This article contains information about principles, methods, ASTM standards of cargo calculations on LNG and LPG tankers.
- Principle
- Weight or Mass
- Density
- US System of Stating Density
- Conversion Between Units
- Temperature
- Pressure
- ASTM Tables
- Total Weight of Liquid Cargo
- Pure Products
- Mixed Products
- Total Weight of Vapour Cargo
- Pure Products
- Mixed Products
- Step-by-step Calculation for Both LPG and LNG Cargoes
- Discharging Calculations
- Cargo Calculation Form
- Vessel Experience Factors
Principle
The tank liquid level (i. e. the innage or sounding) and liquid temperature are used to calculate the total weight of liquefied gas in each cargo tank.
The method of calculation involves:
- Obtaining the tank volume (m3) from the tank calibration tables using the corrected liquid level;
- Obtaining the weight (tonnes) using the formula:Weight = Volume × Density
The liquid weight must be corrected to a standard temperature and density when using the formula. There are 3 different correction methods that can be used:
1 Method 1
Correct the tank volume at the measured temperature to the reference temperature of the density.
This is known as the VCF method (Volume Correction Factor) and is employed when using the ASTM tables.
2 Method 2
Correct the density at the reference temperature to the tank measured temperature.
This is the DCC method (Density Correction Coefficient), which is mostly used with chemicals.
3 Method 3
Correct both tank volume and density to a reference temperature.
Except in the case of certain LNG trades, it is normal practice to include the total weight of cargo vapour in the tank. See Cargo Total Weight Calculation of Liquefied Gas on the LNG and LPG Carriers“Total Weight of Liquid Cargo” and Cargo Total Weight Calculation of Liquefied Gas on the LNG and LPG Carriers“Total Weight of Vapour Cargo”.
Weight or Mass
Newton’s law states:
where:
- P – is the gravity force or weight in newton [N].
- m – is the mass in kg.
- g – is the acceleration of the Earth gravity = 9,81 m/s2.
This is the scientific distinction between weight and mass. However, the marine industry generally uses kilogrammes or metric tonnes as its measurement of weight.
The terms “mass” and “weight” have distinct meanings when used for cargo calculations:
1 Mass
Weight due to the earth’s gravity, excluding any other external force. Synonyms include: “Real weight” or “weight in vacuo”.
2 Weight
Weight due to the earth’s gravity but reduced by the value of the Archimedes force because of air buoyancy. The Apparent Weight (AIR) is always smaller than the Real Weight (VAC). Synonyms include: “apparent weight” or “weight in air”.
Liquefied gases are usually calculated using “weight in vac”. This is the case for butane, propane, LPG, ethylene, propylene, etc, with some exceptions being butadiene, isobutylene or LPG when transported by truck to the final customer (because the weight of the truck itself is included).
The calorific value of an LNG cargo is calculated by the terminal according to its exact composition.
Note: LNG cargo quantities are usually converted from weight (in vac) to energy units such as joule, calorie or BTU (British Thermal Unit). This is because LNG is actually purchased in energy units.
| 1 metric tonne of LNG is equal to the following: | |
|---|---|
| approx. equivalent units | derived units |
| 2,394 m3 of LNG liquid | or 84,56 ft3 |
| or 15,06 US barrels | |
| or 632,5 US gallons | |
| 1 420 m3 of NG gas | or 52 890 ft3 |
| 52,89 millions BTU | or 13,33 millions kCal |
Density
The value known as density will vary with the different units of measurement.
It is important to avoid any confusion between the different units of measurement. It is also necessary to be capable of converting from one system to another as the ship will have no influence over the unit of density provided by the shore.
The “density” or “true density” or “density in vacuo” is the real weight [kg] of 1 m3 of a product, measured at 15 °C in vacuum. (Units: kg/m3).
The “apparent density” is the apparent weight [kg] of 1 1 m3 of a product, measured at 15 °C in air. (Units: kg/m3).
The “relative density” (T1/T2) is the ratio of the real weight of a volume of a given product at the temperature T1 to the real weight of the same volume of pure water at the temperature T2, normally taken as 60 °F/60 °F. Units: none (ratio).
Specific gravity is not used by the petroleum industry anymore, but it is still common in the chemical industry.
The “specific gravity” (T1/T2) is the ratio of the apparent weight of a volume of a given product at the temperature T1 to the apparent weight of the same volume of pure water at the temperature T2. Units: none.
US System of Stating Density
The “API gravity” (60 °F) is a method of expressing relative density:
This formula was first used to define the price of the crude oil in US$/US Barrel. It is not normally used for liquid gas.
For liquids, API rates:
Heavier than water < 10° API
Water = 10° API
Lighter than water > 10° API.
Conversion Between Units
The conversion TRUE DENSITY ↔ APPARENT DENSITY is done using the ASTM table 56 (short):
1 Input:
- Density at 15 °C from 0,5000 to 0,6530 [kg/litre].
2 Output:
- Factor for Converting Weight in Vacuo to Weight in Air.
- Factor for Converting Weight in Air to Weight in Vacuo.
The conversion:
- True density ↔ relative density (T1/T2) ↔ API gravity,
is achieved using the ASTM tables 21 and 51.
Table 21:
1 Input:
- Relative Density (60/60 °F) from 0,500 to 0,653.
2 Output:
- API Gravity at 60 °F [°API].
- True density at 15 °C [kg/litre].
Table 51:
1 Input:
- Density at 15 °C from 0,500 to 0,653 [kg/litre].
2 Output:
- Relative Density 60°/60° F.
- API Gravity at 60 °F [°API]
Temperature
The normal temperature units are °C. However, the temperature used in formulae based on the ideal gas law is given in Kelvin (K). Degrees Kelvin is the temperature scale starting at 0 °K, the “absolute zero” (the lowest possible temperature, which is equal to – 273,15 °C).
Degrees Kelvin is the temperature scale starting at 0 °K, the “absolute zero” (the lowest possible temperature, which is equal to -273,15 °C).
The method of determining the average tank temperature depends on the position of the temperature sensors. There are usually 3 sensors fitted in the tank to measure the liquid phase (i. e. top, middle, bottom) and one for the vapour phase.
For a fully laden tank, the mean temperature of the liquid may be calculated as follows:
where:
- T1 = bottom temperature;
- T2 = middle temperature;
- T3 = top temperature.
Pressure
Pressure is defined as a force applied to a given surface. Using the standard units, a pressure is expressed in newton per square metre (N/m2) or Pascal (Pa). The Pascal is a small unit: 100 000 Pa = 1 bar.
The bar is the most used unit of the metric system. It is nearly equal to kilos per square centimetre (kgf/cm2), which is easy to “visualise” mentally.
Note:
- “nearly” because strictly speaking 1 kgf = 9,8066 N (not 10 N);
- so 1 bar = 1/0,98066 = 1,01972 kgf/cm2.
PSI (pounds per square inch) is the most used unit in the non-metric system (e. g. USA).
- 1 bar = 14,50377 PSI.
| TEMPERATURE | 0 °C | 32 °F | (212-32)/100×°C+32 → °F |
| 273,15 K | Hence: 1,8×°C+32 → °F | ||
| 100 °C | 212 °F | °C+273,15 → K | |
| 373,15 K |
The pressure obtained from reading a gauge is the relative pressure, i. e. the pressure relative to the ambient atmospheric pressure. The relative pressure can be positive or negative.
To differentiate between the types of pressure (i. e. absolute and relative), it is a good practice to add the letter “g” (gauge) at the end of the relative pressure unit (e. g. tank pressure 30 mbarg = 30 millibars read on a gauge).
The atmospheric pressure varies around a mean value of 101 325 Pa (roughly 1 bar), called the standard atmosphere. (This is 1013,25 mb, i. e. mean world pressure).
If the current atmospheric pressure taken from the bridge barometer is 1 025 mbar, then the absolute pressure to be used in formulas with our 30 mbarg reading is:
On a semi-pressurised ship, a cargo tank may be capable of 50 % vacuum. This means that the cargo tank that can withstand a pressure of -0,5 barg or 0,5 bar (absolute, assuming an atmospheric pressure of 1 bar).
| PRESSURE | 1 bar | 14,50377 PSI | PSI = Pounds per Square Inch [lbf/in2] |
| 100 000 Pa (≡ N/m2) | PSI G: Gauge pressure (relative pres.) | ||
| 100 K Pa | PSI A: Absolute pressure | ||
| 0,98692 atm | |||
| 1,01972 kgf/cm2 | |||
| 2 088,54288 lbf/ft2 | |||
| 750,06376 mmHg (0 °C) | |||
| 10,19744 mH2O (4 °C) | |||
| 1 atm | 101 325 Pa | atm or Std Atm | |
| 760,00210 mmHg (0 °C) | |||
| 10,33256 mH2O (4 °C) |
ASTM Tables
The Petroleum Measurement Tables are published by the ASTM (American Society for Testing and Materials), API (American Petroleum Institute) and IP (British Institute of Petroleum).

The current standard is ASTM D1250-04 (2004). As for the previous 1980 edition of the ASTM tables, the range of densities excludes the densities of LPG and LNG gasses. The tables used on gas carriers are a reprint of the “Petroleum Measurement Tables” 1953 edition (published as ASTM-IP-API Petroleum Measurement Tables for Light Hydrocarbon Liquids, The Institute of Petroleum, London, 1986).
Read also: Essential Operations with Gas for a Modern LNG Carriers in Typical Trading Cycle
This reprint contains the tables 21, 51, 56 mentioned above and also tables 53 and 54:
Table 53:
1 Input:
- Observed Density from 0,420 to 0,689 [kg/litre] (= True Density at Observed Temperature).
- Observed Temperature from -46 °C (min) to +60 °C (max) [°C].
2 Output:
- Density at 15 °C [kg/litre] (the Hydrometer Correction is included).
Table 54:
1 Input:
- Density at 15 °C from 0,500 to 0,655 [kg/litre].
- Observed Temperature [°C].
2 Output:
- VCF (Volume Correction Factor) to 15 °C.
Total Weight of Liquid Cargo
Pure Products
For pure products such as ammonia (NH3) or propylene (C3H6), there are precalculated tables available that detail the liquid density (together with the vapour pressure and vapour density), according to the temperature.
Knowing the value of density, we can use the following formula:
To convert weight in vac to weight in air, use table 56.
| Saturated densities of propylene (99,9 % by volume) | |||
|---|---|---|---|
| Temperature [°C] | Vapour pressure [bar] (abs) | Vapour density (vac) [kg/m3] | Liquid density (vac) [kg/m3] |
| -50,0 | 0,912 | 0,912 | 611,9 |
| -49,5 | 0,933 | 0,933 | 611,3 |
| -49,0 | 0,955 | 0,955 | 610,6 |
| -48,5 | 0,977 | 0,977 | 610,0 |
| -48,0 | 1,000 | 1,000 | 609,4 |
| -47,5 | 1,023 | 1,023 | 608,8 |
| -47,0 | 1,046 | 1,046 | 608,2 |
| -46,5 | 1,070 | 1,070 | 607,5 |
| -46,0 | 1,095 | 1,095 | 606,9 |
| -45,5 | 1,119 | 1,119 | 606,3 |
| -45,0 | 1,144 | 1,144 | 605,7 |
| … | … | … | … |
Mixed Products
The composition of a mixed product such as LPG or LNG will vary for each loading operation, therefore pre-calculated tables providing the density according to the temperature are not possible.
1 Densities Provided from the Shore
The ship will use the density as calculated by the terminal at a given reference temperature.
The terminal will determine the mixture density using one of two possible methods:
- A physical measurement of the density using a pressure hydrometer. The measurement will need to comply with the ASTM D 1657 method. Note: This measured density is not an accurate value.
- A computation of the density using the exact composition of the mixture. The composition itself is determined by physical measurement but this is very accurate (using a gas chromatograph/ mass spectrometer). The most popular computation method for density is the COSTALD equation (COrresponding STAte Liquid Density). This is a complex equation beyond the scope of this book.
2 Calculating the Weight of the Product
Before loading, the terminal will give the ship the true density at 15 °C or the relative density at 60 °F/60 °F.
Knowing the density at 15 °C and the temperature of the cargo, allows the VCF (Volume Correction Factor) at 15 °C to be calculated.
Sometimes only an approximate density is given at this stage and a corrected value is provided during the loading operation.
Now the following calculation can be made to determine weight:
Method of calculation
There are two methods that can be used to compute the weight in vacuo of the cargo, they differ by the order that they are introduced to the calculation.
The first method corrects the density at the reference temperature to the density at the measured temperature and then multiplies this by the liquid volume at the measured temperature:

The second method corrects the tank volume at the measured temperature to the tank volume at the density reference temperature (15 °C) and then multiplies it by the density at reference temperature:
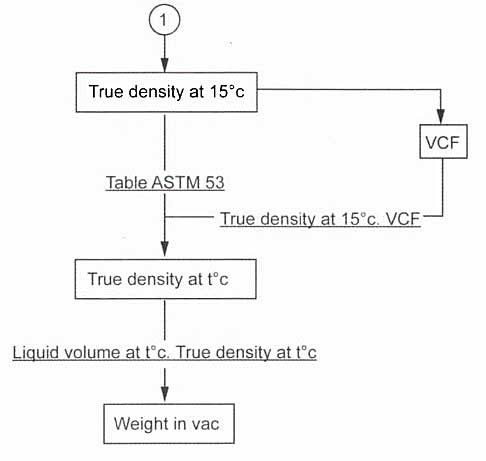
The second method has the advantage of providing the liquid volume at 15 °C as an intermediate result. It is sometimes useful to know this volume for commercial purposes.
If the terminal provides the relative density at 60 °F/60 °F instead of the true density at 15 °C, it will be beneficial to convert the relative density to the true density using table 21, as the tank calibration tables are nearly always in cubic metres (m2).
To convert “weight in vac” to “weight in air”, use table 56.
Total Weight of Vapour Cargo
Pure Products
For pure products such as ammonia, there are precalculated tables that provide the saturated vapour density (together with the saturated vapour pressure) according to the temperature.
With no agitation in the tank, such as from a pump, compressor, suction, condensate or spray return, the tank can be classified as being in equilibrium (a saturated condition). This can be verified as the Piping System of pressure vessels on gas tankerstank pressure will be equal to the saturated vapour pressure indicated in the table if equilibrium has been reached.
If the cargo is not in a state of equilibrium, the formula for mixed products must be used.
The volume of vapour is equal to:
Therefore, the weight in vacuum is:
Mixed Products
Although somewhat laborious, the following calculation may need to be carried out when loading mixed products. In this case, the vapour density at the vapour cargo temperature is calculated using the following formula derived from the ideal gas law (PV = nRT):
where:
- ρvap = vapour density [kg/m3].
- MW = Molecular Weight of the gas mixture components [grams/mole].
- p = vapour pressure in tank [bars].
- ps = standard pressure = 1,01325 bar (or 1 atm).
- Ts = standard temperature = 288,15 K (or 15 °C).
- z = compression factor [ ].
- z = 1 for an ideal gas or a real gas in standard conditions (15 °C et 1 atm).
- z<1 (more compressible) for a real gas in usual conditions.
z is usually very close to 1 (about 0,96-0,98 for a fully refrigerated LPG cargo) and ignored.
This is not the case for a fully pressurised cargo, where the value “z” can be ascertained from a diagram.
For common gases, the Molecular Weight is:
| Saturated Hydrocarbons | MW [grams/mole] |
|---|---|
| Methane CH4 | 16,045 |
| Ethane C2H6 | 30,069 |
| Propane C3H8 | 44,096 |
| Butane C4H10 | 58,124 |
| Unsaturated Hydrocarbons | MW [grams/mole] |
| Ethylene C2H4 | 28,054 |
| Propylene C3H6 | 42,080 |
| Butylene C4H8 | 56,108 |
| Butadiene – 1,3 C4H6 | 54,091 |
| Non Hydrocarbons | MW [grams/mole] |
| Ammonia NH3 | 17,032 |
| Vinylchloride CH2CHCl | 62,500 |
The Molecular Weight of a mixture can be calculated if the mole fractions of the mixture components (results of the gas analysis) are known:
where:
- MWi = molecular weight of the component i.
- Yi = mole fraction for the component i.
Knowing the true density, the weight in vacuum can be calculated as for a pure product:
Note: on some LNG trades, the weight of the LNG vapour is not calculated. The molecular weight of the methane is only about one third of the propane or one quarter of the butane. Compared to the liquid weight on large LNG tankers, the vapour weight can be seen as very small and is, on occasions, ignored.
Step-by-step Calculation for Both LPG and LNG Cargoes
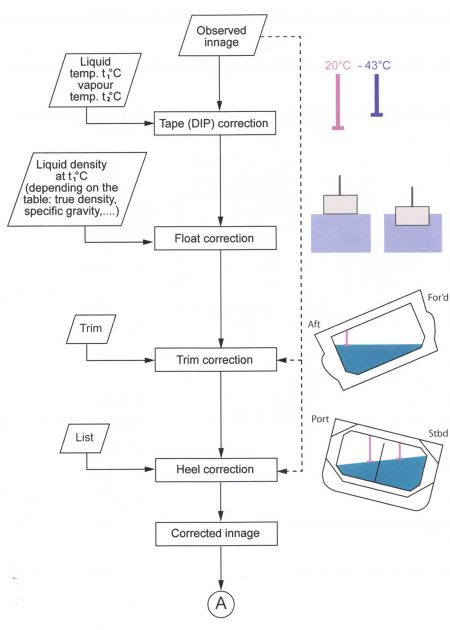
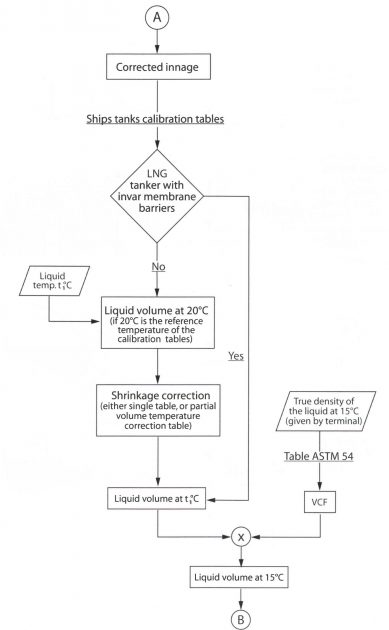
Notes on correcting innages and soundings
Assume a reading from a float gauge system (Note: if tank radar system is used, no tape or float corrections are required).
The float gauge reading provides the observed innage (not the ullage).
The corrected innage can be calculated taking into account:
- The shrinkage of the tape (due to the low temperature);
- The immersion of the float;
- The trim (if the tape is not exactly at the middle of the tank);
- The list (if the tape is not exactly at the middle of the tank).
Using the ship’s tank tables, the (corrected) innage can be converted to a liquid volume. This liquid volume will be given at a reference temperature (for instance 20 °C).
Except where the tank material is INVAR (i. e. Gaz Transport LNG Carriers), a shrinkage correction is applied to this liquid volume to correct it to the temperature of the cargo.
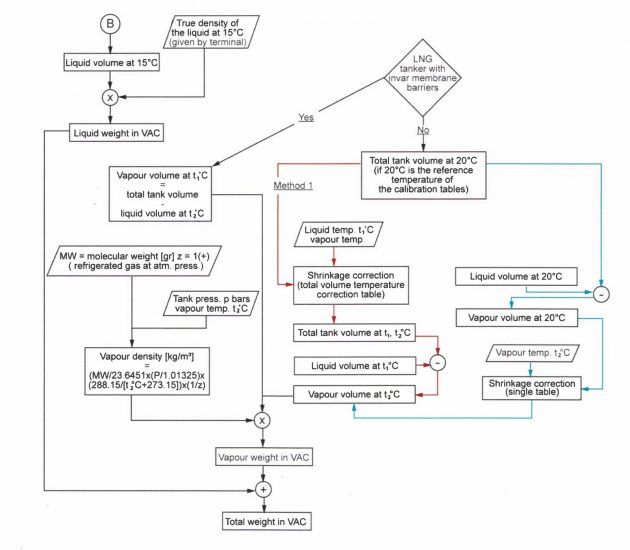
Discharging Calculations
1 Full Discharge
To ascertain the quantity of cargo discharged, the quantity of product and vapour remaining on board is subtracted from the total quantity of cargo and vapour (where applicable) that was on board prior to discharge.
2 Part Cargoes
The calculation of the innage or sounding at which to stop when discharging a part cargo is called a reverse calculation. When discharging stops, the total quantity of cargo on board will therefore be:
The calculation starts with the knowledge of the remaining weight in vac and completes in reverse the steps 1 to 3 until we pre-compute the observed innage. This will be the level at which discharging should stop.
where:
- weight of vapour = liquid volume to discharge × vapour density at T2 °C
And therefore:
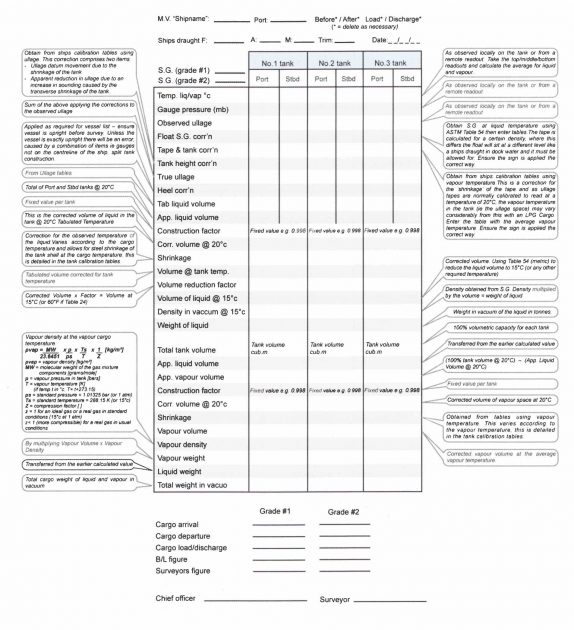
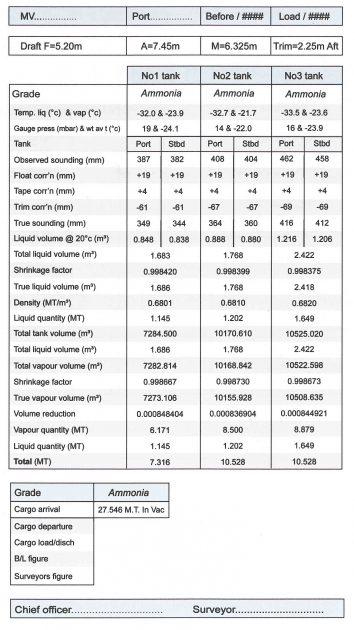
Cargo Calculation Form
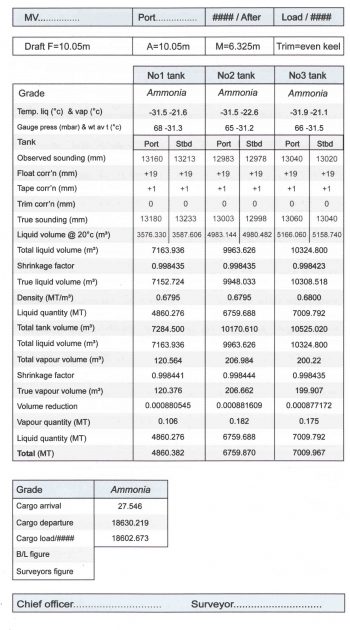
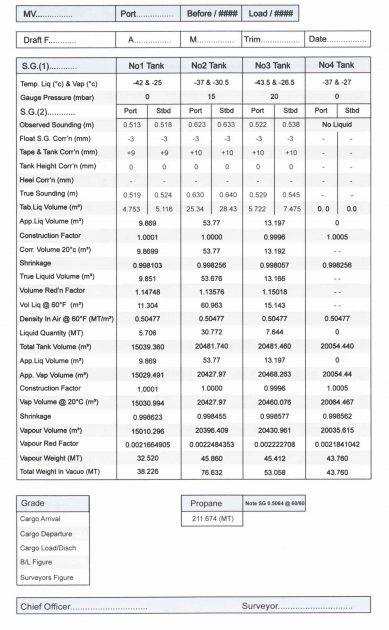
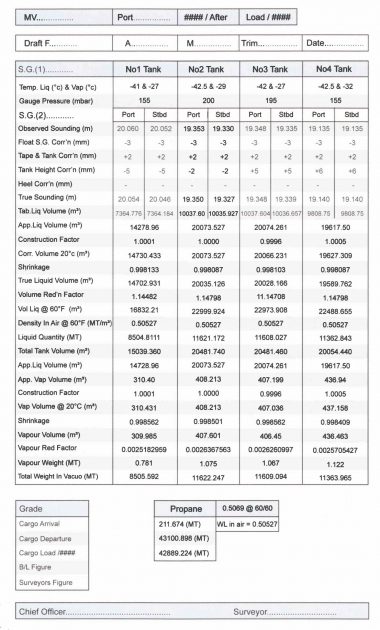
Vessel Experience Factors
After loading or discharging, it is established practice to compare the shore figures for the quantity loaded or discharged to the ship’s figures. Each set is exposed to differing levels of accuracy and so are unlikely to agree. The ratio of disagreement is not constant but varies by a mean value that is known as the Vessel’s Experience Factor (VEF). The VEF is commonly used at the loading port to provide an approximate check of the accuracy of the Bill of Lading and the ship’s figures. However, this practice is rarely conducted at discharge ports although there is no reason why similar techniques could not be employed.
The Institute of Petroleum stipulates that the following voyage types should not be used for the calculation of a VEF value:
- The first voyage after dry-dock;
- Ship-to-ship transfers;
- Voyages where the Bill of Lading is based on the ship’s figures;
- Voyages before any structural changes to the ship’s cargo carrying capacity.
Within the liquid cargo industry, general opinion is that part cargoes (i. e. <80 % of capacity) should not be included for the calculation of a VEF.
Vessel Experience Factor (Loading) (VEFL) = The adjusted mean value of the Vessel Loading Ratio (VLR) that is obtained after several voyages.
Vessel Experience Factor (Discharge) (VEFD) = The adjusted mean value of the Vessel Discharge Ratio (VDR) that is obtained after several voyages.
