Scattering Mechanism of Over-Horizon UHF Propagation

Explore the scattering mechanism of over-horizon UHF propagation through a detailed analysis of basic equations, perturbation theory for field moment calculations, and the interaction of diffracted fields with turbulent refractive index fluctuations.

СодержаниеСвернуть

Basic Equations
Perturbation Theory: Calculation of Field Moments
Scattering of a Diffracted Field on the Turbulent Fluctuations in the Refractive Index

As discussed in Atmospheric Boundary Layer and Basics of the Propagation Mechanisms“Atmospheric Boundary Layer and Key Propagation Mechanisms”, the analytical study of wave propagation through a turbulent troposphere is complicated due to the high dynamic range of the turbulent fluctuations of the refractive index as well as the presence of the boundary surface.

In UHF Propagation in an Evaporation Duct“Exploring UHF Propagation in Evaporation Ducts” we studied the impact of the random component of the dielectric permittivity of the troposphere on UHF propagation in an evaporation duct. It was shown that wave scattering on random inhomogeneities of the refractive index leads to a non-coherent redistribution of the energy between the waveguide modes, the loss of coherence results in additional attenuation of the trapped modes. Using the language of quantum mechanics, we have found the perturbations to the eigenvalues of the discrete spectrum of the localised states. The results obtained in UHF Propagation in an Evaporation Duct“Exploring UHF Propagation in Evaporation Ducts” are valid at distances from the source, on the one hand, long enough to filter all leaked modes and, on the other hand, not too long so that the scattering in the upper layers of the troposphere can be neglected in comparison with the field carried by the trapped modes.

In the absence of tropospheric ducts it is sometimes convenient to solve the transport equations for the coherence function in the continuum spectrum. Such a solution has been obtained for multiple wave scattering in a random medium (uniform on average) over the flat boundary surface. The results demonstrated that anisotropic inhomogeneities of the refractive index may have a significant impact on the signal level. The multiple scattering in the case of strong anisotropy was studied in Refs, where the following was shown:

Compared with the case of isotropic fluctuations of

δ ε (\vec{r}),

when the attenuation of the coherent component of the received field is defined by the square of the phase fluctuations, multiple scattering on anisotropic fluctuations with a factor of anisotropy α = L_⟂/L_|| ≪ 1 1 results in lesser attenuation of the coherent component by a factor of (kL_⟂α) with the same value of L_|| and the scale of the frequency correlation increases (kL_⟂α)^-2 times.

Similar results were obtained, where the authors derived integro-differential equations for the field moments which account for diffraction on the random inhomogeneties and variations in the trength of scattering with small scattering angles. The important result is that the Markov approximation is not applicable with extremely large parameters of anisotropy. In such cases the two-scale model may provide a sufficient tool for analysis.

In this article we suggest a technique for calculating the coherent signal component, with allowance for both diffraction by the earth and wave scattering on random inhomogeneities of the refractive index. Theoretically, the coherent component is defined as the complex amplitude averaged over a statistical ensemble of realisation. If the ergodicity and locally frozen hypotheses hold, the ensemble averaging is equivalent to such over an infinitely long interval. For practical purposes, however, the component coherent over a finite interval of time is of interest. According to data provided in Refs, in about 60 % of experiments performed on trans-horizon links up to 300 km in length, the received amplitude distribution is different from Rayleigh law. This difference is ascribed to the effect of the coherent component. Therefore, it seems necessary to analyse all the factors influencing the coherent component, its range and wavelength dependences, etc.

The approach can be formulated in the following way. For the electromagnetic field component, coherent over time T, we derive, using the Markov approximation, a parabolic-type equation allowing for the additional decay of the coherent signal due to scattering on small-scale fluctuations of the refractive index. Further, we analyse the possibility of replacing in the equation the average (over time T) dielectric constant, which is a “slowly varying” random function of all three variables, with a random function depending on a single coordinate, i. e. height over the interface. Through this procedure, the problem of wave propagation through a three-dimensional random medium is reduced to that for a random stratified medium. The field component averaged over time T can be represented in this approach as a normal wave (i. e. modal) series with random propagation constants and height gain functions for each mode. These are determined with the aid of the perturbation technique formulated in Wave Field Fluctuations in Random Media over a Boundary Interface“Understanding Wave Field Fluctuations in Random Media”, in which the unperturbed refractive index profile is that averaged over the ensemble of the realizations, and the random stratification due to large-scale anisotropic inhomogeneities is considered as a perturbation. The approach permits one to obtain closed-form expressions for statistical moments of any order and analyse the correlation between the signal levels and the turbulent troposphere.

It seems noteworthy that at decimetre wavelength the attenuation rate of the coherent component (T ≤ 1 min) is not normally very high, hence at links about 200 km long the coherent intensity practically coincides with the whole decimetre signal. The basic observation is that the approach suggested in this article is better suited to wave propagation effects at frequencies below 1 GHz, where the effect of the ducting is also week.

Basic Equations

Consider a vertically polarized field whose attenuation function (Understanding Parabolic Approximation in Wave Propagation: Analytical Methods and Applicationssee this equation) is governed by the parabolic equation:

2 j \frac{\partial W}{\partial x} + ∆_{⊥} W + k^{2} [ε_{M} (x, γ, z) - 1] W = 0 E q . 1

where ε_M(x, γ, z) = ε(x, γ, z)+2z/2.

As is known, scattering on the fluctuation in the dielectric permittivity brings about additionnal attenuation of the coherent component of the field which can be described by the factor e^-γx. In the Markov process approximation, the decrement of attenuation γ is given by:

γ = \frac{π k^{2}}{4} \int d^{2} \vec{κ} Φ_{ε} (0, {\vec{κ}}_{⊥}), w i t h \vec{κ} = \{κ_{x}, κ_{γ}\} .

Substitution of a Kolmogorov turbulence spectrum in the above equation would result in a divergence of the integral at small

\vec{κ}

. The reason for this is that the ensemble average usually implied in theoretical calculations allows for arbitrarily large phase distortions due to very large inhomogeneities or over an infinitely long time interval. In practice, however, the coherence over a finite time interval and the dependence of the coherent amplitude on the time of average is of interest.

Let us average Eq. (1) over a finite time T, denoting the average values as <…>_T, and make use of the locally “frozen”, stationary turbulence hypothesis. This hypothesis implies that variations of the random field

ε (\vec{r}, t)

with time result solely from the motion of the turbulent flow at a velocity

\vec{ν}

which can be a random value itself. Introducing:

δ ε_{T} = ε_{M} (\vec{r}) - {<ε_{M} (\vec{r})>}_{T}

and transforming Eq. (1) to the integral equation form we obtain:

{<W (\vec{r})>}_{T} = W (0, γ, z) {<\exp (j \frac{k}{2} \int_{0}^{x} d x^{'} δ ε_{T} (x^{'}, γ, z))>}_{T} - \frac{1}{2 j k} {<\int_{0}^{x} d x^{'} \exp (j \frac{k}{2} \int_{x^{'}}^{x} d x^{''} δ ε_{T} (x^{''}, γ, z)) \cdot [∆_{⊥} + k^{2} [{<ε_{M} (\vec{r})>}_{T} - 1]] W (\vec{r})>}_{T} . E q . 2

Instead of averaging the functionals depending on δε_T over time T, one can perform averaging over the ensemble of ε as δε does not contain greater time-scales than T. On the other hand, the term

{<ε_{M} (\vec{r})>}_{T}

may be considered invariant over times t ≤ T. Assuming statistical independence of the fluctuations in δε_T and

\vec{ν}

, we can perform averaging over

\vec{ν}

independently of δε_T. Suppose we wish to first perform the averaging over δε_T. Introduce definition

W_{T} \equiv {<W (\vec{r})>}_{T}

and then the term W_T will obey the equation:

2 j \frac{\partial W_{T}}{\partial x} + ∆_{⊥} W_{T} + [k^{2} ({<ε_{M} (x, γ, z)>}_{T} - 1) - 2 j k γ_{T}] W_{T} = 0 E q . 3

provided that the wave propagation can be regarded as a Markovian process, i. e. the conditions below are met:

L_{∥} ≪ k L_{z}^{2}, σ_{ε}^{2} k^{2} L_{∥}^{2} ≪ 1 . E q . 4

Here:

L_{∥} = \sqrt{L_{x}^{2} + L_{γ}^{2}}, L_{z}

are, respectively, the horizontal and the vertical scales of the inhomogeneities and

σ_{ε}^{2}

is the root mean square magnitude of fluctuations in ε.

The attenuation rate γ_T averaged over the fluctuations in Eq. (3) is given by the relation:

γ \approx \frac{{πk}^{2}}{4} \int_{|κ_{γ}| > κ_{γ T}} d κ_{γ} \int_{κ_{z}^{2} > κ_{z T}^{2}} d κ_{z} Φ_{ε} (0, κ_{γ}, κ_{z}) E q . 5

and:

κ_{γ T} = {(ν_{γ} T)}^{- 1}, κ_{z T} = {(\int_{0}^{T} (T - τ) B_{ν z} (τ) d τ)}^{- 1 / 2}; E q . 6

ν_γ can be estimated as a mean value of the horizontal transfer velocity:

ν_{∥} = \sqrt{ν_{x}^{2} + ν_{γ}^{2}},

while the vertical component of the velocity

\vec{ν}

can be regarded as solely random with the correlation function B_νz.

We can assume, for further estimates, that κ_zT ≈ (σ_νzT)^-1. The conditions (4) were obtained in Refs for a spatially uniform field of δε. The inequalities (4) impose some limitations to an averaging time T, since under “frozen” turbulence conditions L_|| = ν_||T, L_z = σ_νzT, therefore instead of Eq. (4) we obtain:

\frac{k^{2} σ_{ν z}^{2} T}{ν_{∥}} ≪ 1, k^{2} C_{ε}^{2} ν_{∥}^{8 / 3} T^{8 / 3} ≪ 1 E q . 7

and:

σ_{ε}^{2} = 1 / 2 C_{ε}^{2} L_{∥}^{2 / 3}

for “locally uniform” turbulence.

The function

{<ε_{M} (\vec{r})>}_{T}

involved in Eq. (3) is a much slower function of x and γ than

ε_{M} (\vec{r}),

at least with sufficiently long averaging time. It should be noted that vertical variations of the averaged dielectric permittivity are much more rapid than the horizontal-plane variations.

Establish at which times of averaging the x and γ dependence of

{<ε_{M} (\vec{r})>}_{T}

can be totally neglected in Eq. (3). In other words, for which T the term

{<ε_{M} (\vec{r})>}_{T}

can be replaced by a vertical profile eTi ðzÞ related to some fixed (generally, arbitrary) values x = x_i and γ = γ_i, i.e:

ε_{T i} (z) = {<ε (x_{i}, γ_{i}, z)>}_{T} . E q . 8

The set of functions ε_Ti(z) can be regarded as an ensemble of realisations of some random function ε_T(z). Averaging over that ensemble will be denoted herein-after by a horizontal bar above the character, e. g.

{\bar{ε}}_{T} (z) .

The substitution of ε_T(z) instead of

{<ε_{M} (\vec{r})>}_{T}

corresponds to the introduction of a vertically stratified random medium whose “instantaneous” profile ε_T(z) is the same along the entire propagation path. The slow variations of

{<ε_{M} (\vec{r})>}_{T}

are equivalent to altered realisations of ε_T(z). Obviously, the transition of the vertically stratified medium can only be justified if the amount of fluctuations (over time T) in the coherent component that are due to the difference between

{<ε_{M} (\vec{r})>}_{T}

and ε_T(z) is small. Introducing:

ε_{1} (x, γ, z) = {<ε_{M} (x, γ, z)>}_{T} - ε_{T} (z) E q . 9

we can present W_T (x, γ, z) as:

W_{T} (\vec{r}) = W_{T}^{0} (\vec{r}) \exp (Ψ (\vec{r})) E q . 10

where Ψ = V+jS is a complex phase and

W_{T}^{0} (\vec{r})

satisfies the equation:

2 j \frac{\partial W_{T}^{0}}{\partial x} + ∆_{⊥} W_{T}^{0} + [k^{2} (ε_{T} (z) - 1) - 2 j k γ_{T}] W_{T}^{0} = 0 . E q . 11

Let

W_{T}^{0} (\vec{r}, {\vec{r}}_{0})

denote the propagation factor of the field from a point source at

{\vec{r}}_{0} = \{0, 0, z_{0}\} .

Within the first-order approximation of Rytov’s method, the complex phase of Eq. (10) is:

Ψ = - \frac{k^{2}}{W_{T}^{0} (\vec{r}, {\vec{r}}_{0})} \int_{0}^{x} d x^{'} \int d^{2} {\vec{ρ}}^{'} G (\vec{r}, {\vec{r}}^{'}) ε_{1} (\dot{\vec{r}}) W_{T}^{0} ({\vec{r}}^{'}, {\vec{r}}_{0}), E q . 12

where:

{\vec{ρ}}^{'} = \{x^{'}, γ^{'}\}, {\vec{r}}^{'} = \{x^{'}, {\vec{ρ}}^{'}\}, G (\vec{r}, {\vec{r}}^{'}) = - \frac{1}{4 π (x - x^{'})} W_{T}^{0} (\vec{r}, {\vec{r}}^{'}) . E q . 13

We will consider the case when the reception point

{\vec{r}}^{'}

is shadowed from the transmitter by the terrestrial sphere. The complex phase fluctuations represented by Eq. (12) depend essentially on the vertical profile of

ε_{1} (\vec{r}) .

ε_{1} (\vec{r})

contains spectral components characterised by small vertical scales l_z ≪ m/k, then the mechanism of trans-horizon propagation is a resonance scattering in the higher tropospheric layers, i. e. the troposcatter described by the Booker and Gordon theory. In this case the fluctuations in the log-amplitude V are very high.

To reduce the standard of fluctuations in the log-amplitude V determined by Eq. (10) it is necessary to suppress the multi-scale random variations of

ε_{1} (\vec{r})

by choosing a sufficiently long averaging time T. The minimum vertical scale sizes of the

ε_{1} (\vec{r})

inhomogeneities which are related to the average time as l_z = σ_νzT should meet the condition l_z ≫ m/k. The resultant condition on the averaging time is:

T ≫ \frac{m}{k σ_{ν z}} . E q . 14

In contrast to the “standard” troposcatter mechanism, the scattering of waves satisfying the above conditions occurs in the region of the troposphere which is in the shadow zone with respect to both receiver and transmitter. Hence, the propagation factor

W_{T}^{0} (\vec{r}, {\vec{r}}_{0})

and the Green function

G (\vec{r}, {\vec{r}}^{'})

are most conveniently represented as modal series, Understanding Parabolic Approximation in Wave Propagation: Analytical Methods and Applications“Parabolic Approximation to the Wave Propagation” and Wave Field Fluctuations in Random Media over a Boundary Interface“Understanding Wave Field Fluctuations in Random Media”. Rought estimates for

W_{T}^{0} (\vec{r}, {\vec{r}}_{0})

and

G (\vec{r}, {\vec{r}}^{'})

values can be obtained by retaining just the first terms of these expansions, i.e:

W_{T}^{0} (\vec{r}, {\vec{r}}^{'}) = - 2 \exp (j \frac{π}{4}) \frac{m}{k} \sqrt{\frac{π m (x - x^{'})}{a}} \frac{χ (z) χ (z^{'})}{N} \cdot \exp \{j q \frac{x - x^{'}}{2 k} + j \frac{k}{2} \frac{{(γ - γ^{'})}^{2}}{x - x^{'}} - γ_{T} (x - x^{'})\} . E q . 15

Estimating the integral in Eq. (12) we will first assume ε_T(z) to correspond to the standard tropospheric refraction, i. e. ε_T(z) = 1+2 z/2. Explicit expressions for the values involved in Eq. (15) are:

q = (k^{2} / m^{2}) τ_{1} e^{j π / 3}, τ_{1} = 2, 338, N = - 4 m / k \sqrt{τ_{1}} e^{j π / 3} and χ (z) = w_{1} (τ_{1} e^{j π / 3} - k z / m),

where w₁ is the Airy function defined in the Appendix. Performing the integration in Eq. (15) and averaging over the ensemble of

ε_{1} (\vec{r})

on the assumption of statistically independent fluctuations thereof, we can arrive at the following results.

With:

T ≫ \frac{\sqrt{λ x}}{ν_{∥}} E q . 16

the mean-square log-amplitude fluctuations are:

<V^{2}> = 4 \cdot 10^{- 4} π^{3 / 2} C_{ε_{1}}^{2} L_{∥}^{- 7 / 3} x^{3} E q . 17

where

C_{ε_{1}},

is the structure constant of ε₁. The structure function has been assumed to obey the “two-thirds” law, i. e. the spectrum of ε₁ takes the form (Atmospheric Boundary Layer and Basics of the Propagation Mechanismssee this equation). Thus, provided the following inequalities hold:

a) 4 \cdot 10^{- 4} π^{3 / 2} C_{ε_{1}}^{2} ν_{∥}^{- 7 / 3} T^{- 7 / 3} x^{3} ≪ 1,

b) k^{2} C_{ε}^{2} ν_{∥}^{8 / 3} T^{8 / 3} ≪ 1, E q . 18

c) T \max \{\frac{m}{k ν_{z}}, \frac{\sqrt{λ x}}{ν_{∥}}, \frac{ν_{∥}}{k σ_{ν z}^{2}}\},

the term <ε_M(x, γ, z)>_T in Eq. (3) can be replaced by ε_T(z) without introducing considerable error in

W_{T} (\vec{r}) .

Substituting:

C_{ε_{1}}^{2} \approx C_{ε}^{2} = 10^{- 14} {cm}^{- 2 / 3}, λ = 10 cm, T = 30 s, ν_{∥} = 10 m s^{- 1}, σ_{ν z} = 1 m s^{- 1,}

we see that the principal inequality (18a) can hold at x ≤ 103 km.

Perturbation Theory: Calculation of Field Moments

Thus, calculation of the coherent field amplitude averaged over time T has been reduced to solving Eq. (11). If ε_T(z) is a regular function, Eq. (11) can be solved by known methods, with the solution presentable in the form (14). Actually, the problem consists in determining the propagation constants q and the height-gain functions χ(z). Depending on the specific form of ε_T(z), this can be done either analytically or numerically. However, this is a rare occasion. Generally, ε_T(z) is a random function whose only known parameters are the vertical stratification scale L_z and the root mean square fluctuation strength

{<ε_{T} {(z)}^{2}>}^{1 / 2} .

We further assume that averaging over the statistical ensemble is equivalent to averaging over time:

<ε_{T}^{2}> = ε_{T}^{2}

i. e. the validity of the ergodicity theorem. An analytical solution to Eq. (11) cannot be written, we should aim instead at evaluating the mean level of

W_{T} (\vec{r})

and the root mean square fluctuations

σ_{W} = \sqrt{W_{T}^{2}}

thereof from knowledge of the ε_T(z) statistics. Averaging over the statistical ensemble we can write:

ε_{T} (z) = ε_{T} (z) + ∆ ε (z), ∆ ε = 0 E q . 19

assuming specifically:

ε_{T} (z) = ε_{0} (z) = 1 + 2 \frac{z}{a} . E q . 20

To determine the propagation constants and height gain functions, we will make use of the perturbation theory described in Wave Field Fluctuations in Random Media over a Boundary Interface“Understanding Wave Field Fluctuations in Random Media”. Representing q and χ as:

q = q_{0} + δ q, E q . 21

χ (z) = χ_{0} (z) \exp (\int_{0}^{z} d z^{'} ς (z^{'})), E q . 22

where q₀ and χ₀ are governed by the unperturbed Eq. (11) with ε_T(z) = ε₀(z). We can obtain the random correction term δq and ς(z) in the form:

δ q = - \frac{k^{2}}{N^{2}} \int_{0}^{\infty} ∆ ε (z) χ_{0}^{2} (z) d z, E q . 23

ς (z) = \frac{1}{χ_{0}^{2} (z)} \int_{0}^{z} [δ q - k^{2} ∆ ε (z^{'})] χ_{0}^{2} (z^{'}) d z^{'} . E q . 24

Now we single out of W_T(x, γ, z; z₀) the value W₀, i. e. the solution to Eq. (11) with ε_T(z) = ε₀(z), to obtain:

W_{T} (x, γ, z; z_{0}) = W_{0} (x, γ, z; z_{0}) \cdot \exp \{j \frac{δ q}{2 k} x + \int_{0}^{z} ς (z^{'}) d z^{'} + \int_{0}^{z_{0}} ς (z^{'}) d z^{'} +\} . E q . 25

The factor W_T (x, γ, z; z₀) is a random function of a “slow” time t > T. Within each realization of the signal, the factor W_T is the coherent component of the total signal received during the “short” intervals t ≤ T. During the “long” time-interval t ≫ T, the factor W_T undergoes relatively slow random variations owing to changes of realisation of ε_T. The part of W_T fluctuating at the change of realisations Δε(z) is given by the exponent of Eq. (25).

We can specify the intensity J₀ of the coherent component W_T (x, γ, z; z₀) given ε₀(z) in the form (20):

J_{0} = {|W_{0}|}^{2} = \frac{π m x}{4 a τ_{1}} {|w_{1} (τ_{1} e^{j π / 3} - \frac{k z}{m})|}^{2} {|w_{1} (τ_{1} e^{j π / 3} - \frac{k z_{0}}{m})|}^{2} \cdot \exp (- \frac{m x}{a} τ_{1} \sqrt{3} - 2 γ_{T} x) E q . 26

where 2γ_T is the extra attenuation rate due to the energy transfer to the incoherent part of the signal. Generally, the attenuation rate γ_T given by Eq. (5) undergoes random variations as the medium realisation changes, because of the non-uniformity in the small scale fluctuations of

ε_{M} (\vec{r}) .

In the following study, we shall restrict ourself to the case where the

ε_{M} (\vec{r}) .

fluctuations of scale sizes l_|| < ν_|| and l_|| < ν_zT are statistically uniform, i. e. γ_T = const.

As can be observed from Eqs. (23) to (25), the random value W_T should be distributed log-normally, in view of the central limiting theorem. Note that similar distributions are actually observed in the experiment. For instance, the integral distribution of the amplitude measured over 1 to 5 min intervals reveals log-normal statistics.

To simplify further the derivations, we will assume the receiver and transmitter heights to be equal, i. e. z = z₀, and consider the intensity J_T of the coherent (over time T) signal component averaged over the statistical ensemble, viz.

\bar{J_{T}} = <{|W_{T}|}^{2}> = J_{0} \exp \{- \frac{x^{2}}{8 k^{2}} <{(δ q - δ q^{*})}^{2}> + j \frac{x}{2 k} <(δ q - δ q^{*}) \int_{0}^{z} [ς (z^{'}) + ς^{*} (z^{'})] d z^{'}> + 2 \int_{0}^{z} d z^{'} \int_{0}^{z} d z^{''} <[ς (z^{'}) + ς^{*} (z^{'})] [ς (z^{''}) + ς^{*} (z^{''})]>\} . E q . 27

Further calculations are straightforward but cumbersome. As a specific example, consider one of the correlators involved in Eq. (27):

\int_{0}^{z} d z^{'} \int_{0}^{z} d z^{''} <ς (z^{'}) ς (z^{''})> = <{(δ q)}^{2}> [\int_{0}^{z} \frac{d z^{'}}{χ_{0}^{2} (z^{'})} \int_{0}^{z^{'}} d z^{''} χ_{0}^{2} (z^{''})] - 2 \frac{k^{4}}{N} \int_{0}^{z} \frac{d z^{'}}{χ_{0}^{2} (z^{'})} \int_{0}^{z^{'}} d z_{1} χ_{0}^{2} (z_{1}) \int_{0}^{z} \frac{d z^{''}}{χ_{0}^{2} (z^{''})} \int_{0}^{z^{''}} d z_{2} χ_{0}^{2} (z_{2}) \int_{0}^{\infty} d z_{3} χ_{0}^{2} (z_{3}) <∆ ε (z_{2}) ∆ ε (z_{3})> + k^{4} \int_{0}^{z} \frac{d z^{'}}{χ_{0}^{2} (z^{'})} \int_{0}^{z} \frac{d z^{''}}{χ_{0}^{2} (z^{''})} \int_{0}^{z^{'}} d z_{1} \int_{0}^{z^{''}} d z_{2} χ_{0}^{2} (z_{1}) χ_{0}^{2} (z_{2}) <∆ ε (z_{1}) ∆ ε (z_{2})> . E q . 28

Other terms in the exponent of Eq. (27) can be expressed in a similar way. After lengthy but straightforward calculations, somewhat simplified with

z ≪ m / k \sqrt{τ_{1}},

we can arrive at:

J_{T} = J_{0} \exp \{- \frac{x^{2}}{8 k^{2}} <{(δ q - δ q^{*})}^{2}> + j \frac{x z^{2}}{6 k} [<{(δ q)}^{2}> - <{(δ q^{*})}^{2}>] + j \frac{k x z^{2}}{90 m^{2}} [τ_{1} e^{- j \frac{π}{3}} <{(δ q^{*})}^{2}> - τ_{1} e^{j \frac{π}{3}} <{(δ q)}^{2}>] - \frac{k x}{m^{2}} \frac{τ_{1} \sqrt{3}}{90} z^{4} <{|δ q|}^{2}> + \frac{z^{4}}{18} <{(δ q + δ q^{*})}^{2}>\} . E q . 29

The corresponding terms δq can be expressed via the Fourier transform of Δε(z), viz.

\tilde{ε} (κ) = \frac{1}{2 π} \int_{- \infty}^{\infty} d z e^{- j κ z} ∆ ε (z), E q . 30

δ q = - k^{2} \int_{- \infty}^{\infty} d κ \cdot \tilde{ε} (κ) V (κ) E q . 31

where the function V(κ) is given by:

V (κ) = \frac{1}{N} \int_{0}^{\infty} d z \cdot χ_{0}^{2} (z) e^{j κ z} . E q . 32

It has the meaning of the scattering coefficient from the first mode back to itself again, due to inhomogeneities Δε(z) of the scale-size l = 2π/κ.

According to the inequality (14), the major contribution to the random component of the vertically stratified Δε(z) is given by sufficiently large inhomogeneities with κ = κ_z ≪ k/m. For this case V(κ) can be represented by an asymptotic expansion:

V (κ) = 1 + j \frac{m κ}{k} τ_{1} e^{j π / 3} + O ({(\frac{m κ}{k})}^{2}) . E q . 33

Defining the spectral density of the fluctuations as:

Φ_{1} (κ) = \sqrt{2 π} σ_{∆ ε}^{2} L_{z} \exp (- \frac{κ^{2} L_{z}^{2}}{2}), E q . 34

with L_z = σ_νzT, we shall substitute Eq. (33) into Eq. (29) with an account of the spectrum in the form (34). Then the average intensity

J_{T}

becomes:

J_{T} = J_{0} \exp \{\frac{3 π x^{2}}{4 L_{z}^{2}} m^{2} σ_{∆ ε}^{2} τ_{1}^{2} - x \frac{k^{5} z^{4} σ_{∆ ε}^{2} τ_{1} \sqrt{3}}{180 m^{2}} - \frac{4}{3} π σ_{∆ ε}^{2} (k z^{4})\} . E q . 35

The range of validity of Eq. (35) is dictated, according to the perturbation method employed, by the demand that the second-order correction to W_T(x, z; z₀) be small.

Analyzing Eqs. (27) and (29) we find that the corrections to the propagation constants take the major role in the second-order corrections overall, and these can be evaluated as:

δ q^{(2)} \approx \frac{m^{2}}{k^{2}} {(δ q)}^{2} . E q . 36

Noting that

δ q ~ k^{2} σ_{∆ ε}

we will demand that the terms containing the range (distance) squared in the exponent are small, whence:

σ_{∆ ε}^{3} k^{2} x^{2} m^{2} ≪ 1 . E q . 37

Substituting

σ_{∆ ε}^{2} \approx 10^{- 13},

we find that the requirements of Eq. (37) can be met for x ≤ 150 km at λ = 10 cm (f = 3 GHz) and x ≤ 700 km at λ = 30 cm (f = 1 GHz).

Shown in Figure 1 are the range dependences of the average intensity

J_{T}

as calculated from Eq. (35) for f = 3 GHz and f = 1 GHz. The parameter values assumed for the calculation are:

z = z_{0} = 10 m, σ_{∆ ε}^{2} \approx 10^{- 13}, L_{s} = 20 m

and a = 8 500 km. Range dependences J₀ are also shown for comparison. As can be seen from Figure 1 and from Eq. (35), the presence of random gradients dε_T/dz ~ σ_Δε/L_z in the refractive index results in a sharp increase in the signal strength. This can be regarded as a kind of “trapping” or localization of the radiated field near the earth’s surface, however, in this case it is of a random nature.

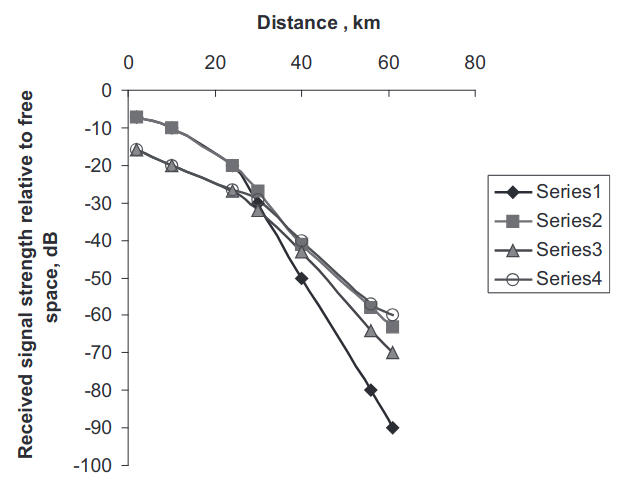
Graph - received field — Fig. 1 Range dependence of the average intensity of the received field, 10log(JT ):

Received field strength at frequency 3 GHz in the absence of fluctuations in the refractivity (
$σ_{∆ ε}^{2} = 0$
);
Received field strength at frequency 3 GHz,
$10 \log (\bar{J_{T}})$
in the presence of fluctuations in the refractivity
$σ_{∆ ε}^{2} \approx 10^{- 13};$
Received field strength at frequency 1 GHz in the absence of fluctuations in the refractivity(
$σ_{∆ ε}^{2} = 0$
);
Received field strength at frequency 1 GHz,
$10 \log (\bar{J_{T}})$
in the presence of fluctuations in the refractivity
$σ_{∆ ε}^{2} \approx 10^{- 13} .$

Making use of Eqs. (25), (27) and (35), we can evaluate the square of the standard of the intensity fluctuations, viz.

σ_{J}^{2} = J_{T}^{2} - {J_{T}}^{2} = {J_{T}}^{2} \{\exp [\frac{3 π x^{2}}{2 L_{z}^{2}} m^{2} σ_{∆ ε}^{2} τ_{1}^{2} - x \frac{k^{5} z^{4} σ_{∆ ε}^{2} τ_{1} \sqrt{3}}{90 m^{2}} - \frac{2}{9} π σ_{∆ ε}^{2} {(k z)}^{4}] - 1\} . E q . 38

Figure 2 provides range dependences of the fluctuation standard

σ_{J}^{2} (x)

and the variation index:

β_{J}^{2} (x) = σ_{J}^{2} (x) / {J_{T}}^{2} (x)

calculated for the same parameter values. The latter magnitude

β_{J}^{2}

characterizes the relative fluctuations in the intensity (i. e. the depth of “slow” fading). As observed from Eq. (38) and from Figure 2, the mean square magnitude of the intensity fluctuations is proportional to the average intensity and grows with the range as the first and major term in the exponent (38).

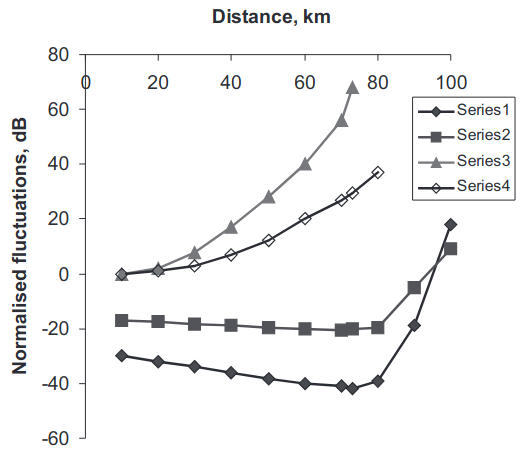
Graph - range dependences — Fig. 2 Range dependences of the fluctuation standard and the variation index in the presence of fluctuations in the refractivity with $σ_{∆ ε}^{2} \approx 10^{- 13} :$

Fluctuation standard
$σ_{J}^{2} (x)$
at frequency 3 GHz;
Fluctuation standard
$σ_{J}^{2} (x)$
at frequency 1 GHz;
Variation index
$β_{J}^{2} (x)$
frequency 3 GHz;
Variation index
$β_{J}^{2} (x)$
at frequency 1 GHz.

We believe that Eqs. (35) and (38) can provide an explanation for the increase in the fading depth which is observed experimentally with increase in the mean levels of the signal. According to the field measurements, the fading depth increases with the path length up to ~200 km, such behavior is also in agreement with the theoretical result provided by Eq. (38). The above theory, developed in this section, introduces a two-scale model of fluctuations in the refractive index: small-scale fluctuations treated as a Kolmogorov turbulence and large-scale fluctuations Δε which are treated as a random stratification Δε(z).

Within the limits of this theory, the signal strength should demonstrate strong correlation with the fluctuation standard

σ_{∆ ε}^{2}

of the dielectric permittivity near the earth’s/ocean’s surface. As

σ_{∆ ε}^{2}

increases, the field intensity should grow, even with small gradients of the average profile of the refractive index, i. e. without ducting or enhanced refraction. This increase in the signal strength is due to multiple scattering of the lowest propagation mode on the “layered” inhomogeneities whose vertical scale sizes are commensurate with Λz = m/k, the vertical scale size of the mode oscillations, as shown in Figure 3. A one-dimensional analogy (along the z-coordinate) to this phenomenon is the stochastic parametric resonance considered in Refs.

To analyse cases of ducted radio wave propagation in an atmospheric duct over the sea’s surface, the common approach is to attempt to compare the measured data with theoretical predictions for ε_M(z) profiles recovered from meteorological measurements. To a certain degree, controlled by the validity of the hydrodynamic theory of an evaporation duct, such profiles correspond to the ensemble averaged dependences

ε_{T} (z),

with the random stratification Δε(z) apparently disregarded.

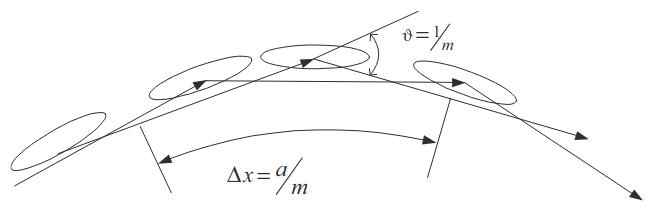
Yet, as can be seen from the above theory, the random component of Δε(z) can play the dominant part in cases where the average profile does not reveal a strong near-surface inversion, like an evaporation duct or for frequencies significantly below 10 GHz when an evaporation duct, even if present, is normally insufficient for the ducting mechanism at these frequencies.

Scattering of a Diffracted Field on the Turbulent Fluctuations in the Refractive Index

Long-range tropospheric propagation due to re-emission of the energy of electromagnetic waves by inhomogeneities of the refractive index has been known since the 1940s. The simple mechanism of the single scattering was first developed by Booker and Gordon and then updated taking into account the Kolmogorov the- ory of the turbulent spectrum of fluctuations in the refractive index. The theory of single scattering was proposed to explain the phenomenon of the long-range propagation in the absence of super-refractive anomalies in the refractive index profiles. It takes into account scattering by inhomogeneities located in the region formed by the intersection of the directional diagrams of the receiving and transmitting antennas, as shown in Figure 4.

Single scattering — Fig. 4 Geometry of single scattering in the troposphere

According to Refs, the mean intensity J_s of the scattered field I_s normalised on the intensity in a free space I_FS is expressed as follows:

J_{s} = \frac{I_{0}}{I_{F S}} = 16 σ_{0} \frac{V}{R^{2}} E q . 39

where V is the effective scattering volume and R is the distance between the receiver and transmitter, and σ₀ is the effective scattering cross-section.

The effective scattering cross-section σ₀ from a unit volume to a unit solid angle is given by:

σ_{0} = \frac{π k^{2}}{2} Φ_{ε} (\vec{q}), E q . 40

where

\vec{q}

is the scattering vector and

Φ_{ε} (\vec{q})

is the spectral density of the fluctuations in the dielectric permittivity

δ ε (\vec{r}) .

The scattering vector

\vec{q}

has the components q_x = q_γ = 0 and q_z = 2k sin (ϑ/2), where x and γ are coordinates along the surface of the earth and z is along the normal to it, k is the wavenumber and ϑ is the scattering angle, Figure 4.

For the inertial interval of the turbulence spectrum s₀ is determined by the relation:

σ_{0} = 0, 052 k^{1 / 3} C_{ε}^{2} {(2 \sin \frac{ϑ}{2})}^{- 11 / 3}, E q . 41

where C_ε is a structure constant, Understanding Parabolic Approximation in Wave Propagation: Analytical Methods and Applications“Parabolic Approximation to the Wave Propagation”.

The above Booker–Gordon theory provides rather good estimates of the signal strength of the scattered field as well as describing the range dependence of the receiving signal strength. However, there are several factors which, in the majority of observations, are not in agreement with the theory of single scattering, for example, the dependence on wavelength, elevation angle, and the cumulative distribution of the scattered field.

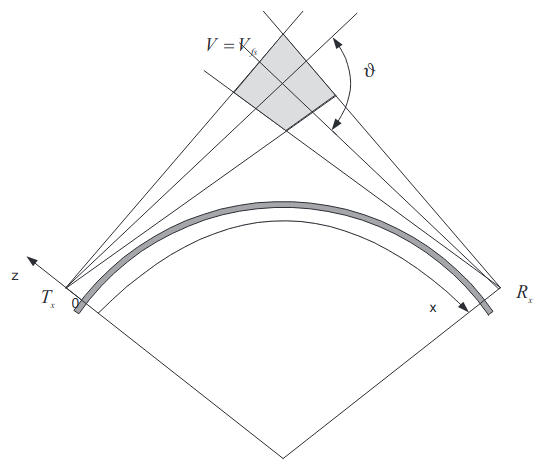
In this section we attempt to estimate the intensity of the signal over the horizon due to scattering of the waves in the volume located in the geometric shadow relative to both the transmitter and receiver, as shown in Figure 5.

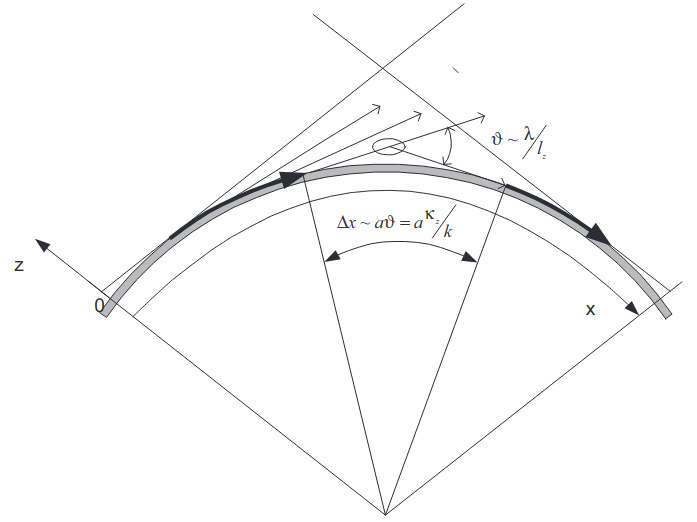
Geometry of single scattering in a diffracted field — Fig. 5 Geometry of the single scattering of the diffracted field

Consider the case of normal refraction, in which the modified dielectric constant of the troposphere ε_M(x, γ, z) = ε₀(z) + δε(x, γ, z), ε₀ = 1 + 2z/a. Here δε(x, γ, z) is a random component of the dielectric permittivity, <δε> = 0.

We shall define the mean intensity J_s of the scattered field normalised at an intensity in a free space via the attenuation factor W:

J_{s} = \frac{<I_{s}>}{I_{F S}} = <{|W|}^{2}> . E q . 42

The attenuation factor can be represented in the form W = W₀+W₁, where W₀ is the solution of the equation:

2 j k \frac{\partial W_{0}}{\partial x} + \frac{\partial^{2} W_{0}}{\partial γ^{2}} + \frac{\partial^{2} W_{0}}{\partial z^{2}} + k^{2} [ε_{0} (z) - 1] W_{0} = 0 . E q . 43

and W₁ is defined in the Born approximation by the expression:

W_{1} = - k^{2} \int_{x_{0}}^{x} d x^{'} \int_{- \infty}^{\infty} d γ^{'} \int_{0}^{\infty} d z^{'} G (x - x^{'}, γ, z; γ^{'}, z^{'}) \cdot δ ε (x^{'}, γ^{'}, z^{'}) W_{0} (x^{'} - x_{0}, γ^{'}, z^{'}, γ_{0}, z_{0}) E q . 44

where

\vec{r}

and

{\vec{r}}_{0}

are the vector-coordinates of the receiver and transmitter respectively:

\vec{r} = \{x, γ, z\}, {\vec{r}}_{0} = \{x_{0}, γ_{0}, z_{0}\} .

Later we will set x₀ = 0 and γ = γ₀ = 0.

We also restrict the integration volume for discussion of the scattering of a diffracted field in the shadow region by the inequalities:

z^{'} < \min \{\frac{{(x^{'} - ∆ x_{0})}^{2}}{2 a}, \frac{{(x - x^{'} - ∆ x)}^{2}}{2 a}\}, ∆ x_{0} < x^{'} < x - ∆ x . E q . 45

Here:

∆ x_{0} = \sqrt{2 a z_{0}}, ∆ x = \sqrt{2 a z} .

We note that the Booker–Gordon theory takes account of scattering only in the radiated region bounded by the inequality:

z^{'} > \{\frac{{(x^{'} - ∆ x_{0})}^{2}}{2 a}, \frac{{(x - x^{'} - ∆ x)}^{2}}{2 a}\} . E q . 46

We can define the Green function

G (\vec{r}, {\vec{r}}^{'})

in terms of the attenuation factor:

G (\vec{r}, {\vec{r}}^{'}) = \frac{1}{4 π (x - \vec{x})} W_{0} (\vec{r}, {\vec{r}}^{'}), E q . 47

which is represented in shadow region in the series of normal waves, Understanding Parabolic Approximation in Wave Propagation: Analytical Methods and Applications“Parabolic Approximation to the Wave Propagation”:

W_{0} (\vec{r}, {\vec{r}}^{'}) = - 2 e^{j π / 4} {[\frac{π m (x - x^{'})}{a}]}^{1 / 2} \frac{m}{k} \exp \{j \frac{k {(γ - γ^{'})}^{2}}{2 (x - x^{'})}\} \cdot \sum_{n = 1}^{\infty} \exp \{j q_{n} \frac{x - x^{'}}{2 k}\} \frac{χ_{n} (z) χ_{n} (z_{0})}{N_{n}} E q . 48

where q_n is a complex propagation constant:

q_{n} = \frac{k^{2}}{m^{2}} τ_{n} e^{j π / 3}, τ_{n} = {[\frac{3}{2} π (n - \frac{1}{4})]}^{2 / 3}, N_{n} = - 4 \frac{m}{k} \sqrt{τ_{n}} e^{j π / 3} . E q . 49

The height-gain functions χ_n(z) satisfy the equation:

\frac{d^{2} χ_{n}}{d z^{2}} + [k^{2} (ε_{0} (z) - 1) - q_{n}] χ_{n} = 0 E q . 50

and boundary conditions:

χ_{n} (z = 0) = 0, \frac{d}{d z} \arg χ_{n} (z) > 0 with z \to \infty . E q . 51

For the case of normal refraction χ_n(z) can be represented in terms of the Airy function, χ_n(z) = w₁(t_n-μz), where μ = k/m and t_n = q_n/μ².

We shall substitute Eqs. (47) and (48) into Eq. (44) and take into account in the double summation over the modes only diagonal terms which do not oscillate with distance. Integrating in Eq. (44) over dy and assuming statistical uniformity of the fluctuations in the refractive index and their isotropy in the x-, γ-planes, we can obtain the equation:

{<{|W_{1}|}^{2}>}_{n} = 2 \frac{{(π k)}^{2} m}{a x} F (z, z_{0}) \exp (- \frac{m x}{a} τ_{n} \sqrt{3}) \cdot \int_{0}^{x_{1} / 2} d x^{'} [{(x^{'} - ∆ x_{0})}^{2} + {(x - ∆ x - x^{'})}^{2}] \int_{- \infty}^{\infty} d κ_{γ} \int_{- \infty}^{\infty} d κ_{z} Φ_{ε} (0, κ_{γ}, κ_{z}) |V_{n} (κ_{z}, x^{'})| E q . 52

for the intensity of the scattered field in the nth mode

{<{|W_{1}|}^{2}>}_{n},

where:

F (z, z_{0}) = \frac{m^{2}}{k^{2} {|N_{n}|}^{2}} {|χ_{n} (z)|}^{2} {|χ_{n} (z_{0})|}^{2}

is a factor describing the dependence of the mean intensity of the scattered field on altitude and x₁ = x-Δx-Δx₀.

The function V_n(κ_z, x^′) in Eq. (52) has the meaning of a coefficient of re-scattering from the nth mode into the nth mode by inhomogeneities with the scale l_z = 2π/κ_z and is defined by:

V_{n} (κ_{z}, x) = \frac{1}{N_{n}} \int_{0}^{x^{2} / 2 a} d z χ_{n}^{2} (z) \exp (j κ_{z} z) . E q . 53

With:

κ_{z} < κ / m τ_{n} and x ≫ (a / m) \cdot \sqrt{τ_{n} / 2}

the major contribution to integral (53) comes from the altitude’s interval 0 < z < mτ_n/2k. The upper limit in Eq. (53) in this case can be replaced by infinity by means of introducing a smooth limiting function which compensates the growth of:

χ_{n}^{2} (z) at z \to \infty .

Let us introduce such a function in the form of exponent exp(-βz). After transition to non-dimensional variables α = β m/k, ς = kz/m and q = κ_zm/k we can deform the contour of integration over ς in V_n(κ_z, x) into a ray with arg ς = π/3. With α ≠ 0 we can neglect the contribution from integration over the arc of infinite radius, and for V_n(κ_z, x) we then obtain:

V_{n} (κ_{z}, x) \approx V_{n} (κ_{z}) = \frac{1}{\sqrt{τ_{n}}} \int_{0}^{\infty} d ς v^{2} (ς - τ_{n}) e^{- q^{*} ς}, E q . 54

where:

q^{*} = (α - j q) e^{j π / 3}, v (ς - τ_{n})

is the Airy function. We can further put parameter α = 0 and expand the exponent into a series over powers of q^*ς:

V_{n} (κ_{z}) = \frac{1}{\sqrt{τ_{n}}} e^{- q^{*} τ_{n}} \sum_{m = 1}^{\infty} P_{m} \frac{{(q^{*})}^{m}}{m!} {(- 1)}^{m}, E q . 55

where:

P_{m} = \int_{- τ_{n}}^{\infty} d x \cdot x^{m} ν^{2} (x) . E q . 56

The recurrent formulas for integrals (56) are provided in the Airy Functions – Comprehensive Guide“In-Depth Exploration of Airy Functions and Their Applications”.

With |q|τ_n ≪ 1, we can retain only the first term in series (55). Taking into account that ν(-τ_n) = 0, we obtain the asymptotic expression:

V_{n} (κ_{z}) ≅ 1 + \frac{j}{3} (\frac{κ_{z} m τ_{n}}{k}) \exp (j \frac{π}{3}) + O ({(\frac{κ_{z} m τ_{n}}{k})}^{2})

which determines the contribution of non-resonant scattering by inhomogeneities having vertical scales l_z greater than the maximum characteristic scale mτ_n/κ of oscillations in

χ_{n}^{2} (z) .

when:

k τ_{n}^{2} / m ≪ κ_{z} ≪ 2 k x / a,

the stationary point of the integrand in Eq. (53):

z_{s t} = \frac{m}{k} (\frac{τ_{n}}{2} + {(\frac{κ_{z} m}{2 k})}^{2})

makes the main contribution to V_n(κ_z, x). In this case the resonant scattering of the nth mode occurs at the altitude z_st at which the scale of

χ_{n}^{2} (z) .

is equal to the vertical scale of the inhomogeneities, and we have for V_n(κ_z, x) the expression:

V_{n} (κ_{z}, x) ≅ \frac{1}{2} {(\frac{k}{κ_{z} m τ_{n}})}^{1 / 2} e^{j π / 12} H (z_{s}) \exp \{- j \frac{κ_{z} m t_{n}}{k} - j \frac{1}{12} {(\frac{κ_{z} m}{k})}^{3}\}, E q . 57

H (z_{s}) = \int_{- \infty}^{z_{s}} \exp (j ξ^{2}) d ξ, z_{s} = \frac{1}{4 \sqrt{κ_{z}}} {(\frac{m}{k})}^{3 / 2} [{(\frac{2 k x}{a})}^{2} - κ_{z}^{2}] . E q . 58

When κ_z > 2kx/a, the upper limit of integration makes the main contribution to the integral V_n(κ_z, x):

V_{n} (κ_{z}, x) ≅ \frac{1}{2} {(\frac{a}{2 m k x τ_{n}})}^{1 / 2} e^{j π / 12} \exp \{- j \frac{m x t_{n}}{a} - j \frac{2}{3} {(\frac{m x}{a})}^{3}\} . E q . 59

This equation corresponds to non-resonant scattering by inhomogeneities with scales l_z < πa/kx.

Let us substitute into Eq. (52) the asymptotes (Hybrid Representation in Action: Fock’s Contour Integral and the Attenuation Factorsee this equation) and specify the spectrum of fluctuations in the refractive index

Φ_{ε} (\vec{κ})

by Atmospheric Boundary Layer and Basics of the Propagation Mechanismssee this equation:

Φ_{ε} (\vec{κ}) = \frac{0, 063 σ_{ε}^{2} L_{z} L_{∥}^{2}}{{(1 + κ_{∥}^{2} L_{∥}^{2} + κ_{z}^{2} L_{z}^{2})}^{11 / 6}}, E q . 60

where:

κ_{∥} = \sqrt{κ_{x}^{2} + κ_{γ}^{2}} .

This spectrum takes into account the finite external scales along the vertical (L_z) axis and horizontal plane (L_||) and the anisotropy of the inhomogeneities α = L_z/L_|| ≠ 1.

Taking then account of the fact that for x ≫ a/mτ_n (for f ~ 10 GHz, a/mτ_n ~ 10 km) small-scale inhomogeneties with κ_z ≫ k/mτ_n make the main contribution to the scattering, and bearing in mind that mτ_n ≫ 1, we obtain for the intensity of the scattered field J_s the following expression:

J_{s d} \approx <{|W_{1}|}^{2}> = \frac{0, 055 π^{3} C_{ε}^{2} α^{- 5 / 3}}{12 τ_{1}^{3}} {(\frac{a}{2})}^{1 / 3} k^{- 1 / 3} {(\frac{x_{1}}{a})}^{- 8 / 3} \cdot F (z, z_{0}) \exp (- \frac{m ξ}{a} τ_{1} \sqrt{3}) E q . 61

where:

ξ = \sqrt{2 a} (\sqrt{z} + \sqrt{z_{0}}) .

We have taken into account the contribution of the first mode with n = 1, the scattering of the other modes can be estimated similarly, however, the contribution of the modes with higher indices n decays as n^–2.

The contribution of the large-scale inhomogeneities to the intensity of the scattered field is exponentially small which can be explained as follows: The wave diffracted over the sphere’s surface creates the secondary waves sliding along the tangent to that surface. These waves then scatter on the imhomogeneities of the refractive index at the scattering angle ϑ ~ λ/l_z.

The scattered wave touches the spherical surface at the distance from the point of initial detachment Δx ~ aϑ = a κ_z/k, and thereafter diffracts along the earth’s surface arriving at the receiving point. Along the path x₁ derived along the geodesic curve, the wave attenuation is determined by:

\exp (- m x_{1} / a τ_{1} \sqrt{3}) .

For the scattered wave the distance along the geodesic x₁ is given by x₁ = x–Δx, since at the interval Δx the wave propagates under free-space conditions, as shown in Figure 5. As observed, for κ_z < k/mτ_n, Δx < am/τ_n, hence the larger the inhomogeneities participating in wave scattering, the shorter the “free-space” interval and, therefore, the larger the attenuation along the geodesic interval.

When x ≫ am/τ_n, the contribution of the large-scale inhomogeneties to single scattering, with κ_z < k/mτ_n, can be neglected. With greater κ_z the scattering takes place in the higher layers of the troposphere at larger angles ϑ, thus increasing the “free-space” interval and decreasing the attenuation of the scattered wave.

In contrast to Eqs. (39) to (41), the dependence of the signal strength on the altitude z enters not only through the scattering angle ϑ = x₁/a but also through the height-gain function

χ_{n} (z) .

In the range of altitudes z ≪ x²/2a and distances:

x (a / m) \sqrt{τ_{n} / 2},

the scattering angle ϑ can be assumed to be independent of altitude, i. e. ϑ ~ x/a; then the dependence of J_sd on z is determined by the factor:

\exp [- (m / a) \sqrt{2 a z} τ_{n} \sqrt{3}] \cdot {|χ_{n}|}^{2} .

Substituting the asymptotes of χ_n(z) into Eq. (60) and assuming z₀ ≫ mτ_n/2k, we obtain:

J_{s d} ~ z^{2} λ^{2 / 3}, with z ≪ \frac{m}{k \sqrt{τ_{n}}}, E q . 62

J_{s d} ~ z^{- 1 / 2} λ, with z ≫ \frac{m τ_{n}}{2 k},

and with z = mτ_n/2k function J_sd(z, λ) has a maximum in which the value of |χ_n(z)| is of the order of one.

We note that in the majority of experiments the wavelength dependence of the scattered field is proportional to the wavelength, J_sd(λ)~λ^m, where 0,7 < m < 1,4.

Let us consider the case of elevated antennas when z, z₀ > mτ₁/2k and compare the intensity of the scattered diffracted field J_sd with the intensity J_s calculated from formula (39) with the spectrum defined by expression (60). Extracting from Eq. (61) the effective scattering cross-section rd with anisotropy factor accounted for, i. e:

σ_{d} = 0, 052 C_{ε}^{2} k^{1 / 3} α^{- 8 / 3} {(2 \sin ϑ / 2)}^{- 11 / 3},

we can represent the intensity of the scattered diffraction field in a form similar to Eq. (39):

J_{s d} = 16 \frac{σ_{d} V_{d}}{x^{2}}, E q . 63

where V_d is the effective scattering volume, which is defined by the equation:

V_{d} = 0, 0087 \frac{π^{3} x^{3} α}{16 m τ_{1}^{4} k \sqrt{z \cdot z_{0}}} . E q . 64

Without even numerical calculation we may conclude that the contribution of the diffracted field will be an order of magnitude less than the contribution of the scattering in a “free-space” volume, defined by formula (39) according to the Booker–Gordon theory. The value of the theory developed in this section is that it provides the correct frequency and height dependence of the scattered field, compared with the “free-space” single scattering theory.

The correct estimation of the scattered field should require calculation of the additional terms in the scattered field not accounted for here. We may notice that given practical antennas we always have two terms in the incident field : direct wave + reflected from the ground wave( comprising the line-of-sight mechanism) and diffracted field. For simplicity, the reflected wave is omitted in the Booker–Gordon single-scattering theory, and the contribution from the transition (between line-of-sight and shadow region) is also omitted. The intensity of the total scattered field should contain four terms:

J_{t o t a l} = \frac{I_{t o t a l}}{I_{F S}} = 16 σ_{0} \frac{V_{f s}}{x^{2}} + 16 σ_{d} \frac{V_{d}}{x^{2}} + 16 σ_{d, 0} \frac{V_{d, f s}}{x^{2}} 16 σ_{0, d} \frac{V_{f s, d}}{x^{2}} E q . 65

where the first term represents the contribution from the scattering in a free-space volume V_fs, as given by Eq. (39) (V_fs ≡ V), the second term is scattering of the diffracted field given by Eq. (64) and two last terms represent scattering of the line-of- sight waves into the diffracted field in the volume V_{fs, d}. (Figure 6) and the diffracted field into the free-space waves in the volume V_d,fs.

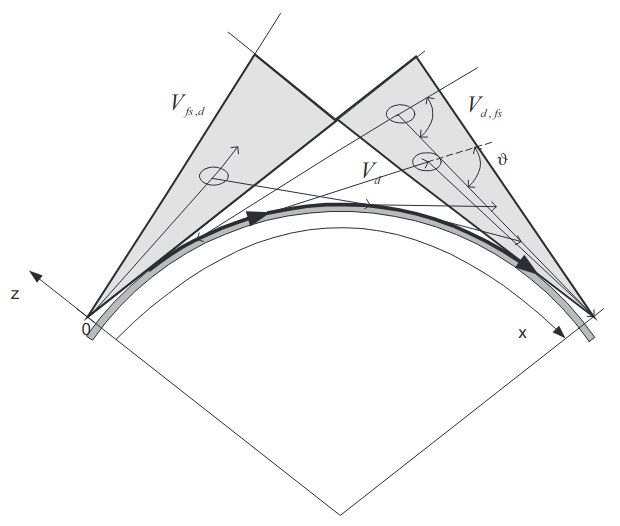
Scattering volumes — Fig. 6 Schematic diagram of the scattering volumes for diffracted-to-diffracted field (V_d), diffracted to free-space field (V_{d, fs}) and free-space to diffracted field (V_{fs, d})

A combination of these four terms may provide observable levels of the scattered field as well as frequency and height dependence in agreement with experiment.

Author

Olga Nesvetailova

Freelancer

Literature

Ivanov, V., Kinber, B., Korzenevitch, I. and Stepanov, B. Impact of the earth surface on long-range tropospheric propagation, Radiotech. Electron., 1980, 25 (10), 2033–2042.
Saitchev, A., Slavinsky, M. Equations for moment-functions of waves propagating in random media with anisotropic inhomogeneities, Radiophys. Quant. Electron., 1985, 28 (1), 75–83.
Kukushkin, A., Fuks, I. and Freilikher, V. Impact from random stratification on a coherent component of the field over horizon, Radiophys. Quant. Electron., 1983, 28 (8), 1064–1072.
Long-range UHF Propagation in the Troposphere, Eds. Vvedensky, B., Kolosov, M., Kalinin, A. and Shifrin, J., Soviet Radio, Moscow, 1965, 416 pp.
Shur, A. Signal Characteristics of Tropospheric Radiolinks, Swyaz, Moscow, 1972, 105 pp.
Shifrin, J. Problems of Statistical Antenna Theory, Soviet Radio, Moscow, 1970, 384 pp.
Kalinin, A., Troitzky, V. and Shur, A. The study of long-range UHF tropospheric propagation, in Radiowave Propagation , Eds. Kolosov, M., Armand, N., Katzelenbaum, B. and Sokolov, A., Nauka, Moscow, 1975, pp. 127– 153.
Rytov, S.M., Kravtsov, Y.A. and Tatarskii, V.I. Introduction to Statistical Radiophysics: Part 2, Random Fields, Nauka, Moscow, 1978, 464 pp.
Tatarskii, V.I. The Effects of Turbulent Atmosphere on Wave Propagation, IPST, Jerusalem, 1971.
Feinberg, E. Radiowave Propagation over the Earth’s Surface, Nauka, Moscow, 1961, 547 pp.
Booker, H., Gordon, W. A theory of radio scattering in the troposphere, 1950, Proc. IRE, 1950, 38 (4), 401–412.
Klatskin, V.I. Stochastic Equations and Waves in Random Media, Nauka, Moscow, 1980, 336 pp.
Rotheram, S. Radiowave propagation in the evaporation duct, 1974, The Marconi Rev., 1974, 37 (192), 18–40.

Footnotes