Прочность дока - определение продольных усилий от веса

В данном материале показаны формулы, которые помогают вычислить усилия взаимодействия плавучего дока и судна, во время ввода и вывода судна. Прочность дока рассчитывается и предусматривается во время проектирования и конструирования.

СодержаниеСвернуть

Определение продольных усилий от собственного веса дока на тихой воде
Определение продольных усилий, действующих на систему док—судно при постановке судов
Влияние неравномерной балластировки при погружении и всплытии дока на продольные усилия
Влияние сухих отсеков в доке на продольные усилия
Влияние приема жидкого балласта на продольные усилия
Определение статических составляющих продольных изгибающих моментов и перерезывающих сил на волнении

Определение продольных усилий от собственного веса дока на тихой воде

Определение изгибающих моментов и перерезывающих сил от собственного веса дока принципиально ничем не отличается от такой же задачи для любого судна, т. е. сводится к определению перерезывающих сил и изгибающих моментов по формулам

$N_{1} (x) = \int_{0}^{x} (q_{Д} - γ ω) d x, Ф о р м . 1$

$M_{1} (x) = \int_{0}^{x} N_{1} (x) d x = \int_{0}^{x} \int_{0}^{x} (q_{Д} - γ ω) d x d x . Ф о р м . 2$

Упрощенная форма корпуса доковКонструкции и проектирование корпусов плавучих доков позволяет сократить громоздкие вычисления, связанные с разбивкой весовой нагрузки по 20 теоретическим шпациям. Вес корпуса дока удобно разбить на вес понтонов и вес башен. Каждую из этих частей веса корпуса дока легко распределить по длине, так как ординаты кривых веса будут пропорциональны ширине и высоте понтонов или высоте башен в каждом сечении.

При ориентировочных расчетах вес корпуса дока (особенно ремонтного, имеющего симметричные оконечности) можно считать равномерно распределенным по длине. Для понтонных (самодокующихся) доков обычно производят разбивку весов и сил поддержания не по теоретическим шпациям, а по участкам, равным длинам отдельных понтонов (с учетом промежутков между ними). Такой способ позволяет определить усилия в сечениях между понтонами дока, где они воспринимаются только башнями (рис. 1).

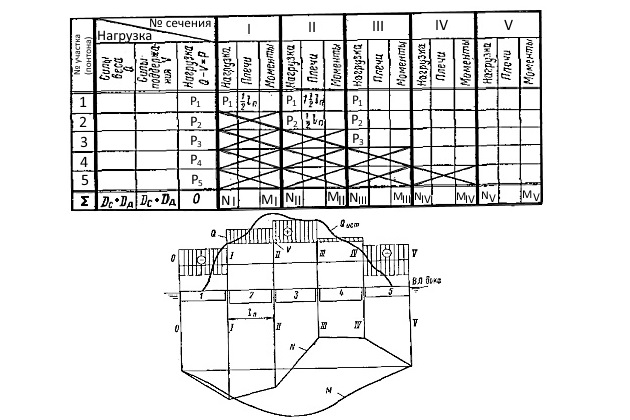
Прочность дока — Рис. 1 Схема определения изгибающих моментов и перерезывающих сил самодокующегося дока

Для вычисления изгибающих моментов в различных сечениях дока при распределении нагрузки по теоретическим шпациям или понтонам (отсекам) можно воспользоваться диаграммой Б. Г. Сизова, а для моментов в сечениях между понтонами — и лучевыми графиками В. В. Козлякова, построенными с использованием линий влияния. Эти же графики и диаграммы могут быть применены для оценки влияния балласта, принятого в отдельные отсеки, и для вычисления момента от судна, если его вес разбит по теоретическим шпациям или понтонам дока.

Вследствие незначительного влияния собственного веса дока на суммарный изгибающий момент дока с поднятым судном, для приближенных вычислений влияние собственного веса дока можно учесть (как рекомендует М. А. Ловягин) увеличением на 20% изгибающего момента от веса судна и балласта, т. е.

$M_{0} \approx 1, 2 (M_{2} + M_{3}) . Ф о р м . 3$

При погружении дока величины изгибающих моментов и перерезывающих сил от собственного веса при прогибе обычно несколько уменьшаются. Одной из причин этого является форма башен дока. Обычно длина башен несколько меньше длины понтонов. В результате, начиная с момента входа башен в воду, появляется некоторый дополнительный перегибающий момент, разгружающий прогиб.

Определение продольных усилий, действующих на систему док—судно при постановке судов

Определение суммарных изгибающих моментов системы док—судно М₀ и соответствующих перерезывающих сил N₀ от веса докуемых судов и дока, сводящееся к построению и двукратному интегрированию весовых эпюр дока, судна и балласта, а также сил поддержания достаточно трудоемко и в большинстве случаев нецелесообразно. Дело в том, что величина и характер распределения весовой нагрузки судов могут изменяться в широких пределах, в зависимости от классов и типов докуемых судов, их размерений, положения в доке (рис. 2), а также от количества и размещения жидкого балласта в доке, принимаемого для устранения крена, дифферента и уменьшения прогиба дока. Предусмотреть заранее при проектировании дока варианты нагрузки системы док—судно достаточно точно невозможно.

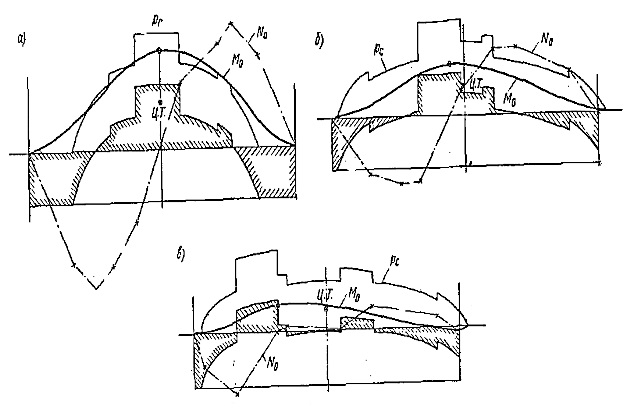
Прочность дока - эпюры нагрузок — Рис. 2 Эпюры нагрузок, изгибающих моментов и перерезывающих сил при постановке в док судов различных типов одинарного докового веса: а — для пассажирского судна; б — для сухогрузного судна; в — для танкера

Исключение составляют случаи, когда проектируемые доки (чаще всего транспортные) предназначены для докования или транспортировки определенных судов. Уточнять величины М₀ и N₀ и их распределение между судном и доком следует при доковании судов, не предусмотренных проектом дока, особенно при использовании его полной грузоподъемности.

Предлагается к прочтению: Элементы теории подруливающего устройства

Для приближенного определения наибольших значений изгибающих моментов системы док—судно посредине килевой дорожки используют аппроксимацию истинных эпюр распределения весовой нагрузки судна простейшими кривыми, например прямоугольником, трапецией, параболами различных степеней, эллипсом и т. д. Наиболее близкие к действительным результаты получаются при параболическом распределении веса судна по предложению И. Н. Сиверцева:

$q_{c} = b_{c} \frac{D_{c}}{L_{c}} [1 - {(\frac{2 x}{L_{c}})}^{m}] Ф о р м . 4$

где

$m = \frac{φ_{c}}{1 - φ_{c}}$

(например, при φ_с=0,8, m=4, b_c=1,25), или по полуэллипсу (по Я. А. Копержинскому и М. А. Ловягину)

$q_{c} = 1, 28 \frac{D_{c}}{L_{c}} {[1 - {(\frac{2 x}{L_{c}})}^{2}]}^{\frac{1}{2}}, Ф о р м . 5$

что справедливо при

$φ_{c} = 0, 75 - 0, 80 .$

В обоих этих случаях статический момент от сил веса судна на миделе дока приблизительно равен

$M_{2}^{с т} = (0, 100 \div 0, 101) D_{c} L_{c} . Ф о р м . 6$

При приближенном определении М₂ истинное распределение сил поддержания по длине дока также целесообразно заменить приближенной зависимостью. В этом случае момент сил поддержания относительно миделя дока равен

$M_{с . п} = - k D_{c} L_{Д}, Ф о р м . 7$

где

k определяется по табл. 1.

Следовательно, приближенное значение изгибающего момента на миделе системы док—судно можно вычислить по формуле

$M_{0} \approx 1, 2 (0, 100 D_{c} L_{c} - k D_{c} L_{Д} \pm 0, 01 B_{Д} L_{Д}^{2}), Ф о р м . 8$

Таблица 1. Зависимость коэффициента k статического момента сил поддержания относительно мидель-шпангоута $M_{c . п} = k D L$ от коэффициента продольной остроты $φ = \frac{δ}{β}$
$φ = \frac{δ}{β}$	0,5	0,6	0,7	0,8	0,9	1,0
k	0,0772	0,0845	0,0930	0,1016	0,114	0,125

где коэффициент 1,2 учитывает влияние собственного веса дока,
составляющая
$\pm 0, 01 B_{Д} L_{Д}^{2}$
— влияние неравномерности откачки или налива балласта [см. формулы (Формула 10), (Формула 11)]. Знак этой составляющей принимается по знаку большей из первых двух.

При распределении веса судна по квадратичной параболе с коэффициентом полноты φ_с изгибающий момент от веса судна с учетом сил поддержания по формуле (Формула 7) при φ_д = 1,0 и k = 0,125 равен (по В. В. Козлякову):

$M_{2} = - \frac{D_{c} L_{Д}}{8} (1 - \frac{3 φ_{c} - 1}{2 φ_{c}} \cdot \frac{L_{c}}{L_{Д}}) . Ф о р м . 9$

Коэффициенты полноты эпюр φ_с и максимальных ординат весовых нагрузок некоторых типов судов

b_{c} (q_{c m a x} = b_{c} \frac{D_{c}}{L_{c}})

приведены в табл. 2.

Таблица 2. Коэффициенты φ_c и b_c для некоторых типов судов
Тип судна	φ_c	b_c
Надводные суда и ледоколы	0,70	1,5
Пассажирские суда	0,75	1,3
Грузовые суда	0,80	1,25
Баржи и подобные им суда	0,85	1,1

В некоторых случаях специально рассчитанной балластировкой дока почти полностью «снимается» изгибающий момент системы док—судно на тихой воде, благодаря чему появляется возможность эксплуатации дока в условиях волнения на незащищенных акваториях или перевод доков с какими-либо грузами морем.

Погашение изгибающего момента на тихой воде соответствующей балластировкой применяется также для транспортных доков при выходе их в крупные водохранилища или в море, когда появляется возможность увеличить осадку дока. Это позволяет в некоторых случаях рассчитать корпус транспортного дока на усилия от веса судна и небольшого речного волнения или только на дополнительные усилия в крупных водохранилищах и морях (после погашения усилий от веса судна) в зависимости от того, какие из этих усилий являются большими.

Рекомендуется к прочтению: Вопросы теории корабля и технические графики

При погружении дока с «длинным» судном (L_с > 1,20 ÷ 1,25L_д) изгибающие моменты могут быть больше, чем во всплытом состоянии, вследствие увеличения сил поддержания в средней части судна. Это обстоятельство следует учитывать при доковании «длинных» судов, особенно при расчете концевых реакций, и в необходимых случаях регулировать их приемом большего количества балласта в средние по длине отсеки дока.

Влияние неравномерной балластировки при погружении и всплытии дока на продольные усилия

С самого начала погружения дока возникает некоторая разность уровней воды в балластных отсеках, вызываемая различными расстояниями отсеков от забортных отверстий и балластных насосов, а также маневрами с балластом для регулирования крена, дифферента и прогиба дока. В процессе погружения или всплытия дока с судном разность уровней балласта против расчетной составляет в различных отсеках не менее 0,3 м.

Пусть n — число отсеков по длине дока, m — число отсеков по одну сторону миделя, в которых повышается или понижается уровень балласта на величину ΔT_б. Считая, что док сидит «на ровный киль», получим следующее выражение дополнительного изгибающего момента:

$M_{3} = ∆ T_{б} γ B_{Д} L_{Д} \frac{m}{n} (\frac{L_{Д}}{2} - \frac{L_{Д}}{2} \cdot \frac{m}{n}) - ∆ T_{б} γ B_{Д} L_{Д} \frac{m}{n} \cdot \frac{L_{Д}}{4} =$

$= ∆ T_{б} γ B_{Д} L_{Д}^{2} (\frac{1}{4} - \frac{1}{2} \cdot \frac{m}{n}) \frac{m}{n} . Ф о р м . 10$

При n = 6, m = 2, ΔT_б = 0,3 м

$M_{3} \approx \frac{0, 3}{36} γ B_{Д} L_{Д}^{2}$

При n = 8, m = 2, ΔT_б = 0,3 м

$M_{3} \approx \frac{0, 3}{32} γ B_{Д} L_{Д}^{2} .$

Можно принимать

$M_{3} \approx 0, 01 B_{Д} L_{Д}^{2} \approx 0, 01 \frac{D_{Д} L_{Д}}{Т_{Д}} Ф о р м . 11$

В случае большей, чем указано выше, разности в уровнях балласта, необходимой по условиям правильной посадки дока, должен быть произведен более точный расчет изгибающих моментов и перерезывающих сил.

Влияние сухих отсеков в доке на продольные усилия

Наличие сухих отсеков рассматривается как снятие весов, равных объему этих отсеков в тот момент времени, когда уровень воды в балластных отсеках дока достигает верхней границы сухих отсеков, т. е. когда они создают максимальную плавучесть. На рис. 2, а приведен пример определения М и N при погружении дока с двумя сухими отсеками в понтоне, а на рис. 2, б — для секционного дока, имеющего сухой отсек — коффердам посредине длины дока.

Влияние приема жидкого балласта на продольные усилия

Чаще всего производится балластировка крайних отсеков понтона для уменьшения прогибающих усилий от веса докуемого судна. Пример вычисления изгибающих моментов и перерезывающих сил от приема «разгружающего» балласта приведен на рис. 3.

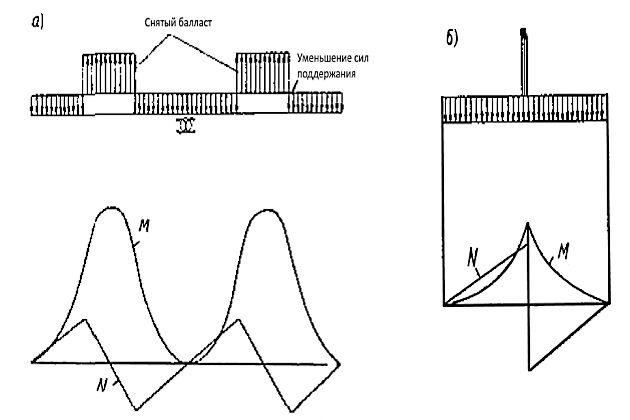
Прочность дока - эпюры изгибающих моментов — Рис. 3 Эпюры изгибающих моментов при погружении дока с сухими отсеками: а — при двух сухих отсеках в понтоне; б — при сухом коффердаме в секционном доке

По мере погружения дока влияние «разгружающего» балласта, в результате заполнения остальных балластных отсеков, уменьшается и становится равным нулю в тот момент, когда уровень балласта в отсеках достигает уровня «разгружающего» балласта.

Рис. 4 Пример построения эпюр изгибающих моментов и перерезывающих сил от приема «разгружающего» балласта

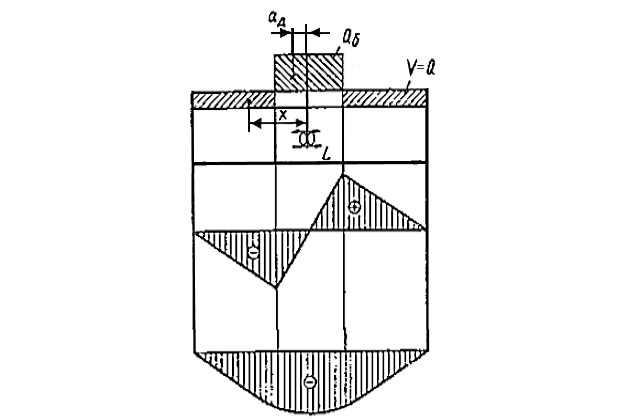
Если вода в отсеках оставляется при всплытии дока, количество балласта в них может быть любым (в пределах полного объема отсеков). Если же отсеки заполняются при погружении дока, уровень воды в них не может быть больше осадки дока с судном и принятым балластом.

Определение статических составляющих продольных изгибающих моментов и перерезывающих сил на волнении

В общем виде формула дополнительного изгибающего момента на волнении имеет вид

$M = γ \cdot 2 r B L^{2} ω Ф о р м . 12$

где

γ — удельный вес воды;
r — полувысота волны;
В и L — ширина и длина дока;
ω — функция, характеризующая форму корпуса.

В случае, если высота волны не ограничивается какими-либо условиями (эксплуатацией дока в защищенных от больших волн акваториях, переводом доков по внутренним водным путям с ограниченной высотой волны и т. п.), высота волны может быть принята «стандартной», т. е.

$h_{c} = 2 r_{c} = \frac{L}{20} + 1 п р и L ⩽ 60 м; Ф о р м . 13$

$h_{c} = 2 r_{c} = \frac{L}{30} + 2 п р и 60 ⩽ L ⩽ 120 м; Ф о р м . 14$

$h_{c} = 2 r_{c} = \frac{L}{20} п р и L ⩽ 120 м; Ф о р м . 15$

$\begin{array}{r} h_{с} = 2 r_{c} = \sqrt{1 + 0, 4 L} - 1 \\ h_{с} = 2 r_{c} = 0, 64 \sqrt{L} - 1 \end{array}\} д л я в о л н л ю б о й д л и н ы . Ф о р м . 16$

В этом случае формула (Формула 12) может быть представлена в виде

$M = \frac{γ B L^{3}}{K} Ф о р м . 17$

где

К — численный коэффициент, зависящий от формы обводов.

Для определенных акваторий с ограниченной высотой волны последняя определяется справочными гидрометеорологическими данными.

Численные коэффициенты в формуле (Формула 12) в зависимости от коэффициентов полноты α или δ предложены ЦНИИМФ, В. В. Давыдовым, Б. Н. Смоляковым (с учетом «косого» курса на волнении), а также Александером, Шмидтом, Суехиро и Фостером, Кингом, Суоном и для прямоугольного понтона — М. А. Ловягиным.

Численные коэффициенты в формуле (Формула 17) предложены В. А. Никитиным, Ранкиным, Виветом, Суехиро, Фостером и Мюрреем.

В работе изложен общий метод определения изгибающих и крутящих моментов и перерезывающих сил для прямоугольного понтона на косинусоидальном волнении при произвольном соотношении длин волны и понтона и любом курсовом угле по отношению к направлению бега волн.

Плавучий док в Гамбурге
Источник: pixabay.com

Результаты расчета дополнительных статических изгибающих моментов на вершине и подошве волны по данным различных авторов приведены в табл. 3. Там же приведены результаты расчета по формуле (Формула 12), в которой коэффициент ω вычислен по близким прототипам. В 12-й строке даны «точные» значения моментов, полученные удифферентовкой дока на вершине и подошве волны по масштабу Бонжана.

Как видно из таблицы, наиболее близкие результаты для дока дает формула ЦНИИМФ. Для прямоугольного понтона при α = δ = 1 все формулы дают одинаковую величину момента, равную

$M \approx \frac{γ 2 r B L^{3}}{4 π^{2}} .$

При «косой» постановке дока на волну изгибающие моменты и перерезывающие силы рекомендуется вычислять по формулам Б. И. Смолякова.

В расчетах дополнительных изгибающих моментов и перерезывающих сил ремонтных доков практически невозможно учесть такое явление, как срезание вершин волн стапель-палубой и накат волн на стапель-палубу. Вследствие этого не имеет смысла уточнение приближенных формул, а тем более точная постановка ремонтного дока на вершину и подошву волны.

Для уменьшения действующих на волнении усилий и ударов волн в днище при переводе морем иногда рекомендуют притопление доков. При притоплении дока, когда осадка его будет такова, что подошва волны не оголяет стапель-палубу (Т > h_п + r), величина дополнительных изгибающих моментов и перерезывающих сил, казалось бы, должна уменьшаться в отношении

\frac{2 b_{б}}{D}

, где b_б — ширина башни дока. Однако эксперименты, проведенные в бассейне ЛКИ, не подтвердили это положение, что объясняется опозданием фазы входа волны во внутридоковое пространство и разрушением ее формы между башнями.

Таблица 3. Сравнительная таблица дополнительных статических составляющих изгибающих моментов на волнении (по различным данным)
№ п/п	Автор	Формула	Момент на вершине волны M_в.в.^mм	Момента на подошве волны М_п.в.^mм
1	ЦНИИМФ	$M = ω γ 2 r B L^{2}$	19 500	-20 400
2	В. В. Давыдов	$M_{в . в} = \frac{γ r B L^{2}}{20 + 75 (1 - α)}$ $M_{п . в} = \frac{γ r B L^{2}}{20 + 52 (1 - α)}$	19 100	-19 800
3	В. Л. Никитин	$M = \frac{D L^{2}}{K δ T} \cdot \frac{2 r}{2 r_{c}} = \frac{γ B L^{3}}{K} \cdot \frac{2 r}{2 r_{c}}$	20 300	-20 300
4	Мюррей	$M = \frac{B L^{3}}{K}$	17 900	-17 900
5	Фостер	$M = K \frac{B L^{3}}{160} \cdot \frac{2 r}{2 r_{c}}$	20 100	-20 100
6	Александер	$M = \frac{2 r α B L^{2}}{K}$	19 700	-19 700
7	Суехиро	$M = ω γ 2 r B L^{2}$	17 400	-17 400
8	Суон	$M = γ B L^{3} \frac{2 r}{λ} \cdot \frac{ω λ}{L}$	19 900	-19 900
9	М. Л. Ловягин	$M = \frac{γ 2 r B L^{2}}{4 π^{2}}$	20 900	-20 900
10	По прототипу I	$M = γ 2 r B L^{2} \cdot ω_{п р о т}$	18 500	-19 100
11	По прототипу II	$M = γ 2 r B L^{2} \cdot ω_{п р о т}$	16 800	-19 900
12	По статической удифферентовке на волне	–	19 700	-20 500

Если величина дополнительных изгибающих моментов на волнении известна, величина максимальной дополнительной перерезывающей силы может быть вычислена по формуле

$N m a x \approx \frac{3, 5 M}{L} Ф о р м . 18$

при синусоидальном законе распределения перерезывающих сил по длине дока.

Сноски