Для осуществления регулирования движения судов с помощью береговых систем управления движением, а также для управления судами в процессе расхождения двух и более судов при прохождении мелководных и других участков (акваторий портов, узкостей и проливов) необходим количественный учет динамических закономерностей судов при переходе с одной скорости движения на другую путем изменения режима работы движителей.
К наиболее часто встречающимся видам таких режимов работы движителей относятся:
- — режим работы движителей от нулевого числа оборотов до оборотов малого, среднего или при особых обстоятельствах в аварийных случаях полного хода при нулевой скорости движения судна в начале маневра;
- — режим работы движителей от оборотов малого или среднего хода до оборотов среднего или полного хода при установившейся скорости в начале маневра;
- — режим работы движителей от оборотов полного, среднего, малого хода до оборотов среднего, малого или самого малого хода при начальной установившейся скорости движения.
При этих режимах работы определяются динамические закономерности движения судов при уменьшении скорости движения.
Эти режимы работы движителей определяют динамические закономерности движения судов.
Для упрощения решений уравнений движения судна при переходных режимах работы движителей будем считать величину упора винта постоянной и переходные процессы работы движителей от одного режима к другому происходящими мгновенно. Такое допущение оправдывается тем, что переходные процессы в двигателях или движителях в 15-20 раз и более происходят быстрее, чем у судна. Например, время реверса лопастей у винта регулируемого шага на крупнотоннажных танкерах типа «Крым» составляет с команды «полный вперед» до команды «стоп» в режиме «море» 46 с, в режиме «порт» (маневренный режим) – 39 с; с команды «средний вперед» до команды «стоп» — в режиме «порт» – 35 с, с команды «малый вперед» до команды «стоп» в режиме «порт» – 27 с. Время реверса двигателя при аварийной остановке судна у крупнотоннажного танкера типа «Маршал Жуков» составляет с начала полного переднего хода до полного заднего хода 50 с, до среднего заднего хода – 30 с, с начала среднего переднего хода до полного заднего хода – 15 с и т. д. В то же время переходные процессы у судна занимают в этих случаях 10-15 мин и более.
Читайте также: Основы маневренности крупнотоннажных судов
Уравнения движения судна при разгоне от нулевой скорости до установившейся скорости при работе движителей на полный, средний или малый ход можно получить из уравнений движения судна, подставив vv = 0; ω = 0. Тогда
где:
- P (n) – сила упора винта на полном среднем или малом переднем ходу, Н (принимается постоянной);
- R (v) – сопротивление корпуса судна, Н.
Принимаем R (v) пропорциональным квадрату скорости, тогда уравнение (Формула 1) преобразуется следующим образом:
где:
- R уст – сопротивление корпуса при скорости установившегося движения (Vуст), Н.
После разделения переменных, интегрирования уравнения (Формула 2) и определения постоянной интегрирования получим:
Из этой формулы определим закон изменения скорости
Делая подстановку в формулу 4, учитывая, что dS/dt = v и интегрируя, получим длину пройденного судном пути S за время t:
Обозначим
тогда
где:
После подстановки новой переменной получим
Интеграл приводится к виду:
Проделав подстановку, получим
Постоянную интегрирования С2 определим из начальных условий при t = 0, S = 0: C2 = a·ln(l/2). После подстановки C2 формула приобретает окончательный вид:
Используя формулы 4 и 5, построим графики инерционных стартовых характеристик крупнотоннажных судов (НМП), удобные для использования на мостике судна. Ключ к использованию графика указан на рис. 1.
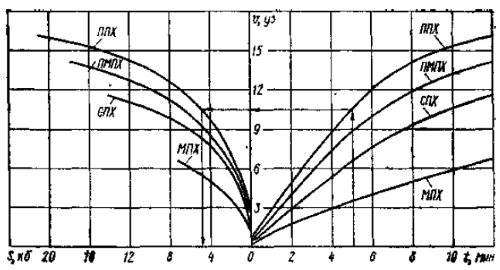
При разгоне судна от скорости малого хода до среднего или полного хода или от среднего хода до полного хода дифференциальное уравнение движения судна будет аналогично уравнению (Формула 1). Время переходного процесса можно определить из уравнения (Формула 3), изменив начальные условия при определении постоянной интегрирования С0. При t = 0 v = vн = v0 (начальная скорость до начала разгона при изменении режима работы машины на средний или полный ход). Тогда постоянная интегрирования С0 будет равна:
Подставляя значение С0 в формулу 3, получим
Из формулы 7 определим закон изменения скорости
Произведя замену С = vуст, получим
Делая подстановку в формулу 8 dS/dt = v и интегрируя, получим:
Обозначим
тогда
где:
После подстановки новых значений в уравнение (Формула 9) получим
Интеграл приведем к виду:
Перейдя к прежней переменной и определив постоянную интегрирования, получим
На рис. 2 представлены графики динамических характеристик крупнотоннажных судов при увеличении оборотов машин с малого хода до среднего и полного.
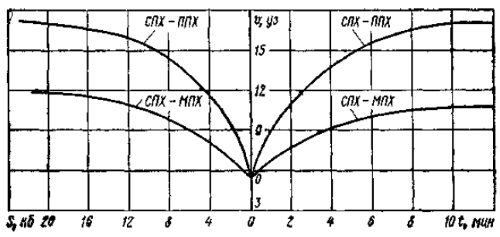
Дифференциальное уравнение, описывающее движение судна при уменьшении оборотов движителей до среднего, малого или самого малого хода, будет иметь вид, аналогичный уравнению (Формула 2). Его решение будет отличаться только знаками и значением постоянных интегрирования. На основании уравнения (Формула 2) имеем
где:
- T1 = P (n) — упор винта после снижения оборотов двигателя.
Обозначим
Делая подстановки и разделяя переменные, получим
где:
- С0 — постоянная интегрирования.
При t = 0 и v = v0
Тогда
Из уравнения (Формула 12) определим закон изменения скорости
где:
- C1 = vУCT — установившаяся скорость после уменьшения оборотов двигателя.
Делая подстановку dS/dt = v и интегрируя уравнения (Формула 13), получим
Введем новую x = e2C/ta. Получим 2C1t/a1 = ln x, переменную:
где:
Тогда
Обозначим
После подстановки новой переменной в уравнение (Формула 14) получим
Интеграл формулы 15 приводится к виду:
Делая подстановку полученных значений интеграла в формулу 15, переходя к прежней переменной и определив постоянную интегрирования С0, получим
По формулам 13 и 16 можно построить графики динамических характеристик судов. В качестве примера такие графики для крупнотоннажных танкеров НМП приведены на рис. 3, рис. 4.
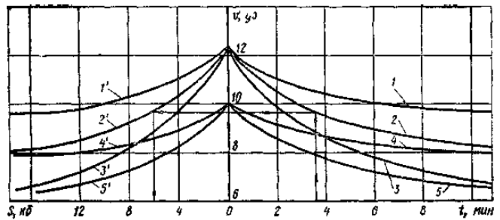
1 — 1′ — с полного манёвренного переднего хода до среднего хода, 2 — 2′ — с полного маневренного переднего хода до чалого переднего хода 3 — 3′ — с полного маневренного переднего хода до самою малого переднего хода, 4 — 4′ — со среднего переднего хода до малого переднего хода, 5 — 5′ — со среднего переднего хода до самого малого переднего хода
Ключ к использованию графиков показан на рисунках.
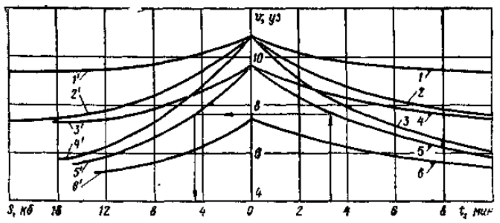
1 — 1′ — с полного маневренного переднего хода до среднего переднего хода, 2 — 2′ — с полного маневренного переднего хода до малого переднего хода, 3 — 3′ — с полного маневренного переднего хода до самого малого переднего хода, 4 — 4′ — со среднего переднего хода до малого переднего хода, 5 — 5′ — со среднего переднего хода до самого малого переднего хода, 6 — 6′ — с малого переднего хода до самого малого переднего хода
Для проверки точности расчетов динамических характеристик судов по приведенной выше методике были проведены натурные испытания различных типов крупнотоннажных судов внутреннего плавания и крупнотоннажных танкеров НМП типа «Крым», «Борис Бутома», «Маршал Жуков».
При натурных испытаниях, проводившихся на Черном море в районе порта Геленджик в октябре 1979 г., после подачи команды об изменении режима работы двигателей через каждые 20 с наблюдателем определялись полярные координаты судна по отношению к неподвижному точечному ориентиру (бую) с помощью судовой радиолокационной станции «Океан».
Предлагается к прочтению: Уравнения движения судна
Затем по полученным координатам судна определялся график изменения пути и скорости судна по времени. В дополнение к РЛС координаты судна определялись с помощью высокоточной фазовой радиогеодезической системы.
На рис. 5 приведены результаты натурных и расчетных величин при маневрах танкера «Маршал Жуков» водоизмещением 127,2 тыс. т при изменении режима работы двигателя с полного маневренного переднего хода на средний передний ход.
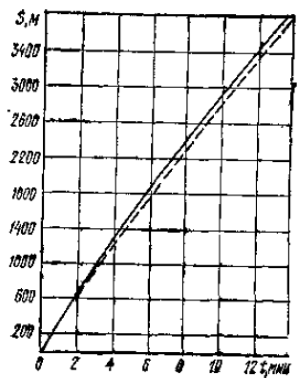
Высокая сходимость натурных и расчетных данных позволяет сделать заключение о приемлемости изложенной методики для инженерных практических расчетов.
Приведенные графики динамических характеристик судов с 1977 г. были внедрены на крупнотоннажных пассажирских и грузовых судах внутреннего плавания и с 1980 г. — на всех крупнотоннажных танкерах типа «Крым», «Борис Бутома», «Маршал Жуков» и «София» Новороссийского морского пароходства.

