Движение судна и расчеты по законам действующих сил

Векторные и кинематические уравнения в инерциальной системе отсчета. Для составления уравнений движения судна, необходимых для изучения маневренности судна, прежде всего нужно выбрать систему отсчета: инерциальную (неподвижную) или неинерциальную (подвижную).

Если рассматривать движение судна в инерциальной системе отсчета, то уравнение движения в общем случае определяется на основании второго закона динамики двумя векторными уравнениями:

m_{1} \frac{d v}{d t} = F; Ф о р м . 1

J_{1} = \frac{d ω_{c}}{d t} M_{c} Ф о р м . 2

Первое уравнение (формула 1) представляет собой равенство главного вектора (результирующей силыОпределение результирующих сил инерции многоцилиндрового двигателя) внешних сил F произведению массы судна с учетом присоединенной массы воды m₁ на линейное ускорение судна dv_c/dt. Это уравнение характеризует поступательное движение центра инерции или центра тяжести судна.

Второе уравнение (формула 2) представляет собой равенство вектора главного момента внешних сил относительно вертикальной оси вращения судна М_с произведению момента инерции судна с учетом присоединенного момента инерции масс воды относительно той же оси J₁ на угловое ускорение dω/dt. Это уравнение характеризует вращательное движение судна.

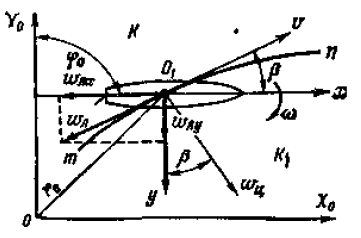
Положение судна на плоскости в инерциальной системе отсчета К с осями Х₀ ОУ₀ в любой момент времени можно определить, задав радиус-вектор r₀ произвольной точки судна O₁ и угол курса φ₀ (рис. 1). Тогда кинематические уравнения движения в инерциальной системе отсчета в полярных координатах будут иметь вид:

r_{o} = r_{o} (t); Ф о р м . 3

φ_{0} = φ_{0} (t); Ф о р м . 4

В теории маневренности большое распространение получила неинерциальная система отсчета K₁ с началом в центре тяжести судна и правой системой координат, при которой положительное направление оси O_1x — это направление в сторону носа судна, оси O_1y — в сторону правого борта, оси r — вниз. Ось O_1x совпадает с диаметральной плоскостью судна.

Систем отчета — Рис. 1 Инерциальная (К) и неинерциальная (К1) системы отчета

Для того чтобы решить задачу о движении судна, необходимо знать законы действующих на судно сил и их моментов, которые можно подразделить на два вида:

силы и моменты инерционной природы (внутренние силы), возникающие в результате действующих на судно ускорений,
и силы и моменты гидроаэродинамической природы (внешние силы).

При составлении уравнений будем считать, что движение судна происходит в горизонтальной плоскости с изменяющейся линейной скоростью v и угловой скоростью ω.

Силы и моменты инерционной природы. В неинерциальной, жестко связанной с судном, системе отсчета К₁ при движении по криволинейной траектории m—n на судно будут действовать два ускорения: линейное ω_л = dv/dt и центростремительное ω_ц = ωv. В общем случае при движении по криволинейной траектории скорость судна уменьшается, поэтому вектор ускорения ω_л будет направлен в противоположную сторону вектору скорости v и отклонен от отрицательного направления оси O_1x на величину угла дрейфа β. Вектор центростремительного ускорения ω_ц всегда направлен в сторону поворота и отклонен от оси О₁γ на угол β.

Как видно из рис. 1, проекция векторов ω_л и ω_ц на оси координат неинерциальной системы К₁ соответственно равны:

ω_{л х} = - ω_{л} \cos β = - \frac{d v}{d t} - \cos β = - \frac{d v_{x}}{d t}; Ф о р м . 5

ω_{л у} = ω_{л} \sin β = \frac{d v}{d t} \sin β = \frac{d v_{y}}{d t}; Ф о р м . 6

ω_{л х} = ω_{ц} \sin β = ω v \sin β = ω v_{у}; Ф о р м . 7

ω_{ц у} = ω_{ц} \cos β = ω v \cos β = ω v_{x} . Ф о р м . 8

Ускорения ω_л и ω_ц вызовут появление сил инерции F_л и F_ц, которые будут равны произведению соответствующих масс на величину ускорений и направлены в сторону, противоположную ускорениям (рис. 3).

Неинерциальные системы — Рис. 3 Инерциальные силы (F_л и F_ц) и их проекции на оси неинерциальной системы

Обозначим коэффициенты присоединенных масс воды по оси О₁х-λ₁₁, по оси О₁у-λ₂₂, тогда масса судна с учетом присоединенной массы воды вдоль оси O₁х будет равна m(1 + λ₁₁), вдоль оси О₁у – m(1+λ₂₂). После суммирования проекций инерционных сил по оси O₁x и О₁у будем иметь следующие выражения для сил инерционной природы:

F_{х л} - F_{ц х} = m (1 + λ_{11}) \frac{d v_{x}}{d t} \cdot m (1 + λ_{22}) ω v_{y}, Ф о р м . 9

F_{у л} - F_{ц у} = - m (1 + λ_{22}) \frac{d v_{у}}{d t} - m (1 + λ_{11}) ω v_{х} . Ф о р м . 10

Если скорость судна при движении по кривой будет увеличиваться, то знаки сил F_xл и F_yл изменятся на обратные.

При неустановившемся движении по криволинейной траектории угловая скорость поворота ω является переменной величиной, поэтому на судно будет действовать угловое ускорение dω/dt = φ″. При увеличении угловой скорости судна вектор углового ускорения будет направлен вдоль вектора угловой скорости ω, т. е. вниз, в сторону положительного значения оси z (рис. 2).

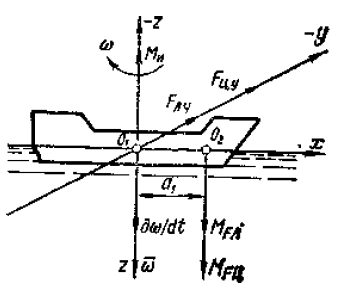
Угловое ускорение вызывает появление инерционного углового момента М_и, который препятствует повороту судна.

Угловой инерционный момент направлен в сторону, противоположную угловому ускорению, и численно равен произведению момента инерции судна (с учетом присоединенного момента инерции от масс воды) на угловое ускорение

М_{и} = - J (1 + λ_{66}) \frac{d ω}{d t}, Ф о р м . 11

где:

λ₆₆ — коэффициент присоединенного момента инерции от масс воды.

Так как фактически ось вращения судна при движении по криволинейной траектории находится не в точке О₁, а в точке О₂, т. е. сдвинута к носу судна на величину а₁, то в создании инерционных моментов будут участвовать проекции инерционных сил F_лy и F_цy. Проекции сил F_лx и F_цx пересекают ось вращения и моментов не создают.

Моменты от сил F_лy и F_цy способствуют повороту судна, поэтому их векторы M_Fл и M_Fu в рассматриваемом случае совпадают по направлению с вектором угловой скорости и и будут направлены вниз. Модули этих моментов будут равны M_Fл = F_лya₁; M_Fu=F_цya₁. Определим суммарный момент:

M_{F л} + М_{F ц} = m (1 - λ_{22}) \frac{d v_{y}}{d t} a 1 + m (1 + λ_{11}) ω v_{x} a_{1} . Ф о р м . 12

Учитывая, что ωа₁ = v_v, произведение (dv_v-/dt) а₁ = ωv_xa₁= v_xv_y, можем записать

M_{F л} + М_{F ц} = m (2 + λ_{22} + λ_{11}) v_{x} v_{y} . . . Ф о р м . 13

Если движение судна по криволинейной траектории происходит с увеличением скорости поступательного движения, то момент изменит знак на обратный, в этом случае будем иметь:

M_{F л} + М_{F ц} = m (1 + λ_{22}) \frac{d u_{y}}{d t} a_{1} + m (1 + λ_{11}) ω v_{x} a_{1}, Ф о р м . 14

или в окончательном виде

M_{F л} + M_{F ц} = m (λ_{11} - λ_{22}) v_{x} v_{y} . Ф о р м . 15

Суммарный инерционный момент при увеличении скорости поворота судна и уменьшении линейной скорости движения будет иметь вид:

M_{и} + M_{F л} + M_{F ц} = - J (1 + λ_{66}) \frac{d ω}{d t} + m (2 + λ_{22} + λ_{11}) v_{x} v_{y} . Ф о р м . 16

Этот момент при увеличении скорости поворота и линейной скорости судна будет равен:

M_{и} + М_{F л} + М_{F ц} = J (1 + λ_{66}) \frac{d ω}{d t} + m (λ_{22} - λ_{11}) u_{x} u_{y} . Ф о р м . 17

Значение именно этого момента приводится в большинстве работ по управляемости судов.

Силы и моменты аэрогидродинамической природы, силы тяжести и водоизмещения. Все внешние силы и моменты, действующие на судно, могут быть разбиты на пять категорий:

аэродинамические силы и моменты, возникающие на надводной части корпуса судна;
гидродинамические силы и моменты на корпусе судна;
силы веса и водоизмещения;
управляющие силы и моменты, создаваемые рулями, движителями и подруливающими устройствами;
возмущающие силы и моменты, обусловленные воздействием течений, волнением, гидродинамическим воздействием корпуса судна с грунтом дна и берегов или корпусом другого судна.

Обычно при определении сил и моментов, действующих на судно, принято опираться на так называемую гипотезу стационарности, согласно которой величины аэро- и гидродинамических сил полностью определяются кинематическими параметрами движения судна в данный момент времени. Силы и моменты, действующие при прямолинейном движении с углами дрейфа, называют позиционными, а силы и моменты, обусловленные вращением судна, – демпфирующими.

Проекции главного вектора и главного момента гидродинамических сил на оси связанной системы координат определяются следующими формулами:

[\begin{matrix} {F_{x}}_{1} \\ {F_{y}}_{1} \\ F_{z_{1}} \end{matrix}] = \frac{1}{2} ρ_{1} S u^{2} [\begin{matrix} {C_{x}}_{1} \\ {C_{y}}_{1} \\ {C_{z}}_{1} \end{matrix}]; Ф о р м . 18

[\begin{matrix} {М_{x}}_{_{1}} \\ {М_{y}}_{_{1}} \\ М_{z_{1}} \end{matrix}] = \frac{1}{2} ρ_{1} S u^{2} L [\begin{matrix} {m_{x}}_{_{1}} \\ {m_{y}}_{_{1}} \\ {m_{z}}_{_{1}} \end{matrix}]; Ф о р м . 19

где:

p₁ — массовая плотность воды, кг/м²;
S, L — площадь, м², и длина, м, корпуса судна;
v — скорость судна, м/с;
C_у1, C_v₁, C_z₁ — характеристики (коэффициенты) продольной, нормальной и поперечной гидродинамических сил соответственно;
m_х1, m_у1, m_г1 —характеристики (коэффициенты) гидродинамических моментов крена, рыскания и дифферента соответственно.

Проекции главного вектора и главного момента аэродинамических сил на те же оси определяются аналогично.

На капитанском мостике должны находиться таблицы и графики, позволяющие вахтенному помощнику капитана достаточно быстро произвести приближенный расчет сил, воздействующих на судно от внешних факторов. В качестве примера (табл. 1) приведен расчет сил давления ветра на нефтерудовоз типа «Маршал Буденный», произведенный по формуле:

F_{в} = 0, 59 С_{в} {u^{2}}_{в} (А_{с} \cos^{2} Θ + B_{c} \sin^{2} Θ), Ф о р м . 20

где:

F_B — сила воздействия ветра, Н;
C_В — коэффициент, учитывающий уменьшение скоростного напора ветра по высоте (по исследованиям автора C_В=0,7 — при стоянке судна у причалов;
C_В— = 0,8 — на свободной поверхности воды);
v_В — скорость ветра, м/с;
Ас — лобовая парусность судна, м²;
В_C — боковая парусность судна, м²;
9 — курсовой угол ветра, °.

Ниже приведена зависимость от скорости сил течения на подводную часть корпуса того же судна при осадке 16,5 м на глубокой воде.

Таблица 1. Воздействие ветра на нефтерудовоз типа “Маршал Буденный”
Скорость ветра, м/с	Воздействие ветра при Θ = 90°, Н		Воздействие ветра при Θ = 45°, Н
Скорость ветра, м/с	Судно в балласте	Судно в грузе	Судно в балласте (поперечная составляющая)	Судно в балласте (продольная составляющая)
10	1,96·10⁵	1,47·10⁵	9,81·10⁴	3,92·10⁴
20	7,65·10⁵	6,78·10⁵	3,43·10⁵	1,18·10⁵
30	1,67·10⁶	1,42·10⁶	7,85·10⁵	1,96·10⁵
40	2,94·10⁶	2,35·10⁶	1,37·10⁶	3,92·10⁵

Расчет произведен по формуле:

F_{1} = K {u^{2}}_{Т} S_{K} \sin Θ Ф о р м . 21

где:

F_T — сила воздействия воды от течения, Н;
К — коэффициент, равный 343,35;
S_k2 — площадь боковой поверхности подводной части корпуса судна, м²;
v — скорость течения, м/с;
Θ — курсовой угол течения, °.

Скорость течения, м/с (уз)	0,25 (0,5)	0,51 (1)	1,03 (2)	1,54 (3)
Воздействие течения при знак – 90 °.	7,8·10⁴	3,14·10⁵	1,29·10⁶	2,88·10⁶

В качестве примера на рис. 4 приведены графики сил сопротивления воды корпусу судна на глубокой воде для крупнотоннажных танкеров при движении без учета угла дрейфа.

Рис. 4 Сила сопротивления корпуса крупнотоннажных танкеров.
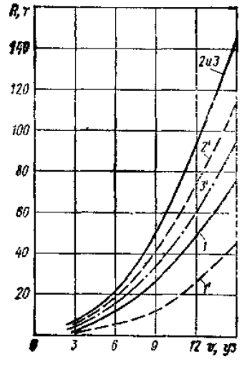
1 – танкер “Лисичанск” в грузу; 1′ – танкер “Лисичанск” в балласте, 2 – нефтерудовоз “Борис Бутома” в грузу; 2′ – нефтерудовоз “Борис Бутома” в балласте, 3 – нефтерудовоз “Маршал Жуков” в грузу; 3′ – нефтерудовоз “Маршал Жуков” в балласте

На рис. 5 для этих же судов приведены силы упора винта при оборотах полного хода в зависимости от скорости движения на переднем и заднем ходу.

Упор винта — Рис. 5 Зависимость силы упора винта крупнотоннажных танкеров от скорости на переднем ходу и при реверсировании.
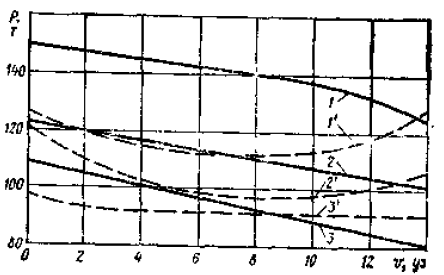
1 – нефтерудовоз “Маршал Жуков” на переднем ходу; 1′ – нефтерудовоз “Маршал Жуков” при реверсировании; 2 – нефтерудовоз “Борис Бутома” на переднем ходу; 2′ – нефтерудовоз “Борис Бутома” при реверсировании; 3 – танкер “Лисичанск” на переднем ходу; 3′ – танкер “Лисичанск” при реверсировании

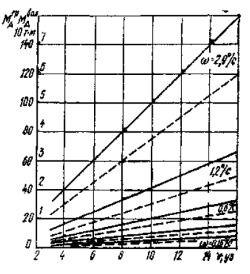
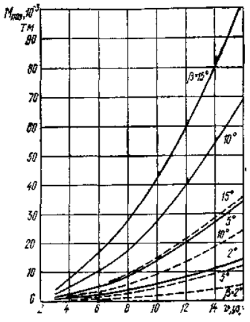
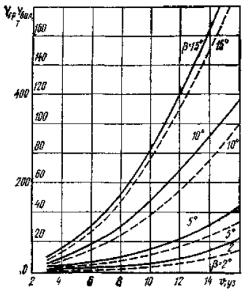
На рис. 6 показаны графики поперечных сил на корпусе для нефтерудовоз а «Борис Бутома», а на рис. 7 и рис. 8 — значение позиционных и демпфирующих моментов, воздействующих на корпус того же теплохода в грузу (М_Д^ГР) и в балласте М_д^бал в зависимости от скорости и угла дрейфа.

Поперечная сила — Рис. 6 Зависимость поперечной силы от скорости для нефтерудовоза “Борис Бутома” при различных значениях угла дрейфа β (сплошная линия – в грузу; штриховая – в балласте)

У крупнотоннажных судов при движении на участках пути (проливах, реках), где имеется течение и уклон поверхности воды, под действием веса возникают значительные силы соскальзывания.

Позиционный момент — Рис. 7 Зависимости позиционного момента от скорости нефтерудовоза “Борис Бутома” при различных углах дрейфа β (сплошная линия – в грузу; штриховая – в балласте)

В практике управления судами типа «Крым» и крупнотоннажными одновинтовыми судами других типов Новороссийского морского пароходства имелись случаи, когда вследствие тех или иных технических причин главный двигатель мог работать только на малых оборотах, обеспечивая скорость движения в спокойной воде 6-8 уз. При движении в проливе Дарданеллы, а иногда в Эгейском море, где скорость встречного течения не превышает 3-5 уз, судно, имеющее ход относительно воды 6-8 уз, останавливалось. И после длительной многочасовой попытки преодолеть участок судно, заняв положение под углом к течению, начинало сноситься в сторону берега. Для предотвращения возникавшей аварийной ситуации машина останавливалась, и на заднем ходу судно выходило из пролива.

Демпфирующий момент — Рис. 8 Зависимость демпфирующего момента от скорости нефтерудовоза “Борис Бутома” при различных значениях угловой скорости v (сплошная линия – в грузу; штриховая – в балласте)

После одной-двух неудачных попыток капитаны обращались в пароходство с просьбой выслать для проводки буксировщик, в ожидании которого крупнотоннажное судно простаивало 2-3 сут.

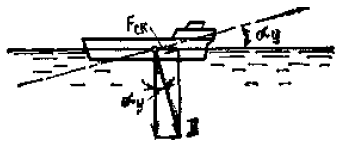
Причиной невозможности преодолеть участки пути со скоростями течения 5 уз, когда крупнотоннажное судно способно развивать скорость 6-8 уз, является действие силы соскальзывания F_ск, которая, как видно из рис. 9, равна:

F_{c k} = D \sin α_{y}, Ф о р м . 22

где:

D — весовое водоизмещение судна, Н;
α_v — угол, характеризующий продольный уклон поверхности воды, °.

Продольный уклон i = sin α_v поверхности воды можно определить, воспользовавшись широко известным в гидротехнике уравнением Шези, имеющим вид:

v_{т . c p} = C \sqrt{i H}, Ф о р м . 23

где:

v_{т. ср} — средняя скорость течения, м/с;
C — коэффициент Шези, Н — глубина.

При ориентировочных расчетах можно принимать С ≈ 22.

Соскальзывание — Рис. 9 Сила соскальзывания

На основании формулы 24 i = v_т²/C²Н, тогда сила соскальзывания, действующая на судно, для практических расчетов может быть определена по формуле:

F_{C K} = \frac{D}{H} (\frac{u_{T}}{C})^{2} . Ф о р м . 24

Если упор двигателя F_д ≤ F_CK + R_T (R_T — сопротивление сил трения на корпусе судна от течения), то проход данного участка пути невозможен. Как показывают расчеты, величина силы соскальзывания, действующей на судно водоизмещением 100 тыс. — 150 тыс. т, может достигать в проливах 15-25 т, что при скорости 7-8 уз приводит к потере скорости 2-3 уз.

Управляющими силами на крупнотоннажных судах являются силы давления на рули и силы упора подруливающих устройств. Рулевая сила P_v в случае расположения руля за гребным винтом может быть определена по формуле:

P_{y} = 52 r_{1} C_{p} S_{p} {v^{3}}_{c p} (x_{p} + β), Ф о р м . 25

где:

r₁ — поправочный коэффициент, учитывающий влияние сопротивления корпуса, r₁≈1,2, С_р — коэффициент, зависящий от относительного удлинения руля λ = h_p/l_p (здесь h_p — высота, l_p — длина руля);
C_p — определяется по графику, (рис. 12, а);
S_P — площадь руля, м²;
v_p — средняя скорость воды, набегающей на руль, м/с;
α_p — угол перекладки руля, °;
β — угол дрейфа, °.

На танкерах типа «Крым» и других крупнотоннажных судах устанавливаются водометные подруливающие устройства (ВПУ). Рабочим органом ВПУ является осевой насос, который всасывает воду, а затем выбрасывает ее через одно из двух сопел, расположенных перпендикулярно бортам.

Перо руля — Рис. 10 К определению силы давления на перо руля:
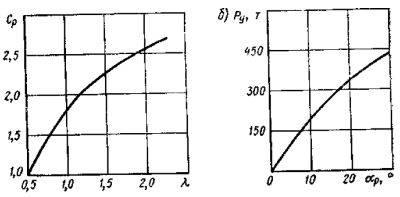
а – судно водоизмещением 180 тыс. т; б – рулевая сила танкера

Сила упора ВПУ на танкере «Крым» составляет 57,8 кН. Величина упора изменяется перекрытием поперечных каналов с помощью затворов. Время изменения направления упора с одного борта на другой не более 30 с. Разработан нормализованный ряд ВПУ, приведенный в табл. 2.

Таблица 2. Нормализованный ряд ВПУ
Типоразмер (индекс) ВПУ	Номинальная мощность привода, Вт	Тяга, кН (не менее)	Диаметр осевого насоса, м	Типоразмер (индекс) ВПУ	Номинальная мощность привода, Вт	Тяга, кН (не менее)	Диаметр осевого насоса, м
1	22·10³	2,94	0,42	5	315·10³	41,7	1,43
2	45·103	6,87	0,7		500·10³	57,8	–
	75·10³	9,6	–	6	500·10³	67,7	–
3	110·10³	1,4	0,87		800·10³	92	1.85
4	200·10³	25,5	1,1	7	800·10³	116	–
					1250·10³	158	2.60

На очень малых ходах обычные рули малоэффективны. Существующие носовые ВПУ эффективны в использовании, когда скорость судна равна нулю или не превышает 3 уз. ВПУ не только способствуют сокращению времени выполнения ряда маневров, но при плавании в узкостях, проливах, реках, каналах могут оказать судоводителю неоценимую помощь при расхождении с другими судами, когда требуется снизить до минимума скорость или остановиться, при постановке на якорь, особенно при ветре и в других случаях.

Предлагается к прочтению: Основы маневренности крупнотоннажных судов

Из сравнения сил упора, создаваемых ВПУ, с силами воздействия ветра можно сделать вывод что для гарантированного управления крупнотоннажными судами при сильных ветрах существующие ВПУ обладают недостаточной силой упора. Возмущающие силы под действием волнения трудно поддаются расчету. Как показывают исследования Д. Н. Ньюмена, сила от воздействия волн может быть выражена следующим соотношением:

F_{y α} = K_{y} D \frac{{h^{2}}_{в}}{{λ^{2}}_{в}}, Ф о р м . 26

где:

K_У — коэффициент, равный 0,05 (зависит от глубины воды);
D — водоизмещение судна;
h_в — высота волны, м;
λ_в — длина волны, м.

Короткие волны, которые почти полностью гасятся судном, передают ему почти всю свою кинетическую энергию, в результате чего возникает значительный напор в направлении распространения волн, в то же время длинные волны возбуждают только колебательные движения, не создавая горизонтального напора.

Вращающий момент, порождаемый волнением F_{м. в}, может быть выражен следующим образом:

F_{м . в} = К_{м} D \frac{{h^{2}}_{в}}{{λ^{2}}_{в}} \sin ψ_{н}, Ф о р м . 27

где:

K_м — коэффициент момента;
ψ_в — угол волновой атаки, °.

При волнении, направленном в корму F_{м. в.} достигает наибольшего значения и судно трудно удерживается на курсе. Крупные суда очень подвержены действию длинных волн в отношении влияния на стабилизацию курса.

Уравнения движения судна в неинерциальной системе отсчета. Для рассматриваемого случая движения точки m_i, расположенной на диаметральной плоскости судна, можно считать сложным движением: движением относительно неинерциальной системы и движением переносным в отношении инерциальной системы отсчета. Тогда в силу общих геометрических свойств сложного движения абсолютное ускорение точки m_i будет равно:

ω_{i а б с} = ω_{i о τ а} + ω_{i п е р} . Ф о р м . 28

На основании второго закона Ньютона можно записать m_iω_{i абс} = F_i, или

m_{i} (ω_{i о τ 1} + ω_{i п е р}) F_{i} . Ф о р м . 29

Второе соотношение можно переписать так:

m_{i} ω_{i о τ} = F_{i} - m_{i} ω_{i п е р} . Ф о р м . 30

Формулу 30 можно трактовать как запись закона Ньютона применительно к неинерциальной системе отсчета. Второй член в правой части формулы 30 имеет размерность силы. На основании этой формулы, распространяя массу точки m_i на всю массу судна, с учетом соответствующих присоединенных масс воды можем записать уравнения движения судна в неинерциальной системе отсчета:

\begin{matrix} m (1 + λ_{11}) \frac{d v_{x}}{d t} - m (1 + λ_{22}) ω v_{y} = Σ F_{x}; \\ m (1 + λ_{22}) \frac{d v_{y}}{d t} + m (1 + λ_{11}) ω v_{x} = Σ F_{y}; \\ J (1 + λ_{66}) \frac{d ω}{d t} + m (λ_{22} - λ_{11}) v_{x} v_{y} = Σ M_{z} . \end{matrix}} Ф о р м . 31

В левой части уравнений стоят инерционные члены, в правой — силы и моменты неинерционной природы. Интегрируя систему (формула 31), можно найти три функции v (t), β(t), ω (t). В свою очередь эти функции позволяют определить изменения угла курса φ(t) и угла скорости ψ(t). Далее по значениям v (t), ψ(t) и β(t) можно определить координаты центра тяжести судна x (t) и у (t) и на их основе построить траекторию движения судна в горизонтальной плоскости.

Автор статьи

Владимир Филатов

Старший помощник капитана

Список литературы

Войткунский Я. И., Першиц Р. Я., Титов И. А. Справочник по теории корабля. Л.: Судостроение, 1973. 511 с.
Гапоненко В. И. Устройство и эксплуатация нефтегаваней. М.: Транспорт, 1978. 85 с.
Демин С. И. Вопросы управления морскими судами. М.: Рекламинформбюро ММФ СССР, 1977. 73 с.
Дремлюг В. В. Эффективность плавания судов при не однородных гидрометеорологических условиях. М.: Рекламинформбюро ММФ СССР, 1977. 28 с.
Ковалев А. Г. Коллектив и социально-психологические проблемы руководства. 2-е изд., доп. М.: Политиздат, 1978. 279 с.
Кокрофт А. Н., Ламейер Д. Н. Толкование МППСС-72. М. – Транспорт, 1981. 280 с.
Корнараки В. А. Справочник лоцмана. М.: Транспорт, 1975. 168 с.
Крука Д. М. Научные основы управления социалистическим производством. М.: Экономика, 1978. 280 с.
Лесков М. М., Баранов Ю. К., Гаврюк М. И. Навигация. М.: Транспорт, 1980. 335 с.
Лесков М. М. и др. Использование систем дистанционной отдачи якорей как одного из средств повышения безопасности мореплавания. М.: ЦБНТИ ММФ, сер. «Безопасность мореплавания», вып. № 8 (138), 1981. 15 с.
Матевосян В. Г. Методы конкретных ситуаций. М.: ЦРИА «Морфлот», 1980. 28 с.
Матевосян В. Г., Ольшамовский С. Б., Шишкин Е. А. Оптимальное торможение супертанкеров. М.: ЦРИА «Морфлот», 1981. 29 с.
Мастушкин Ю. М. Управляемость промысловых судов. М.: Пищевая промышленность, 1981. 232 с.
Наставление по организации штурманской службы на судах ММФ. М.: ЦРИА «Морфлот», 1982. 100 с.
Новиков Б. Я. Штурманский метод предвычисления скорости и направления смещения тайфуна на сутки вперед. ЦБНТИ ММФ, сер. «Морской транспорт»., сер. «Судовождение и связь», вып. 5 (150), М., 1982. 32 с.
Общие положения об установлении путей движения судов. ГУНиО МО, 1979. 23 с.
Океанские пути мира. ГУНиО МО, 1980. 203 с.
Ольшамовский С. Б., Земляновский Д. К., Шепетов И. А. Организация безопасности плавания судов. М.: Транспорт, 1979. 196 с.
Ольшамовскйй С. Б. Судовождение и правила плавания на внутренних судоходных путях. М.: Транспорт, 1976. 216 с.
Ольшамовский С. Б., Миронов А. В. Маневренность крупнотоннажных судов. – Морской флот, № 3, 1980, с. 21-22.
Ольшамовский С. Б., Перекрестов А. Н. Исследование расхождений крупнотоннажных судов в море. ЦБНТИ ММФ, сер. «Безопасность мореплавания», вып. № 2 (152), 1983. 10-18 с.
Логосов С. Г. Безопасность плавания в портовых водах. М.: Транспорт, 1977. 135 с.
Погосов С. Г. Швартовка крупнотоннажных судов. М.: Транспорт, 1976. 172 с.
Рекомендации по обеспечению безопасности плавания судов в осенне-зимний период и в штормовых условиях. М.: Рекламинформбюро ММФ, 1977. 59 с.
Руководство по оценке точности кораблевождения. ГУМО, 1970. 86 с.
Руководство по использованию навигационных радиолокационных станций в кораблевождении. ГУМО, 1969. 44 с.
Сазонов А. Е., Родионов А. И. Автоматизация судовождения. М : Транспорт, 1977. 106 с.
Сборник руководящих документов по безопасности мореплавания. М.: Рекламбюро ММФ, 1973. 428 с.
Таратынов В. П. Судовождение в стесненных водах. М.: Транспорт, 1980. 127 с.
Удалов В. И., Ольшамовский С. Б. Предупреждение столкновений судов. М.: ЦРИА «Морфлот», 1980. 21 с.
Удалов В. И., Ольшамовский С. В., Ворощук Н. А. Учет гидрометеоусловий при выборе навигационного пути. М.: ЦРИА «Морфлот», 1979. 17 с.
Цурбан А. И. Определение маневренных элементов судна. М.: Транспорт, 1977. 127 с.
Яскевич А. П., Зурабов Ю. Г. Новые МППСС. М.: Транспорт, 1975. 232 с.

Сноски