С появлением и развитием вычислительной техники стали разрабатывать и широко внедрять аналитические методы в практику проектирования формы корпуса судна и плазовых работПлазовые работы. Имеется множество методов аналитического описания линий и поверхностей теоретического чертежа, позволяющих задавать их в виде уравнений, совокупность которых представляет математическую модель формы корпуса. В САПР судов обводы корпуса генерируются на основе заданных проектных характеристик судна, таких, например, как:
- Длина между перпендикулярами;
- Высота борта на мидель-шпангоуте;
- Ширина максимальная;
- Осадка;
- Коэффициенты общей полноты и полноты мидель-шпангоута;
- Абсцисса центра величины;
- Ширина горизонтального киля;
- Радиус скулы;
- Длина цилиндрической вставки и ее границы;
- Длина носовой и кормовой частей корпуса от границ цилиндрической вставки до перпендикуляров;
- Объем и размеры бульба;
- Диаметр гребного винта;
- Характеристики кормового подзора;
- Формообразующие линии палуб и штевней и т. п.
В некоторых САПР количество подобных проектных характеристик судна превышает 80.
Чаще всего уравнения ватерлиний и шпангоутов задают в виде полиномов (сплайнов) кубических или более высоких степеней. Могут применять также уравнения полушироты вида:
у(х) = а + вх + с × еm+nх × (к + Ɩх)
Где:
- е — основание натуральных логарифмов;
- Коэффициенты а, в, с, k, Ɩ, m и n являются функциями от осадки судна.
Математическая модель формы корпуса может быть представлена и в виде совокупности уравнений, аппроксимирующих теоретические линии, заданные таблицей ординат теоретического чертежа. Координаты точек линий теоретического чертежа и формообразующих линий корпуса (штевней и главной палубы) образуют цифровую модель формы корпуса — основу для создания аппроксимирующей математической модели.
Названные способы задания формы корпуса приняты в современных САПР. Однако ни одна из существующих систем автоматического генерирования обводов корпуса не дает их окончательно согласованными и сглаженными в особенности в оконечностях судна. Согласование и сглаживание теоретических линий корпуса выполняется в этих системах в диалоговом режиме на ПК.
Кроме того, после согласования и сглаживания линий изготавливают деревянную модель корпуса, которую буксируют в опытовом бассейне для определения сопротивления воды при различных скоростях движения судна. По результатам буксировочных испытаний форму обводов в отдельных районах корпуса корректируют.
Для замены трудоемких графических операций согласования и сглаживания обводов корпуса разработаны и внедрены в практику судостроения графоаналитические методы, позволяющие использовать вычислительную технику.
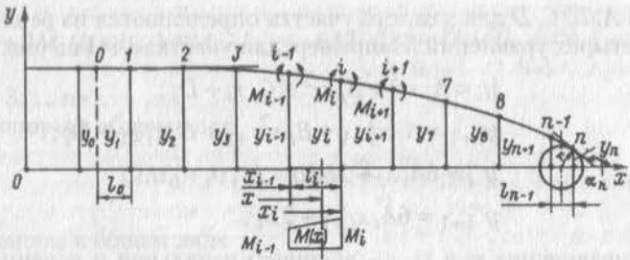
Для совместного сглаживания кривых, лежащих во взаимно перпендикулярных плоскостях, например, ватерлиний и шпангоутов, можно пользоваться достаточно простым методом разностей таблично заданных функций. Для ватерлинии (или шпангоута) с равностоящими полуширотами yi конечные разности (рис. 1) первого и второго порядков:
∆ уi = yi+1 – yi, ∆2уi = ∆ i+1 – ∆ i
Если полушироты не равноотстоящие, то применяют разделенные разности первого и второго порядков
Свойства разностей аналогичны свойствам производных аналитических непрерывных функций, поэтому, вычисляя и анализируя величины и знаки разностей, можно судить о гладкости кривой. Критерии гладкости состоят в том, что первые и вторые разности должны возрастать или убывать монотонно, а вторые разности не должны менять знак.
Немонотонное изменение величин вторых разностей свидетельствует о скрытой негладкости, т. е. о немонотонном изменении кривизны кривой на разных участках, а перемена знака вторых разностей – о наличии точек перегиба, в которых вторые разности обращаются в нуль.
Процесс сглаживания на основе метода разностей состоит в вычислении первых и вторых разностей, их анализе и при необходимости во внесении поправок в значения полуширот с повторяющимся пересчетом первых и вторых разностей до достижения критериев гладкости. При этом сглаживание ватерлиний и шпангоутов выполняется совместно.
Новые полушироты не должны отличаться от исходных более, чем на величину поправки εi предел изменения которой составляет от +20 до ±30 мм для того, чтобы не допустить резкого изменения формы корпуса, отраженной в теоретическом чертеже. На основе этого чертежа при проектировании судна выполняют кораблестроительные расчеты, изменения результатов которых также не должны превышать допускаемых величин. Процесс сглаживания батоксов выполняется аналогично.
В современных системах генерирования обводов корпуса сглаживание выполняется в диалоговом режиме. ПК вычисляет и вычерчивает на дисплее кривую вторых разностей, по гладкости которой оператор судит о гладкости ватерлинии. Сглаживая в необходимых случаях кривую вторых разностей, оператор пересчитывает полушироты ватерлинии и выводит ее на дисплей.
Диалог продолжается до тех пор, пока ватерлинии (шпангоуты) не стали, по мнению оператора, достаточно гладкими. Внося поправки в полушироты, следует оценивать их влияние и на гладкость шпангоутов и батоксов, которую нужно проверять тем же способом, что и гладкость ватерлиний.
Математическая модель формы корпуса, обводы которого сглажены методом разностей, может быть представлена совокупностью уравнений типа аппроксимирующих ватерлинии и шпангоуты по участкам.
у – Ах3 + Вх2 + Cx + D
Коэффициенты А, В, С, D для каждого участка определяются из решения системы четырех уравнений. Например, для участка i, i+1 на рис. 1.
- yi = Ai xi3 = Bi xi2 + Ci xi + Di ;
- yi = Ai x3i+1 = Bi x2i+1 + Ci xi+1 + Di ;
- y”i = 6Ai xi + 2Bi ;
- y’i+1 = 6Ai xi+1 + 2Bi .
В этих уравнениях xi и xi+1 — абсциссы начальной и конечной точек участка, а yi и yi+1 полушироты этих точек. Вторые производные y’i и y’i+1 определяют из решения системы уравнений (1), известной из теории разностей. Например, для сглаженной ватерлинии, показанной на рис. 1.
y’0 + 4y’1 + y’2 = 6 δy’12 ;
y’1 + 4y’2 + y’3 = 6 δy’22 ;
y’n-2 + 4y’n-1 + y’n = 6 δy2n-1 .
В системе (1) количество неизвестных на два больше количества уравнений, поэтому для ее решения устанавливают граничные условия. Кривизна в точке 0 выхода ватерлинии на цилиндрическую вставку равна нулю, а в точке n равна 1/r, где r — радиус сечения форштевня в точке n. Следовательно, y’0 =0, а y’n = 1/r и количество неизвестных вторых производных становится равным количеству уравнений.
Второй подход к решению задач аппроксимации и сглаживания кривых теоретического чертежа основан на математическом моделировании изогнутой рейки. Для вычерчивания обводов корпуса на теоретическом чертеже или на плазе используют длинные тонкие гибкие деревянные или пластмассовые рейки. Их изгибают и прижимают грузами в точках, по которым прочерчивают кривые. Изогнутая рейка аналогична многоопорной неразрезной балке со смещенными относительно друг друга опорами (рис. 1).
Участки линии изогнутой рейки между точками-опорами описываются, как показано дальше, уравнениями кубических парабол, поэтому их использование для аппроксимации точечно заданных линий называют методом кубических сплайнов (от англ, spline — рейка). Методом сплайнов можно воспользоваться и для сглаживания теоретических линий корпуса, заданных таблицей ординат и теоретическим чертежом.
В точках прижима рейки к плоскости стола действуют изгибающие моменты Mi силы трения и реакции опор R. Известно, что для незагруженной внешней нагрузкой балки постоянного сечения жесткостью EI со смещенными абсолютно жесткими опорами для i-й опоры уравнения трех моментов имеют вид:
Где:
- i = 2, 3,…, n – 1.
Для 0-ой опоры в общем виде:
Для n-й опоры в общем виде:
Если изогнутый участок ватерлинии в точке 0 плавно сопрягается с участком цилиндрической вставки, т. е. с участком, параллельным оси х, то у‘0 = 0. В точке n производная:
у‘0= tgan
Где:
- an – угол между касательной к ватерлинии в точке n и осью х.
Названные граничные условия соответствуют жесткой заделке рейки на крайних опорах. На каждом участке изгиба рейки прогибы ее малы по сравнению с длиной участка. Тогда, как известно, кривизна
1/R(x) ≈ y'(x)
Где:
- R(x) — радиус кривизны.
Изгибающие моменты М(х) = EJ у'(х). Если оперировать рейкой, для которой принято EJ = 1, то у’ (х) = М(х), т. е. вторая производная от упругой линии рейки в каждой ее точке равна изгибающему моменту или кривизне линии в этих точках. При отсутствии в пролетах балки внешней нагрузки изгибающие моменты вдоль пролетов изменяются линейно. Силами трения между рейкой и столом в пределах между опорными точками пренебрегаем, после чего для сечения х на участке i – 1, г (см. рис. 1) можно записать:
Дважды интегрируя (3) с учетом граничных условий у(xi–1) = уi–1; у(xi) = уi, получаем уравнение изгиба рейки на участке i-1, i, т. е. кубический сплайн:
Таких уравнений будет столько, сколько участков. Входящие в них опорные моменты определяют решением системы уравнений трех моментов с учетом граничных условий на крайних опорах. Однако, прежде чем получить окончательные уравнения (4), необходимо проверить и обеспечить гладкость линий, для чего должны быть соблюдены критерии гладкости, которые аналогичны критериям для разностей таблично заданных кривых.
Если имеются S-образные ватерлинии и шпангоуты, то они должны разделяться заданной точкой перегиба и их выпуклая и вогнутая части должны рассматриваться отдельно. Под монотонным возрастанием у‘(х) понимают, например для ватерлинии на рис. 1, соблюдение условия на основе чего можно считать, что и величины у‘(х) изменяются монотонно.
у‘n > у‘n-1 > у‘n-2 > … > у‘i+1 > у‘i > у‘i-1 > … > у‘1 > у‘2 > у‘1 (5)
Сглаживание ватерлинии состоит в следующем. По начальным значениям полуширот yi взятым из таблицы ординат, и заданным граничным условиям y0 = 0 и y’n = tgan решают системы уравнений (2) — (4) и в первом приближении определяют все Мi = y’i. Затем y’i – анализируют по их знакам и выполнению условия (5).
Если некоторые y’ имеют знаки, обратные остальным y’, и не выполняется условие (5), вносят поправки в величины y’, т. е. их приводят к условию (5) и одинаковым знакам, что равносильно сглаживанию эпюры моментов Мi, ограниченной осью х и возрастающей ломаной линией, состоящей из прямых отрезков между опорными точками кривой.
Принимая сглаженные значения y’i – и оставшиеся неизменными значения остальных y’i, вычисляют новые величины полуширот yi, путем решения относительно них системы уравнений (2) — (2, б). При этом y0 и y’n принимают равными исходным значениям. Входящие в систему (2) — (2, б) моменты Мi, в этом случае известны. Неизвестными являются полушироты yi. Новые значения yi сравнивают с исходными. Их разность не должна превышать отмеченной ранее поправки ±εi.
Сглаживание шпангоутов и батоксов выполняют аналогично. При этом оценивают взаимное влияние вносимых поправок на гладкость всех кривых. Сглаживание кривых по рейке, как и при использовании разностей, выполняется в диалоговом режиме между оператором и ПК.
Участок ватерлинии, идентичный картинке на экране дисплея ПК, показан на рис. 2. Участок состоит из 4 частей, разделенных на 10 интервалов каждая. В точках разбиения восстановлены перпендикуляры, равные величинам у'(х), отображающим кривизну ватерлинии. Для вывода на экран задаются их масштабом. Из рис. 2, а видно, что величины у'(х) на 3-м участке убывают, а затем вновь возрастают. В точке (i) у'(х) = 0, а затем величины у'(х) становятся отрицательными.
Следовательно, на 3-м участке кривая имеет скрытую негладкость, а в точке i — точку перегиба. Оператор, меняя кривизну ватерлинии, добивается ее гладкости, т. е. монотонного возрастания перпендикуляров по всей ватерлинии (рис. 2, б), что легко наблюдается визуально. После сглаживания ватерлинии определяют окончательные значения Мi, и составляют уравнения (4) для каждого участка ватерлинии.
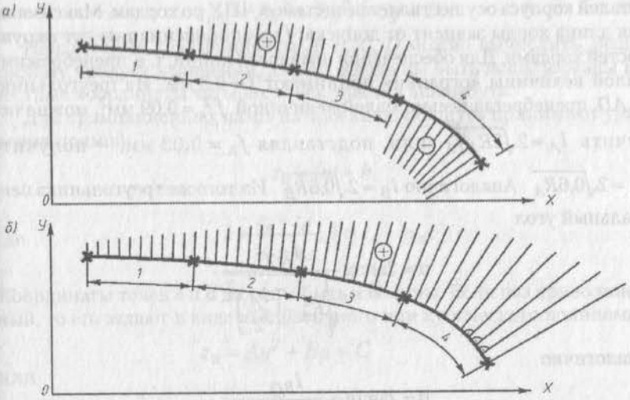
а — не сглаженной;
б — сглаженной
Подставляя в эти уравнения абсциссу конструктивных шпангоутов х, вычисляют их полушироты. Аналогично формируются уравнения шпангоутов и батоксов, которые в совокупности с уравнениями ватерлиний представляют математическую модель корпуса в аппроксимированном виде.
Для вычерчивания теоретического чертежа чертежной машиной кубические сплайны аппроксимируют дугами окружностей, как показано на рис. 3. Для этого на каждом участке через точки А и В проводят дуги двух окружностей, сопрягающиеся в точке К. Координаты (xА, yА), (xВ, yВ) и угловые коэффициенты касательных у'(xА) и у'(xВ) известны из сплайна.
Задача решается на ПК итерационно с оценкой качества аппроксимации. Качество проверяют путем сравнения заштрихованной площади S с суммарной площадью двух круговых колец шириной δ и радиусами RА и RB, найденными в процессе решения задачи:
S < (αRА + βRB)δ
Где:
- δ -максимально допустимое отклонение дуг окружностей от сплайна;
- α и β — центральные углы.
Радиусы:
Где:
- y’А(xА) и y’В(xВ) – вторые производные от сплайна в точках А и В.
Движение рабочего органа деталей корпуса осуществляется системой ЧПУ по хордам. Максимальная длина хорды зависит от допуска ƒ на аппроксимацию дуг окружностей хордами. Для обеспечения плавности линий, т. е. пренебрежимо малой величины «огранки» принимают ƒ= 0,3 мм.
Из треугольника O1 AD, пренебрегая весьма малой величиной ƒ2А = 0,09 мм2, можно получить:
Или, подставляя ƒА = 0,03 мм, получить:
Аналогично:
Из того же треугольника центральный угол:
Аналогично:
Получив математическую модель корпуса судна, переходят к решению тех же задач, что и Плазовые работы, подготовка и выполнение масштабированияпосле плазовой разбивки. Выполняют решения на чертежных машинах, используя ПК и математические методы.
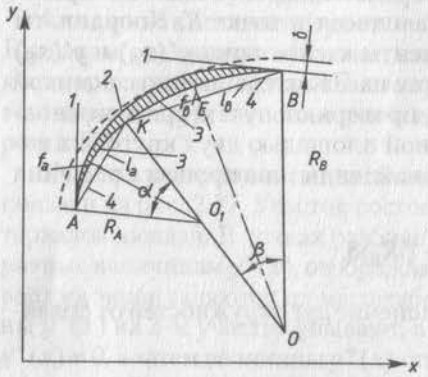
1 – касательная;
2 – кубический сплайн;
3 – дуги окружностей;
4 – хорды
При определении формы и размеров деталей корпуса требуется предварительная трассировка пазов наружной обшивки и теоретических линий продольного набора. Трассировка пазов заключается в расчете координат точек пересечения пазов на проекции «корпус» с линиями шпангоутов и стыков. Пазы на проекции «корпус», как показано на рис. 4, по участкам или по всему корпусу принимают за прямые линии или в виде слабоизогнутых кривых линий.
Поскольку каждый участок шпангоута между ватерлиниями аппроксимирован своим уравнением, их суммарное количество по всем шпангоутам весьма велико, что усложняет задачу трассировки пазов. Для упрощения целесообразно каждый шпангоут разделить на несколько участков и каждый участок аппроксимировать кубическим полиномом вида:
zшп = Ay3 + By2 + Ay + D
Неизвестные коэффициенты А, В, С, D можно вычислить, решив ему четырех уравнений, для чего должны быть использованы изтные координаты четырех точек участка шпангоута.
Для прямолинейных пазов на проекции «корпус» принимают уравнения прямой:
zп = ky + b
Где:
Координаты точек e и d должны быть известны. Если паз криволинейный, то его задают в виде квадратичного или кубического полинома:
zп = Ay2 + By + C
Или:
zп = Ay3 + By2 + Су + D
Входящие в полиномы неизвестные коэффициенты A, B, C и D можно вычислить, решив системы трех или четырех уравнений при известных координатах трех или четырех точек проекции паза, например, Точек a, b, с, i.
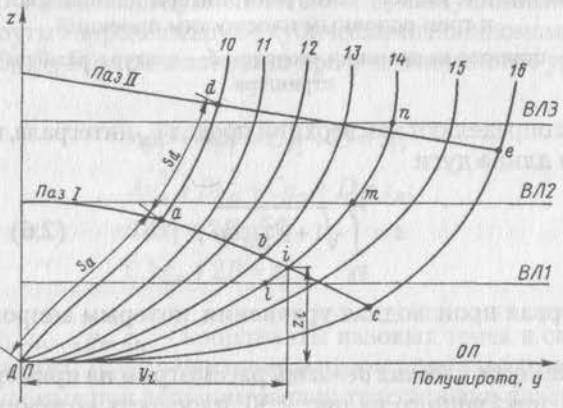
Решая систему уравнений zп = zшп для каждого шпангоута, можно определить координаты уп точек пересечения паза со шпангоутами, а подставив эти координаты в уравнение паза, определить ординаты zп. Точки пазов могут задаваться и криволинейными координатами, т. е. длинами дуг шпангоутов или стыков, в частности, длинами sa, sd и т. д. в виде цепочки размеров от ДП судна. В этом случае координаты у указанных точек определяют как верхний предел ув интеграла, по которому вычисляется длина дуги:
Где:
- z’шп — первая производная уравнения, которым аппроксимирован шпангоут.
Расчет размеров плоских деталей рассмотрим на примере днищевого стрингера, показанного на рис. 5, плоскость которого перпендикулярна ОП и наклонена к ДП и ПМШ.
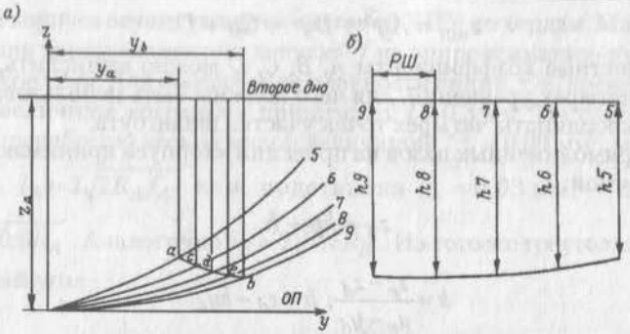
а — стрингер на проекции «корпус»;
б — контур и размеры стрингера
Все шпангоуты аппроксимированы уравнениями так же, как и теоретическая линия стрингера — линия пересечения его плоскости с внутренней поверхностью наружной обшивки. Совместное решение уравнений позволяет определить координаты у и z точек а, с, d, е, b. Вычтя координаты z этих точек из высоты второго дна zд, можно найти величину отрезков hi = zд–z. Растянутая шпация:
Где:
Зная hi и РШ, можно построить контур стрингера и проставить его размеры. Здесь уа и уb — полушироты точек а и b.
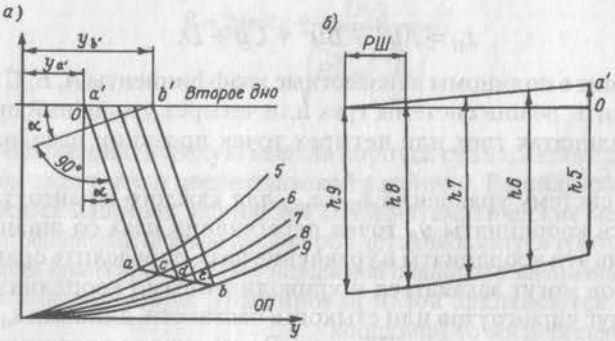
а — стрингер на проекции «корпус»;
б — контур и размеры стрингера
Рассмотрим случай, когда деталь, показанная на рис. 6, наклонена ко всем трем основным плоскостям корпуса судна. Координаты точек а, с, d, е, b находят как и в предыдущем случае. Линии пересечения стрингера плоскостями шпангоутов параллельны друг другу. Необходимо вычислить sinα по формуле:
Тогда:
По этим данным, как видно из рис. 6, б можно однозначно задать контур и размеры стрингера.
Ранее был рассмотрен графический способ развертывания деталей двоякой кривизны методом геодезических линий. Такие детали аналитически можно разворачивать методом наименьших площадей. Применяя метод наименьших площадей, как показано на рис. 7, поверхность детали аппроксимируют многогранной поверхностью. Ребрами поверхности являются отрезки, соединяющие точки разбиения шпангоутов, а гранями — треугольники. Фактически применяют метод триангуляции поверхности.
Все шпангоуты аппроксимируют кубическими полиномами с коэффициентами Ai, Bi, Сi, Di, определяемыми при решении систем уравнений:
Ay31 + By21 + Су1 + D = z1 ;
Ay3n + By2n + Суn + D = zn ;
6Ax1 + 2B = z’1 ;
6Axn + 2B = z’n .
Где:
- у1, z1, …, уi, zi,…. yn, zn — координаты пазовых точек в системе осей корпуса судна 0zyx;
- z1, zn — величины вторых производных в пазовых точках, получаемые при решении задачи трассировки пазов.
Длину Ɩi каждого шпангоута между верхним и нижним пазами вычисляют по формуле (6). Ею же пользуются для вычисления длины средних линий шпангоутных полос, равных полусумме длин образующих их дуг шпангоутов.
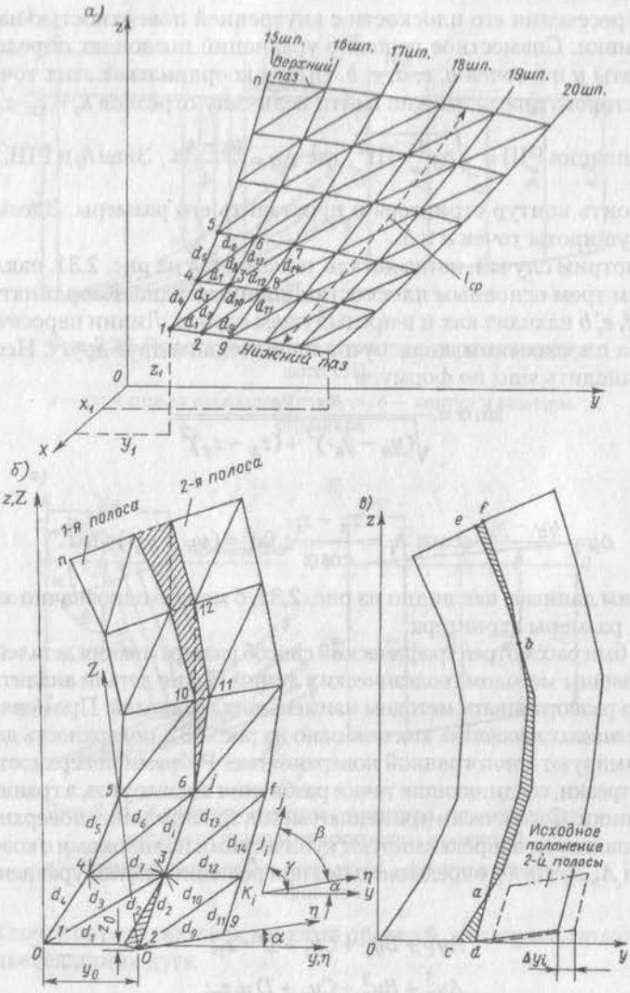
а — развертываемая деталь (в аксонометрии);
б — обкатывание первой полосы второй;
в — сдвиг второй полосы влево
Из всех полос выбирается полоса с максимальной длиной средней линии и разделяется на N частей, состоящих из двух треугольников каждая. Обычно принимается N = 10 (на рис. 7 для упрощения взято N = 5). Для определения координат у точек разбиения шпангоутов указанной полосы, равных верхнему пределу интеграла (6), при длинах дуг si = Ɩi / 10; 2Ɩi / 10; …; 9Ɩi / 10 используют также формулу (6).
Зная у, можно вычислить координаты z тех же точек. Координаты х точек разбиения каждого шпангоута определены в системе осей координат 0zyx с началом в плоскости z0y, как расстояния, кратные шпации. Имея значения координат вершин треугольников, вычисляют их площади. Например, площадь треугольника ifk (рис. 7, б)
Тогда первое значение суммарной площади полосы:
Затем полосу разбивают на N + 1 частей и аналогичным образом вычисляются координаты точек разбиения, площади треугольников и второе значение суммарной площади полосы — S2. Если S2 – S1 меньше принятой из практики величины точности аппроксимации поверхности детали δ, то количество участков разделения всех полос окончательно считается равным N. В противном случае процесс разбиения на большее количество участков продолжается до удовлетворения принятой величины точности аппроксимации.
Величина точности считается достаточной при выполнении условия δ ≤ (0,0001 – 0,001). После окончания итерационного процесса и определения количества участков разделения полос вычисляют длины ребер треугольников. Например, ребра d1, d2, d3 треугольника 1, 2, 3 (рис. 7, а):
Процесс собственно развертывания многогранной поверхности начинают с развертывания на плоскость отдельных ее полос. Выполнение развертки каждой полосы заключается в последовательной стыковке смежных треугольников, составляющих полосу в плоской системе осей координат y0z (рис. 7, б). Для этого вычисляют координаты вершин треугольников в собственной, связанной с первым треугольником, плоской системе координат η0С, которая выбирается так, чтобы начало ее координат совпадало с вершиной 1, а ось η0 совпадала со стороной 1 – 2 первого треугольника.
Таким образом, собственная система осей координат η0С первой полосы совпадаете общей системой координат y0z. Из принятого способа выбора собственной системы координат первой полосы следует, что координаты точек 1 и 2 С1 = Z1 = С2 = Z2 = 0, а координата точки 2 η2 = y2 = d1. Координаты точки 3 вычисляются из очевидной системы уравнений:
y23 + z23 = d23 и (y3 – y2)2 + z23 = d23
Далее производят стыковку второго треугольника с первым, т. е. вычисляют координаты вершины 4 в системе координат y0z, третьего треугольника со вторым и т. д. Координаты точки 4 вычисляют из системы уравнений:
y24 + z24 = d24 и (y3 – y4)2 + (z4 – z3)2 = d27
В общем виде координаты точки j вычисляют из системы уравнений:
(yj – yi)2 + (zj – zi)2 = d2i и (yj – y4)2 + (zj – z4)2 = d27
И т. д. до вычисления координат всех вершин треугольников первой полосы в общей системе координат y0z.
Аналогично вычисляют координаты вершин треугольников каждой из полос в ее собственной системе координат. В результате полного перебора всех составляющих треугольников первой полосы получают ее развертку на плоскости y0z. Затем первая полоса «обкатывается» второй полосой (рис. 7, б) и вычисляют заштрихованные площади «расстыковки». Окончательным из всех возможных будет то положение второй полосы, при котором площадь «расстыковки» окажется наименьшей.
Площади «расстыковки» также разделяют на треугольники, после чего вычисляют сумму их площадей. Для определения площадей координаты вершин треугольников второй «перекатываемой» полосы пересчитывают для каждого ее положения из собственной системы координат η0С с началом отсчета в точке 2 в общую систему координат y0z «обкатываемой» полосы по формулам преобразования координат. Например, для точки i:
yi = y0 + ηi cosα – Сi sinα ;
zi = z0 + ηi sinα – Сi cosα .
Откуда:
y0 = yi + ηi cosα + Сi sinα ; (7)
z0 = zi + ηi sinα – Сi cosα . (8)
В выражениях (7) и (8) y0, z0 и угол α неизвестны. Для их определения вычисляют тригонометрические функции угла α = γ – β, где, как следует из схемы наклона осей на рис. 7, б, γ и β — углы наклона ребра i-j к осям 0η и 0y. Тогда:
sinα = cosα(γ – β) = sinγ cosβ – sinβ cosγ (9)
cosα = sinα(γ – β) = sinγ cosβ – sinγ cosβ (10)
Подставляя (11 и 12) в (9 и 10), получаем:
Где:
- y = yj – yi ;
- z = zj – zi ;
- η = ηj – ηi ;
- C = Cj – Ci .
Значения у0 и z0 определяют после подстановки (13) в (7) и (8). Далее по формулам преобразования координат вычисляют координаты вершин треугольников второй полосы в общей системе координат y0z для всех положений этой полосы относительно первой. Например, для точки «к» координаты yk и zk получают решением систем уравнений:
(yk – y0)2 + (zk – z0)2 = d210 ;
(yk – yi)2 + (zk – zi)2 = d212 .
Площади заштрихованных треугольников вычисляют по формулам, аналогичным формуле для sifk. Корректировку контура развертки для учета пластических деформаций гибки осуществляют последовательными приближениями. Как следует из рис. 7, в, сдвигая вторую полосу влево на некоторую величину ∆yi, пересчитывают координаты у точек контура второй полосы и определяют площади заштрихованных участков acd, bef и ab, а также отношение суммы площадей acd и bef к площади ab.
По данным практики для парусовидной детали оно должно составлять 1:3. Если это условие не соблюдено, то полоса вновь сдвигается на величину ∆yi — шаг итерации — и приближения повторяют, пока указанное соотношение будет выполнено. После корректировки вычисляют окончательные координаты пазовых вершин треугольников, но которым контур развертки рассчитывается и появляется на дисплее ПК.
Математическую модель раскроя профильного проката создают на основе выполнения двух условий:
Где:
- Zj — целевая функция, представляющая суммарную длину заготовок;
- Ɩj — длина i-й детали;
- Lj — длина j-й заготовки;
- n — количество деталей.
Задачу решают последовательно для каждой заготовки, что позволяет учесть несколько вариантов длины заготовок. Условие Lj ≥ Lj+1 приводит к рациональному построению алгоритмов раскроя и уменьшает вероятность случая, когда для какой-либо детали не находится заготовки соответствующей длины, поскольку весь металл уже использован для раскроя более коротких деталей.
Раскрой листового проката осуществляют перебором вариантов расположения деталей на картах раскроя, т. е. математически моделируют на ПК ручной (графический) раскрой. Перед составлением карт раскроя контуры деталей предварительно упрощают: криволинейные контуры деталей заменяют ломаными линиями, мелкие вырезы исключают, крупные внутренние вырезы заменяют вписанными многоугольниками.
ПК размещает первую крупную деталь в прямоугольнике оконтурованного заказного листа с пересчетом собственных координат детали в систему координат листа. Затем методом последовательных перемещений и поворотов с ней стыкуется вторая деталь до тех пор, пока критерий размещения не окажется удовлетворительным. После этого две детали объединяются в общий контур, к ним присоединяется третья деталь и т. д.
Небольшие группы деталей плотно укладывают в прямоугольники — фрагменты карт раскроя — с последующим размещением полученных фрагментов в пределах заданных заказных листов. Можно составить несколько вариантов планов раскроя.
Сформированные и принятые технологами карты раскроя для визуального наблюдения вычерчиваются графопостроителем. При неудовлетворительном коэффициенте использования металла (менее 0,82—0,86) деловые отходы и свободные области на картах раскроя заполняют вручную или эти карты расформировывают, а детали собирают для размещения в следующей группе совместного раскроя.
Получение геометрических данных о форме лекал постелей для сборки секций зависит от расположения плоскости основания постели.
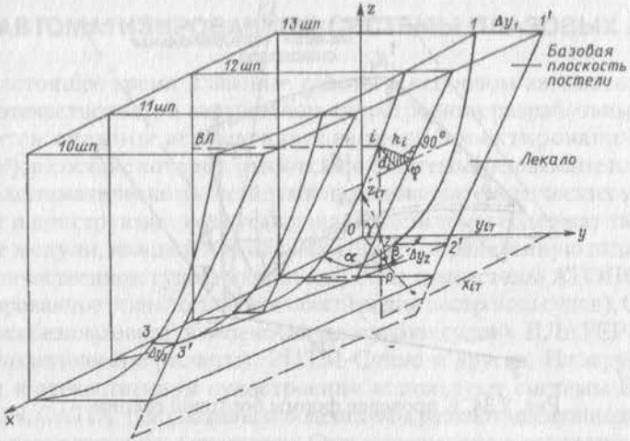
В случаях, когда плоскость основания постели (например, для сборки бортовой или днищевой секции) параллельна диаметральной или основной плоскостям, форму лекал или высоты стоек постели определяют в системе главных координат судна. Когда криволинейные бортовые секции имеют значительную кривизну, плоскость основания постели наклоняют для уменьшения высоты лекал или стоек и удобного, близкого к горизонтальному, расположения секций в постели. Стенд, на котором устанавливают съемные лекала, имеет тогда высоту 0,7—0,8 м. Стоечная постель имеет ту же высоту.
На рис. 8 показана дважды усеченная постель, базовая плоскость которой наклонена к ПМШ ик ДП. Ее лекала лежат в плоскостях шпангоутов под углом φ к базовой плоскости. Положение базовой плоскости задается полуширотами yi трех точек, например, точек 1′, 2′ и 3′, отстоящих от точек 1, 2 и 3 шпангоутов на ∆y1, ∆y2 и ∆y3, выбранных так, чтобы наименьшая высота лекал была более 200 мм. Высоты точек лекал определяют по формуле:
hi = di/ sinφ
Где:
- di — отстояние точки i от базовой плоскости по перпендикуляру к ней.
Отстояние точек наружной обшивки от базовой плоскости:
Где:
- p — длина перпендикуляра, опушенного из начала координат на базовую плоскость;
- xiТ yiТ ziТ — теоретические (плазовые) координаты точки i в системе основных координат судна;
- α, γ, β — углы между осями координат и перпендикуляром р.
Координаты xiТ yiТ ziТ следует принимать для точек конструктивных шпангоутов на пересечениях с ватерлиниями.
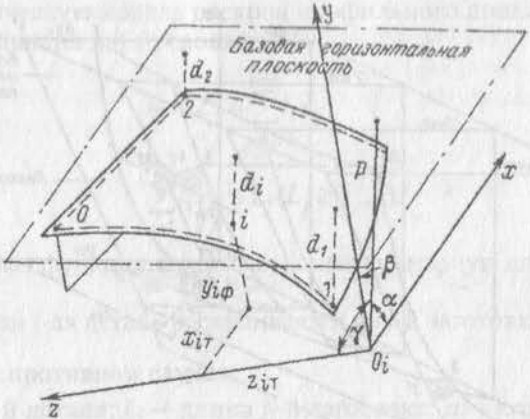
Для определения трех неизвестных косинусов и длины перпендикуляра нужно составить и решить систему, состоящую из четырех уравнений, используя формулу для di, учитывая, что di точек 1′, 2′ и 3′ равны нулю, так как эти точки находятся в базовой плоскости, а их полушироты
у’ = yiТ + ∆yi
Где:
- i = 1,2,3.
В качестве четвертого уравнения используется равенство:
cos2α +cos2β -kos2γ = 1
Угол φ между базовой плоскостью постели и плоскостями шпангоутов равен углу между перпендикулярами к этим плоскостям (перпендикуляром р и осью 0x), т. е. φ = α. Определив косинусы угла и величину р, можно вычислить di и hi для всех точек i лекал постели.
Для проверки формы бортовой секции, занимающей согласно рис. 9 произвольное положение на опорах в цехе, нужно вычислить отклонения ∆yi фактических полуширот точек наружной поверхности обшивки yiф от их теоретических (плазовых) значений yiT по формуле:
Где:
- di — отстояние по вертикали проверяемой i-й точки от базовой горизонтальной плоскости, проходящей через наиболее высокую точку секции в плоскости крайнего шпангоута (величину di замеряют при помощи теодолита или шлангового уровня).
Косинусы углов α, γ и β между базовой горизонтальной плоскостью и основными плоскостями проекций судна, т. е. между перпендикуляром р и основными осями координат, можно определить, решив совместно систему, состоящую из трех уравнений, составленных по (14) для точек 0 (d0=0), 1 и 2 (величины d1 и d2 замеряют на секции), и равенства для суммы квадратов косинусов углов.
