Приступая к изучению двигателей внутреннего сгорания, необходимо иметь четкое представление о термодинамических особенностях того или иного типа двигателей, их эффективности в зависимости от ограничений, накладываемых условиями эксплуатации. Такое представление может быть получено путем рассмотрения идеальных циклов ДВС.
Идеальный цикл — это упрощенная термодинамическая схема рабочего цикла, не имеющая каких-либо потерь энергии, кроме неизбежной передачи тепла холодному источнику. Идеальный цикл — это эталон, к которому надо стремиться. При этом практический интерес представляет экономичность цикла и параметры, ее определяющие.
Цикл поршневого двигателя со смешанным подводом тепла
Напомним основные особенности идеальных циклов:
- а) рабочее тело в цикле — идеальный газ;
- б) количество идеального газа — постоянно;
- в) сжатие и расширение газа происходит по адиабате;
- г) процессы сгорания топливаРасчет процесса сгорания топлива и выпуска газов условно заменяются процессами подвода и отвода тепла при постоянном давлении или постоянном объеме.
Как 2-тактные, так и 4-тактные двигатели имеют одинаковые идеальные циклы.
Из курса термодинамики известно, что для современного поршневого дизеля с непосредственным впрыском топлива в цилиндр идеальным является цикл со смешанным подводом теплоты (рис. 1).
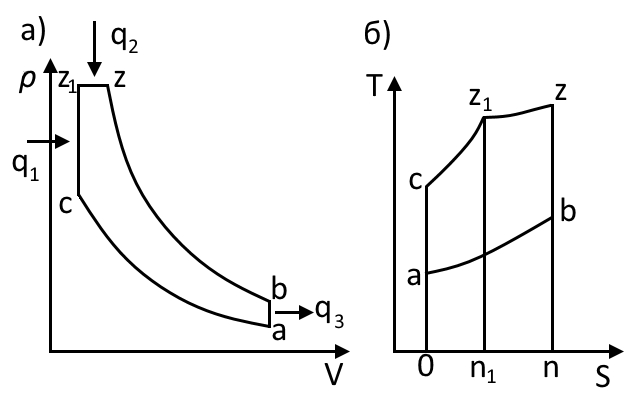
В верхней части рисунка дано изображение цикла в осях «давление-объем», где площади под кривыми численно равны работе в процессе расширения или сжатия. В нижней части рисунка цикл изображен в осях «температура-энтальпия», где площади под кривыми численно равны количеству подведенной или отведенной теплоты. Подвод теплоты в цикле осуществляется частично при постоянном объеме (для теплоты q1 определяется площадью ocz1n1), частично при постоянном давлении (доля q2 определяется площадью n1z1zn). Отведенная теплота q3 определяется площадью oabn.
Термический КПД цикла равен:
где:
- q1 — количество подведенного тепла (площадь oczn на диаграмме T-S);
- q3 — количество тепла, переданное холодному источнику (площадь abno).
Доли подведенной и отведенной теплоты, выраженные через теплоемкости газа Cv и Cp и температуры в точках цикла, равны:
Выразим температуры через параметры цикла:
Выполнив преобразования исходной зависимости (Формула 1) с учетом приведенных равенств найдем:
где:
- k = Cp/Cv — показатель адиабаты.
- ε – степень сжатия;
- λ – степень повышения давления;
- ρ – степень предварительного расширения.
Если принять ρ = 1 – расчетная формула становится справедливой для идеального цикла карбюраторного двигателя (цикл быстрого горения). При λ = 1 – формула справедлива для “дизельного” цикла (цикл компрессорного дизеля с воздушным распыливанием топлива и сгоранием при постоянном давлении).
Рекомендуется к прочтению: Последовательно-параллельный комбинированный наддув
Как видно из приведенной зависимости, для любого идеального цикла термический КПД растет с ростом степени сжатия ε. При равной степени сжатия цикл быстрого горения имеет более высокий КПД, “дизельный” цикл – минимальный КПД.
Однако у дизеля величина степени сжатия больше в 1,5-2 раза по сравнению с карбюраторным двигателем, у которого ε ограничивается детонационными качествами топлива (бензина), что реально обеспечивает более высокие значения ηt у дизелей.
Что касается максимальных значений степени сжатия у дизелей – величины ε ограничиваются требованиями механической напряженности двигателя. Чем выше степень сжатия – тем выше давление сжатия и соответственно давление сгорания в цилиндре, больше механические напряжения в деталях.
Если выдвинуть требования – при сравнении циклов исходить из одинакового давления сгорания, то более экономичным оказывается цикл “компрессорного” дизеля, затем следует цикл со смешанным подводом тепла; цикл быстрого горения имеет минимальный термический КПД. Такое положение объясняет тенденцию изменения показателей рабочего процесса и регулировки современных дизелей по мере их форсировки – ограничения по механическо напряженности заставляют изменять цикл со смешанным подводом теплоты в сторону цикла сгорания при постоянном давлении (уменьшать долю q1 и увеличивать долю q2). Реально это осуществляется за счет уменьшения угла опережения подачи топлива и даже перенесения всего впрыска топлива за ВМТ.
Идеальный цикл комбинированного двигателя
Современный дизельный агрегат представляет собой Элементы движения, распределительный вал, шатун и другие составляющие ДВСпоршневой двигатель внутреннего сгорания, оснащенный турбокомпрессором ТК (газовой турбиной с сидящим на одном валу с ней компрессором, рис. 2). Газы совершают полезную работы сначала в цилиндре (перемещая рабочий поршень), а затем в газовой турбине. Если газовая турбина отдает часть полезной работы на общий фланец отбора мощности – такой двигатель в полной мере может быть назван комбинированным.
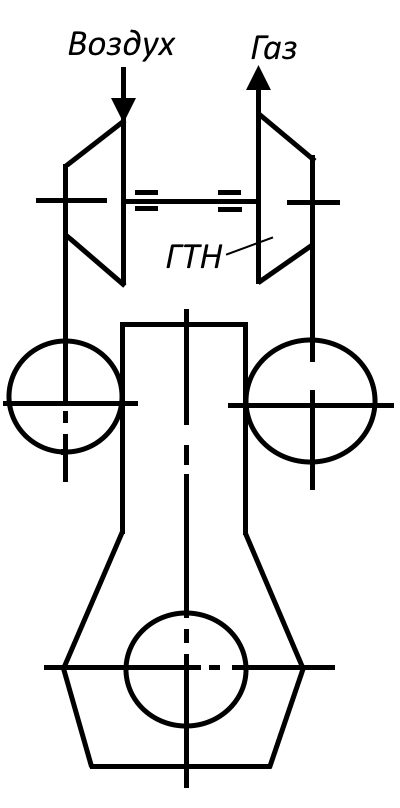
Реально в современных двигателях газовая турбина используется только для приводы воздушного компрессора, подающего воздух в цилиндры под более высоким давлением, чем давление окружающей среды. Энергия газов, преобразованная в механическую работу в газовой турбине, передается в компрессоре воздуху, и при отсутствии охлаждения воздуха возвращается в цилиндр. Двигатель с такой схемой использования энергии может быть назван комбинированным условно.
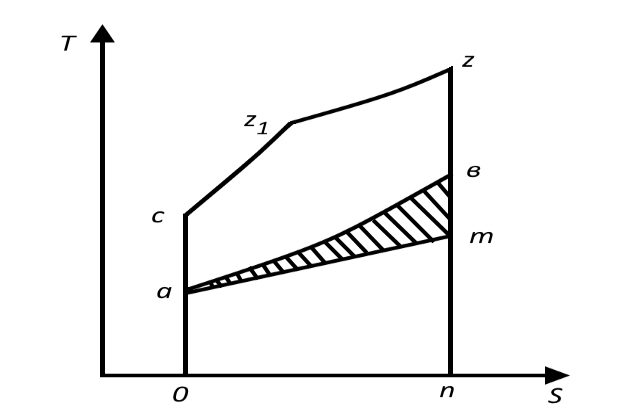
Идеальный цикл двигателя в осях P-V дан на рис. 3, в осях T-S на рис. 4. Он состоят из цикла acz1zb поршневого двигателя со смешанным подводом теплоты и упрощенного цикла турбокомпрессора без охлаждения воздуха bmoa.

В цикле ТК обозначено:
- bm — адиабатное расширение рабочего тела в газовой турбине;
- mo — передача тепла холодному источнику q3 при P = const (истечение газа из газовой турбины при постоянном давлении);
- oa — адиабатное сжатие воздуха в компрессоре;
В осях P-V полезная работа определяется площадью диаграммы.
Будет интересно: Последовательный комбинированный наддув
Как видно из рисунка 3, полезная работа в комбинированном двигателе acz1zbmo при прочих равных условиях больше полезной работы цикла поршневого двигателя acz1zb на величину, определяемую площадью bmoa.
Поскольку количество подведенного тепла считается неизменным, следовательно, полезная работа увеличена за счет уменьшения количества отводимого тепла. Это видно из рис. 4, где уменьшение отведенного тепла по сравнению с циклом поршневого двигателя определяется заштрихованной площадью bmoa.
Определим термический КПД идеального цикла комбинированного двигателя. Для этого обозначим:
— суммарная степень сжатия в компрессоре и в цилиндре;
- Δδ = Vm/Vo — отношение объема газа на выходе из турбины к объему газа на входе в компрессор..
Остальные обозначения — те же, что и в циклах поршневых ДВС. Тогда:
Так как:
а температуры определяются равенствами:
то:
Учитывая, что Cp/Cv = k, и выполнив алгебраические преобразования, окончательно получим:
Из этого равенства видно, что термический КПД комбинированного двигателя зависит от тех же факторов, что и цикл поршневого двигателя. Увеличение ηi комбинированного двигателя по сравнению с поршневым определяется двумя факторами: возрастанием суммарной степени сжатия
и влиянием дополнительного расширения в турбине, характеризуемым отношение Vm/Vo = Δδ.
Любое увеличение суммарной степени сжатия и степени последующего расширения в турбине приводит к уменьшению правой части равенства (Формула 9) и к соответствующему увеличению термического КПД цикла. Это – один из определяющих факторов, благодаря которому удалось поднять эффективный КПД современных двигателей до небывалой ранее величины 50-52 %.
