Навигационная безопасность плавания судов в плотных потоках

Для обеспечения безопасности мореплавания при движении судов в плотных потоках, а также для регулирования движения судов с помощью систем управления движением, большое значение имеет правильное установление безопасных дистанций между движущимися друг за другом судами.

В исследованиях потоков судов определение безопасных дистанций между судами производили двумя методами:

динамическим – путем установления закономерностей движения судов при торможении;
статистическим – путем натурных изучений реальных судопотоков.

Во втором случае определяли «зоны навигационной безопасности», т. е. безопасные дистанции в направлении по курсу судна и в перпендикулярном ему направлении.

Рассмотрим первый разработанный нами способ. Будем полагать, что дистанция между двумя движущимися в одном направлении с одинаковыми скоростями судами будет безопасной, если судоводитель сзади идущего судна будет иметь возможность избежать столкновения при экстренном торможении (работой движителей на задний ход) идущего впереди судна. На рис. 1 показан графически процесс торможения следующих одно за другим двух судов.

График торможения судна — Рис. 1 График процесса торможения судов, следующих одно за другим

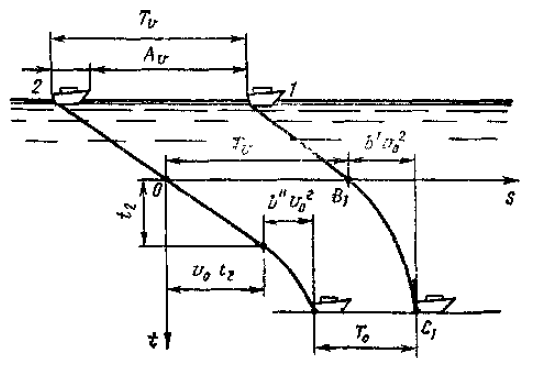
Предположим, вначале на расстоянии A_v суда движутся друг за другом со скоростью v₀. Судоводитель судна 1, обнаружив препятствие, внезапно остановил машины, дал движителям полный задний ход; торможение началось в точке B₁, и судно 1 остановилось в точке C₁. Движение судна 1 на переменном режиме с уменьшением скорости можно разделить на два периода:

– с момента прекращения подачи топлива в двигатель до полной остановки винта;
– с момента запуска двигателя на задний ход до момента остановки судна.

Силой сопротивления винтов в периоде можно пренебречь и тогда дифференциальное уравнение движения в этом периоде будет иметь вид

m (1 + λ_{11}) \frac{d v}{d t} = - R_{0} (\frac{v}{v_{0}})^{2}, Ф о р м . 1

где:

m – масса судна, кг;
λ₁₁ – коэффициент присоединенной массы воды;
v – текущая скорость судна, м/с;
R₀ – сопротивление воды движению судна, Н, при скорости v₀;
v₀ – начальная скорость судна, м/с.

Введем обозначение

α_{1} = R_{0} m (1 + λ_{11}) {v^{2}}_{0},

разделяя переменные и интегрируя, получим:

t_{1} = - \frac{1}{α_{1}} |\frac{v^{- 2 + 1}}{- 2 + 1}| \begin{matrix} v_{s} \\ v_{0} \end{matrix}

Длительность первого периода будет равна

t_{1} = \frac{1}{α_{1}} (\frac{1}{v_{2}} - \frac{1}{v_{0}}) Ф о р м . 2

Скорость в конце первого периода движения можно определить из выражения (Формула 2):

v_{2} = \frac{v_{0}}{1 + α_{1} v_{0} t_{1}} Ф о р м . 3

Учитывая, что dl/dt = v, можем определить путь, проходимый в первом периоде, по формуле:

l_{1} = \begin{matrix} t_{2} \\ \int \\ 0 \end{matrix} \frac{v_{0} d t}{1 + α_{1} v_{0} t} = \frac{1}{α_{1}} \ln (1 + α_{1} v_{0} t_{2}),

или

t_{1} = {v^{2}}_{0} b_{1},

где:

b_{1} = \frac{m + λ_{11}}{R_{0}} \ln (1 + α_{1} v_{0} t_{2}) .

Упор винта, как показывают натурные испытания, незначительно зависит от скорости судна, поэтому в первом приближении будем принимать величину упора постоянной.

Уравнение движения во втором периоде будет иметь вид:

m (1 + λ_{11}) \frac{d v}{d t} = - [T_{з . х} + R_{2} (\frac{v}{v_{2}})^{2}], Ф о р м . 4

где:

T_{з. х} – упор винта на заднем xoдy, Н;
R₂ – сопротивление воды движению судна 1 при скорости v₂, H.

Обозначим C²₂ = T_{з. х}v²₂/R₂, a′₁ = R₂/m · (l+ λ₁₁ )v²₂. После разделения переменных уравнения и интегрирования получим

t_{2} = - \frac{1}{α'_{1}} \begin{matrix} 0 \\ \int \\ v_{2} \end{matrix} \frac{d v_{2}}{v_{2} + C_{2}} = - \frac{1}{α ‘_{1} C_{2}} |a r c t g \frac{v}{C_{2}}| \begin{matrix} 0 \\ v_{2} \end{matrix},

откуда

t = \frac{1}{α'_{1} C_{2}} a r c t g \frac{v_{2}}{C_{2}} .

Для определения зависимости величинах скорости движения судна во втором периоде от времени необходимо полученное выражение для t₂ проинтегрировать в общем виде, т. е. вместо t₂ подставить текущее время t, а нижний предел интеграла заменить текущей скоростью v. После интегрирования и преобразований получим:

v = C_{2} t g (a r c t g \frac{v_{2}}{C_{2}} - α_{1}' C_{2} t)

Далее, заменяя v на dl₂/dt, получим

l_{2} = C_{2} \begin{matrix} t_{2} \\ \int t g \\ 0 \end{matrix} (a r c t g \frac{v_{2}}{C_{2}} - α_{1}' C_{2} t) d t .

После интегрирования будем иметь

l_{2} = \frac{1}{α_{1}'} \ln \frac{\cos (ε_{2} - α_{1}' C_{2} t_{2})}{\cos ε_{2}}, Ф о р м . 5

где:

ε_{2} = a r c t g \frac{v_{2}}{l_{2}} .

Упор винта во втором периоде торможения можно определить по формуле:

T_{з . х} = T_{шв . з . х} = \frac{R_{т}}{R_{н}} \frac{M_{шв}}{D_{в}}, Ф о р м . 6

где:

к_т, к_м – коэффициенты упора и момента на швартовах;
M_шв – момент двигателя при работе на швартовых который может приниматься равным номинальному моменту M_Н, Нм;
D_в – диаметр винта, м.

Общий путь торможения l_Т, проходимый судном с уменьшением скорости движения в первом и втором периодах, запишется в виде:

l_{T} = l_{1} - l_{2} = b_{1} {v^{2}}_{0} + b_{2} {v^{3}}_{2} = b' v_{2}, Ф о р м . 7

где:

b' = \frac{\ln (1 + λ_{11})}{R_{2}} \ln \frac{(\cos ε_{2} - α_{1}' C_{2} t_{2})}{\cos ε_{2}};

b' = b_{1} + b_{2} .

Момент начала снижения скорости движения впереди идущим судном (если звуковой сигнал «Мои машины работают на задний ход» не услышан) не будет сразу обнаружен судоводителем идущего сзади судна. Только после уменьшения расстояния между судами на определенную величину Δl судоводитель сзади идущего судна осознает опасность и предпримет действие, направленное к остановке своего судна (подаст команду «Стоп»).

Предлагается к прочтению: Районы регламентированного движения

С момента подачи этой команды и до момента прекращения подачи топлива в цилиндры двигателя или закрытия стопорного клапана у паровой машины (турбины) не наблюдается существенного падения частоты вращения двигателя. Выключение двигателя после подачи команды «Стоп» при хорошо натренированной команде происходит по истечении 4-6 с. При наличии дистанционного управления двигателями это время может быть принято равным 1-2 с.

В течение указанного времени судно 2 (см. рис. 1) будет двигаться с постоянной скоростью v₀. Путь, проходимый судном 2 на постоянной скорости,

l' = v_{0} t_{2}, Ф о р м . 8

где:

t₂ = t_CP + t_P + t_Д + t_{И. К}.

Здесь

t_СР – время, в течение которого судоводитель замечает сокращение расстояния между судами, с;
t_p – время реакции судоводителя (t_p = 1,0 ÷ 1,5 с);
t_Д – время действия (1 ÷ 2 с);
t_{И. К} – время исполнения команды, с.

На основании исследований, посвященных изучению способности человека обнаружить внезапные изменения скорости прямолинейного движения объекта, можно сделать вывод, что порог различия изменений скорости прямолинейного движения зависит от исходной скорости. Для скоростей движения водоизмещающих судов этот порог может быть принят равным 20-30 % исходной скорости. В этом случае время может быть определено по выражению t_ср ≈ m (1 + λ₁₁) v₀²/4R₀.

Из графика (см. рис. 1) нетрудно установить, что T_v + b′v₀² = T₀ + b″v₀ + v₀t₂. Делая подстановку, T_v = L + A_V, T₀ = L + A₀ = 1,2L, определим величину безопасного интервала:

A_{v} = 0, 3 L + (3 + t_{н . к}) v_{0} + (\frac{m (1 + λ_{11})}{M R_{0}} + b ″ - b') {v^{2}}_{0} . Ф о р м . 9

Обозначим m(1 + λ₁₁)/4R₀ = b^′″, тогда

A_{v} = 0, 2 L + (b ″' + b ″ - b') {v^{2}}_{0} + (3 + t_{н . к}) v_{0} . Ф о р м . 11

Таким образом, величина безопасного интервала в потоке судов зависит от скорости движения, габаритов судов, инерционных параметров судов и психологических факторов судоводителей. Исходя из конкретных характеристик потока судов, условий плавания на том или ином участке и установленных скоростей движения с помощью формулы 10 можно решать задачу об обосновании безопасных дистанций между судами.

На рис. 2 приведен график безопасных дистанций основных типов крупнотоннажных судов. Анализируя полученные зависимости, можно видеть, что с уменьшением скорости движения безопасные дистанции судов уменьшаются по линейному закону.

Рис. 2 График безопасных дистанций между судами в потоке судов.
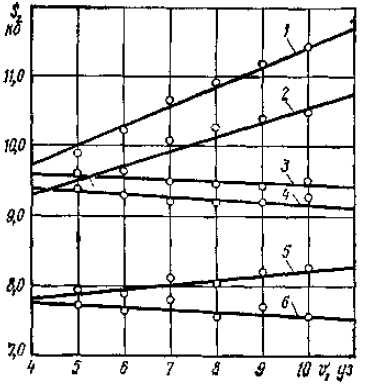
1 – судно типа «Борис Бутома» движется за судном типа «Крым»; 2 – судно типа «Борис Бутома» движется за судном типа «София»; 3 – судно типа «Крым» движется за судном типа «Борис Бутома»; 4 – судно типа «Крым» движется за судном типа «София»; 5 – судно типа «София» движется за судном типа «Крым»; 6 – судно типа «София» движется за судном типа «Борис Бутома»

По исследованиям научного сотрудника технического факультета из университета Осака К. Тагути, средние статистические безопасные дистанции в потоке судов имели значение (рис. 3)

A v_{c p} \approx 8 L,

или

A v \approx L + 0, 33 L v_{0}^{1, 6} + Δ М, Ф о р м . 11

где:

ΔΜ – запас дистанции, м.

Дистанция — Рис. 3 Безопасные дистанции по статистическим данным.
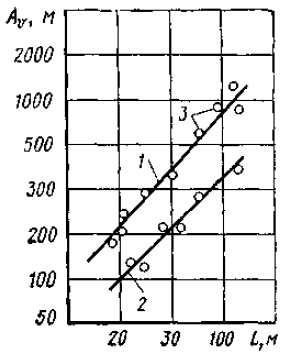
1 – до впереди идущего судна; 2 – до судна идущего по траверзу; 3 – опытные точки по натурным измерениям

В направлении, перпендикулярном курсу судна, ширину зоны рекомендуется определять по формуле:

A_{n} \approx 0, 6 L {v^{0, 4}}_{0}, или A_{n} \approx 3, 5 L . Ф о р м . 12

Таким образом, зона навигационной безопасности (ЗНБ) ограничена дистанцией 8L впереди судна и 3,5L в перпендикулярном направлении. Приведенные данные показывают, что полученные расчетным путем безопасные дистанции подтверждаются статистическими исследованиями потока судов.

Разработанные графики по определению безопасных дистанций между судами внедрены на крупнотоннажных танкерах типа «Крым», «Маршал Жуков», «Борис Бутома», «София» Новороссийского морского пароходства.

Установленные безопасные дистанции при движении в кильватерной колонне практически будут выдерживаться с определенной степенью приближения. Судоводитель реагирует на величину дистанции до впереди идущего судна, определив ее визуально (или, например, с помощью дальномерного устройства РЛС), и с помощью ДАУ изменяет частоту вращения двигателей. Скорость судна изменяется до тех пор, пока величина дистанции не достигает нужной безопасной величины. Этот цикл регулирования по мере надобности повторяется.

Рассмотрим математическую модель этого процесса управления в потоке судов. В системе маршрутных координат положение судна вдоль судового хода в любой момент времени определяется одной координатой х. Тогда положение n-го судна в момент t будет определяться координатой х(n, t), а следующего впереди него судна с номером n – 1 в тот же момент времени – координатой х(n – l, t). В этом случае скорость n-го судна можно записать в виде:

dх(n, t)/dt, а (n – 1)-го судна dx(n – 1, t )/dt;
ускорение n-го судна d²х(n, t)/dt², a (n – 1)-го d² х (n – 1, t)/dt².

Будем полагать, что ускорение n-го судна в процессе управления изменяется судоводителем пропорционально относительной скорости впереди идущего судна, т. е. чем больше скорость изменения дистанции между судами, или относительная скорость, тем стремительнее судоводитель n-го судна изменяет режим движения. Однако ускорение n-го судна практически начинает изменяться не сразу после изменения относительной скорости между судами, а через некоторый промежуток времени запаздывания T₃, равный реакции рассматриваемой системы, который можно определить экспериментальным путем.

Изложенный принцип управления математически можно выразить в виде следующего дифференциального уравнения:

\frac{d^{2}}{d t^{2}} x (n_{1} t + T_{2}) = α_{k} |\frac{d}{d t} x (n - 1, t) - \frac{d}{d t} x (n_{1} t) . Ф о р м . 13

где:

α_K – коэффициент пропорциональности, с^-1.

Из уравнения (формула 13) видно, что чем больше значение α_K тем быстрее каждый судоводитель реагирует на изменение скорости впереди идущего судна. Поэтому с физической стороны коэффициент α_K характеризует чувствительность (внимательность) судоводителя на изменение обстановки движения. Приближенно можно считать

α_{К} = 1 / t_{C P} .

Для того чтобы приведенная математическая модель задавала управление, следует поставить цель или требования, которые преследует управление. К их числу можно отнести:

поддержание наиболее равномерного потока судов, что может быть достигнуто, если минимизировать ускорения (замедления) α судов, движущихся в кильватерной колонне;
скорость судов v должна иметь некоторое значение v₂, равное скорости головного судна.

Таким образом, критерием качества управления может быть минимизация интеграла

I = \begin{matrix} t_{1} \\ \int \\ t_{0} \end{matrix} {|λ α^{2} + v (v - v_{2})^{2}|}^{2} d t . Ф о р м . 14

где:

λ, μ – соответствующие положительные весовые коэффициенты.

При минимизации I необходимо принимать во внимание следующие ограничения: судно имеет наибольшее ускорение α_u(v), быстро убывающее с увеличением скорости движения, и предел замедления α_u. Верхний и нижний пределы ускорения определяются соотношениями α_i ≤ α ≤ α_u(v).

Существуют ограничения сверху на скорость v_u, определяемые условиями движения, и ограничение снизу – требование, чтобы судно не двигалось задним ходом: 0 ≤ v ≤ v_u.

Отыскание минимума критерия качества управления производится с использованием динамического программирования, вариационного исчисления, принципа максимума (Л. С. Понтрягина) и др.

Сноски

Безопасные дистанции между судами