Диаграмма динамической остойчивости судна ДДО

Остойчивость судна простыми словами – это его способность восстанавливать равновесие после внешнего воздействия (крена). Понимание этого фундаментального свойства имеет решающее значение для безопасности судна.

В нашей статье мы подробно рассмотрим виды остойчивости судов – статическую и динамическую. Особое внимание будет уделено механизму, лежащему в основе этих понятий: работе кренящего момента и действию противодействующего восстанавливающего момента. Неконтролируемый кренящий момент таит в себе опасность кренящего момента, которая может привести к опрокидыванию. Изучение диаграмм остойчивости дает ключ к расчету критических углов крена, что позволяет обеспечить надежное восстановление равновесия судна в любых условиях и понять, в чем разница между статической и динамической остойчивостью.

Основные характеристики остойчивости судна описывают его способность сопротивляться крену и восстанавливать равновесие. Ключевыми показателями являются метацентрическая высота, которая определяет начальную остойчивость при малых углах крена, и плечо статической остойчивости.

Понимание и контроль факторов, влияющих на остойчивость судна, таких как вертикальное распределение груза, метацентрическая высота и наличие свободных поверхностей в танках, являются критически важными условиями для безопасной эксплуатации и мореплавания.

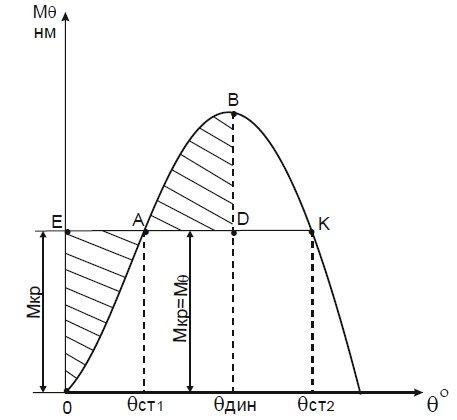
При статическом приложении кренящего момента восстанавливающий момент постепенно увеличивается вместе с нарастанием угла крена, и эти моменты взаимно уравновешивают друг друга в течение всего процесса статического накренения судна. Движение судна происходит равномерно, без угловых ускорений. Предположим теперь, что к судну, находящемуся в прямом положении, внезапно приложен кренящий момент, величина которого не связана с углом наклонения. Тогда график его действия можно изобразить на диаграмме статической остойчивости прямой линией ЕК параллельно оси (так действует, например, момент шквального ветра, обрыв тяжелого груза, подвешенного на шкентеле вываленной за борт грузовой стрелы, обрыв буксирного троса). Под действием этого момента судно быстро накреняется.

Что такое динамическая остойчивость судна?

Динамическая остойчивость – это способность судна противостоять действию внезапно приложенного кренящего момента, не опрокидываясь.

Угол крена, на который наклоняется судно при внезапном действии кренящего момента, называется динамическим углом крена θ_дин. Динамический угол крена θ_дин определяют из условия равенства работ кренящего и восстанавливающего момента:

А К Р = A θ . Ф о р м . 1

Следовательно, мерой динамической остойчивости служит работа восстанавливающего момента Aθ, которую надо совершить, чтобы накренить судно на угол θ_дин. (Напомним, что мерой статической остойчивости является восстанавливающий момент). Работа постоянного кренящего момента при наклонении судна до угла θ_дин равна произведению момента на угол крена:

А К Р = М К Р θ_{д и н} Ф о р м . 2

На рисунке эта работа графически представлена площадью прямоугольника ОEDθ_дин.

Предлагается к прочтению: Диаграмма статической остойчивости (ДСО) и ее свойства

Поскольку восстанавливающий момент М_КР как функция угла крена задается Диаграмма статической остойчивости (ДСО) и ее свойствадиаграммой статической остойчивости, работу восстанавливающего момента Aθ, необходимую для накренения судна на угол θ_дин, графически можно изобразить площадью фигуры OABθ_дин. Тогда условие (1) можно записать в виде:

S О Е D θ_{д и н} = S О А В θ_{д и н} Ф о р м . 3

Как видно из рисунка, обе площади включают общую для них площадь ОАDθ_дин, поэтому приходим к выводу, что равенство работ кренящего и восстанавливающего моментов будет соблюдено, если заштрихованные на рисунке площади (S_ABD и S_ОЕА) будут равны.

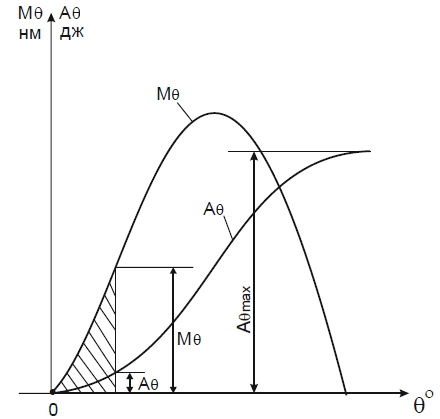
График восстанавливающего момента — Рис. 2

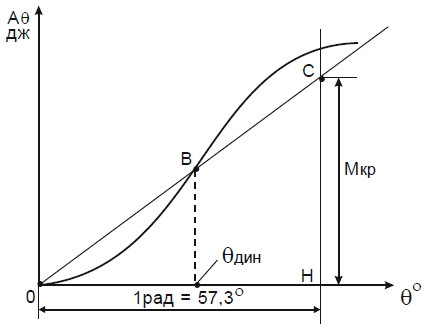
Отсюда получаем правило, которое используется для графического решения уравнения (1): при заданном динамическом кренящем моменте M_КР положение ординаты Bθ_дин подбирают таким образом, чтобы заштрихованные площади оказались равными. Тогда пересечение с осью ординаты Bθ_дин даст искомый угол динамического крена. Определить динамический угол крена по диаграмме статической остойчивости можно лишь приближенно. Задачи, связанные с динамической остойчивостью, решаются быстрее и точнее с помощью так называемой диаграммы динамической остойчивости, которая представляет собой кривую, выражающую зависимость работы восстанавливающего момента от угла крена.

Построение такой диаграммы, являющейся интегральной кривой по отношению к диаграмме статической остойчивости, производится следующим образом. На оси абсцисс намечают несколько точек, соответствующих выбранным углам крена, и восстанавливают перпендикуляр до пересечения с кривой диаграммы статической остойчивости. Вычислив работу восстанавливающего момента (выраженную графически соответствующими площадями) при накренении судна от прямого положения (θ = 0) до заданного угла крена, на перпендикулярах откладывают ординаты, которые в заданном масштабе определяют вычисленные значения площадей. Точки ординат соединяют плавной кривой, которая является диаграммой динамической остойчивости при данном состоянии нагрузки судна. На практике диаграмму динамической остойчивости строят по рассчитанным плечам динамической остойчивости методом определения интегральных сумм плеч статической остойчивости и расчета на основании этих сумм плеч динамической остойчивости.

График динамической остойчивости — Рис. 3

Что такое плечо статической остойчивости?

Плечо статической остойчивости – это горизонтальное расстояние между двумя силами, образующими восстанавливающую пару, возникающую при наклонении судна на некоторый угол.

Чтобы определить динамический угол крена на диаграмме динамической остойчивости следует отложить на оси абсцисс один радиан (57,3 град.) и в полученной точке Н восстановить перпендикуляр, на котором в масштабе работы откладывается отрезок НС = M_КР. Соединив точку С прямой с началом координат, получим график работы постоянного кренящего момента. Абсцисса точки пересечения прямой ОС с диаграммой динамической остойчивости (точка В) определяет искомый угол θ_дин.

С помощью диаграммы динамической остойчивости может быть решена обратная задача об отыскании динамически приложенного кренящего момента M_КР по заданному углу крена θ_дин.

Определение минимального опрокидывающего момента по диаграмме статистической и динамической остойчивости

Предельные наклонения судна с помощью диаграмм статической и динамической остойчивости можно изобразить следующим образом:

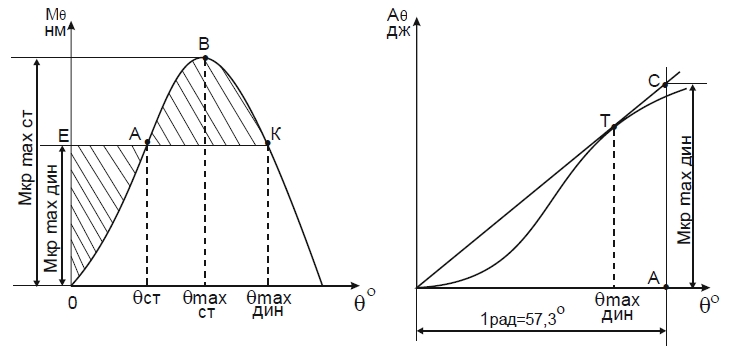
График предельного наклонения судна — Рис. 4

Мы видим, что предельный кренящий момент, действующий статически, всегда больше предельного кренящего момента, действующего динамически. Таким образом, для судна быстрое нарастание кренящего момента всегда более опасно, чем медленное.

Рассматривая вопросы, связанные с действием внезапно приложенного кренящего момента, мы исходим из предположения, что начальному положению судна соответствует угол крена, равный нулю (прямое положение). Между тем в практике эксплуатации судов бывают случаи, когда к началу действия внезапного кренящего момента судно уже находится в накрененном положении в результате действия какого-то кренящего момента. В этой ситуации при решении задач динамической остойчивости возможны два случая:

судно плавает с начальным углом крена в том же направлении, в котором приложен внезапный кренящий момент;
судно имеет начальный крен в сторону, противоположную действию внезапного кренящего момента.

Ограничимся рассмотрением способа решения задач по определению минимального опрокидывающего момента для второго, более опасного случая. Внезапно приложенный кренящий момент, при котором динамический угол крена достигает значения статического угла неустойчивого равновесия, называется минимальным опрокидывающим моментом – M_опр.

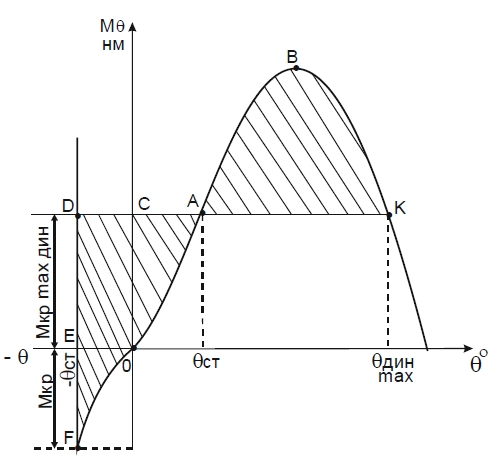
Допустим, что судно имеет крен -θ_СТ1, созданный первоначально действующим моментом М_КР. Кроме того, на судно действует внезапный кренящий момент M_КР.дин. в направлении, противоположном M_КР, т. е. судно имеет крен на тот борт, со стороны которого подействовал внезапный кренящий момент.

В этом случае минимальный опрокидывающий момент определяют следующим образом. Диаграмму статической остойчивости продолжают в область отрицательных значений абсцисс на участке, равном углу крена -θ_СТ1. Затем на оси абсцисс откладывают в соответствующем масштабе угол крена -θ_СТ1, через полученную точку Е проводят вертикальную линию до пересечения с диаграммой (точка F) и продолжают ее вверх. После этого подбирают такое положение по высоте линии DK, параллельной оси абсцисс, чтобы заштрихованные площади FDA и АВК оказались равными. Найденная ордината ОС соответствует значению минимального опрокидывающего момента М_{КР max} _дин. При наличии крена судна на угол -θ_СТ1, созданного первоначальным кренящим моментом М_КР, абсцисса точки К определяет угол крена θ_max _дин, который при этом получит судно.

По диаграмме динамической остойчивости значения опрокидывающего момента и вызываемого им крена определяют следующим образом:

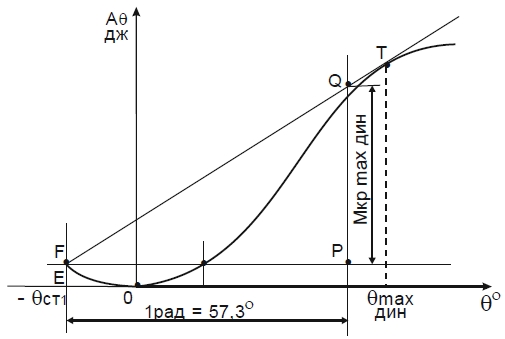
Диаграмма динамической остойчивости — Рис. 6

Продолжают диаграмму в область отрицательных значений абсцисс на участке, равном углу -θ_СТ1. Затем на левой части оси абсцисс отмечают точку Е, соответствующую первоначальному углу крена -θ_СТ1, и через нее проводят вертикальную линию до пересечения с диаграммой (точка F). Из точки F проводят касательную FT и горизонтальную прямую, параллельную оси абсцисс, на которой откладывают отрезок FP, равный одному радиану (57,3 град.). Из точки Р восстанавливают перпендикуляр до пересечения с касательной FT в точке Q. Отрезок РQ в масштабе оси ординат равен минимальному опрокидывающему моменту М_{КР max} _дин. При наличии первоначального крена судна на угол -θ_СТ1, абсцисса точки Т дает значение угла крена θmax _дин, вызванного моментом М_{КР max} _дин.