При постройке судна возможно некоторое перераспределение масс, вследствие чего возникают расхождения между расчетными и действительными значениями аппликат Ц.Т. судна и метацентрической высоты. В связи с этим Регистр предписывает уточнять проектные данные о положении Ц.Т. построенного судна путем проведения так называемого опыта кренования. Опыту кренования подвергаются головные суда строящихся серий, каждое пятое судно серии, а также новые суда несерийной постройки. Кроме того, опыту кренования подвергают каждое судно после капитального ремонта или переоборудования и суда, остойчивость которых неизвестна или вызывает сомнения.
Опыт кренования основан на использовании формулы, определяющей угол крена при перемещении груза в поперечно-горизонтальном направлении. Зная массу груза P, перемещаемого в поперечно – горизонтальном направлении, плечо его переноса ly, водоизмещение судна D и угол крена θ, возникающий после перемещения груза, можно вычислить метацентрическую высоту судна:
где:
- Mкр – кренящий момент, вызванный переносом груза.
Массу перемещаемого груза, который принято называть крен – балластом, определяют взвешиванием, плечо lу – непосредственным замером, водоизмещение D – по кривой водоизмещения или масштабу Бонжана исходя из замеренной осадки судна в момент кренования. Определив в результате опыта значение угла θ и подставив его в формулу 1, получают метацентрическую высоту судна h. Затем можно вычислить и аппликату ZG Ц.Т., предварительно определив по метацентрической диаграмме величину Zm:
Опыт кренования проводится в тихую погоду при спокойном состоянии поверхности воды и отсутствии течения. Скорость ветра не должна превышать 3 м/с. Судно не должно касаться стенки причала, грунта или находящегося рядом судна.
Следует проводить кренование порожнего судна, но со снабжением, находящимся на своих местах. Цистерны различного назначения должны быть осушены либо запрессованы. Начальный крен не должен превышать 0,5-1 град. Крен – балласт принимают на судно в таком количестве, чтобы обеспечить максимальные углы крена 2-4 град.
Для определения углов крена пользуются весками (нити с подвешенными грузами), сообщающимися сосудами, инклинографами различных типов и другими спец – приборами.
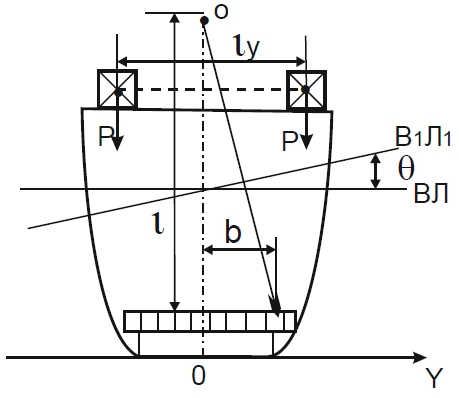
При использовании весков на больших судах длина нити должна быть 4,0-6,0 м, а на малых – не менее 1,5 м. Груз веска, с укрепленной на нем крылаткой, из двух взаимно перпендикулярных пластинок, опускают в бак с водой или маслом, чтобы колебания веска быстрее прекращались. Весков должно быть не меньше двух (лучше три). Места подвешивания выбирают по длине судна. Для отсчета углов крена, вблизи нижнего конца веска, укрепляют горизонтальную деревянную рейку с нанесенной шкалой. Угол крена, соответствующий перемещению крен – балласта, определяют по формуле:
где:
- b – отклонение веска, измеренное по рейке;
- l – длина веска, измеренная от точки подвеса до шкалы, по которой отсчитываются отклонения.
Кривые элементов теоретического чертежа
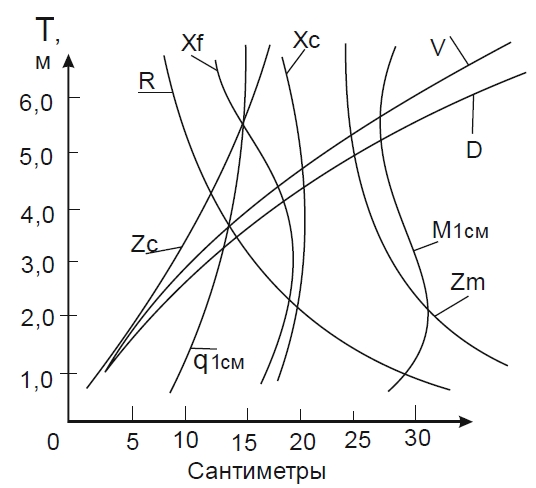
Кривые элементов теоретического чертежа представляют собой диаграмму, которая объединяет кривые, определяющие зависимость изменения значений теоретических элементов судна (V, Xс, Zс, Zm, Xf, q1см, r, R, M1см) от его осадки. Поскольку речь идет об элементах судна, связанных с плавучестью и остойчивостью, т. е. со статикой судна, эту совокупность кривых часто называют кривыми плавучести и начальной остойчивости.
Следует заметить, что к элементам теоретического корпуса, кроме основных элементов плавучести и элементов остойчивости при малых углах наклонения, следует отнести также геометрические характеристики обводов, и, в первую очередь, коэффициенты полноты формы корпуса судна (коэффициент общей полноты – δ, коэффициент полнотыКоэффициенты полноты, форма корпуса и мореходные качества буксиров площади ватерлинии – α, коэффициент полноты площади мидель – шпангоута – β), поэтому кривые этих элементов также включают в кривые элементов теоретического чертежа.
Количество кривых на диаграмме может доходить до 15-20. Для того чтобы определить необходимые значения элементов теоретического чертежа по кривым плавучести и начальной остойчивости, на оси осадок нужно наметить точку, соответствующую заданной осадке, и провести прямую, параллельную оси абсцисс. Отстояние точки пересечения прямой с соответствующей кривой от линии отсчета в выбранном масштабе определяет искомые элементы теоретического чертежа.
Примеры таких кривых приведены ниже на рисунках 3-6.
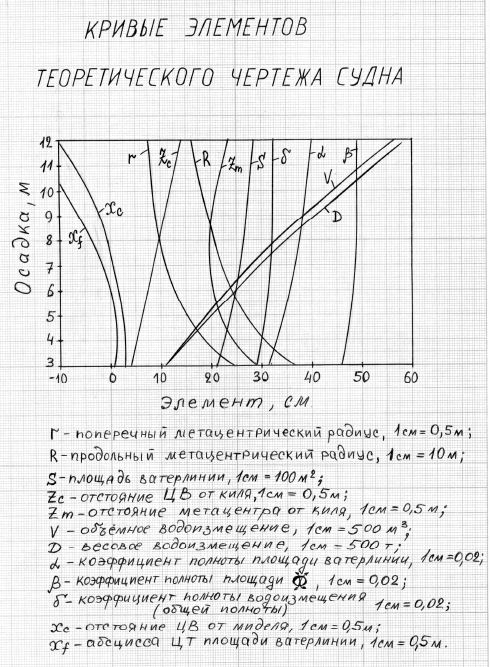
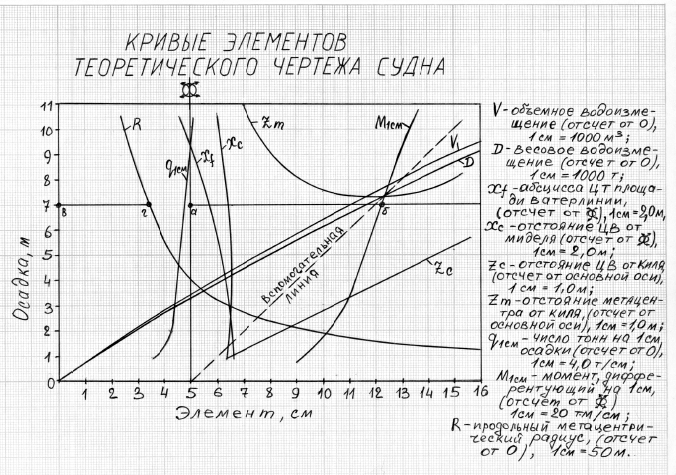
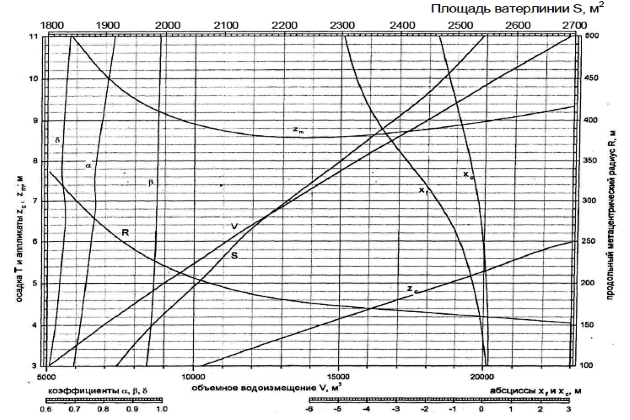
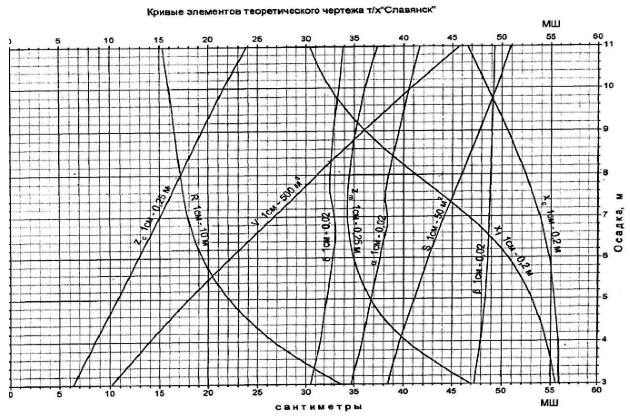
Очень часто зависимость теоретических элементов судна от осадки приводят в документации судна не в виде кривых, а в виде таблицы, которая носит обычно название таблицы гидростатических элементов судна. Пример такой таблицы приводится ниже.
| Гидростатические элементы судна | |||||||
|---|---|---|---|---|---|---|---|
| HydroSHIP | HUDROSTATIC PARTICULARS | PAGE: 28 | |||||
| DRAUGHT EXT. (m) | VOLUME (m^3) | DISPLAC (tonnes) | KM (m) | LCB (m) | LCF (m) | T1 (t/cm) | MT1 (tm/cm) |
| 3.75 | 3989.5 | 4089.3 | 7.409 | -2.35 | -2.49 | 12.13 | 63.5 |
| 3.76 | 4001.4 | 4101.5 | 7.401 | -2.35 | -2.49 | 12.13 | 63.6 |
| 3.78 | 4013.3 | 4113.7 | 7.392 | -2.35 | -2.48 | 12.14 | 63.6 |
| 3.79 | 4025.2 | 4138.0 | 7.384 | -2.35 | -2.48 | 12.14 | 63.6 |
| 3.80 | 4037.1 | 4150.2 | 7.376 | -2.35 | -2.48 | 12.14 | 63.7 |
| 3.81 | 4049.0 | 4162.4 | 7.367 | -2.35 | -2.48 | 12.15 | 63.7 |
| 3.82 | 4060.9 | 4174.6 | 7.359 | -2.35 | -2.47 | 12.15 | 63.8 |
| 3.83 | 4072.8 | 4199.0 | 7.351 | -2.35 | -2.47 | 12.15 | 63.8 |
| 3.84 | 4084..7 | 4211.2 | 7.342 | -2.35 | -2.47 | 12.16 | 63.9 |
| 3.85 | 4096.6 | 4223.4 | 7.334 | -2.35 | -2.46 | 12.16 | 63.9 |
| 3.86 | 4108.5 | 4235.6 | 7.326 | -2.35 | -2.46 | 12.16 | 63.9 |
| 3.87 | 4120.3 | 4247.8 | 7.318 | -2.35 | -2.46 | 12.17 | 64.0 |
| 3.8 | 4144.2 | 4260.0 | 7.311 | -2.35 | -2.45 | 12.17 | 64.0 |
| 3.89 | 4156.1 | 4272.3 | 7.304 | -2.35 | -2.45 | 12.17 | 64.1 |
| 3.90 | 4168.1 | 4284.5 | 7.297 | -2.35 | -2.45 | 12.18 | 64.1 |
| 3.91 | 4180.0 | 4296.8 | 7.290 | -2.35 | -2.44 | 12.18 | 64.2 |
| 3.92 | 4192.0 | 4309.0 | 7.284 | -2.35 | -2.44 | 12.18 | 64.2 |
| 3.93 | 4203.9 | 4321.2 | 7.277 | -2.35 | -2.44 | 12.19 | 64.3 |
| 3.94 | 4215.8 | 4333.5 | 7.270 | -2.35 | -2.43 | 12.19 | 64.3 |
| 3.95 | 4227.8 | 4345.7 | 7.263 | -2.35 | -2.43 | 12.19 | 64.4 |
| 3.96 | 4239.7 | 4358.0 | 7.256 | -2.35 | -2.42 | 12.20 | 64.4 |
| 3.97 | 4251.7 | 4370.2 | 7.249 | -2.35 | -2.42 | 12.20 | 64.4 |
| 3.98 | 4263.6 | 4382.4 | 7.242 | -2.36 | -2.42 | 12.21 | 64.5 |
| 3.99 | 4275.6 | 4394.7 | 7.235 | -2.36 | -2.41 | 12.21 | 64.5 |
| 4.00 | 4287.5 | 4406.9 | 7.228 | -2.36 | -2.41 | 12.21 | 64.6 |
| 4.01 | 4299.4 | 4419.2 | 7.221 | -2.36 | -2.41 | 12.22 | 64.6 |
| 4.02 | 4311.4 | 4431.4 | 7.214 | -2.36 | -2.40 | 12.22 | 64.7 |
| 4.03 | 4323.3 | 4443.6 | 7.207 | -2.36 | -2.40 | 12.2 | 64.7 |
| 4.04 | 4335.3 | 4455.9 | 7.200 | -2.36 | -2.39 | 12.23 | 64.8 |
| 4.05 | 4347.2 | 4468.1 | 7.194 | -2.36 | -2.39 | 12.23 | 64.8 |
| 4.06 | 4359.1 | 4480.4 | 7.187 | -2.36 | -2.39 | 12.23 | 64.9 |
| 4.07 | 4371.1 | 4492.7 | 7.180 | -2.36 | -2.38 | 12.24 | 64.9 |
| 4.08 | 4383.1 | 4505.0 | 7.174 | -2.36 | -2.38 | 12.24 | 65.9 |
| 4.09 | 4395.2 | 4517.4 | 7.169 | -2.36 | -2.37 | 12.25 | 65.0 |
| 4.10 | 4407.2 | 4517.4 | 7.163 | -2.36 | -2.37 | 12.25 | 65.0 |
| 4.11 | 4419.2 | 4529.7 | 7.157 | -2.36 | -2.36 | 12.26 | 65.1 |
| 4.12 | 4431.2 | 4542.0 | 7.152 | -2.36 | -2.36 | 12.26 | 65.1 |
| 4.13 | 4443.2 | 4554.3 | 7.146 | -2.36 | -2.35 | 12.26 | 65.2 |
| 4.14 | 4455.3 | 4566.6 | 7.140 | -2.36 | -2.35 | 12.27 | 65.2 |
| 4.15 | 4467.3 | 4579.0 | 7.135 | -2.36 | -2.34 | 12.27 | 65.3 |
| 4.16 | 4479.3 | 4591.3 | 7.129 | -2.36 | -2.34 | 12.27 | 65.3 |
| 4.17 | 4491.3 | 4603.6 | 7.123 | -2.36 | -2.33 | 12.28 | 65.4 |
| 4.18 | 4503.3 | 4615.9 | 7.118 | -2.36 | -2.33 | 12.28 | 65.4 |
| 4.19 | 4515.4 | 4628.3 | 7.112 | -2.36 | -2.32 | 12.28 | 65.5 |
Остойчивость при больших углах крена – Плечо остойчивости
В предыдущих темах рассматривалась остойчивость судна при наклонении его от положения равновесия на малые (начальные) углы крена. При этом в основу изучения теории начальной остойчивости были положены следующие допущения:
- при Крен судна при поперечном перемещении грузакрене судна перемещение Ц.В. происходит по дуге окружности;
- поперечный метацентр находится в точке, которая является центром этой окружности и не изменяет своего положения при наклонениях;
- значение поперечного метацентрического радиуса остается неизменным;
- равнообъемные ватерлинии пересекаются по прямой, проходящей через Ц.Т. площади ватерлинии, расположенный в ДП судна.
Однако в процессе эксплуатации судна часто возникают наклонения на большие углы крена. В этих случаях применение перечисленных выше допущений приводит к неверным результатам. Поэтому была разработана теория остойчивости судна при больших углах наклонения.
При больших углах наклонения судно нельзя считать прямостенным в пределах изменения формы подводного объема; симметрия входящей и выходящей частей площади наклонной ватерлинии значительно нарушается, что приводит к смещению оси пересечения двух равнообъемных ватерлиний. Перемещение Ц.В. при больших углах крена происходит уже не по дуге окружности, а по кривой переменной кривизны. Это равносильно тому, что поперечный метацентр не остается в постоянной точке m на ДП, как это было при малых углах крена, а смещается в новую точку. Следовательно, и расстояние между метацентром и Ц.В. – поперечный метацентрический радиус – является переменной величиной. Из сказанного следует, что метацентрическая высота тоже изменяется и уже не может служить критерием Понятия об остойчивости судна в различных условиях кренапоперечной остойчивости. По этим соображениям, решая вопросы остойчивости при больших углах крена, нельзя пользоваться метацентрической формулой поперечной остойчивости и всеми полученными на ее основании формулами, в которые входит значение поперечной метацентрической высоты.
Восстанавливающий момент, являющийся мерой статической остойчивости судна при больших углах крена, будет равен:
Основная задача расчета остойчивости при больших углах крена сводится к определению плеча ιст восстанавливающего момента в зависимости от угла крена θ.
Предлагается к прочтению:
Влияние на остойчивость судна подвешенных грузов
Крен судна при поперечном перемещении груза

Как удачно, что здесь приводятся формулы для практического расчета, а то ищешь, а везде только теория