Динамика двигателя судна, условия и оценка работы

Динамика двигателя включает в себя обширную информацию про движение КШМ под действием изменяющегося давления и сил инерции, что и рассмотренно ниже.

а) переменного давления газов в цилиндре;

б) сил инерции поступательно движущихся масс и моментов от этих сил;

в) центробежных сил вращающихся масс и моментов от этих сил;

г) крутящего момента двигателя и противоположного ему опрокидывающего момента;

д) крутильных и осевых колебаний, возникающих в валопроводе и коленчатом валу, как в упругой колебательной системе.

Суммарное влияние этих факторов определяет “динамику” двигателя — его механическую напряженность, характер изменения давления в подшипниках коленчатого вала и условия смазки подшипников, неравномерность вращения вала, вибрацию двигателя и корпуса судна.

Силы, определяющие механическую напряженность двигателя

Строго говоря, механические напряжения в деталях двигателя вызываются не только воздействием перечисленных выше динамических факторов, но и:

1. Статическими усилиями затяга деталей крепежа при сборке дизеля;
2. Изменением “внешних” условий — деформацией корпуса судна при его различной осадке или при волнении моря.

Статические усилия затяга деталей крепежа (шпилек, фундаментных болтов, анкерных связей и т. д.) создают в них растягивающие напряжения, а в стягиваемых деталях — напряжения сжатия. Так, благодаря предварительному затягу анкерных связей блок цилиндров всегда работает на сжатие. Подробно вопрос о механической напряженности наиболее ответственных деталей из-за статических усилий рассматривается при расчетах их прочности.

Изменение внешних условий приводит порой к весьма неблагоприятным последствиям. Деформация корпуса и фундамента двигателя вызывает трещины в блоках цилиндров, разрыв крепежных шпилек, износ клиньев фундамента, превышение допустимого уровня изгиба коленчатого вала (иначе — превышение допустимых раскепов коленчатого вала). Вопросы предотвращения этих нежелательных явлений решаются путем обеспечения достаточной жесткости корпуса судна и фундамента при его постройке, а также учетом последующих деформаций корпуса при монтаже двигателя на судовом фундаменте.

К примеру, если при загрузке судна и увеличении осадки его корпус в месте установки двигателя прогибается вверх, то необходимо заранее, еще при монтаже двигателя на судовом фундаменте, монтировать коленчатый вал с упреждающим прогибом вниз (обеспечивая так называемый положительный раскеп коленчатого вала). Вопросы влияния внешних условий на механическую напряженность двигателя носят конкретный характер для каждого судна и выходят за пределы настоящей статьи.

Рассмотрим более подробно усилия, определяющие механические напряжения в наиболее ответственных деталях механизма движения и возникающие при работе двигателя (без учета статических и внешних факторов).

На кривошипно-шатунный механизм действует 4 рода сил: давления газов P_г, силы инерции P_j, силы веса P_g и силы трения P_тр (рис. 1). Сила от давления газов на поршень равна: P_г = p_гF_n.

где:

• p_г – давление газов в цилиндре;
• F_n – площадь поршня.

Эта сила приложена к поршневому пальцу — в тронковых двигателях — или к поперечине крейцкопфа — в крейцкопфных двигателях.

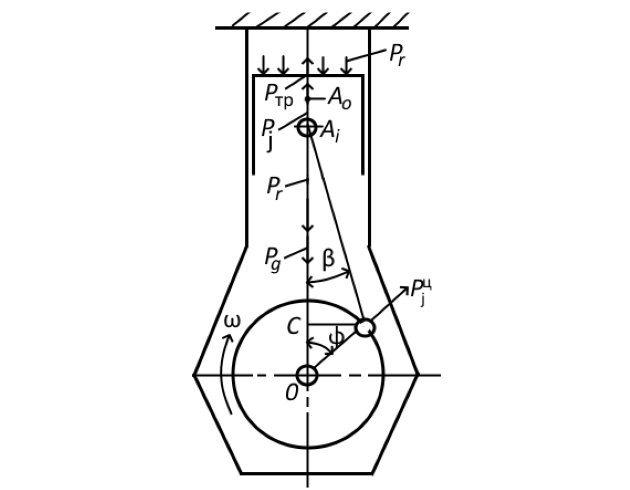
Силы инерции определяются переменной величиной или переменным направлением вектора скорости. В связи с этим в кривошипно-шатунном механизме наблюдаются как силы инерции поступательно движущихся масс, определяемые переменной скоростью движения поршня, так и центробежные силы инерции вращающихся масс. Величина сил инерции от поступательно движущихся масс может быть определена как:

$P_j = M_s{j}_s = \left(G_s/g\right) j_s, Форм. 1$

где:

• M_s = G_s/g – масса поршня и поступательно движущейся части шатуна;
• g – ускорение свободного падения;
• j_s – ускорение поступательно движущихся масс.

Ускорение j_s может быть найдено из уравнения перемещения поршня S = f(τ) (обозначения см. рис. 1):

$S = O{A}_o – O{A}_i = O{A}_o – \left(OC + CA\right) = R + L – \left(R\cos \phi + L\cos \beta \right) = R + L\left(R/R\right) – R\left(\cos \phi + \left(L/R\right) \cos \beta \right).$

где:

• OA_o = L + R:
• L – длина шатуна;
• R – радиус кривошипа;
• φ – угол поворота кривошипа от ВМТ;
• β – угол между шатуном и осью цилиндра.

Обозначим: R/L = λ; тогда:

$S = R \left[\left(1 + 1 / \lambda \right) – \left(\cos \phi + \left(1 / \lambda \right) \cos \beta \right)\right]. Форм. 2$

Так как:

$R\sin \phi = L\sin \beta , R/L = \sin \beta /\sin \phi = \lambda ; \sin \beta = \lambda \sin \phi ;$

то:

$\cos \beta = \sqrt{1 – Si{n}^2 \beta } = \sqrt{1 – \lambda 2·Si{n}^2\phi }.$

Раскладывая равенство cosβ в биноминальный ряд и взяв первые 2 члена разложения, получим приближенное равенство:

$\cos \beta \approx 1 – \left(1/2\right) \left({\lambda }^2 {\sin }^2 \phi \right). Форм. 3$

Подставим это равенство в формулу 2. Получим:

$S \approx R \left[1 + 1/\lambda – \cos \phi – 1/\lambda + 1/\lambda \left(1/2\right) \left(\lambda 2 {\sin }^2 \phi \right)\right] = R \left(1 – \cos \phi + \left(1/2\right) \lambda {\sin }^2 \phi \right).$

Так как:

$\cos 2\phi = {\cos }^2\phi – {\sin }^2\phi = 1 – 2 \sin 2\phi ;$

${\sin }^2\phi = \left(1/2\right) \left(1 – \cos 2\phi \right),$

то:

$S = R \left[\left(1 – \cos \phi \right) + \left(\lambda /4\right) \left(1 – \cos 2\phi \right)\right]. Форм. 4$

Взяв производные от пути по времени, найдем законы изменения скорости и ускорения движения поршня:

$C = dS/d\tau = \left(dS/d\phi \right) \left(d\phi /d\tau \right) = R\omega \left(\sin \phi + \left(\lambda /2\right)\sin 2\phi \right), Форм. 5$

$J = dC/d\tau = \left(dC/d\phi \right) \left(d\phi /d\tau \right) = R{\omega }^2 \left(\cos \phi + \lambda \cos 2\phi \right), Форм. 6$

где:

• ω = dφ/dτ – угловая скорость коленчатого вала.

Тогда сила инерции P_j определится зависимостью:

$P_j = M_s R{\omega }^2 \left(\cos \phi + \lambda \cos 2\phi \right).$

Первое слагаемое этого равенства называется силой инерции поступательно движущихся масс 1-го порядка:

$P_j^1 = Ms R{\omega }^2 \cos \phi . Форм. 7$

Второе слагаемое называется силой инерции II-го порядка:

$P_j^{11} = M_s R{\omega }^2 \lambda \cos 2\phi . Форм. 8$

Как видно, амплитуды сил инерции поступательно движущихся масс возрастают пропорционально квадрату угловой скорости (или частоты вращения).

Если при разложении cosβ в биноминальный ряд взять не два члена разложения (формулы 3), а более, то тогда можно найти силы инерции 3-го, 4-го и т. д. порядков. Однако амплитуды этих сил невелики, их обычно не учитывают.

Характер изменения величин

дан на рис. 2. Как видно из рисунка, период колебания величины

$P_j^1$

равен периоду вращения коленчатого вала, а период колебания

$P_j^{11}$

— в 2 раза больше (за 1 оборот коленчатого вала сила

$P_j^{11}$

дважды меняет свою величину и на-правление). Сила инерции 1-го порядка имеет максимум в ВМТ и НМТ. При нахождении поршня в этих положениях скорость его равна 0, а ускорение — максимально.

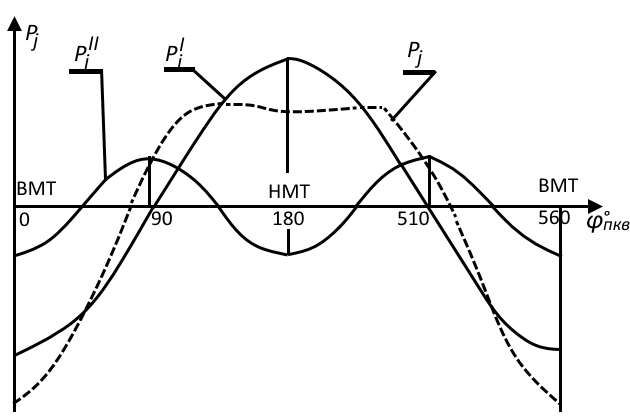
В ВМТ силы инерции действуют против направления сил от давления газов, стремятся оторвать поршень вверх. В НМТ, наоборот, — при остановке поршня силы инерции действуют вниз, по направлению действия сил давления газов. При повороте коленчатого вала на 90° от ВМТ сила инерции 1-го порядка равна нулю:

$P_j^1 = 0.$

Силы инерции 2-го порядка как в ВМТ, так и в НМТ равны по величине и по направлению и действуют против сил от давления газов на поршень. Максимальные значения силы

Причиной появления сил инерции 2-го порядка является конечная длина шатуна. Так, если принять длину шатуна бесконечной: L = ∞, то λ = R / L = 0; соответственно

$P_j^{11} = 0.$

В реальном двигателе из-за конечной длины шатуна при повороте коленчатого вала на 90° после ВМТ поршень проходит более половины своего хода. Эта разница может быть найдена с помощью зависимости 4:

$∆S = S_{\phi =90} – 1/2 S = R \left(1 + \left(1/4\right) \lambda 2\right) – R = 1/2 \lambda R = R^2 / 2L. Форм. 9$

Величина ΔS = R²/2L носит название “поправка профессора Брикса Ф. А. на конечную длину шатуна”. Она указывает, насколько поршень проходит более 1/2 своего хода при повороте кривошипа на 90° от ВМТ. Следовательно, в диапазоне φ = 0 + 90° пкв средняя скорость поршня больше, чем при φ = 90 + 180° пкв. Это обстоятельство оказывает свое влияние на соответствующее изменение ускорения поршня и появление силы инерции 2-го порядка.

Центробежные силы инерции вращательно движущихся масс кривошипа равны:

$P_j^{ц} = M_R j_{ц} = M_R R{\omega }^2, Форм. 10$

где:

• M_R – вращающиеся массы;
• j_ц = Rω² – центробежное ускорение.

Механические напряжения, возникающие в днище головки поршня,определяются только воздействием сил от давления газов. Условия же работы головного соединения определяются уже не только давлением газов, но и силами инерции поршня, его весом и силами трения между поршнем и втулкой цилиндра. Для оценки механической напряженности головного, мотылевого соединений и шатуна вводится понятие суммарной движущей силы P_Σ, равной алгебраической сумме сил от давления газов P_г, сил инерции поступательно движущихся масс P_j, сил веса поступательно движущихся масс P_g и сил трения P_тр:

$P_{\Sigma } = P_{г} + P_j + P_g + P_{тр}. Форм. 11$

Приложив силу P_Σ в центре головного подшипника, можно найти нормальное усилие N, действующее на тронк поршня, и усилие S, направленное по шатуну (рис. 3):

$N = P_{\Sigma } tg \beta \approx P_{\Sigma } Sin\beta = P_{\Sigma } \lambda Sin\phi , Форм. 12$

$S = P_{\Sigma } / Cos\beta . Форм. 13$

В зависимости (Формула 12) принято допущение: tgβ ≅ Sinβ. При малых углах это допущение не дает большой погрешности. Разложив усилие S на составляющие, найдем касательную T и радиальную R силы, действующие в кривошипношатунном механизме:

$T = S Sin\left(\phi + \beta \right) = P_{\Sigma }Sin\left(\phi + \beta \right) / Cos\beta ; Форм. 14$

$R = S Cos\left(\phi + \beta \right) = P_{\Sigma }Cos\left(\phi + \beta \right) / Cos\beta . Форм. 15$

Механическая напряженность кривошипа определяется совместным воздействием сил S и

$P_j^{ц}$

. Касательная составляющая силы S — сила T — обеспечивает крутящий момент на валу двигателя и определяет касательные напряжения вала.

Оценка механической напряженности в условиях эксплуатации

Уровень механической напряженности определяет условия смазки, износы, работоспособность подшипников, других узлов, возможность появления усталостных разрушений и т. д. При эксплуатации абсолютные величины показателей механической напряженности не контролируются ввиду сложности их определения. Однако механическая напряженностьИзменение механической напряженности может быть оценена по косвенным показателям.

Максимальные напряжения в деталях движения и в подшипниках определяются максимальной движущей силой. Величина этой силы может быть принята равной:

$P_{\Sigma }^{max} \approx P_z – P_j^{max},$

где:

• P_z – усилие от максимального давления сгорания.

Можно написать:

$P_j^{max} = M_s R{\omega }^2 \left(1 + \lambda \right) = M_s R {\left(\pi n/30\right)}^2 \left(1 + \lambda \right) = k_j n^2$

здесь

$k_j = M_s R {\left(\pi /30\right)}^2 \left(1 + \lambda \right).$

Тогда:

$P_{\Sigma }^{max} \approx P_z – k_j n^2. Форм. 16$

Работоспособность деталей зависит не только от максимальной движущей силы, но и от амплитуды ее изменения, определяющей усталостные разрушения. В 2-тактных двигателях изменение движущей силы может быть принято от 0 (в НМТ) до

$P_{\Sigma }^{max}$

(в районе ВМТ). Поэтому амплитуда силы 2-тактных ДВС равна:

$∆P_{\Sigma } = 1/2 P_{\Sigma }^{max} \approx 1/2 \left(P_z – k_j n^2\right). Форм. 17$

В 4-тактных двигателях диапазон изменения силы — от (-P_j^max) в конце такта выталкивание газов до

$P_{\Sigma }^{max}$

— в начале рабочего хода; амплитуда действующей силы определится равенством:

$∆P_{\Sigma } = 1/2 \left(P_{\Sigma }^{max} + P_j^{max}\right) \approx 1/2 P_z. Форм. 18$

Следовательно, 4-тактные двигатели при прочих равных условиях имеют большую амплитуду ΔP_Σ, чем 2-тактные, и являются более напряженными.

Максимальные касательные напряжения в шейках коленчатого вала зависят от максимального касательного усилия

$T_{\Sigma }^{max}$

:

$T_{\Sigma }^{max} = T + ∆T_{\Sigma },$

где:

• ${\overline{T}}_{\Sigma }$

  – среднее касательное усилие;

• ΔT_Σ – амплитуда отклонения касательного усилия.

Работа за один оборот коленчатого вала двигателя любой тактности, выраженная через средее касательное усилие, равна:

$L = {\overline{T}}_{\Sigma } 2\mathrm{\pi R}. \mathrm{Форм}. 19$

С другой стороны, можно эту работу выразить через среднее индикаторное давление:

$L = p_i F 2R i/m, Форм. 20$

где

• i – число цилиндров;
• m – коэффициент тактности;
• 2R = S – ход поршня;
• F – площадь поршня.

Приравняв правые части зависимостей 19 и 20, можно найти:

${\overline{T}}_{\Sigma } = p_i F 2R i/\left(2\mathrm{\pi R} \mathrm{m}\right) = K_m p_i, Форм. 21$

где:

• K_m = F i/(πm) – величина, постоянная для каждого двигателя.

Как показывают расчеты динамики, независимо от тактности дизеля амплитуда касательных усилий выражается приближенным равенством:

$∆T_{\Sigma } \approx 0,2 P_z, Форм. 22$

С учетом равенства 21 и 22 величина

$T_{\Sigma }^{max}$

выразится зависимостью:

$T_{\Sigma }^{max} \approx K_m p_i + 0,2 P_z. Форм. 23$

Из приведенных формул видно, что при неизменной частоте вращения величины

$P_{\Sigma }^{max}, ∆P_{\Sigma }, ∆T_{\Sigma }$

полностью определится величиной максимального давления в цилиндре (давление сгорания)

P_z, а

$T_{\Sigma }^{max}$

— величина P_z и P_i. Следовательно, в условиях эксплуатации для конкретного скоростного режима вполне обоснованным и наиболее объективным критерием механической напряженности двигателя является максимальное давление цикла P_z и среднее индикаторное давление P_i.

Расчетное определение сил, действующих в кривошипно-шатунном механизме

Расчетное определение сил, действующих в кривошипно-шатунном механизме, и последующая расчетная оценка механической напряженности может быть выполнена с помощью совмещенных би-центровой диаграммы проф. Брикса, индикаторной диаграммы и диаграммы сил инерции Толле (рис. 4). Для упрощения расчетов все силы относятся к 1 см² площади поршня, т. е. имеют размерность давления.

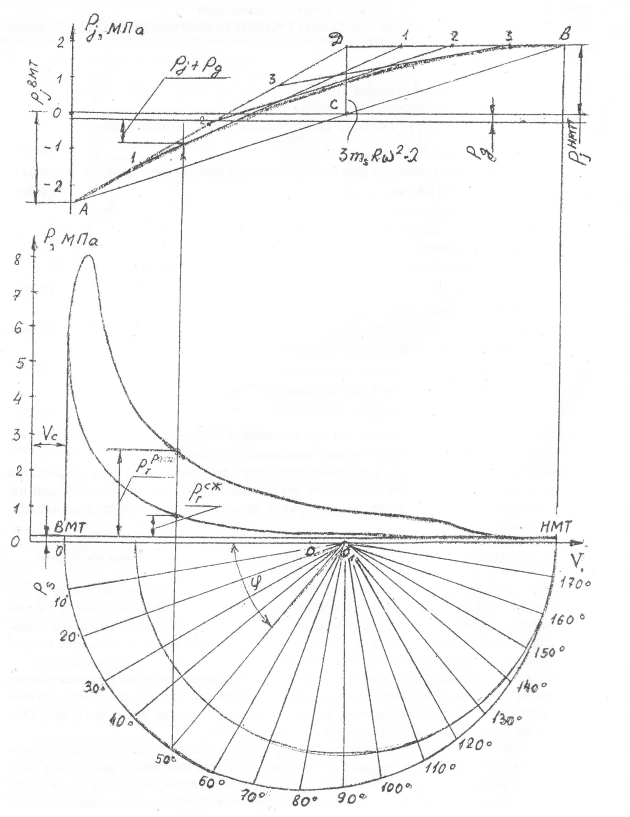
Индикаторная диаграмма берется по данным расчета индикаторного процесса или же принимается по данным индицирования реального двигателя. Диаграмма Брикса обычно строится под индикаторной диаграммой, как это показано на рисунке. Поправка Брикса ОО₁ на конечную длину шатуна рассчитывается по формуле 9.

Диаграмма Толле позволяет упростить определение сил инерции поступательно движущихся масс в функции от угла поворота коленчатого вала. При построении диаграммы силы инерции, действующие по направлению действия сил давления газов, считаются положительными. Таким образом, в ВМТ сила инерции поступательно движущихся масс равна:

$P_j^{вмт} = –\left(M_s/F\right) R{\omega }^2 \left(1 + \lambda \right) = –m_s R{\omega }^2 \left(1 + \lambda \right){10}^{–2}, МПа. Форм. 24$

Соответственно в НМТ:

$P_j^{нмт} = m_s R{\omega }^2 \left(1 – \lambda \right){10}^{–2}, МПа. Форм. 25$

Здесь:

• m_s = M_s/F – масса поступательно движущихся частей, отнесенная к 1 см² площади поршня, кг/см²;
• R – радиус кривошипа, м;
• ω – угловая скорость, l/с;
• λ = R/L – отношение радиуса кривошипа к длине шатуна.

Как было отмечено, величина M_S, кг, складывается из массы поршня и поступательно движущейся части шатуна: M_S = M_П + M_ШS. Для определения величины поступательно движущейся массы шатуна M_шs делается допущение, что масса шатуна сосредоточена в 2-х точках: в центре поршневого пальца – поступательная масса M_ШS, в центре кривошипа – вращающаяся масса M_ШR (рис. 5).

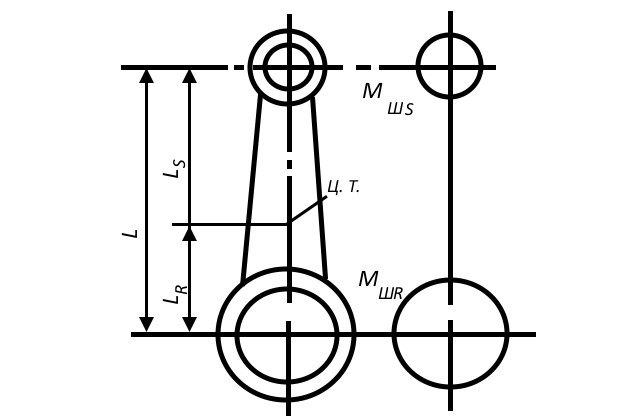
Величины M_ШS и M_ШR находятся из равенств:

$M_{Ш} = M_{ШS} + M_{ШR};$

$M_{ШR}/L_S = M_{ШS} + L_R, Форм. 26$

где:

• L_R и L_S – расстояние от центра тяжести шатуна соответственно до центра кривошипа и центра поршневого пальца.

Обычно L_R = 0,25 ÷ 0,52 L (верхние значения – для малооборотных ДВС).

Отложив ординаты

$P_j^{вмт} и P_j^{нмт}$

на диаграмме Толле и найдя точки A и B, соединяют их прямой и находят точку С. Из точки С восстанавливают перпендикуляр, на котором откладывается величина CD = 3m_sRω²λ. Найденная точка D соединяется с точками A и B, отрезки AD и DB делятся на равное количество частей. Найденные точки 1, 2, 3 и т. д. соединяются прямыми, как это показано на рис. 4. К этим прямым проводится касательная кривая, которая и определяет величину сил инерции в функции от хода поршня (или объема цилиндра).

 
Для нахождения давления газов и сил инерции в функции угла поворота коленчатого вала диаграмма Брикса разбивается из точки O₁ лучами через 5 ÷ 15° пкв. Для каждого угла поворота коленчатого вала давление газов и сила инерции находится путем восстановления ординаты из точки пересечения соответствующего луча с полуокружностью радиуса R, проведенной из точки О.

При определении давления газов необходимо учитывать лишь избыточное давление, без учета давления в подпоршневой области (P_o или P_s). Силы трения P_тр при расчете P_Σ обычно не учитывается – в дальнейшем они учитываются механическим КПД. Силы веса поступательно движущихся частей, отнесенные к 1 см² площади поршня, откладываются вниз от оси абсцисс на диаграмме Толле. В дальнейшем ординаты P_j + P_g снимаются от линии, проходящей параллельно оси абсцисс на расстоянии P_g.

$P_g = m_{s}9.81 {10}^{–2}, МПа.$

Определение сил динамики ведется в табличной форме в пределах φ = 0 ÷ 360° пкв для 2-тактных ДВС и φ = 0 ÷ 720° пкв для 4-тактных ДВС (табл. 1)

 
Расчет сил P_Σ, N, R, Т₁ ведется по формулам 11-15. Тригонометрические функции рассчитываются или принимаются по справочникам в зависимости от величины λ. Касательные усилия T₁ первого цилиндра (столбец 10) повторяются в последующих столбцах с учетом угла заклинки кривошипов и последовательности работы цилиндров. Так, если в 6-цилиндровом 2-тактном двигателе последовательность работы цилиндров 1-5-3-4-2-6, то для 5-го цилиндра необходимо повторить записи T₁ со смещением по фазе на 60° пкв, для 3-го на 120° пкв и т. д.

В многоцилиндровом двигателе коленчатый вал воспринимает и передает суммарный крутящий момент, определяемый суммарным касательным усилием T_Σ = ΣT_i. Расчетом T_Σ для каждого значения φ заканчивается построение таблицы сил динамики. По данным таблицы строятся кривые сил динамики. Примерный вид кривых динамики для 6-цилиндрового 2-тактного дизеля на рис. 6.

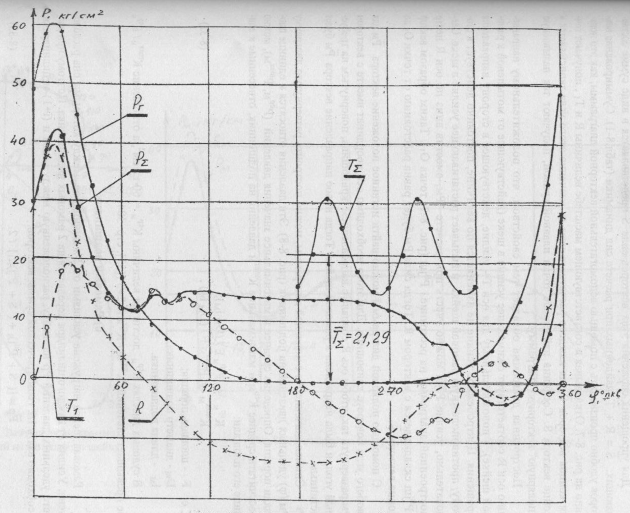
Правильность расчета сил динамики проверяется путем определения среднего касательного усилия по всем цилиндрам и нахождения индикаторной мощностиИндикаторная и эффективная мощность двигателя дизеля. Среднее касательное усилие можно найти путем планиметрирования площади под кривой T_Σ(φ) или же аналитическим путем – суммированием ординат под кривой T_Σ(φ):

${\overline{T}}_{\Sigma } \approx \Sigma T_x/k, Форм. 27$

где:

• k = 360m/(Δφ i) – число ординат, приходящихся на один период кривой T_Σ(φ);
• m – коэффициент тактности двигателя;
• i – число цилиндров;
• Δφ – шаг по оси абсцисс, с которым определяются ординаты T_x.

По найденному значению

${\overline{T}}_{\Sigma }$

рассчитываются крутящий момент и индикаторная мощность двигателя:

$M_{кр} = {\overline{T}}_{\Sigma } R F, Форм. 28$

$N_i = M_{кр} 2\mathrm{\pi } \mathrm{n}/0.06, \mathrm{кВт}. \mathrm{Форм}. 29$

Найденная индикаторная мощность сравнивается с мощностью, определенной по индикаторной диаграмме. Считается допустимым расхождение не более 3-4 %.

Рекомендуем к прочтению: Параметры топливоподачи и факторы, их определяющие

Для расчета центробежной силы, действующей в кривошипе, необходимо вращающиеся массы шатуна (M_ШR), мотылевой шейки (M_МШ), щек (M_Щ) и противовесов (M_ПР) привести к одному радиусу по формуле: M′ = Mr/R (из условия

$P_j^{ц} = M r{\omega }^2 = M\prime R{\omega }^2$

, где M′ – приведенная масса, r – расстояние от центра тяжести массы до оси коленчатого вала, R – радиус приведения). Обычно массы приводятся к радиусу кривошипа R. В случае, когда 2 противовеса расположены противоположно колену, неуравновешенные приведенные массы равны:

$M_R = M_{ШR} + M_{MШ} + 2M{\prime }_{Щ} – 2M{\prime }_{ПР}. Форм. 30$

Центробежные силы вращающихся масс определяются зависимостью 10:

$P_j^{ц} = M_R R{\omega }^2.$

Найденные силы динамики являются исходными при оценке условий работы подшипников, расчетах неравномерности вращения коленчатого вала, оценке уравновешенностиПонятие уравновешенности. Действие неуравновешенного двигателя на фундамент и корпус судна и прочностных расчетах деталей двигателя.

Оценка условий работы подшипников коленчатого вала

Условия работы подшипников в общем случае могут быть оценены комплексом параметров — скоростью скольжения цапфы относительно подшипника, средним и максимальным давлением на подшипник, отношением максимального давления к среднему. Последнее отношение характеризует степень ударности нагрузки на подшипник и определяет надежность его работы.

Относительная скорость скольжения в подшипниках судовых дизелей весьма умерена. Она обычно находится в пределах: C_n = 3-12 м/сек (нижние значения — для малооборотных дизелей). Поэтому основным фактором, определяющим надежность работы подшипников судовых ДВС, является величина и характер изменения давления на подшипники.

Давление на головной подшипник полностью определяется величиной и характером изменения суммарной движущей силы P_Σ, определенной при расчетах сил динамики (табл. 1). Для оценки давлений на мотылевой и рамовый подшипники также используются данные табл. 1.

Мотылевый подшипник

Сила P_м, действующая на мотылевый подшипник, определяется геометрической суммой векторов (рис. 3):

${\overline{P}}_{м} = \overline{S} + {\overline{P}}_j^{цш}, Форм. 31$

где:

• $\overline{S}$

  – вектор силы, действующей по шатуну;

• ${\overline{P}}_j^{цш}$

  – вектор центробежной силы вращательно движущихся масс шатуна (

  $P_j^{цш} = M_{ШR} R{\omega }^2$

  ).

Для упрощения сложения этих векторов сила 

$\overline{S}$

представляется в виде сумме составляющих:

$\overline{S} = \overline{R} + \overline{T},$

, найденных при расчете сил динамики (табл. 1). Суммирование векторов удобно производить с помощью вспомогательной векторной диаграммы, как это показано на рис. 7.

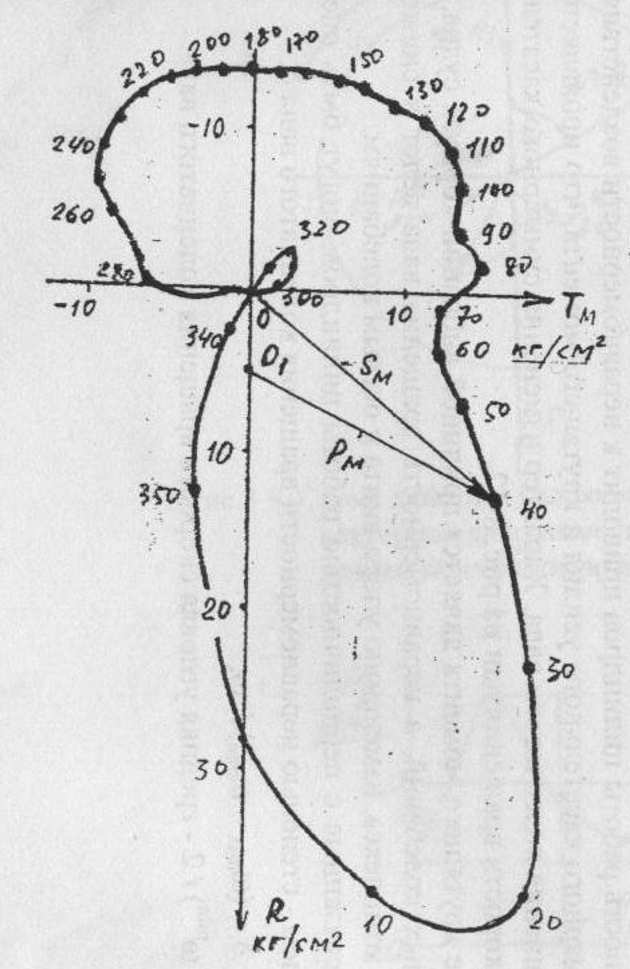
Откладывая в соответствующем масштабе величины R_i и T_i, получают точки концов векторов 

${\overline{S}}_i$

для каждого расчетного угла φ. Значение этого угла записывается в конце вектора

$\overline{S}$

. Соединив найденные точки плавной кривой, получают так называемую “полярную” векторную диаграмму.

Построенная диаграмма обладает тем свойством, что положительному направлению оси R соответствует сжимающее усилие в щеке (действующее от мотылевой к рамовой шейке), а положительному для оси T — усилие, действующее в сторону направления вращения. Центробежное усилие не изменяется по величине, постоянно действует в сторону, противоположную рамовой шейке, и вызывает растягивающее усилие в щеке. Следовательно, усилие

${\overline{P}}_j^{цш}$

можно учесть при расчете

${\overline{P}}_{м}$

, сместив вниз по оси R центр построенной диаграммы на расстояние

${\overline{P}}_j^{цш}$

(рис. 7, точка О₁. Таким образом вектор

${\overline{P}}_j^{цш}$

складывается с вектором R. Тогда сила P_м будет равна расстоянию от точки O₁ до конца вектора

$\overline{S}$

.

С помощью полярной диаграммы можно найти истинное положение вектора

${\overline{P}}_{м}$

для любого угла поворота кривошипа. Для этого необходимо оси координат вместе с вектором P_м развернуть так, чтобы ось R совпала с направлением кривошипа, повернутым на требуемый угол, и была направлена к рамовой шейке. Тогда новое направление вектора

${\overline{P}}_{м}$

будет истинным.

 
Снимая значение P_м с полярной диаграммы, можно построить развернутую диаграмму P_м(φ) удельных давлений на подшипник (рис. 8).

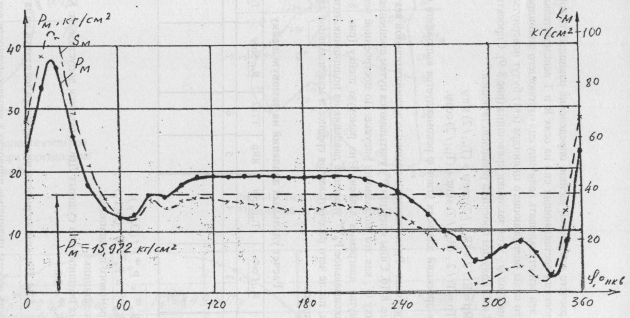
Эти давления относятся к единице площади поршня. Определив среднее и максимальное значения давлений (

$P_{м}^{ср}, P_{м}^{max}$

), можно рассчитать среднее

$K_{м}^{ср}$

и максимальное

$K_{м}^{max}$

давления на подшипник, отнесенные к единице его площади:

$K_{м}^{ср} = P_{м}^{ср} F/\left(D_{М}{l}_{М}\right);$

$K_{м}^{max} = P_{м}^{max} F/\left(D_{М}{l}_{М}\right), Форм. 32$

где:

• F – площадь поршня;
• D_М – диаметр подшипника;
• l_М – длина подшипника.

В судовых дизелях при баббитовой заливке подшипников

$K_{м}^{ср}$

достигает величины

$K_{м}^{ср} = 60$

бар, а отношение

$K_{м}^{max}/K_{м}^{ср}$

не превышает значений:

$K_{м}^{max}/K_{м}^{ср} = 2÷3.$

В современных дизелях с высокими параметрами рабочего процесса средние давления достигли велчины

$K_{м}^{ср} = 70–80$

бар, отношение

$K_{м}^{max}/K_{м}^{ср} = 3,5$

, что потребовало более прочного материала для заливки подшипников.

Рамовый подшипник

Рамовая шейка нагружена усилиями от 2-х цилиндров, между которыми она расположена. Усилия от каждого цилиндра передается на 2 рамовых подшипника. Поэтому при расчете удельных давлений P_p на шейку, расположенную между i-тым и (i+1)-м цилиндрами, необходимо взять 1/2 геометрической суммы векторов:

${\overline{P}}_p = \left[{\left(\overline{S} + {\overline{P}}_j^{ц}\right)}_i + {\left(\overline{S} + {\overline{P}}_j^{ц}\right)}_{i+1}\right]/2. Форм. 33$

Центробежное усилие

$P_j^{ц}$

определяется массой не только вращающейся части шатуна, но и массой щеки, мотылевой шейки и противовесов:

$P_j^{ц} = m_R R{\omega }^2. Форм. 34$

Как и при расчете мотылевой шейки, определение равнодействующей P_p удобно выполнять через проекции составляющих сил на осях R и T вспомогательной векторной диаграммы. Если на эти оси откладывать величину сил отстающего цилиндра (примем, что это — i-тый цилиндр), то силы опережающего цилиндра (i+1) будут повернуты в сторону направления вращения на угол Ψ — угол заклинки кривошипа (рис. 9).

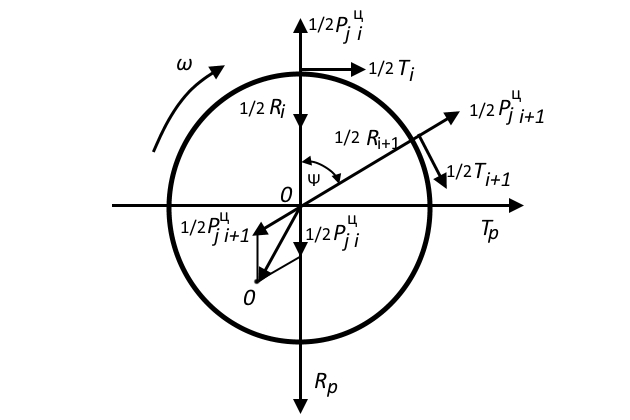
Спроектировав силы R_i+1/2 и T_i+1/2 на оси R и T, получим проекции равнодействующей:

$R_p = R_i/2 + \left(R_{i+1}/2\right) \cos \psi + \left(T_{i+1}/2\right) \sin \psi ;$

$T_p = T_i/2 – \left(R_{i+1}/2\right) \sin \psi + \left(T_{i+1}/2\right) \cos \psi . Форм. 35$

Расчет этих проекций для всех углов φ рекомендуется выполнять в табличной форме (табл. 2):

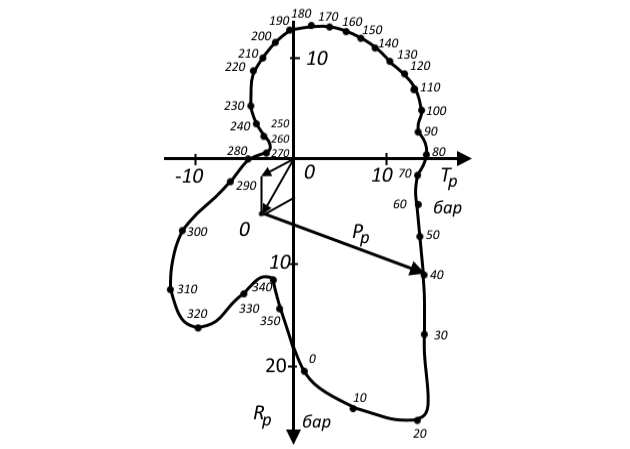
Равнодействующая

${\overline{P}}_p$

находится с помощью вспомогательной векторной диаграммы. Силы инерции i-того

$(P_j^{ц}{ }_i/2)$

и (i+1)-ого

$(P_j^{ц}{ }_{i+1}/2)$

цилиндров учитываются путем смещения центра диаграммы из точки О в точку О′, как это показано на рисунке. По построенной векторной диаграмме строится развернутая диаграмма давлений на рамовую шейку (рис. 11), определяются среднее

$P_p^{ср}$

и максимальное

$P_p^{max}$

удельные давления на подшипник, отнесенные к единице площади поршня, после чего рассчитывается среднее и максимальное давление на единицу площади подшипника:

$K_p^{ср} = P_p^{ср} F/\left(D_p{l}_p\right);$

$K_p^{max} = P_p^{max} F/\left(D_p{l}_p\right), Форм. 36$

где:

• D_p – диаметр рамового подшипника;
• l_p – длина подшипника.

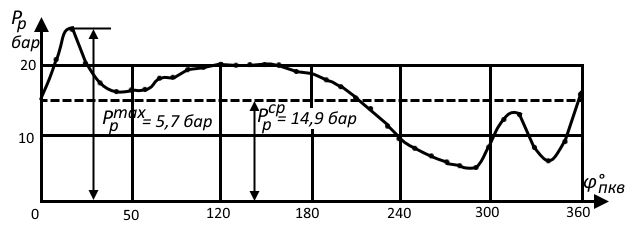
Для рамовых подшипников судовых ДВС считается допустимым:

$K_p^{ср} = 50$

бар, отношение

$K_p^{max}/K_p^{ср} = 3,0.$

Неравномерность вращения коленчатого вала

Периодичность работы цилиндров приводит к неравномерности воздействия на коленчатый вал суммарного касательного усилия и крутящего момента, что проявляется в неравномерности вращения коленчатого вала. Характер изменения суммарного касательного усилия и угловой скорости вращения дан на рис. 12.

Изменение крутящего момента является причиной вибрации корпуса судна, возникновения крутильных колебаний, а неравномерность вращения вала ведет к снижению КПД движительного комплекса, изменению упора винта и осевым колебаниям.

Явления, связанные с периодичностью работы цилиндров, могут быть оценены численно показателем — степенью неравномерности вращения коленчатого вала δ:

$\delta = \left({\omega }_{max} – {\omega }_{min}\right)/\overline{\omega }, Форм. 37$

где:

• $\overline{\omega } = \left({\omega }^{max} + {\omega }^{min}\right)/2, l/с$

  – средняя угловая скорость вращения коленчатого вала.

Рассмотрим, какие факторы определяют величину δ. Для этого на основании теоремы об изменении кинетической энергии системы запишем:

$∆A = \mathfrak{I} \left({{\omega }^2}_{max} – {{\omega }^2}_{min}\right)/2, Форм. 38$

где:

• ΔA – избыток (или недостаток) работы движущих сил по сравнению с работой сил со-противления;
• $\mathfrak{I}$

  – момент инерции вращающихся масс валопровода.

Величина ΔA в соответствующем масштабе определяется площадью ΔF₁ = ΔF₂ на рис. 12. Преобразуем равенство 38. Запишем:

$2∆A/\mathfrak{I} = \left({\omega }_{max} + {\omega }_{min}\right) \left({\omega }_{max} – {\omega }_{min}\right) = 2 \overline{\omega } \left({\omega }_{max} – {\omega }_{min}\right).$

Тогда:

$\delta = \left({\omega }_{max} – {\omega }_{min}\right)/\overline{\omega } = ∆A/\left(\mathfrak{I} {\overline{\omega }}^2\right), Форм. 39$

Так как:

$\overline{\omega } = \mathrm{\pi n}/30;$

$\mathfrak{I} = m{r}^2 = \left(G/g\right) r^2,$

То:

$\delta = ∆A \left(g/G{r}^2\right) {\left(30/\mathrm{\pi n}\right)}^2 \approx 900 ∆A/\left(G{r}^2{n}^2\right). Форм. 40$

В этих равенствах:

• n – частота вращения, об/мин;
• G – приведенный вес вращающихся частей, кг;
• r – радиус инерции вращающихся частей, м;
• g – ускорение свободного падения, м/сек²;

Если взять не радиус, а диаметр инерции вращающихся масс: D = 2r, то равенство 40 можно записать в виде:

$\delta \approx 3 600 ∆A/\left(G{D}^2{n}^2\right). Форм. 41$

Величина GD² – это маховый момент вращающихся масс; он связан с момент инерции зависимостью:

$G{D}^2 = M g {\left(2r\right)}^2 = M{r}^2 4g = 39,2 \mathfrak{I} кг {м}^2. Форм. 42$

Как видно из равенств  формул 39 и 41, неравномерность вращения коленчатого вала прямопропорциональна величине избыточной (или недостающей) работы ΔA и обратно пропорциональна моменту инерции вращающихся деталей

$\mathfrak{I}$

(или маховому моменту GD²) и квадрату частоты вращения n².

Избыточная работа может быть найдена с помощью графика T_Σ(φ), построенного по итогам расчета сил динамики в кривошипно-шатунном механизме (рис. 12). Определив площадь ΔF наибольшей площадки между кривой T_Σ(φ) и линией

${\overline{T}}_{\Sigma }$

, можно рассчитать ΔA:

$∆A = ∆F F m_f, Форм. 43$

где:

• F – площадь поршня, см²;
• m_f = m_p m_φ – масштаб площади диаграммы, кгм/см²мм²;
• m_p – масштаб оси ординат, кг/см²мм;
• m_φ = π 2R/lт – масштаб оси абсцисс, м/мм;
• R – радиус кривошипа, м;
• l_m – длина оси абсцисс, соответствующая 360° пкв, мм;
• ΔF – избыточная площадь, мм².

$\mathfrak{I} = {\mathfrak{I}}_{кв} + {\mathfrak{I}}_{мех} + {\mathfrak{I}}_{р} + {\mathfrak{I}}_{в} + {\mathfrak{I}}_{гр}. Форм. 44$

Моменты инерции каждого элемента определяются с помощью зависимости:

$\mathfrak{I}x = {М}_x r^2, Форм. 45$

где:

• M_x – масса вращающегося элемента, кг/сек²/м;
• r – его радиус инерции, м.

При расчетах судовых дизелей радиусы инерции мотылевых шеек, щек, противовесов обычно принимаются равными расстоянию от оси коленчатого вала до центра тяжести элемента. Вращающуюся массу шатуна считают сосредоточенной в центре мотылевой шейки. Для сплошного вала, вращающегося относительно своей оси, радиус инерции равен:

$r = 0,5d\sqrt{2},$

где:

• d – диаметр вала.

В практике расчетов степени неравномерности вращения коленчатого вала часто пользуются другим способом, отличным от рассмотренного выше, не связанным с необходимостью определения численной величины избыточной работы ΔA. Для этого зависимость 39 преобразуется следующим образом:

$\delta = \left(∆A/\left(\mathfrak{I}{\left(\mathrm{\pi n}/30\right)}^2\right)\right) N_i/N_i.$

Индикаторная мощность N_i может быть выражена через работу A_o, совершаемую двигателем за один оборот коленчатого вала:

$N_i = A_o n/\left(60 75\right) илс.$

Тогда:

$\delta = \left(∆A N_i/\left(\mathfrak{I}{\left(\mathrm{\pi n}/30\right)}^2\right)\right)\left(60 75/\left(A_o n\right)\right) = \left(60 75 {30}^2/{\mathrm{\pi }}^2\right) \left(Ni/\left(\mathfrak{I}{n}^3\right)\right) ∆A/A_o$

Или:

$\delta = 0,41 {10}^6 \left(N_i/\left(\mathfrak{I}{n}^3\right)\right) ∆A/A_o.$

Отношение работы ΔA/A_o численно равно отношению избыточной площади ΔF к площади F_o под линией

${\overline{T}}_{\Sigma }$

(рис. 6) на протяжении 360° пкв независимо от тактности двигателя. Поэтому можно записать:

$\delta = 0,41 {10}^6 \left(Ni/\left(\mathfrak{I}{n}^3\right)\right) ∆F/F_o. Форм. 46$

Если мощность дана в N_i кВт, момент инерции

$\mathfrak{I}$

кг м², то формула имеет вид:

$\delta = 0,548 {10}^7 (N_i/\left(\mathfrak{I}{n}^3\right)) ∆F/F_o. Форм. 47$

Обычно степень неравномерности вращения коленчатого вала находится в пределах:

• δ = 1/200 ÷ 1/300 – для дизель-генераторов переменного тока;
• δ = 1/100 ÷ 1/150 – для дизель-генераторов постоянного тока;
• δ = 1/30 ÷ 1/40 – для главных судовых дизелей (без учета вращающихся масс валопровода и винта).

В двигателях малой и средней размерности момент инерции определяется главным образом массой маховика. Поэтому требуемая степень неравномерности вращения коленчатого вала обеспечивается выбором соответствующего маховика. В судовых малооборотных двигателях маховик практически не влияет на неравномерность вращения коленчатого вала — он выполняет роль приводного зубчатого колеса валоповоротного механизма.

На малых нагрузках главных двигателей, а также при отключении цилиндров в аварийных случаях неравномерность вращения повышается в 2-3 раза. Соответственно растет вибрация корпуса судна.

Крутильные и осевые колебания валопровода

Валопровод любого судна представляет собой колебательную систему, поскольку включает в себя 2 разнородных накопителя энергии: упругость вала (потенциальная энергия) и массу (кинетическая энергия). При изменении внешнего воздействия на валопровод потенциальная энергия “закрученного” вала превращается в кинетическую энергию колеблющихся масс и наоборот — возникают крутильные колебания валопровода. При этом в валопроводе развиваются дополнительные касательные напряжения, иногда приводящие к самой серьезной аварии — поломке коленчатого вала. Характерным признаком разрушения вала из-за крутильных колебаний является расположение плоскости разлома под углом ~45° к оси вала.

Величина касательных напряжений при крутильных колебаниях при прочих равных условиях зависит от 2-х факторов:

1. От амплитуды изменения крутящего момента (или суммарного касательного усилия);
2. От совпадения частоты изменения внешнего воздействия и собственной частоты колебаний валопровода. Дизельная силовая установка имеет значительные отклонения M_кр от его среднего значения и поэтому требует особого внимания с точки зрения крутильных колебаний (по сравнению с паротурбинной и газотурбинной силовыми установками, у которых M_кр = const).

По Правилам Регистра перед установкой дизеля на судно выполняется расчет валопроводаРемонт валопроводов и судовых гребных винтов на крутильные колебания — определяются собственная частота колебаний, величина дополнительных касательных напряжений на различных частотах вращения, устанавливаются зоны критических оборотов, опасные для работы дизеля. На головном судне расчеты проверяются экспериментально и уточняются. Материалы расчета на крутильные колебания выдаются на судно. Рассмотрим факторы, определяющие собственную частоту колебаний валопровода. Для этого в простейшем случае для одноузловой колебательной системы (рис. 13) запишем уравнение крутильных колебаний в виде:

$\mathfrak{I} \left(d^2 \phi /d{\tau }^2\right) + c\phi = 0, Форм. 48$

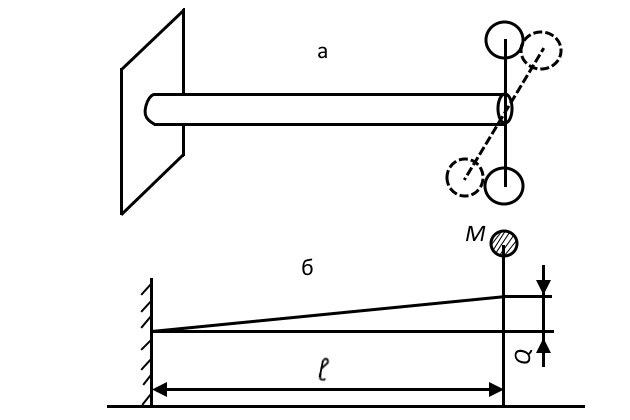
где:

• $\mathfrak{I}$

  – момент инерции массы M относительно оси вала;

• φ – угол отклонения массы от равновесного состояния;
• C – жесткость вала;
• τ — время.

Жесткость вала определяется зависимостью:

$C = \left(C_{II} W_p\right)/l, Форм. 49$

где:

• G_II – модуль упругости материала вала II рода;
• W_p – полярный момент инерции поперечного сечения вала (для круглового вала W_p = πd⁴/32);
• l – длина вала.

Угол закрутки вала φ зависит от величины скручивающего момента M_кр и жесткости вала C:

$\phi = M_{кр}/C = M_{кр}l/\left(G_{II}{W}_p\right).$

Угловая частота колебаний со связана с жесткостью C и моментом инерции

$\mathfrak{I}$

известной зависимостью:

$\omega = \sqrt{C/\mathfrak{I}}, l/сек. Форм. 50$

Подставив это равенство в формулу 48, получим:

$d^2\phi /\left(d{\tau }^2\right) + {\omega }^2\phi = 0$

Решением этого дифференциального уравнения является уравнение вида:

$\phi = B \sin \omega \tau + A \cos \omega \tau . Форм. 51$

Приняв начальные уравнения: τ = 0; dφ/dτ = 0; φ = A, получим решение: φ = A cos ωτ.

Как видно, крутильные колебания рассматриваемой схемы являются гармоническими с максимальной угловой амплитудой A и угловой частотой ω.

Из зависимостей 49 и 50 можно найти период колебаний T и собственную частоту колебаний ν:

$T = 2\mathrm{\pi }/\mathrm{\omega } = 2\mathrm{\pi } \sqrt{\mathfrak{I}·\mathrm{l}/\left({\mathrm{G}}_{\mathrm{II}}·{\mathrm{W}}_{\mathrm{p}}\right)}, \mathrm{с}; \mathrm{Форм}. 52$

$\nu = \left(30/\mathrm{\pi }\right)\omega = \left(30/\mathrm{\pi }\right)\sqrt{G_{II}·W_p/\left(\mathfrak{I}·l\right)}, кол/мин. Форм. 53$

Из равенства 53 можно сделать вывод, что собственная частота колебаний снижается при увеличении момента инерции (увеличении массы), увеличении длины валопровода, уменьшении полярного момента (уменьшении диаметра вала) и не зависит от величины крутящего момента. Этот вывод справедлив и для любой сколь угодно сложной крутильной системы.

В случае 2-массовой колебательной системы (рис. 14) угловая амплитуда в точке “y” равна 0. Это — узел колебаний. Как видно, узел один, поэтому система называется одноузловой. Частота собственных (свободных) колебаний такой системы определяется по формуле:

$\omega = \sqrt{\left({\mathfrak{I}}_1 + {\mathfrak{I}}_2\right)·C_{1–2}/\left({\mathfrak{I}}_1·{\mathfrak{I}}_2\right)}, Форм. 54$

где:

• ${\mathfrak{I}}_1 и {\mathfrak{I}}_2$

  – моменты инерции масс M₁ и M₂;

• C_1-2 – жесткость вала.

При 3-х массах возможна одно- и двухузловая форма колебаний (рис. 15).

Частота собственных колебаний определяется зависимостью:

$\omega = \sqrt{A \pm \sqrt{A^2 – B}}, Форм. 55$

где:

• (+) при 2-узловой схеме;
• (-) при 1-узловой схеме;

$A = C_{1–2} \left({\mathfrak{I}}_1 + {\mathfrak{I}}_2\right)/\left(2{\mathfrak{I}}_1 {\mathfrak{I}}_2\right) + C_{2–3}\left({\mathfrak{I}}_2 + {\mathfrak{I}}_3\right)/\left(2{\mathfrak{I}}_2 {\mathfrak{I}}_3\right), Форм. 56$

$B = C_{1–2} C_{2–3} \left({\mathfrak{I}}_1 + {\mathfrak{I}}_2 + {\mathfrak{I}}_3\right)/\left({\mathfrak{I}}_1 {\mathfrak{I}}_2 {\mathfrak{I}}_3\right). Форм. 57$

Дизельная силовая установка представляет собой многомассовую многоузловую колебательную систему. Для ее расчета применяют более сложные методы (метод Терских, Толле, Хольцера и др.), дающие достаточно близкие данные к истинным.

При расчетах, не требующих высокой точности (к примеру, при проверке валопровода в эксплуатационных условиях, когда необходимо определить критическую частоту вращения коленчатого вала после демонтажа элементов движения) валопровод может быть представлен в виде 2-х или 3-массовой колебательной системы.

В этом случае массы всех цилиндров считаются сосредоточенными в центре тяжести двигателя, что позволяет рассчитать собственную частоту колебаний валопровода наиболее важных форм — одноузловой (по формуле 54) и 2-узловой (по формуле 55).

При расчетах системы валопровода на крутильные колебания гребной и коленчатые валы заменяются общим приведенным (эквивалентным) валом, имеющем по всей длине неизменный диаметр d_o и обладающий такими же упругими свойствами, что и действительный вал. По условию упругой эквивалентности, должно быть равенство углов скручивания при действии одного и того момента:

$\phi = M_{кр} l/\left(G_{II} W_p\right) = M_{кр} l_o/\left(G_{II} W_{po}\right), Форм. 58$

где:

• l_о = l W_po/W_p – приведенная длина вала;
• W_po = πd _о⁴/32 – полярный момент инерции приведенного вала;
• 2r_o = d_o – диаметр приведенного вала.

Действительные массы заменяются приведенными массами по формуле (из условия

):

$m_o = m r^2/{r_o}^2. Форм. 59$

Расчет обычно выполняется в относительной форме — приведенная масса одного цилиндра и приведенная длина между 2-мя цилиндрами принимаются равными 1; элементы остальных участков выражаются в долях от принятого за единицу.

После определения собственных частот колебаний валопровода определяются резонансные частоты и запретные (критические) частоты вращения коленчатого вала. Резонансными будут являться частоты, рассчитанные по формуле:

$n_{рез} = {\nu }_{собств}/K, Форм. 60$

где:

• K = 1, 2, 3, 4… – последовательный ряд целых чисел.

При совпадении частоты вращения коленчатого вала с найденными резонансными частотами в валопроводе развиваются крутильные колебания, увеличивается амплитуда колебаний, появляются дополнительные скручивающие моменты. Однако не все резонансные частоты являются опасными для работы двигателя. Силы трения в колебательной системе (силы “упругого гистерезиса”) препятствуют развитию крутильных колебаний.

Лишь на некоторых частотах дополнительные скручивающие моменты могут привести к разрушению вала. Для определения этих частот проводится расчет дополнительных напряжений в валопроводе от крутильных колебаний на резонансных частотах и устанавливаются запретные зоны работы двигателя.

Наиболее опасными являются частоты вращения, определяемые зависимостью:

$n = {\nu }_{собств}/\left(i m\right), Форм. 61$

где:

• i – число цилиндров;
• m – коэффициент тактности двигателя.

При такой частоте вращения частота вспышек работающих цилиндров совпадает с собственной частотой колебаний валопровода.

К примеру, на судах типа “Лисичанск” собственная частота колебаний валопровода в 1-узловой форме равна ν_собств= 387 кол/мин. Резонансными являются частоты 387; 193,5; 129; 96,75; 77,4; 64,5; 55,3; 48,4; 43; 38,7;…. Поскольку главный двигатель является 9-цилиндровым 2-тактным, то наиболее опасной является частота вращения n = 387/9 = 43 об/мин.

Расчет на прочность позволил установить, что дополнительные касательные напряжения при этом — более 350 кг/см², что выше допустимого (рис. 16). Фирма-строитель установила зону запретных частот вращения n_кр = 40-47 об/мин. На остальных резонансных частотах в зоне работы двигателя дополнительные касательные напряжения не выходят за пределы 100 кг/см²; эти частоты вращения не являются опасными.

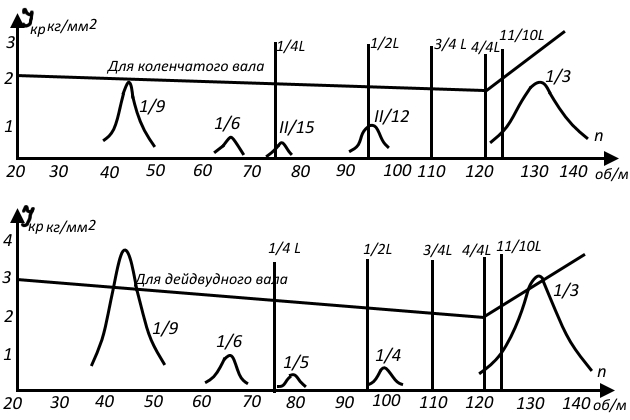
Если при проектировании силовой установки выяснилось, что критические скорости вращения находятся в зоне рабочих режимов двигателя (к примеру, в режиме среднего хода), то имеется 2 выхода:

1. Зона критических оборотов смещается путем: а) изменения жесткости валопровода (варьированием длины и диаметра вала); б) изменением массы маховика или противовесов на кривошипах; в) разделением крутильной системы с помощью эластичных муфт;
2. Амплитуда крутильных колебаний уменьшается путем установки успокоителей — антивибраторов или демпферов. В антивибраторе создаются колебания, противоположные крутильным, что способствует уменьшению амплитуды крутильных колебаний. В демпферах энергия крутильных колебаний срабатывается главным образом за счет трения в упругих элементах.

Природа осевых колебаний валопровода аналогична природе крутильных колебаний. Вал обладает упругостью не только при его скручивании, но и при сжатии в осевом направлении, что и определяет осевые колебания валопровода при изменении величины внешнего воздействия — упора винта. Как указывалось выше, переменный упор винта вызывается главным образом неравномерностью вращения коленчатого вала. Опыты показывают, что развитие крутильных колебаний способствует и развитию осевых колебаний.

Последствием осевых колебаний могут быть вибрация корпуса судна, разрушение муфт валопровода, разрушение упорного подшипника и его корпуса, обрыв противовесов коленчатого вала, разрушение коленчатого вала.

Наиболее действенным средством предотвращения развития осевых колебаний является установка осевых демпферов (рис. 17). Обычно демпферы — гидравлические, поршневого типа, в которых энергия осевых колебаний срабатывается путем перетекания жидкости из одной полости цилиндра в другую через отверстия малого диаметра.

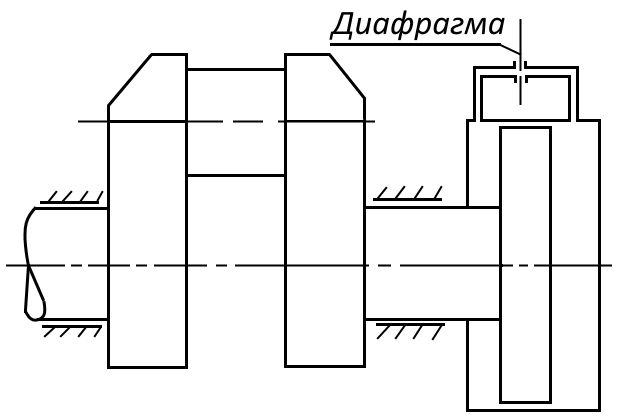
Расчет осевых колебаний выполняются по тем же формулам, что и расчет крутильных колебаний. Однако в формулы необходимо подставлять:

• вместо момента инерции

  $\mathfrak{I}$

  — массу M;

• вместо крутильной жесткости вала C — осевую жесткость C_o;
• вместо угла закрутки φ — линейную дифференциацию Δl.