В этой статье подробно рассмотрено понятие уравновешенности дизельных судовых двигателей, объясняется определение сил инерции, результирующих факторов и других составляющих для выявления действия на корпус судна.
- Понятие уравновешенности. Действие неуравновешенного двигателя на фундамент и корпус судна
- Общие положения уравновешенности
- Действие неуравновешенного двигателя на фундамент и корпус судна
- Возможности уравновешивания двигателя, предупреждения и ослабления вибраций
- Определение результирующих сил инерции многоцилиндрового двигателя
- Определение результирующих моментов в двигателе от сил инерции
- Анализ уравновешенности некоторых кривошипных систем
Понятие уравновешенности. Действие неуравновешенного двигателя на фундамент и корпус судна
Понятие уравновешенности включают в себя данные по силам инерции, моментам этих сил, о форме коленчатого вала и количество цилиндров.
Общие положения уравновешенности
При работе двигателя у каждого цилиндра возникают силы инерции, неуравновешенные в пределах одного цилиндра:
- – силы инерции вращающихся масс кривошипа;
- – силы инерции поступательно движущихся масс I-го порядка;
- – силы инерции поступательно движущихся масс II-го порядка.
Здесь обозначено:
- MR – неуравновешенные массы вращающихся частей кривошипа (определяются по формуле Динамика двигателя судна, условия и оценка работы“Неуравновешенные массы”);
- MS – масса поступательно движущихся частей;
- ω = πn/30 – угловая скорость вращения коленчатого вала;
- λ = R/L – отношение радиуса кривошипа к длине шатуна;
- φ – угол поворота коленчатого вала.
Силы инерции вращающихся масс
всегда действуют по радиусу кривошипа от центра, силы
— по оси цилиндра.
В результате действия сил инерции в многоцилиндровом двигателе равнодействующая сил отдельных цилиндров может быть равна 0:
В этом случае говорят: двигатель уравновешен по силам инерции. Если же равнодействующие не равны 0 — двигатель неуравновешен.
В неуравновешенном двигателе равнодействующий вектор
лежит в плоскости, перпендикулярной оси вала, и вращается вместе с валом — как и в единичном цилиндре. Векторы
лежат в плоскости, проходящей через оси цилиндров. В вертикальном двигателе векторы
всегда вертикальны.
Величина результирующего вектора
не зависит от угла поворота коленчатого вала, в отличие от величины векторов
, которые являются функцией от угла φ и изменяются соответственно по законам cosφ и соs2φ.
Помимо сил инерции, в двигателе действуют моменты от этих сил. Если в многоцилиндровом двигателе результирующий момент от сил инерции отдельных цилиндров не равен 0:
— то двигатель неуравновешен по моментам от сил инерции. Двигатель может быть неуравновешен по моментам даже в том случае, когда суммарный вектор от сил инерции равен 0.
Момент от сил инерции вращающихся масс
постоянен по величине, не зависит от угла φ и вращается вместе с коленчатым валом. Результирующие моменты
перемены по величине, действуют в плоскости, проходящей через оси цилиндров, изменяются по тем же законам, что и силы инерции (cosφ, cos 2φ).
Условие полной уравновешенности двигателя – равенство нулю всех равнодействующих от сил и моментов инерции вращающихся и поступательно движущихся масс.
Действие неуравновешенного двигателя на фундамент и корпус судна
Корпус любого судна представляет собой упругую систему, в которой могут развиваться колебания в 2-х, реже — в 3-узловой форме (рис. 1). Если частота изменения крутящего момента, упора винта, неуравновешенных сил и моментов от сил инерции совпадут с частотой собственных колебаний корпуса судна, то возникает вибрация корпуса, способная привести к самым серьезным последствиям.
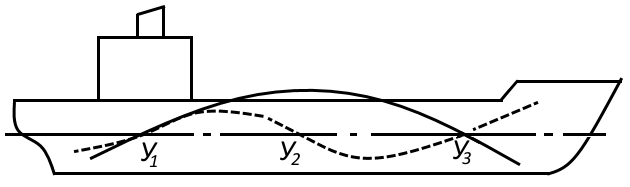
Наиболее существенным фактором, определяющим амплитуду вибраций, является наличие неуравновешенных сил и моментов от сил инерции. Неуравновешенные центробежные силы
вращаются вместе с двигателем, действуют за 1 оборот Ремонт коленвала и других основных подвижных деталей дизелейколенчатого вала во все стороны, стремятся то оторвать двигатель от фундамента, то сдвинуть его в сторону или прижать вниз. В таких же направлениях неуравновешенный момент стремится развернуть двигатель.
Поскольку неуравновешенные силы инерции 1-го и 2-го порядков поступательно движущихся масс
действуют в плоскости, проходящей через оси цилиндров, и изменяются по законам cosφ, cos2φ, то эти силы стремятся то поднять, то прижать двигатель к фундаменту. Неуравновешенные моменты от сил инерции поступательно движущихся масс
стремятся опрокинуть двигатель “через голову” на торец в той же плоскости, проходящей через оси цилиндров.
Возможности уравновешивания двигателя, предупреждения и ослабления вибраций
Оптимальным решением при проектировании силовой установки является выбор для судна полностью уравновешенного двигателя. Уравновесить двигатель можно 3-мя путями:
- Выбором соответствующего числа цилиндров и последовательности их работы;
- Уравновешиванием с помощью противовесов каждого цилиндра индивидуально;
- Уравновешиванием с помощью противовесов результирующих сил и моментов в многоцилиндровом двигателе.
Первый путь позволяет добиться полной уравновешенности самым простым путем. В 4-тактных ДВС этого можно достичь, применив 6-ти или 8-цилиндровую компоновку двигателя. Однако возможности этого пути в “ходовом” диапазоне чисел цилиндров и их тактности ограничены. Более подробно этот вопрос будет рассмотрен при анализе уравновешенности кривошипных систем.
2-й и 3-й пути используются в случаях, когда невозможно применение двигателя с оптимальным с точки зрения уравновешенности числом цилиндров и углом заклинки кривошипов (к примеру, для установки на судно требуется 2-тактный малооборотный дизель с числом цилиндров 6, неуравновешенный по моментам от сил инерции).
Индивидуальное уравновешение центробежных сил возможно с помощью 2-х противовесов, расположенных противоположно колену кривошипа (рис. 2). Массы противовесов Mпр и расстояние их центров тяжести от оси вала ρ должны удовлетворять равенству: 2Mпр ρ = MR R, где MR — масса вращающихся частей кривошипа, R — его радиус. В таком случае, неуравновешенные центробежные силы в данном цилиндре и соответственно моменты от этих сил равны 0.
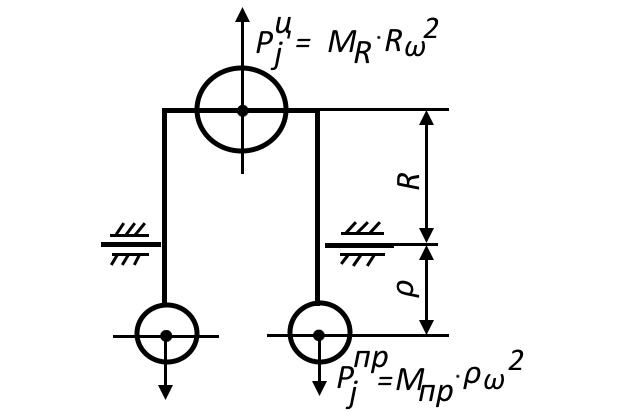
в ВМТ, то при повороте колена на 90° сила инерции
становится равной 0, а центробежная сила противовесов не изменяется по величине, будет действовать в горизонтальной плоскости и стремиться сдвинуть двигатель в сторону.
Вывод о невозможности уравновесить силы и моменты от сил инерции поступательно движущихся масс с помощью противовесов на кривошипе внутри одного цилиндра справедлив и для многоцилиндрового двигателя.
Сила инерции I порядка может быть уравновешена в 1 цилиндре с помощью 2-х валов, вращающихся в противоположные стороны с угловой скоростью, равной скорости коленчатого вала (рис. 3).
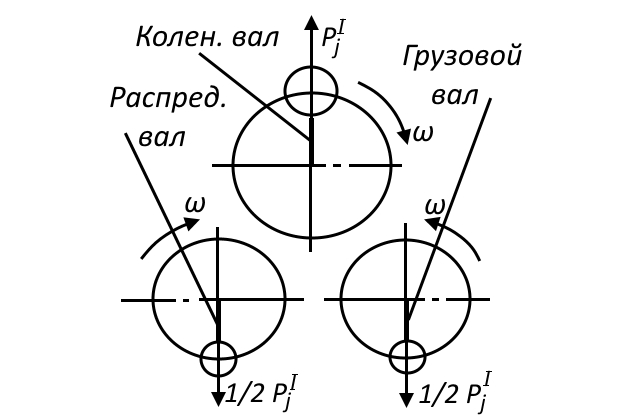
На валах укреплены противовесы, развивающие совместно центробежную силу
Тогда горизонтальные составляющие центробежных сил противовесов будут поглощать друг друга, а вертикальные — уравновешивать текущие значения
. При равенстве 0 силы инерции 1-го порядка, момент этой силы относительно центра тяжести двигателя также будет равен нулю.
Силу инерции II порядка и момент от этой силы можно уравновесить аналогичным образом; однако частота вращения вспомогательных валов с противовесами должны быть в 2 раза больше частоты вращения коленчатого вала.
В многоцилиндровом двигателе нет необходимости уравновешивать каждый цилиндр порознь. Можно уравновесить лишь результирующие неуравновешенные силы и моменты от всех цилиндров. Пути уравновешивания результирующих сил в многоцилиндровом двигателе аналогичны одноцилиндровому двигателю.
Для уравновешивания результирующих моментов следует применять противовесы, разнесенные по длине двигателя и установленные на коленчатом валу (при уравновешивании
) или на 2-х вспомогательных валах (при уравновешивании
).
В судовых ДВС довольно часто применяются противовесы для уравновешивания центробежных сил и моментов от этих сил. Уравновешивание сил I и II порядка и моментов от этих сил с помощью вспомогательных валов применяется на новых моделях малооборотных двигателей.
В главных ДВС иногда применяют противовесы на коленчатом валу, назначение которых — частично переводить амплитуды сил и моментов от сил инерции поступательно движущихся масс из вертикальной в горизонтальную плоскость. При этом уменьшаются максимальные амплитуды неуравновешенных сил и моментов в вертикальной плоскости, хотя и создаются дополнительные неуравновешенные силы и моменты в горизонтальной плоскости.
Будет интересно: Ремонт вспомогательных механизмов и систем
В случае применения на судне неуравновешенного по силам или моментам двигателя, его необходимо правильно расположить. При неуравновешенных силах инерции для предупреждения вибраций двигатель следует устанавливать как можно ближе к узлу колебаний (рис. 1), при неуравновешенных моментах инерции — как можно дальше от узлов.
Для ослабления вибраций главные двигатели устанавливаются на усиленные фундаменты. Частоты вращения, на которых наблюдается повышенная вибрация корпуса, стараются проходить, возможно, быстрее при увеличении или уменьшении оборотов. Вспомогательные двигатели (и некоторые главные сравнительно небольшой мощности) устанавливаются на фундаменты, на амортизаторы (резиновые, пружинные или резинометаллические).
Частоты вращения, на которых наблюдается повышенная вибрация корпуса, стараются проходить возможно быстрее при увеличении или уменьшении оборотов.
Определение результирующих сил инерции многоцилиндрового двигателя
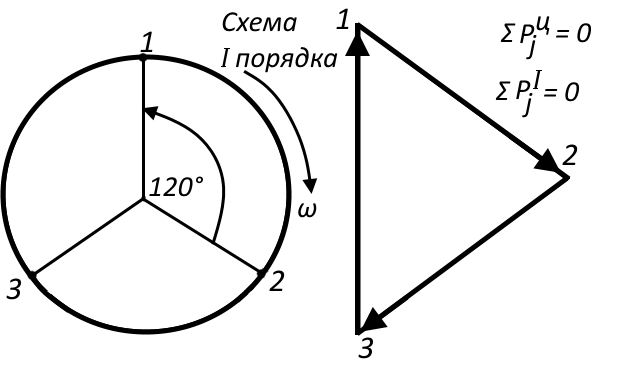
Результирующий вектор центробежных сил в многоцилиндровом двигателе может быть найден графическим путем с помощью схемы кривошипов I порядка и силового многоугольника (рис. 4).
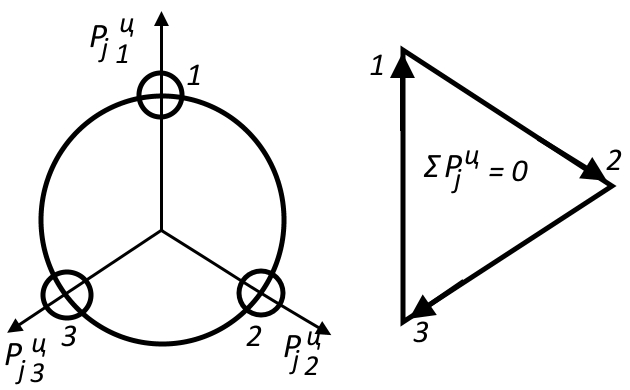
Схема кривошипов I порядка получается путем проектирования кривошипов всех цилиндров на плоскость, перпендикулярную оси коленчатого вала, при этом кривошип 1-го цилиндра устанавливается в ВМТ. Очевидно, что схема 1 порядка определяется последовательностью вспышек в цилиндрах. Поскольку центробежные силы каждого цилиндра направлены по радиусу кривошипа, то результирующий вектор можно найти суммированием векторов
отдельных цилиндров, как это показано на рисунке.
Векторы сил инерции
откладываются в выбранном масштабе при построении силового многоугольника в любой последовательности: можно суммировать векторы последователь 1, 2, 3 и т. д. цилиндров, можно их суммировать по порядку вспышек — результат не изменится.
Как видно из рисунка, для 3-цилиндрового двигателя силовой многоугольник замкнулся, следовательно, результирующий вектор равен 0:
, двигатель уравновешен по центробежным силам. В общем случае многоугольник может не замкнуться. Тогда результирующий вектор
равен расстоянию от начала 1-го вектора силового многоугольника до конца последнего суммируемого вектора. Результирующий вектор
является постоянно действующим по величине и вращается вместе с коленчатым валом двигателя.
Результирующий вектор сил инерции поступательно движущихся масс 1 порядка также может быть найден чисто алгебраическим путем. Поскольку
изменится по закону косинуса (
), то для каждого цилиндра приведенного на рисунке примера 3-цилиндрового двигателя эти силы равны:
Все векторы
направлены по вертикальной оси, то результирующий вектор
находится как алгебраическая сумма:
Как видно, 3-цилиндровый двигатель уравновешен и по силам инерции поступательно движущихся масс 1-го порядка.
- Если двигатель уравновешен по центробежным силам, то он уравновешен и по силам инерции поступательно движущихся масс I-гo порядка (и наоборот);
В случае неуравновешенности двигателя, отношение максимальных значений неуравновешенных сил
равно отношению весов (или масс) вращательно и поступательно движущихся частей:
то для 3-цилиндрового двигателя можно написать:
Тогда:
Следовательно, 3-х цилиндровый двигатель уравновешен по силам инерции II-го порядка. Для упрощения нахождения результирующей силы
удобно пользоваться графическим способом — с помощью схемы кривошипов II-го порядка и фиктивного многоугольника сил инерции II-го порядка. Как и в предыдущем случае, истинная величина силы
каждого цилиндра заменяется фиктивной силой
, действующей по направлению кривошипов в так называемой “схеме II порядка” (рис. 6). Схема II порядка получается из схемы 1-го порядка путем поворота кривошипа каждого цилиндра на угол, в 2 раза больше истинного. Так, если кривошип был расположен через 120° пкв относительно 1-го цилиндра, то он повернется на 240° пкв в схеме II-го порядка. Проекция фиктивной силы
на вертикальную ось в схеме II порядка даст истинное значение силы для каждого цилиндра.

Максимальное значение результирующей силы
равно численно равнодействующему вектору силового многоугольника. Это значение неуравновешенная сила
примет при повороте кривошипа на 1/2 угла между равнодействующим вектором и вертикалью (при совпадении фиктивной равнодействующей с вертикалью). Когда равнодействующий вектор займет горизонтальное положение, то мгновенное значение результирующей силы
будет равно нулю.
В настоящей статье рассмотрен пример, когда массы MR, MS и радиусы кривошипов всех цилиндров одинаковы. В общем случае массы и радиусы могут отличаться (к примеру, при наличии навешанного продувочного насоса, при отключении цилиндров и т. д.). Это учитывается масштабным фактором — при построении силового многоугольника для каждого цилиндра откладывается своя величина вектора силы инерции.
Определение результирующих моментов в двигателе от сил инерции
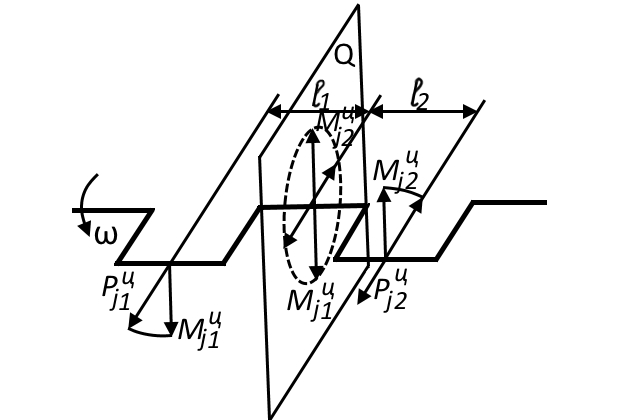
Если силы инерции в многоцилиндровом двигателе внутри каждого цилиндра не равны нулю, то результирующий момент от всех цилиндров необходимо определять как сумму векторов относительно центра тяжести двигателя по формуле:
где:
- Mji = Pji li – момент от сил инерции цилиндра относительно центра тяжести двигателя;
- Pji – сила инерции цилиндра;
- li – расстояние от оси цилиндра до центра тяжести двигателя.
Центр тяжести двигателя можно найти с помощью так называемого “веревочного многоугольника” (рис. 7). Для этого определяют вес каждого цилиндра, отсека приводов и маховика. Веса суммируют графически, последовательно откладывая по одной прямой в выбранном масштабе величины G1, G2, G3 и т. д., как это показано на рис. 7. Точку 1 на оси первого цилиндра выбирают произвольно примерно на уровне середины суммарного вектора ΣGi. Эта точка соединяется линиями с концами векторов G1, G2, G3, … Линия a-1 продолжается до пересечения с осью 2-го цилиндра, находится точка 2. Из точки 2 проводится прямая, параллельная b-1 и т. д.
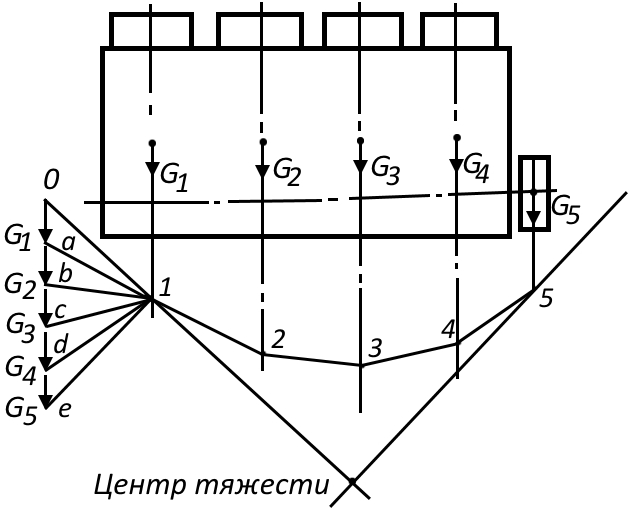
Центр тяжести находится в точке пересечения прямой О-1 и линии, проведенной из точки 5 параллельно отрезку e-1.
При оценке уравновешенности двигателя по моментам от сил инерции удобно пользоваться графическим способом. В основу его положена возможность представления момента в виде вектора. Вектор перпендикулярен плоскости действия момента и направлен таким образом, чтобы при взгляде навстречу вектору направление действия момента соответствовало направлению хода часовой стрелки (рис. 8).

Моменты от центробежных сил изображаются векторами, вращающимися вместе с коленчатым валом в плоскости, перпендикулярной плоскости кривошипа (рис. 9). Эти векторы можно спроектировать на плоскость, проходящую через центр тяжести двигателя перпендикулярно оси вала. В результате проектирования векторов моментов на эту плоскость получается новая схема кривошипов, радиусы которой будут перпендикулярны радиусам кривошипов схемы 1-го порядка.
Учитывая, что векторы моментов
каждого цилиндра перпендикулярны соответствующим радиусам в схеме 1-го порядка, условились при определении результирующего момента
пользоваться схемой 1-го порядка. При этом векторы моментов всех цилиндров как бы поворачиваются на 90° в сторону, противоположную направлению вращения коленчатого вала. Как видно из рис. 9, при таком условном повороте векторы моментов цилиндров, расположенных слева от плоскости отсчета моментов, совпадают с направлением радиуса кривошипа. Для цилиндров, расположенных справа от плоскости отсчета, направление вектора момента противоположно направлению центробежной силы (вектор момента направлен к центру кривошипа в схеме 1-го порядка).
При графическом суммировании векторов моментов с помощью схемы 1 порядка замыкающий вектор силового многоугольника даст истинную величину неуравновешенного момента
. Его истинное направление для данного момента времени может быть найдено путем поворота равнодействующего вектора
на 90° в сторону направления вращения.
На рис. 10 дан пример определения результирующего момента
для 5-цилиндрового двигателя. Отсчет моментов ведется относительно плоскости, проходящей между 3 и 4-ым цилиндрами (маховик сместил центр тяжести в сторону фланца отбора мощности). Векторы моментов каждого цилиндра отличаются по величине, поскольку у каждого цилиндра свое плечо действия силы относительно плоскости отсчета. Направление моментов цилиндров 1, 2 и 3 совпадают с направлением кривошипов, поскольку цилиндры расположены слева от плоскости отсчета. Моменты 4 и 5-го цилиндров, расположенных справа от плоскости отсчета, направлены к центру кривошипов в схеме 1-го порядка. Истинное направление вектора
находится путем поворота результирующего вектора на 90° по часовой стрелке (в сторону направления вращения).
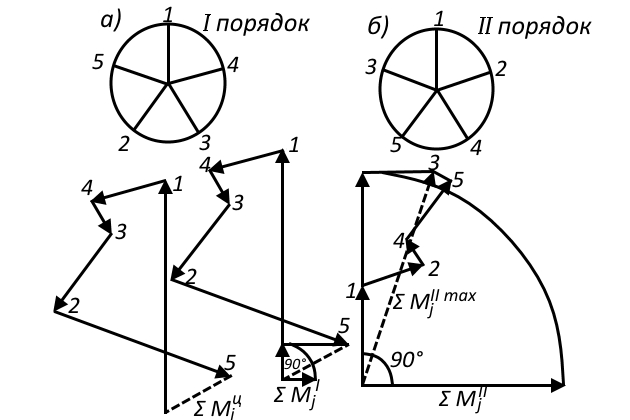
Аналогичным построением находится результирующий момент от фиктивных сил инерции поступательно движущихся масс 1-го порядка. Найденная равнодействующая силового многоугольника моментов также будет фиктивной. Истинная величина неуравновешенного момента
определится для данного момента времени как проекция найденной равнодействующей на вертикальную ось, а истинное направление — путем поворота этой проекции на 90° в сторону направления вращения. Таким образом, вектор
расположен в горизонтальной плоскости (рис. 10).
Максимальное значение вектора
будет в момент, когда кривошипный механизм повернется на угол, образованный равнодействующей силового многоугольника и вертикалью. Это значение равно величине равнодействующей. Если же равнодействующая силового многоугольника займет горизонтальное положение, то мгновенное значение
будет равно нулю.
Силовые многоугольники моментов
и
подобны, т. к. они построены по общей схеме кривошипов, а плечи действия сил у них одинаковы. Следовательно, если
, то
. В противном случае отношение максимальных значений результирующих моментов равно отношению величины вращательно MR и поступательно Ms движущихся масс цилиндра:
Суммарный результирующий момент
от сил инерции 2-го порядка определяется аналогично результирующему моменту
от сил инерции 1-го порядка. Влияние Cos2φ учитывается схемой кривошипов 2-го порядка (рис. 10, б). Максимальное значение вектора момента цилиндра находится как:
Как и в предыдущем случае, направление моментов при построении силового многоугольника зависит от положения цилиндра относительно плоскости отсчета. Если цилиндр расположен слева от плоскости отсчета, то направление момента
совпадает с направлением кривошипа в схеме II-го порядка. Если цилиндр расположен справа, то момент направлен к центру кривошипа. Мгновенная величина
находится как проекция фиктивного равнодействующего вектора силового многоугольника моментов на вертикальную ось. Истинное направление действия момента
определяется поворотом этой вертикальной проекции на 90° в сторону направления вращения. Максимальное значение неуравновешенного момента
численно равно равнодействующей силового многоугольника. Это значение момента будет достигнуто при повороте кривошипа на 1/2 угла между равнодействующей и вертикальной осью (когда равнодействующая займет вертикальное положение). Если равнодействующая силового многоугольника займет горизонтальное положение, то мгновенное значение
будет равно нулю.
Как это указывалось ранее, при уравновешенности по силам инерции анализ уравновешенности по моментам можно производить относительно любой плоскости. В частности, плоскость отсчета можно взять проходящей через ось крайнего цилиндра. Тогда все цилиндры находятся по одну сторону от плоскости отсчета, и направления их моментов совпадают с направлением кривошипов соответствующей схемы. Это облегчает построение силовых многоугольников и оценку уравновешенности системы.
Если двигатель V-образный, с противоположно движущимися поршнями, т. д., то анализ уравновешенности может проводиться путем анализа уравновешенности каждого ряда с последующим геометрическим сложением результирующих неуравновешенных сил и моментов, действующих одновременно.
Анализ уравновешенности некоторых кривошипных систем
Чтобы иметь грамотное представление о характере воздействия конкретного двигателя на фундамент и корпус судна, необходимо проанализировать его уравновешенность. Такой качественный анализ для простейших кривошипных систем может быть дан на основе чисто логических рассуждений с помощью схем кривошипов I и II-го порядков.
В любом многоцилиндровом двигателе кривошипы отдельных цилиндров смещены друг относительно друга на вполне определенный угол — угол заклинки кривошипов. Его величина определяется равенством:
где:
- m – коэффициент тактности;
- i – число цилиндров.
Как видно, угол заклинки для конкретного двигателя с определенным числом цилиндров — величина постоянная; она вполне определяет уравновешенность по силам инерции. Уравновешенность же по моментам определяется и порядком вспышек в цилиндрах, что отображается последовательностью расположения кривошипов в схеме 1 порядка.
В одноцилиндровом 2-х или 4-х тактном двигателе (рис. 11, а) все силы неуравновешенны:
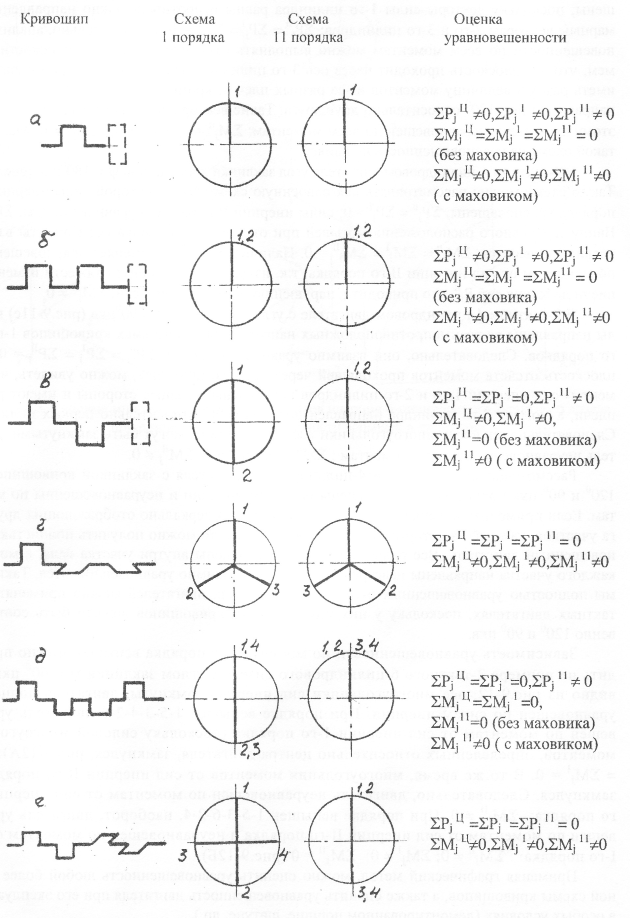
Если в двигателе отсутствует маховик, то центр тяжести проходит через ось цилиндра, плечо моментов от сил инерции равно нулю. Следовательно, все моменты уравновешены. Если же в двигателе имеется маховик, то плечо действия сил инерции равно расстоянию от сил цилиндра до центра тяжести. Двигатель неуравновешен по всем силам и по всем моментам.
В 4-тактном 2-цилиндровом двигателе угол заклинки Ψ = 360° пкв (рис. 11, б). Схема кривошипов такого двигателя аналогична 1-цилиндровой компоновке. Уравновешенность также подобна 1-цилиндровому двигателю: все силы неуравновешены (так как силы инерции цилиндров действуют в одном направлении в схемах кривошипов I и II порядков). При отсутствии маховика центр тяжести проходит между 1 и 2-м цилиндрами, плечи действия сил одинаковы, моменты 1 и 2-го цилиндров направлены навстречу друг другу и полностью уравновешиваются. При наличии маховика центр тяжести смещается. Моменты оказываются неуравновешенными, т. к. плечи действия сил в 1 и 2-м цилиндрах становятся разными.
Читайте также: Общие методы ремонта и повышения ресурса деталей
В 2-тактном 2-цилиндровом двигателе угол заклинки кривошипов Ψ = 180° пкв (рис. 11, в). Направление действия сил в схеме кривошипов 1-го порядка — противоположное. Следовательно, силы инерции 1-го порядка полностью уравновешены:
. Силы инерции
в схеме II порядка направлены в одну сторону: поэтому
. Поскольку силы инерции I-го порядка уравновешены, то плоскость отсчета моментов можно взять проходящей через ось 1-го цилиндра; при этом силы инерции
2-го цилиндра создадут момент относительно этой плоскости. Следовательно, двигатель неуравновешен по моментам 1 -го порядка:
Плоскость отсчета моментов от сил
должна проходить через центр тяжести двигателя (т. к.
). Если центр тяжести находится между 1 и 2-м цилиндрами (маховик отсутствует), то моменты
цилиндров направлены навстречу друг другу и взаимно уравновешиваются:
. Если же двигатель имеет маховик, то центр тяжести смещается, плечи действия сил инерции
цилиндров – разные, двигатель неуравновешен по моментам от сил инерции II-го порядка:
В 2-тактном 3-цилиндровом двигателе угол заклинки кривошипов Ψ = 120° пкв (рис. 11, г). Схема кривошипов 4-тактного двигателя с углом заклинки Ψ = 240° пкв аналогична 2-тактному двигателю. Как было выяснено в пункте “Определение результирующих сил инерции многоцилиндрового двигателя”, все силы инерции в такой схеме уравновешены, поскольку векторы силы 1-го цилиндра равны и противоположно направлены суммарным векторам 2-го и 3-го цилиндров:
Следовательно, анализ уравновешенности по всем моментам можно выполнять относительно любой плоскости.
Примем, что эта плоскость проходит через ось 3-го цилиндра. Тогда 1-й и 2-й цилиндры будут иметь разную величину моментов из-за разных плеч и, кроме того, векторы этих моментов направлены под 120° относительно друг друга. Такие векторы не могут уравновеситься. Поэтому двигатель неуравновешен по всем моментам:
Маховик в такой схеме на уравновешенность не влияет.
В 4-тактном 4-цилиндровом двигателе угол заклинки кривошипов Ψ = 180° пкв (рис. 11, д). Такую схему можно рассматривать как сдвоенную схему “В”, в которой силы инерции 1-го порядка уравновешены:
силы инерции II порядка неуравновешенны:
Ввиду зеркального расположения мотылей при отсутствии маховика все моменты взаимно уравновешиваются:
Наличие маховика изменяет уравновешенность по моментам от сил инерции II-го порядка, т. к. из-за смещения центра тяжести изменяются плечи действия сил
, что приводит к нарушению уравновешенности:
В 2-тактном 4-цилиндровом двигателе с углом заклинки Ψ = 90° пкв (рис. 11, е) все силы направлены во взаимопротивоположных направлениях в системах кривошипов I-го и II-го порядков. Следовательно, они взаимно уравновешиваются:
Взяв плоскость отсчета моментов проходящей через ось 4-го цилиндра, можно увидеть, что моменты сил инерции 1-го и 2-го цилиндров направлены в разные стороны и имеют разные плечи, а момент 3-го цилиндра направлен под углом 90° относительно первых цилиндров. Следовательно, силовые многоугольники всех моментов не могут быть замкнутыми. Двигатель неуравновешен по всем моментам:
Рассмотренные схемы 3-х и 4-цилиндрового двигателя с заклинкой кривошипов под 120° и 90° пкв полностью уравновешены по силам инерции и неуравновешенны по моментам. Если применить коленчатый вал, состоящий из 2-х зеркально отображающих друг друга участков, каждый из которых имеет 3 или 4 колена, то можно получить полностью уравновешенный двигатель. Все силы инерции уравновешены внутри участка вала, а моменты каждого участка направлены навстречу друг другу и взаимно уравновешиваются. Такие схемы полностью уравновешенных 6-ти и 8-цилиндровых двигателей можно применять в 4-тактных двигателях, поскольку у них угол заклинки кривошипов должен быть соответственно 120° и 90° пкв.
Зависимость уравновешенности по моментам от порядка вспышек можно проследить на примере 2-тактного 6-цилиндрового дизеля с углом заклинки Ψ — 60° пкв. Как видно из рис. 12, все многоугольники сил инерции замкнуты, двигатель полностью уравновешен по силам инерции и в случае “А”, и в случае “Б”.
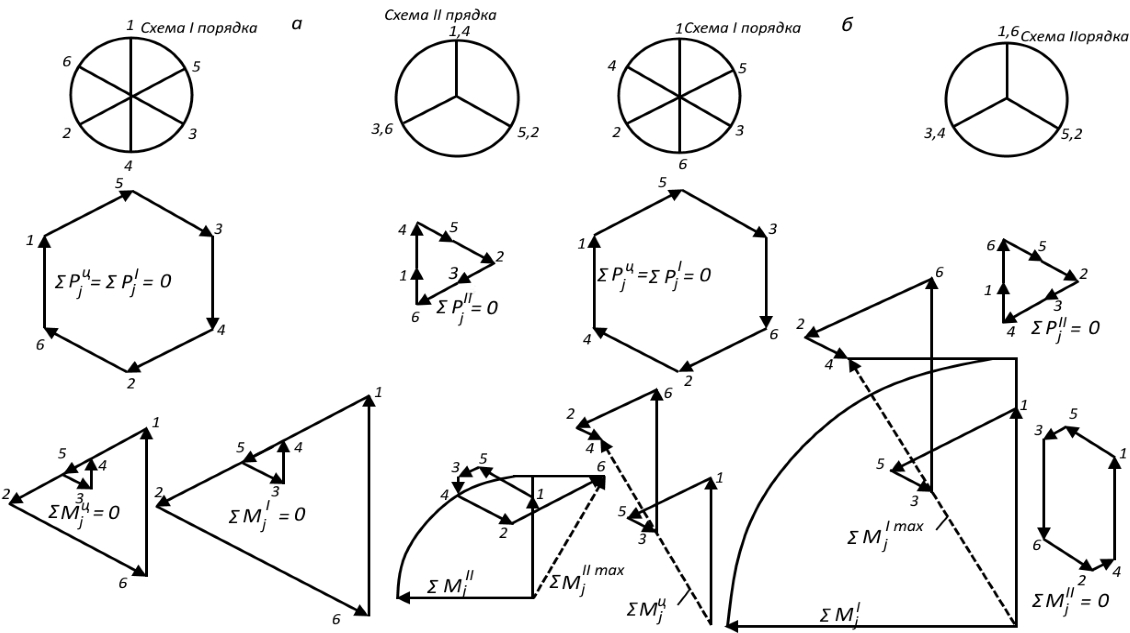
При порядке вспышек 1-5-3-4-2-6 (случай “А”) двигатель уравновешен по моментам от сил инерции 1-го порядка (поскольку силовой многоугольник моментов, определенных относительно центра двигателя, замкнулся, рис. 12, а):
В то же время, многоугольник моментов от сил инерции II-го порядка не замкнулся. Следовательно, двигатель неуравновешен по моментам от сил инерции II-го порядка:
При порядке вспышек 1-5-3-6-2-4 (случай “Б”), наоборот, двигатель уравновешен по моментам от сил инерции II-го порядка и неуравновешен по моментам от сил I-го порядка:
(рис. 12, б). Для обеспечения полной уравновешенности дизеля необходимо применять иные конструктивные решения по сравнению со случаем “А”.
Применяя графический метод, можно оценить уравновешенность любой более сложной схемы кривошипов, а также оценить уравновешенность двигателя при его эксплуатации в особых условиях (демонтированном поршне, шатуне, др.).
🤝 Поддержите нашу работу
Нашли опечатку? Выделите и нажмите CTRL+Enter
