Продольные усилия на волнении для плавучего дока

Известно несколько динамических факторов, существенно влияющих на величину продольных усилий, а именно: эффект Смита, влияние присоединенных масс воды, удары волн в оконечности и общая вибрация корпуса на волнении.

СодержаниеСвернуть

Диаграмма изменения (при погружении и всплытии) усилий, вызывающих общий продольный изгиб дока
Суммарные (расчетные) усилия, вызывающие общий продольный изгиб системы док—судно. Учет гибкости дока
Проверка прочности и устойчивости корпуса дока при общем продольном изгибе. Взаимное влияние продольного и поперечного изгибов
Проверка устойчивости пластин
Проверка устойчивости балок
Проверка устойчивости перекрытий
Устойчивость башен доков в горизонтальной плоскости (применение задачи Ф. С. Ясинского)

Эффект Смита. Так называемый эффект Смита выражается в отступлении от прямой пропорциональности между гидростатическим давлением и осадкой судна на волнении: действительное давление на вершине волны меньше гидростатического, на подошве — больше. Это явление приводит к уменьшению изгибающего момента на волнении, что может быть учтено введением поправочного коэффициента Смита в формулы (Формула 12Расчет общей продольной прочности дока) и (Формула 17Расчет общей продольной прочности дока).

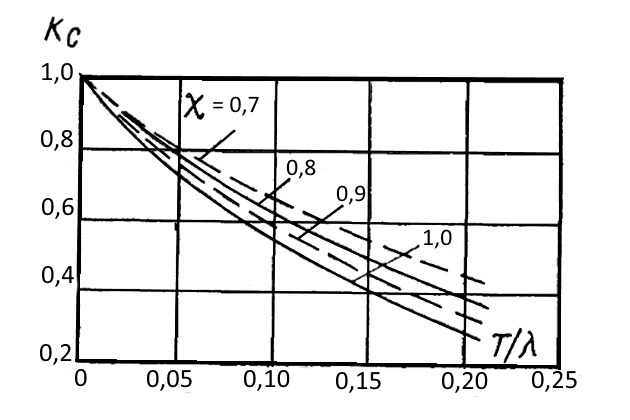
Коэффициент Смита может быть определен по графикам рис. 1 в зависимости от отношения Т/λ и коэффициента вертикальной остроты

χ = \frac{δ}{α}

. Для прямоугольных понтонов он может быть приближенно вычислен по формуле

$K_{c} = 1 - 2 π \frac{T}{λ} Ф о р м . 1$

Рис. 1 Зависимость коэффициента Смита от отношения осадки судна к длине волны и коэффициента вертикальной остроты

Влияние присоединенных масс воды, т. е. инерционных усилий при качке на волнении, а также демпфирования изучено теоретически на основании гидродинамической теории качки М. Д. Хаскинда и экспериментально на моделях доков. Приближенно это влияние можно оценить по формуле А. А. Курдюмова:

$K_{и} = 1, 15 (1 - \frac{2 B}{λ}) Ф о р м . 2$

Динамические (ударные) составляющие изгибающих моментов и перерезывающих сил. Величина динамической (ударной) составляющей изгибающего момента на подошве волны определяется по формуле с учетом влияния дифферента:

$M_{Д}^{П . В} = - 0, 2 [a + b (δ - 0, 6) + c \frac{∆}{0, 04}] B^{2} L \frac{h_{p}}{\bar{λ_{p}}}, Ф о р м . 3$

$\begin{array}{r} г д е α = f (\frac{T}{L}, F r) \\ b = f (\frac{T}{L}, F r) \\ c = f (\frac{T}{L}, F r) \end{array}\}$
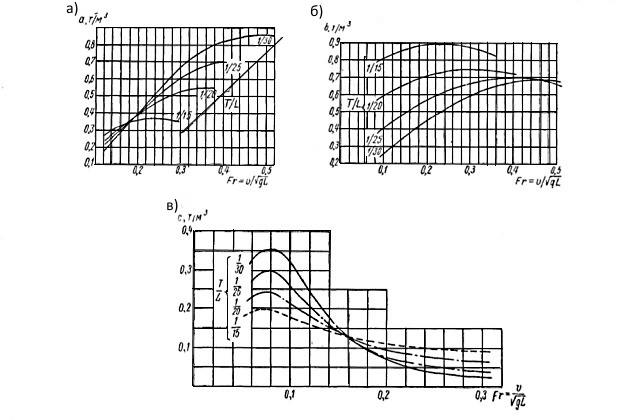
— коэффициенты, определяемые по рис. 2;
δ — коэффициент общей полноты дока;
$∆ = \frac{T к - T н}{L}$
— дифферент дока;
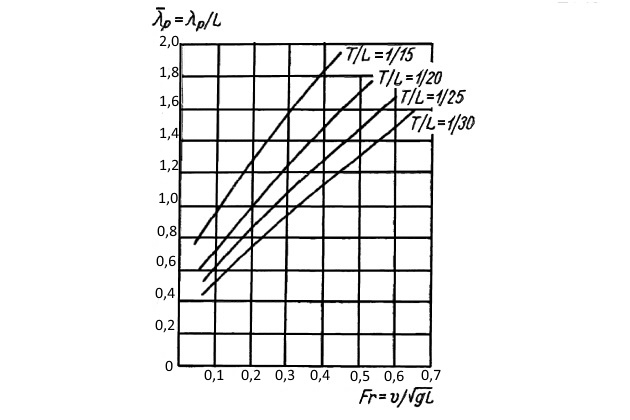
λ_р — относительная длина резонансной волны, определяемая по рис. 3

$7, 5 \sqrt{\frac{T}{L}} \cdot \frac{F r + 0, 4 \sqrt{λ_{p}}}{λ_{p}} = 1 . Ф о р м . 4$

Скорость буксировки на волнении определяется по формуле

$F r = F r_{T . B} - ∆ F r, Ф о р м . 5$

где

$F r = \frac{υ}{\sqrt{g L}},$

а потеря скорости на волнении при ходе против волны

$∆ F r = (0, 3 δ - 0, 08) (4 + \frac{F r_{T . B}}{0, 55 - 0, 5 δ}) (0, 15 \frac{B}{T} + 0, 6) \frac{A}{10}, Ф о р м . 6$

$A = 1 п р и h_{p} ⩾ h_{0};$

$A = \frac{2 h_{p}}{h_{0}} - 1 п р и \frac{h_{0}}{2} ⩽ h_{p} ⩽ h_{0};$

$A = 0 п р и h_{p} ⩽ \frac{h_{0}}{2};$

h₀ вычисляется по формулам (Формула 13Расчет общей продольной прочности дока) — (Формула 16Расчет общей продольной прочности дока);
h_р вычисляется по тем же формулам при длине волны
$λ_{p} = λ_{p} L$
.

На вершине волны

$М_{Д}^{В . В} = (0, 56 δ + 0, 06) М_{Д}^{П . В} . Ф о р м . 7$

Соответствующие динамические составляющие перерезывающих сил равны

$N_{Д} \approx \frac{(3, 0 \div 3, 5) М_{Д}}{L} . Ф о р м . 8$

Зависимость коэффициентов уравнения ударной составляющей — Рис. 2 Зависимость коэффициентов уравнения динамической (ударной) составляющей изгибающего момента от относительной скорости и отношения осадки к длине: а — коэффициент а; б — коэффициент b; в — коэффициент c

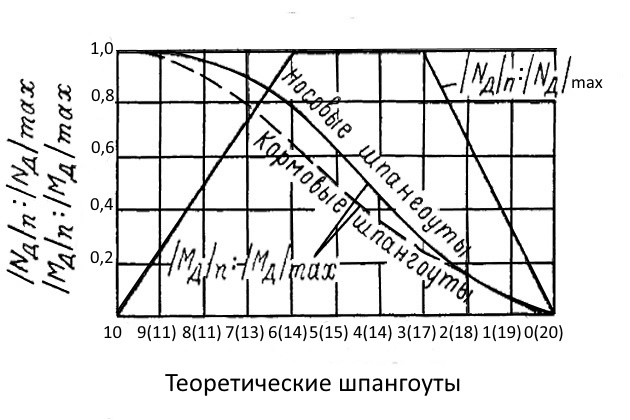
Динамические составляющие изгибающих моментов и перерезывающих сил по длине дока распределяются как показано на рис. 4. Величины ударных составляющих продольных усилий при незначительных скоростях буксировки доков обычно малы, но в случаях некоторых сочетаний Т/λ и Fr могут составить существенную часть общего изгибающего момента.

Рис. 3 Зависимость относительной длины синхронной волны от относительной скорости и отношения осадки к длине

Суммируя статические и динамические моменты, нужно учесть, что их максимальные величины действуют при различных длинах волн (обычно λ_p < L). При относительных скоростях буксировки Fr < 0,2 с увеличением Т/λ динамические составляющие могут повыситься, и на это следует обратить внимание, в частности, при расчленении доков на секции и притоплении доков.

Рис. 4 Эпюры относительных величин динамических (ударных) составляющих изгибающих моментов и перерезывающих сил

Учет изгибающих моментов от общей вибрации корпуса на волнении. Этот вопрос имеет значение только для очень гибких доков, у которых период собственных колебаний близок к кажущемуся периоду волн. Ввиду того, что период собственных колебаний доков обычно меньше 1 сек., а кажущийся период опасных волн не меньше чем 2—3 сек., этими моментами до сих пор пренебрегали. Их следует вычислять только для транспортных доков с низкими башнями.

Диаграмма изменения (при погружении и всплытии) усилий, вызывающих общий продольный изгиб дока

При погружении и всплытии дока происходит изменение усилий, вызывающих различные деформации дока, в частности, общий продольный изгиб. Анализ изменения этих усилий был дан выше. Для наглядного представления об изменении усилий при погружении или притоплении и отыскания наиболее опасной осадки можно построить диаграммы (рис. 5).

Суммарные (расчетные) усилия, вызывающие общий продольный изгиб системы док—судно. Учет гибкости дока

Для системы ремонтный док—судно расчетными усилиями при доковании являются суммы усилий от собственного веса дока, веса докуемых судов, неравномерной балластировки и влияния сухих отсеков, а также от веса «разгружающего» балласта, если в нем возникает необходимость. Конструкция дока (если это не предусмотрено заданием на проектирование и назначением дока) не проектируется на восприятие полного изгибающего момента, приходящегося на корпус дока.

Практикой докостроения рекомендуется следующее:

При расчете прочности доков, предназначенных для текущего ремонта и окраски судов, желательно, чтобы величина изгибающего момента, воспринимаемого доком, была равна М_д ≈ 0,60 М₀;
Для доков капитального и аварийного ремонта судов подъемной силой до 5 000 т желательно, чтобы М_д ≈ 1,0 М₀. Для доков длиной свыше 125 м это условие трудно выполнимо и продольные связи дока (особенно понтонного) получаются чрезмерно большими. Часть изгибающего момента системы док—судно (25—75%) можно погашать «разгружающим» балластом; в этом случае для доков длиной 125 м М_д ≈ 0,75 М₀, а для доков длиной около 250 м М_д ≈ 0,25 М₀;
Если док предназначен к эксплуатации и подъему судов на плохо защищенных от волнения акваториях, следует учитывать дополнительные усилия от волнения с учетом динамических поправок и добавок.

Для ремонтных доков при переводе морем расчетными усилиями обычно являются усилия от волнения (статические и динамические).

Предлагается к прочтению: Прочность плавучих доков и общие характеристики внешних сил

Если ремонтный док должен быть переведен морем и общая прочность его при действии суммарного момента не может быть обеспечена, часть этого момента может быть погашена моментом от приема «разгружающего» балласта.

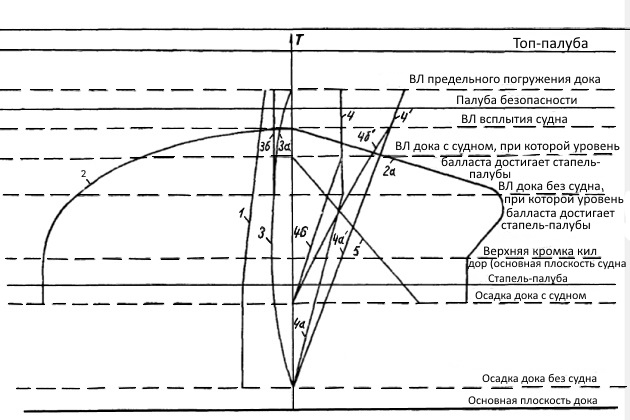
Рис. 5 Изменение усилий, вызывающих общий продольный изгиб дока, при погружении и всплытии: 1 — изменение М и N от собственного веса дока (влияние башен); 2 — изменение М и N от веса докуемого судна при прогнутом доке; 2, а — то же, при перегнутом доке с судном, длина которого на 20—25% превосходит длину дока; 3 — изменение М и N от неравномерной балластировки (3, а — при отсутствии воздушных подушек в балластных отсеках; влияние неравномерности балластировки исчезает при полном заполнении балластных отсеков; 3, б — при наличии воздушных подушек в балластных отсеках; влияние неравномерности сохраняется до полного погружения дока); 4 — изменение М и N от влияния сухих отсеков в понтонах (положительное значение — сухие отсеки в середине длины дока; 4, а — для дока без судна; 4, б — для дока с судном); 4′ — то же, от влияния сухих отсеков в башнях (положительное значение — сухие отсеки в середине длины дока;
$4_{а}^{'}$
— для дока без судна;
$4_{б}^{'}$
— для дока с судном); 5 — изменение М и N от «разгружающего» балласта (обычно в концевых отсеках понтона)

Если прочность дока при действии момента М₀ или М_д на неограниченном волнении (т. е. на синхронной волне) недостаточна и необходимые подкрепления невозможны, определяется предельная высота волны h_max и курсовые углы по отношению к бегу волн, при которых обеспечивается прочность дока и соответственно ограничиваются условия перевода.

Транспортные доки должны проектироваться на восприятие следующих усилий:

При транспортировке судна, не воспринимающего момент, по мелководью (по внутренним водным путям или мелким проливам) — на усилия М₀ и N₀. Для достижения минимальной осадки дока с судном количество «разгружающего» или любого другого жидкого балласта в нем должно быть по возможности наименьшим.

Величины моментов должны вычисляться при высоте волны h, наибольшей для заданных акваторий (для судов разряда «М» Речной Регистр устанавливает размеры расчетной волны λ = 40 м; h = 3,0 м);

Если док транспортирует судно, корпус которого может воспринимать изгибающие моменты, производится распределение изгибающего момента М₀ между судном (М_с) и доком (М_п);
При выходе транспортного дока в море или в крупное водохранилище, где появляются волны большей высоты, но возможно притопление дока, часть величины моментов может быть погашена. Все сказанное об изгибающих моментах относится и к перерезывающим силам.

Для относительно длинных (в частности, транспортных) и самодокующихся доков величина суммарного изгибающего момента может вычисляться с учетом влияния гибкости дока, то есть с учетом изменения сил поддержания за счет формы упругой линии дока (док рассматривается как балка на упругом основании жесткостью к = γВ_д).

Полный изгибающий момент на тихой воде с учетом гибкости на миделе дока равен

$М_{0}^{(u)} (\frac{l}{2}) = М_{0} (\frac{l}{2}) β (u), Ф о р м . 9$

где

$β (u) = \frac{1}{1 + 0, 08 u^{4} α};$

$u = \frac{L_{Д}}{2} \sqrt[4]{\frac{γ B}{4 E I}};$

EI — приведенная жесткость системы док—судно;
α — коэффициент полноты ватерлинии.

Дополнительный момент на волнении равен (по В. В. Козлякову)

$М_{B}^{(u)} = М_{B} \cdot f_{2} (u), Ф о р м . 10$

где f₂(u) определяется по табл. 1 (при а = 1 и λ — L_д).

Таблица 1. Уменьшение дополнительного статического момента на волнении за счет гибкости дока
u	0	0,50	1,00	1,10	1,20	1,30	1,35	1,40	1,45	1,50
f₂(u)	1,0	0,990	0,890	0,845	0,794	0,738	0,710	0,680	0,648	0,620

При несимметричной относительно диаметральной плоскости нагрузке дока, балластировке или установке судов суммарный изгибающий момент M_д распределяется между башнями не поровну. Для правильного учета работы каждой башни нагрузку от несимметрично расположенных весов (машинных и котельных отделений, грузовых кранов, балласта под башнями) следует распределять по длине для каждой башни отдельно, а вес несимметрично расположенных судов и несимметричного балласта в понтоне между башнями распределять по башням в виде реакций от понтонов, после чего определять изгибающий момент для каждой башни отдельно. Это особенно важно для определения напряжений и стрелок прогиба у самодокующихся доков.

Проверка прочности и устойчивости корпуса дока при общем продольном изгибе. Взаимное влияние продольного и поперечного изгибов

Рекомендуется обратить внимание на следующие специфические вопросы расчета общей прочности доков:

При проверке прочности ремонтного дока обычно можно ограничиться расчетом миделевого сечения. Для сильно облегченных транспортных доков, имеющих длину, значительно превышающую длину судна, возникает необходимость в проверке прочности по нескольким сечениям, так как силы поддержания в оконечностях не компенсируются нагрузкой судна, а усилия воспринимаются только корпусом дока. Такая же необходимость может возникнуть при постановке в любой длинный док короткого судна;
При вычислении элементов поперечного сечения понтонного дока в состав эквивалентного бруса корпуса включают обычно только продольные связи башен и иногда — соединительные листы между понтонами в плоскостях стенок башен («юбки»);
Если корпус дока построен из отдельных секций, соединенных по периметру на заклепках или болтах, отдельной проверке должны быть подвергнуты поперечные сечения по этим соединениям;
Кроме учета влияния площади вырезов в палубах, следует определить толщину и конфигурацию усиленных листов на палубах и в наружной обшивке в районе вырезов для их компенсации и погашения концентрации напряжений. К вырезам по наружной обшивке, подлежащим подкреплениям для снижения концентрации напряжений, относятся большие вырезы для приемных и отливных клинкетов (если они не расположены на разрезных понтонах) и т. п.;
При проверке общей прочности доков вычисление элементов сечения корпуса производится методом последовательных приближений, с учетом редуцирования связей. Устойчивость жестких связей корпуса (продольных ребер жесткости, перекрытий и башен в целом) обеспечивается полностью (см. ниже), и редуцирование их производить не приходится. Пластины (листы) конструкций корпуса, имеющих продольную систему набора, т. е. с отношением сторон пластин
$\frac{a}{b} > 1$
(а — сторона, направленная вдоль корпуса, b — поперек корпуса), редуцируются по соотношению их эйлеровых и действующих в жестких связях корпуса напряжений, то есть

$φ = \frac{σ_{э}}{σ_{ж . с}} . Ф о р м . 11$

Влияние начальной погиби и поперечной нагрузки для пластин при продольной системе набора не учитывается.

Редуцирование пластин при поперечной системе набора корпуса, т. е. при отношении сторон

\frac{a}{b} < 1

, производится по формуле

$φ = \frac{σ_{п л}}{σ_{ж . с}} = \frac{α}{m}, Ф о р м . 12$

где

σ_пл — установившиеся в пластине цепные напряжения («+» — растяжения; «—» — сжатие);
$α = \frac{σ_{п л}}{σ_{э}}$
— отношение цепных напряжений в пластине к ее эйлеровому напряжению, которое в этом случае определяется формулой (для стальных пластин с E = 2·10⁶кг/см²)

$σ_{э} = 200 {(\frac{100 δ}{α})}^{2} {[1 + {(\frac{a}{b})}^{2}]}^{2}; Ф о р м . 13$

$m = \frac{σ_{ж . с}}{σ_{э}}$
— отношение напряжении в жестких связях корпуса к эйлеровому напряжению пластины.

Зависимость между напряжениями в жестких связях корпуса и напряжениями в пластинах, имеющих отношение сторон

\frac{a}{b} < 1

, с учетом начальной погиби пластин и действующей на них поперечной нагрузки, выражается известным уравнением И. Г. Бубнова — С. П. Тимошко — П. Ф. Папковича:

$m = α - \frac{3 (1 - μ^{2})}{δ^{2} {[1 + {(\frac{a}{b})}^{2}]}^{2}} \cdot [{(\frac{h_{1} + c_{1}}{1 + \frac{α}{ρ}})}^{2} - с_{1}^{2} + {(\frac{b_{1}}{1 + α})}^{2} - b_{1}^{2} + h_{1}^{2} λ (α)], Ф о р м . 14$

где

b₁ — стрелка начальной синусоидальной погиби;
с₁ — стрелка начальной косинусоидальной погиби;
h₁ — стрелка прогиба пластины под действием поперечной нагрузки. Для стальных пластин, гнущихся по цилиндрической поверхности,

$h_{1} = 1, 35 p δ {(\frac{α}{100 δ})}^{4};$

р — давление на пластину, кг/см² (q = 10р, м. вод. ст.);
μ = 0,3 — коэффициент Пуассона;

$ρ = \frac{4}{k};$

k — коэффициент, учитывающий влияние на устойчивость пластин жесткости набора на кручение. При проверке устойчивости пластин корпуса пластины считаются свободно опертыми и жесткость набора на кручение не учитывается; при этом не учитывается также отступление от закона Гука для пластин, т. е. k = 1 и Q = 4. Рекомендуется принимать следующие значения начальной погиби пластин (все размеры в миллиметрах):

1) по рекомендации Л. Я. Резницкого

$b_{1} = 0, 5 δ;$

$с_{1} = 0, 2 δ; Ф о р м . 15$

2) при учете только синусоидальной погиби

$b_{1} = \frac{S}{1500 δ} (55 + δ);$

$с_{1} = 0; Ф о р м . 16$

3) по «Нормам прочности морских судов» Регистра 1962 г.

$\begin{matrix} b_{1} = 0; \\ c_{1} = \frac{δ + 2 \sqrt{δ}}{\frac{100 δ}{S} +} п р и S ⩽ 800, \end{matrix}$

или

$c_{1} = \frac{δ + 2 \sqrt{δ}}{\frac{δ}{8} + 1} п р и S > 800 . Ф о р м . 17$

Для величин b₁ и c₁ по формулам (Формула 15) зависимость между m и а по уравнению (Формула 14) вычислена Я. Б. Каганером (табл. 2). При значениях b₁ и c₁ по формуле (Формула 16) величины m и

φ = \frac{α}{m}

для нескольких значений толщины листов δ вычислены Н. Н. Рудневым, В. А. Бияковым, А. И. Брайниным и Э. Н. Гариным (табл. 3). При значениях b₁ и c₁ по формулам (Формула 16) и (Формула 17) редукционные коэффициенты приведены на рис. 6.

Таблица 2. Результаты решения уравнения (формула 14) при b₁ = 0,5δ; c₁ = 0,2δ
$α$	$m_{q = 0}$	$m_{q = 4, 0 м}$	$m_{q = 7, 5 м}$	$φ = \frac{α}{m_{q = 0}}$	$α$	$m_{q = 0}$	$m_{q = 4, 0 м}$	$m_{q = 7, 5 м}$	$φ = \frac{α}{m_{q = 0}}$
$α$	$m_{q = 0}$	$m_{q = 4, 0 м}$	$m_{q = 7, 5 м}$	$φ = \frac{α}{m_{q = 0}}$	$α$	$m_{q = 0}$	$m_{q = 4, 0 м}$	$m_{q = 7, 5 м}$	$φ = \frac{α}{m_{q = 0}}$
– 1,000	-∞	-∞	-∞	0	0,25	0,508	0,457	0,404	0,492
-0,975	-1091,6	-1091,7	-1091,8	0,001	0,50	0,902	0,856	0,809	0,554
-0,950	-273,1	-273,2	-273,4	0,003	0,75	1,24	1,20	1,16	0,604
-0,925	-121,7	-121,8	-121,9	0,008	1,00	1,55	1,52	1,48	0,644
-0,90	-68,5	-68,6	-68,7	0,013	1,50	2,12	2,10	2,06	0,706
-0,85	-30,6	-30,7	-30,8	0,028	2,00	2,67	2,64	2,62	0,750
-0,80	-17,2	-17,3	-17,4	0,046	2,50	3,20	3,17	3,15	0,782
-0,75	-11,0	-11,1	-11,2	0,068	3,0	3,71	3,69	3,68	0,808
-0,70	-7,64	-7,72	-7,81	0,092	4,0	4,74	4,72	4,71	0,844
-0,65	-5,58	-5,67	-5,73	0,116	5,0	5,75	5,74	5,73	0,869
-0,60	-4,22	-4,30	-4,38	0,142	7,5	8,27	8,26	8,26	0,907
-0,55	-3,28	-3,36	-3,44	0,168	10,0	10,8	10,8	10,8	0,932
-0,50	-2,58	-2,65	-2,73	0,194	15,5	15,8	15,8	15,8	0,950
-0,40	-1,64	-1,71	-1,78	0,244	20,0	20,8	20,8	20,8	0,962
-0,30	-1,03	-1,09	-1,16	0,292	30,0	30,8	30,8	30,8	0,974
-0,20	-0,593	-0,657	-0,657	0,337	40,0	40,8	40,8	40,8	0,981
-0,10	-0,268	-0,329	-0,392	0,373	50,0	50,8	50,8	50,8	0,984
0,00	-0,001	-0,117	-0,057	–	60,0	60,8	60,8	60,8	0,987

Схема расчета элементов сечения корпуса во втором и следующих приближениях при использовании уравнения (Формула 14) приведена в табл. 4.

Рис. 6 Редукционные коэффициенты пластин для различных отношений
$\frac{b}{t}$
(поперечная система набора): а — при синусоидальной погиби; б — при косинусоидальной погиби

При использовании величины

φ = \frac{α}{m} = f (σ_{ж . с})

расчет производится по обычной схеме. При редуцировании связей и вычислении элементов сечения корпуса в высших приближениях учитываются напряжения от местного изгиба.

Таблица 3. Значение α, m и $φ = \frac{α}{m}$ для пластин при начальной синусоидальной погиби $b_{1} = \frac{S}{1500 δ} (55 + δ)$ и $S = 600 (c_{1}) = h_{1} = 0$
α	$δ = 6$		$δ = 8$		$δ = 10$		$δ = 12$		$δ = 14$		$δ = 18$		$δ = 20$
α	m	φ	m	φ	m	φ	m	φ	m	φ	m	φ	m	φ
-0,9													-2,42	0,37
-0,8									-2,11	0,38			1,17	0,68
-0,7					-2,62	0,27	-1,7	0,41	-1,25	0,56	-0,92	0,76	-0,85	0,82
-0,6	-7,05	0,08			-1,59	0,38	-1,1	0,54	-0,88	0,68
-0,5	-4,19	0,12	-1,67	0,30	-1,07	0,47	-0,8	0,62	-0,66	0,76	-0,57	0,88	-0,5	0,91
-0,4	-2,59	0,15	-1,09	0,37	-0,74	0,54					-0,44	0,91
-0,3	-1,58	0,19	-0,71	0,42	-0,49	0,61	-0,4	0,75
-0,2	-0,89	0,22	-0,44	0,46	-0,31	0,64			-0,3	0,87
-0,1			-0,19	0,53	-0,14	0,71
0,5	1,19	0,42	0,72	0,69	0,61	0,82	0,56	0,90	0,53	0,94	0,51	0,98
1,0	1,91	0,52	1,29	0,77	1,14	0,88	1,07	0,93	1,04	0,96	1,02	0,98
1,5	2,53	0,59			1,66	0,92	1,58	0,95	1,55	0,97	1,52	0,99
2,0	3,1	0,65					2,09	0,96	2,05	0,98	2,02	0,99
2,5	3,63	0,69					2,5	0,97	2,55	0,98
5,0	6,19	081

Таблица 4 (часть 1). Вычисление элементов сечения корпуса в высших приближениях при поперечной системе набора с использованием уравнения (формула 14)
№ связей	Наименование связей	Редуцируемая площадь Fn	Отстояние от оси сравнения zn	Отстояние от нейтральной оси $z_{0 n}^{(i - 1)}$	$σ_{ж . с}^{(i - 1)} = \frac{M \cdot z_{0 n}^{(i - 1)}}{I^{(i - 1)}}$	$m_{2}^{(i)} = \frac{σ_{ж . с}^{(i - 1)}}{σ_{э}}$	$m^{(i)} = m_{1} + m_{2}^{(i)}$	$α^{(i)} = f (m^{i})$
1
2
·
·
·
n

Таблица 4 (часть 2). Вычисление элементов сечения корпуса в высших приближениях при поперечной системе набора с использованием уравнения (формула 14)
№ связей	$α_{2}^{(i)} = α^{(i)} - α_{1}$	$φ^{(i)} = \frac{α_{2}^{(i)}}{m^{(i)}}$	$∆ φ^{(i)} = φ^{(i)} - φ^{(i - 1)}$	$∆ F_{n}^{(i)} = F_{n} \cdot ∆ φ^{(i)}$	$∆ F_{n}^{(i)} \cdot z_{0 n}^{(i)}$	$∆ F_{n}^{(i)} \cdot {z_{0 n}^{(i)}}^{2}$	$∆ i_{n}^{(i)} = \frac{∆ F_{n}^{(i)} h^{2}}{12}$
№ связей	$α_{2}^{(i)} = α^{(i)} - α_{1}$	$φ^{(i)} = \frac{α_{2}^{(i)}}{m^{(i)}}$	$∆ φ^{(i)} = φ^{(i)} - φ^{(i - 1)}$	$∆ F_{n}^{(i)} = F_{n} \cdot ∆ φ^{(i)}$	$∆ F_{n}^{(i)} \cdot z_{0 n}^{(i)}$	$∆ F_{n}^{(i)} \cdot {z_{0 n}^{(i)}}^{2}$	$∆ i_{n}^{(i)} = \frac{∆ F_{n}^{(i)} h^{2}}{12}$
1
2
·
·
·
n
				$\sum_{n} ∆ F_{n}^{(i)}$	$\sum_{n} ∆ F_{n}^{(i)} \times z_{0 n}^{(i)}$	$\sum_{n} ∆ F_{n}^{(i)} \times {z_{0 n}^{(i)}}^{2}$	$\sum_{n} ∆ i_{n}^{(i)}$
Дальнейшие вычисления: $∆ z^{(i)} = \frac{\sum_{n} ∆ F_{n}^{(i)} \cdot z_{0 n}^{(i)}}{\sum_{n} ∆ F_{n}^{(i)}};$ $∆ I^{(i)} = \sum_{n} ∆ F_{n}^{(i)} \cdot {z_{0 n}^{(i)}}^{2} + \sum_{n} ∆ i_{n}^{(i)} - ∆ z^{(i)} \sum_{n} ∆ F_{n}^{(i)} \cdot z_{0 n}^{(i)};$
$I^{(i)} = I^{(i - 1)} - ∆ I^{(i)};$ $W_{n}^{(i)} = \frac{I (i)}{z_{0 n}^{(i - 1)} - ∆ z^{(i)}};$ $σ_{ж . с}^{(i)} = \frac{M}{W_{n}^{(i)}} .$

Учет действующих напряжений от местного изгиба производится одновременно с редуцированием связей при напряжениях от общего изгиба (см. табл. 2Коэффициенты φ_c и b_c для некоторых типов судов).

При редуцировании пластин корпуса «жесткая» часть их, равная 0,22—0,25 короткой стороны опорного контура с каждой стороны пластины (т. е. всего 0,44—0,50 короткой стороны), не редуцируется. При наличии начальной погиби пластины редуцируются не только при сжатии, но и при растяжении (см. табл. 2, 3, рис. 6).

6 Для проверки устойчивости связей корпуса и их редуцирования необходимо определить эйлеровы (критические) напряжения конструкций (это относится ко всем сжатым связям корпуса).

При определении эйлеровых (критических) напряжений связей корпуса их разделяют на четыре категории:

агибкие связи корпуса (пластины);

бжесткие связи корпуса (продольные ребра жесткости, карлингсы, стрингеры и т. п.);

всистемы перекрестных связей корпуса (перекрытия);

гобъемные конструкции в целом (башни и понтоны дока).

Проверка устойчивости пластин

Эйлеровы напряжения пластин вычисляются по известным формулам, приведенным в учебниках, руководствах и справочниках по строительной механике. При продольной системе набора корпуса эйлеровы напряжения пластин рекомендуется доводить до действующих в соответствующих пластинах напряжений при расчетном изгибающем моменте.

Устойчивость некоторых пластин корпуса, относящихся к категории «жестких» связей корпуса (пластин палубных стрингеров топ-палубы, ширстрека бортов и внутренних стенок башен, скуловых листов по борту и днищу, угловых листов внутренних стенок башен и стапель-палубы, среднего листа стапель-палубы, горизонтального киля, листов днищевых стрингеров и вертикального киля при низких неразрезных понтонах), желательно обеспечивать до предела текучести материала в топ-палубе.

Рекомендуется к прочтению: Металлические плавучие доки — общие сведения и классификация

Желательно, чтобы была обеспечена устойчивость всех пластин корпуса при действии предельных моментов. Этого достигают уменьшением расстояния между продольными ребрами жесткости, причем по конструктивным и технологическим соображениям оно не должно быть меньше 350 мм. Для небольших доков, когда толщина листов увеличивается из соображений износа и коррозии, доведение эйлеровых напряжений до действующих нерационально.

При поперечной системе набора корпуса величину эйлеровых напряжений пластин регламентировать невозможно. В этом случае пластины воспринимают цепные напряжения, определяемые уравнением (Формула 14), которые всегда меньше эйлеровых напряжений (—1 < а < 1) и меньше напряжений в жестких связях корпуса (а < m).

Для пластин, одинаково сжатых в двух направлениях (стапель-палуба при установке судов, днище на вершине волны и т. п.), устойчивость проверяется по формуле

$σ_{1 э} = σ_{2 э} = 200 {(\frac{100 δ}{α})}^{2} [1 + {(\frac{a}{b})}^{2}] . Ф о р м . 18$

Проверка устойчивости балок

Определение теоретических эйлеровых напряжений сжатых стержней производится по формуле

$σ_{э} = \frac{π^{2} E I}{{(μ l)}^{2} F} = \frac{{(2 υ_{э})}^{2} E I}{l^{2} F}, Ф о р м . 19$

где μ или 2υ_э — коэффициенты, характеризующие опирание стержней;
I — момент инерции стержня с присоединенным пояском, равным меньшей из величин
$b_{1} = \frac{l}{6}$
или b₁ = 0,5b;
F = f + bδ ( f — площадь профиля, δ — толщина пластины, b — расстояние между балками).

Наиболее полные таблицы устойчивости балок с различными закреплениями можно найти в справочниках В. В. Давыдова, Н. В. Маттес, И. Н. Эиверцева и Ю. А. Шиманского. Для продольных ребер жесткости принимается μ = 1 или 2υ_э = π.

Исправленные эйлеровы (критические) напряжения стержней с учетом отступления от закона Гука определяются по формуле

$σ_{э}^{'} = φ σ_{Т}, Ф о р м . 20$

где
$φ = \frac{σ_{э}^{'}}{σ_{Т}}$
функция отношения теоретических эйлеровых напряжений к пределу текучести:
$φ = f (\frac{σ_{э}}{σ_{Т}})$
.

Зависимости

φ = \frac{σ_{_{э}}^{‘}}{σ_{Т}} = f (\frac{σ_{э}}{σ_{Т}})

для стали и алюминиевомагниевых сплавов приведены на рис. 7.

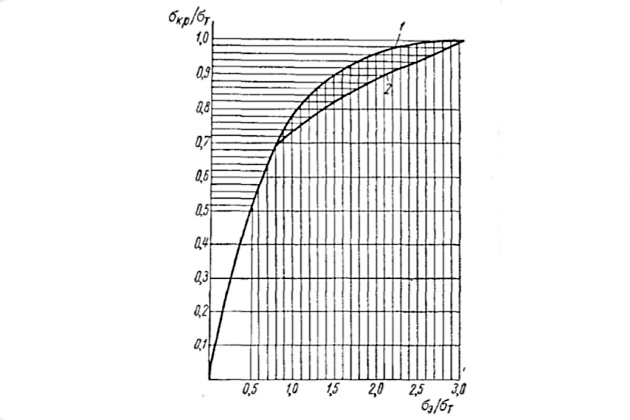
Графики исправленных эйлеровых напряжений — Рис. 7 Графики исправленных эйлеровых (критических) напряжений (отступление от закона Гука): 1 — для сталей; 2 — для алюминиевомагниевых сплавов

Устойчивость балок продольного набора корпуса должна быть обеспечена до напряжений, возникающих в них при действии на корпус предельного момента.

Проверка устойчивости перекрытий

При поперечной системе набора (рис. 8) устойчивость перекрытия проверяется как устойчивость пластины, подкрепленной поперечными упругими ребрами жесткости (бимсами).

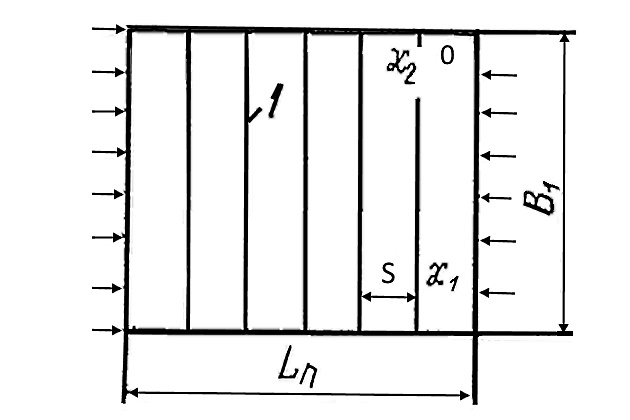
Рис. 8 Условные обозначения для расчета устойчивости перекрытий при поперечной системе набора

Бимсы считаются упруго заделанными на бортах (шпангоутах), при этом коэффициент опорной пары бимса у борта может быть определен по формуле

$ϰ = \frac{1}{1 + \frac{2}{3} \cdot \frac{I}{I_{1}} \cdot \frac{l}{B_{1}}}, Ф о р м . 21$

где

I — момент инерции бимса;
I₁ — момент инерции шпангоута (при проверке топ-палубы) или сумма моментов инерции шпангоутов, примыкающих сверху и снизу к нижним палубам (промежуточной палубе, палубе безопасности и др);
l — пролет шпангоута между топ-палубой и нижележащей палубой (при проверке топ-палубы) или полусумма верхнего и нижнего пролетов шпангоута (при проверке нижних палуб);
В₁ — пролет бимса (ширина башни на уровне соответствующей палубы).

Эйлеровы напряжения пластины на поперечных упругих ребрах (при поперечной системе набора) определяются по формуле (для стальных пластин)

$σ_{э} = λ \cdot 200 {(\frac{100 δ}{S})}^{2} \cdot {[1 + {(\frac{S}{B_{1}})}^{2}]}^{2} . Ф о р м . 22$

Значение параметра λ в этой формуле определяется по графику, приведенному на рис. 9, в зависимости от величины х, характеризующей относительную жесткость бимсов и вычисляемой по формуле

$χ = 100 {(\frac{μ}{π})}^{4} \cdot {(\frac{S}{B_{1}})}^{3} \cdot \frac{I}{B_{1} δ^{3}} . Форм . 23$

Входящий в формулу (Формула 23) коэффициент μ характеризует закрепление бимсов и определяется по табл. 5, в зависимости от коэффициента опорной пары бимсов ℵ (Формула 21), причем предполагается, что бимсы на бортах и внутренних стенках башен закреплены одинаково.

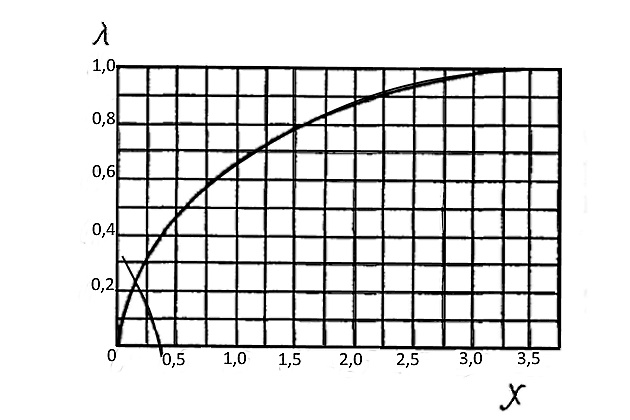
Зависимость значений для формулы 22 — Рис. 9 Зависимость λ = f (χ) в формуле (Формула 22) для расчета устойчивости перекрытий при поперечной системе набора

При χ = 3,67 параметр λ становится равным единице и эйлеровы напряжения пластин (Формула 22) определяются как для пластин, свободно опертых на жесткий контур, т. е. устойчивость пластин определяется устойчивостью одного поля между бимсами. Жесткость, соответствующая величине λ = 1 и χ = 3,67, называется критической:

$I_{к р} = 0, 0367 {(\frac{π}{μ})}^{4} \cdot {(\frac{B_{1}}{S})}^{3} \cdot B_{1} \cdot δ^{3} . Ф о р м . 24$

Таблица 5. Зависимость ${(\frac{π}{μ})}^{4}$ в функции от ℵ
ℵ	0,00	0,25	0,50	0,75	1,00
${(\frac{π}{μ})}^{4}$	1,000	0,799	0,595	0,393	0,195

Таблица 5. Зависимость

{(\frac{π}{μ})}^{4}

в функции от ℵ

ℵ

0,00

0,25

0,50

0,75

1,00

{(\frac{π}{μ})}^{4}

1,000

0,799

0,595

0,393

0,195

При продольной системе набора необходимая или критическая жесткость поперечных балок (бимсов) определяется по формуле

$I = {(\frac{π}{μ})}^{4} \cdot {(\frac{B_{1}}{α})}^{3} \cdot \frac{B_{1}}{b} \cdot i \cdot η \cdot χ_{j m a x} (λ), Ф о р м . 25$

где

обозначения те же, что в формуле (Формула 24) и, кроме того, i — момент инерции продольных ребер жесткости (с присоединенным пояском);
η — коэффициент, учитывающий отступление от закона Гука, равный в этом случае отношению
$η = \frac{σ_{э}^{'}}{σ_{э}}$
и определяемый с помощью графика (см. рис. 7).

Если устойчивость перекрытия, как это обычно бывает, должна быть обеспечена до предела текучести материала, т. е.

$σ_{э}^{'} = σ_{Т},$

то для стали

$η = \frac{σ_{э}^{'}}{σ_{э}} = \frac{σ_{Т}}{σ_{э}} = \frac{1}{2, 8} .$

Параметр λ для перекрытий, имеющих продольную систему набора, определяется по формуле

$λ = \frac{\frac{1}{η} σ_{э}^{'}}{σ_{э}^{0}} = \frac{\frac{1}{η} σ_{э}^{'}}{\frac{π^{2} E i}{a^{2} f}},$

т. е. величина λ является отношением эйлеровых напряжений перекрытия в целом к эйлеровым напряжениям продольных ребер жесткости, вычисленным в предположении, что бимсы являются для них жесткими опорами (Формула 19).

При σ_э = σ_т для стальных конструкций

λ = \frac{2, 8 σ_{Т}}{σ_{э}^{0}}

Функция

χ_{j m a x} (λ)

определяется по табл. 21 в зависимости от числа пролетов продольных ребер жесткости между поперечными переборками

𝑘 = \frac{L_{п е р}}{a}

при наиболее неблагоприятном числе полуволн потери устойчивости j.

Значение λ = 1 соответствует критической жесткости бимса. Устойчивость перекрытий должна обеспечиваться при восприятии корпусом предельных моментов. В случае необходимости выполнить расчеты устойчивости более сложных перекрытий следует обратиться к пособию А. З. Локшина.

Таблица 6 для определения функции $χ j_{m a x} (λ)$ в формуле (Формула 25)
λ	K	2	3	4	5	6	7	8	∞
0,0		-0,0616	-0,0123	-0,0039	-0,0016	-0,0008	-0,0004	-0,0002	0,0000
0,1		-0,0371	-0,0012	-0,0023	-0,0024	-0,0020	0,0016	0,0013	0,0032
0,2		-0,0125	-0,0099	-0,0076	0,0064	0,0099	0,0097	0,0086	0,0106
0,3		0,0125	0,0210	0,0149	0,0225	0,0211	0,0215	0,0225	0,0230
0,4		0,0379	0,0323	0,0379	0,0387	0,0379	0,0402	0,0379	0,0410
0,5		0,0636	0,0436	0,0636	0,0551	0,0636	0,0590	0,0636	0,0640
0,6		0,0989	0,0716	0,0898	0,0895	0,0898	0,0924	0,0898	0,0924
0,7		0,1168	0,1214	0,1168	0,1292	0,1214	0,1284	0,1282	0,1292
0,8		0,1444	0,1751	0,1513	0,1714	0,1751	0,1660	0,1745	01744
0,9		0,1730	0,2347	0,2342	0,2162	0,237	0,2388	0,2342	0,2384
0,95		0,1878	0,2679	0,2851	0,2786	0,2622	0,2810	0,2851	–
1,00		0,2026	0,3040	0,3480	0,3662	0,3780	0,3850	0,3912	0,4050

Устойчивость башен доков в горизонтальной плоскости (применение задачи Ф. С. Ясинского)

Для расчета устойчивости башен дока в горизонтальной плоскости может быть применено (по предложению Э. Н. Гарина) решение задачи Ф. С. Ясинского об устойчивости верхних поясков вертикальных ферм мостов.

При проверке башен дока на устойчивость в качестве «верхнего пояска» условно можно равной половине расстояния от нейтральной оси до топ-палубы. При таком допущении как бы учитывается полная величина сжимающих усилий, действующих в башнях при прогибе дока (рис. 10).

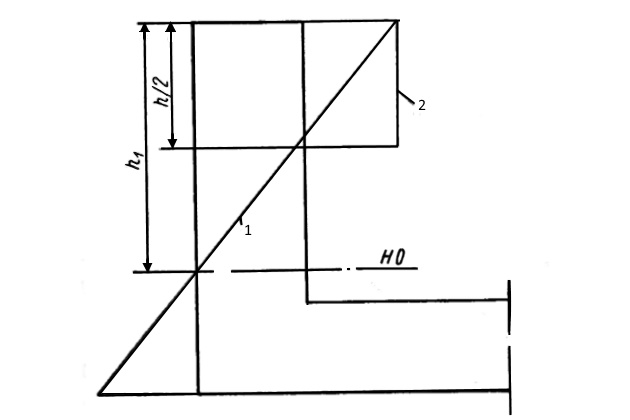
Рис. 10 Условное распределение сжимающих напряжений при расчете устойчивости башни дока в горизонтальной плоскости с использованием задачи Ф. С. Ясинского: 1 — истинная эпюра напряжений; 2 — условная эпюра напряжений

«Верхний поясок» башни рассматривается как балка, лежащая на сплошном упругом основании, образованном вертикальным набором башен (с присоединенными поясками наружной обшивки и внутренних стенок башен). При этом вертикальный набор башен считается упруго заделанным на поперечном наборе понтона.

Предлагается к прочтению: Расчет общей продольной прочности дока

Коэффициент жесткости упругого основания определяется по формуле

$𝑘 = \frac{E}{S (\frac{H^{3}}{3 I_{б}} + \frac{H^{2} B}{2 I_{п}})} = \frac{E}{\frac{S H^{3}}{3 I_{б}} (1 + \frac{3}{2} \cdot \frac{B}{H} \cdot \frac{I_{б}}{I_{п}})} . Ф о р м . 26$

Эйлеровы напряжения «верхнего пояска» башни определяются по формуле

$σ_{э} = \frac{π^{2} E I}{{(β L)}^{2} F} . Ф о р м . 27$

В формулах (Формула 26) и (Формула 27) приняты следующие обозначения:

L, В, Н — соответственно длина, ширина и высота дока;
I_б, I_п — соответственно моменты инерции поперечного набора башен и понтона с присоединенными поясками, приведенные к одной шпации S;
I — момент инерции условного «верхнего пояска» относительно вертикальной оси инерции;
S — шпация дока;
β — коэффициент «приведенной» длины башен, характеризующий влияние упругого основания, определяемый по табл. 7 в зависимости от характеристики относительной жесткости упругого основания

$α = \frac{k L^{4}}{16 E I} . Ф о р м . 28$

Таблица 7. Значения коэффициента $β = f (α)$
α	0	1	3	5	10	15	20
β	∞	2,22	1,28	0,993	0,703	0,574	0,542
α	50	100	150	200	300	500	> 1 000
β	0,431	0,340	0,277	0,261	0,236	0,206	0,176

По существующим к обеспечению устойчивости продольных связей требованиям устойчивость башен должна быть обеспечена при действии предельных моментов. Для этого необходимо, чтобы эйлеровы напряжения были минимум в 2,8 раза больше предела текучести (см. рис. 7). Следовательно, должно выдерживаться соотношение

$\frac{π^{2} E I}{{(β L)}^{2} F} ⩾ 2, 8 σ_{T} . Ф о р м . 29$

Как показывают выполненные расчеты, проверка устойчивости башен необходима при проектировании доков с относительно узкими и высокими башнями, а также при понтонах, имеющих малую жесткость (малая высота понтона или большая ширина дока), особенно при сталях повышенного сопротивления.

Совершенно необходима проверка устойчивости верхних связей продольных ферм док-понтонов.

Необходимость в проверке устойчивости понтонов может возникнуть только при относительно низких и широких неразрезных понтонах (используется метод, изложенный в п. «в», причем для фермы должен быть определен эквивалентный момент инерции).

7Суммирование напряжений при общем продольном изгибе. Нормальные напряжения в продольных связях понтона дока от изгиба перекрытия (σ₂), вследствие большого отношения длины к ширине понтона, незначительны и в большинстве случаев их можно не вычислять.

При определении суммарных нормальных и касательных напряжений в корпусе следует учитывать напряжения от поперечного изгиба при плоском напряженном состоянии стапель-палубы и днища, а также нормальные и касательные напряжения от скручивания корпуса.

В отдельных случаях не следует пренебрегать усилиями сжатия по торцам дока.

8Взаимное влияние продольного и поперечного изгибов дока еще не подвергалось теоретическому исследованию

Качественно оно сводится к следующему:

Общий продольный изгиб дока (его башен) приводит к появлению различной податливости опор для поперечных связей понтонов дока, в результате чего несколько изменяются поперечные изгибающие моменты и перерезывающие силы. Наряду с этим жесткость башни на кручение создает некоторые моменты на концах понтонов;
В результате поперечного изгиба понтонов, т. е. их «цилиндричности», несколько увеличивается жесткость корпуса при продольном изгибе или соответственно в результате общего продольного изгиба несколько увеличивается общая жесткость понтонов при поперечном изгибе;
Неравномерный по длине дока поперечный изгиб понтонов вызывает кручение башен, в результате чего возникают дополнительные нормальные и касательные напряжения в башнях от стесненного кручения, суммирующиеся с напряжениями от общего продольного изгиба, а также создается некоторая степень заделки понтонов на башнях;
Суммарная стрелка прогиба от продольного и поперечного изгиба дока несколько увеличивает силы его поддержания, в результате чего уменьшаются как продольные, так и поперечные изгибающие моменты;
Пояски понтона монолитного дока (днище и стапель-палуба) находятся в плоском напряженном состоянии (в результате совместного продольного и поперечного изгиба). Для приближенного учета плоского напряженного состояния величину напряжений в днище и в настиле стапель-палубы можно определять по формулам

$\begin{array}{r} σ_{1} = σ_{п р о д} - μ σ_{п о п е р}, \\ σ_{2} = σ_{п о п е р} - μ σ_{п р о д}, \end{array}\} Ф о р м . 30$

где

σ_прод и σ_попер — напряжения от продольного и поперечного изгибов;
σ₁ и σ₂ — приведенные продольные и поперечные напряжения при плоском напряженном состоянии.

Сноски