Электронавигационные приборы

Общие принципы функционирования гирокомпасов типа “Standard-14” и “TG-5000”, основные свойства гироскопа с тремя степенями свободы

Простейшим вариантом гироскопа с тремя степенями свободы является гироскоп в кардановом подвесе (рис. 1).

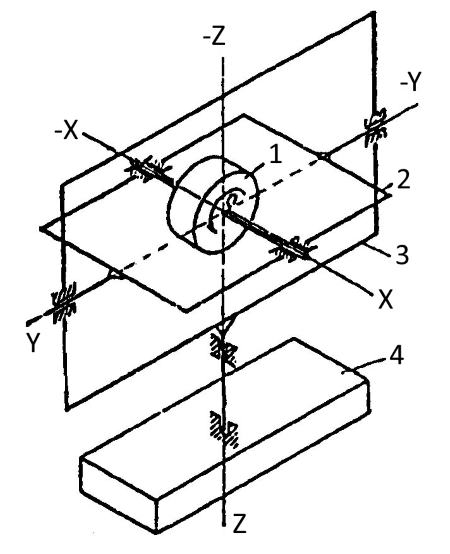
Ротор 1 подвешен в системе колец так, что он может вращаться вокруг оси Х – Х относительно внутреннего кольца 2 (собственное вращение), внутреннее кольцо – вокруг оси Y – Y относительно внешнего кольца 3, а последнее – вокруг оси Z – Z относительно основания 4. Точка 0 пересечения осей Х – Х, Y – Y и Z – Z является центром подвеса гироскопа.

Рассматриваемый гироскоп имеет следующие свойства:

1. Главная ось свободного гироскопа стремится удержать неизменным свое направление в инерциальном пространстве. Это означает, что если главная ось направлена на какую-либо звезду, то при любых перемещениях основания, на котором установлен гироскоп, она будет неизменно указывать на эту звезду, изменяя свою ориентацию по отношению к системе координат, связанной с Землей. Впервые указанное свойство было использовано Л. Фуко для доказательств суточного вращения Земли.
2. Под действием внешней силы, приложенной к внутреннему или внешнему кольцу и создающей момент, не совпадающий по направлению с главной осью гироскопа, последняя будет двигаться не по направлению действия силы (как это было бы при невращающемся роторе), а перпендикулярно этому направлению. Подобное свойство гироскопа называется прецессией. Прецессионное движение происходит с постоянной угловой скоростью, т. е. является безынерционным.
3. Под действием импульса силы (удара) главная ось гироскопа практически не изменяет первоначального направления, а лишь совершает быстрые колебания около положения равновесия. Эти колебания называют нутацией. Они особенно хорошо заметны при небольшой угловой скорости собственного вращения ротора.

Свойства гироскопа с тремя степенями свободы используются в таких устройствах, как гирокомпасы, гирогоризонты, гиростабилизаторы индикаторного типа.

Суточное вращение Земли и принцип построения гирокомпаса

Гироскопическим компасом (гирокомпасом) называется навигационное гироскопическое устройство, предназначенное для указания плоскости истинного меридиана и позволяющее на этой основе определять курс судна и пеленги ориентиров, а также осуществлять стабилизацию в азимуте различных судовых устройств.

Гирокомпас (ГК) является механическим компасом. В силу этого качества определение положения плоскости истинного меридиана с помощью ГК должно основываться на некоторой механической характеристике Земли. Единственной механической характеристикой Земли, идентифицирующей определенную плоскость (плоскость истинного меридиана наблюдателя), является ее кинематическая характеристика – угловая скорость суточного вращения Земли ω.

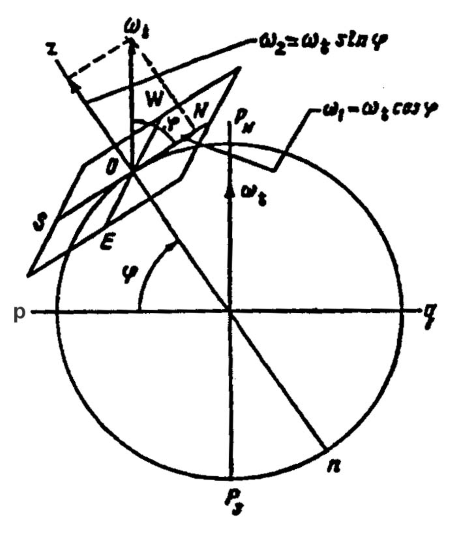
На рис. 2 изображена сферическая модель Земли – шар средним радиусом R = 6370 км. На этом рисунке показаны: вектор угловой скорости ω = 7,29х10^-5 с^-1 суточного вращения Земли, вектор горизонтальной ω₁ составляющей, вектор вертикальной составляющей ω₂, причем;

ω₁ = ωcosφ       ;       ω₂ = ωsinφ.                    (1)

При точке О (место наблюдателя) построены основные плоскости и линии горизонтной системы координат ONEn. Более удобное и более естественное изображение системы координат ONEn представлено на рис. 3, где использована вспомогательная сфера произвольного радиуса.

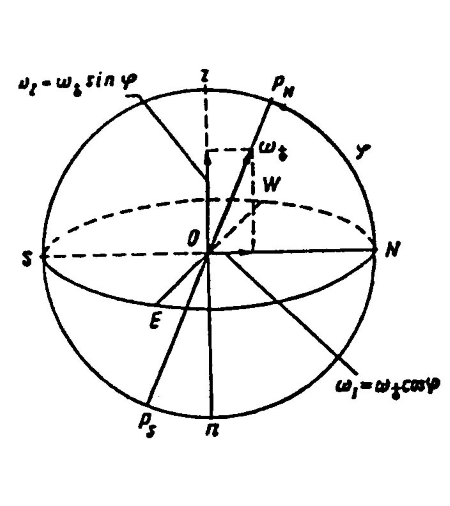
Имея в виду главное назначение ГК – определение курса судна (а таковым является угол, лежащий в горизонтальной плоскости), следует считать в принципе непригодным для этой цели устройство, которое указывает положение плоскости истинного меридиана, располагаясь вдоль вектора ω (этот вектор, как известно, образует с плоскостью горизонта угол, равный широте φ места.)

Поставленным требованиям отвечает горизонтальная составляющая вектора угловой скорости суточного вращения Земли ω₁ = ωcosφ, направленная вдоль линии пересечения плоскостей истинного горизонта и истинного меридиана, т. е. вдоль так называемой полуденной линии NS (вследствие суточного вращения Земли, именно над этой линией происходит верхняя или нижняя кульминация любого светила).

Вследствие вращения плоскости истинного горизонта с угловой скоростью ω₁, наблюдаемое движение главной оси свободного гироскопа по отношению к этой плоскости существенно различается в зависимости от того, располагается его главная ось ОХ вдоль NS (вдоль вектора ω₁) или отклонена от этой линии к востоку либо к западу. В последних двух случаях, вследствие вращения плоскости истинного горизонта, для любого наблюдателя, связанного с этой плоскостью, происходит угловое отклонение оси ОХ относительно плоскости истинного горизонта: либо видимый подъем, либо опускание. Этим только различается поведение гироскопа слева и справа от плоскости меридиана.

Известно только одно механическое устройство, способное идентифицировать отклонение какого-либо тела от плоскости истинного горизонта – это маятник (в широком понимании). Существенным обстоятельством является то, что при появлении указанного отклонения у маятника возникает восстанавливающий момент силы тяжести, пропорциональный углу его отклонения от плоскости горизонта. Объединение (непосредственное или косвенное, т.е. путем дистанционной связи) двух механических устройств: свободного (астатического) гироскопа и маятника в единую систему, т.е. придание гироскопу маятникового эффекта, приводит к возникновению у такой системы свойства избирательности по отношению к плоскости истинного меридиана. В этом состоит общий принцип построения гирокомпасов маятникового типа.

Способ технической реализации гирокомпаса с непосредственным управлением

В настоящее время принято делить все существующие гирокомпасы на два больших класса: с непосредственным и с косвенным управлением. Гирокомпасы “Standard-14” и “TG-5000” являются гирокомпасами с непосредственным управлением.

Гирокомпасами с непосредственным управлением называются такие гирокомпасы, чувствительный элемент которых представляет собой астатический гироскоп, механически связанный с маятниковым устройством, которое управляет его движением с помощью момента силы тяжести, пропорционального углу отклонения главной оси гироскопа от плоскости горизонта. Очень часто в литературе такие гирокомпасы называют маятниковыми. Существует несколько способов технической реализации гирокомпаса с непосредственным управлением. Наиболее известный и широко распространенный способ состоит в жестком соединении астатического гироскопа с разбалансированной массой, создающей чувствительному элементу положительный маятниковый эффект, иначе говоря, придающий ему нижнюю маятниковость.

На рис. 4 представлена модель такого гирокомпаса. Он состоит из ротора 1 гироскопа, гирокамеры 2, разбалансированной массы 3, горизонтального 4 и вертикального 5 колец карданного подвеса и направляющих опор 6 вращения. Расстояние OG, на которое смещен вниз центр массы чувствительного элемента, называется метацентрической высотой “а”.

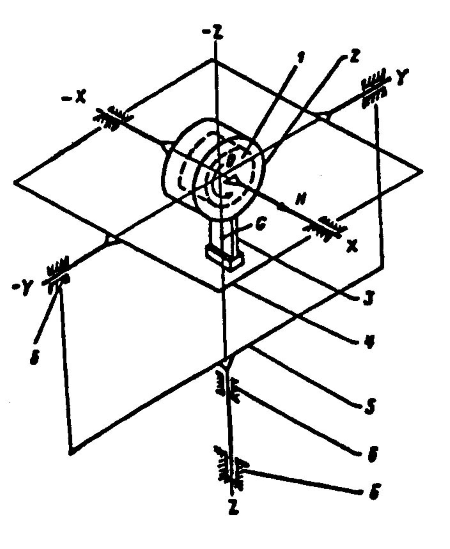
Рассмотрим поведение главной оси гирокомпаса, обладающего положительным маятниковым эффектом, по отношению к плоскости горизонта и меридиана. На рис. 5 изображена горизонтная система координат ONEn и показаны горизонтальная ω₁ = ωcosφ и вертикальная ω₂ = ωsinφ составляющие угловой скорости суточного вращения Земли.

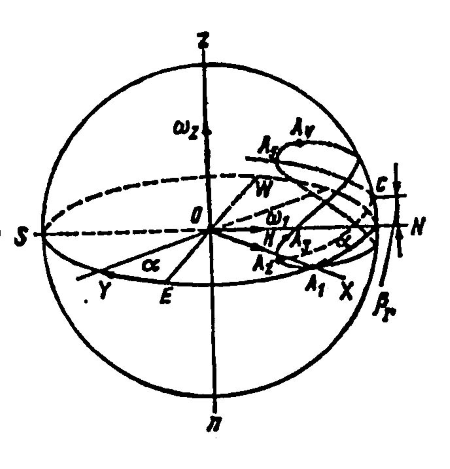
Предположим, что первоначально главная ось гироскопа расположена горизонтально и отклонена от плоскости истинного меридиана к востоку на угол α (позиция А₁). В этом положении, т. е. при горизонтальном расположении оси ОХ гироскопа, сила тяжести Р = Mg не создает момента относительно какой-либо оси гироскопа. Вращение плоскости горизонта со скоростью ω₁ вызывает непрерывное опускание восточной половины горизонта. В результате этого главная ось гироскопа видимым образом, т. е. по отношению к плоскости горизонта, поднимается. Указанный подъем происходит со скоростью, определяемой полезной составляющей ω_у = ω₁sinα.

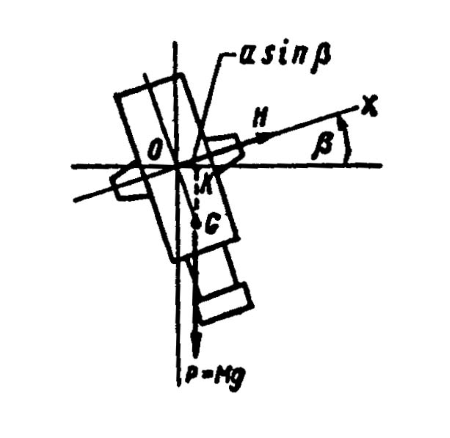
Как только главная ось гироскопа поднимется над плоскостью горизонта на некоторый угол, возникает момент силы тяжести (рис. 6);

L_у = P · α · sinβ = M · g · α · sinβ.

Обозначив;

M · g · α = B,                    (2)

где В – модуль маятникового момента, окончательно получим;

L_у = В · sinβ.                   (3)

Под действием момента L_у возникнет прецессионное движение со скоростью ω_pz = L_у/H, которое будет направлено в стороны совмещения оси ОХ с плоскостью истинного меридиана. Однако существует некоторый начальный интервал времени, в который угол в еще настолько мал (и, следовательно, еще настолько мал момент L_у ), что угловая скорость прецессии ω_pz в это время меньше угловой скорости ω₂ вращения плоскости меридиана. В результате этого увеличивается угловое расстояние между осью ОХ гироскопа и меридианом, т. е. ось ОХ удаляется от него (участок траектории А₁ А₂ на рис. 5). Поскольку угол β увеличивается, при некотором его значении β_r наступит момент, в который скорость прецессии гироскопа сравняется со скоростью вращения меридиана. На рис. 5 это положение иллюстрируется точкой А₂ перегиба траектории.

В последующем, например позиция А₃, значение угла в (рис. 7), постепенно нарастая, превысит значение β_r (см.рис. 5), следовательно, скорость ω_pz прецессии превысит скорость ω₂ (позиция А₃). В результате гироскоп неизбежно настигнет плоскость меридиана, но, имея при этом максимальное возвышение, обгонит ее и окажется над западной половиной горизонта. Поскольку последняя непрерывно поднимается, ось ОХ гироскопа начнет видимым образом опускаться (позиция А₄), продолжая тем не менее прецессировать со скоростью, большей ω₂, до тех пор, пока значение угла β не станет снова равным β_r (позиция А₅). В этот момент произойдет второй перегиб траектории.

Вращение плоскости истинного меридиана со скоростью ω₂ можно исключить из рассмотрения, если определять поведение главной оси гироскопа по отношению к плоскости, соединяющей точки перегиба А₂ – А₅, т. е. по отношению к плоскости, приподнятой на угол β_r над истинным горизонтом. В этой постановке задачи удобнее всего определять движение конца главной оси гироскопа двумя линейными скоростями (см. рис. 7): V₁, вызванной прецессионным движением под действием момента В sin (β – β_r, и V₂ видимого движения по отношению к плоскости А₂ – А₅, которая вращается с той же скоростью ω₁, что и плоскость истинного горизонта.

Равенство скоростей V₁ у точек траектории, имеющих одинаковый угол (β – β_r), т. е. расположенных симметрично слева и справа относительно меридиана, а также равенство абсолютных значений при противоположном направлении скоростей V₂ у этих же точек доказывают симметричность восходящей и нисходящей ветвей траектории относительно линии А2 – А5 и плоскости меридиана и, следовательно, замкнутость траектории, что соответствует незатухающим колебаниям.

Таким образом, гироскопический чувствительный элемент, обладающий положительным маятниковым эффектом, в принципе, становится гирокомпасом, так как он приобрел свойства избирательности по отношении к плоскости истинного меридиана, поскольку центр его колебаний располагается точно в плоскости истинного меридиана. Указанный центр в условиях неподвижного основания всегда может быть определен путем осреднения крайних отклонений оси гироскопа в азимуте.

Полное решение задачи реализации морского гирокомпаса требует погашения его незатухающих колебаний, т. е. демпфирования, чтобы в плоскости истинного меридиана располагалась не геометрическая точка (центр колебаний), а материальная ось гироскопа. Способ демпфирования колебаний, применяемый в гирокомпасе “St-14”, рассматривается далее.

Двухгирокомпасный маятниковый чувствительный элемент

Чувствительный элемент двухгироскопного гирокомпаса представляет собой сферу 1 (рис. 8) с установленными внутри нее двумя гироскопами 2 (отсюда происходит термин “гиросфера”Подъем и установка гиросферы). Сфера герметична, имеет гидростатический подвес, одновременно выполняющий роль электролита, обеспечивающего бесконтактный подвод питания внутрь сферы.

В большинстве моделей гирокомпасов “Standard” фирмы «Аншютц» использовалось электромагнитное центрирование гиросферы (рис. 9, а ), осуществляемое помощью катушки, питающейся переменным током.

В последних моделях гирокомпасов фирмы «Аншютц» (“St-14”, “St-20”) (рис. 9, б) применяется гидродинамический способ центрирования, реализуемый с помощью встроенной миниатюрной помпы.

Немецкая фирма «Плат» «Plath» применяет в своих гирокомпасах (рис. 9, в) подвес гиросферы на основе поддерживающей жидкости 1 , а центрирование осуществляет механическим способом при помощи вертикальной иглы 2 и камниевой опоры 3.

Центр массы гиросферы (точка G) смещен вдоль вертикальной оси гиросферы Z-Z вниз относительно ее центра подвеса – геометрического центра (точка О). В результате этого в гравитационном поле гиросфера обладает положительным маятниковым эффектом.

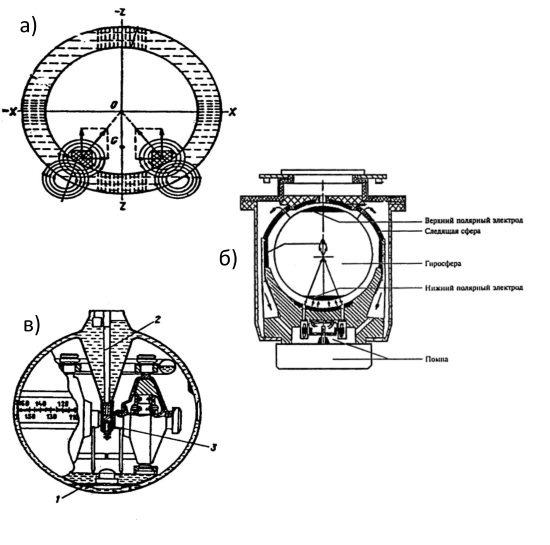
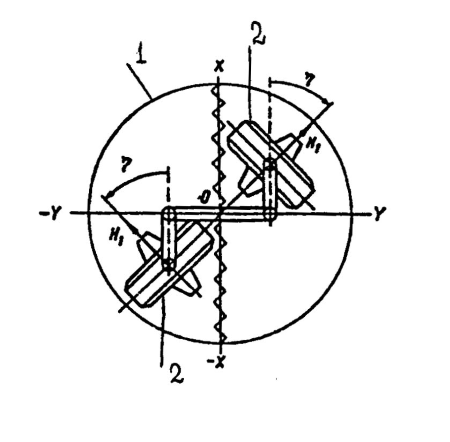
Рассмотрим подробнее гироузел чувствительного элемента (рис. 8). Два практически одинаковых по своим характеристикам гиромотора, представляющих собой асинхронные электродвигатели, питающиеся трехфазным переменным током, расположены так, что их главные оси образуют с осью Х – Х гиросферы углы п, в неработающем гирокомпасе равные 45^о.

Между гиромоторами (условимся называть их в дальнейшем просто гироскопами) установлена упругая кинематическая связь типа антипараллелограмма, включающая в себя два рычага, коромысло и две пружины. Эта связь дает возможность гироскопам поворачиваться вокруг их вертикальных осей (параллельных оси Z – Z) только на равные углы и в противоположные стороны, т. е. либо сходиться, либо расходиться.

Демпфирование колебаний чувствительного элемента гирокомпаса “Standard”

Для того чтобы чувствительный элемент гирокомпаса стал пригодным для целей судовождения, т. е. для непрерывного определения курса судна, необходимо, чтобы его физическая ось ОХ стабильно располагалась в плоскости истинного меридиана. Это равнозначно требованию о том, чтобы указанная плоскость стала положением его статического равновесия (а не динамического, как в режиме незатухающих колебаний).

Таким образом, ставится задача, состоящая в следующем: главная ось чувствительного элемента, имея перед пуском гирокомпаса любое произвольное отклонение от плоскости истинного меридиана, спустя некоторое время должна прийти в эту плоскость и оставаться в ней (практически в ее малой окрестности) неограниченно долгое время.

Чтобы обеспечить такое поведение чувствительного элемента, необходимо задемпфировать его колебания, т. е. сделать их из незатухающих затухающими.

Из теории колебаний известно, что демпфирование можно реализовать с помощью момента, имеющего сдвиг по фазе на 90^о по отношению к маятниковому моменту (принцип действия цистерн “Фрама”, применяющихся для снижения качки корабля на волнении).

Техническим устройством, с помощью которого в гирокомпасе “St-14” создается дополнительный маятниковый момент, обладающий необходимым сдвигом по фазе по отношению к основному маятниковому моменту, является гидравлический маятник (система сообщающихся сосудов, заполненных жидкостью), который устанавливают внутри чувствительного элемента и жестко скрепляют с его оболочкой (рис. 10).

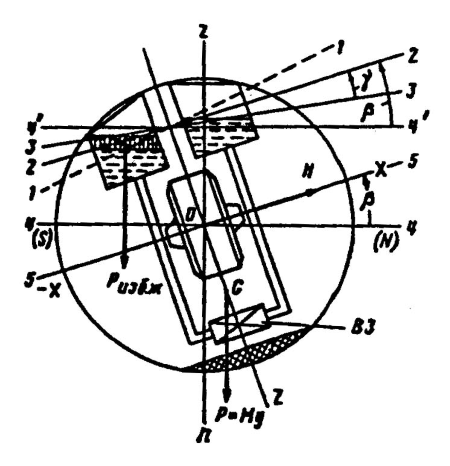
Сосуды и соединительная трубка располагаются вдоль оси Х – Х. При такой установке перетекание жидкости происходит в плоскости ХОZ, т. е. моменты от возникающего избытка жидкости создаются вокруг оси Y – Y.

Подбирая подходящую жидкость (весьма вязкое минеральное масло) и изготовляя соединительную трубку с малой площадью рабочего сечения, можно добиться необходимой силы вязкого трения, связывающего жидкость с гиросферой, и обеспечить требуемое запаздывание в колебаниях жидкости по отношению к колебаниям гиросферы по углу β. Следует особо подчеркнуть, что при данном способе демпфирования колебаний сохраняется непосредственное управление движением чувствительного элемента, осуществляемое силой тяжести, действующей как на твердый, так и на гидравлический маятники.

Одногироскопный маятниковый чувствительный элемент с жидкостно-торсионным подвесом

Одно из самых последних достижений в мировой гирокомпасной технике является создание одногироскопного маятникового гирокомпаса, наиболее важной отличительной чертой которого является высокая точность в условиях качки, что долгие годы считалось недостижимым для такого типа гирокомпасов.

К таким гирокомпасам относится гирокомпас “TG – 5000”. Рассматриваемый гирокомпас занимает промежуточное положение между двухгироскопным маятниковым гирокомпасом с автономным чувствительным элементом и корректируемым гирокомпасом с косвенным управлением, поскольку в одних обстоятельствах его поведение адекватно или близко первому из упомянутых аналогов, а в других обстоятельствах – второму.

Основное принципиальное отличие рассматриваемого одногироскопного маятникового гирокомпаса от уже изученного двухгироскопного, также маятникового гирокомпаса, заключается в системе подвеса чувствительного элемента, который может быть классифицирован как жидкостно-торсионный.

В отличие от гирокомпаса “St-14”, положение центра массы одногироскопного маятникового чувствительного элемента гирокомпаса “TG-5000” не локализовано в линейном отношении внутри следящей сферы.

Обратимся к рис. 11, на котором изображена гиросфера 1 с торсионным (проволочным) подвесом 2, находящаяся внутри следящей сферы 3 и полностью погруженная в высоковязкую силиконовую непроводящую жидкость 4.

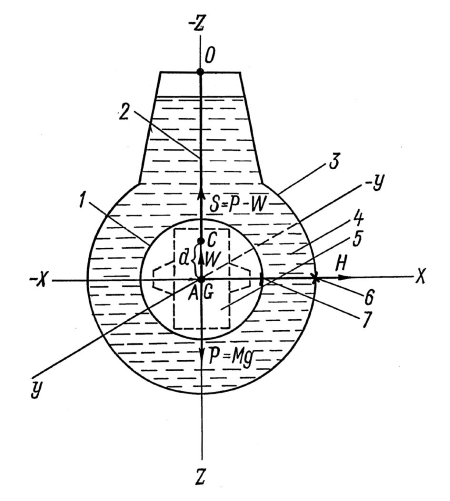
Гиросфера обладает небольшой отрицательной плавучестью. Внутри нее расположен жестко связанный с ней гиромотор 5. Двухкоординатный датчик угла индукционного типа, вырабатывающий электрические сигналы, пропорциональные углам рассогласования гиросферы со следящей сферой, образован ротором 7 и статором 6.

Обратим особое внимание на следующие четыре точки, отмеченные на рис. 11:

• точка G – центр массы гиросферы, точка, в которой приложенаравнодействующая сил веса всех элементов гиросферы Р;
• точка А – центр плавучести (он же в данном случае и геометрический центр) гиросферы, точка, в которой приложена равнодействующая архимедовых сил поддержания W;
• точка С – центр крепления торсиона к гиросфере, точка, в которой приложена сила его натяжения S;
• точка О – центр подвеса гиросферы, точка, в которой торсион закреплен в следящей сфере.

Существенное отличие подвеса рассматриваемого гирокомпаса состоит в том, что он не локализует положение центра подвеса как в гирокомпасах “St-14” по отношению к следящей сфере. Этот факт является следствием того, что центр подвеса вынесен за пределы гиросферы, что и позволило придать чувствительному элементу эффект положительного маятника при совпадающем положении центра массы с центром плавучести.

Введем следующие обозначения для параметров подвеса: расстояние GC = d, расстояние CO = ρ.

Обладание положительным маятникообразным эффектом обеспечивает непосредственное управление движением чувствительного элемента со всеми вытекающими отсюда последствиями, в частности, появление свойства избирательности по отношению к плоскости истинного меридиана.

Действительно, в положении, изображенном на рис. 11, когда чувствительный элемент расположен так, что его главная ось (вектор кинетического момента) находится в горизонтальной плоскости, а точки G, А, С, О находятся на одной вертикальной прямой, сила натяжения торсиона, образовавшаяся как разность силы тяжести Р и архимедовой силы W;

S = P – W,                    (4)

не создает момента относительного какой-либо оси гиросферы.

Однако, если ось ОХ чувствительного элемента, будучи отклоненной, например, к востоку от плоскости истинного меридиана, начнет по этой причине приподниматься над плоскостью истинного горизонта, образовывая угол β, то положение радикально изменяется. Как видно из рис. 12 сила натяжения торсиона S создает вместе с силой (Р – W) момент относительно оси Y – Y гиросферы, причем вектор момента будет направлен в сторону отрицательных значений указанной оси, т. е. к западу.

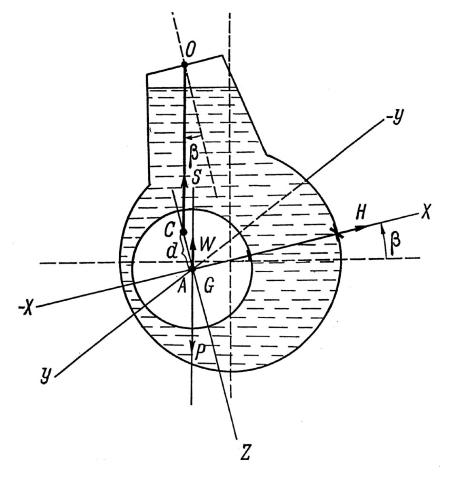
В результате действия момента L_y возникает прецессионное движение также к западу, т. е. в сторону плоскости истинного меридиана. Таким образом, сложилась уже знакомая ситуация, подробно рассмотренная в п. 1.3 с конечным выводом о том, что чувствительный элемент приобрел свойство избирательности по отношению к плоскости истинного меридиана, совершая вокруг нее незатухающие эллиптические колебания.

Нетрудно найти величину момента L_y. Из рис. 12 вытекает:

L_y = (P -W)d sinβ ≈ (P – W)dβ.                    (5)

Поскольку разность Р – W характеризует остаточный вес гиросферы в жидкости, то можно записать:

P – W = Δ Md,                    (6)

(величину Δ M обычно называют дифферентом массы). По аналогии с двухгироскопным компасом будем называть произведение Δ Md модулем маятникового момента, обозначив его символом В, т. е.:

B = Δ Md.                    (7)

Таким образом, окончательно имеем следующее выражение для горизонтального управляющего момента:

L_y = B·β,                    (8)

т. е. такое же, как в гирокомпасе “St-14” (см. формулу (3)), со всеми аналогичными последствиями.

Демпфирование колебаний чувствительного элемента гирокомпаса типа “TG-5000”

Дальнейший анализ поведения чувствительного элемента гирокомпаса требует введения в рассмотрение двухканальной следящей системы, которая обеспечивает непрерывное согласование положения следящей сферы с гиросферой. Для этой цели (рис. 13) следящая сфера подвешена в двухосном кардановом подвесе, образованном рамками 1 и 2.

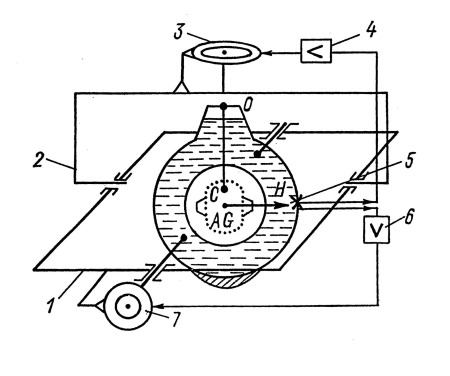
Горизонтальный канал следящей системы включает в себя датчик угла 5 (его горизонтальную координату), усилитель 4 и азимутальный следящий двигатель 3. Аналогично построен и вертикальный канал: датчик угла 5 (вертикальная координата), усилитель 6 и вертикальный следящий двигатель 7. Остальные элементы конструкции уже были показаны на рис. 11.

Движение гиросферы по углу α непрерывно отрабатывается горизонтальным каналом следящей системы. В результате такой отработки торсион все время раскручивается и тем самым гиросфера остается свободной от действия вертикального упругого момента.

При движении гиросферы по углу β происходит отработка вертикального канала следящей системы. В результате происходящего при этом поворота следящей сферы (см. рис. 12) гиросфера изменяет свое относительное расположение внутри следящей сферы, смещаясь в сторону ее опустившейся части. Отметим, что, невзирая на такое движение следящей сферы, вязкая жидкость, окружающая гиросферу, оказывает на нее весьма слабое воздействие, поскольку период указанного движения очень большой.

Необходимость вертикального канала следящей системы (как известно, в двухгироскопном маятниковом компасе он отсутствует) вызывается примененным способом погашения колебаний гиросферы. Сущность способа заключается в следующем (см. рис. 13). Сигнал рассогласования, пропорциональный углу β, который вырабатывается датчиком угла 5 (вертикальная координата) кроме того, что он идет на отработку положения следящей сферы по вертикальному каналу следящей системы, параллельно, через усилитель 4, поступает на азимутальный следящий двигатель 3 в виде дополнительного сигнала (который сверх того пропорционален рассогласованию по углу α). Происходит дополнительная отработка следящего двигателя 3, вследствие чего гиросфера оказывается под воздействием вертикального упругого момента, который является управляющим моментом и может быть представлен в следующем виде:

L_z = Dβ,                    (9)

где D – модуль вертикального демпфирующего момента.

Этот момент пространственно сдвинут по фазе на 90⁰ по отношению момента L_y = Вβ.

Момент L_z вызовет прецессионное движение гиросферы в плоскости углов β и при правильном подборе его знака указанное движение будет таким, что конец вектора Н будет стремиться к совпаданию с плоскостью истинного горизонта.

Совместное воздействие горизонтального маятникового момента L_y и вертикального упругого момента L_z обеспечивает движение конца вектора Н по сходящейся спирали, т. е. создается требуемый режим затухающих колебаний гиросферы. После завершения колебаний гиросфера придет в устойчивое положение равновесия по отношению к плоскости истинного меридиана и истинного горизонта.

Скоростная девиация гирокомпаса и ее учет

В предыдущих параграфах было установлено, что гироскопическое устройство,обладающее маятниковым эффектом, приобретает свойство избирательности по отношению к азимутальным направлениям, так как имеет своим положением равновесия плоскость истинного меридиана, т. е. ту вертикальную плоскость, которая содержит вектор горизонтальной составляющей суточного вращения Земли ω₁ = ω cosφ.

Ввиду такой закономерности, естественно, возникает следующий вопрос: не могут ли в процессе использования гирокомпаса сложиться такие условия, при которых в плоскости горизонта, кроме упомянутой горизонтальной составляющей ω₁, появятся какие-то дополнительные векторы угловой скорости, в результате чего произойдет смещение положения равновесия главной оси чувствительного элемента в сторону от плоскости истинного меридиана? Нетрудно прийти к заключению, что источником таких дополнительных угловых скоростей может быть движение основания (объекта) гирокомпаса по сферической поверхности Земли. По этой причине необходимо выявить совокупность угловых скоростей, которые будут восприниматься чувствительным элементом гирокомпаса, установленного на судне, движущемся с постоянной скорость и на постоянном курсе.

Движение судна считается заданным, если известен его курс ИК и скорость V (рис. 14).

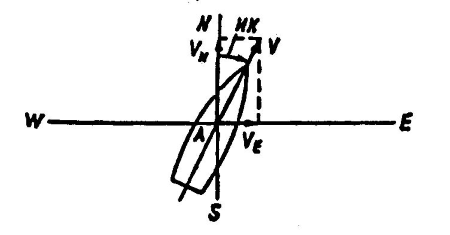
Другим вариантом определения движения является задание составляющих скоростей:

V_N – вдоль меридиана и V_E – вдоль параллели (см. рис. 14). Связь между двумя вариантами устанавливается следующими соотношениями:

V_N = Vcos ИК;     V_E = Vsin ИК.                    (10)

Поскольку движение судна происходит по земной сфере, существование линейных скоростей неизбежно вызовет появление некоторых угловых движений. Для определения существующих угловых скоростей обратимся к рис. 15, на котором положение судна на земной сфере задано координатами φ и λ, а его движение – составляющими V_N и V_E скорости.

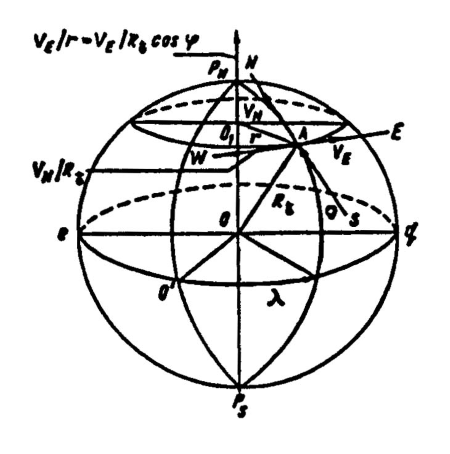
Отчетливо видно, что движение с линейной скоростью V_N по дуге большого круга, имеющего радиус, равный R, приводит к возникновению угловой скорости, вектор которой равен по величине отношению V_N/R и направлен по линии EW к W.

Соответственно движение с линейной скоростью V_E, происходящее по дуге параллели радиусом r = Rcosφ, приводит к появлению угловой скорости, вектор которой равен отношению V_E/Rcosφ.

Пользуясь тем свойством, что вектор угловой скорости является свободным вектором, т. е. его можно переносить параллельно самому себе в любую точку, нанесем этот вектор на ось вращения Земли, т. е. на ось P_NP_S по направлению к P_N.

Теперь установлена совокупность угловых скоростей (поле угловых скоростей), которые воспринимаются чувствительным элементом гирокомпаса, установленного на движущемся судне. Указанное поле угловых скоростей включает в себя составляющие ω₁ и ω₂ угловой скорости суточного вращения Земли (переносные угловые скорости) и составляющие V_N/R и V_E/Rcosφ угловой скорости вращения судна относительно Земли. Все перечисленные составляющие показаны на рис. 16, из которого отчетливо видно каким образом они разложены по осям горизонтной системы координат ONEn.

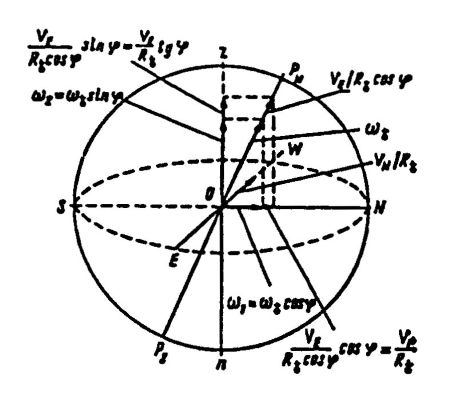
В итоге поле угловых скоростей однозначно характеризуется следующими
тремя составляющими: а) по оси N – S по направлению к N; б) по оси E – W по направлению к Е; в) по оси Z – n по направлению к n, т. е. соответственно:

$U_1=(\omega \cos \varphi +\frac{V_E}{R}); U_2=–\frac{V_N}{R}; U_3=–(\omega \sin \varphi –\frac{V_E}{R}tg\varphi ). \left(11\right)$

С позиций, изложенных в п. 1.8. главный интерес представляет тот факт, что в плоскости истинного горизонта оказались вместо единственной составляющей ω₁ = ωcosφ, как это имело место в случае неподвижного основания, три составляющие, в том числе V_N/R – ортогональная к ωcosφ.

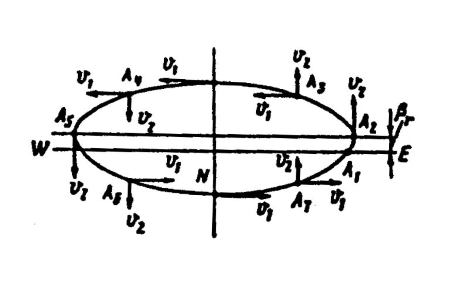
На рис. 17 показана плоскость истинного горизонта (вид с зенита) и
расположенные в этой плоскости составляющие U₁ и U₂, данные в развернутом виде.

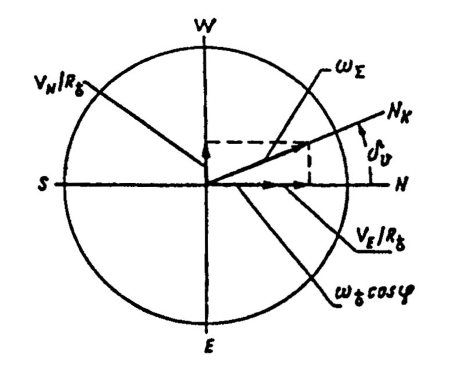
Положение вектора равнодействующей ω_Σ по отношению к истинному
меридиану определяется углом δ_v, тангенс которого находят по формуле:

$tg{\delta }_V=–\frac{V_N/R}{\omega \cos \varphi +V_E/R} \left(12\right)$

или после простых преобразований, с учетом значений, приведенных в формуле (10):

$tg{\delta }_V=–\frac{V \cos ИК}{R\omega \cos \varphi +V\sin ИК} \left(13\right)$

(знак “минус” означает, что при заданных исходных условиях угол δ_v имеет западное наименование). Поскольку положение равновесия главной оси ОХ чувствительного элемента гирокомпаса теперь располагается в вертикальной плоскости, содержащей вектор равнодействующей ω_Σ указанная плоскость получает название плоскость компасного меридиана, а ее угловое отклонение от плоскости истинного меридиана δ_v – скоростная девиация гирокомпаса.

Формула (13), совершенно точная с математической точки зрения, противоречива с практической точки зрения, поскольку для определения погрешности курса – угла δ_v – необходимо знать истинное значение последнего. Для устранения этого недостатка преобразуем формулу (13) с помощью известного из навигации общего соотношения:

ИК = КК +δ_v.                    (14)

Используя уравнения (14), представим выражение (13) в виде:

$\frac{\sin {\delta }_V}{\cos {\delta }_V}=–\frac{V \cos (KK+{\delta }_V)}{R\omega \cos \varphi +V \sin (KK+{\delta }_M)},$

что тождественно равно следующему выражению:

sinδ_vRωcosφ = – V[cos(KK + δ_v)cosδ_v + sin (KK + δ_v) sinδ_v]

или:

sin δ_vRωcosφ = – Vcos KK,

откуда:

$\sin {\delta }_V=–\frac{V \cos KK}{R\omega \cos \varphi }. \left(15\right)$

Основные закономерности скоростной девиации, вытекающие из анализа формулы (15), состоят в следующем.

1. Возникновение скоростной девиации обуславливается наличием у судна северной составляющей скорости движения.
2. Девиация линейно зависит от скорости судна.
3. Девиация имеет полукруговой характер зависимости от компасного курса (максимальные по абсолютному значению девиации достигаются на курсах 0 и 180^о, нулевые – на курсах 90 и 270^о ).
4. Зависимость девиации от широты определяется функцией 1/cosφ, поэтому особенно резкое увеличение ее численного значения происходит в широтах выше 60^о.
5. Скоростная девиация не зависит от параметров гирокомпаса, т. е. ее величина одинакова для всех типов гирокомпасов.

Скоростная девиация в гирокомпасе “St-14” учитывается с помощью таблиц, а в гирокомпасе “TG-5000” – путем ее исключения из показаний всех репитеров с помощью корректора полуавтоматического типа (см. ниже).

Инерционные девиации

Инерционные девиации у гирокомпасов “St-14” и “TG-5000” возникают в результате маневрирования судна, т. е. при изменении скорости судна или его курса.

Указанные девиации возникают из-за наличия у чувствительного элемента маятникового эффекта.

Девиация, возникающая в результате воздействия сил инерции на маятниковое устройство, называется инерционной девиацией первого рода. Единственным способом предупреждения ее появления является придание периоду незатухающих колебаний гирокомпаса значения 84,4 мин. Однако период незатухающих колебаний гирокомпаса зависит от широты места судна и по этой причине инерционная девиация первого рода полностью отсутствует только в одной определенной широте, называемой расчетной широтой гирокомпаса (обозначается φ*).

Например, для гирокомпаса “St-14” расчетная широта φ* равняется 54^о (широта Гамбурга). При плавании вне расчетной широты у гирокомпаса обязательно будет возникать при маневрировании инерционная девиация первого рода. У сертифицированных гирокомпасов эта девиация сравнительно невелика и ее пределы лимитируются резолюцей ИМО А-424.

Из-за наличия в конструкции гирокомпаса какого-либо устройства для погашения его колебаний при маневрировании возникает инерционная девиация второго рода. В гирокомпасах “St-14” и “TG-5000” не существует каких-либо приспособлений для предотвращения возникновения этой девиации. Величина девиации второго рода не зависит от широты места и может суммироваться (в φ > φ*) c инерционной девиацией первого рода.

Интеркардинальная девиация (девиация на качке)

Интеркардинальной девиацией называется девиация гирокомпаса, возникающая при качке судна на волнении. Эта девиация появляется из-за существования у чувствительного элемента гирокомпаса маятникового эффекта.

В гирокомпасе “St-14” величина интеркардинальной девиации снижается до величины, предписываемой резолюцией ИМО, путем применения системы двух, связанных между собой гироскопов.

В гирокомпасе “TG-5000” снижение девиации осуществляется путем использования в подвесе чувствительного элемента жидкости чрезвычайно высокой вязкости.

Предлагается к прочтению:
Связь для передачи корреспонденции
«Система судовых сообщений» и «Маршрутные донесения с судов»