Параметры сжиженного газа, его внутренние процессы – температура, давление, энергия и т. п. важно учитывать во время транспортировки на газовозах. Поэтому уделим этому пристальное внимание.
- Идеальный газ
- Критические температура и давление
- Уравнение состояния идеального газа (уравнение Менделеева-Клапейрона)
- Основы термодинамики
- Внутренняя энергия и энтальпия
- Теплота
- Расчет температуры смеси жидкой фазы груза
- Закон Дальтона
- Взаимные превращения жидкостей и газов
- Испарение
- Кипение
- Работа при изменении объёма газа
- Энтропия
- Теплопроводность
- Расчет изоляции грузовых танков
- Диаграмма Молье
В данном материале подробно рассмотрим варианты состояний сжиженных веществ, критические показатели смесей и как их избежать при перевозке химических и нефтяных веществ.
Идеальный газ
Количественные зависимости между двумя параметрами газа при фиксированном значении третьего параметра называются газовыми законами.
Процессы же, протекающие при постоянстве одного из параметров, называются изопроцессами.
Идеальный газ – это газ, который имеет следующие свойства:
- размеры молекул малы по сравнению с расстояниями между ними;
- молекулы взаимодействуют друг с другом и со стенками сосуда только в момент соударения;
- все соударения абсолютно упруги;
- рассматриваются любые газы, в которых число молекул очень велико;
- молекулы распределены по всему объёму равномерно;
- молекулы движутся хаотично, то есть все направления движения молекул равноправны;
- скорость молекул может принимать любые значения;
- к движению отдельной молекулы применимы законы классической механики.
Критические температура и давление
Теоретически, все газы можно сжижать при охлаждении их до определенной температуры или же путем их сжатия. Некоторые газы необходимо предварительно охладить перед их сжатием. Рассматривая этот вопрос подробнее, можно установить, что все газы имеют строго определенную температуру и давление, при которых их можно обратить в жидкость (рис. 1). Такие параметры называются критическими.
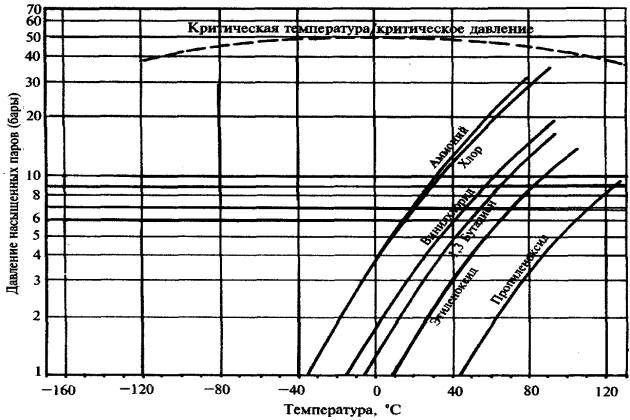
- Критическая температура газа – это температура, выше которой газ не может быть сжат до состояния жидкости, каким бы высоким ни было давление.
- Критическое давление газа – это минимальное давление, при котором газ, находящийся при критической температуре, может быть сжат до состояния жидкости.
| Таблица 1. Значения критических давлений и температур для некоторых газов | |||
|---|---|---|---|
| Название газа | Химическая формула | Критическая температура (°С) | Критическое давление (бар) |
| Аммиак | NH3 | 132,4 | 112,0 |
| Гелий | Не | -268,0 | 2,3 |
| Водород | Н2 | -240,0 | 12,8 |
| Углекислый газ | СО2 | 31,0 | 73,0 |
| Метан | СН4 | -82,1 | 45,8 |
| Азот | N2 | -147,1 | 33,9 |
| Кислород | О2 | -118,8 | 51,4 |
| Пропан | С3Н8 | 96,8 | 42,1 |
| Вода | Н2О | 374,0 | 218,0 |
| Винил хлорид | С2Н3Cl | 156,5 | 56,9 |
Уравнение состояния идеального газа (уравнение Менделеева-Клапейрона)
Состояние идеального газа характеризуют три инструментально измеряемых параметра:
- P – давление, (Па);
- v – удельный объём (м3/кг) или плотность (ρ, кг/м3);
- T – температура, (K).
Существует общая зависимость, связывающая между собой эти параметры, которая называется уравнением состояния. Параметры состояния, изменяющиеся в процессе, не зависят от пути процесса и определяются только начальным и конечным состояниями.
Для идеального газа уравнение состояния имеет самый простой вид и называется уравнением Клапейрона-Менделеева:
в котором
есть массовая газовая постоянная число 8 314 Дж/(кмоль K), определенное Д. И. Менделеевым, универсальная газовая постоянная для мольного количества газа, а μ – мольное число газа, равное его молярной массе.
Уравнение, устанавливающее связь между давлением, температурой и объёмом газов было получено французским физиком Бенуа Клапейроном. А в форме уравнения состояния идеального газа его впервые использовал Д. И. Менделеев.
Как видно, два параметра определяют третий в любом термодинамическом процессе с неизменным количеством идеального газа.
Многие процессы, происходящие в природе и осуществляемые в технике, можно приближенно рассматривать как процессы, в которых меняются лишь давление и температура.
Тщательная экспериментальная проверка газовых законов современными методами показала, что эти законы достаточно точно описывают поведение реальных газов при небольших давлениях и высоких температурах, в противном случае наблюдаются значительные отступления от уравнения состояния.
Это объясняется двумя причинами:
- при сильном сжатии газов объём незанятого молекулами пространства становится сравним с объёмом, занимаемым самими молекулами,
- при низких температурах становится заметным взаимодействие между молекулами.
Пример 1:
Какой объём займут 96 г кислорода при 3-х (300 000 Па) барах давления и температуре +77 °С.
Решение
- прежде всего, определим, сколько молей составляют 96 г кислорода.
- далее нам надо определить, сколько молей кислорода составляет 96 г,
- теперь, используя уравнение Менделеева-Клайперона, мы можем определить объём:
В периодической таблице элементов мы видим, что атомная масса кислорода составляет 15,9994. Это значит, что один моль кислорода (6,02 · 1023 атомов) будет иметь массу ~16 г. Соответственно молекула кислорода, состоящая из 2-х атомов, будет иметь массу 32 г/моль.
заметим, что Дж = Н · м, а Па = Н/м2.
Пример 2:
Определим, какое количество паров (масса) содержится в танке объёмом 5 000 м3 после выгрузки бутана (С4Н10), если манометрическое давление в танке составляет 0,1 бара, а температура +5 °С?
Решение:
Из уравнения состояния идеального газа
Определим искомую величину
Для нашего примера давление p будет равно сумме манометрического и атмосферного давлений
или же 1,11 · 105 Па, а температура T = 273 + 5 °С.
Подставляя известные величины в выражение (Формула 1) получим массу паров бутана, оставшихся в грузовом танке после выгрузки сжиженного газа.
Основы термодинамики
Термодинамика возникла как наука о взаимном превращении двух форм энергии – теплоты и механической работы. В настоящее время термодинамика занимается исследованием практически всех явлений, связанных с получением или потреблением энергии, совершением работы, переносом вещества и т. д.
Техническая термодинамика исследует соотношения между параметрами термодинамических систем и совершаемой работой. Материальные тела, входящие в состав термодинамических систем делятся на:
- горячие источники теплоты и холодные теплоприемники;
- рабочие тела.
Состоянием системы называют определенное сочетание её свойств в данный момент времени.
Параметром состояния системы называют такой её показатель, изменение которого обязательно связано с изменением состояния системы.
Всякое изменение состояния тела или системы, связанное с теплообменом или механическим воздействием, называют термодинамическим процессом.
Параметры состояния, изменяющиеся в процессе, не зависят от пути процесса и определяются только начальным и конечным состояниями. Повторим, что, основными параметрами системы, представляющей собой не перемещающийся объём газа как рабочего тела, являются:
- температура (T, K);
- давление (p, Па);
- удельный объём (v, м3/кг) или плотность (ρ, кг/м3).
Напомним также, что все три основных параметра находятся в определенном математическом соотношении, называемом уравнением состояния. Для идеального газа оно имеет вид уравнения Клапейрона-Менделеева:
в котором
есть массовая газовая постоянная число 8 314 Дж/(кмоль K), определенное Д. И. Менделеевым, универсальная газовая постоянная для мольного количества газа, а μ – мольное число газа, равное его молярной массе.
Основу термодинамики составляют два её закона, или начала:
- первый закон термодинамики – это всеобщий закон сохранения и превращения энергии;
- второй закон термодинамики определяет направление самопроизвольного процесса в изолированной термодинамической системе.
Внутренняя энергия и энтальпия
Тело, как система составляющих его частиц обладает внутренней энергией. Внутренняя энергия не зависит ни от механического движения тела, ни от его местоположения относительно других тел и является исключительно функцией состояния тела.
Кинетическая энергия движения частиц зависит от температуры, а потенциальная энергия взаимодействия зависит от расстояния между частицами, т. е. от объёма тела.
Если потенциальная энергия взаимодействия молекул равна нулю, газ называется идеальным, а его внутренняя энергия равна сумме кинетической энергии движения молекул и пропорциональна его абсолютной температуре.
Изменение внутренней энергии определяется формулой:
где:
- ΔT – изменение температуры, K;
- m – масса газа, кг;
- cν – удельная массовая теплоёмкость газа в изохорном процессе (ν = const), Дж/(кг K).
Удельную внутреннюю энергию относят к 1 кг массы газа:
которая является функцией состояния неподвижного вещества.
Сумма внутренней энергии и энергии введения газа в объём V под давлением p – есть полная энергия, называемая энтальпией:
В термодинамических процессах интерес представляет не само по себе значение внутренней энергии или энтальпии, а их изменение при переходе тела из состояния 1 в состояние 2, поскольку изменение параметров состояния в термодинамической системе не зависит от вида процесса.
где:
- cp = cν + R – удельная массовая теплоёмкость в изобарном процессе (p = const), R – Дж/(кг K) – массовая газовая постоянная.
- m – масса вещества;
- – разность удельных энтальпий вещества в конце и начале процесса (h2 – h1).
- n – количество тел, участвующих в теплообмене.
- c – удельная теплоемкость;
- m – масса тела;
- ΔT = T2 – T1, при нагревании T2 > T1, а при охлаждении T2 < T1.
- pT – общее давление смеси газов;
- pA + pB – парциальное давление каждого газа;
- nA – количество молей газа А в объёме;
- nB – количество молей газа В в объёме;
- R – универсальная газовая постоянная, равная 8,314 Дж/(K·моль);
- T – абсолютная температура смеси газов;
- V – объём смеси газов в куб. метрах.
- gi – массовая концентрация газа и;
- ri – молярная концентрация газа.
- Gi и Gсм – масса газа и масса смеси газов;
- ni и nсм – количества вещества газа и смеси газов (моль).
- n – число молей;
- Mr – молярная масса;
- m – масса вещества.
- число молей пропана: 100 г : 44,1 г/моль = 2,27 моль;
- число молей бутана: 400 г : 58,1 г/моль = 6,88 моль;
- общее число молей смеси 9,15 моль.
- парциальное давление пропана составит: 0,248 · 3,69 бар = 0,915 бар;
- парциальное давление бутана составит: 0,752 · 0,78 бар = 0,587 бар;
- давление насыщенных паров смеси 1,502 бар;
- давление в танке (манометрическое) ≈ 0,5 бар.
- содержание пропана в газовой фазе: 0,915 бар : 1,502 бар = 0,609 → 60,9 %;
- содержание бутана в газовой фазе: 0,587 бар : 1,502 бар = 0,391 → 39,1 %.
- испарение;
- кипение.
- Если испарение происходит в замкнутом сосуде, температура во всех точках сосуда одинакова, но её величина ниже, чем температура кипения. В таком случае внутри сосуда достигается состояние равновесия между жидкостью и паром, и процесс испарения прекращается c достижением в этом паре парциального давления насыщения, соответствующего температуре в сосуде.
- Если же испарение происходит в открытом сосуде, равновесие не достигается практически никогда, а скорость испарения зависит от многих факторов. Обычно скорость испарения пропорциональна разности между давлением насыщенного пара при температуре испарения и действительным давлением пара над поверхностью жидкости.
- Если же давление насыщенных паров жидкости и фактическое давление паров равны, испарение сопровождается обратным процессом, который называется конденсацией.
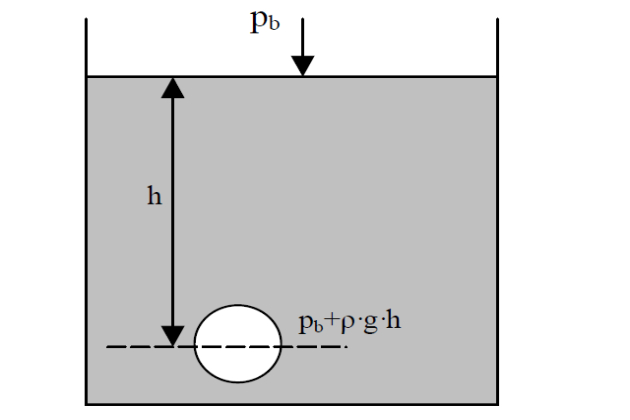
- pb – барометрическое давление;
- h – высота столба жидкости;
- ρv – плотность жидкости;
- g – ускорение свободного падения.
- F – сила, действующая на поршень, (Н);
- L – расстояние пройденное поршнем, (м);
- S – площадь поршня, (м2);
- p – давление газа, (Па);
- ΔV – объём цилиндра на ходе поршня (м3 ).
- dq – элементарный удельный теплообмен;
- ds – удельная энтропия.
- ς (м) – толщина изоляции;
- λ (Вт/(м·К)) – удельная теплопроводность материала;
- Q (Вт) – тепловой поток;
- A (м2) – площадь изоляции;
- T1 (°K) – температура теплой поверхности изоляции;
- T2 (°K) – температура холодной поверхности изоляции.
- Из таблицы 2 выбираем значение удельной теплопроводности полиуретановой пены, -0,023 Вт/м·K,
- подставим известные нам значения в формулу:
- если произойдет отделение изоляции танка от его переборок (например при образовании льда между переборкой танка и изоляцией), то приток тепла будет значительно больше, поскольку в том месте, где отстала изоляция сталь будет единственным изоляционным материалом между грузом и окружающей средой. Как можно найти из таблицы, удельная теплопроводность стали составляет 50,2 Вт/м·K,
- при толщине стали 20 мм, приток тепла в танк составит:
Для практических расчетов, связанных с определение результата энергообмена в том или ином процессе, используется формула:
где:
Информация о термодинамических параметрах сжиженных газов, перевозимых на судах, даётся или в графической форме, или в табличной форме. Основными параметрами для входа в график являются инструментально измеряемые параметры, такие как температура и давление газа.
Теплота
Количество теплоты в физике обозначается символом Q и связано с изменением внутренней энергии частиц, из которого состоит тело.
Теплоту, полученную телом, считают положительной, а теплоту, отданную телом, считают отрицательной.
В изолированной системе справедливо уравнение теплового баланса:
где:
В общем случае количество теплоты, переданной при охлаждении или полученной при нагреве тела, определяется по формуле:
где:
В таблице 2 приведены значения изобарной теплоёмкости для некоторых газов. Значения теплоёмкости изменяются от нуля до бесконечности в зависимости от термодинамического процесса, в котором протекает теплообмен.
| Таблица 2. Удельная изобарная теплоёмкость и удельная скрытая теплота парообразования (Latent Heat of Vaporization) для некоторых газов | |||
|---|---|---|---|
| Название газа | Удельная изобарная теплоемкость Дж/кг·K | Скрытая теплота парообразования при р = 101,3250 кПа (кДж/кг·K) | |
| Перегретый пар | Жидкость | ||
| Ethane | 1.706 | 3.807 | 489,36 |
| Propane | 1.625 | 2.476 | 425,73 |
| n-Butane | 1.652 | 2.366 | 385,26 |
| i-Butane | 1.616 | 2.366 | 366,40 |
| Etylene | 1.514 | — | 482,77 |
| Propylene | 1.480 | 2.443 | 437,88 |
| Butylene | 1.483 | 2.237 | 390,60 |
| Ammonia | 2.079 | 4.693 | 1.366 |
| 1,2- Butadiene | 1.446 | 2.262 | 449,60 |
| 1,3-Butadiene | 1.426 | 2.124 | 418,70 |
Расчет температуры смеси жидкой фазы груза
Теплота всегда передается от более тёплого тела к менее теплому, иными словами, от тела с высокой температурой – к телу с низкой температурой.
Предположим, что два вещества смешаны без образования химической реакции, т. е. не возникает выделения или поглощения тепла. В этом случае можно сказать, что тепло переданное, равно теплу полученному. При этом, мы предполагаем, что не происходит передачи тепла окружающей среде.
Такое определение используется на практике при перевозке газовой смеси сжиженных пропана и бутана, с разной теплоемкостью и разными температурами при их смешивании на борту судна.
В этом случае мы заранее можем сосчитать температуру смеси сжиженных газов, зная первоначальные параметры каждого газа до их смешения. А, имея в наличии температуру смеси, мы можем определить и давление в танке, и плотность груза.
Прежде всего, выразим в виде формул уже известное равенство – теплота, полученная равна теплоте отданной:
где левая половина равенства определяет теплоту одной жидкости, а правая – теплоту другой. Наиболее просто это можно рассмотреть на примере.
Пример:
Смешиваются 5 кг пропана при температуре tp = -40 °С и 8 кг бутана при температуре tb = +2 °С. Удельная теплоёмкость пропана cр = 2 476 Дж/кг·K, а для бутана cb = 2 366 Дж/кг·K.
Определим температуру смеси газов (Tm)
Решение:
Ясно, что Tb > Tm > Tp и можно записать ΔTp = (Tm – Tp), а для бутана ΔTb = (Tb – Tm)
для нашего случая
рассчитаем температуру смеси по формуле (Формула 1):
В общем случае расчет температуры смеси можно выразить формулой:
Закон Дальтона
Давление смеси газов равно сумме парциальных давлений каждого из газов, составляющих смесь.
Используя буквенные обозначения, закон Дальтона можно выразить следующим образом:
где:
Для вычисления давления смеси используются понятия:
При перевозке смеси сжиженных газов, важно знать, какое давление будет в танке при данной температуре. Это требуется для установки параметров компрессорной установки.
Рассмотрим несколько простых методов расчета давления паров, если известны молярный или весовой состав смеси, погруженной на борт,
Пример:
Судно должно погрузить смесь 100 тонн пропана и 400 тонн бутана, температура смеси составляет -8 °С (смотри расчет температуры смеси газов). Давление насыщенных паров для пропана при этой температуре, определенное по графику или взятое из таблицы, составляет 3,69 бара. А давление насыщенных паров бутана, составит при этой температуре 0,78 бара. Необходимо определить давление насыщенных паров смеси (то есть общее давление в танке) и процентный состав газовой фазы над поверхностью жидкости.
Решение:
Рассчитаем молярное соотношение пропана и бутана в составе смеси. Для этого определим молярную массу пропана (С3Н8) и бутана (С4Н10). С помощью периодической таблицы элементов находим, что один атом углерода имеет массу 12,01115 г/моль, а атом водорода – 1,00797 г/моль.
| Расчет молярного соотношения пропана и бутана в составе смеси | |
|---|---|
| Наименование вещества | Численное выражение |
| Молярная масса пропана | |
| Молярная масса бутана | |
Теперь определим количество молей каждого вещества в смеси. Соотношение масс пропана и бутана 100 тонн : 400 тонн, но если использовать не тонны, а граммы, то соотношение останется тем же самым 100 г : 400 г. Расчет количества вещества (молей) будем производить по соотношению:
где:
Рассчитаем парциальное давление пропана и бутана, используя закон Рауля:
молярный состав пропана в жидкой фазе:
молярный состав бутана в жидкой фазе:
Состав смеси в газовой фазе (над поверхностью жидкости) можно рассчитать следующим образом:
Как можно видеть, газ, всасываемый компрессором в систему повторного сжижения, состоит на 60,9 % из паров пропана и на 39,1 % из паров бутана, несмотря на то, что в жидкой фазе пропана содержится всего 24,8 %.
Важно, производить такие расчеты заранее, с тем, чтобы определить установочное давление для предохранительных клапанов на танках (MARVS – Maximum Allowed Relieve Valve Setting) и максимально допустимое давление конденсации смеси в системе повторного сжижения, поскольку пропан имеет более высокое давление конденсации, нежели бутан.
Следует иметь ввиду, что все газы, перевозимые на судах, фактически представляют из себя смесь целого ряда различных газов. Например, промышленный пропан содержит в своем составе от 95 до 98 % пропана, 1-3 % этана и около 1 % бутана.
Взаимные превращения жидкостей и газов
В природе и в технике мы часто встречаемся с изменением агрегатного состояния вещества (рис. 3), в частности с превращением жидких и твердых тел в газообразное состояние.
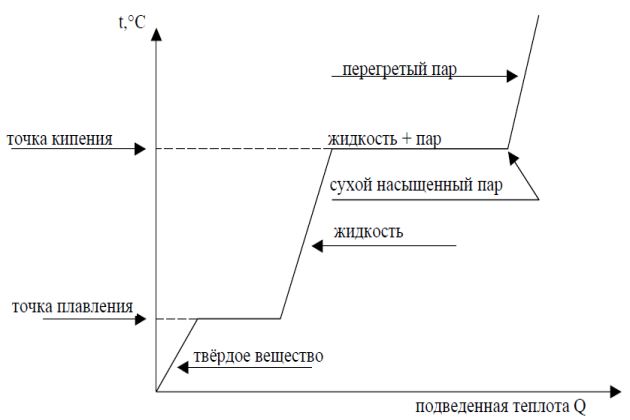
Для жидкостей существуют два способа перехода в газообразное состояние:
Испарение
Испарение происходит с открытой, свободной поверхности, отделяющей жидкость от газа, например, с поверхности жидкости в открытом сосуде, с поверхности водоёма и т. д.
При испарении, молекулы, вылетевшие с поверхности жидкости, должны преодолеть силу притяжения соседних молекул, следовательно, совершить некоторую работу. Поэтому, чтобы произошло испарение, испаряющемуся веществу необходимо сообщить некоторое количество теплоты, черпая её из запаса внутренней энергии самой жидкости.
Если к испаряющейся жидкости не подводить теплоту извне, то жидкость охлаждается.
Кипение
Второй способ преобразования жидкости в пар – кипение, которое отличается от испарения тем, что образование паров происходит по всему объёму жидкости (рис. 4).
Поэтому данная жидкость, находясь под определенным давлением, кипит при вполне определённой температуре.
Обычно температуру кипения той или иной жидкости, в том числе и для сжиженных газов, приводят для атмосферного давления.
Пузырьки газа, возникающие в процессе кипения, насыщены парами груза.
Когда давление насыщенного пара внутри пузырьков превышает давление на поверхности жидкости, пузырьки всплывают и лопаются. Жидкость начинает кипеть. Если увеличить давление над жидкостью, то температура кипения увеличится, если давление понизить, то и температура кипения уменьшится.
В практике это факт используется очень часто. Например, в паровых установках вода кипит при температуре 281 °С при давлении в 65 бар, а в установках по производству дистиллированной воды, наоборот, вода кипит при температуре 40 °С и давлении насыщенных паров 0,0738 бар. На высоте около 5 000 метров атмосферное давление составляет 513 мбар, что соответствует температуре кипения воды 82 °С.
Простейший же способ охладить до наинизшей температуры сжиженный газ – сделать так, чтобы его давление насыщенных паров было равно атмосферному давлению, то есть, сообщить атмосферу грузового танка с окружающей атмосферой, что и достигается при срабатывании предохранительного клапана на грузовом танке.
Для того чтобы подсчитать количество теплоты, необходимое для превращения в пар жидкости любой массы, нужно удельную теплоту парообразования (r) умножить на массу.
Эта формула часто используется при определении необходимого количества жидкого груза для Охлаждение груза перед погрузкой в грузовые танкизахолаживания грузовых танков без использования судовой установки повторного сжижения (см. статью Подготовка грузовых танков«Грузовые операции на судне, продувка, захолаживание танков»).
Работа при изменении объёма газа
Одним из основных термодинамических процессов, совершающихся в большинстве тепловых машин, является процесс расширения газа с совершением работы. При изобарном расширении газа от объёма V1 до объёма V2, происходит перемещение поршня в цилиндре на расстояние L (рис. 5).
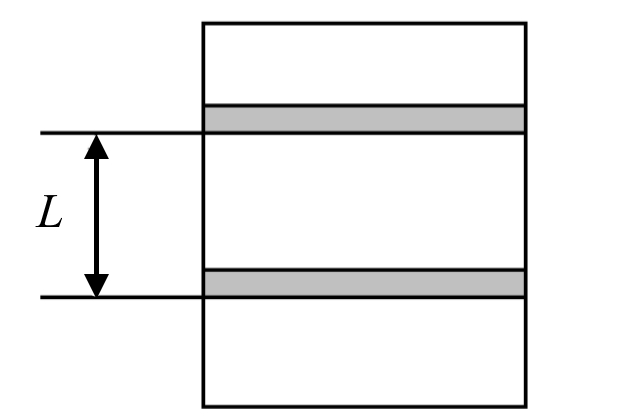
При этом работа «A» совершаемая газом, будет равна (рис. 6):
где:
При изохорном процессе изменения объёма газа не происходит, следовательно работа в данном случае будет равна «0».

При изотермическом расширении газа (т. е. при неизменной температуре), работа выразится площадью фигуры под гиперболой (рис. 7).
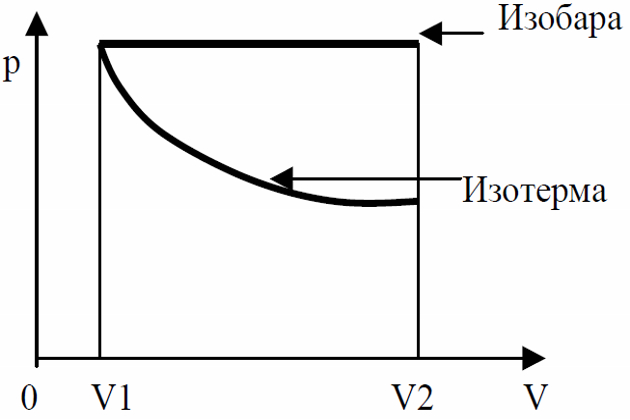
При расширении газа направление вектора силы давления газа совпадает с направлением вектора перемещения поршня, поэтому работа, совершаемая газом в этом случае, будет положительной, а работа внешних сил – отрицательной. При сжатии газа направление вектора внешней силы совпадает с направлением перемещения поршня, поэтому работа внешних сил будет положительной (A > 0), а работа газа – отрицательной (A < 0).
Энтропия
Энтропия является также одним из параметров состояния системы и характеризует её энергоспособность. Увеличение энтропии системы указывает на снижение её энергоспособности.
где:
Выразив удельный теплообмен через внутреннюю энергию тела и работу изменения объёма, для процесса 1-2 можно записать:
Таким образом, изменение энтропии определяется изменением измеряемых параметров системы (p, V, T). В теплотехнике для графического представления состояний газа и отображения термодинамических процессов в тепловых двигателях широко используется так называемая энтропийная диаграмма (T-s).
Теплопроводность
Теплопроводность – это процесс передачи теплоты (энергии) вследствие хаотичного теплового движения молекул или атомов.
Иными словами, применительно к телам, можно сказать, что теплопроводность – это перенос энергии от более нагретых участков тела к менее нагретым его участкам вследствие теплового движения и взаимодействия частиц. Помимо теплопроводности теплота может передаваться конвекцией и излучением.
Конвекция, происходящая без вмешательства извне, называется естественной, если же неоднородно нагретую массу газа или жидкости перемешивать с помощью насоса или вентилятора, то происходит вынужденная конвекция.
В практике перевозки сжиженных газов теплопроводность материалов используется при расчете изоляции грузовых танков.
Расчет изоляции грузовых танков
Для расчетов притока теплоты через изоляцию грузовых танков, мы воспользуемся следующей формулой:
где:
Для наглядности рассмотрим использование этой формулы на конкретном примере.
Пример:
Определить количество теплоты, которое проникает через изоляцию одного грузового танка судна вместимостью 75 000 м3. Танк изолирован полиуретановой пеной, наполненной фреоном, толщиной 100 мм, тепловоспринимающая поверхность танка 690 м2. Температура окружающей среды составляет +30 °С, а температура груза -40 °С.
Как видим, приток тепла через переборку танка будет на несколько порядков выше, чем приток тепла через 10 см слой изоляции. Правда этот расчет не является реалистичным, поскольку на практике мы не сталкиваемся с тем, чтобы вся изоляция танка отвалилась. Даже в таком, гипотетическом случае, на внешней поверхности танка будет образовываться слой льда, который будет выполнять роль своего рода изолирующего материала. В этом случае приток тепла в танк будет значительно ниже.
| Таблица 3. Теплофизические характеристики некоторых материалов | |||
|---|---|---|---|
| Тип изоляции | Теплопроводность, Вт/м·K | Плотность, Кг/м3 | Теплоёмкость, кДж/кг·K |
| Неподвижный воздух | 0,024 | 1,29 | 1,0 |
| Полистирол (пена) | 0,038 | 25 | 1,34 |
| Эбонит (разрыхленный) | 0,029 | 65 | 1,38 |
| Полиуретан (пена) | 0,023 | 40 | 1,26 |
| PVC (пена) | 0,033 | 40 | 1,34 |
| Бакелит | 0,041 | 32 | 1,34 |
| Стекловата (в матах) | 0,035 | 20 | 0,84 |
| Стекловата насыпью | 0,041 | 60 | 0,84 |
| Минеральная вата в матах | 0,035 | 45 | 0,84 |
| Минеральная вата насыпью | 0,041 | 100 | 0,84 |
| Перлит | 0,035 | 50 | 0,84 |
| Сталь | 50,2 | 7 800 | 0,46 |
Диаграмма Молье
Наиболее важным в практическом плане является понимание того, как можно рассчитать время охлаждения груза в зависимости от имеющегося оборудования на борту судна. Поскольку возможности судовой установки по сжижению газов во многом определяют время стоянки судна в порту, то знание этих возможностей и правильное их использование позволят нам заранее планировать стояночное время, поможет избежать ненужных простоев и претензий к судну.
Диаграмма, которая приводится ниже (рис. 8), рассчитана только для пропана, но метод её использования для всех газов одинаков.
| Таблица 4. Множители для образования десятичных кратных и дольных единиц и их наименование | |||
|---|---|---|---|
| Число | Порядок измерения | Название | Сокращенное обозначение |
| 1 000 000 000 000 | 1012 | Тера | Т |
| 1 000 000 000 | 109 | Гига | Г |
| 1 000 000 | 106 | Мега | M |
| 1 000 | 103 | Килок | |
| 100 | 102 | Гекто | г |
| 10 | 10 | Дека | да |
| 0,1 | 10-1 | Деци | д |
| 0,01 | 10-2 | Санти | с |
| 0,001 | 10-3 | Мили | м |
| 0,000001 | 10-6 | Микро | мк |
| 0,000000001 | 10-9 | Нано | н |
| 0,000000000001 | 10-12 | Пико | п |
Диаграмма с осями давления – энтальпия иногда называется диаграммой Молье. В ней используется логарифмическая шкала абсолютного давления (p log) – на вертикальной оси, на горизонтальной оси (h) – натуральная шкала удельной энтальпии (рис. 8, 9). Давление – в МПа (мега Паскалях), 0,1 МПа = 1 бар, поэтому в дальнейшем будем использовать бары. Удельная энтальпия измеряется в кДж/кг. В дальнейшем при решении практических задач мы будем постоянно использовать диаграмму Молье (но только её схематичное изображение, с тем, чтобы отчетливее понимать физику тепловых процессов, происходящих с грузом).
На диаграмме мы можем заметить своего рода «сачок», образованный кривыми. Границы этого «сачка» представляют собой пограничные кривые смены агрегатных состояний сжиженного газа, а именно переход жидкости в насыщенный пар. Все что находится слева от «сачка» представляет собой переохлажденную жидкость, а все то, что справа от «сачка» относится к перегретому пару (рис. 9).
Пространство между этими кривыми представляет собой различные состояния смеси насыщенных паров пропана и жидкости отражает процесс фазового перехода. На ряде примеров, рассмотрим практическое использование диаграммы Молье.

Пример 1:
Проведите линию, соответствующую давлению в 2 бара (0,2 Мpа) через участок диаграммы, отражающий смену фаз (рис. 10). Найдем энтальпию для 1 кг кипящего пропана при абсолютном давлении 2 бара.
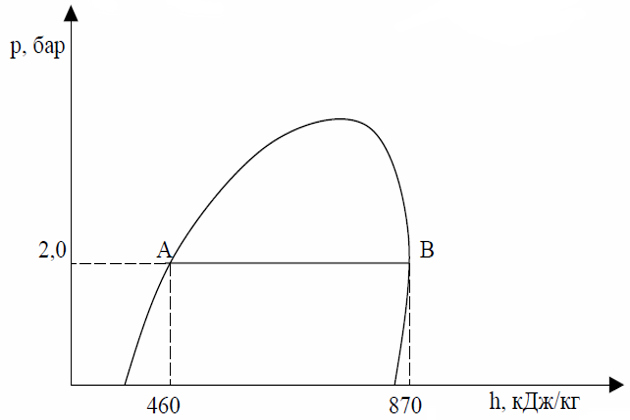
Как уже отмечалось выше, кипящий жидкий пропан характеризуется левой кривой диаграммы. В нашем случае это будет точка «А». Проведя из точки А вертикальную линию к шкале h, мы определим значение энтальпии, которое составит 460 кДж/кг. Это означает, что каждый килограмм пропана в данном состоянии (в точке кипения при давлении 2 бара) обладает энергией в 460 кДж. Следовательно, 10 кг пропана обладают энтальпией 4 600 кДж.
Далее определим величину энтальпии для сухого насыщенного пара пропана при том же давлении в 2 бара. Для этого проведем вертикальную линию из точки «В» до пересечения со шкалой энтальпии. В результате найдем, что максимальное значение энтальпии для 1 кг пропана в фазе насыщенных паров составит 870 кДж. Внутри диаграммы линии, направленные из точки критического состояния газа вниз, отображают количество частей газа и жидкости в фазе перехода. То есть 0,1 означает, что смесь содержит 1 часть паров газа и 9 частей жидкости. В точке пересечения давления насыщенных паров и этих кривых мы определим состав смеси (её сухость или влажность).
Температура перехода постоянна в течение всего процесса конденсации или парообразования. Если пропан находится в замкнутой системе (в грузовом танке), в ней присутствуют и жидкая и газообразная фазы груза. Можно определить температуру жидкости, зная давление паров, давление паров по температуре жидкости.
Давление и температура связаны между собой, если жидкость и пар находятся в равновесном состоянии в замкнутой системе. Заметим, что кривые температуры, расположенные в левой части диаграммы, следуют почти вертикально вниз, пересекают фазу парообразования в горизонтальном направлении, и в правой части диаграммы опять опускаются вниз почти вертикально.
Пример 2:
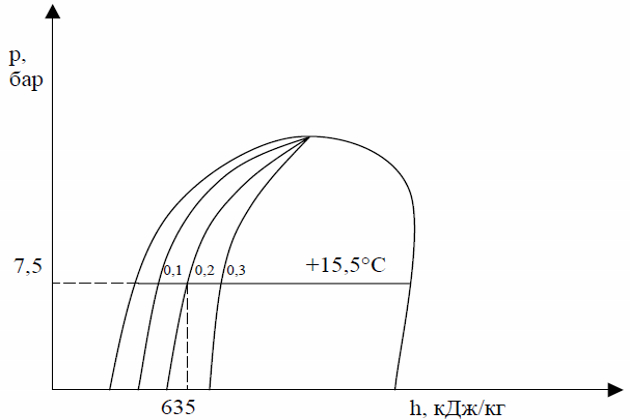
Предположим, что мы имеем 1 кг пропана в стадии смены фаз (часть пропана жидкость, а часть – пар). Давление насыщенных паров составляет 7,5 бар, а энтальпия смеси (пар-жидкость) равна 635 кДж/кг. Необходимо определить, какая часть пропана находится в жидкой фазе, а какая в газообразной?
Отложим на диаграмме, прежде всего известные величины, давление паров 7,5 бар и энтальпию 635 кДж/кг. Далее мы можем определить, что точка пересечения давления и энтальпии лежит на кривой, которая обозначена 0,2. А это, в свою очередь означает, что мы имеем пропан в стадии кипения и 2 (20 %) части пропана находятся в газообразном состоянии, а 8 частей (80 %) находятся в жидком состоянии.
Также можно определить температуру жидкости, которая составляет 60 °F или же +15,5 °С (для перевода температуры мы будем использовать таблицу термодинамических характеристик пропана – см. таблицуТаблицы и графические приложения по специализированной подготовке персонала газовоза «Термодинамические параметры пропана»).
Чтобы найти давление в танке (манометрическое давление) необходимо помнить, что оно меньше давления насыщенных паров (абсолютного давления) на величину атмосферного давления, равного 1 013 мбар. В дальнейшем для упрощения расчетов мы будем использовать значение атмосферного давления равное 1 бару. То есть в нашем случае давление насыщенных паров или абсолютное давление равно 7,5 бар, то манометрическое давление в танке составит 6,5 бар.
Ранее уже упоминалось, что жидкость и пары в равновесном состоянии находятся в замкнутой системе при одной и той же температуре. Это верно, однако на практике можно заметить, что пары, находящиеся в верхней части танка (в куполе) имеют температуру значительно выше, чем температура жидкости. Это обусловлено нагревом танка. Однако, такой нагрев не влияет на давление в танке, которое соответствует температуре жидкости (точнее сказать температуре на поверхности жидкости). Пары непосредственно над поверхностью жидкости имеют ту же самую температуру, что и поверхность жидкости, и, как раз на поверхности жидкости, и происходит смена фаз вещества.
Как видно (рис. 8-11), на диаграмме Молье кривые плотности направлены из левого нижнего угла диаграммы «сачка» в правый верхний угол. Значение плотности в диаграмме может быть дано в lb/ft3 Для пересчета в СИ используется переводной коэффициент 16,02 (1,0 lb/ft3 = 16,02 кг/м3).
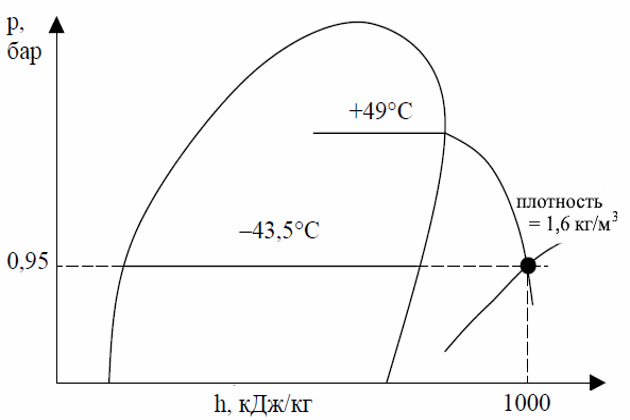
Пример 3:
В этом примере будем использовать кривые плотности. Требуется определить плотность перегретого пара пропана при абсолютном давлении 0,95 бара и температуре +49 °С (120 °F). Также определим удельную энтальпию этих паров. Процесс определения искомых параметров виден из рисунка 12.
В наших примерах используются термодинамические характеристики для одного газа – пропана. В подобных расчетах для любого газа меняться будут только абсолютные величины термодинамических параметров, принцип же остается тот же самый для всех газов.
В дальнейшем для упрощения, большей точности расчетов и сокращения времени будем использовать таблицы термодинамических свойств газов.
Практически вся информация, заложенная в диаграмме Молье, приведена в табличной форме.
С помощью таблиц можно определить численное значение параметров груза, но трудно представить себе как идет процесс охлаждения, если не использовать хотя бы схематичное отображение диаграммы «p – h».
Пример 4:
В грузовом танке при температуре -20 °С находится пропан. Необходимо определить как можно точнее давление газа в танке при данной температуре. Далее необходимо определить плотность и энтальпию паров и жидкости, а также определить разность энтальпии между жидкостью и парами. Пары над поверхностью жидкости находятся в состоянии насыщения при той же температуре, что и сама жидкость. Атмосферное давление в нашем случае составляет 980 миллибар. Необходимо нарисовать упрощенную диаграмму Молье и отобразить все параметры на ней (рис. 13).
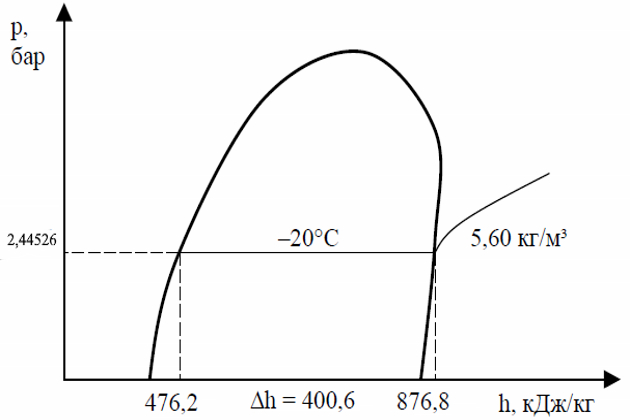
Используя таблицу, определяем давление насыщенных паров пропана. Абсолютное давление паров пропана при температуре -20 °С – 2,44526 бар. Давление в танке будет равно:
абсолютное давление – атмосферное давление = давлению в танке (избыточное или манометрическое давление)
2,44526 бар – 0,980 бар = 1,46526 бар.
В колонке, соответствующей плотности жидкости находим, что плотность жидкого пропана при -20 °С составит 554,48 кг/м3. Далее находим в соответствующей колонке плотность насыщенных паров, которая равна 5,60 кг/м3.
Энтальпия же для жидкости составит 476,2 кДж/кг, а для паров 876,8 кДж/кг. Соответственно разность энтальпии составит (876,8 – 476,2) = 400,6 кДж/кг.
Несколько позже мы рассмотрим использование диаграммы Молье в практических расчетах работы установок повторного сжижения.
