Качество в судостроении

Роль измерений в обеспечении качества

Для постройки судна, соответствующего проекту, и обеспечения работы систем, реализующих функции механизированных или ав­томатизированных производств (контроль технологических пара­метров, регулирование, управление), необходима постоянная ме­трологическая информация отечности и качестве его изготовления, которую получают путем измерений. Единство измерений в разных местах, в разное время, разными методами и средствами позволяет сопоставлять их результаты. Близость полученных результатов к истинному значению измеряемой величины характеризует точность из­мерений.

Разность между результатом измерения величины Х_р и истинным ее значением Х_и определяет абсолютную погрешность измерения ∆ = |Х_Р -Х_и|. В силу несовершенства измерительных средств, методов измерения и органов чувств наблюдателя истинное значение всегда ос­тается неизвестным, поэтому понятие «истинная величина» использу­ют лишь при решении теоретических задач метрологии. На практике пользуются значением величины, найденным экспериментальным пу­тем и максимально приближающимся к истинному. За действительную величину при многократных измерениях часто принимают среднее арифметическое результатов отдельных измерений.

Погрешности разделяют на систематические 0 и случайные η со­ставляющие, тогда;

∆ = η+0.

Систематические погрешности остаются постоянными или законо­мерно изменяются при повторных измерениях одной и той же величи­ны. Причины их появления — определенные, неслучайные факторы. Например, неточное нанесение штрихов на шкалу прибора вносит одну и ту же ошибку во все результаты измерений. Систематические погреш­ности почти всегда могут быть выявлены опытным путем специально разработанными приемами и методами, а затем исключены из резуль­татов измерений внесением поправок.

Возникновение случайных погрешностей измерений определяют мно­гочисленные факторы, проявляющиеся нерегулярно и с непредсказуе­мой частотой, например, изменение внимания оператора при снятии показаний приборов или вариации показаний средств измерений из-за их технического несовершенства. Поэтому случайные погрешности нельзя исключать из результатов измерений подобно систематическим. Тем не менее если отдельные значения случайной погрешности предска­зать невозможно, то совокупность их при многократных измерениях од­ной и той же величины подчиняется закономерностям, описываемым методами теории вероятности и математической статистики.

Среди случайных погрешностей выделяют грубые погрешности, суще­ственно превышающие некоторую ожидаемую погрешность, независимую от наблюдателя (например, из-за скачка напряжения в электрической сети), и промахи, резко искажающие результат по вине наблюдателя (на­пример, ошибки при записи или считывании показаний прибора). Те и другие обычно исключают из результатов измерений.

Требования к качеству судов и отдельных судовых конструкций ус­танавливает нормативная документация. Они (требования) всегда со­держат некоторый разброс каждого из задаваемых параметров, огра­ниченный верхним и нижним пределами. Ограниченный пределами интервал значений параметров называют полем допуска, а разность меж­ду наибольшим и наименьшим значениями — допускаемым отклоне­нием или допуском. Наряду с допускаемыми отклонениями в изделиях могут встречаться несоответствия требованиям, установленным техни­ческой документацией, или дефекты, приводящие к ухудшению каче­ства или к невозможности нормальной эксплуатации таких изделий.

Примерами дефектов могут служить:

• Трещины в стальных конструк­циях;
• Непровары в сварных швах;
• Потеки на окрашенной поверхности;
• Отклонения формы или размеров деталей и конструкций за установ­ленные пределы.

Повышение точности изготовления корпусных деталей и конструк­ций — важнейшая задача судостроительного производства. Следует иметь в виду, что высокая точность требует и значительных затрат на обработку. Например, изготовить какую-либо деталь с точностью со­блюдения линейных размеров до 0,1 мм технологически сложнее и дороже, чем с точностью 1,0 мм, так как необходимы иные оборудование, оснастка и квалификация рабочего. С другой стороны, чем выше точ­ность изготовления собираемых элементов, тем менее трудоемки сбо­рочные работы, так как уменьшается объем пригонки, а следовательно, и затраты.

Установить оптимальную точность для каждого конкретного слу­чая весьма сложно. Все технологические процессы могут быть опи­саны только с позиций теории вероятности и математической статис­тики, когда результаты каждого конкретного действия (измерения величины, откладывания размера, оценки погрешности резки и пр.) рассматривают как случайные величины. Погрешности размеров де­талей и конструкций обычно подчиняются закону нормального распределения.

Допускаемые отклонения размеров от номинальных устанавливают с учетом функционального назначения узла, конструкции или изделия. Задают их конструкторы. В просторечии их называют «допуски, как нужно». Технологи с учетом законов распределения погрешностей при использовании определенной технологии и имеющегося оборудования устанавливают «допуски, как можно». В конечном счете конструктив­ные допуски должны быть обеспечены принятой технологией.

Предельные значения допускаемых отклонении (их границы) ста­раются назначить так, чтобы вероятность выхода за них была мала. Например, для закона нормального распределения устанавливают гра­ницы ± Зσ, т. е. поле допуска δ = 6σ. Вероятность попадания случайно­го отклонения в поле допуска δ = 6σ составляет 99,73%, а вероятность выхода за его пределы – 0,27% (в меньшую и большую стороны). Не­обходимо все же помнить, что вероятность выхода размера за границы допуска есть всегда и возможны ошибки, приводящие к грубым погреш­ностям, превышающим расчетные. Вероятность того, что фактический размер выйдет за пределы поля допуска, называют процентом риска Р, параметр, который называют коэффициентом риска t, зависит от соот­ношения между средним квадратическим отклонением σ и выбранной величиной поля допуска δ:

Погрешность средства измерения является одной из составляющих суммарной погрешности результата измерения. Например, на точность измерения одного из самых распространенных в судостроении измерительных инструментов – рулеток – помимо погрешности шкалы δ_ш, указанной в паспорте средства измерения, влияют погрешности натя­жения ленты δ_н = Ɩ∆ P/EF, температурная δ_тт = Ɩ(α₁∆t₁ – α₂∆t₂) и завися­щая от квалификации разметчика погрешность отсчета размера и со­вмещения рисок шкалы δ₀.

Здесь:

• Ɩ — измеряемый размер;
• ∆P — разность между фактическим и нормальным натяжениями рулетки;
• E — модуль нормальной упругости материала ленты;
• F — площадь поперечного се­чения ленты;
• α₁ и α₂ — коэффициенты линейного расширения измеряемого объекта и ленты рулетки;
• ∆t₁ и ∆t₂ — отклонения от нормальной температуры измеряемого объекта и ленты рулетки.

Реальная погрешность измерения рулетками:

${∆}_{\sum _{}}=\sqrt{{{\mathrm{\delta }}^2}_{\mathrm{ш}}+{{\mathrm{\delta }}^2}_{\mathrm{н}}+{{\mathrm{\delta }}^2}_{\mathrm{т}}+{{\mathrm{\delta }}^2}_0}$

Отличается от паспортных данных о погрешности средства измерения δ_ш.

Для оценки ожидаемой точности изготовления деталей и конструкций выполняют расчет размерных цепей. Размерной цепью называют замкну­тый контур, образованный взаимосвязанными размерами — звеньями. В размерной цепи выделяют замыкающее звено, связывающее поверхно­сти или оси, расстояние или угол между которыми нужно обеспечить или измерить, т. е. звено, из-за кото­рого ведут расчет размерной цепи. Остальные звенья называют состав­ляющими. Составляющее звено счи­тают положительным (увеличивающим), если с его увеличением при постоянстве всех остальных составляющих звеньев увеличивается замыкающее звено, и отрицательным (уменьшающим), если при его уве­личении замыкающее звено уменьшается.

Различают плоские размерные цепи, в которых все звенья лежат в одной плоскости (или в параллельных плоскостях) и пространствен­ные. Плоские размерные цепи с параллельными звеньями называют линейными.

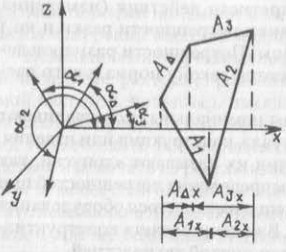
Любая размерная цепь может быть превращена в систему линейных цепей путем проецирования всех звеньев на оси выбранной системы ко­ординат. Например, четырехзвенная пространственная размерная цепь, показанная на рис. 12.1, может быть преобразована в три линейные:

А_∆х = A₁cosα₁ + А₂cosα₂ + A₃cosα₃

А_∆у = A₁cosβ₁ + A₂cosβ₂ + A₃cosβ₃

А_∆z = A₁cosγ₁ + A₂cosγ₂ + A₃cosγ₃

Где:

• cosα_i, cosβ_i, cosγ_i, — направляющие косинусы каждого звена (на ри­сунке показана только первая линейная цепь).

Под расчетом размерной цепи понимают взаимную расчетную увяз­ку размеров ее звеньев, по заданным допускам составляющих звеньев находят допуск замыкающего звена (прямая задача, поверочный расчет) или по заданному допуску замыкающего звена находят допуски составляющих звеньев (обратная задача, проектный расчет).

Обе задачи можно решать либо методом максимума-минимума, либо вероятностным методом.

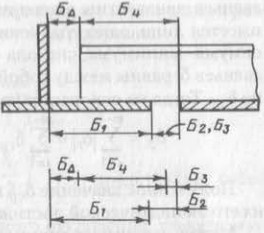
Рассмотрим размерную цепь, приведенную на рис. 2. Замыкаю­щим звеном Б_∆ в ней является величина зазора между торцом ребра жесткости и плоскостью вертикального листа при стыковании двух секций. Обозначим Б_i, номинальные размеры звеньев, μ_i — допускае­мое верхнее, а ν_i — допускаемое нижнее отклонения от номинальных размеров. Тогда возможное большее значение звена будет Б_i + μ_i, а возможное меньшее значение Б_i + ν_i. Допуски звеньев:

δ_i = (Б_i + μ_i) – (Б_i + ν_i) = μ_i – ν_i

Размерная цепь имеет следующие со­ставляющие звенья:

• Б ^{μ1 ν1}₁ — расстояние от вертикального листа до кромки полотнища;
• Б ^{μ2 ν2}₂ — зазор между кромками полотнищ;
• Б ^{μ3 ν3}₃ — усадка сварного шва после сварки;
• Б ^{μ4 ν4}₄ — выход ребра жест­кости за кромку полотнища.

Расчет по методу максимума-мини­мума включает поиск:

• Номинального размера замыкающего звена как суммы разме­ров звеньев цепи (уменьшающие звенья имеют знак минус):
  ${\mathrm{Б}}_{∆\mathrm{ном}}={\mathrm{Б}}_1+{\mathrm{Б}}_2–{\mathrm{Б}}_3–{\mathrm{Б}}_4=\sum _{i=1}^{m–1}{\mathrm{Б}}_i$

  Где: m = 4 — количество звеньев размерной цепи;

• Наибольшего размера (с учетом величин отклонений) замыкаю­щего звена, как суммы наибольших размеров увеличивающих звеньев и наименьших размеров уменьшающих звеньев Б_∆max = (Б₁ + μ₁) + (Б₂ + μ₂) – (Б₃ + ν₃) – (Б₄ + ν₄);

• Наименьшего размера замыкающего звена сложением наимень­ших размеров увеличивающих звеньев и наибольших размеров умень­шающих Б_∆min = (Б₁ + ν₁) + (Б₂ + ν₂) – (Б₃ + ν₃) – (Б₄ + μ₄).

По определению разность между Б_∆max и Б_∆min – допуск замыкаю­щего звена:

Таким образом, независимо от значений номинальных размеров и от расположения полей допусков относительно звеньев размерной цепи (симметрично или ассиметрично) допуск замыкающего звена равен сумме абсолютных величин допусков всех составляющих звеньев. До­пуск любого размера δ_i, в отличие от отклонений μ_i и ν_i – всегда пред­ставляет собой положительную величину. Для того чтобы предупре­дить возможные ошибки при расчетах, в формуле (1) использован знак абсолютной величины.

Обратную задачу решают чаще. По заданной величине δ_∆ определя­ют допуски δ_i звеньев цепи. Задача имеет бесконечное число решений, поскольку для определения m-1 неизвестных величин (в цепи из m звеньев неизвестны значения от m-1 допусков составляющих звеньев) имеется лишь одно уравнение размерной цепи. Применяя метод мак­симума-минимума, сначала считают, что все допуски составляющих звеньев δ_i равны между собой и равны некоторой неизвестной величи­не δ_ср. Тогда на основании уравнения (1) можно записать

Полученное значение δ_ср корректируют для каждого звена, исходя из его экономической достижимости.

Метод максимума-минимума прост, нагляден и позволяет получать надежные результаты. Вместе с тем он дает завышенные требования к точности звеньев размерной цепи. Поэтому, когда известны характерис­тики рассеяния (или законы распределения) погрешностей звеньев, рас­чет ведут вероятностным методом, основанном на сложении квадратов средних квадратических отклонений независимых случайных величин:

Если принять σ_i=σ_cp, то:

${\mathrm{\sigma }}_{∆}={\mathrm{\sigma }}_{\mathrm{cp}}\sqrt{m–1}$

Учитывая, что величины σ и δ связаны между собой через коэффициент риска t=δ/2σ, имеем пра­во считать, что:

${\mathrm{\delta }}_{∆}={\mathrm{\delta }}_{\mathrm{cp}}\sqrt{m–1}$

Определив по заданному допуску замы­кающего звена среднюю величину допуска звеньев размерной цепи δ_ср, получим:

${\mathrm{\delta }}_{\mathrm{cp}}={\mathrm{\delta }}_{∆}\sqrt{m–1}$

Этот допуск будет в:

$\sqrt{m–1}$

раз больше, чем при расчете по методу максимума-минимума. Разница в результа­тах расчетов по двум описанным методам тем значительнее, чем боль­ше звеньев содержится в размерной цепи.

Для более точного расчета размерной цепи с учетом ожидаемого процента риска и законов распределения отклонений размеров звень­ев выразим среднее квадратическое отклонение через коэффициент риска каждого звена t_i и допуск δ_i: σ_i = δ_i/2t_i. Подставив полученное соот­ношение в уравнение (2) и возведя обе его части в квадрат, получим:

$\frac{{\mathrm{\delta }}_{∆}^2}{4t_{∆}^2}=\sum _{i=1}^{m–1}\frac{{\displaystyle {\mathrm{\delta }}_i^2}}{{\displaystyle 4{\mathrm{t}}_i^2}}$

Введя коэффициент относительного рассеяния λ^‘_i = 1/t²_i, значение поля допуска замыкающего звена размерной цепи приведем к виду:

${\mathrm{\delta }}_{∆}=t_{∆}\sqrt{\mathit{\sum }_{i\mathit{=}\mathit{1}}^{m\mathit{–}\mathit{1}}{{\lambda }_i}^{\mathit{‘}}{\delta }_i^{\mathit{2}}} \left(3\right)$

Поскольку допуск для всех звеньев ранее принят одинаковым и рав­ным δ_ср, а также считая λ^‘₁ = λ^‘₂ = … = λ^‘_m-1 = λ^‘_ср, получаем:

${\mathrm{\delta }}_{\mathrm{cp}}=\frac{{\mathrm{\delta }}_{∆}}{{\displaystyle {{\displaystyle t}}_{∆}}\sqrt{{\mathrm{\lambda }}_{\mathrm{cp}}^{‘}(m–1)}}$

Коэффициент:

${\mathrm{\lambda }}_i^{‘}=\frac{1}{{\mathrm{t}}_i^2}={\left(\frac{2{\mathrm{\sigma }}_i}{{\mathrm{\delta }}_i}\right)}^2={\left({\mathrm{\sigma }}_{\mathrm{i}}:\frac{{\displaystyle {\mathrm{\delta }}_{\mathrm{i}}}}{{\displaystyle 2}}\right)}^2$

Представляет собой квадрат отношения среднего квадратического отклонения, характеризу­ющего случайные составляющие производственной погрешности при дан­ном законе распределения, и половины предписанного допуска звена.

Практически во всех случаях решения размерных цепей рассеяние отклонений замыкающего звена подчинено нормальному закону распределения. Для нормального закона хорошо известно отношение λ^‘_i = 1/9. Значение t_∆ в выражении (3) также следует считать соот­ветствующим нормальному закону, тогда:

${\mathrm{\delta }}_{∆}=\sqrt{\sum _{i=1}^{m–1}{\mathrm{\delta }}_i^2} \left(3а\right)$

Координата середины поля допуска замыкающего звена:

$\mathrm{\xi }=\sum _{i=1}^n{\mathrm{\xi }}_{0i}^{\mathrm{ув}}–\sum _{n+1}^{m–1}{\mathrm{\xi }}_{0i}^{\mathrm{ув}}$

Где:

• ${\xi }_{0i}^{ув}$

  – координата середины поля допуска увеличивающего звена размерной цепи;

• ${\xi }_{0i}^{ум}$

  – то же для уменьшающего звена;

• n — количество увеличивающих звеньев.

Проведем расчет размерной цепи, показанной на рис. 2, задаваясь значениями допусков звеньев цепи:

${\mathrm{Б}}_1^{+3};{\mathrm{Б}}_2^{\frac{+1}{–2}};{\mathrm{Б}}_3^{\pm 0,3};{\mathrm{Б}}_4^{–3};$

Примем t_∆ = 3 (процент риска будет равен 0,27) и будем считать, что погрешности звеньев следуют нормальному закону распределения (λ^‘_i = 1/9).

По методу максимума-минимума допуск замыкающего звена δ_∆ = 3 + 3 + 0,6 +3 = 9,6 мм, верхняя граница допуска замыкающего звена μ_∆ = (+3) + (+1)- (-0.3)- (-3) = +7,3 мм и нижняя граница допуска замыкающего звена ν_∆ = (0) + (-2) – (+0,3) – 0 = – 2,3 мм.

Поскольку δ_∆ = μ_∆ – ν_∆ = (+7,3) – (-2,3) = 9,6 мм, можно считать, что для замыкающего звена справедлив допуск

${\mathrm{Б}}_{∆}^{\frac{+7,3}{–2,3}}.$

При использовании для расчета вероятностного метода имеем:

Координата середины поля допуска замыкающего звена ξ_∆ = (ξo1 + ξ02) – (ξ03 + ξ04) = [(+1.5) + (-0,5)]- [0 + (-1,5)] = +2,5 мм, откуда верхняя граница допуска замыкающего звена:

${\mathrm{\mu }}_{∆}={\mathrm{\xi }}_{{}_{∆}}+\frac{{\mathrm{\delta }}_{∆}}{2}=+2,5+\frac{5,2}{2}=+5,1 \mathrm{мм}$

А его нижняя граница:

${\mathrm{\nu }}_{∆}={\mathrm{\xi }}_{{}_{∆}}–\frac{{\mathrm{\delta }}_{∆}}{2}=+2,5–\frac{5,2}{2}=–0,1 \mathrm{мм}$

Проверка расчета подтверждает результат:

  δ_∆ = μ_∆ – ν_∆ = 5,1 – (0,1) = 5,2 мм.

Допускаемые расчетные размеры замыкающего звена полученные вероятностным методом

${\mathrm{Б}}_{∆}^{\frac{+5,1}{–0,1}}.$

Величина допуска на зазор между ребром жесткости и листом, най­денного обоими методами, не гарантирует качественной сварки дета­лей. Исходя из требуемых режимов сварки, допуск замыкающего зве­на должен быть около 2 мм, т. е. δ_∆ = 2 мм, откуда средний допуск на звенья той же размерной цепи по методу максимума-минимума 2/(5—1) = 0,5 мм, вероятностным методом:

$2/3\sqrt{(5–1)÷9}=1,0 \mathrm{мм}$

Результаты расчетов показывают, что требуемая для качественной сварки точность звеньев рассмотренной цепи выше, чем реально дос­тижимая при сборке корпусных конструкций. Выход можно найти в расширении допуска на звенья цепи. Увеличив до 32% (t = 1) допус­тимый процент риска получения погрешностей, превышающих приня­тые, найдем, что средний допуск составит уже 3 мм, но тогда примерно треть всех сопряжений не уложится в сборочные допуски. Тем не ме­нее этим приемом, т. е. увеличением процента риска широко пользу­ются на практике. По существу в корпусостроении все допуски на де­тали и конструкции назначены с процентом риска, отличающимся от нуля. Если обеспечить точность звеньев размерной цепи невозможно, то при изготовлении деталей в определенных местах оставляют излиш­ки металла — припуски, которые удаляют при сборочных работах.

Повышение точности замыкающего звена может быть достигнуто как увеличением точности каждого из составляющих звеньев, так и сокращением количества звеньев в размерной цепи, к чему всегда сле­дует стремиться при разработке технологии сборки, например, перехо­дя от подетального к узловому монтажу.

При изготовлении деталей и конструкций для достижения необхо­димой точности замыкающего звена размерной цепи могут использовать:

• Полную взаимозаменяемость, когда любую деталь, узел или секцию при сборке устанавливают на место без каких-либо пригоночных работ;
• Неполную (частичную) взаимозаменяемость, при которой неко­торая часть деталей, узлов, секций требует при сборке пригонки;
• Групповую взаимозаменяемость, при которой детали, изготовлен­ные с относительно большими допусками, по фактическим размерам разделяют на несколько групп. Внутри каждой группы обеспечивают полную взаимозаменяемость. В судокорпусостроении этот метод не применяют.

Требуемой точности изделий достигают регулированием и пригон­кой. При регулировании заданный размер замыкающего звена выдер­живают не удалением припуска, а перемещением деталей относительно баз или базовых деталей и, в некоторых случаях, установкой компенсационных звеньев (прокладок, вставок и т. н.). Поджатие дета­лей при сборке (используют их гибкость) рассматривают как регулирование.

Пригонкой достигают точности, оставив припуски в местах сопря­жения собираемых элементов, а затем удалив лишний материал при сборочных работах. Несмотря на то, что количество припусков стре­мятся уменьшить за счет повышения точности изготовления деталей и конструкций, пригонка все же является одним из основных способов обеспечения требуемых зазоров под сварку.

В судокорпусостроении допуски на размеры деталей и конструк­ций в чертежах обычно не указывают. Их задают, исходя из накоплен­ного опыта, в нормативно-технической документации, например, в отраслевых стандартах.

Рекомендуется к прочтению:
Плазовое обеспечение корпусных цехов
Автоматизированные системы плазовых работ