Перекладка руля и маневренность крупнотоннажных судов

Закономерности движения судна при перекладке руля характеризуют одно из важнейших качеств судна, обеспечивающих безопасность плавания, называемое управляемостью. Фундаментальные основы науки об управляемости судов заложены трудами советских ученых А. М. Васина, К. К. Федяевского, В. М. Лаврентьева, Г. А. Фирсова, И. Т. Хановича, Р. Я. Першица, В. Г. Соболева, А. В. Васильева и др., а также зарубежных ученых И. Ф. Кемпфа, Д. Дэвидсона, К. Гупшиса, Л. Мотора, И. Окада, Н. Дьедонне, X. Тимме, К. Номото и др.

Современное состояние теории управляемости позволяет с необходимой для практики судовождения точностью определить характеристики управляемости судов с использованием расчетов и данных эксперимента.

Для обеспечения безопасности мореплавания важное значение, особенно при управлении Крупнотоннажное судно как объект управлениякрупнотоннажными судами, приобретают умение судоводителей правильно оценивать характеристики управляемости судна и на их основе прогнозировать траекторию движения с переложенным рулем. Выполнение безопасных и эффективных маневров в сложных условиях плавания невозможно без знаний закономерностей движения судна при перекладке руля, а именно таких характеристик, как характеристика кривой линии, описывающей движение центра тяжести судна, называемой циркуляцией, изменения угловой скорости движения и величины угла дрейфа судна на циркуляции. Именно поэтому большое значение придается повышению специальной подготовки судоводителей, направленной на изучение управляемости и маневренных качеств особенно крупнотоннажных судов.

Предлагается к прочтению: Оптимальные способы торможения судов

В связи с этим в ряде стран созданы специальные центры подготовки судоводителей на тренажерах различного типа по управлению судами. Признано необходимым иметь на каждом судне «Информацию капитану о маневренных элементах судна», которая должна учитывать специфику конкретного типа судна и динамику влияния различных факторов на управляемость в разнообразных условиях плавания.

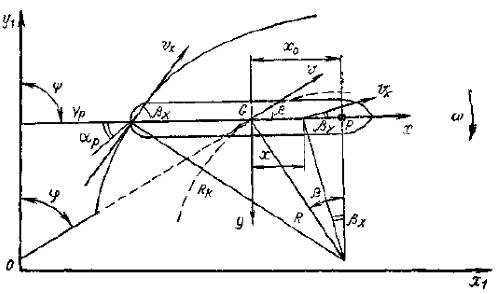
При перекладке руля на угол α_p движущееся прямолинейно со скоростью v₀ судно будет осуществлять криволинейное движение, при этом кинематика движения судна в горизонтальной плоскости характеризуется следующими величинами (рис. 1):

поступательной скоростью центра тяжести судна v;
угловой скоростью вращения co,
углом скорости φ;
углом дрейфа β₀ при центре тяжести G;
углом курса ψ;
координатами центра тяжести х, у;
радиусом кривизны траектории R из центра тяжести (ц. т.) судна.

Будем считать, что ц. т. судна находится в плоскости миделя. Перечисленные характеристики в неустановившийся (эволюционный) период циркуляции являются функциями времени t.

Вычисление угла дрейфа — Рис. 1 Изменение угла дрейфа по длине судна

В соответствии с этим угловая скорость судна определяется как производная от угла курса по времени:

ω = d φ / d t . Ф о р м . 1

Как видно из рис. 1, существует соотношение

ψ = φ + β . Ф о р м . 2

Поэтому можно записать

ω = d φ / d t + d β / d t . Ф о р м . 3

Обозначим через dl дифференциал дуги траектории ц. т. судна. Тогда получим dl = rdφ:

r = d l / d φ = d l d t / d t d φ = v d φ / d t

Таким образом, имеем dφ/dt = v/r и соответственно находим

φ = v r + d β / d t . Ф о р м . 4

При установившейся циркуляции dβ/dt = 0. В этом случае

ω_{ц} = - v_{ц} r_{ц} . Ф о р м . 5

Точки судна, расположенные на ДП судна в направлении носа и кормы от ц. т., движутся по траектории различной кривизны. Поэтому углы дрейфа β (х) в различных по длине судна точках х будут различными.

Точка P с абсциссой х₀ называется полюсом поворота. В соответствии с обозначениями на рис. 1 имеем

t g β (x) = (x_{0} - x) / r \cdot \cos β_{0} . Ф о р м . 6

Если углы дрейфа не выходят за пределы 15-20° (что имеет место при выполнении большинства маневров крупнотоннажными судами), то можно принять tgβ(x) ≈ sin(β_x) ≈ β(x); cosβ (x) ≈ 1. Тогда β(х₀ – х)/r.

Поскольку в рассматриваемый момент времени β₀ = x₀/r = v/ω, то соответственно получим β(x) = β₀ – ωx/v. Введем безразмерные обозначения:

x = x/L,

где:

L – расчетная длина судна на конструктивной ватерлинии;
ω = L/R – безразмерная угловая скорость поворота судна на циркуляции.

Тогда получим

β (x) = β_{0} - x (ω) . Ф о р м . 7

Угол дрейфа после перекладки руля достигает наибольшего значения в кормовой оконечности судна.

На рис. 2 показана кривая изменения угла дрейфа β₀ в зависимости от угловой скорости поворота ω°/с, полученная Тадзима для танкера водоизмещением 360 тыс. т. Максимальное значение β составляет 25°.

График изменение угла дрейфа — Рис. 2 Изменение угла дрейфа танкера

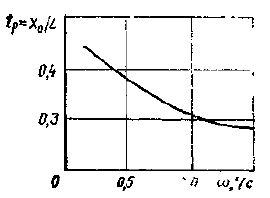
На рис. 3 для того же судна приведена кривая изменения положения полюса поворота, характеризуемая величиной его удаления от миделя судна, выраженной в относительной безразмерной величине (длинах судна). При угловых скоростях до 0,5 °/с полюс поворота смещен от миделя к носу судна на расстоянии около 0,4L; при больших угловых скоростях около 0,3L.

График положения полюса поворота судна — Рис. 3 Изменение положения полюса поворота у танкера

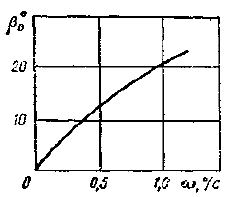
Из соотношения sinβ₀ = x₀/r ≈ β₀ можем записать приближенное выражение

β_{0} \approx (0, 3 \div 0, 4) L r . Ф о р м . 8

Изменение угла дрейфа β с течением времени можно определить по формуле:

β = β_{0} (1 - е^{t / T}), Ф о р м . 9

где:

T – постоянная времени для данного судна, определяемая по результатам натурных испытаний.

В табл. 1 приведены значения углов дрейфа для крупнотоннажных судов.

Таблица 1. Углы друйфа
Характеристики судна	Танкер	Нефтерудовоз	Рудовоз	Танкер
`L`, м	244	224,3	172,0	183,0
`B`, м	35,4	30,6	24,8	28,0
`T`, м	12,3	11,6	9,6	10,1
`W`, т	81 860	63 234	32 756	43 448
`V`, м/с	15,9	16,3	16,5	15,5
`Ap`, °	35	35	35	35
`β0`, °	18	20	20	15

Определить угловую скорость поворота судна можно на основании решения с некоторыми упрощениями третьего уравнения в системе:

J z (1 + λ_{66}) d ω / d t + m (λ_{11} - λ_{22}) v_{x} v_{y} = Σ М_{г} . Ф о р м . 10

Ввиду малого значения вторым членом уравнения в правой части можно пренебречь. Допустим, что момент руля M_P при отклонении его на угол α_p и позиционный момент на корпусе судна пропорциональны углу поворота руля и характеризуются выражением M_an = M_a + M_n = K_a α_p, где K_a – суммарный момент при повороте руля на 1°. Момент сопротивления воды вращению судна (демпфирующий момент) пропорционален угловой скорости поворота судна со, т. е. M_R = K_1ω = K₁(dφ/dt).

Принимая во внимание равенства dω/dt = d²φ/dt² и M = M_α + M_R – M_P, преобразуем уравнение (формула 10) следующим образом:

J (l + λ_{66}) d^{2} φ / d t^{2} = К_{α} α_{p} — K d φ / d t,

или

d^{2} φ / d t^{2} + N_{ω} d φ / d t = N_{α} α_{p}, Ф о р м . 11

где:

N_{ω} = K_{1} / J (1 + λ_{66}),

N_{α} = К_{α} / J (д + λ_{66}) .

Уравнение (формула 11) можно записать в виде:

T d ω / d t + ω = K α_{p}, Ф о р м . 12

где:

T = J (l + λ_{66}) N_{ω}, с

K = N_{α} / N_{ω}, 1 / с .

Если при постоянном угле перекладки руля α_p судно получает постоянную угловую скорость ω_уст, тогда ускорение поворота судна dω/dt = 0. Это означает, что момент руля и позиционный момент на корпусе N_a α_p будут равны демпфирующему моменту или моменту сопротивления воды вращению N_ω · ω, или ω_уст = N_a α_р/N_ω = Kα_p. Из этого выражения следует, что конечная угловая скорость поворота будет того же порядка, что и угол перекладки руля α_p. Судно с большим значением коэффициента K будет иметь сравнительно небольшой диаметр циркуляции.

В результате проведенных нами натурных испытаний получены следующие значения постоянных K₁ и T для крупнотоннажных танкеров (табл. 2).

Таблица 2. Значение постоянных `K₁` и `T`
Тип судна	Водоизмещение, тыс. т	`ω_уст` °	`K₁`, с	`T`, с
Танкер “Крым”	182,0	0,75	0,02	50
ОБО “Маршал Жуков”	127,0	0,52	0,015	95
Нефтерудовоз “Борис Бутома”	133	0,82	0,023	80
Танкер “София”	50	0,87	0,022	55
Танкер “Бухарест”	25,5	0,76	0,02	27

Проинтегрируем неоднородное дифференциальное уравнение первого порядка (формула 12), приведя к виду:

\frac{d ω}{d t} + \frac{l}{T} ω = \frac{K}{T} α_{p} Ф о р м . 13

с помощью подстановки ω = U · V. Получаем

dω = udv + vdu;

где:

u и v – неизвестные функции t.

Перепишем уравнение 13 в виде:

\frac{d ω}{d t} + T^{- 1} ω = \frac{K^{α} p}{T},

или

d ω + T^{- 1} ω d t = d t \frac{K^{α} p}{T} .

Применяя подстановку ω = U · V, получим

u d v + v d u + T^{- 1} v u d t = d t \frac{K^{α} p}{T},

или

u d v + v (d υ + T^{- 1} u d t) = d t \frac{K^{α} p}{T} d t . Ф о р м . 14

Поставим условие, чтобы выражение в скобках равнялось нулю:

du + T^-1udt = 0,

или

du/u = – Т^-1dt.

Интегрируя, имеем lnu = – ƒ T^-1d t = – t/T. Потенцируя, получим u = e^-t/T. Постоянную интегрирования здесь не пишем, так как достаточно будет какого-нибудь отличного от нуля решения этого уравнения. Подставим найденную функцию и в уравнение 14, учтя, что выражение в скобках равно нулю:

u d v = d t \frac{K^{α} p}{T};

e^{t / T} d u = d t \frac{K^{α} p}{T};

d v = \frac{K^{α} p}{T} e^{t / T} d t .

Интегрируя, получим

u = \frac{K^{α} p}{T} \int e^{t / T} d t = K^{α} p e^{t / T} + C,

где:

С — постоянная интегрирования.

Подставляя найденные функции u и v в исходную подстановку, получим

ω = e^{t / T} (K^{α} p e^{t / T} + C)

ω = K^{α} p + C e^{t / T} .

При t = 0 ω = 0, тогда С = -Ka_p, или

ω = Κ^{α} p (1 - е^{t / T}) . Ф о р м . 15

Формулу 14 можно записать в виде:

ω = ω_{у с т} (1 - е^{- t / T}) . Ф о р м . 16

Проинтегрируем уравнение 13, преобразовав его следующим образом:

\frac{d^{2} φ}{d t^{2}} + \frac{1}{T} \frac{d φ}{d t} = \frac{K^{α} p}{T}

Так как dφ/dt = ω с учетом выражения (формула 16) можно записать:

\frac{d^{2} φ}{d t^{2}} + \frac{ω_{у с т}}{T} - \frac{ω_{у с т}}{T} e^{- t / T} = \frac{ω_{у с т}}{T},

или

\frac{d^{2}}{d t} (\frac{d φ}{d t}) - \frac{ω_{у с т}}{T} e^{- t / T} .

Интегрируя, получим:

\frac{d φ}{d t} = \frac{ω_{у с т}}{T} \int e^{- t / T} d t = - ω_{у с т} e^{t / T} + C_{1},

где:

С₁ – постоянная интегрирования.

При t = 0 dφ/dt = 0, тогда с₁ = ω_уст. Подставив значение C₁ получим:

\frac{d φ}{d t} = - ω_{у с т} C^{- t / T} + ω_{у с т} .

Разделив переменные и интегрируя, получим:

ω = - ω_{у с т} \int e^{- t / T} d t - \int ω_{у с т} d t + c_{2},

где:

c₂ – постоянная интегрирования;

φ = ω_{у с т} T e^{- t / T} + ω_{у с т} t + c_{2} .

При t = 0 φ = 0, тогда с₂ = – ω_устT или

φ = ω_{у с т} (t - T + T e^{- t / T}) . Ф о р м . 17

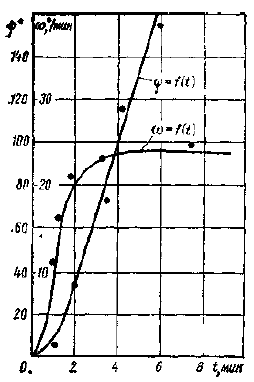
На рис. 4 показаны рассчитанные по формулам 15 и 16 закономерности изменения угла поворота φ и угловой скорости поворота ω груженого танкера «Маршал Жуков», двигавшегося с начальной скоростью 8,25 уз после перекладки руля на правый борт. Расчетные данные сопоставлены с результатами натурных испытаний, проведенных нами в 1979 г. на Черном море в районе Новороссийска. Расчетные данные удовлетворительно совпадают с натурными величинами, что позволяет сделать заключение о практической приемлемости формул 15 и 16 для решения поставленной задачи.

График угловой скорости судна — Рис. 4 Изменение угловой скорости `ω` и угла поворота `φ` теплохода «Маршал Жуков» (кружками на рисунке обозначены опытные значения, полученные по натурным испытаниям)

Важное значение для решения многих задач судовождения имеет знание судоводителями закономерностей изменения скорости судна, движущегося по криволинейной траектории с переложенным рулем. Натурные изменения показывают, что при перекладке руля на борт у крупнотоннажных судов скорость поступательного движения v уменьшается в течение 4-6 мин. При этом величина уменьшения скорости v пропорциональна величине угловой скорости поворота судна ω.

Аналитическое определение падения скорости при движении с переложенным рулем представляет большие сложности. По рекомендации И. Г. Хановича и Г. В. Соболева, падение скорости при повороте судна можно определить по формуле:

\frac{v}{v_{0}} = \frac{1}{\sqrt[3]{1 + C 1 {ω^{2}}_{у с т}}}, Ф о р м . 18

где:

С₁ – опытный коэффициент.

По результатам проведенных натурных испытаний крупнотоннажных судов С₁ = 40. На рис. 5 показана кривая снижения скорости при установившейся циркуляции, рассчитанная по формуле 18. На кривой нанесены опытные точки для трех крупнотоннажных судов.

График снижения скорости судна — Рис. 5 Снижение скорости теплохода «Борис Бутома» при перекладке руля на левый борт (кружками обозначены опытные значения, полученные по натурным испытаниям)

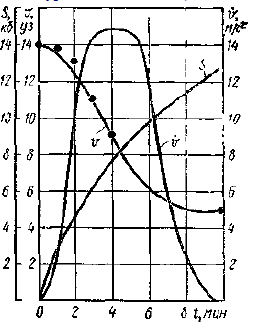
На рис. 6 показано изменение установившейся угловой скорости и безразмерной линейной скорости v = v/v₀ при различных перекладках руля нефтерудовоза «Борис Бутома» при полной загрузке судна.

График скорости теплохода — Рис. 6 Снижение скорости на установившейся циркуляции.
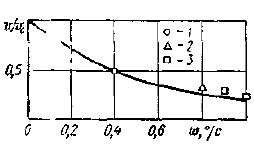
1 – теплоход «Маршал Жуков»; 2 – теплоход «Борис Бутома»; 3 – судно водоизмещением 250 тыс. т

Падение скорости хода при перекладке руля на 35° достигает 60 % и 25 % при перекладке руля на 10°; при этом величина угловой скорости поворота составляет 0,8 и 0,4°/с соответственно. Аналогичные закономерности наблюдаются и у танкеров типа «Крым» и «Маршал Жуков».

Как показали натурные испытания, текущее значение скорости хода судна v, движущегося с переложенным рулем, можно определить по формуле:

v_{t} = 0, 5 v_{0} + 0, 5 v_{0} e^{- 6 t / R_{ц}}, Ф о р м . 19

где:

v₀ – скорость в начале маневра, м/с;
t – время, с;
R_ц – радиус установившейся циркуляции, м.

На рис. 6 приведены опытные точки и рассчитанные по формуле 19 кривые изменения скорости на груженном теплоходе «Борис Бутома» при перекладке руля на левый борт. Экспериментальные данные хорошо согласуются с теоретической кривой. На рис. 5 также показана кривая изменения ускорения (замедления) поступательного движения v и пройденного расстояния S, кб.

Наиболее полно поворотливость судна характеризует его циркуляция. Циркуляцией называется кривая линия, которую описывает центр тяжести судна при перекладке руля. Поворотливость обычно характеризуют диаграммой управляемости судна, выражающей зависимость между углом перекладки руля (α_p) и безразмерной угловой скоростью судна

ω = L/R_ц,

здесь:

L – длина судна;
R_ц – радиус установившейся циркуляции.

На рис. 7 приведены диаграммы управляемости крупнотоннажных судов, построенные по результатам натурных испытаний. Близость ординат начала диаграмм к нулю указывает на то, что крупнотоннажные суда обладают высокой эксплуатационной устойчивостью на курсе.

Диаграммы управляемости судна — Рис. 7 Диаграммы управляемости крупнотоннажных судов.
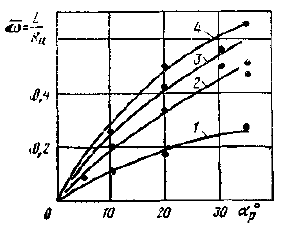
1 – «София»; 2 – плавбаза; 3 – «Крым»; 4 – «Маршал Жуков»

Аналитически циркуляцию можно рассчитать путем численного интегрирования системы дифференциальных уравнений с помощью ЭВМ, например, по методу Рунге-Кутта.

Сноски

Закономерности движения крупнотоннажных судов при перекладке руля