Эффективность любого судна, от быстроходного катера до грузового транспорта с большим водоизмещением судна, напрямую зависит от гребного винта. Поэтому точный расчет гребных винтов судов является ключевым этапом проектирования, определяющим ходовые качества и экономичность эксплуатации.
Процесс подбора винта – это не просто выбор стандартных размеров. Инженеру необходимо выполнить сложный расчет пропеллера, учитывая уникальное взаимодействие винта и корпуса, а также жесткие характеристики двигателей внутреннего сгорания.
Главная цель – максимизировать скорость и минимизировать потери. Это требует детального анализа факторов, влияющих на коэффициент полезного действия (КПД), включая геометрические параметры, режим движения (относительная поступь) и гидродинамические явления, такие как сильно развитая кавитация.
- Основные понятия и определения
- Геометрические характеристики гребных винтов
- Гидродинамические характеристики гребных винтов
- Диаграммы для расчета гребных винтов
- Коэффициенты взаимодействия винта и корпуса
- Кавитация гребного винта
- Проектирование гребных винтов
- Выбор исходных данных
- Выбор числа лопастей, дискового отношения и элементов эквивалентного профиля
- Определение наибольшей скорости судна и элементов некавитирующих гребных винтов
- Проверка отсутствия кавитации гребных винтов и уточнение оптимальной величины дискового отношения
- Определение наибольшей скорости катера и элементов кавитирующих гребных винтов
- Особенности определения наибольшей скорости и элементов гребных винтов катеров на подводных крыльях
Ошибки в расчете приводят к недокруту двигателя и перерасходу топлива. Современный подход опирается на детальный гидродинамический анализ и использование специальных диаграмм, что позволяет определить оптимальный винт и обеспечить заданные режимы работы. Таким образом, точный расчет становится основой для успешных ходовых испытаний и долгосрочной эксплуатации судна.
Основные понятия и определения
В зависимости от назначения катеров и моторных лодок, формы их обводов, мощности двигателей и развиваемых скоростей условия работы ГВ могут сильно изменяться, что существенно отражается на конструктивных особенностях винтов и методах их проектирования.
При этом наибольшее влияние на выбор основных элементов проектируемых ГВ оказывают следующие обстоятельства:
- недостаточная точность расчетных методов определения сопротивления катеров и моторных лодок и отсутствие данных по буксировочным испытаниям моделей для большинства малотоннажных судов;
- сложное взаимодействие между винтом и корпусом у многих типов быстроходных катеров, обусловленное наличием косого обтекания и развитой кавитацией;
- сильно развитая кавитация ГВ, возникающая при достаточно высоких скоростях и приводящая к уменьшению упора и КПД винтов;
- относительно жесткие характеристики двигателей внутреннего сгорания, не допускающие практически никакой перегрузки ни по мощности, ни по частоте вращения;
- наличие горба сопротивления у глиссирующих и крылатых судов, требующее повышенных запасов мощности двигателей на промежуточных режимах движения.
Указанные особенности проектирования и эксплуатации катеров и моторных лодок во многих случаях не позволяют расчетным путем установить окончательные элементы оптимального ГВ. С целью обеспечения заданных режимов работы двигателей и получения наибольших скоростей на ходовых испытаниях обычно производится доводка ГВ, в результате которой уточняются его основные элементы – диаметр, шаг и дисковое отношение. Для облегчения и ускорения процесса доводки ГВ иногда принимают решение об изготовлении и испытании двух или даже трех вариантов винтов с различными элементами, изменяющимися по определенному закону.
Геометрические характеристики гребных винтов
Действие гребного винта определяют следующие основные геометрические элементы и характеристики.
Диаметр винта D = 2R, представляющий собой диаметр окружности, описываемой самой удаленной от оси винта точкой лопасти.
Радиус винта R = 0,5 D – расстояние от оси винта до наиболее удаленной точки, называемой краем лопасти.
Геометрический, или конструктивный, шаг Н, характеризующий возможное перемещение винта за один оборот при движении без скольжения. Конструктивный шаг сечения лопасти, расположенного на радиусе r, находится по формуле:
где:
- tg ν тангенс шагового угла на радиусе r.
Отношение шага винта к его диаметру называют шаговым отношением. Различают винты постоянного шага Н = const и переменного, у которых шаг вдоль радиуса изменяется по какому-либо закону Н = f(r).
Дисковое отношение Θ, представляющее отношение суммарной площади A всех z лопастей к площади диска, ометаемого винтом, Ad = 0,25 π D2:
Поскольку винтовая поверхность не совмещается с плоскостью без искажения, то под площадью лопасти A/z понимается величина поверхности, ограниченная спрямленным контуром лопасти, который соединяет кромки развернутых на плоскость и затем спрямленных сечений лопасти, расположенных на различных радиусах.
Средняя ширина лопасти, равная отношению площади лопасти к ее длине:
где:
- dс = 2rс – диаметр ступицы ГВ.
Приведенный, или относительный, радиус лопасти, представляющий собой отношение радиуса центра давления (ЦД) лопасти R0 к наибольшему радиусу гребного винта R. Обычно принимается, что ЦД, характеризующий точку приложения к лопасти равнодействующей всех гидродинамических сил, совпадает с центром тяжести спрямленной площади лопасти. При нормальных образованиях лопасти приведенный радиус находится в пределах:
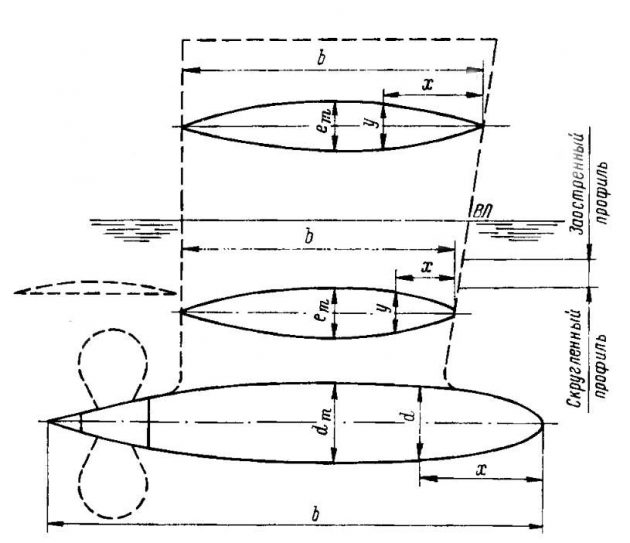
Профиль сечения лопасти, под которым понимается спрямленный на плоскость след сечения лопасти винта соосным с ним круговым цилиндром на заданном радиусе. Правильный выбор формы лопастных сечений имеет большое значение для повышения эффективности катерных гребных винтов. На практике чаще всего применяют профили авиационного и сегментного типа (рис. 1). У профилей авиационного типа максимальная толщина находится на расстоянии ~ 1/3 хорды от входящей кромки, которая обычно имеет скругленную форму. У сегментных профилей наибольшая толщина расположена преимущественно посредине хорды и кромки заострены. Прямая линия, проходящая через входящую кромку профиля (носик) и выходящую (хвостик), называется кромочной линией.
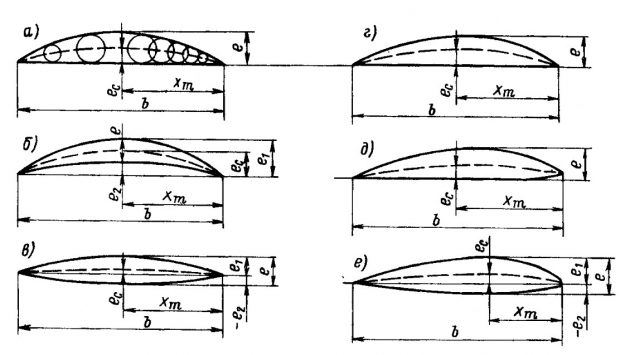
а – плоско-выпуклый сегментный профиль; б – вогнуто-выпуклый профиль; в – двояковыпуклый профиль; г – плоско-выпуклый острокромочный профиль с приполненной входящей кромкой; д – профиль Вальхнера (со скругленной приполненной и приподнятой входящей кромкой); е – авиационный профиль
Длина профиля b, измеренная вдоль кромочной линии и характеризующая ширину лопасти на радиусе r, представляет собой хорду профиля. Наибольшая толщина профиля e определяется как алгебраическая сумма отложенных от кромочной линии максимальных ординат e1 и e2 верхнего и нижнего контуров профиля. Ордината e2 принимается положительной при вогнутом нижнем контуре и отрицательной – при выпуклом. Отношение наибольшей толщины профиля к его хорде называют относительной толщиной:
где:
- δ1 = e1/b – относительная кривизна засасывающей стороны профиля;
- δ2 = e2/b относительная кривизна нагнетающей стороны.
Гидродинамические характеристики гребных винтов
Упор и момент, развиваемые вращающимся гребным винтом, обычно представляют в следующем виде:
- K1 – коэффициент упора ГВ;
- K2 – коэффициент момента;
- n – частота вращения винта, с-1;
- ρ – плотность воды (плотность пресной воды ρ = 1 000 кг/м3, морской ρ = 1 015-1 025 кг/м3).
Упор и момент не являются постоянными величинами, а зависят от режима работы винта т. е. от частоты его вращения n и осевой скорости перемещения νp, определяющих углы атаки элементов лопастей винта на различных радиусах.
Если бы винт двигался не в жидкости, а в твердой среде, то за один оборот он перемещался бы вдоль собственной оси на расстояние, равное его шагу H. При частоте вращения винта n окружная скорость его любого соосного сечения была бы и = 2πrn, а скорость осевого перемещения Hn. Однако при движении в воде реальная скорость перемещения винта νp меньше скорости Hn.
Отношение:
представляет собой скольжение относительно геометрического шага.
В качестве безразмерной кинематической характеристики гребного винта принимают относительную поступь:
Относительная поступь определяет режим работы гребного винта и оказывает решающее влияние на углы атаки различных сечений лопастей. Изображенная на рис. 2 диаграмма скоростей элемента лопасти винта, расположенного на радиусе r, характеризует соотношение между осевой и окружной составляющими скорости w на различных режимах движения без учета вызванных скоростей. Диаграмма показывает, что с уменьшением расчетной скорости натекания воды на винт νp, т. е. с уменьшением поступи винта углы атаки элемента лопасти будут возрастать.
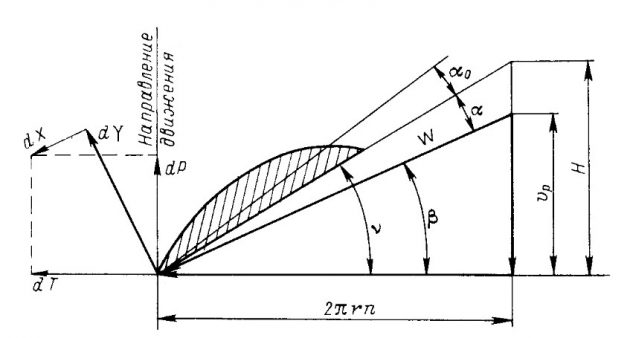
Это, в свою очередь, будет приводить к увеличению подъемной силы каждого элемента лопасти d Y и, следовательно, к увеличению упора винта P и его момента M. Наибольших значений углы атаки, а также упор и момент винта достигнут при поступи, равной нулю, т. е. при работе винта на швартовах:
С другой стороны, при увеличении скорости νp и поступи винта λp будут уменьшаться углы атаки элементов сечений при одновременном уменьшении упора и момента винта в целом. Такое уменьшение будет происходить до тех пор, пока при некотором значении линейной поступи H1 = νp1/n, называемом поступью или шагом нулевого упора, упор винта не обратится в нуль и гребной винт перестанет быть движителем.
Вращающий момент становится равным нулю при еще большем значении поступи H2 = νp2/n называемом шагом нулевого момента (рис. 3). При поступи, превышающей H2, винт начнет сам создавать вращающий момент, т. е. будет работать как турбина. В диапазоне между поступями нулевого упора H1 и нулевого момента H2 винт не может быть использован ни как движитель, ни как турбина.
Отношение:
определяет область бездействия (или парализации) ГВ и называется паралью. Величина парали характеризует профильные потери лопастей ГВ.
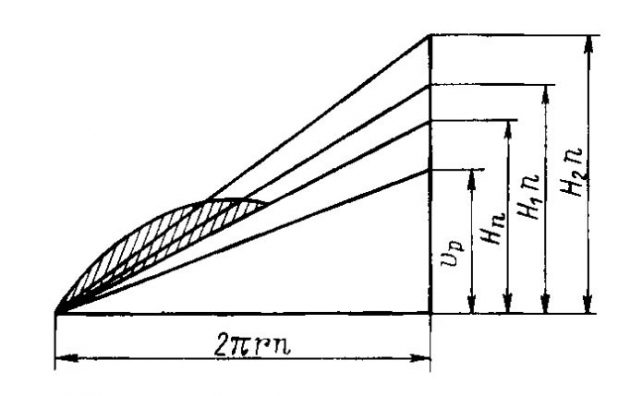
Отношение шага нулевого упора Н1 к диаметру винта D называется шаговым отношением нулевого упора:
При этом скольжение винта относительно шага нулевого упора, обозначаемое s1, будет равно нулю. Относительная поступь и скольжение винта связаны между собой следующими зависимостями:
При изучении действия ГВ и их проектировании принято рассматривать главным образом коэффициенты упора и момента, являющиеся важнейшими безразмерными динамическими характеристиками:
Переход к безразмерным характеристикам позволяет использовать имеющиеся зависимости и закономерности независимо от абсолютных размеров ГВ. Обычно величины коэффициентов упора и момента винта изображают в виде функций относительной поступи K1 = f1(λp) и K2 = f2(λp).
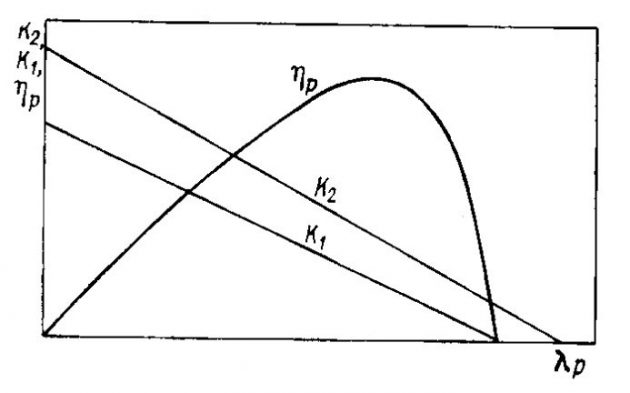
Совместно с кривыми K1 и K2 строят также кривую изменения коэффициента полезного действия (КПД) винта, представляющего собой отношение полезной мощности ГВ Pνρ к мощности затраченной Nв. Необходимая для вращения винта с заданной частотой мощность определяется по формуле:
КПД винта при различных значениях поступи:
Типичный характер изменения зависимостей K1 = f1(λp), K2 = f2(λp) и ηp = f3(λp), называемых иначе кривыми действия ГВ в свободной воде, представлен на рис. 4.
Важной характеристикой режима работы ГВ является коэффициент нагрузки по упору:
Действие ГВ полностью характеризуется тремя независимыми параметрами: коэффициентом упора K1, коэффициентом момента K2 и относительной поступью λp. С их помощью однозначно определяются КПД винта ηp (Формула 16) коэффициент нагрузки σp (Формула 17) и другие необходимые параметры. Это обстоятельство также используется при построении расчетных диаграмм для проектирования ГВ.
Диаграммы для расчета гребных винтов
Наибольшее распространение для определения элементов ГВ в отечественной практике получили диаграммы, на которых в совмещенном виде представлены кривые действия целой серии ГВ в свободной воде, т. е. при отсутствии корпуса судна.
Все элементы и характеристики ГВ, входящих в серию (дисковое отношение, число лопастей, профилировка сечений и т. д.), полностью одинаковы, за исключением шагового отношения, которое изменяется с определенным интервалом. Диаграммы, построенные в координатных осях K1 – λp, состоят из двух основных семейств кривых. Первое семейство составляют кривые коэффициентов упора ГВ K1 = f(λp), которые для винтов, отличающихся только шаговым отношением, располагаются эквидистантно.
Второе семейство образуют кривые ηp = f(λp, H/D), отвечающие одинаковым значениям КПД этой же серии винтов. Такие диаграммы позволяют относительно просто находить значения шагового отношения H/D и КПД ηp любого винта серии, а также определять необходимую мощность двигателя по заданному упору ГВ P, скорости его поступательного движения νp, частоте вращения n или диаметру D.
Аналогичным образом при совмещении семейств кривых коэффициентов момента K2 = f(λp) и КПД ηp = f(λp, H/D) строятся диаграммы в осях K2 – λp. Эти диаграммы удобны при определении элементов ГВ по заданной мощности двигателей, в силу чего их иногда называют “машинными“. Для сокращения размеров „машинную” диаграмму часто строят в виде зависимостей
или
.
В конечном итоге оба типа диаграмм приводят к одним и тем же результатам как по элементам проектируемых ГВ, так и по величине наибольшей достижимой скорости судна. Однако следует отметить, что в зависимости от величин диаметра и частоты вращения по каждой диаграмме может быть подобрано бесконечное количество ГВ, нормально загружающих двигатель, но имеющих различные значения КПД и обеспечивающих различную скорость.
С целью достижения наибольшей скорости необходимо стремиться выбирать оптимальный ГВ, т. е. винт, обладающий наивысшим для заданных условий КПД. Для ускорения определения элементов оптимальных винтов на диаграммах построены линии оптимальных частот вращения nopt и оптимальных диаметров Dopt, образующих на каждой диаграмме область оптимальных ГВ.
Аналогичные коэффициенты для диаграмм K2 – λp имеют вид:
В этих формулах Nв – мощность на гребном валу, кВт.
Имеется много таких диаграмм для широкого диапазона дисковых отношений, числа лопастей и профилировки их сечений. Часть из них получена Э. Э. Папмелем расчетным путем. Другие построены на основании экспериментальных материалов. Принципиальной особенностью диаграмм Папмеля, отличающей их от всех других диаграмм такого типа, является то, что в них в качестве одной из независимых переменных выбрано не геометрическое шаговое отношение H/D, а шаговое отношение нулевого упора H1/D, являющееся важнейшей гидродинамической характеристикой.
Связь шагового отношения нулевого упора с геометрическим шаговым отношением достаточно хорошо выражается формулой:
где:
- δ0 – относительная кривизна средней линии профиля сечения, расположенного на приведенном радиусе лопасти R0.
Для возможности практического проектирования ГВ и выполнения расчетов ходкости на рис. 5-11 приведены наиболее употребительные расчетные диаграммы двух и трехлопастных винтов с различными дисковыми отношениями.
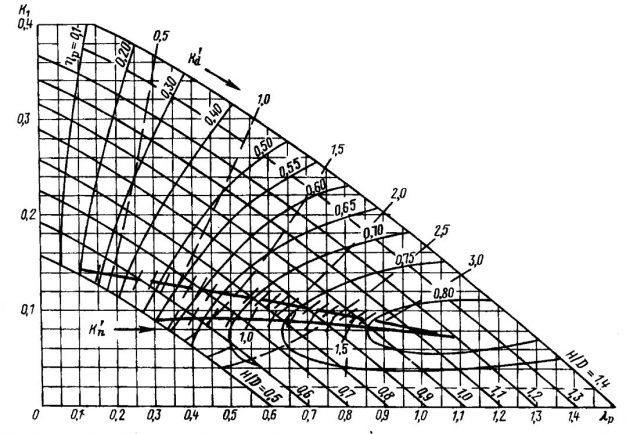
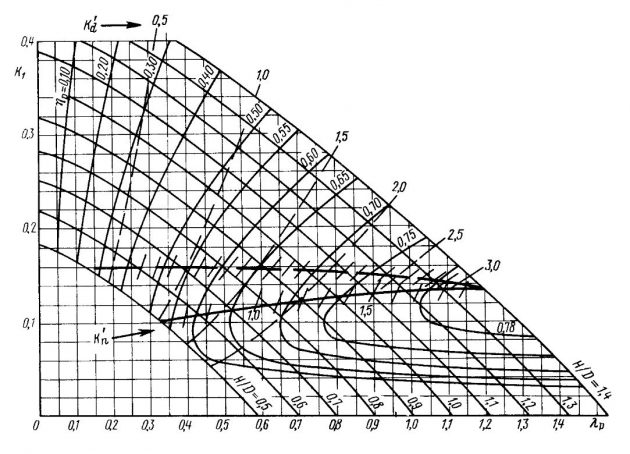
Каждая диаграмма соответствует указанным на ней основным характеристикам ГВ. Винты с дисковыми отношениями 0,3-0,5 предназначены для катеров и моторных лодок с умеренными скоростями, т. е. до 50 км/ч. Эти винты являются некавитирующими. До радиуса r = 0,6R они имеют авиационный профиль сечений лопастей, который далее переходит в сегментный.
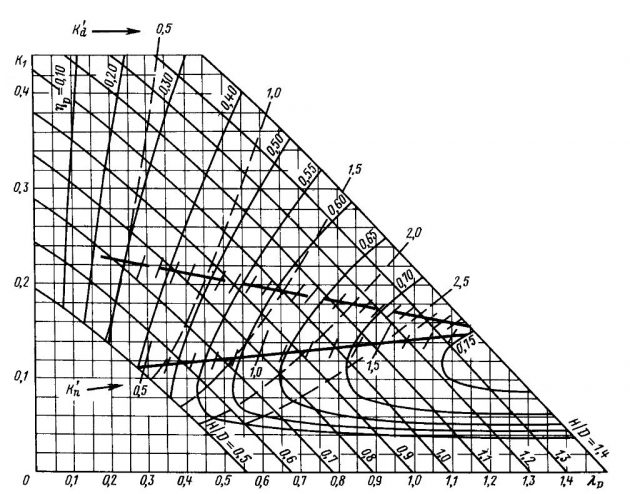
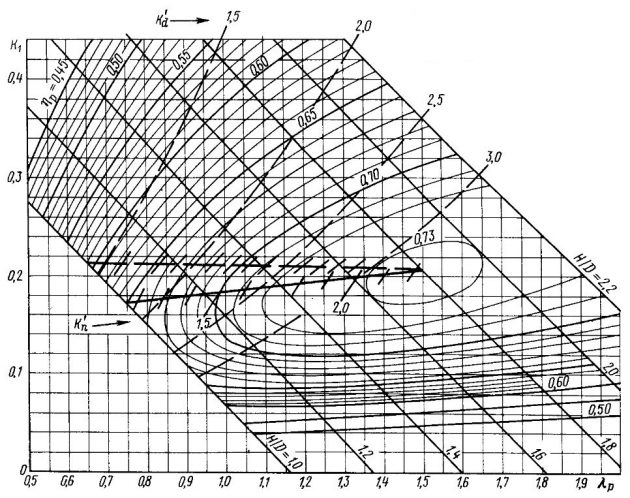
ГВ с дисковыми отношениями Θ = 0,8-1,0 применяются на быстроходных судах и имеют сегментную вогнуто-выпуклую профилировку сечений лопастей, которая позволяет отдалить наступление кавитации винтов или ослабить ее влияние.
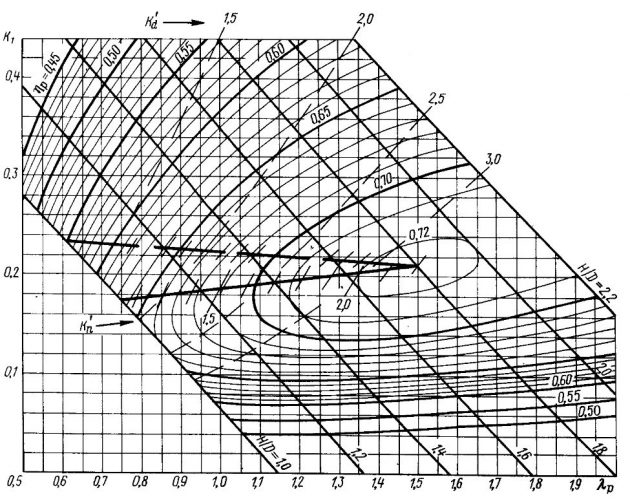
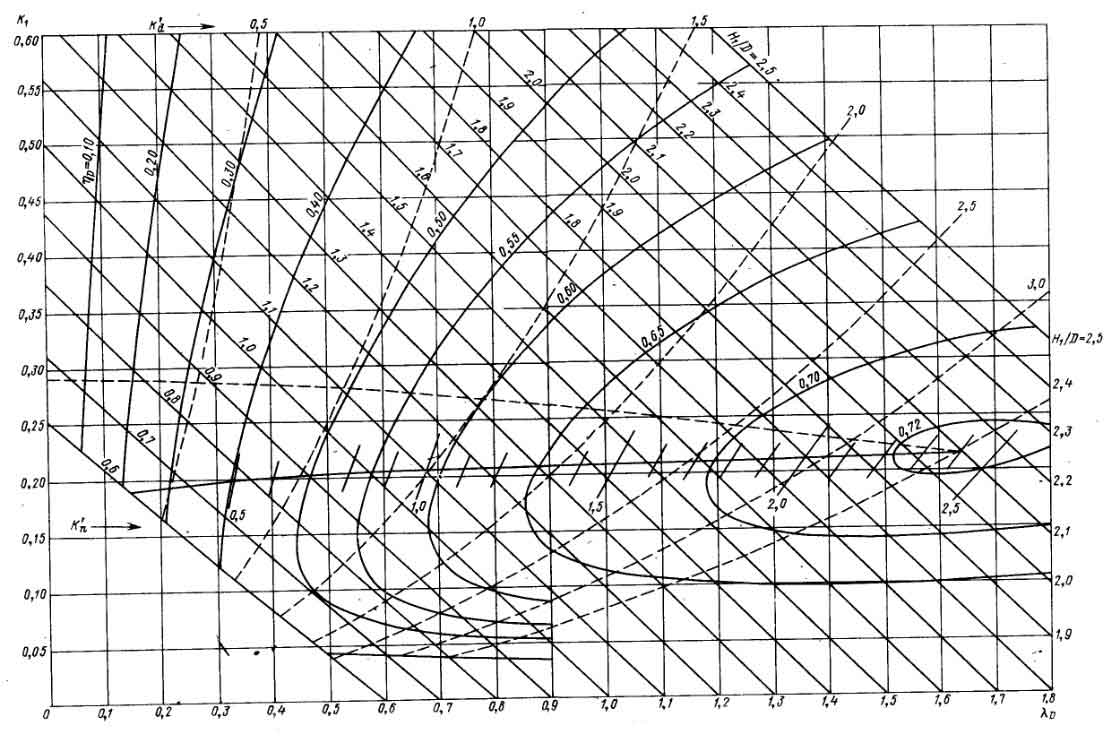
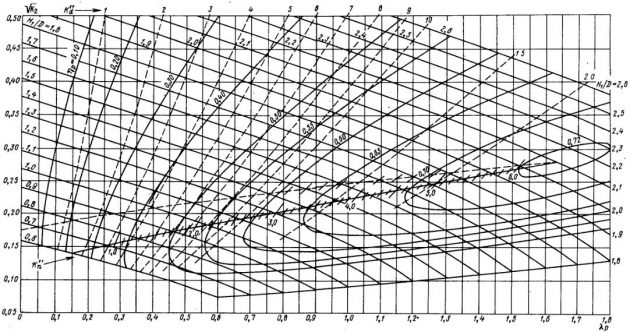
Диаграммы для винтов с Θ = 1 построены по шаговому отношению нулевого упора H1/D. Все остальные диаграммы – по геометрическому шаговому отношению. Это обязательно следует учитывать при проектировании ГВ.
Коэффициенты взаимодействия винта и корпуса
Между корпусом катера и работающим ГВ возникает сложное гидромеханическое взаимодействие. По мере движения катера, в пространство, освобождаемое его кормой, устремляется вода, которая вместе с прилегающей к корпусу массой жидкости увлекается катером в сторону своего движения и создает так называемый попутный поток. Попутный поток, набегая на ГВ, изменяет условия его работы. Наличие попутного потока, направленного в основном в сторону движения катера, уменьшает скорость натекания воды на винт:
где:
- w – коэффициент попутного потока.
В свою очередь, ГВ, воздействуя на поток впереди себя, изменяет характер обтекания судна. В результате такого взаимодействия основные характеристики ГВ – упор, момент и КПД – при работе за корпусом катера, как правило, отличаются от соответствующих характеристик этого же винта в свободной воде. Работающий за корпусом катера ГВ понижает давление впереди себя и вызывает увеличение скорости обтекания кормовой оконечности. Возникающая при этом дополнительная сила, называемая силой засасывания, повышает сопротивление катера и должна быть уравновешена дополнительным упором ГВ. Влияние силы засасывания учитывается безразмерным коэффициентом засасывания:
где:
- P – полный упор винта, передаваемый на упорный подшипник;
- Pe = P (1 – t) – полезная тяга одного винта, равная доле приходящегося на него сопротивления;
- Ke = K1(1 – t) – коэффициент тяги винта.
Значения коэффициентов попутного потока и засасывания, называемых иначе коэффициентами взаимодействия винта и корпуса, определяют по результатам анализа испытаний самоходных моделей или близких катеров-прототипов. При отсутствии таких материалов можно пользоваться приближенными формулами. Для неглиссирующих одновинтовых катеров со стационарными двигателями коэффициент попутного потока:
где:
- δ – коэффициент общей полноты.
Для двухвинтовых катеров коэффициент попутного потока несколько уменьшается:
Коэффициент засасывания на рабочем режиме зависит от коэффициента попутного потока:
Можно также, по предложению Э. Э. Папмеля, определять вначале коэффициент засасывания на швартовах:
а затем на любых промежуточных режимах работы винта:
В среднем для относительно тихоходных водоизмещающих катеров коэффициент попутного потока достигает значений w = 0,15-0,20. Для катеров переходного режима w = 0,06-0,10.
При использовании подвесных моторов коэффициенты взаимодействия находятся в пределах:
Угловая колонка имеет значительно большие габариты, чем нога подвесного мотора. Это приводит к увеличению коэффициентов взаимодействия. При отношении диаметра винта к диаметру гондолы D/dm = 1,5-2,5 и удлинении гондолы br/dm = 4-6 для кормового расположения винта коэффициенты взаимодействия принимают:
При носовом расположении ГВ гондола находится полностью в потоке от винта, что приводит к возрастанию ее сопротивления и увеличению коэффициента засасывания.
На быстроходных катерах с наклонными гребными валами, ГВ, находящиеся под плоским глиссирующим днищем или кормовым крылом, обтекаются почти невозмущенным потоком. При наличии достаточных зазоров пограничный слой не попадает на диск винта. Попутный же поток от кронштейнов и гребного вала настолько мал, что его можно не учитывать. Таким образом, у глиссирующих моторных лодок и катеров на подводных крыльях попутный поток и сила засасывания практически отсутствуют. Однако при проектировании ГВ в этом случае необходимо учитывать влияние косого обтекания винтов, которое является следствием наклонного расположения гребных валов и изменения дифферента на ходу. При отсутствии кавитации можно принять, что наклонное положение ГВ к потоку будет приводить к уменьшению расчетной скорости обтекания до величины ν cos υ и к снижению упора до P cos υ, что, по аналогии, принято учитывать при помощи условных коэффициентов попутного потока w и засасывания t:
Значения коэффициентов w и t находят по формуле:
где:
- v° = 57,3 v – угол скоса потока в градусах и радианах.
Обычно при определении условного коэффициента попутного потока под скосом потока v понимается угол между осью валопровода и днищем (кормовым крылом) катера, а при определении коэффициента засасывания – угол между валопроводом и направлением движения катера.
Для нахождения условных коэффициентов взаимодействия винта и корпуса при косом обтекании винтов быстроходных катеров и моторных лодок могут быть также использованы приведенные рекомендации.
Наличие коэффициентов попутного потока и засасывания приводит к изменению пропульсивного коэффициента, под которым понимается отношение буксировочной мощности катера или лодки на заданной скорости движения NR = Rν = Peν к мощности, подводимой к винту, NB = 2πnM:
Заменив в данном выражении скорость судна ν и тягу винта Pe их значениями с учетом влияния корпуса, получим:
Входящее в пропульсивный коэффициент отношение:
принято называть коэффициентом влияния корпуса.
Кавитация гребного винта
Неизбежным спутником роста скоростей судов различного назначения является кавитация ГВ, под которой понимается образование разрывов сплошности в капельной жидкости, происходящих вследствие понижения давления до некоторого критического значения. Область разрыва, называемая каверной, представляет собой полость, заполненную парогазовой смесью.
В качестве основного критерия подобия кавитации как при моделировании условной работы кавитирующих ГВ, так и при их проектировании используется безразмерная характеристика, называемая числом кавитации:
где:
- pa = 101 300 Па – атмосферное давление;
- hs – глубина погружения оси винта, м;
- pd – давление насыщенных паров воды, Па (для температуры воды 12 °C принимают pd = 1 300 Па);
- γ – объемный вес воды (для пресной воды γ = 9 810 Н/м³, для морской γ = 10 000 Н/м³);
- νp – расчетная скорость натекания воды на винт, м/с.
В практике кавитацию ГВ условно разделяют на две стадии. Первая стадия кавитации характеризуется тем, что полости, образующиеся на засасывающей поверхности лопастей, невелики и замыкаются на самих лопастях. Гидродинамические характеристики ГВ – его упор и момент – при этом практически не изменяются. Вредным последствием первой стадии кавитации часто является эрозия винта – разрушение металла лопастей в местах замыкания кавитационных каверн.
Особенно интенсивно развивается эрозия при неравномерном обтекании ГВ.
По мере увеличения скорости потока νp и уменьшения числа кавитации κ первая стадия кавитации переходит во вторую, при которой происходит изменение гидродинамических характеристик ГВ, в связи с чем его упор, момент и КПД уменьшают свои значения. Размеры кавитационных каверн при этом увеличиваются и замыкание их происходит за пределами лопастей. Сильно развитую вторую стадию кавитации, когда обтекание лопастей происходит со срывом струй и каверна уходит далеко за профиль, называют суперкавитацией.
Режим работы кавитирующего ГВ, под которым обычно понимается винт, кавитирующий во второй стадии, определяется двумя независимыми параметрами – относительной поступью λp и числом кавитации κ. Действие кавитирующего винта на различных режимах его работы характеризуется безразмерными коэффициентами упора K1φ, момента K2φ и КПД ηрφ, учитывающими влияние кавитации. Примерный вид кривых действия кавитирующего винта, иллюстрирующий эти зависимости при различных числах кавитации, показан на рис. 12. Коэффициенты упора и полезного действия кавитирующего винта на любом режиме работы могут быть представлены в виде:
где:
- φ1 и ηφ – коэффициенты, характеризующие уменьшение упора и КПД винта вследствие кавитации.
Практическое проектирование кавитирующих гребных винтов всегда вызывало большие трудности. Разработанный в 30-х годах метод Папмеля имеет недостаточную точность. Методы расчета кавитирующих винтов, основанные на вихревой теории, в силу своей сложности и громоздкости, не могут применяться для практического проектирования винтов быстроходных катеров и моторных лодок.
Предлагаемый ниже метод разработан на основании анализа и обобщения многочисленных экспериментальных материалов по испытаниям моделей ГВ в кавитационной трубе. Для облегчения влияния конкретных конструктивных особенностей ГВ на его действие при обработке и систематизации материалов испытаний было использовано известное допущение о возможности замены реальной лопасти гребного винта эквивалентным крыльевым профилем, на котором все явления развиваются точно так же, как и на всей лопасти винта в целом.
Размеры и форма этого профиля выбираются таким образом, чтобы его действие, отнесенное к суммарной площади всех лопастей винта как при отсутствии кавитации, так и при ее наличии, было эквивалентно действию самого ГВ. В качестве эквивалентного профиля в данном методе принято сечение, проходящее через ЦД лопасти винта и наилучшим образом характеризующее как основные геометрические элементы лопасти, так и ее гидродинамические особенности.
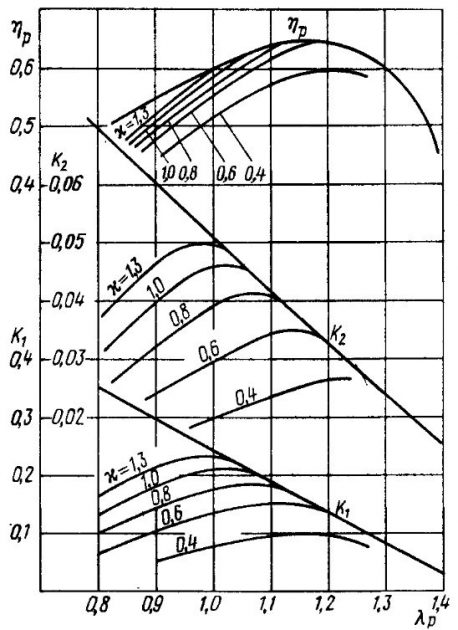
В результате исследований и анализа были установлены следующие, общие для большинства трехлопастных винтов, закономерности наступления и развития второй стадии кавитации.
1 Уменьшение упора и КПД ГВ вследствие влияния кавитации начинается всегда при вполне определенном критическом значении его относительной поступи λpk, зависящем в основном от величин шагового отношения нулевого упора H1/D, дискового отношения Θ, числа кавитации κ и относительной толщины эквивалентного профиля δ.
2 Уменьшение коэффициентов φ1 и ηφ после возникновения второй стадии кавитации у всех ГВ происходит по одним и тем же законам, которые определяются следующими основными параметрами:
- отношением действующей относительной поступи гребного винта на данном режиме работы λp к его критической поступи λpk;
- значением числа кавитации κ;
- относительной кривизной засасывающей стенки эквивалентного профиля δ1. Таким образом, в общем случае коэффициенты φ1 и ηφ могут быть выражены следующими функциональными зависимостями:
Влияние же остальных элементов ГВ (шагового отношения H/D, дискового отношения Θ, формы контура лопасти и т. д.) на характер и степень развития кавитации настолько мало, что при практическом расчете кавитационных характеристик винтов им можно пренебречь. Отсутствие влияния указанных параметров на кавитационные характеристики винтов свидетельствует о достаточной универсальности полученных зависимостей и расчетных диаграмм.
3 Уменьшение числа кавитации κ сдвигает момент наступления второй стадии кавитации в сторону увеличения критической относительной поступи при одновременном более интенсивном падении гидродинамических характеристик винта для данного отношения поступей λ
4 Увеличение относительной толщины δ = e/b при прочих равных условиях также увеличивает значение критической относительной поступи λpk, при которой начинается уменьшение упора винта.
5 Увеличение относительной кривизны засасывающей стороны эквивалентного профиля лопасти δ1 = e1/b при числах кавитации k < 1,5 и прочих равных условиях уменьшает интенсивность падения коэффициента φ1 при кавитации ГВ.
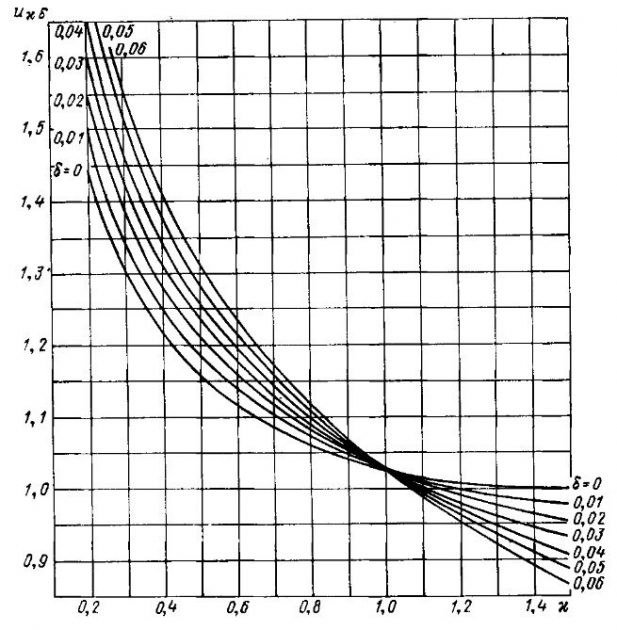
Критическая относительная поступь ГВ с достаточной для проектных расчетов точностью может быть определена по формуле:
Коэффициент p = 1,05-1,10 учитывает ускорение момента наступления второй стадии кавитации вследствие увеличения чисел Рейнольдса и усиления неравномерности обтекания натурных винтов по сравнению с модельными. Зависимость
, учитывающая влияние числа кавитации κ и относительной толщины эквивалентного профиля δ на критическую поступь ГВ λpk, приведена на рис. 13. Приближенное значение критической относительной поступи может быть также найдено по формуле:
Коэффициенты φ1 и ηφ при проектировании кавитирующих винтов находятся по специальным диаграммам кавитационных характеристик. На этих диаграммах представлены зависимости коэффициентов уменьшения упора φ1 и КПД ηφ от отношения расчетной относительной поступи ГВ, имеющего определенные параметры, к его критической поступи λp/λpk при различных числах кавитации κ = 0,2÷1,4. Такой диапазон чисел кавитации охватывает практически все наиболее интересные режимы движения быстроходных моторных лодок и катеров в пределах от 40 до 130 км/ч. При этом, однако, следует иметь в виду, что значения коэффициентов φ1 для числа кавитации κ = 0,2 получены экстраполяцией.
Определяющей характеристикой при выборе расчетной диаграммы является относительная кривизна засасывающей стороны эквивалентного профиля δ1 = e1/b, независимо от величин шагового и дискового отношений ГВ в реальных пределах их изменения. Всего построено восемь диаграмм для различных значений относительной кривизны, изменяющихся от δ1 = 0,024 до δ1 = 0,052 с интервалом △δ1 = 0,004. Диаграммы для винтов с кривизной δ1 = 0,032, 0,040 и 0,048 приведены на рис. 14-16.
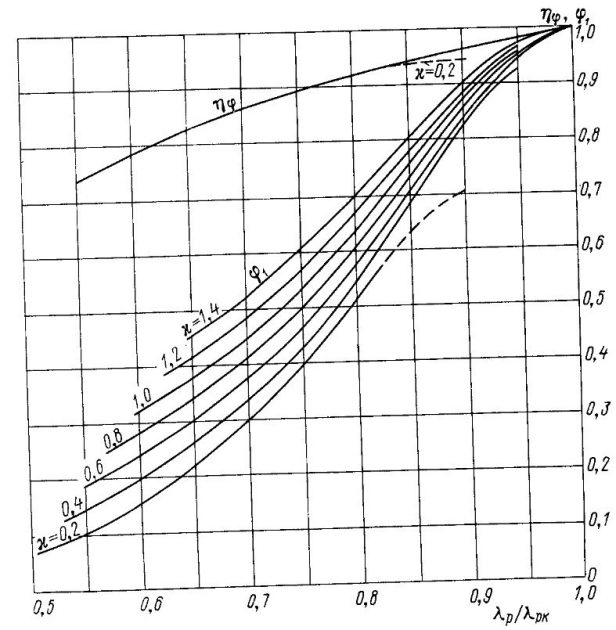
Для определения кавитационных характеристик ГВ по приведенным диаграммам необходимо для всего диапазона скоростей судна найти числа кавитации κ и отношения расчетных относительных поступей λp к критическим λpk.
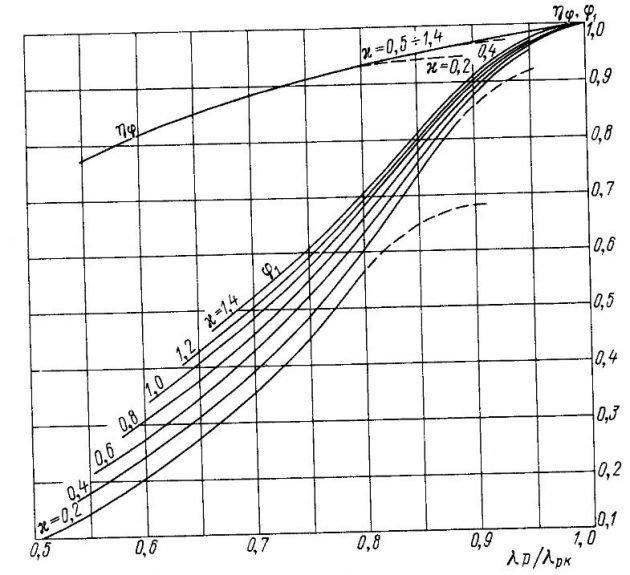
Далее по значению кривизны лопасти δ1 = e1/b на приведенном радиусе рассматриваемого винта выбирается расчетная диаграмма φ1-λp/λpk, с помощью которой находят значения коэффициента уменьшения упора φ1 = f(λp/λpk, κ) и КПД ηφ = f(λp/λpk, κ) от влияния кавитации, а также значения коэффициента упора K1φ = K1φ1 и КПД ηpφ = ηpηφ в заданных условиях кавитации.
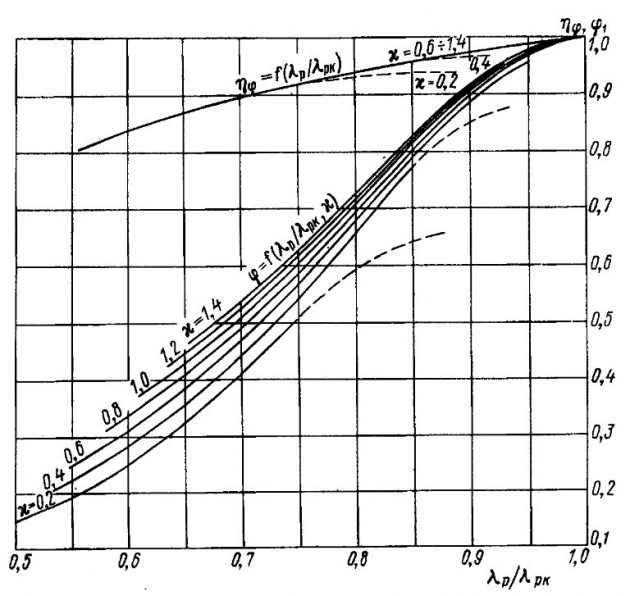
При несовпадении относительной кривизны эквивалентного профиля проектируемого винта δ1 с диаграммой, коэффициенты φ1 и ηφ находят по диаграммам, имеющим наиболее близкие значения δ1, или путем интерполяции.
Все элементы и характеристики ГВ при отсутствии кавитации, используемые для расчета по приведенным формулам и диаграммам его гидродинамических характеристик в условиях кавитации, считаются известными или определяются одним из общепринятых способов, например по расчетным диаграммам K1 – λp.
Необходимо отметить, что предлагаемые кавитационные диаграммы и методы их использования полностью применимы при проектировании и анализе действия кавитирующих ГВ, имеющих нормальные образования, наиболее распространенные в современной практике – эллиптический контур лопасти при сегментном плоско-выпуклом или вогнуто-выпуклом профиле сечений с максимальной толщиной, находящейся посередине сечения или на некотором расстоянии от нее. Пределы изменения относительной толщины эквивалентного профиля этих винтов составляют δ = 0,024 – 0,06, дискового отношения Θ = 0,6 – 1,2, шагового отношения (постоянного или переменного вдоль радиуса) H/D = 1,0 – 2,2.
Проектирование гребных винтов
Выбор исходных данных
Настоящий раздел относится в основном к моторным лодкам и катерам со стационарными двигателями, так как подвесные моторы обычно поставляются с готовыми ГВ. Однако приведенные рекомендации полностью пригодны и для проектирования новых ГВ для различных подвесных моторов.
В начале проектирования ГВ должны быть известны или установлены предварительным расчетом следующие исходные данные:
- теоретический чертеж катера или лодки с главными размерениями и коэффициентами, с расчетными значениями водоизмещений и осадок;
- кривые сопротивления и эффективной мощности корпуса с выступающими частями в зависимости от скорости R = f(νκ) и NR = f(νκ);
- чертежи, характеризующие расположение ГВ, корпуса катера, подводного крыла и выступающих частей, со сведениями о наибольшем допустимом диаметре винта и глубине его погружения на максимальной скорости, об углах наклона гребных валов, об углах ходового дифферента и т. д.;
- коэффициенты взаимодействия винта и корпуса;
- количество двигателей или гребных валов zв;
- номинальная или располагаемая мощность двигателей Ne, кВт, и соответствующая частота их вращения nдв, об/мин (с-1);
- внешняя и ограничительная характеристики двигателей Nвн = f(nдв) и Norp = f(nдв).
Желательно также иметь универсальную характеристику, позволяющую на ходовых испытаниях определять мощность двигателя в зависимости от частоты вращения и часового расхода топлива. При наличии редуктора или вертикальной колонки должно быть указано их передаточное отношение ip.
Практика показывает, что для обеспечения достаточного запаса мощности на ухудшение состояния корпуса и увеличение высоты волнения выбор элементов ГВ целесообразно производить для полного водоизмещения при условии использования около 90 % располагаемой мощности на номинальной частоте вращения двигателей. У катеров на подводных крыльях (КПК) запас мощности может достигать даже 20 %, так как он должен обеспечивать преодоление горба сопротивления и выход на крылья в условиях волнения. При назначении расчетной мощности двигателя следует учитывать также потери мощности на трение валопровода в упорном и опорном подшипниках и в дейдвуде. КПД валопровода в среднем составляет ηв = 0,96 – 0,98. Угловые вертикальные колонки имеют ηм ≈ 0,90.
Для головных катеров и моторных лодок, в особенности быстроходных, целесообразно проектировать два-три варианта гребных винтов, обеспечивающих различную загрузку двигателей при заданной частоте вращения. Наличие нескольких вариантов винтов позволяет в процессе ходовых испытаний выбрать для последующего серийного изготовления винты с наиболее оптимальными элементами как по скорости катера, так и по загрузке двигателей даже в случае недостаточной достоверности некоторых исходных данных, использованных при их проектировании.
Выбор числа лопастей, дискового отношения и элементов эквивалентного профиля
С уменьшением количества лопастей КПД ГВ на рабочих режимах возрастает. Наибольшим КПД обладают двухлопастные винты (на 6-12 % выше, чем трехлопастные).
Широкое применение двухлопастных винтов ограничивается сильной вибрацией, возникающей вследствие резкого уменьшения частоты и увеличения амплитуды импульсных давлений, создаваемых на днище катера каждой лопастью. Кроме того, двухлопастным винтам свойственна в большей мере, чем трехлопастным, так называемая гидродинамическая неуравновешенность, при которой из-за различий в шаге, профилировке или площади лопасти винта развивают неодинаковый, а в косом потоке даже периодически изменяющийся упор. При этом равнодействующая сил упора обеих лопастей не совпадает с осью винта. Внеосевые переменные нагрузки вызывают изгиб гребного вала и дополнительно усиливают вибрацию концевого кронштейна и корпуса катера.
Применение двухлопастных ГВ на быстроходных катерах с двигателями значительной мощности связано с осуществлением ряда конструктивных мер – специального подкрепления кронштейна и днища в районе действия винта, увеличения зазоров между винтом и корпусом, повышения частоты вращения винта и т. д. Одновременно должны быть повышены требования к изготовлению двухлопастных винтов с целью достижения близких значений шага обеих лопастей и хорошей их балансировки.
Указанные трудности использования двухлопастных винтов привели к тому, что несмотря на некоторое снижение КПД, наибольшее распространение в малом катеростроении получили трехлопастные ГВ, менее опасные в отношении вибрации и пульсирующих давлений.
Кавитирующие ГВ обычно проектируют также трехлопастными.
Дисковое отношение некавитирующих ГВ следует выбирать таким образом, чтобы при обеспечении необходимой прочности лопастей оно не снижало бы гидродинамических качеств винтов. При этом на наиболее длительных эксплуатационных режимах должно быть исключено возникновение кавитации и появление эрозии ГВ.
Как рассчитать диаметр гребного винта по мощности двигателя? Ориентировочная величина дискового отношения, удовлетворяющего данным условиям, находится с помощью рис. 17 или по формуле:
где:
- P – упор ГВ на режиме полного хода, кН;
- D – ожидаемый диаметр ГВ, м.
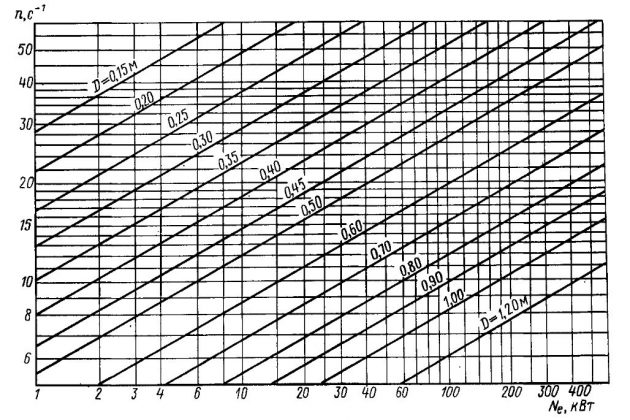
Предварительная оценка оптимального диаметра ГВ может быть произведена по частоте его вращения и мощности двигателя (рис. 18). Если найденный диаметр винта окажется больше максимально допустимого по условиям его размещения, то дисковое отношение определяют по максимально допустимой величине D. В дальнейшем оптимальный диаметр винта и дисковое отношение уточняются во втором приближении для достижения их наилучших значений, обеспечивающих наивысший КПД.

Однако, независимо от результатов расчета, принимать дисковое отношение менее Θ = 0,3 не следует, так как это будет приводить к снижению КПД винта из-за увеличения толщин лопастей и ухудшения их гидродинамических качеств. С другой стороны, излишнее увеличение дискового отношения также нежелательно, так как одновременно с повышением упора и момента, винта вследствие возрастания профильных потерь снижается его КПД. Кроме того, при больших дисковых отношениях становится заметным стеснение потока, увеличиваются скорости обтекания лопастей и усиливается их взаимодействие. Это способствует появлению и углублению кавитации.
В тех случаях, когда не удается избежать наступления кавитации даже при увеличении дискового отношения до Θ = 1,0 – 1,2, следует проектировать кавитирующие винты. Дисковое отношение кавитирующих ГВ обычно находится в пределах Θ = 0,9 – 1,2. Верхний предел дисковых отношений принимают для винтов с большими шаговыми отношениями (H/D = 1,4 – 1,8), у которых неблагоприятное влияние гидродинамической решетки менее заметно. Практика показывает, что выбор дисковых отношений в указанных пределах приводит к умеренным потерям пропульсивных качеств ГВ от кавитации и не вызывает значительных трудностей при их изготовлении.
При проектировании суперкавитирующих ГВ нет необходимости в значительном увеличении дискового отношения и его принимают A/Ad = 0,5 – 0,8.
С дисковым отношением ГВ непосредственно связаны основные элементы эквивалентного профиля. С увеличением дискового отношения возрастает ширина лопастей и соответственно уменьшаются их относительные характеристики. Относительная толщина эквивалентного профиля может быть найдена по простой эмпирической зависимости:
Полученная по данной формуле толщина эквивалентного профиля обычно удовлетворяет условию прочности и обеспечивает приемлемые кавитационные характеристики ГВ.
Если проектируемый винт является кавитирующим или работает вблизи кавитационного режима, то для уменьшения влияния кавитации или отдаления момента ее наступления необходимо стремиться к обеспечению безударной работы сечений лопастей.
Увеличение диапазона углов безударного входа, при которых сглаживается пик разрежения у входящей кромки, достигается сегментной вогнуто-выпуклой профилировкой лопастных сечений с плавно изменяющейся вдоль радиуса кривизной.
Увеличение относительной кривизны влияет на гидродинамические характеристики ГВ подобно увеличению его шагового отношения. Близкое к оптимальному распределение вогнутости лопасти вдоль ее радиуса получается, если относительная кривизна средней линии эквивалентного профиля соответствует:
где:
- Cy – коэффициент подъемной силы, который находится по формуле Папмеля:
По полученным значениям δ и δ1 легко определяется относительная кривизна засасывающей стенки профиля, необходимая для выбора расчетной кавитационной диаграммы:
В начальной стадии проектирования винта, когда отсутствуют значения коэффициентов K1 и Cy, относительную кривизну в первом приближении можно найти по формуле:
в которой относительная вогнутость нагнетающей стенки эквивалентного профиля
В дальнейшем при уточнении величины дискового отношения могут быть также уточнены и элементы эквивалентного профиля.
Определение наибольшей скорости судна и элементов некавитирующих гребных винтов
Определение величин диаметра и шага ГВ, обеспечивающих его согласование с механической установкой и оказывающих решающее влияние на КПД винта и скорость судна, осуществляется по расчетной диаграмме (численный пример расчета смотрите в статье Малотоннажные суда на подводных крыльях“Суда на подводных крыльях”), выбранной в соответствии с установленными значениями дискового отношения и числа лопастей винта.
Увеличение диаметра винта в реально допустимых пределах повышает его КПД.
При этом необходимо учитывать возможность размещения ГВ за корпусом катера или лодки. У водоизмещающих малых судов диаметр винта ограничивается осадкой, так как приближение кромок лопастей к свободной поверхности воды связано с опасностью прорыва к ним воздуха. У быстроходных глиссирующих катеров и КПК излишнее увеличение диаметра винта, расположенного под днищем или крылом, будет ухудшать условия его работы вследствие увеличения угла наклона гребного вала и усиления влияния косого потока.
Большое влияние на диаметр винта оказывает частота его вращения. Уменьшение частоты вращения винта требует соответствующего увеличения диаметра. Для каждой частоты вращения в зависимости от сопротивления корпуса и скорости судна можно с помощью коэффициента
найти оптимальную величину диаметра винта, при которой его КПД достигает максимального значения. И наоборот, каждому значению диаметра винта соответствует оптимальная частота вращения, определяемая при помощи коэффициента
. Гидродинамическая связь диаметра винта с частотой вращения осуществляется через шаговое отношение H/D и относительную поступь λp, определяющую режим работы винта.
Шаговое отношение весьма сильно влияет на характеристики коэффициентов упора и момента винта. Зависимость КПД от шагового отношения более сложна. Наибольшие значения КПД по мере увеличения шагового отношения до H/D ≈ 2,0 – 2,2 также возрастают, а затем начинают убывать. Рабочие значения КПД винта определяются величинами H/D и λp и могут колебаться в значительных пределах, поэтому правильный выбор шагового отношения и других элементов винта имеет чрезвычайно важное значение.
В зависимости от заданных расчетных условий при проектировании некавитирующих ГВ и определении скорости катеров и лодок можно выделить следующие наиболее типичные случаи.
- Определение наибольшей скорости катера и оптимального диаметра гребного винта при заданной частоте его вращения.
- Определение наибольшей скорости катера и оптимальной частоты вращения при заданной (ограниченной) величине диаметра винта.
- Определение наибольшей скорости катера или лодки при заданных значениях диаметра и частоты вращения ГВ.
Во всех случаях расчета мощность двигателей считается известной. Расчет удобнее всего производить в табличной форме. Перед таблицей приводят известные постоянные величины – мощность двигателей ΣNe, кВт, частоту вращения n, с-1, или диаметр винта D, м, коэффициенты взаимодействия w и t, количество гребных валов zв и т. д.
Для первого случая задания можно использовать таблицу, составленную по следующей схеме:
Данную схему можно применить также и для второго случая задания, т. е. для определения оптимальной частоты вращения по заданному диаметру винта. При этом в статье Гидродинамические характеристики гребных винтов и технология построения паспортных диаграмм“Характеристики гребных винтов” схемы и далее вместо коэффициента
используется коэффициент
[см. формулы 18 и 19], а в статье Гидродинамические характеристики гребных винтов и технология построения паспортных диаграмм“Выбор количества ГВ, направления их вращения и расположения относительно корпуса” вычисляется искомое значение nopt = vp/Dλp.
Полученные значения мощности двигателей ΣNe, диаметра винта D, шагового отношения H/D и КПД винта ηp откладывают на графике в зависимости от скорости судна νk. Наибольшая скорость катера, а также все элементы и характеристики гребного винта определяются абсциссой точки пересечения кривой необходимой мощности двигателей со значением располагаемой мощности. Для полученной скорости целесообразно произвести контрольный расчет.
Если полученный диаметр винта Dopt будет превышать максимально допустимый, т. е. величина диаметра окажется ограниченной, то расчет следует производить по несколько измененной схеме для заданных значений диаметра D и частоты вращения ГВ n. При этом основные характеристики, влияющие на эффективность гребного винта – его шаговое отношение и КПД – находятся по соответствующей диаграмме K1 – λp в точке действия винта, определяемой значениями его поступи λp и коэффициента упора K1, полученными для каждой заданной скорости судна. Последовательность расчета видна из приведенной схемы и дополнительных пояснений не требует:
Элементы проектируемого винта соответствуют скорости, при которой необходимая мощность двигателей совпадает с располагаемой.
С помощью приведенных расчетных схем по диаграммам K1 – λp можно также найти мощность двигателей, требующуюся для достижения заданной скорости катера. При этом достаточно ограничиться лишь столбцом первого приближения, поскольку добиваться совпадения необходимой мощности с располагаемой уже не нужно.
При использовании диаграмм K2 – λp определение оптимального диаметра винта по известным значениям мощности Ne, кВт, и частоты вращения двигателя n, с-1, производят по следующей схеме:
Оптимальная частота вращения винта находится по аналогичной схеме с помощью коэффициента
. Коэффициенты взаимодействия w и t в данных схемах также предполагаются известными.
Если диаметр и частота вращения ГВ заданы, то схема определения его элементов по диаграммам K2 – λp еще более упрощается:
Проверка отсутствия кавитации гребных винтов и уточнение оптимальной величины дискового отношения
После определения основных элементов ГВ необходимо проверить их на отсутствие второй стадии кавитации. Такая проверка с достаточной надежностью и простотой производится по формуле:
которая показывает, что для отсутствия кавитации необходимо, чтобы рабочая относительная поступь проектируемого винта λp всегда была больше его критической поступи λpk при действующем числе кавитации κ. При практической проверке ГВ на кавитацию следует по формулам 41 или 42 вычислить значения его критической поступи на различных режимах работы, включая максимальный, и сравнить их с величинами действительной поступи винта на тех же режимах:
- (см. рис. 13);
При значениях поступей λp < λpk для исключения кавитации дисковое отношение винта следует увеличить. Если же рабочая поступь винта будет существенно превышать критическую, то для повышения КПД дисковое отношение целесообразно уменьшить. Уточнить оптимальное дисковое отношение винта можно по формулам:
или:
При пользовании формулой 51 значения функции
снимаются с рис. 13. Формула 52 позволяет непосредственно определять дисковое отношение винта, не пользуясь указанным графиком.
Поскольку данные формулы получены из условия, характеризующего начало уменьшения упора при кавитации, то для предохранения от эрозии винта, возникающей в первой стадии кавитации, дисковое отношение, особенно в косом потоке при большой неравномерности обтекания винта, принимают с некоторым запасом. Достаточный запас дискового отношения обеспечивает коэффициент ускорения кавитации в формулах 51 и 52, близкий к p = 1,2.
При равномерном осевом обтекании ГВ этот коэффициент может быть уменьшен.
Определение наибольшей скорости катера и элементов кавитирующих гребных винтов
Если в результате попыток спроектировать некавитирующий ГВ окажется, что необходимая для этой цели величина дискового отношения будет превышать значение Θ = 1,0 – 1,2, то, очевидно, следует перейти к проектированию кавитирующего винта. При этом для определения основных характеристик проектируемого винта при отсутствии кавитации используется одна из диаграмм K1 – λp. Учет же влияния кавитации на действие этого винта производится по универсальной диаграмме φ1 – λp/λpk, выбранной в зависимости от элементов принятого эквивалентного профиля. Относительную толщину эквивалентного профиля кавитирующего винта устанавливают в соответствии с ранее приведенными рекомендациями. Дисковое отношение для уменьшения влияния кавитации на действие винта, как уже указывалось, целесообразно принимать близким к Θ = 1. Число лопастей по тем же соображениям принимают z = 3.
В результате расчета должны быть определены наибольшая скорость катера или моторной лодки при полном использовании мощности двигателей, а также наивыгоднейшие элементы кавитирующего ГВ, включая оптимальные значения его диаметра, частоты вращения, шагового отношения и КПД. При этом следует иметь в виду, что одним из самых существенных требований к проектируемому ГВ является условие согласования его элементов с механической установкой и сопротивлением катера.
Это означает, что из бесконечного количества вариантов необходимо выбрать такой гребной винт с оптимальной комбинацией элементов, который, несмотря на влияние кавитации на скорость катера, сможет обеспечить достижение максимальной скорости при заданных мощности и частоте вращения двигателей. Поскольку гидродинамические характеристики ГВ при появлении кавитации сильно изменяются, то решение данной задачи сопряжено с определенными трудностями.
При проектировании кавитирующего ГВ необходимо иметь возможность определять ожидаемое уменьшение упора и КПД винта от влияния кавитации на любом заданном режиме работы с тем, чтобы заранее предусмотреть соответствующее увеличение его шага для компенсации этого уменьшения. Неточность в определении элементов кавитирующего винта приведет к тому, что он будет не согласован с двигателем.
Для расчета элементов кавитирующего винта может быть использована схема, представленная в табл. 1. Схема позволяет определить скорость судна и шаговое отношение винта в условиях кавитации при заданных величинах его диаметра и частоты вращения. Если оптимальные значения диаметра или частоты вращения винта должны быть найдены, то расчет по аналогичной схеме производят для нескольких вариаций искомого параметра при постоянной ожидаемой скорости. Порядок расчета ясен из таблицы и не требует пояснений. Задаются тремя значениями скорости, близкими к ожидаемой ее величине, и находят соответствующие им значения сопротивления R, поступи винта λp, числа кавитации κ и т. д. Далее в строке 8 для каждой принятой скорости судна задаются тремя коэффициентами упора K1 позволяющими в условиях кавитации обеспечить тягу Pe, близкую к необходимой, и по диаграмме K1 – λp, имеющей выбранное дисковое отношение, определяют значения шаговых отношений нулевого упора H1/D и КПД винта ηp при отсутствии кавитации.
Таблица 1. Расчет скорости и элементов кавитирующего ГВ ( ) | |||||
|---|---|---|---|---|---|
| 1 | νк, км/ч | ||||
| 2 | νp = 0,278 νк(1-w), м/с | ||||
| 3 | R = f(νк) = zвPe, кН | ||||
| 4 | NR = 0,278 νкR, кВт | ||||
| 5 | |||||
| 6 | |||||
| 7 | |||||
| 8 | K1 | ||||
| 9 | |||||
| 10 | |||||
| 11 | |||||
| 12 | |||||
| 13 | |||||
| 14 | |||||
| 15 | |||||
| 16 | |||||
| 17 | |||||
Если расчетная диаграмма построена не по H1/D, а по геометрическому шаговому отношению H/D, то шаговое отношение H1/D находят на пересечении кривой H/D с осью λp. Для учета влияния кавитации на характеристики винта вычисляют величины λpk и отношения поступей λpλpk.
Затем по соответствующей диаграмме φ1 – λp/λpk находят коэффициенты уменьшения упора φ1 и КПД ηφ кавитирующего винта. С помощью этих коэффициентов определяют развиваемую ГВ тягу на каждом режиме и потребляемую при этом мощность двигателей. Значения коэффициентов упора K1 и потребной мощности ΣNe = f(K1), при которых тяга винтов будет равна сопротивлению катера, находят путем построения полученных для каждой скорости судна зависимостей Pe = f(K1) и ΣNe = f(K1) совместно с кривой сопротивления. Для проверки этих значений K1 и ΣNe производят контрольные расчеты в дополнительных столбцах табл. 1. Зависимости K1 = f(νk), Pe = f(νк) и ΣNe = f(νk), построенные по результатам контрольных расчетов, позволяют определить наибольшую достижимую скорость катера, а также необходимые значения тяги и коэффициента упора винта. Эти величины соответствуют точке, в которой необходимая мощность двигателей становится равной располагаемой мощности.
Исходя из найденных значений наибольшей скорости и коэффициента упора в последнем столбце табл. 1 также производят контрольный расчет, позволяющий окончательно уточнить основные элементы и характеристики проектируемого кавитирующего ГВ для заданных условий эксплуатации. При этом следует обратить внимание на правильный выбор величины коэффициента ускорения наступления кавитации p в натурных условиях. Для кавитирующих ГВ, работающих при относительно равномерном осевом обтекании, а также при небольших (до 6-8°) углах скоса потока этот коэффициент составляет около p = 1,05÷1,10. При увеличении углов наклона гребных валов и усилении неравномерности потока у быстроходных глиссирующих и крылатых катеров коэффициент ускорения кавитации может возрасти до значения p = 1,20.
Особенности определения наибольшей скорости и элементов гребных винтов катеров на подводных крыльях
Ддя преодоления горба сопротивления и обеспечения выхода катера на крылья необходимо при скорости, равной (0,4÷0,6) νm, приложить значительную мощность. Однако вследствие ограничений, накладываемых внешними характеристиками двигателей внутреннего сгорания, эта мощность не всегда может быть развита на промежуточном режиме работы при неполных оборотах Влияние гребного винта фиксированного шага (ВФШ) и руля на управляемость суднаГВ фиксированного шага, спроектированного на режим максимальной скорости, в особенности при наличии кавитации. При движении на волнении данное явление еще более усугубляется вследствие увеличения сопротивления и дополнительного возрастания мощности, необходимой для выхода катера на глиссирование или на крылья, поэтому необходимо стремиться к созданию возможно большего запаса мощности.
Обычно это достигается рациональным выбором расчетного режима и проектированием так называемого легкого ГВ за счет неполного использования мощности двигателя на режиме наибольшей скорости при заданной частоте вращения винта, т. е. практически за счет снижения максимальной скорости катера. Запас мощности двигателей на режиме наибольшей скорости у КПК, например, принимают в пределах 10-20 %. Конкретная величина необходимого запаса мощности определяется типом внешней характеристики двигателя, величиной горба сопротивления и ожидаемым его увеличением на волнении. Выбирая элементы ГВ для КПК из условия получения наибольшей скорости, всегда необходимо проверять их на режиме выхода на крылья.
Такая проверка осуществляется при построении паспортной диаграммы. Желательно, чтобы запас мощности на горбе сопротивления КПК составлял не менее 20 %.
Применение вертикальных колонок в силу отсутствия наклонных валов исключает косое обтекание ГВ, что улучшает условия их работы, а также уменьшает опасность появления кавитации винтов или их эрозии. Вне корпуса катера колонка состоит из вертикальных валов, находящихся в стойке хорошо обтекаемой формы, и нижнего редуктора с гребным валом, заключенных, в обтекаемую гондолу (рис. 19).
Верхняя часть стойки, пересекающая свободную поверхность воды, для улучшения волнообразования и уменьшения опасности прорыва воздуха, имеет заостренный сегментный профиль. Под ватерлинией для уменьшения сопротивления профиль стойки плавно скругляется и переходит в симметричный авиационный.
Возникновение кавитации элементов колонки приводит к резкому возрастанию ее сопротивления и ухудшению условий работы винта. Поэтому профили стойки и гондолы должны обладать увеличенным диапазоном углов безударного входа и высокими антикавитационными качествами. Относительные ординаты профилей стойки и гондолы, удовлетворяющие указанным условиям, приведены в табл. 2. Отношение длины гондолы к ее наибольшему диаметру следует принимать в пределах b/dm = 4÷6. При этом ступица винта должна плавно сопрягаться с обводами гондолы.
Критическое число начала кавитации колонок, разработанных в соответствии с данными рекомендациями, при осевом обтекании приближенно определяют в зависимости от относительной толщины профиля:
При движении с дрейфом критическое число кавитации быстро возрастает. При создании вертикальных угловых колонок приходится учитывать ряд противоречивых требований. Для снижения сопротивления самой колонки необходимо уменьшать ее габариты, что возможно при повышении частоты вращения ГВ.
Повышение же частоты вращения винта понижает его КПД и увеличивает опасность появления кавитации.
Рассмотрим, какая применяется методика оценки эффективности гребного винта. Выбор оптимальных соотношений между размерами колонки и характеристиками ГВ производится путем сравнительного анализа эффективности винта при различной частоте вращения с учетом кавитации, если она имеет место, и соответствующего изменения сопротивления колонки. Для приближенного определения сопротивления колонки в ньютонах рекомендуется формула:
где:
- Sк – площадь смоченной поверхности колонки, м2;
- ν и νк – скорость в метрах в секунду и километрах в час соответственно.
Указанные особенности необходимо учитывать. При определении наибольшей скорости и проектировании ГВ для КПК как с наклонными гребными валами, так и с угловыми вертикальными колонками. При этом проектирование некавитирующих винтов в зависимости от условий задания производится по одной из приведенных выше схем. Для кавитирующих ГВ используется табл. 1.
| Таблица 2. Относительные ординаты профилей гондолы и стойки угловой колонки | ||||
|---|---|---|---|---|
| № ординаты | Абсцисса профиля x/b | Относительный диаметр гондолы d/dm | Относительные ординаты профиля стойки | |
| ниже ВЛ y/em | выше ВЛ y/em | |||
| 1 | 0 | 0 | 0 | 0 |
| 2 | 0,0125 | 0,216 | 0,206 | 0,050 |
| 3 | 0,025 | 0,328 | 0,320 | 0,0975 |
| 4 | 0,050 | 0,480 | 0,464 | 0,190 |
| 5 | 0,075 | 0,582 | 0,561 | 0,2775 |
| 6 | 0,100 | 0,662 | 0,650 | 0,360 |
| 7 | 0,150 | 0,781 | 0,775 | 0,510 |
| 8 | 0,200 | 0,863 | 0,859 | 0,640 |
| 9 | 0,250 | 0,920 | 0,917 | 0,750 |
| 10 | 0,300 | 0,958 | 0,956 | 0,840 |
| 11 | 0,350 | 0,983 | 0,982 | 0,910 |
| 12 | 0,425 | 1,0 | 1,0 | 0,977 |
| 13 | 0,500 | 0,987 | 0,990 | 1,0 |
| 14 | 0,600 | 0,920 | 0,930 | 0,960 |
| 15 | 0,700 | 0,785 | 0,820 | 0,840 |
| 16 | 0,800 | 0,595 | 0,650 | 0,640 |
| 17 | 0,900 | 0,350 | 0,420 | 0,360 |
| 18 | 0,950 | 0,192 | 0,250 | 0,190 |
| 19 | 1,0 | 0 | 0 | 0 |
🤝 Поддержите нашу работу
Нашли опечатку? Выделите и нажмите CTRL+Enter

Качественный материал, для владельцев малых яхт или крупных моторных лодок самое то. Отлично!