Расчеты прочности основных деталей дизеля

На прочность деталей СДВС влияет множество факторов, которые обусловлены напряженными изменениями и возможными деформациями.

Расчет коленчатого вала

Для судового механика расчет прочности деталей двигателя важен не с точки зрения получения конечного конструкторского результата, а с точки зрения получения понятия как работает та или иная деталь, какие требования выдвигаются классификационным обществом к ее размерам, какие внешние условия способствуют снижению или, наоборот, повышению вероятности выхода детали из строя. При этом наибольший интерес представляет оценка показателей прочности самой ответственной детали двигателя коленчатого вала.

Требования Регистра России к диаметру коленчатого вала

Правила классификационных обществ, под надзором которых изготавливаются двигатели, выдвигают определенные требования к размерам коленчатого вала. Эти требования обобщают опыт того или иного классификационного общества. Регистр России дает такую эмпирическую формулу для определения минимально допустимого диаметра шеек коленчатого вала:

$d = 0,115k·\sqrt[3]{D^2\sqrt{{\left(P_{z}L\right)}^2 + {\left(\phi ·t·S\right)}^2}}, Форм. 1$

где:

• D – диаметр цилиндра, см;
• S – ход поршня, см;
• L – расстояние между серединами рамовых шеек, см;
• P_z – максимальное давление в цилиндре, кг/см²;
• t – коэффициент, учитывающий степень форсировки двигателя;
• t = 8,5 + p_i – для 2-тактных ДВС;
• t = 8,5 + 0,75 p_i – для 4-тактных ДВС;
• p_i – среднее индикаторное давление, кг/см²;
• k – коэффициент, учитывающий механические свойства материала коленчатого вала.

$k = \sqrt[3]{{\sigma }_{в}/\left(2{\sigma }_{в} – 44\right)}, Форм. 2$

где:

• σ_в – предел прочности материала коленчатого вала при растяжении, кг/мм²; если материал имеет σ_в более 80 кг/мм², то в формулу подставляется значение σ_в = 80 кг/мм²;
• φ – коэффициент, учитывающий число цилиндров.

 
Приведенная формула 1 применима к расчету минимального диаметра коленчатого вала без сверлений в шейках или же при диаметре сверлений менее 0,4 от наружного диаметра шейки. Это требование всегда выполняется для судовых двигателей.

Расчет коленчатого вала в 1-м расчетном положении

Коленчатый вал – это многоопорная статически неопределимая неразрезная балка. Расчет такой балки как многоопорной мало того, что сложен, – расчет дает малую точность. Поэтому в практике расчетов используется более простой и в то же время более надежный метод. Рассчитывается лишь одно колено, лежащее на 2 опорах (рамовых подшипниках), остальная часть коленчатого вала отбрасывается. Балка получается статически определимой. Опорные точки расчетного вала считаются расположенными посредине подшипников, вал принимается абсолютно жестким. В качестве расчетного выбирается то колено, к которому подводится наибольший крутящий момент от выше расположенных цилиндров. В общем случае расчет коленчатого вала проводится в его 3-х опасных положениях:

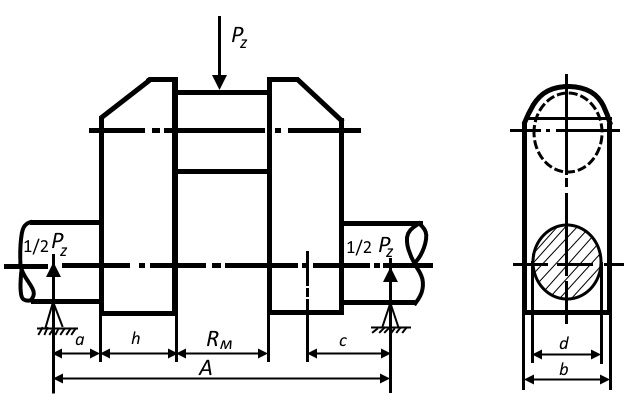
1. В верхней мертвой точке кривошипа при допущении, что в этот момент давление в цилиндре – максимальное (P = P_z), рис. 1;
2. В положении максимального касательного усилия в цилиндре;
3. В положении вала, когда весь двигатель развивает максимальное касательное усилие (максимальный крутящий момент).

2-е и 3-е расчетные положения коленчатого вала могут не совпадать для высокооборотных двигателей. Для судовых двигателей 2-е и 3-е расчетные положения всегда совпадают. Поэтому в судовых двигателях можно ограничиться анализом прочности коленчатого вала лишь в 1-м и 2-м расчетных положениях.

Читайте также: Уравновешенность двигателя, анализ и определение результирующих сил
 
Для определения расчетного колена в 1-м положении кривошип каждого цилиндра мысленно устанавливается в верхнюю мертвую точку и определяется суммарное касательное усилие, подводимое к этому цилиндру от выше расположенных цилиндров. То колено, к которому подводится наибольшее по абсолютной величине суммарное касательное усилие, будет являться расчетным.

Расчетное колено определяется с помощью вспомогательной таблицы (таблица 2). На основании расчета сил динамики в 1-й строке таблицы для цилиндра No. 1 записываются значения касательного усилия T₁ через угол Ψ, равный углу чередования вспышек в цилиндрах (в приведенном примере Ψ = 60°). В соответствии с порядком работы цилиндров записи 1-й строки повторяются во всех ниже расположенных строках для 2, 3, 4-го и т. д. цилиндров.

Так, если последовательность вспышек 1-5-3-4-2-6, то в 5-м цилиндре повторится то же, что и в 1-м цилиндре, через 60° поворота коленчатого вала, в 3-ем – через 120° пкв и т. д. Заполнив таблицу, необходимо найти сумму касательных усилий от выше расположенных цилиндров для каждого колена в момент его нахождения в ВМТ. То колено, к которому подходит максимальное усилие ΣT, является расчетным. В приведенном в табл. 2 примере расчетным является колено No 6.

 
Найденное значение максимального касательного усилия ΣТ^мах позволяет найти скручивающий момент на расчетном колене в 1-м положении и напряжения кручения в рамовой и мотылевой шейках:

$M_{кр} = \Sigma T^{мах} F_n R, Форм. 3$

${\tau }_{кр} = M_{кр}/W_P, Форм. 4$

где:

• F_n – площадь поршня;
• R – радиус кривошипа;
• W_Р= 0,2 d³ – полярный момент сопротивления кручению рамовой или мотылевой шейки;
• d – диаметр шейки.

Изгибающий момент в колене определяется усилием от давления газов в цилиндре P_z. Это усилие распределяется поровну на 2 рамовых опоры и определяет реакции опор. С учетом величины плеч действия силы реакции опор (рис. 1) изгибающие моменты равны:

• на рамовой шейке

$M_{ир} = 0,5 P_z{F}_n a; Форм. 5$

• на мотылевой шейке

$M_{им} = 0,5 P_z{F}_n 0,5A; Форм. 6$

• на щеке колена:

$M_{иш} = 0,5 P_z{F}_n c; Форм. 7$

Соответственно напряжения изгиба определятся как:

• на рамовой шейке

${\sigma }_{ир} = M_{ир}/W_{рам}; Форм. 8$

• в мотылевой шейке

${\sigma }_{им} = M_{иш}/W_{м}; Форм. 9$

• в щеке (от реакции P_z/2)

${\sigma }_{ищ}^{\prime } = M_{ищ}/W_{щ}^{\prime }; Форм. 10$

• в щеке (от крутящего момента)

${\sigma }_{ищ}^{″} = M_{кр}/W_{щ}^{″}; Форм. 11$

Моменты сопротивления изгибу здесь равны:

• для рамовой и мотылевой шейки

$W = 0,1 d^3; Форм. 12$

• для щеки (от усилия P_z)

$W_{щ}^{\prime } = b h^2/6; Форм. 13$

• для щеки (от усилия крутящего момента)

$W_{щ}^{″} = b2 h/6. Форм. 14$

Напряжение сжатия в щеке σ_сж и максимальное суммарное напряжение в щеке σ_щ рассчитываются по формулам:

${\sigma }_{сж} = P_z F_n/2 bh; Форм. 15$

${\sigma }_{щ} = {\sigma }_{щ}^{\prime } + {\sigma }_{щ}^{″} + {\sigma }_{сж}. Форм. 16$

Сложные напряжения в рамовой и мотылевой шейках определяются по зависимости:

${\sigma }_{рам, м} = \sqrt{{\sigma }_{и}^2 + 4{\tau }_{кр}^2}. Форм. 17$

Расчет коленчатого вала во 2-м расчетном положении

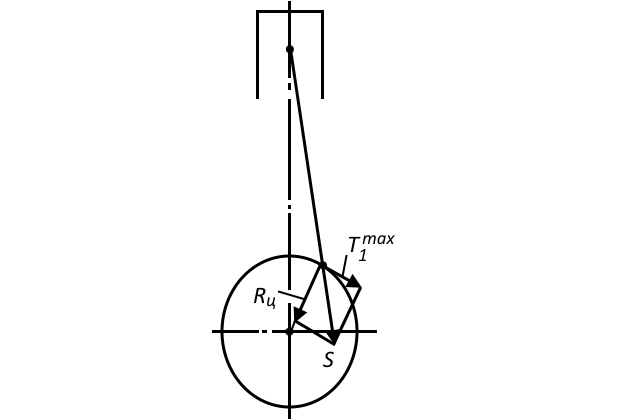
2-е расчетное положение коленчатого вала определяется на основе расчета сил динамики (таблица 1). Угол положения коленчатого вала, при котором в цилиндре достигается максимальное касательное усилие

, обычно наблюдается при повороте кривошипа на 20-30° после ВМТ (рис. 2).

Расчетным считается то колено, к которому в положении

$T_1^{мах}$

подводится максимальное суммарное касательное усилие от выше расположенных цилиндров. Для определения расчетного колена строится таблица (таблица 3), аналогичная предыдущему случаю. В 1-й строке таблицы записывается значение T₁ начиная с

$T_1^{мах}$

, через угол заклинки кривошипов Ψ. В последующих строках эти записи повторяются со сдвигом по фазе с учетом порядка работы цилиндров. Просуммировав в каждой графе усилия T₁ от выше расположенных цилиндров, определяют ΣT и выбирают ΣT^мах. Для приведенного в таблице примера максимальное усилие ΣT^мах получено в 4-м цилиндре. Это колено является расчетным.

 
Крутящий момент на расчетном колене равен:

• в кормовой рамовой шейке

$M_{кр} = \left(T_1^{мах} + \Sigma T^{мах}\right)F_n R; Форм. 18$

• в мотылевой шейке

$M_{кр} = \left(0,5 T_1^{мах} + \Sigma T^{мах}\right)F_n R. Форм. 19$

Напряжение кручения в шейках рассчитывается по формуле 4. Кроме того, напряжение кручения возникает и в щеках колена под действием силы

$T_1^{мах}$

, которая создает крутящий момент, равный:

$M_{кщ} = 0,5 T_1^{мах} F_n c. Форм. 20$

Напряжение кручения будет разным для широкой и узкой стороны щеки, имеющих разный полярный момент сопротивления, равный:

• на середине широкой стороны щеки

$W\prime = k b h^2, Форм. 21$

• на середине узкой стороны щеки

$W″ = k b^2 h. Форм. 22$

Коэффициент k определяется соотношением размеров щеки b/h (обозначение см. рис. 1.), может быть найден из табл. 4.

 
Напряжение изгиба в шейках коленчатого вала во 2-м расчетном положении определяется силой S_φ, равной (рис. 2):

$S_{\phi } = \sqrt{{\left(T_1^{max}\right)}^2 + R_{\phi }^2}, Форм. 23$

где:

• R_φ – радиальная сила кривошипа при угле φ, соответствующем силе

  $T_1^{max}.$

Сила R_φ, определяется по данным расчета сил динамики.

Величина изгибающего момента на шейках и в щеках определяется равенствами:

• на рамовой шейке

$M_{ир} = M_{кр} = 0,5 S_{\phi } F_n a; Форм. 24$

• на мотылевой шейке

$M_{им} = M_{км} = 0,5 S_{\phi } F_n 0,5 A; Форм. 25$

• на щеке колена (от реакции R_φ/2)

$M_{ищ} = 0,5 R_{\phi } F_n c; Форм. 26$

Напряжения изгиба в этих элементах определяются по тем же расчетным формулам, что и для 1-го расчетного положения коленчатого вала (зависимости 8-11). Напряжения сжатия в щеке определяются воздействием радиальной силы R_φ:

${\sigma }_{сж} = 0,5 R_{\phi } F_n/bh. Форм. 27$

Сложные напряжения рассчитываются по формулам:

• в рамовой и мотылевой шейках:

${\sigma }_{рам, м} = \sqrt{{\sigma }_{и}^2 + 4{\tau }_{к}^2}; Форм. 28$

• в щеке на середине широкой стороны:

${\sigma }_{щ}^{\prime } = \sqrt{{\left({\sigma }_{и}^{\prime } + {\sigma }_{сж}\right)}^2 + 4{\tau }_{щ}^2}; Форм. 29$

• в щеке на середине узкой стороны:

${\sigma }_{щ}^{″} = \sqrt{{\left({\sigma }_{и}^{″} + {\sigma }_{сж}\right)}^2 + 4{\tau }_{щ}^2}. Форм. 30$

Сложные напряжения для углеродистой стали должны находится в пределах:

• Для рамовой шейки – 40-80 МПа;
• Для мотылевой шейки – 60-100 МПа;
• Для щеки колена – 80-120 МПа.

Расчет шатуна

Изменение напряжения в стержне шатуна определяется изменением суммарной движущей силы цилиндра. Для 2-х тактного двигателя амплитуда изменения суммарной движущей силы численно равна ее максимальному значению:

$P_{\Sigma } = P_Z – P_j^{вмт}.$

В 4-тактном двигателе в конце такта выталкивания шатун нагружен растягивающими усилиями от сил инерции, амплитуда P_Σ возрастает до величины: P_Σ = P_z.

Однако как в 2-х, так и 4-тактных двигателях в качестве расчетного принимается усилие от максимального давления в цилиндре P_z. Напряжение сжатия в стержне шатуна от этого усилия равно:

${\sigma }_{сж} = P_z F_n/{f_{ст}}^{min}, Форм. 31$

где:

• f_ст^min – минимальное сечение стержня шатуна.

Сила от давления P_z не только сжимает стержень, но и вызывает его продольный изгиб. Напряжения от продольного изгиба, прежде всего, определяются силами инерции стержня шатуна, которые при работе двигателя стремятся шатун изогнуть. В предельном случае продольного изгиба шатун может быть поломан. Оценка показателей прочности стержня шатуна производится 2-мя путями:

1. Расчетом степени надежности стержня (по отношению к критической силе, ломающей шатун);
2. Расчетом напряжений изгиба и суммарного условного напряжения.

Критическая сила, ломающая шатун, рассчитывается в зависимости от степени гибкости стержня. Степень гибкости – это отношение длины шатуна L к радиусу инерции поперечного сечения i. Для судовых двигателей отношение L/i находится в пределах: 110 > L/i > 50. Для такого случая ломающие критические напряжения могут быть найдены по формулам:

• для углеродистых сталей

${\sigma }_{к} = \left(3 350 – 6,2 L/i\right) кг/с{м}^2; Форм. 32$

• для легированной стали

${\sigma }_{к} = \left(4 700 – 23 L/i\right) кг/с{м}^2. Форм. 33$

Тогда критическая сила равна:

$P_{к} = {\sigma }_{к} f_{ст}. Форм. 34$

Степень надежности стержня шатуна ε определится отношением:

$\epsilon = P_{к}/P_z{F}_n. Фрм. 35$

Считается допустимым:

• ε = 4-6,5 – для тихоходных двигателей;
• ε = 3-4,5 – для быстроходных двигателей.

Сила инерции вращающихся масс, действующая на единицу длины шатуна при работе двигателя, изменяется от 0 (у верхней головки) до максимального значения q – у нижней головки (рис. 3).

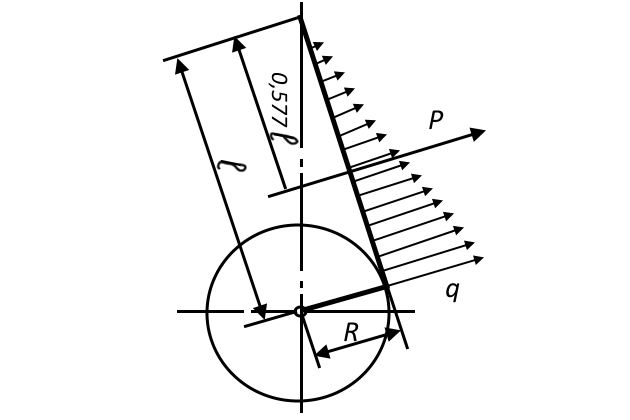
Величина q равна:

$q = m {\overline{\omega }}^2 R, Форм. 36$

где:

• m = f_ст ρ – масса единицы длины шатуна (произведение площади поперечного сечения стержня f_ст на плотность ρ);
• R – радиус вращения нижней головки;
• $\overline{\omega } = \mathrm{\pi } \mathrm{n}/30$

  – угловая скорость коленчатого вала.

Как известно, при подобном изменении сил инерции по длине стержня величина равнодействующей равна: P^мах = q L/2, а максимальное значение изгибающего момента определяется равенством:

$M^{мах} = q L^2/16. Форм. 37$

Момент M^мах соответствует сечению, расположенному на расстоянии 0,577 L от верхней головки шатуна. Напряжение изгиба в этом сечении составит:

${\sigma }_{и} = M^{мах}/W, Форм. 38$

где:

• W – момент сопротивления поперечного сечения стержня (для круглого сечения W = 0,1 d³).

Суммарное условное напряжение в стержне шатуна равно сумме напряжений сжатия и изгиба:

${\sigma }_{\Sigma } = {\sigma }_{сж} + {\sigma }_{и}. Форм. 39$

Считается допустимым напряжение:

• σ_Σ = 100 МПа – для шатунов из углеродистой стали;
• σ_Σ = 130 МПа – для шатунов из легированной стали.

Расчет шатунного болта, поршневого кольца, анкерной связи и крепежа цилиндра

Шатунный болт

Максимальное напряжение в шатунном болте 4-тактного двигателя возникает в конце такта выталкивания. В этот момент свободные силы инерции поступательно движущихся масс и силы инерции вращающихся масс шатуна, не связанные давлением газа, создают растягивающие усилия в болте. В 2-тактном двигателе в нормальных условиях работы шатунный болт нагружен лишь силами инерции вращающейся массы нижней крышки мотылевого подшипника.

При монтаже мотылевого подшипника усилие затяга шатунных болтов должно быть таким, чтобы при максимальном значении сил инерции не была бы нарушена плотность соединения. Это усилие затяга принимается равным:

$P_{з} = к P_{j\Sigma }Sin {\alpha }_n, Форм. 40$

где:

• к = 1,35-1,50 – коэффициент запаса;
• P_jΣ = P_jS + P_jR – суммарная сила инерции, воспринимаемая болтами;
• $P_{j S} = M_S R {\overline{\omega }}^2 \left(1 + \lambda \right)$

  – максимальная сила инерции поступательно движущихся масс;

• $P_{jR}\prime = M_{шR}\prime R {\overline{\omega }}^2$

  – сила инерции вращающейся части шатуна (за вычетом нижней половины мотылевого подшипника);

• α_n – угол между плоскостью разъема мотылевого подшипника и осью шатуна.

Особо неблагоприятные условия работы шатунных болтов как 2-ух, так и 4-тактных двигателей возникают при задире поршня. Усилие, воспринимаемое шатунными болтами в этом случае, определяется как:

$P_{зад} = q_{зад}{F}_n Sin {\alpha }_n, Форм. 41$

где:

• q_зад – условное давление на единицу площади поршня при задире; принимается в пределах: q_зад = 1,5-2,0 МПа;
• F_n – площадь поршня.

В качестве расчетного усилия P_расч для шатунных болтов независимо от тактности двигателя принимается большее из усилий – P_з или P_зад. Расчетное напряжение растяжения в шатунном болте равно:

${\sigma }_p = 4 P_{расч}/\left(i {\mathrm{\pi d}}^2\right), Форм. 42$

где:

• i – количество шатунных болтов на одном шатуне;
• d – диаметр болта минимальный.

Считается допустимым напряжение в шатунном болте:

• σ_p = 90 МПа – для углеродистых сталей;
• σ_p = 130 МПа – для легированных сталей.

Поршневое кольцо

Поршневые кольца, особенно 1-е поршневое кольцо, – наиболее нагруженные детали двигателя. При их расчетах на прочность обычно определяют:

• Максимальное напряжение изгиба в рабочем положении кольца в цилиндре двигателя (когда кольцо сжато);
• Максимальное напряжение изгиба при надевании кольца на головку поршня (при растяжении кольца);
• Удельное давление кольца на стенку цилиндра за счет сил упругости в его рабочем положении.

На рис. 4 показано поршневое кольцо в 3-х положениях:

1. В рабочем положении;
2. В свободном состоянии;
3. При надевании на поршень.

В рабочем положении кольцо должно быть сжато от свободного состояния до рабочего размера – диаметра цилиндра D. Длина наружной окружности кольца при этом составляет: L′ = π D, стрела прогиба кольца f′ равна:

$f\prime = e – s, Форм. 43$

где:

• e – зазор в замке в свободном состоянии кольца;
• s = e-f′ – зазор в замке в рабочем состоянии.

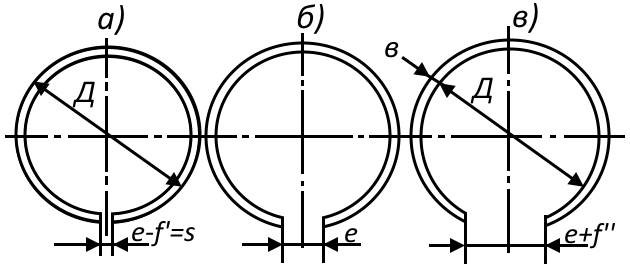
При надевании на поршень кольцо должно быть растянуто так, чтобы его внутренний диаметр был равен наружному диаметру головки D. По сравнению с рабочим положением кольца длина его наружной окружности будет больше и составит: L″ = π (D + 2b), где b – ширина кольца. Если обозначить: f″ – стрела прогиба кольца от свободного состояния до растянутого положения, то разница длин окружности наружного диаметра кольца L″ – L′ даст сумму прогибов при сжатии (f′) и растяжении (f″):

$L″ – L\prime = f\prime + f″ = \mathrm{\pi }\left(\mathrm{D} + 2\mathrm{b}\right) – \mathrm{\pi D}. \mathrm{Форм}. 44$

Откуда:

$f″ = 2\mathrm{\pi b} – \mathrm{f}\prime . \mathrm{Форм}. 45$

С учетом возможности растяжения кольца при надевании на поршень на несколько больший диаметр, чем наружный диаметр головки, для расчета деформации кольца последняя формула принимается с некоторым запасом:

$f″ = 8b – \mathrm{f}\prime . \mathrm{Форм}. 46$

В общем случае уравнение стрелы прогиба кольца как балки определяется равенством:

$f = P L^3/k E J, \mathrm{Форм}. 47$

где:

• P – сила растяжения или сжатия;
• L – длина пролета балки;
• E – модуль упругости материала;
• J – момент инерции расчетного сечения;
• k – коэффициент, учитывающий характер нагрузки и жесткость закрепления концов балки.

Рассматривая поршневое кольцо как одноопорную балку, последнее уравнение может быть преобразовано для расчета напряжений изгиба:

• в рабочем положении кольца:

${\sigma }_{и}^{\prime } = 0,425 E f\prime /b {\left(D/b – 1\right)}^2 Форм. 48$

• при надевании на поршень:

${\sigma }_{и}^{″} = 0,425 E f″/b {\left(D/b – 1\right)}^2 Форм. 49$

Модуль упругости для чугуна может быть принят равным:

• при диаметре цилиндра менее D < 180 мм: E = 10⁵ МПа;
• при диаметрах D > 180 мм: E = 0,825 10⁵ МПа.

Для судовых двигателей допускаемые напряжения изгиба поршневых колец могут быть назначены в зависимости от диаметра цилиндра:

• при D < 175 мм:

  ${\sigma }_{и}^{\prime } = 190 мПа, {\sigma }_{и}^{″} = 220–250 МПа;$

• при 180 < D < 400 мм:

  ${\sigma }_{и}^{\prime } = 160–170 мПа, {\sigma }_{и}^{″} = 175–185 МПа;$

• при D > 410 мм:

  ${\sigma }_{и}^{\prime } = {\sigma }_{и}^{″} = 140–150 МПа.$

Давление поршневого кольца на стенку цилиндра за счет сил упругости P_ц может быть найдено по величине расчетного напряжения изгиба кольца

${\sigma }_{и}^{\prime }$

в рабочем состоянии. После несложных преобразований можно найти:

$P_{ц} = \frac{0,33{\sigma }_{и}^{\prime }·b^2}{D\left(D – b\right)}.$

Эта величина обычно не превышает 0,1 МПа.

Анкерные связи, крепеж цилиндра

Условия работы анкерных связей и крепежа цилиндра (шпилек крепления крышки) подобны. Усилия предварительного затяга этих элементов должны быть такими, чтобы во время работы двигателя, стягиваемые детали (цилиндр, станина, фундаментная рамаУстановка и центровка фундаментной рамы) не разгружались от усилия сжатия. Поэтому все исходные позиции и расчетные формулы, как для анкерных связей, так и для крепежа крышки, идентичны.

Максимальное усилие, возникающее в цилиндре при его работе, определяется давлением сгорания P_z. Для двигателя S70MC при P_z = 15 МПа это усилие составляет около 550 тонн. Оно стремится поднять вверх крышку и блок цилиндра. Усилие на крепеж крышки будет меньше на величину веса крышки, а на анкерные связи – это усилие снизится еще и на величину блока цилиндра в сборе. Однако вес крышки и блока несоизмеримо меньше усилия от давления P_z (для двигателя S70MC вес крышки – 3,84 т, вес втулки – 4,787 т и блока – 0,83 т). Поэтому в качестве исходной величины при расчете анкерных болтов и крепежа цилиндра принимается усилие от давления сгорания P_z.

Усилие предварительного затяга болтов должно быть равно:

$P_d = \lambda P_z \pi D^2/4 i, Форм. 51$

где:

• λ – коэффициент предварительного затяга; принимается в пределах: λ = 1,35-1,80
• i – количество болтов на один цилиндр (при расчете анкерных связей i = 4, при расчете шпилек крышки цилиндра малооборотного двигателя обычно i = 16).

Максимальное усилие P_a, действующее на болты при работе, равно сумме усилия предварительного затяга P_d и усилия от давления сгорания P_z:

$P_a = P_d + P_z \pi D^2/\left(4 i\right). Форм. 52$

Максимальное напряжение растяжения болта определится как:

${\sigma }_a = 4P_a/\left(\pi d_a^2\right). Форм. 53$

Здесь:

• d_a – диаметр анкерного болта или шпильки крепежа крышки.

Допускаемые напряжения для этих деталей могут быть приняты:

• σ_a = 120 МПа – для углеродистых сталей;
• σ_a = 180-200 МПа – для лучших легированных сталей.

Удлинение анкерной связи или шпильки крепления крышки может быть найдено по формуле:

$\delta = \left(4 P_d/{\mathrm{\pi d}}_{\mathrm{a}}^2\right) L_a/E, Форм. 54$

где:

• L_a – длина связи (шпильки);
• E  – модуль упругости стали; может быть принят равным E = (1,5-2,0) 10⁵ МН/м².