Основные законы термодинамики

Законы термодинамики представляют собой фундаментальные принципы, описывающие поведение энергии в системах. Они включают такие базовые положения, как сохранение энергии, второй закон термодинамики (закон энтропии) и третий закон термодинамики (о невозможности достижения абсолютного нуля температуры). Понимание и применение этих законов крайне важно для судомехаников, работающих с судовыми двигателями и системами отопления, так как они обеспечивают основы для эффективной работы и обслуживания этих систем.

Знание законов термодинамики позволяет судомеханикам правильно распределять и управлять энергией внутри судовых систем, обеспечивая оптимальную работу двигателей и поддерживая безопасные температурные режимы. Одним из важных аспектов является уменьшение потерь энергии в виде тепла, что снижает расход топлива и повышает эффективность судовой машины. Кроме того, понимание законов термодинамики позволяет предсказывать и предотвращать возможные поломки и сбои в работе систем, что важно для безопасности судна и его экипажа. Таким образом, знание законов термодинамики является неотъемлемой частью профессиональной подготовки судомехаников и позволяет им эффективно управлять энергетическими процессами на судне.

Первый закон термодинамики

Сущность первого закона термодинамики. Термодинамика как наука, изучающая процессы преобразования различных форм движения материи, опирается на наиболее общий, универсальный закон природы – закон сохранения энергии. Полет самолета, нагревание воды в котле, перемещение электронов по проводникам – различные формы движения материи, но все они количественно измеряются одной величиной – энергией.

Разные формы движения материи часто не совсем точно называют видами энергии:

• механической;
• тепловой;
• электрической энергией.

Раньше для каждого из этих видов энергии была своя единица измерения:

• килограммометр;
• калория;
• ватт-час и т. д..

Системой СИ предусмотрена только одна единица измерения энергии – джоуль. Это возможно лишь потому, что при преобразовании форм движения материи (например, механической в электрическую в генераторе тока) энергия не может исчезать бесследно или создаваться вновь. Неизменность энергии при преобразовании форм движения материи – принцип, называемый законом сохранения энергии или первым началом (законом) термодинамики.

Этот закон не был открыт одним человеком. В древности греческий ученый Архимед в «золотом правиле механики», по существу, коснулся частного случая этого закона. Значительно позже, в эпоху Возрождения, итальянец Леонардо да Винчи это же правило распространил на вращательное движение. Француз Р. Декарт и англичанин Ньютон высказали другие, частные принципы первого закона. М. В. Ломоносов в середине XVIII в. сформулировал первое начало как закон сохранения материи и движения. Количественные соотношения этого закона установили Р. Майнер, Д. Джоуль, X. Ленц, Г. Гельмгольц и С. Карно.

В Теоретические основы теплотехникитепловых машинах происходит преобразование тепловой формы движения материи в механическую форму и наоборот. Обозначим энергию той и другой формы движения соответственно Q и L и согласно первому закону термодинамики получим:

Математически в прежних единицах измерения первый закон выражался более сложным уравнением:

где:

• Q – количество теплоты, ккал Килокалория – тысяча калории; 1 ккал = 4,18 кДжx;
• L – работа, кгс·м;

• A – тепловой эквивалент работы, равный

  $\frac{1}{427}$

  ккал/(кгс·м).

При сгорании одной спички выделяется примерно 1 ккал теплоты. Если бы всю эту теплоту можно было направить в идеальный двигатель, то она могла бы совершить работу, равную 427 кгс·м (поднять семь человек весом по 61 кг на высоту 1 м). Для получения же 1 кгс·м работы потребуется

ккал теплоты; это число и представляет собой тепловой эквивалент работы.

На судах флота до сего времени мощность двигателей часто выражают в лошадиных силах (л. с.). Работа 75 кгс·м, выполненная за 1 с, соответствует одной лошадиной силе. Тепловой эквивалент энергии 1 л. с.·ч = 632 ккал. Единица измерения энергии 1 квт·ч эквивалентна 860 ккал.

Внутренняя энергия. Возьмем два цилиндра. Пусть в каждом из них содержится по 1 кг одного и того же газа при одинаковых начальных температурах, но в первом цилиндре поршень закреплен неподвижно, а во втором он может передвигаться. При нагревании газа во втором цилиндре с закрепленным неподвижно поршнем вся подведенная теплота переходит в энергию хаотического движения молекул газа. Происходит как бы накопление энергии в газе. Эта энергия называется внутренней энергией и измеряется в джоулях на килограмм газа. Она зависит только от температуры и измеряется количеством теплоты, которое нужно подвести к 1 кг газа, чтобы нагреть его от 0 К до данной температуры Т при постоянном объеме. Внутренняя энергия обозначается буквой U и является четвертым параметром состояния газа.

Математическое выражение первого закона термодинамики. При нагревании газа в цилиндре с подвижным поршнем подводимая теплота затрачивается не только на повышение внутренней энергии от U₁ до U₂. Ускоряется беспорядочное движение молекул газа, одновременно растут температуры и давления. Если раньше вес поршня уравновешивался давлением p, то в результате нагревания газа равновесие нарушится. Под действием давления поршень будет перемещаться вверх до тех пор, пока при новом значении объема V₂ давление не возвратится к прежнему значению p. Следовательно, газом будет совершена работа l Дж/кг.

Таким образом, в общем случае не все количество подведенной к газу теплоты q расходуется на увеличение внутренней энергии газа (U₂ – U₁); часть ее затрачивается на совершение работы l:

В прежних единицах измерения первый закон термодинамики записывается так:

Понятие об энтальпии. Если давление газа в цилиндре будет p, то суммарная сила, которая поднимает поршень, составляет pF, где:

• F – площадь поршня.

Работа l, совершаемая газом при перемещении поршня на величину S, будет равна произведению силы pF на путь S:

С другой стороны, произведение FS – есть объем, описываемый при перемещении поршнем; он равен V₂ – V₁.

Следовательно:

Подставив это значение l в уравнение первого закона термодинамики:

перегруппируем:

Величина в скобках (U + pV) называется энтальпией газа, обозначается буквой i и измеряется в Дж/кг или ккал/кг. Таким образом:

Энтальпия, или теплосодержание, является пятым параметром состояния газа. Она численно равна количеству теплоты, затрачиваемой при нагревании 1 кг от 0 К до температуры Т при постоянном давлении. Часть этой теплоты создает внутреннюю энергию газа U, а другая часть используется для совершения механической работы pU расширения при постоянном давлении.

Заменив в уравнении первого Основы термодинамики сжиженных газовзакона термодинамики выражения в скобках через i₂ и i₁, получим:

Это значит, что количество теплоты, затраченной на совершение работы расширения (перемещения поршня) в процессе при постоянном давлении, равно разнице энтальпий.

Численные значения энтальпии могут быть найдены по специальным таблицам или диаграммам.

Работа газа и ее графическое изображение. При расширении, как известно, газ совершает работу. Для определения работы газа удобно пользоваться диаграммой p – v. Она строится в системе координат, в которой по горизонтальной оси откладываются удельные объемы v, а по вертикальной оси – давления p.

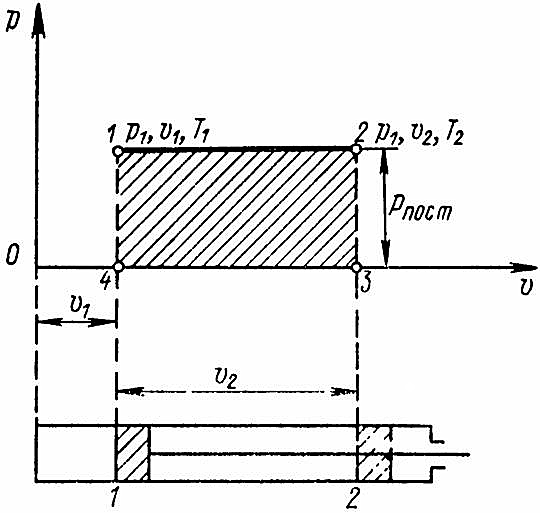
Пусть в начале процесса объем газа равен v₁, а давление p₁. Откладываем на горизонтальной оси отрезок, равный в масштабе v₁, а на вертикальной оси в масштабе отрезок p₁. Из концов отрезков восставляем перпендикуляры. Пересечение этих двух перпендикуляров дает точку 1, которая и будет графически определять состояние газа до подвода теплоты. После нагревания газа его объем увеличится до значения v₂; давление останется по прежнему равным p₁. Состояние газа после нагревания будет характеризоваться точкой 2.

Так как процесс перемещения поршня происходит при постоянном давлении, линия процесса 1-2 пойдет параллельно объемов.

Произведение давления на объем есть работа:

при обозначениях, принятых на рис. 1, p₁ есть высота 1-4; (v₂ – v₁) – основание 3-4, а произведение высоты на основание есть площадь 1-2-3-4-1.

Таким образом, работа l, совершаемая газом в процессе, графически представляет собой площадь, ограниченную линией процесса (1-2), осью объемов и крайними ординатами процесса (1, 4 и 2, 3).

Термодинамические процессы

Основные понятия. Всякое изменение состояния рабочего тела и связанное с этим изменение всех или некоторых параметров его состояния называется термодинамическим процессом, или просто процессом.

Процессы с газами или паром происходят, например, в цилиндрах тепловых двигателей. При воспламенении горючей смеси в цилиндре двигателя внутреннего сгорания смесь имеет более высокие давление и температуру и меньший объем, чем при выходе из цилиндра. Следовательно, при работе в цилиндре двигателя газовая смесь совершает некоторые процессы, в которых изменяются все три основных параметра:

• давление p;
• удельный объем v;
• и температура T.

Подобное же явление наблюдается и при работе паровой машины, только не с газовой смесью, а с паром, который поступает в цилиндр машины с одними параметрами, а выходит из цилиндра с другими параметрами (p, v, Т).

В реальных тепловых двигателях и устройствах (паровой котел, дизель, компрессор, паровая машина) процессы сопровождаются изменением всех параметров состояния. Однако для лучшего понимания явлений целесообразно выделить четыре процесса, каждый из которых соответствует постоянному значению одного параметра:

• изобарный (p = const);
• изохорный (v = const);
• изотермический (T = const);
• адиабатный (без теплообмена).

Эти процессы представляют собой частные случаи так называемых политропных процессов. Исследуют эти процессы, основываясь на первом законе термодинамики:

и уравнении состояния газа:

Графически процессы изображаются в координатах p-v.

Изобарный процесс. Изобарный процесс происходит при постоянном давлении газа: (p = const). Переменными параметрами здесь являются объем и температура.

При нагревании газа, начальные параметры которого составляют p₁, v₁, T₁ (см. рис. 1), поршень переместится из положения 1 в положение 2 и конечное состояние газа выразится параметрами p₁, v₂, T₂. Так как давление газа в течение процесса не меняется, в диаграмме p-v этот процесс изобразится горизонтальной прямой 1-2, которая называется изобарой.

Напишем уравнения состояния газов:

• конечного состояния p₁v₂ = RT₂;
• и начального состояния p₁v₁ = RT₁.

Разделив первое уравнение на второе, получим:

Таким образом, в изобарном процессе объем газа изменяется пропорционально изменению абсолютной температуры.

Рассмотрим теперь, на что расходуется подводимая теплота q при изобарном процессе. Для этого напишем уравнение первого закона термодинамики в общем виде:

При совершении процесса изменяется температура газа (от T₁ до T₂); следовательно, будет изменяться и внутренняя энергия U. Значит, часть теплоты в изобарном процессе пойдет на приращение внутренней энергии U₂ – U₁. А так как во время процесса будет перемещаться поршень, то остальная часть теплоты пойдет на совершение механической работы l по перемещению поршня.

Работа l, совершаемая газом в процессе 1-2, изображается в координатах p-v в некотором масштабе площадью прямоугольника
1-2-3-4.

Изохорный процесс. Изохорный процесс происходит в замкнутом пространстве при постоянном объеме: V = const. Он может совершаться при нагревании или охлаждении газа в баллоне. В тепловых машинах Топлива, масла и другие рабочие среды судовых энергетических установокпроцессы сгорания топлива в некоторых случаях могут быть близкими к изохорным.

Особенностью изохорного процесса является то, что газ при изменении своего состояния не совершает работы.

Обозначим на диаграмме p-v (рис. 2) начальное состояние газа точкой l, определяемой параметрами p₁, v₁ и T₁.

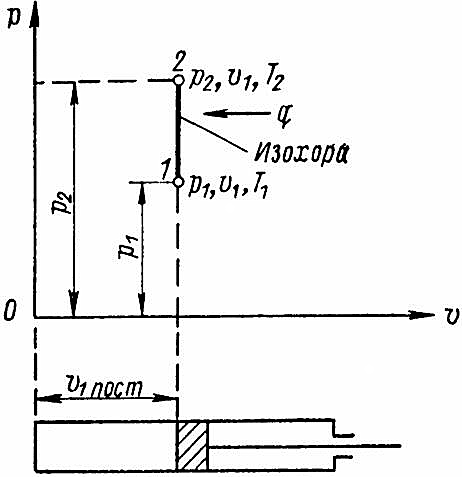
Если подведем к цилиндру при неподвижном поршне определенное количество теплоты q, то температура газа и его давление повысятся до T₂ и p₂, причем линия процесса выразится прямой 1-2, параллельной оси давления. Эта прямая называется изохорой.

Запишем уравнение состояния газа для точек 1 и 2:

Поделив эти уравнения почленно, получим:

Следовательно, в изохорном процессе давление газа изменяется пропорционально его абсолютной температуре, т. е. при нагревании газа происходит повышение давления, а при охлаждении – понижение.

Общее количество теплоты, участвующей в процессе, определим из основного закона термодинамики:

Но так как в изохорном процессе механическая работа не совершается, т. е.:

• l = 0;
• то q = U₂ – U₁.

Следовательно, вся участвующая в изохорном процессе теплота идет на изменение внутренней энергии газа, в результате чего изменяются его температура и давление.

Изотермический процесс. Изотермический процесс происходит при постоянной температуре: T = const. Переменными величинами здесь являются объем газа и его давление, поэтому в изотермическом процессе всегда имеем дело с расширением или сжатием газа.

При сжатии температура газа стремится повыситься, поэтому чтобы достигнуть изотермического сжатия, от газа необходимо отводить теплоту. При расширении, наоборот, температура газа стремится понизиться; следовательно, чтобы расширение было изотермическим, к газу нужно подводить теплоту.

На рис. 3 показаны схемы охлаждаемого цилиндра и графическое изображение изотермического процесса сжатия 1-2 в диаграмме р-v. В начале процесса (точка 1) газ характеризуется параметрами p₁, v₁ и T₁, после окончания сжатия (точка 2) давление увеличивается до p₂, объем уменьшается до v₂, а температура остается прежней T₁.

Напишем уравнение состояния газа для точек 1 и 2:

Следовательно:

Так как произведение давления (ордината p) на объем (абсцисса v) в изотермическом процессе есть величина постоянная, то линия процесса 1-2, именуемая изотермой, представляет собой кривую, называемую равнобочной гиперболой.

Чтобы определить, куда расходуется теплота, участвующая в процессе, воспользуемся уравнением первого закона термодинамики:

Так как в изотермическом процессе температура газа не меняется, то, следовательно, и внутренняя энергия его остается постоянной, т. е. U₂ = U₁.

Отсюда следует:

а поэтому уравнение первого закона термодинамики примет вид:

Из этого уравнения видно, что в изотермическом процессе сжатия работа сжатия l полностью переходит в теплоту q. Эта теплота q для сохранения постоянной температуры газа должна отводиться охлаждающей средой, которая омывает стенки цилиндра. И наоборот, подведенная при изотермическом процессе теплота может полностью быть использована для совершения работы расширения. Значит, изотермический процесс очень выгоден для тепловой машины. К сожалению, в реальных условиях он неосуществим. Работа изотермического сжатия графически в диаграмме р-v изобразится площадью 1-2-3-4-1.

Адиабатный процесс. Адиабатный процесс — это такое изменение состояния газа, при котором к нему не подводится и от него не отводится теплота: q = 0. Иначе говоря, при адиабатном процессе расширение или сжатие газа происходит таким образом, что между газом и внешней окружающей средой нет теплообмена. Этого можно было бы добиться при идеальной изоляции стенок цилиндра теплового двигателя материалами, абсолютно не проводящими теплоту.

В действительности между стенками цилиндра и рабочим газом всегда существует некоторый теплообмен, поэтому чисто адиабатные процессы неосуществимы. Однако при расчетах тепловых машин этот процесс имеет большое значение, так как быстро протекающие процессы могут приближаться к адиабатным.

Если на диаграмме р-v (рис. 4) начальное состояние газа отметить точкой 1, то конечное состояние после адиабатного расширения можно представить точкой 2. Линия процесса 1-2 называется адиабатой. Адиабата по виду похожа на изотерму, но проходит более круто.

При адиабатном процессе все параметры газа p, v и T являются переменными величинами, зависящими одна от другой. Эта зависимость определяется уравнением адиабаты, которое выводится из нее и имеет вид:

Здесь показатель степени k есть отношение массовых теплоемкостей c_p/c_v.

При адиабатном процессе произведение давления на соответствующий объем в степени k есть величина постоянная, т. е.:

или

Последним уравнением пользуются при графическом построении адиабаты.

В связи с тем что в адиабатном процессе внешняя теплота не участвует, возникает вопрос, за счет чего же в этом процессе совершается работа при расширении газа? Для выяснения этого воспользуемся уравнением первого закона термодинамики:

Так как в адиабатном процессе q = 0, то:

откуда:

или:

Следовательно, работа в адиабатном процессе расширения совершается за счет внутренней энергии газа, т. е. теплоты, содержащейся в газе. При этом внутренняя энергия, которая в начале процесса была больше (U₁ > U₂), уменьшается. Графически в диаграмме р-v работа расширения изображается площадью 1-2-3-4-1.

Политропные процессы. Реальные процессы сжатия и расширения в тепловых двигателях близки к политропным.

В политропном процессе взаимосвязь давления с удельным объемом выражается следующим уравнением:

где:

• n – показатель политропы, зависящий от условий протекания процесса;

он может иметь любое численное значение.

Например, если n = 0, то pv⁰ = const, а так как v⁰ = 1, то p = const.

Следовательно, данный процесс протекает при постоянном давлении и является изобарным.

Если n = 1, то уравнение примет вид pv = const, т. е. превратится в уравнение изотермического процесса.

При n = k уравнение политропы превращается в уравнение адиабатного процесса pv^k = const.

Можно показать, что при n = ∞ уравнение политропы обращается в уравнение изохорного процесса. Для этого нужно лишь предварительно из обеих частей уравнения pvⁿ = const извлечь корень степени n:

Подставив затем в это равенство n = ∞, получим v = const.

Из сказанного следует, что ранее рассмотренные процессы:

• изобарный;
• изохорный;
• изотермический;
• и адиабатный;

являются частными случаями политропного процесса.

Взаимное расположение изобары, изохоры, изотермы, адиабаты, проходящих через одну общую точку А в осях р-v, показано на рис. 5.

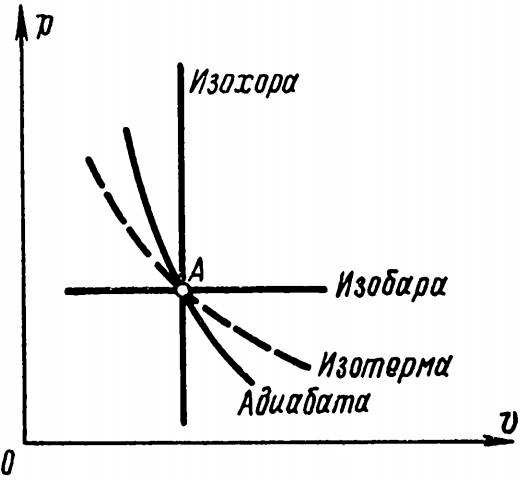
Через эту точку можно провести еще бесконечное количество других линий, подчиняющихся одному общему для всех них уравнению:

Все такие линии называются политропами.

Второй закон термодинамики

Сущность второго закона термодинамики. Первый закон термодинамики выражает всеобщий закон сохранения энергии при преобразовании форм движения материи, но не оговаривает условий таких преобразований. Опыт показал, что между двумя формами передачи энергии – теплотой и работой – имеется существенная разница. Преобразование упорядоченного движения тела в неупорядоченное движение частиц самого тела может происходить без каких-либо дополнительных процессов. Например, резец на токарном станке за счет большей части подаваемой к нему механической энергии производит работу снятия стружки; при этом работа трения резца о металл превращается в теплоту. Кроме того, при трении в подшипниках в передаточных механизмах некоторое количество механической энергии, передаваемое станком, тоже превращается в теплоту.

Превращение работы в теплоту происходит везде, где имеется трение:

• при трении в подшипниках гребного вала;
• трении гребного вала в воде;
• трении при движении жидкостей паров и газов в трубопроводах и т. д.

Обратное преобразование неупорядоченного движения частиц тела в упорядоченное (превращение теплоты в работу) обязательно должно сопровождаться дополнительным процессом. Например, в любом действующем двигателе внутреннего сгорания нельзя превратить в механическую энергию всю теплоту, полученную от сгорания топлива в цилиндрах. Обязательным условием работы двигателя является осуществление дополнительного процесса – передача части теплоты окружающей среде с отработавшими газами и с водой, которая охлаждает двигатель.

Итак, основные положения второго закона термодинамики сводятся к следующему:

1. в непрерывно действующем двигателе теплота не может быть полностью превращена в работу;
2. в то же время любая энергия, затраченная на производство работы, может сполна перейти в равновеликое количество теплоты;
3. переход теплоты от нагретого тела к холодному осуществляется при всех условиях самопроизвольно, тогда как обратный процесс – переход теплоты от холодного тела к горячему – самопроизвольно осуществляться не может;
4. для работы теплового двигателя необходимы по крайней мере два источника теплоты – горячий и холодный, имеющие разные температуры.

В этом и кроется причина, по которой нельзя перевести в работу тепловую энергию окружающего нас атмосферного воздуха или воды морей и океанов: отсутствует второй источник теплоты с более низкой температурой.

Таким образом, второй закон термодинамики раскрывает условия, необходимые для превращения теплоты в работу.

Второй закон термодинамики является очень важным дополнением к первому закону. Первый закон говорит о том, что для получения работы необходимо затратить теплоту и что нельзя получить работу из ничего, т. е. нельзя построить вечный двигатель первого рода. Второй закон термодинамики говорит о невозможности создания вечного двигателя второго рода, т. е. о том, что нельзя построить двигатель, в котором вся теплота, подведенная к рабочему телу, превращалась бы в работу.

Прикладное значение второго закона термодинамики проявляется, в частности, при анализе термодинамических циклов.

Круговые процессы (циклы). В тепловых двигателях превращение теплоты в работу происходит с помощью рабочего тела, которое воспринимает теплоту от внешних источников и расширяется, совершая полезную работу. Для работы тепловой машины требуется постоянное повторение процесса расширения, т. е. рабочее тело после расширения удаляется и заменяется новым, в таком же количестве и в том же составе, или возвращается в первоначальное состояние.

Определенная совокупность термодинамических процессов, в результате которых рабочее тело возвращается в начальное состояние, а величины, характеризующие это состояние (p v, T и др.), принимают прежние значения, называется круговым процессом, или циклом.

Циклы бывают прямые и обратные. В том и в другом циклах осуществляются подвод и отвод теплоты, но в прямом цикле это сопровождается получением работы, а в обратном – ее затратой.

В различных системах координат циклы изображаются замкнутыми линиями. В прямом цикле, показанном на рис. 6, процесс расширения изображается линией АmВ, а в процессе сжатия – линией ВnА, расположенной ниже линии расширения. Прямой цикл, изображенный в системах координат, протекает по часовой стрелке.

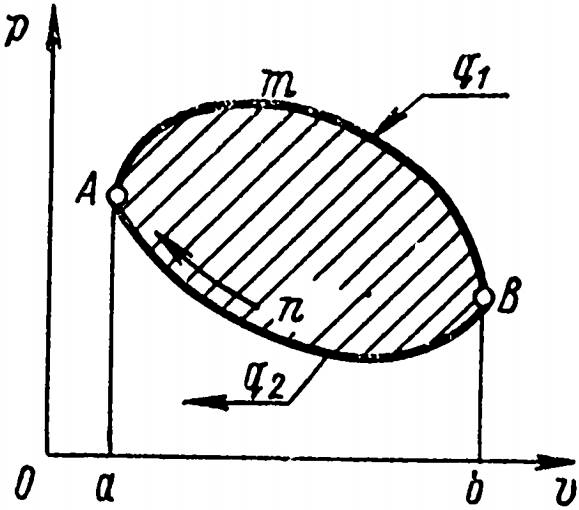
Работа сжатия, осуществляемая внешними силами, изображается площадью аАnВbа. Работа расширения, совершаемая за счет подвода теплоты, изображается площадью aАmВba.

За каждый цикл работа расширения, получающаяся в результате подвода теплоты q₁, расходуется на компенсацию работы сжатия, производимой внешними силами, а избыток механической работы, который изображен заштрихованной площадью, ограниченной линией цикла АmВnА, может быть использован для приведения в действие гребных винтов, электрогенераторов и т. д.

Таким образом, в прямом цикле в процессе расширения подводится теплота, в результате чего совершается внешняя работа, эквивалентная площади АmВnА.

По прямому циклу работают тепловые двигатели – паровые машины и турбины, двигатели внутреннего сгорания и газовые турбины.

Обратными называются циклы, на осуществление которых расходуется работа. Обратный цикл изображен на рис. 7.

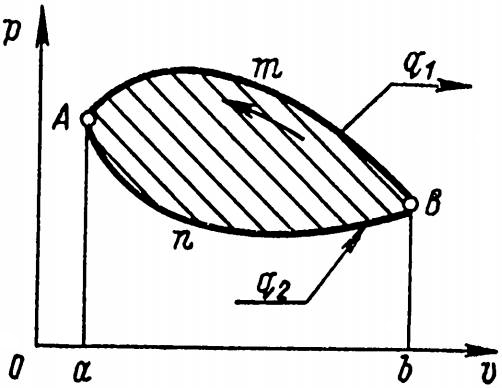
Линия сжатия BmA у обратного цикла проходит выше линии расширения AnB. Обратный цикл протекает против хода часовой стрелки. Работа сжатия в обратном цикле, т. е. работа внешних сил, обозначенная площадью BmАаbB, больше работы расширения (площадь АnВbaA). Поэтому для совершения такого цикла необходима затрата внешней работы, измеряемая заштрихованной площадью, ограниченной линией цикла BmAnB. По обратному циклу работают холодильные машины, отбирающие теплоту от холодного тела и передающие ее горячему, на что и затрачивается внешняя работа.

Прямой цикл сопровождается подводом теплоты. Степень использования теплоты, т. е. выгодность цикла, оценивается термическим коэффициентом полезного действия (КПД), который обозначается буквой η с индексом t.

Если в прямом цикле q₁ – теплота, подведенная во время процесса расширения, a q₂ – теплота, которая отводится во время сжатия, то q₁-q₂ – полезная теплота, превращенная в работу.

Отношение же полезной теплоты ко всей подведенной теплоте и есть термический КПД:

или:

Он показывает, какая часть теплоты в цикле превращается в работу.

Цикл Карно. Из формулы 2 видно, что η_t тем больше, чем при данном q₁ меньше q₂, т. е. чем меньше теплоты отводится. В пределе η_t равно единице, когда q₂ = 0, т. е. когда нисколько теплоты не отводится, а вся она превращается в работу. Однако же, как было выяснено из второго закона термодинамики, в тепловом двигателе вся теплота не может быть превращена в работу, а поэтому не может равняться нулю.

Следовательно, η_t никогда не может достигнуть единицы.

В связи с этим возникает вопрос, по какому циклу должен работать тепловой двигатель, чтобы иметь наивысший возможный η_t. Ответ на этот вопрос дал в 1824 г. французский инженер и ученый Сади Карно. Он предложил цикл, названный его именем.

Цикл Карно – идеальный, практически неосуществимый, так как для реализации этого цикла необходима тепловая машина с идеальной теплоизоляцией; кроме того, рабочее тело должно периодически сообщаться с теплоприемником и теплоотдатчиком.

Цикл Карно, как и любой другой, может быть прямым и обратным.

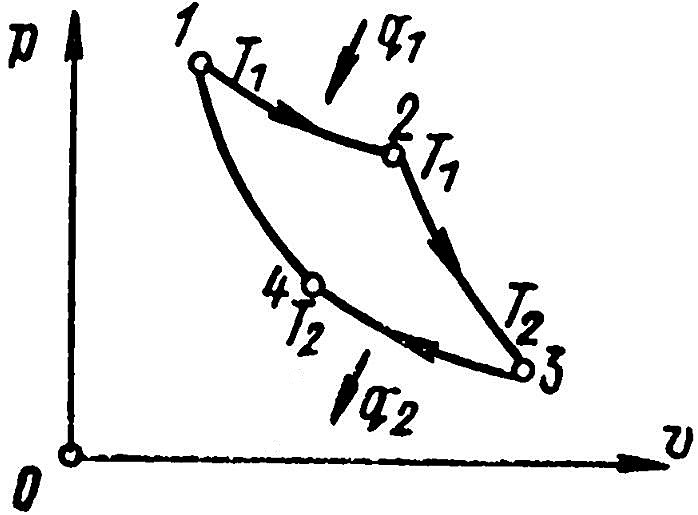
Прямой цикл Карно в графическом изображении (рис. 8) состоит из двух адиабат и протекает в такой последовательности:

• изотермическое расширение 1-2 с подводом теплоты от горячего источника;
• адиабатное расширение 2-3, при котором температура газа понижается от T₁ до T₂;
• изотермическое сжатие 3-4 с отводом теплоты;
• адиабатное сжатие 4-1, при котором температура газа повышается от T₂ до T₁.

Наивысшая температура рабочего тела в цикле принимается T₁ низшая температура T₂.

Термический КПД цикла Карно определяется по формуле, аналогичной выражению термического КПД произвольного цикла:

Из этой формулы следует, что термический КПД наивыгоднейшего из всех возможных циклов – цикла Карно – не может быть равен единице. Это могло бы быть при T₂ = 0 (t₂ = -273 °С) или T₁ = ∞, что практически невозможно.

Прямой цикл Карно имеет для теплотехники огромное значение, так как позволяет определять максимально возможный при данных температурах термический КПД теплового двигателя.

Например, если действительный двигатель внутреннего сгорания имеет высшую температуру в цикле – температуру сгорания рабочей смеси 1 800 °С и низшую – температуру свежей рабочей смеси, поступающей в цилиндр, 50 °С, то его термический КПД не превышает 50 %. Если бы этот двигатель внутреннего сгорания при данных температурах работал по циклу Карно, то максимально возможный термический КПД его был бы равен:

Обратный цикл Карно протекает против хода часовой стрелки. В обратном цикле Карно в результате затраты внешней работы теплота от более холодного тела передается более нагретому. Обратный цикл Карно является идеальным циклом холодильных установок.

Эффективность работы холодильной установки оценивают холодильным коэффициентом, который обозначается буквой ε. Холодильный коэффициент представляет собой отношение теплоты, отобранной от более холодного тела, к теплоте, эквивалентной работе, затраченной на осуществление цикла.

Например, если в обратном цикле Карно от холодного тела отбирается и передается более нагретому телу 1 400 кДж теплоты, а на создание работы по отбору теплоты расходуется 1 000 кДж, то:

Практически холодильный коэффициент цикла Карно определяется по формуле:

где:

• T₁ – температура нагретого тела;
• T₂ – температура холодного тела.

Значение обратного цикла Карно для теплотехники тоже велико, так как позволяет определить максимально возможный для данного диапазона температур холодильный коэффициент. Например, если реальная холодильная установка охлаждает какое-то тело до t₂ = -30 °С и имеет наивысшую температуру рабочего цикла t₁ = +27 °С, то рабочий холодильный коэффициент этой установки составляет 3,2. Если бы эта холодильная установка работала по обратному циклу Карно, то при данном диапазоне температур максимально возможный холодильный коэффициент был бы:

Следовательно, степень совершенства современной холодильной установки составляет:

Понятие об энтропии. Диаграмма Т-S. Цикл Карно является частным случаем общего термодинамического цикла, следовательно, для него можно записать:

или

Отсюда имеем:

Как видим, величина q₂, которая представляет собой теплоту, уходящую в окружающую среду, зависит от двух сомножителей:

• отношения q₁/T₁;
• и температуры T₂.

Если эту температуру считать постоянной величиной, то потеря теплоты q₂ практически зависит только от отношения q₁/T₁. Чем больше это отношение, тем больше потеря q₂.

Учитывая большую роль отношения q/T, ему дали специальное название в термодинамике – энтропия.

Энтропия является параметром состояния и измеряется в тех же единицах, что и массовая теплоемкость, т. е. в кДж/ (кг·К) или ккал/(кг·°C). Обозначают энтропию буквой S:

Таким образом, в термодинамике используются:

• три основных параметра: p, v и T (давление, удельный объем и температура);
• и три дополнительных: U, i и S (внутренняя энергия, энтальпия и энтропия).

В цикле Карно энтропия не изменяется:

Неизменна энтропия и при адиабатном процессе. Однако в реальных циклах и процессах постоянства энтропии не наблюдается.

Чтобы понять физический смысл энтропии, рассмотрим такой пример. Двигатель внутреннего сгорания вращает гребной винт судна. Часть тепловой энергии отдается забортной воде, часть тратится на совершение работы. Полученная работа в конечном итоге расходуется на трение частиц воды, возмущенной гребным винтом, т. е. опять-таки превращается в тепловую энергию, которая поступает в окружающую среду. Эта тепловая энергия уже не может быть превращена в работу, она теряется в окружающей среде бесполезно; в этом случае говорят, что энергия рассеивается. Мерой рассеивания энергии и служит энтропия.

Если учесть, что температура забортной воды T₂ меньше, чем температура газов T в цилиндре двигателя, то получается, что в результате передачи теплоты Q энтропия увеличивается:

.

Так как энтропия является параметром состояния, то ее можно использовать как одну из координат для графического изображения процессов. Наглядной и удобной для расчетов является система координат, в которой по оси абсцисс откладывается энтропия, а по оси ординат – абсолютная температура. Если в такой системе координат нанести линии процессов, получится диаграмма T-S.

Рассмотрим, как будут изображаться в этой диаграмме различные процессы.

Изотермический процесс, как протекающий при постоянной температуре, имеет вид прямой линии 1-2 (рис. 9), параллельной оси абсцисс.

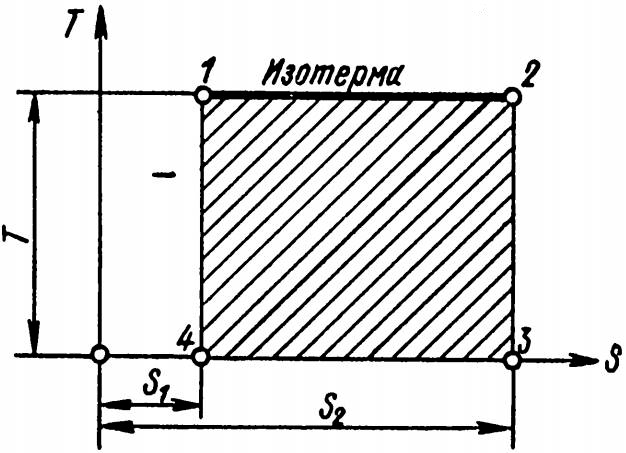
При расширении к рабочему телу подводится теплота, в результате чего энтропия увеличивается от S₁ до S₂.

Произведение энтропии на абсолютную температуру дает количество теплоты, участвующей в процессе. В данном процессе энтропия составляет S₁-S₂, следовательно:

Графически S₁-S₂ представляет собой основание, а T – высоту; произведение этих двух сомножителей дает площадь. Таким образом, в диаграмме T-S площадь, ограниченная линией процесса, ее крайними ординатами и осью абсцисс, определяет количество теплоты, участвующей в процессе.

Напомним, что в диаграмме p-v аналогичная площадь изображает работу.

Адиабатный процесс, как известно, протекает без теплообмена, следовательно, q = 0, a S = const; температура изменяется. Это значит, что адиабата должна идти параллельно оси ординат (рис. 10).

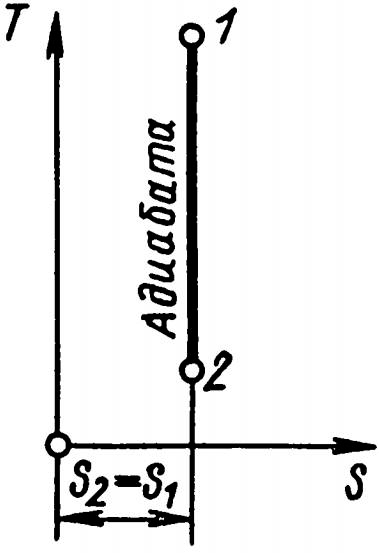
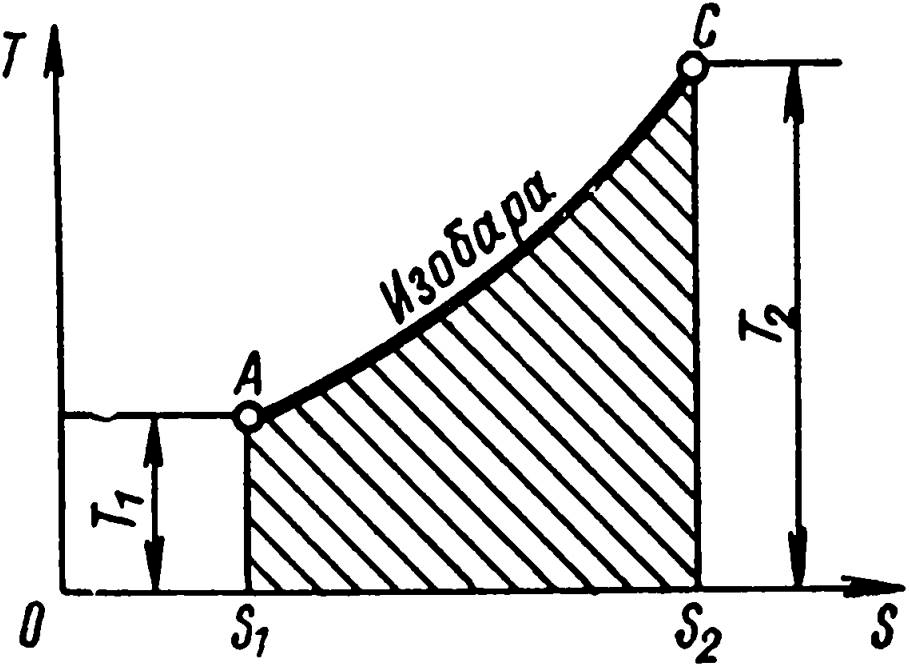
Изохорный (рис. 11) и изобарный (рис. 12) процессы изображаются кривыми АВ и АС, причем изохора идет круче изобары.

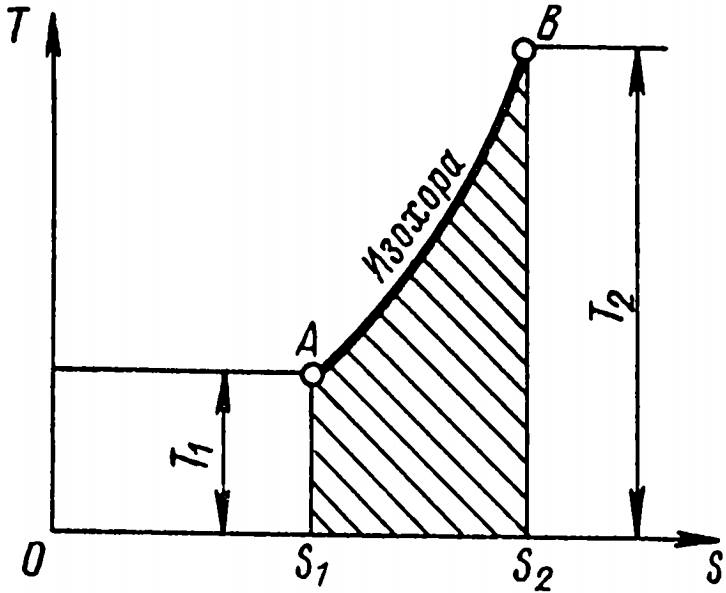
Заштрихованные площади представляют собой количество теплоты, участвующей в процессах.

Рассмотрим, как выглядит цикл Карно в диаграмме T-S (рис. 13).

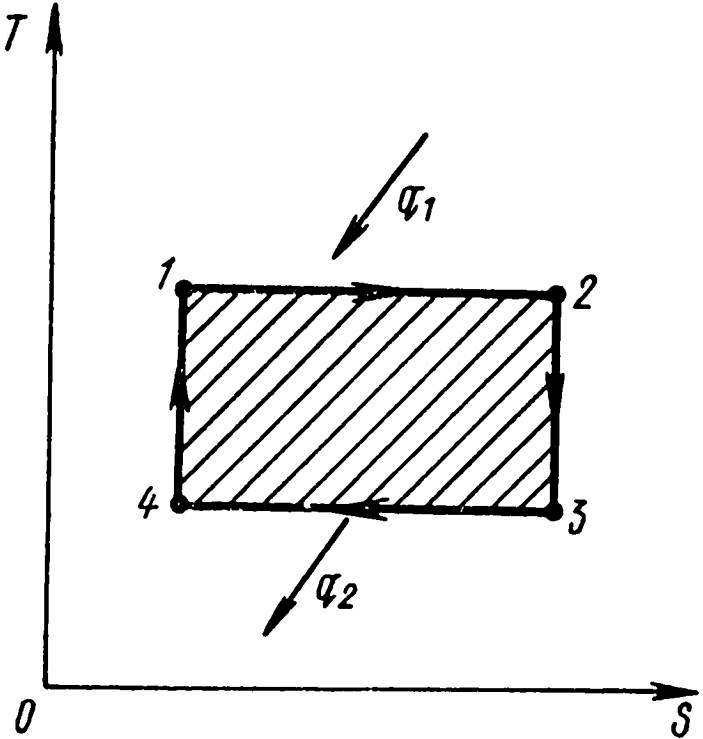
Изотермическое расширение 1-2 изображается прямой, параллельной оси абсцисс; поскольку к рабочему телу подводится теплота, энтропия его увеличивается (процесс направлен вправо от точки 1). При адиабатном расширении температура тела снижается, а так как адиабата в диаграмме T-S изображается вертикально, то процесс от точки 2 направлен по ординате вниз (2-3). Изотермическое сжатие сопровождается отводом теплоты q₂, энтропия при этом уменьшается. Следовательно, процесс сжатия представляет собой отрезок горизонтальной прямой 3-4. Адиабатное сжатие имеет вид прямой 4-1. Площадь диаграммы 1-2-3-4 в масштабе соответствует количеству теплоты, превращенной в работу.

Автор статьи

Виктор Свиридов

Судовой механик

Список литературы

1. Абдульманов X. А. Холодильная техника на судах рыбной промышленности. М., «Пищевая промышленность», 1970.
2. Акимов П. П. Силовые установки морских судов. М., «Транспорт», 1965.
3. Алексеев Г. Д., Карпович В. А. Энергетические установки промысловых судов. Л., «Судостроение», 1972.
4. Аристов Ю. К. Судовые вспомогательные механизмы. М., «Речной транспорт», 1959.
5. Богомольный А. Е. Судовые вспомогательные и рыбопромысловые механизмы. Л., «Судостроение», 1971.
6. Грузберг Я. Ю. Судовые паровые котлы. Л., «Судостроение», 1964,
7. Караев А. А. Энергетика судов будущего. Л., «Судостроение», 1967.
8. Карамушко Ф. Д. и др. Судовые вспомогательные механизмы и системы. М., «Транспорт», 1968.
9. Колесников О. Г. Судовые вспомогательные и холодильные установки. М., «Транспорт», 1967.
10. Конфедератов И. Я. Основы энергетики. М., «Просвещение», 1967.
11. Коршунов Л. П. Силовые установки рыбопромысловых судов. М., «Пищевая промышленность», 1967.
12. Кузовлев В. А. Техническая термодинамика. М., «Транспорт», 1964.
13. Петренко Л. Д. и др. Судовые энергетические установки, вспомогательные и рыбопромысловые механизмы. Л., «Судостроение», 1971.
14. Соловьев Е. М. Пособие мотористу рыбопромыслового судна. М., «Пищевая промышленность», 1966.
15. Соловьев Е. М. Пособие мотористу крупнотоннажного судна рыбопромыслового флота. М., «Пищевая промышленность», 1971.
16. Туркин А. А. Вспомогательные механизмы и технологические холодильные установки промысловых судов. Л., «Судостроение», 1966.