Крен судна при поперечном перемещении груза

Рассмотрим перемещение на судне груза весом ρ в поперечно – горизонтальном направлении к правому борту на расстояние l_у. Такое перемещение груза вызовет крен и смещение Ц.Т. судна в направлении, параллельном линии перемещения груза ρ. Начальная поперечная остойчивость при этом не изменится, т. к. аппликаты Ц.В. и Ц.Т., а также метацентрический радиус и метацентрическая высота не получат никакого приращения. Сила тяжести судна, приложенная в новом Ц.Т., и сила поддержания, приложенная в новом Ц.В., будут действовать по одной вертикали, перпендикулярно новой ватерлинии В₁Л₁.

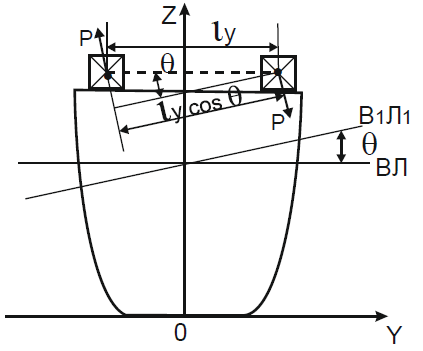
Судно при этом принимает новое положение равновесия, накренившись на угол крена. Из рисунка следует, что момент, который появляется в результате перемещения груза поперек судна, можно определить из выражения:

$Мкр = Р·ly·\cos \theta$

Восстанавливающий момент можно определить по метацентрической формуле остойчивости. Судно находится в равновесии под действием измененной системы сил, поэтому моменты М_кр и Мθ также равны:

$Р·lу·\cos \theta = D\prime ·h·\sin \theta$

Решая это уравнение относительно θ, получим формулу для определения угла крена при поперечном перемещении груза:

$tg\Theta = Р·lyD\prime ·h$

Поскольку угол крена мал, последнее выражение можно записать в виде:

$\Theta = Р·lyD\prime ·h$

Приведенной формулой пользуются в тех случаях, когда углы крена не превышают 10-15 град.

Изменение остойчивости судна при перемещении груза по вертикали

Допустим, что на судне, сидящем на ровном киле и находящемся в равновесии, перемещен по вертикали груз весом Р на расстояние l_z. Поскольку водоизмещение судна от перемещения груза не меняется, первое условие равновесия будет соблюдено (судно сохранит свою осадку). Согласно известной теореме теоретической механики, Ц.Т. судна переместится в точку G₁, находящуюся на одной вертикали с прежним положением Ц.Т. судна G. Сама вертикаль пройдет, как и прежде, через Ц.В. судна C. Тем самым будет соблюдено второе условие равновесия, следовательно, при вертикальном перемещении груза судно не изменит своего положения равновесия (не появится ни крена ни дифферента).

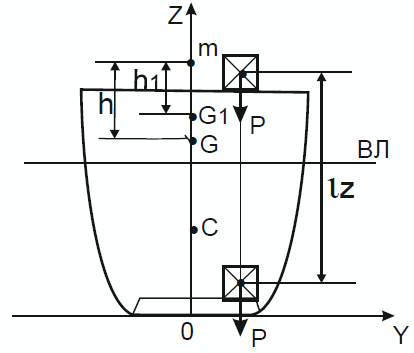
Рассмотрим теперь изменение начальной поперечной остойчивости. Ввиду того, что форма погруженного в воду корпуса судна и форма площади ватерлинии не изменились, положение Ц.В. и поперечного метацентра (т. m) при перемещении груза по вертикали остается неизменным. Перемещается только Ц.Т. судна из точки G в точку G₁. Отрезок GG₁ может быть найден с помощью выражения:

$GG1 = Р·lzD$

Если до перемещения груза поперечная метацентрическая высота была h, то после его перемещения она изменится на величину GG₁. В нашем случае изменение поперечной метацентрической высоты Δh = GG₁ имеет отрицательный знак, т. к. перемещение Ц.Т. судна по направлению к поперечному метацентру, положение которого, как мы установили, остается неизменным, уменьшает метацентрическую высоту. Следовательно, новое значение поперечной метацентрической высоты будет:

$h1 = h–Р·lzD Форм. 1$

Очевидно, что в случае перемещения груза вниз перед вторым членом правой части уравнения новой метацентрической высоты h₁, должен быть поставлен знак плюс (+).

Предлагается к прочтению: Метацентрическая формула начальной поперечной остойчивости

Из выражения (Формула 1) следует, что уменьшение остойчивости судна пропорционально произведению массы груза на его перемещение по высоте. Кроме того, при прочих равных условиях, изменение поперечной остойчивости будет относительно меньше у судна с большим водоизмещением, чем у судна с малым D. Поэтому на больших судах перемещение относительно больших грузов безопаснее, чем на малых судах.

Может оказаться, что значение GG₁ перемещения вверх Ц.Т. судна будет больше самой величины h. Тогда начальная поперечная остойчивость станет отрицательной, т. е. судно не сможет оставаться в прямом положении.

Изменение остойчивости судна от приема или снятия (расходования) грузов

В общем случае, при приеме или снятии груза, происходит изменение средней осадки судна, вследствие изменения водоизмещения, появление крена и дифферента, из-за смещения линии действия силы веса, относительно линии действия силы плавучести, и изменение остойчивости, в результате изменения положения Ц.Т. и Ц.В.

Задачу о влиянии на посадку и остойчивость судна приема некоторого груза весом P в любую точку А с координатами Xp, Yp, Zp можно разделить на две более простые задачи.

В первой из них рассматривают влияние на посадку и остойчивость приема груза весом P, если Ц.Т. принимаемого груза находится в ДП и на одной вертикали с центром тяжести площади действующей ватерлинии.

Во второй задаче рассматривают изменение посадки судна при переносе этого же груза по горизонтали. Такой перенос, как было показано раньше, не отражается на начальной остойчивости, поэтому ниже рассматривается только первая задача.

На палубу судна принят груз весом P, Ц.Т. которого расположен в ДП на расстоянии zр от основной плоскости. До приема груза судно имело водоизмещение D₀ и осадку Т.

После приема груза водоизмещение судна стало

$D_1 = D + Р, а осадка {Т}_1 = Т + \Delta Т.$

При приеме груза меняют положение все три точки, характеризующие поперечную остойчивость; центр величины – из-за изменения осадки судна, а, следовательно, и формы погруженного в воду объема корпуса судна; центр тяжести – вследствие изменения нагрузки судна, а поперечный метацентр – вследствие изменения формы площади ватерлинии и объема, погруженной в воду части корпуса судна.

Читайте также: Поперечная остойчивость судна

Метацентрическая высота, характеризующая остойчивость судна, вследствие всех названных причин, получит следующее изменение:

$∆h = PD+P(T+∆T2h–Zp)$

Новое значение поперечной метацентрической высоты после приема или снятия (расходования) груза будет:

$h1 = h+∆h = h+\pm PD\pm P(T\pm ∆T2–h–Zp)$

Здесь знак плюс соответствует приему груза, знак минус – его снятию (расходованию).