Определение продольного крутящего момента, как и поперечного, подразумевает выполнение расчетов, а также заполнение технической карты. Если расчеты выполнены неверное, и карта заполнена ошибочными данными – это может привести печальным последствиям.
- Общая характеристика скручивания корпуса дока
- Определение продольного крутящего момента от несимметричной загрузки дока
- Определение поперечного крутящего момента от несимметричной загрузки дока
- Определение продольного крутящего момента при статической постановке на «косую волну»
- Учет динамических факторов
- Определение поперечного крутящего момента при статической постановке на «косую волну»
- Определение напряжений при продольном скручивании
- Дифференциальные зависимости стесненного кручения
- Общий порядок расчета
- Вычисление геометрических характеристик, необходимых для определения σω
- Определение геометрических характеристик, необходимых для определения τк, τω
- Вычисление напряжений
Общая характеристика скручивания корпуса дока
Наличие дополнительных нормальных напряжений от скручивания у транспортных доков, корпуса которых проектируют максимально облегченными, может привести к нарушению условий прочности. Важное значение приобретает расчет прочности на скручивание для ремонтных доков при перегоне морем.
Читайте также: Расчет общей поперечной прочности сухого дока
Скручивание относительно продольной оси дока (в дальнейшем будем называть его «продольным») вызывает взаимный поворот и депланацию поперечных сечений. Скручивание относительно поперечной оси («поперечное скручивание») вызывает аналогичные взаимные деформации продольных сечений дока.
Определение продольного крутящего момента от несимметричной загрузки дока
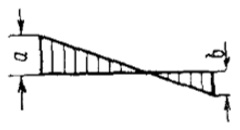
При одновременном (несимметричном) доковании двух или нескольких судов в корпусе дока возникает скручивающий момент. Соответствующей балластировкой док всегда может быть выровнен на ровный киль. В этом случае продольный крутящий момент в каком-либо сечении дока определяется как алгебраическая сумма кренящих моментов, приложенных с одной стороны рассматриваемого сечения. Эпюра крутящих моментов может быть определена как интегральная кривая от кривой распределенных по длине кренящих моментов (рис. 1).
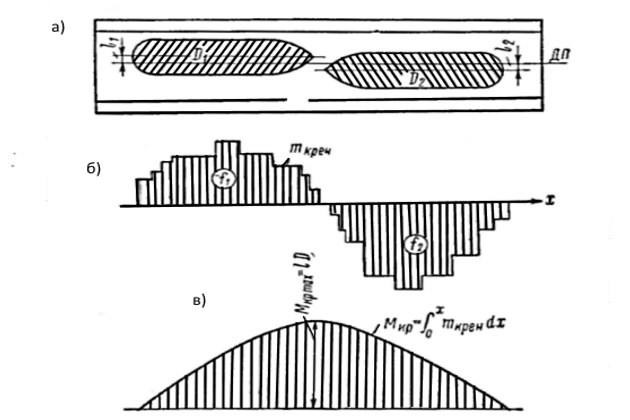
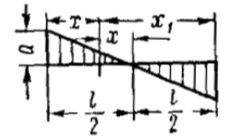
При крене дока, т. е. когда принятый на стапель-палубу несимметричный груз не уравновешен, для определения крутящего момента следует просуммировать эпюры кренящих моментов от грузов с эпюрой распределенных восстанавливающих моментов сил поддержания и проинтегрировать суммарную эпюру (рис. 2).
Определение поперечного крутящего момента от несимметричной загрузки дока
При несимметричном доковании судов, кроме продольного скручивания, возникает также поперечное скручивание корпуса дока.

Поперечный крутящий момент в любом продольном сечении определяется как алгебраическая сумма дифферентующих моментов, приложенных с одной стороны рассматриваемого сечения. Эпюра крутящих моментов есть интегральная кривая от кривой распределенных по ширине дока дифферентующих моментов (рис. 3).
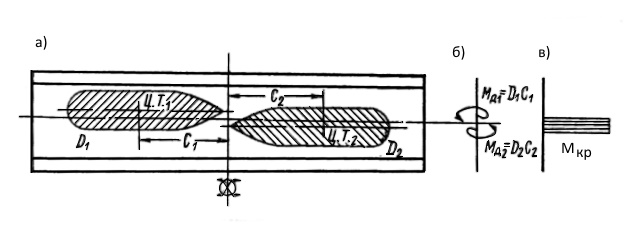
При наличии неуравновешенного дифферента следует учитывать восстанавливающий момент сил поддержания.
Определение продольного крутящего момента при статической постановке на «косую волну»
Вопросу определения Мкр при статической постановке судна на «косую волну» посвящены работы Ю. А. Шиманского, В. В. Давыдова, А. А. Курдюмова, А. И. Максимаджи и Н. Н. Руднева, а также других авторов.
Наиболее удобная формула приближенного определения крутящего момента на миделе приведена в книге В. В. Давыдова в форме
где:
- γ — объемный вес воды;
- r — полувысота расчетной волны;
- B, L — ширина и длина дока;
— коэффициент, значения которого даны в табл. 1;
- λ — длина волны.
| Таблица 1. Значения коэффициента R | |||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |||||||||||||||
| 6 | 8 | 10 | 6 | 8 | 10 | 6 | 8 | 10 | 6 | 8 | 10 | 6 | 8 | 10 | 6 | 8 | 10 | 6 | 8 | 10 | |
| 24 | 18 | 15 | 51 | 41 | 35 | 72 | 60 | 50 | 78 | 72 | 63 | 74 | 78 | 74 | 58 | 76 | 77 | 36 | 68 | 77 | |
Максимальный крутящий момент определяется по формуле (Формула 1) для нескольких значений
(в пределах
).
<
Курсовой угол ψ, соответствующий неблагоприятному
, находится как
Определим максимальный крутящий момент на миделе дока с размерами L = 120 м; B = 20 м.
Для
имеем
Для других элементов волны получим:
| Значения элементов волны | |||
|---|---|---|---|
| 2 | 60 | 4 | 4 900 |
| 3 | 40 | 3,33 | 5 760 |
| 4 | 30 | 3,0 | 5 600 |
| 5 | 24 | 2,8 | 5 000 |
Как видно из примера, наибольший крутящий момент возникает при
, при этом неблагоприятный курсовой угол равен
Обобщенное выражение для
может быть представлено в следующем виде (см. Кильблоки, клетки, упорыКонструкции и проектирование корпусов плавучих доков):
- где значения величин γ, r, λ, В, ψ объяснены выше.
По этой формуле максимальное значение крутящего момента также определяется из расчета для нескольких значений
.
Учет динамических факторов
Приведенные выше формулы носят теоретический характер. Как показал эксперимент, проведенный кафедрой строительной механики корабля ЛКИ (см. Система набора плавучих доковКонструкции и проектирование корпусов плавучих доков), реальная величина крутящего момента значительно ниже подсчитанного по теоретическим формулам. Это объясняется влиянием динамических факторов, сопровождающих процесс волнения.
Динамические крутящие моменты для доков с
могут быть определены по формуле
Значения Кдин, полученные экспериментальным путем, приведены в табл. 2.
| Таблица 2. Значение коэффициента Kдин | ||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0,53 | 0,63 | 0,70 | 0,965 | 1,07 | 1,22 | |||||||||||||||||
| 30 | 45 | 60 | 75 | 30 | 45 | 60 | 75 | 30 | 45 | 60 | 75 | 30 | 45 | 60 | 75 | 30 | 45 | 30 | 45 | 60 | 75 | |
| Kдин | 1,8 | 3,6 | 7,6 | 14,3 | 4,42 | 9,3 | 15,8 | 16,5 | 11,7 | 14,3 | 20,4 | 15,1 | 18 | 23 | 22 | 13,9 | 16,2 | 16,6 | 10,8 | 13,5 | 12,8 | 10,8 |
Динамический крутящий момент можно также определить по формуле
где:
- Мкр — статический крутящий момент, определяемый по формулам (Формула 1)—(Формула 2);
— коэффициент, учитывающий эффект Смита;
— коэффициент, учитывающий дифракцию волн новой поверхности.
Для доков
где
- Т — осадка дока;
- λ — длина расчетной волны.
Определение поперечного крутящего момента при статической постановке на «косую волну»
Поперечный крутящий момент в диаметральной плоскости дока при статической постановке на волну можно определить по следующей формуле1:
Формула (в несколько измененном виде) заимствована из статьи Расчет прочности ферм башенРасчеты местной прочности металлических плавучих доков.
где
— отношение высоты к длине волны;
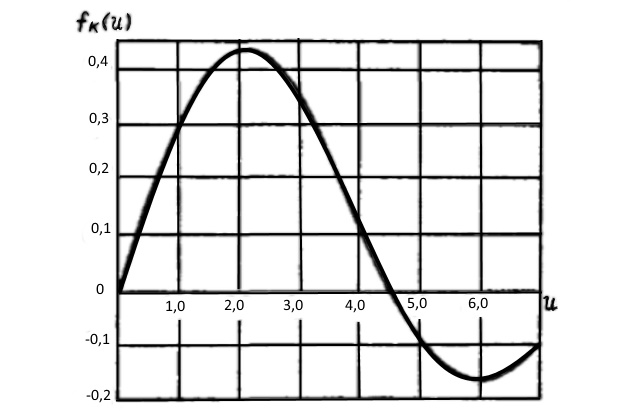
— аргумент функции
;
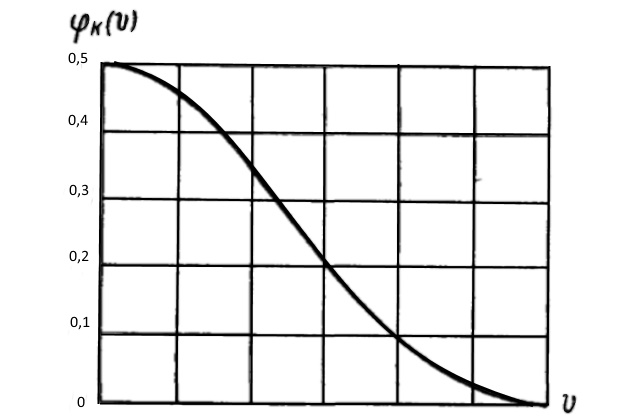
— аргумент функции φk (v).
Графики функций
и φk (v) приведены на рис. 4 и 5.
Максимальное значение поперечного крутящего момента определяется по формуле (Формула 4) для определенного диапазона
и ψ. Расчеты удобно вести в табличной форме.
Специальных исследований о влиянии динамических факторов на величину поперечного крутящего момента не велось, но, очевидно, что это влияние будет таким же, как при продольном скручивании.
Определение напряжений при продольном скручивании
Теория стесненного скручивания тонкостенных стержней замкнутого недеформируемого профиля разработана в 1939—1940 гг. проф. А. А. Уманским применительно к авиаконструкциям. Читатели, интересующиеся основами теории стесненного кручения, могут обратиться к трудам и других авторов. Ниже изложена схема расчета стесненного кручения, основанная на теории A. А. Уманского (см. выше “Определение поперечного крутящего момента от несимметричной загрузки дока”).
Внешний крутящий момент Мz вызывает стесненное скручивание корпуса. Крутящий момент уравновешивается системой внутренних касательных напряжений τk и τω, где τk — касательные напряжения чистого кручения; τω — секториальные касательные напряжения.
Если представить внешний крутящий момент как
где:
- Мk — момент чистого кручения;
- Мω — изгибно-крутящий момент,
то напряжения τk уравновешивают Мk:
а напряжения τω уравновешивают Мω:
Суммарное значение касательных напряжений
Кроме касательных напряжений при стесненном кручении в результате депланации сечений возникает взаимно уравновешенная система так называемых секториальных нормальных напряжений σω. Касательные и нормальные напряжения для одноконтурного профиля определяются следующими зависимостями:
где:
- Bω — изгибно-крутящий бимомент, кг/см²;
— главная секториальная координата (единичная депланация), см²;
- ρ — приведенный радиус одноконтурного профиля, см²;
— главный секториальный статический момент, см4;
- Ia — момент инерции свободного кручения, см4;
- Iω — секториальный момент инерции, см4;
- δ — толщина стенки профиля, см;
- Мк, Мω, Вω — силовые факторы; они зависят от характера внешней скручивающей нагрузки и граничных условий на концах стержня (корпуса дока);
— геометрические характеристики профиля стержня (поперечного сечения корпуса).
Дифференциальные зависимости стесненного кручения
Как следует из теории стесненного кручения, общие выражения для Мк, Мω, Вω имеют вид
где:
— угол закручивания стержня (
— интенсивность угла закручивания);
— коэффициент депланации;
- Iс — направленный момент инерции;
— интенсивность внешнего крутящего момента;
— изгибно-крутильная характеристика.
Общее выражение
и ее производных определяется интегрированием дифференциального уравнения стесненного кручения
При решении дифференциального уравнения стесненного кручения для плавающей балки принимаются следующие граничные условия:
- при z = 0 и z = L (оконечности дока) стеснение отсутствует (депланация свободна), угол поворота не равен нулю;
при
(мидель-шпангоут дока) депланация свободна, угол поворота равен нулю.
В табл. 3 и 4 представлены окончательные выражения Мк, Мω, Вω,
для двух видов распределения внешнего крутящего момента: по линейному закону и косинусоиде. Тот и другой вид распределения момента с достаточной степенью точности могут заменять реальное распределение крутящего момента.
Общий порядок расчета
На первом этапе расчета определяются координаты центра кручения, относительно которого происходит поворот сечений при скручивании:
Таблица 3. Выражения при линейном Mz | |||
|---|---|---|---|
| Величина | Характер эпюр | Уравнения ординат эпюр | Максимум ординат |
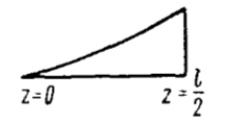
| Mz | 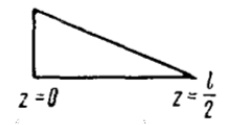 | ||
 | |||
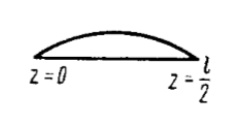 | |||
| Mk |  | ||
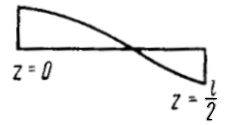 | |||
Таблица 4. Выражения при косинусоидальном Mz | |||
|---|---|---|---|
| Величина | Характер эпюр | Уравнения ординат эпюр | Максимум ординат |
| Mz | 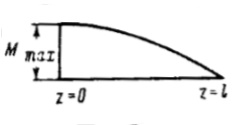 | ||
 | |||
 | |||
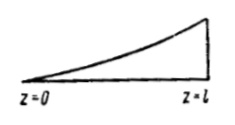
| Mk |  | ||
 | |||
Для симметричного относительно диаметральной плоскости сечения дока ах = 0. Значение аy определяется методом последовательных приближений. Главные секториальные координаты
первого приближения рекомендуется определять относительно центра тяжести сечения. Расчеты
последующего приближения производят относительно положения центра кручения, полученного в предыдущем приближении.
Предлагается к прочтению: Учет динамических факторов при определении дополнительных продольных усилий на волнении
Процесс последовательных приближений сходится достаточно быстро и два-три приближения дают практически приемлемый результат. Главная секториальная координата последнего приближения является окончательным ее значением, все остальные секториальные характеристики определяются относительно центра кручения.
Интегралы типа
вычисляются по правилу Верещагина. С целью упрощения расчетов рекомендуется многосвязный контур поперечного сечения дока заменять двухсвязным (одноконтурным), «размазывая» внутренние продольные переборки понтона и палубу безопасности в башне по внешним стенкам контура профиля. Можно также, делая ошибку в безопасную сторону, вообще пренебречь наличием внутренних конструкций, увеличивающих статическую неопределенность контура профиля.
Момент инерции сечения:
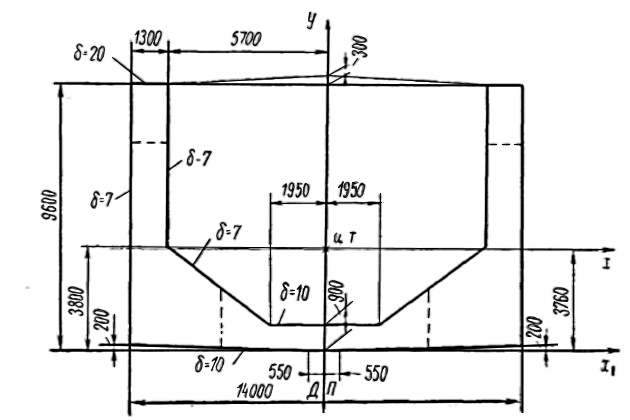
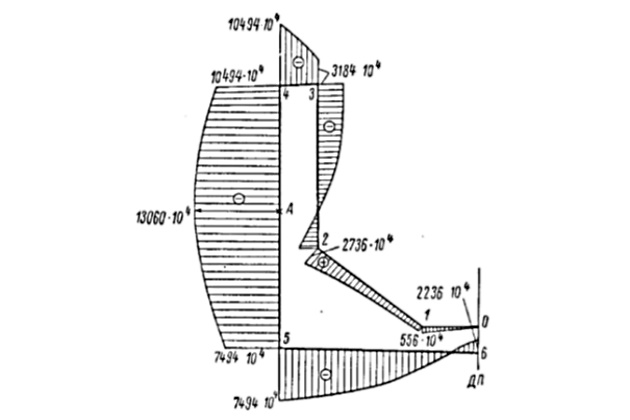
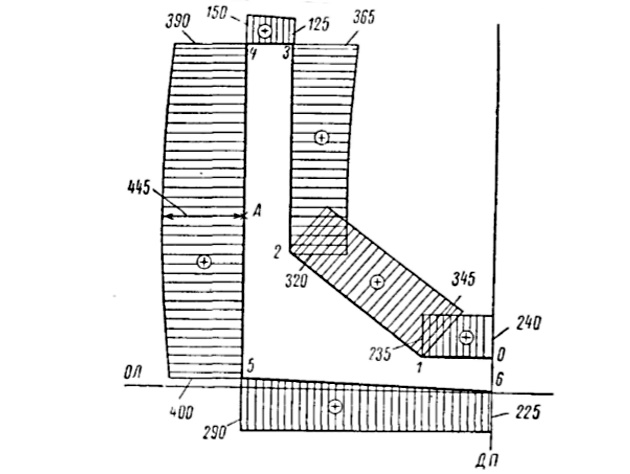
В дальнейшем определение наиболее специфических характеристик будет поясняться численными расчетами применительно к схеме поперечного сечения дока, изображенной на рис. 6 (пунктиром показаны неучитываемые внутренние конструкции).
Вычисление геометрических характеристик, необходимых для определения σω
Определение главной секториальной координаты
для одноконтурного сечения.
где:
- ω — секториальная координата точки сечения:
Этот интеграл берется от определенной начальной точки. За положительное направление обхода принимается направление против движения часовой стрелки. Для сечения, составленного из отрезков прямых,
где:
- ri — длина перпендикуляра, опущенного из полюса на прямолинейный участок контура;
- si — длина прямолинейного участка контура;
— приведенная координата точки сечения:
или, для случая прямолинейных участков,
При распространении интеграла (или суммы) на весь периметр сечения
становится приведенным периметром контура. Так для контура на рис. 6
где:
- δi — толщина прямолинейного участка контура;
- ρ — приведенный радиус одноконтурного профиля
где:
- Ω удвоенная площадь, ограниченная контуром поперечного сечения дока.
Для поперечного сечения, изображенного на рис. 6,
В процессе определения
рекомендуется построить эпюры
.
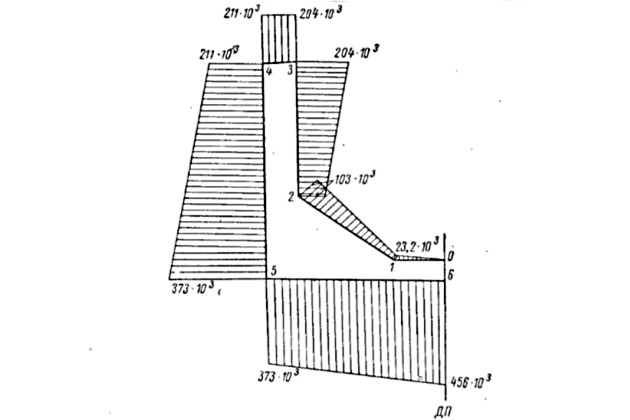
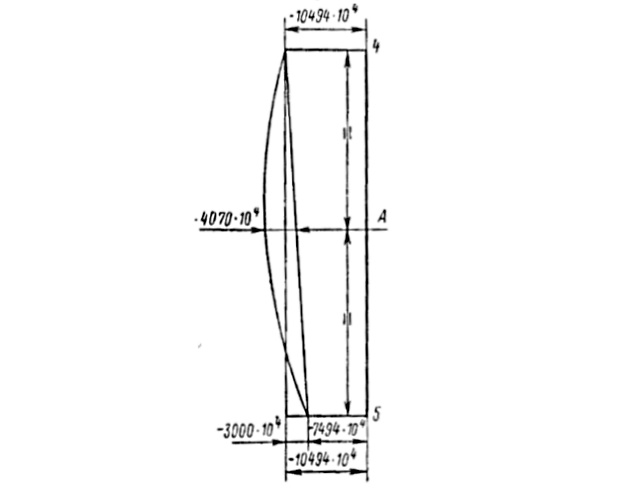
На рис. 7 за «полюс» принят центр тяжести сечения (эпюра r всегда положительна).
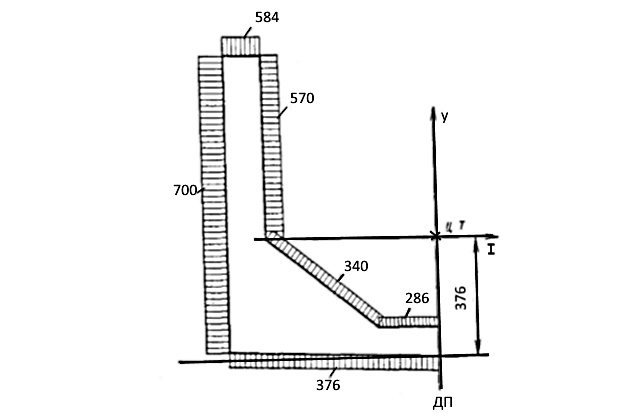
На рис. 8 за начальную точку отсчета принята точка 0. Полюс радиуса-вектора принят в центре тяжести. Знак эпюры со определяется направлением вращения радиуса-вектора: «плюс» — против часовой стрелки.
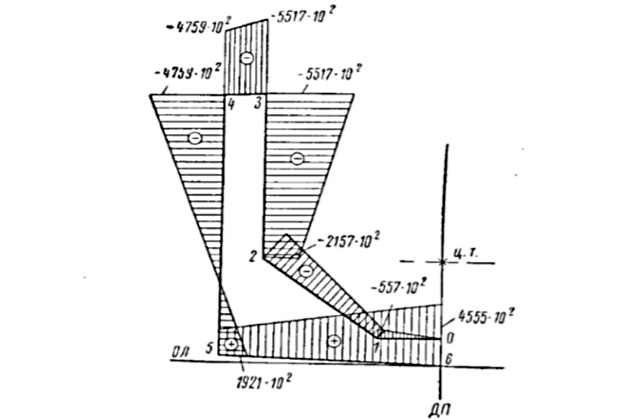
Вычисление ординат эпюры:
Проверка правильности построения эпюры: ордината эпюры в точке 6 должна быть равна
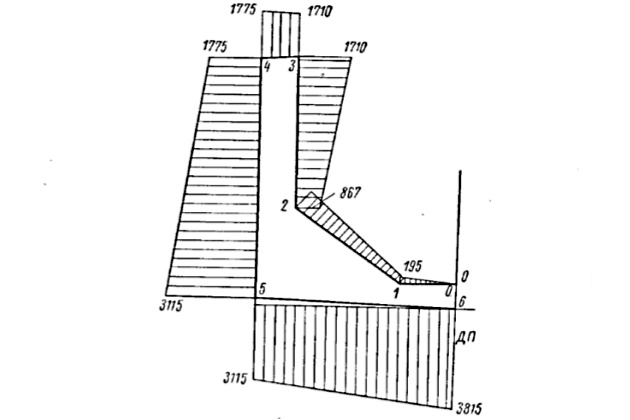
Вычисление ординат эпюры:
На рис. 9 за начальную точку отсчета также принимается точка 0.
Вычисление ординат эпюры:
.
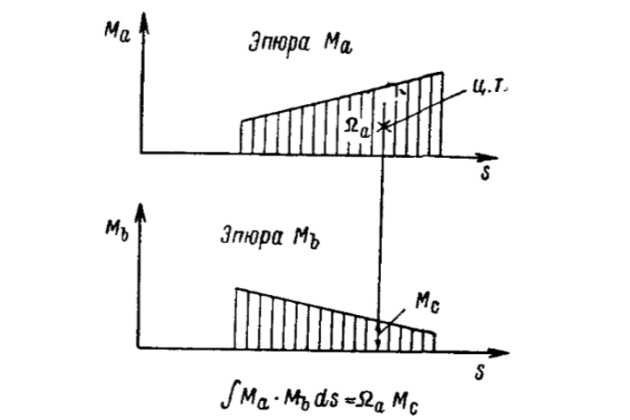
Вычисление этого интеграла производится по правилу Верещагина, которое для функций с прямолинейными эпюрами формулируется так: чтобы проинтегрировать произведение двух функций, необходимо площадь эпюры одной из функций умножить на ординату эпюры другой функции, взятую под центром тяжести площади первой эпюры (рис. 12).
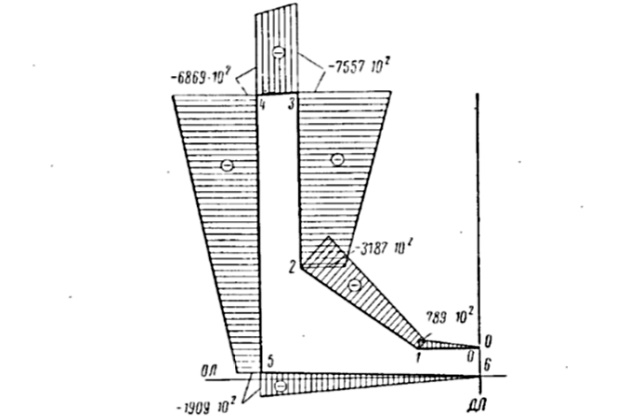
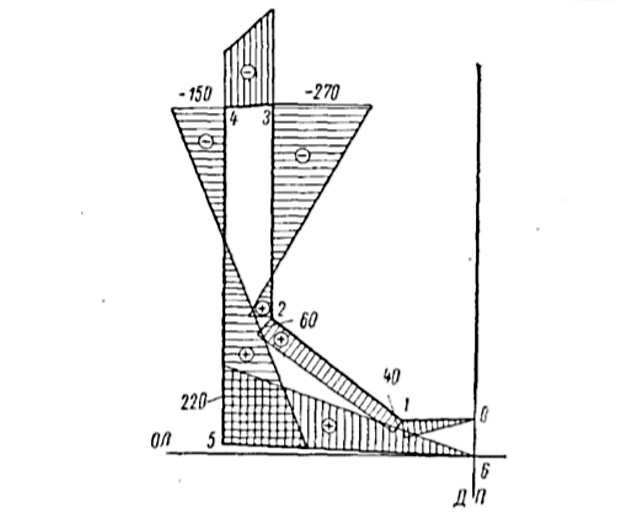
Вычисление ординат эпюры:
В табл. 5 даны формулы метода Верещагина для различных сочетаний прямолинейных эпюр подынтегральных функций.
Таким образом, для вычисления искомого интеграла, кроме уже построенной эпюры
, следует построить эпюру
(рис. 13). Интеграл
, представленный в виде
, вычисляется в форме табл. 6.
.
Для определения
необходимо предварительно вычислить момент инерции корпуса дока относительно вертикальной оси Iу. После определения
в первом приближении (для рассматриваемого примера
) вновь определяется
(снова определяются и строятся эпюры r, ω = rs относительно полученного центра кручения
– значения ρs остаются прежними). Истинное положение центра кручения должно соответствовать условию ау = 0.
| Таблица 5. Значения интегралов | ||||||
|---|---|---|---|---|---|---|
| Эпюра Мb | Эпюра Ма |  |  |  |  |  |
 | ||||||
 | ||||||
 | ||||||
 | ||||||
 | ||||||
 | ||||||
 | ||||||
 | 0 | |||||
| – | – |  |  | – | – | |
| Таблица 6. Расчет выражения | |||||||
|---|---|---|---|---|---|---|---|
| Стержень | Длина см | Формула | |||||
| 0-1 | 195 | 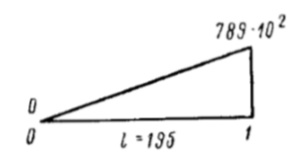 | 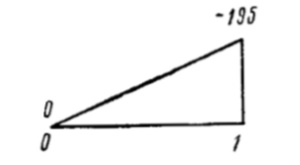 | 10·108 | 10·108 | 10 | |
| 1-2 | 470 | 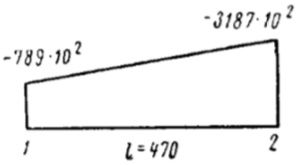 |  | 393·108 | 275·108 | 7 | |
| 2-3 | 590 | 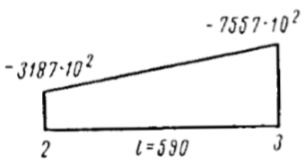 | 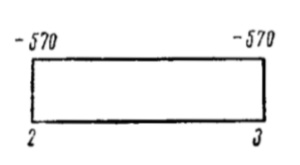 | 1470·108 | 1055·108 | 7 | |
| 3-4 | 130 | 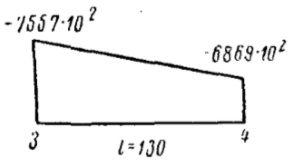 |  | 395·108 | 1190·108 | 20 | |
| 4-5 | 940 |  | 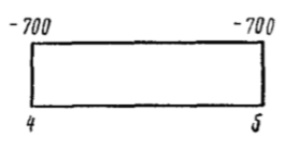 | 2890·108 | 2020·108 | 7 | |
| 5-6 | 700 | 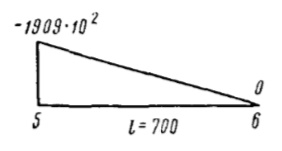 | 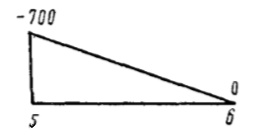 | 311·108 | 311·108 | 10 | |
Это условие является критерием окончания процесса последовательных приближений при определении положения центра кручения. Практически процесс приближения можно останавливать при значениях ау
, близких к нулю, когда значения главных секториальных координат
в последнем приближении мало отличаются от их значений в предыдущем приближении.
Определение геометрических характеристик, необходимых для определения τк, τω
1. Определение главного секториального статического момента
:
где:
— единичный поток касательных усилий;
— секториальный статический момент точки контура поперечного сечения, равный
- (интеграл распространяется от начала отсчета до рассматриваемой точки n).
Для прямолинейной эпюры
на прямолинейных участках контура выражение
будет иметь вид
где:
— главные секториальные координаты начала и конца рассматриваемого участка контура;
- δi — толщина участка;
- Si — длина участка;
f — поправка на криволинейность эпюры
;
Вычислять значения
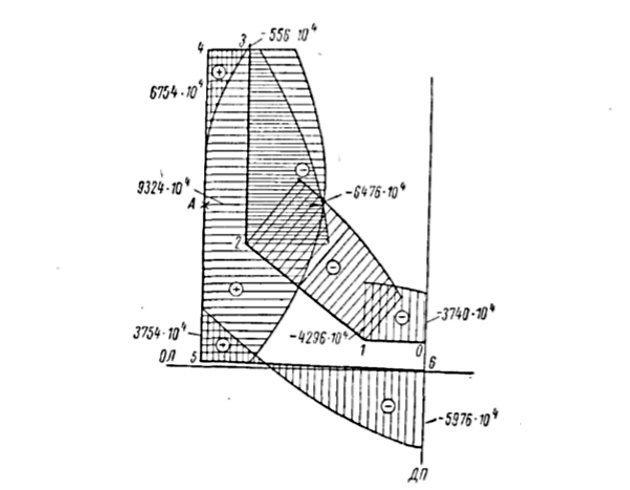
рекомендуется в форме табл. 7. При построении эпюры
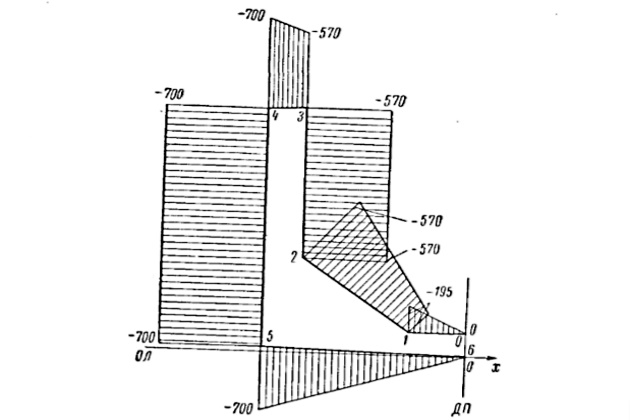
(рис. 14) рекомендуется определить значение статического момента для точки А, расположенной по середине высоты сечения, т. е. для точки максимальных изгибно-крутильных касательных напряжений τω (рис. 18).
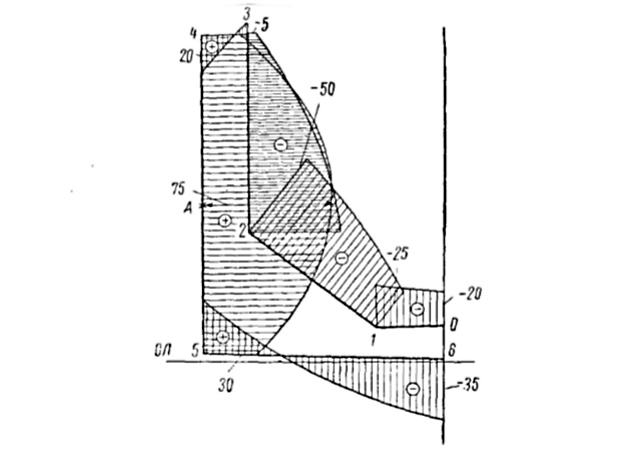
Вычисление ординат эпюры:
Единичный поток касательных усилий
определяется из равенства
где:
— приведенный периметр контура сечения (см. выше);
— приведенная площадь эпюры секториальных статических моментов.
| Таблица 7. Расчет | |||
|---|---|---|---|
| Стержень | Эпюры | Вычисление по участкам | Эпюра по участкам |
| 0-1 | 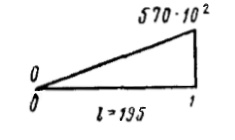 | 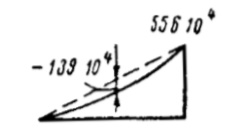 | |
| 1-2 | 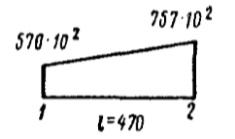 | 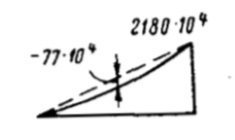 | |
| 2-3 | 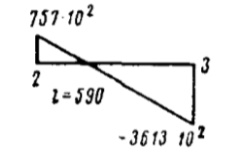 | 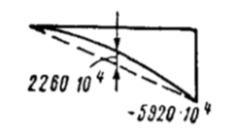 | |
| 3-4 | 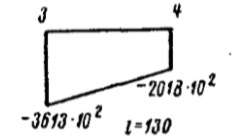 | 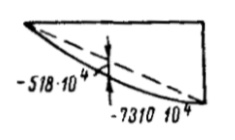 | |
| 4-5 |  | 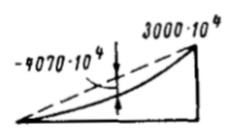 | |
| 5-6 | 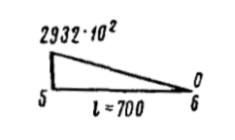 | 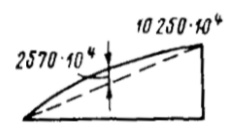 | |
Примечание. Приведенные в таблице эпюры являются результатом окончательного приближения. | |||
Интегральное выражение приведенной площади эпюры секториальных статических моментов для прямолинейных участков контура можно представить в следующем виде:
— ординаты эпюры Sω в начале и конце рассматриваемого участка.
Вычисления по формуле (Формула 22) рекомендуется вести в форме табл. 8.
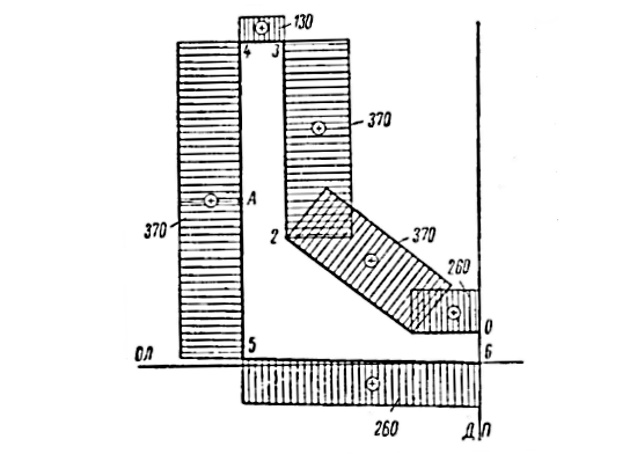
Таким образом,
для всего контура. Теперь можно подсчитать ординаты и построить эпюру
(рис. 16).
Вычисление ординат эпюры:
2. Определение моментов инерции Ia, Ic, Iω. Момент инерции свободного кручения для одноконтурного сечения определяется следующим образом:
| Таблица 8. Расчет | ||
|---|---|---|
| Стержень | Результат | |
| 0-1 | 36·107 | |
| 1-2 | 1070·107 | |
| 2-3 | 1455·107 | |
| 3-4 | -467·107 | |
| 4-5 | -15 750·107 | |
| 5-6 | -457·107 | |
Имея в виду, что
можно написать:
Направленный момент инерции определяется выражением
или, для случая прямолинейных участков сечения с постоянной эпюрой r на отдельных участках,
- где знак суммы распространяется на все участки контура поперечного сечения (r отсчитывается от центра кручения).
Вычислять Ic рекомендуется в форме табл. 9.
Если сумма распространена на половину симметричного сечения, то
Секториальный момент инерции Iω имеет следующее выражение:
или
Интеграл
вычисляется по правилу Верещагина перемножением эпюры
самой на себя. Вычислять интеграл удобно в форме табл. 10. Если сумма распространена на половину симметричного сечения, то
| Таблица 9. Расчет Ic | ||||||
|---|---|---|---|---|---|---|
| Стержень | si, см | ri, см | ||||
| 0-1 | 195 | 1,0 | 412 | 168·103 | 328·105 | 328·105 |
| 1-2 | 470 | 0,7 | 210 | 44,2·103 | 208·105 | 146·105 |
| 2-3 | 590 | 0,7 | 570 | 325·103 | 1920·105 | 1340·105 |
| 3-4 | 130 | 2,0 | 1282 | 1645·103 | 2140·105 | 4280·105 |
| 4-5 | 940 | 0,7 | 700 | 490·103 | 4600·105 | 3220·105 |
| 5-6 | 700 | 1,0 | 322 | 104·103 | 727·105 | 727·105 |
| Примечание. Значения ri в таблице соответствуют окончательному положению центра кручения. Промежуточные вычисления не приводятся. | ||||||
Вычисление напряжений
После определения всех геометрических характеристик вычисляют напряжения. Максимальные значения Вω, Мк, Мω, в зависимости от принятого вида распределения внешнего крутящего момента, вычисляют по формулам, приведенным в табл. 3 и 4. Bω max возникает на ¼ L, а Мω max и Мк max — на миделе дока.
Подставляя значения Вω, Мω, Мк в выражения для напряжений, представим последние в виде
где:
- β1, β2, β3 — численные значения выражений
| Таблица 10. Расчет | |||||
|---|---|---|---|---|---|
| Стержень | Вычисления | ||||
| 0-1 | 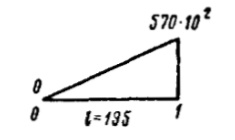 | 1,0 | 21·1010 | 21·1010 | |
| 1-2 | 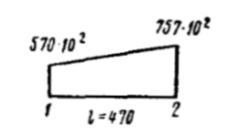 | 0,7 | 176·1010 | 123·1010 | |
| 2-3 | 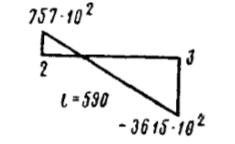 | 0,7 | 2080·1010 | 1460·1010 | |
| 3-4 | 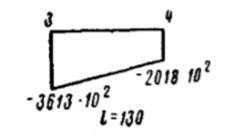 | 2,0 | 1055·1010 | 2110·1010 | |
| 4-5 | 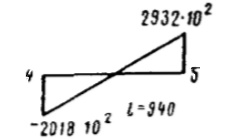 | 0,7 | 2110·1010 | 1480·1010 | |
| 5-6 | 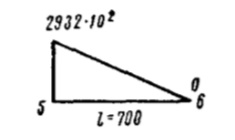 | 1,0 | 2000·1010 | 2000·1010 | |
Примечание. – результат окончательного приближения. | |||||
Такое выражение напряжений в функции от геометрических характеристик позволяет вычислить ординаты и построить эпюры напряжений (рис. 17—20).
Вычисление ординат эпюры:
Полученные нормальные напряжения от скручивания следует просуммировать с нормальными напряжениями от изгиба на соответствующем «косом курсе». Касательные напряжения от скручивания суммируются с касательными напряжениями от изгиба.
Рекомендуется к прочтению: Взаимодействие плавучего дока и судна: усилия между ними и моменты изгиба
При ориентировочных расчетах суммарную величину касательных напряжений от скручивания можно определить как для свободного кручения одноконтурного сечения по формуле Бредта:
Порядок расчета напряжений при поперечном скручивании тот же, что и при продольном. Представляя продольные сечения дока в виде симметричных прямоугольников и пренебрегая (с ошибкой в безопасную сторону) наличием поперечных переборок (рис. 21), можно добиться значительных упрощений. Так, для продольного сечения, показанного на рис. 21, а, формулы основных геометрических характеристик будут иметь вид:
где:
— средняя толщина днища и стапель-палубы понтона;
- δт — толщина торцовых стенок понтона;
- l, h — длина и высота понтона.
Характер изменения
показан на рис. 21, в, г, д.
Вычисление ординат эпюры:
Выражения для ординат эпюр
в точках 0, 1, 2 имеют следующий вид2:
Вычисление ординат эпюры:
2Выражения получены на основании общих формул; промежуточные выкладки (ввиду их простоты) не приводятся.
Вычисление ординат эпюры:
Выражения
(как и для продольного скручивания) могут быть приняты по табл. 3, 43. В этом случае длина скручиваемого плавающего стержня равна ширине дока.
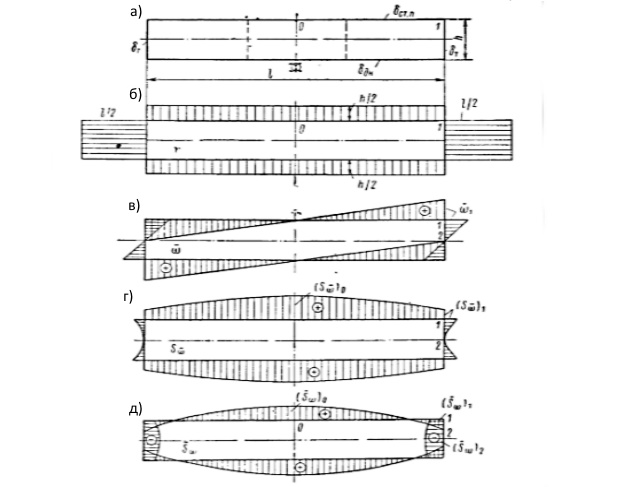
Рис. 21 К расчету поперечного скручивания: а — эскиз продольного сечения; пунктиром показаны поперечные переборки, наличие которых в расчете не учитывается; б — эпюра r; в — эпюра
; г — эпюра
; д — эпюра
3При этом допускается ошибка в безопасную сторону, так как не учитывается непризматичность понтона в поперечном направлении.
