Судно в доке - условия ремонта, достройки и подкрепления

Судно в доке подразумевает, что его постановка была совершена после тщательных расчетов всех изгибающих моментов и усилий их взаимодействия при поднятии. Все показатели применяются для расчета в формулах, приведенных в данном материале.

СодержаниеСвернуть

Постановка задачи об определении реакций и распределении усилий между судном и поднимающим его плавучим доком
Методы решения уравнения совместного изгиба дока и судна
Приближенное определение усилий, действующих на плавучий док и докуемое судно
Приближенные формулы для определения реакций килевой дорожки
Влияние зазора между судном и килевой дорожкой на реакции кильблоков и распределение усилий между судном и доком
Регулирование усилий подбором жесткости кильблоков
Условия ремонта, достройки и подкрепления судов в плавучих доках
Определение усилий при постановке нескольких судов в один док, одного судна в два дока, при неполном доковании судна

Постановка задачи об определении реакций и распределении усилий между судном и поднимающим его плавучим доком

При известных реакциях кильблоков или клеток судно и док можно рассматривать отдельно как две независимые уравновешенные системы: судно — под действием собственного веса и реакций кильблоков (клеток); док — под действием реакций кильблоков (клеток), собственного веса, балласта и сил поддержания.

Введем следующие обозначения:

Е_с, Е_д — модули нормальной упругости материалов судна и дока;
I_с — момент инерции поперечного сечения судна (переменный по длине судна);
I_д — момент инерции поперечного сечения дока (для понтонного дока учитываются только башни), переменный по длине дока;
$υ_{с}$
— стрелка прогиба судна от общего продольного изгиба в доке;
$υ_{Д}$
— стрелка прогиба башен дока (стрелка прогиба дока от общего продольного изгиба с судном);
q_c — весовая нагрузка судна на единицу длины;
q_д — разность между весом дока (с учетом балласта) и силами поддержания, соответствующими положению дока с судном, на единицу длины;
r — интенсивность реакций кильблоков;
k₁ — коэффициент жесткости кильблоков (на единицу длины);
k₂ — коэффициент жесткости днищевых перекрытий судна (на единицу длины);
k₃ — коэффициент жесткости понтона дока при поперечном изгибе (на единицу длины);
f_д — начальная стрелка прогиба от поперечного изгиба понтонов относительно башен под действием веса понтонов, балласта и сил поддержания;
f_c — стрелка прогиба киля судна относительно бортов от местной нагрузки на днищевые перекрытия судна;
Δ — начальный зазор между верхней кромкой кильблоков и килевой линией судна в момент постановки судна на кильблоки за счет начального (строительного) изгиба судна Δ_c, специальной, в необходимом случае, выкладки кильблоков Δ₀, а также за счет температурного зазора Δ_t°;
$\begin{array}{r} P_{c} (0), P_{c} (l) \\ M_{c} (0), M_{c} (l) \end{array}\}$
— веса свешивающихся за килевую дорожку оконечностей судна и моменты этих весов относительно концов килевой дорожки;
$\begin{array}{r} P_{Д} (0), P_{Д} (l) \\ M_{Д} (0), M_{Д} (l) \end{array}\}$
— то же для дока, считая за нагрузку дока разность между его весом (с балластом) и силами поддержания (q_Д);
l — длина килевой дорожки;
$x = 0, x = l, x = \frac{l}{2}$
— координаты правого и левого концов и середины килевой дорожки.

Смещение корпуса судна относительно башен дока равно сумме перемещений днищевых перекрытий судна, кильблоков, понтонов дока и начального зазора:

υ = υ_{c} - υ_{Д} = r (\frac{1}{k_{1}} + \frac{1}{k_{2}} + \frac{1}{k_{3}}) + f_{Д} - f_{с} + ∆,

откуда

r = k (υ_{c} - υ_{Д} + f_{с} - f_{Д} - ∆), Ф о р м . 1

где

\frac{1}{k} = \frac{1}{k_{1}} + \frac{1}{k_{2}} + \frac{1}{k_{3}} .

Дифференциальные уравнения изгиба судна и дока имеют вид

\begin{array}{r} (Е_{с} I_{c} υ_{c}^{″}) ″ = q_{c} - r = q_{c} - k (υ_{c} - υ_{Д} + f_{c} - f_{Д} - ∆), \\ (Е_{Д} I_{Д} υ_{Д}^{″}) ″ = q_{Д} + r = - q_{Д} + k (υ_{c} - υ_{Д} + f_{c} - f_{Д} - ∆) . \end{array}\} Ф о р м . 2

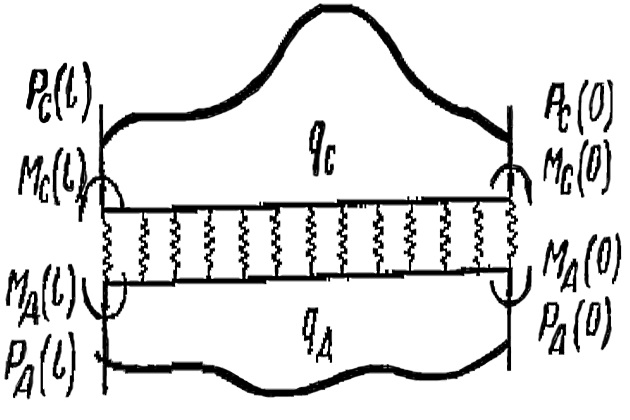
В соответствии с рис. 1 граничные условия на концах килевой дорожки записываются в следующем виде: при х = 0

Е_{с} I_{c} υ_{c}^{″} = M_{c} (0),

(Е_{с} I_{c} υ_{c}^{″})' = Р_{c} (0),

Е_{Д} I_{Д} υ_{Д}^{″} = - М_{Д} (0),

(Е_{Д} I_{Д} υ_{Д}^{″})' = - Р_{Д} (0);

при x = l

Е_{с} I_{с} υ_{с}^{″} = М_{с} (l),

(Е_{с} I_{с} υ_{с}^{″})' = Р_{с} (l),

Е_{Д} I_{Д} υ_{Д}^{″} = - М_{Д} (l),

(Е_{Д} I_{Д} υ_{Д}^{″})' = - Р_{Д} (l) .

Рис. 1 Расчетная схема совместного изгиба судна и плавучего дока

Интегрируя уравнения (Формула 2) два раза, используя граничные условия при х = 0, деля результат интегрирования первого уравнения на E_cI_c, а второго — на E_дI_д и вычитая одно из другого, получаем:

υ^{″} = υ_{c}^{″} - υ_{Д}^{″} = \frac{1}{Е_{с} I_{c}} \int_{0}^{x} \int_{0}^{x} q_{c} d_{x} d_{x} + \frac{1}{Е_{Д} I_{Д}} \int_{0}^{x} \int_{0}^{x} q_{Д} d_{x} d_{x} -

- \frac{1}{E I} \int_{0}^{x} {\int k}_{0}^{x} (υ_{c} - υ_{Д} + f_{c} - f_{Д} - ∆) d_{x} d_{x} +

+ [\frac{P_{c} (0)}{E_{c} I_{c}} + \frac{P_{Д} (0)}{E_{Д} I_{Д}}] x + \frac{М_{с} (0)}{E_{c} I_{c}} + \frac{M_{Д} (0)}{E_{Д} I_{Д}}, Ф о р м . 3

где

\frac{1}{E I} = \frac{1}{E_{c} I_{c}} + \frac{1}{E_{Д} I_{Д}},

т. е.

E I = \frac{E_{c} I_{c} \cdot E_{Д} I_{Д}}{E_{c} I_{c} + E_{Д} I_{Д}} .

Умножив (Формула 3) на EI и снова продифференцировав дважды, получим:

(E I υ ″) ″ + k υ = M ″ - k (f_{c} - f_{Д} - ∆), Ф о р м . 4

где

M = \frac{E I}{E_{c} I_{c}} [\int_{0}^{x} \int_{0}^{x} q_{c} d_{x} d_{x} + P_{c} (0) x + M_{c} (0)] +

+ \frac{E I}{E_{Д} I_{Д}} [\int_{0}^{x} \int_{0}^{x} q_{Д} d_{x} d_{x} + P_{Д} (0) x + M_{Д} (0)] .

Граничные условия для функции

υ

(прогиба приведенной балки) следующие:

\begin{matrix} п р и x = 0 \\ E I υ ″ = \frac{E I}{E_{c} I_{c}} M_{c} (0) + \frac{E I}{E_{Д} I_{Д}} M_{Д} (0) = M (0), \\ (E I υ ″)' = \frac{E I}{E_{c} I_{c}} P_{c} (0) + \frac{E I}{E_{Д} I_{Д}} P_{Д} (0) + (\frac{E I}{E_{c} I_{c}})' [M_{c} (0) - M_{Д} (0)] = P (0); \\ п р и x = l \\ E I υ ″ = - \frac{E I}{E_{c} I_{c}} M_{c} (l) + \frac{E I}{E_{Д} I_{Д}} M_{Д} (l) = M (l), \\ (E I υ ″)' = \frac{E I}{E_{c} I_{c}} P_{c} (l) - \frac{E I}{E_{Д} I_{Д}} P_{Д} (l) + (\frac{E I}{E_{c} I_{c}})' [M_{c} (l) - M_{Д} (l)] = - P (l); \end{matrix}\} Ф о р м . 5

Таким образом, задача об определении реакций кильблоков при постановке непризматического судна в непризматический док сводится к задаче об изгибе балки приведенной жесткости EI, лежащей на сплошном упругом основании приведенной жесткости k и несущей приведенную поперечную нагрузку

q = M ″ - k (f_{c} - f_{Д} - ∆) .

Для определения изгибающих моментов, действующих отдельно на судно и док, сложим оба уравнения (Формула 2) и, проинтегрировав сумму дважды, найдем:

M_{c} (x) + M_{Д} (x) = M_{0} (x), Ф о р м . *

где М₀(х) — изгибающий момент от нагрузки q_c — q_д, то есть изгибающий момент от веса судна, дока, балласта и сил поддержания при нахождении судна в доке.

Предлагается к прочтению: Конструкции и проектирование корпусов плавучих доков

Следовательно, М₀(х) — изгибающий момент, действующий на систему док—судно, вычисленный в предположении, что вес судна является обычной нагрузкой для дока, то есть судно не обладает жесткостью.

С другой стороны,

M (x) = E I υ ” = E I (υ_{c}^{”} - υ_{Д}^{”}) = \frac{E I}{E_{c} I_{c}} M_{c} (x) - \frac{E I}{E_{Д} I_{Д}} M_{Д} (x) . Ф о р м . * *

Решая совместно уравнения (*) и (**), получим следующие выражения для изгибающих моментов, действующих в судне и доке:

\begin{array}{r} M_{c} (x) = \frac{E_{c} I_{c} (x)}{E_{c} I_{c} (x) + E_{Д} I_{Д} (x)} M_{0} (x) + M (x), \\ M_{Д} (x) = \frac{E_{Д} I_{Д} (x)}{E_{с} I_{с} (x) + E_{Д} I_{Д} (x)} M_{0} (x) - M (x) . \end{array}\} Ф о р м . 6

Выражения для перерезывающих сил, действующих в судне и доке, получаются дифференцированием по х выражений (Формула 6):

\begin{array}{r} N_{c} (x) = M_{c}^{'} (x) = [\frac{E_{c} I_{c} (x)}{E_{c} I_{c} (x) + E_{Д} I_{Д} (x)} M_{0} (x)]' + N (x), \\ N_{Д} (x) = M_{Д}^{'} (x) = [\frac{E_{Д} I_{Д} (x)}{E_{c} I_{c} (x) + E_{Д} I_{Д} (x)} M_{0} (x)]' - N (x) . \end{array}\} Ф о р м . 7

Физически первые составляющие выражений (Формула 6), (Формула 7) представляют собой изгибающие моменты и перерезывающие силы от совместного изгиба системы док—судно как общей балки, причем корпус судна и дока участвуют в таком изгибе пропорционально своим жесткостям («первый главный изгиб»). Вторые составляющие характеризуют вертикальное смещение суднаКрен судна при поперечном перемещении груза по отношению к доку («второй главный изгиб»), вызванное неуравновешенностью нагрузок q_с и q_д, различной приведенной жесткостью упругого основания по длине и несоответствием граничных условий «первого главного изгиба» с фактическими граничными условиями на концах килевой дорожки (наличием концевых моментов и сосредоточенных сил).

Методы решения уравнения совместного изгиба дока и судна

1 Энергетический метод впервые был использован Н. В. Красноперовым, а затем П. Ф. Папковичем, П. А. Миняевым, Л. М. Буничем и Ю. А. Шиманским.

В настоящее время для решения уравнения (Формула 4) энергетическим методом рекомендуется пользоваться Справочником, принимая «приведенные» значения нагрузки и жесткостей.

Портовое сооружение для контейнеровозов
Источник: pixabay.com

2 Обычный процесс последовательных приближений при встречающихся на практике соотношениях k (х), EI (х) и l оказывается медленно сходящимся или даже расходящимся. А. Н. Крылов и П. Ф. Папкович предложили способ улучшения сходимости процесса последовательных приближений, не нашедший применения на практике.

При расходящихся последовательных приближениях часто принимают за р-е приближение некоторую среднюю величину между φ_р и φ_р-1 (так называемый обобщенный метод последовательных приближений). По предложению В. В. Варнелло

φ_{p} = α φ_{p - 1} + (1 - α) φ_{p - 1},

где функция φ определяется уравнением

(E I (x) φ_{p - 1}^{″}) ″ = q (x) - k (x) φ_{p - 1} .

Для относительно «жестких» судов α≈0,30, а для относительно «гибких» α≈0,1. А. А. Курдюмов получил для α формулу

α = \frac{1}{1 + 0, 002 \frac{k_{0} l^{4}}{E I_{0}}} = \frac{1}{1 + 0, 129 u^{4}},

где

u = \frac{l}{2} \sqrt[4]{\frac{k_{0}}{4 E I_{0}},} k_{0} и E I_{0}

— средние приведенные коэффициенты жесткости упругого основания и системы док—судно, выраженной уравнением (Формула 4), и доказал, что при такой схеме решения процесс последовательных приближений является сходящимся.

Расчетная схема для определения реакций кильблоков способом последовательных приближений, которой рекомендуется пользоваться, принимая приведенные выше зависимости для φ_р и α, составлена Б. Л. Николаи и А. А. Селиверстовым.

3 А. Н. Крылов в упомянутой уже работе использовал метод численного интегрирования Адамса — Штермера. Полученная им схема расчета очень громоздка и до настоящего времени не применялась.

В решении Л. В. Диковича рассматриваемая балка разбита на ряд участков, в каждом из которых момент инерции, нагрузка и жесткость упругого основания считаются постоянными.

Указанные расчетные схемы решения уравнения (Формула 4), т. е. определения реакций при постановке судна в плавучий док и соответственно точного распределения изгибающих моментов между судном и доком, весьма трудоемки. Поэтому в практических расчетах пользоваться ими рекомендуется лишь в исключительных случаях, когда требуется уточнение усилий, действующих в доке или докуемом судне. Особое внимание следует обратить на соответствующую точность исходных данных.

Грузовое судно “ML RORO”
Источник: pixabay.com

В частности, одной из существеннейших величин, значительно влияющих на результаты расчетов, является величина начального зазора между килевой линией судна и верхней кромкой кильблоков Δ. По расчетам А. А. Курдюмова при зазоре Δ = 0,1 м величина реакций может увеличиваться по сравнению с реакциями при Δ = 0 в 1,7 раза. В то же время начальный (строительный) изгиб докуемого судна обычно неизвестен или известен с большой погрешностью.

Приближенное определение усилий, действующих на плавучий док и докуемое судно

Так как момент М₀(х), изгибающий систему док—судно, может быть определен с любой необходимой точностью, вопрос об определении моментов М_с(х) и М_д(х) сводится к определению момента М(х) = EIυ″ приведенной балки, рассмотренной выше.

Как показывают подсчеты, величина этого момента (при Δ = 0), по сравнению с первыми слагаемыми формул (Формула 6), мала и является только поправкой к ним. Для определения поправки М (х) А. А. Курдюмов и В. В. Козляков воспользовались приближенным приемом, считая, что на длине килевой дорожки судно и док являются призматическими балками (

I_{c} = I_{c}^{0} = c o n s t; I_{Д} = I_{Д}^{0} = c o n s t

)

, а приведенная жесткость упругого основания постоянна по длине (k = k° = const).

В результате принятых допущений уравнение (Формула 4) принимает вид:

E I^{0} υ^{I V} + k^{0} υ = \frac{E_{Д} I_{Д}^{0} q_{c} + E_{c} I_{c}^{0} q_{Д}}{E_{c} I_{c}^{0} + E_{Д} I_{Д}^{0}} - k^{0} (f_{c} - f_{Д} - ∆) . Ф о р м . 8

Так как

(\frac{E I^{0}}{E_{c} I_{c}^{0}})' = 0

граничные условия для уравнения (Формула 8) принимают вид:

при х=0:

\begin{array}{r} \begin{matrix} M (0) = \frac{E_{Д} I_{Д}^{0} M_{c} (0) + E_{c} I_{c}^{0} M_{Д} (0)}{E_{c} I_{c}^{0} + E_{Д} I_{Д}^{0}}, \\ P (0) = \frac{E_{Д} I_{Д}^{0} P_{c} (0) + E_{c} I_{c}^{0} P_{Д} (0)}{E_{c} I_{c}^{0} + E_{Д} I_{Д}^{0}}; \\ п р и x = I \end{matrix} \\ \begin{matrix} M (l) = \frac{E_{Д} I_{Д}^{0} M_{c} (l) + E_{c} I_{c}^{0} M_{Д} (l)}{E_{c} I_{c}^{0} + E_{Д} I_{Д}^{0}}, \\ P (l) = \frac{E_{Д} I_{Д}^{0} P_{c} (l) + E_{c} I_{c}^{0} P_{Д} (l)}{E_{c} I_{c}^{0} + E_{Д} I_{Д}^{0}} . \end{matrix} \end{array}\} Ф о р м . 9

Изгибающий момент М (х) можно представить в виде суммы двух моментов: изгибающего момента от концевых сосредоточенных сил и моментов Р (0), Р (l), М (0), М (l) и изгибающего момента от распределенной нагрузки q [правой части уравнения (Формула 8)]:

M (x) = M^{P . M} (x) + M^{q} (x) . Ф о р м . 10

Изгибающий момент приведенной балки от концевых приведенных усилий посредине длины килевой дорожки равен

M^{P . M} (\frac{1}{2}) = M_{φ 1} (u) + \frac{1}{4} P l \frac{X_{0} (u)}{μ_{0} (u)}, Ф о р м . 11

где:

M = (\frac{1}{2}) [M (0) + M (l)],

P = (\frac{1}{2}) [P (0) + P (l)] .

Изгибающие моменты приведенной балки от концевых приведенных усилий в других сечениях равны

M^{P . M} (x) = M (0) φ [2 u \frac{x}{l}] + M (l) φ [2 u (1 - \frac{x}{l})] +

+ \frac{P (0)}{2 u} i \cdot ξ [2 u \frac{x}{l}] + \frac{P (l)}{2 u} l \cdot ξ [2 u (1 - \frac{x}{l})] . Ф о р м . 12

Для приближенного определения изгибающего момента от нагрузки q можно допустить, что нагрузка судна q_c и начальный зазор Δ представляют собой параболы 2-й степени. Тогда величина изгибающего момента приведенной балки посредине длины килевой дорожки от распределенной нагрузки выразится формулой

M^{q} (\frac{l}{2}) = - \frac{q *}{k^{0}} [1 - φ_{1} (u)], Ф о р м . 13

где

q * = E I^{0} [\frac{E I^{0}}{E_{c} l_{c}^{0}} \cdot \frac{24 (1 - φ_{c}) D_{c}}{φ_{c} L_{c}^{3}} + \frac{8 k^{0} ∆}{l^{2}}],

φ_с — коэффициент полноты эпюры весовой нагрузки судна.

Значения функций

φ_{1} (u), X_{0} (u), μ_{0} (u), φ [2 u \frac{x}{l}], φ [2 u (1 - \frac{x}{l})], ξ (2 u \frac{x}{l}), ξ [2 u (1 - \frac{x}{l})]

в зависимости от аргумента u, u′, u″ приведены в таблице.

Аргументы u, u′, u″ определяются зависимостями

\begin{array}{r} \begin{matrix} u = \frac{1}{2} \sqrt[4]{\frac{k_{0}}{4 E l^{0}}}, \\ u ‘ = 2 u \frac{x}{l}, \end{matrix} \\ u ” = 2 u (1 - \frac{x}{l}) . \end{array}\} Ф о р м . 14

Таблица. Значение функций
$u; u'; u ″ .$	$φ_{1} (u)$	$S (u) = \frac{x_{0} (u)}{μ_{0} (u)}$	$φ (u'); φ (u ″)$	$ξ (u'); ξ (u ″)$
0,0	1,000	1,000	1,000	0,000
0,1	1,000	1,000	0,991	0,090
0,2	0,999	1,000	0,965	0,163
0,3	0,993	0,999	0,927	0,219
0,4	0,979	0,996	0,878	0,261
0,5	0,950	0,991	0,823	0,291
0,6	0,901	0,982	0,763	0,310
0,7	0,827	0,963	0,700	0,320
0,8	0,731	0,944	0,635	0,322
0,9	0,899	0,912	0,571	0,318
1,0	0,852	0,872	0,508	0,300
1,1	0,795	0,820	0,448	0,297
1,2	0,728	0,762	0,390	0,281
1,3	0,653	0,697	0,335	0,263
1,4	0,578	0,628	0,285	0,243
1,5	0,492	0,558	0,238	0,223
1,6	0,411	0,487	0,196	0,202
1,7	0,335	0,419	0,158	0,181
1,8	0,264	0,354	0,123	0,161
1,9	0,201	0,283	0,093	0,142
2,0	0,144	0,149	0,067	0,123
2,2	0,054	0,165	0,024	0,089
2,4	-0,009	0,103	0,006	0,061
2,6	-0,051	0,018	0,025	0,038
2,8	-0,074	0,028	0,037	0,020
3,0	-0,085	0,012	0,042	0,007
3,2	-0,087	0,000	0,043	0,002
3,4	-0,082	0,000	0,041	0,009
3,6	-0,073	-0,014	0,037	0,012
3,8	-0,063	-0,015	0,031	0,014
4,0	-0,052	-0,016	0,026	0,014
4,2	-0,041	-0,017	0,021	0,013
4,4	-0,031	-0,009	0,015	0,012
4,6	-0,022	-0,009	0,011	0,010
4,8	-0,015	-0,010	0,007	0,008
5,0	-0,009	-0,010	0,005	0,006

Используя выражения (Формула 6) и приведенные в настоящем материале приближенные формулы для М (х) = М^{р. м} (х) + М^q(х), можно написать следующие приближенные формулы А. А. Курдюмова и В. В. Козлякова для полных изгибающих моментов, действующих в корпусах дока и судна посредине килевой дорожки:

\begin{array}{r} \begin{matrix} M_{Д} (\frac{l}{2}) = \frac{1}{1 + α} \{M_{0} (\frac{l}{2}) + \frac{α}{2} [M_{0} (0) + M_{0} (l)] φ 1 (u)\} + \\ + \frac{α}{1 + α} \cdot \frac{l}{8} [N_{0} (0) - N_{0} (l)] \cdot \frac{X_{0} (u)}{μ_{0} (u)} - \frac{1}{2} [M_{c} (0) + M_{c} (l)] \times \end{matrix} \\ \begin{matrix} \times φ_{1} (u) - [P_{c} (0) + P_{c} (l)] \frac{l}{8} \cdot \frac{X_{0} (u)}{μ_{0} (u)} + \\ + \frac{E I^{0}}{k_{0}} [\frac{E I^{0}}{E_{c} I_{c}^{0}} \cdot \frac{24 (1 - φ_{c}) D_{c}}{φ_{c} L_{c}^{3}} + \frac{8 k^{0} ∆}{l^{2}}] \cdot [1 - φ_{1} (u)], \\ M_{c} (\frac{l}{2}) = M_{0} (\frac{l}{2}) - M_{Д} (\frac{l}{2}), \end{matrix} \end{array}\} Ф о р м . 15

где

α = \frac{E_{c} I_{c}^{0}}{E_{Д} I_{Д}^{0}} .

По концам килевой дорожки изгибающие моменты в доке равны

\begin{array}{r} M_{Д} (0) = M_{0} (0) - M_{c} (0), \\ M_{Д} (l) = M_{0} (l) - M_{c} (l) . \end{array}\} Ф о р м . 16

Перерезывающие силы можно определить по формулам (Формула 7), пренебрегая величинами N (х) и считая производную

(\frac{E_{c} I_{c} (x)}{E_{Д} I_{Д} (x)})

равной нулю:

\begin{array}{r} N_{Д} (x) \approx \frac{E_{Д} I_{Д} (x)}{E_{c} I_{c} (x) + E_{Д} I_{Д} (x)} N_{0} (x), \\ N_{c} (x) \approx \frac{E_{c} I_{c} (x)}{E_{c} I_{c} (x) + E_{Д} I_{Д} (x)} N_{0} (x) . \end{array}\} Ф о р м . 17

Приближенные формулы для определения реакций килевой дорожки

Наибольшая интенсивность реакций кильблоков в середине длины килевой дорожки обычно определяется по формуле

r (\frac{l}{2}) = b_{c} \frac{D_{c}}{L_{c}}, Ф о р м . 18

где

b_c — не может превосходить максимальной интенсивности весовой нагрузки судна, т. е.

r {(\frac{l}{2})}_{m a x} ⩽ q_{c} m a x Ф о р м . 19

Интенсивность реакций концевых кильблоков определяется по формулам А. А. Курдюмова и В. В. Козлякова

\begin{array}{r} \begin{matrix} r (0) = \frac{1}{1 + α} q_{c} (0) + \frac{α}{1 + α} q_{Д} (0) + \\ + \frac{4 u}{l} [P_{c} (0) - \frac{α}{1 + α} N_{0} (0)] + \\ + \frac{8 u^{2}}{l^{2}} [M_{c} (0) - \frac{α}{1 + α} M_{0} (0) + M_{0}], \end{matrix} \\ \begin{matrix} r (l) = \frac{1}{1 + α} q_{c} (l) + \frac{α}{1 + α} q_{Д} (l) + \\ + \frac{4 u}{l} [P_{c} (l) + \frac{α}{1 + α} N_{0} (l)] + \\ + \frac{8 u^{2}}{l^{2}} [M_{c} (l) - \frac{α}{1 + α} M_{0} (l) + M_{0}], \end{matrix} \end{array}\} Ф о р м . 20

где

M_{0} = M^{q} (\frac{l}{2}) = \frac{E I^{0}}{k_{0}} [\frac{E I^{0}}{E_{c} I_{c}^{0}} \cdot \frac{24 (1 - φ_{c}) D_{c}}{φ_{c} \cdot L_{c}^{3}} + \frac{8 k^{0} ∆}{l^{2}}] \times

\times [1 - φ_{1} (u)] = \frac{0, 376}{1 + α} \cdot \frac{1}{u^{4}} {(\frac{l}{L_{c}})}^{3} \times

\times l [D_{c} \frac{1 - φ_{c}}{φ_{c}} + α D_{б} \frac{1 - φ_{б}}{φ_{б}}] + \frac{8 α}{1 + α} E_{Д} I_{Д}^{0} \frac{1 - φ_{1} (u)}{l^{2}} \times

\times \{∆ c + ∆ 0 - \frac{α_{Д} ∆ t_{Д}^{0} t^{2}}{8 H_{Д}} [1 - \frac{α_{с}}{α_{Д}} \cdot \frac{∆ t_{c}^{0}}{∆ t_{Д}^{0}} \cdot \frac{H_{Д}}{H_{с}}]\} . Ф о р м . 21

В формулу (Формула 21) введен дополнительно член

α D_{б} \frac{1 - φ_{б}}{φ_{б}}

, учитывающий вес балласта, принимаемого в док для изменения моментов или специально для уменьшения концевых реакций.

Интенсивности веса дока у концов килевой дорожки q_д(0) и q_д (l) должны учитывать вес балласта в отсеках, находящихся в этих районах, а также веса малых судов, поставленных в этих районах одновременно с крупным судном, для которого определяются реакции килевой дорожки.

Если отсутствует кривая нагрузки дока (с балластом и малыми судами), величины q_д (0) и q_д (l) можно определять по формулам

\begin{array}{r} q_{Д} (0) = \frac{D_{Д} + Σ D_{c} + D_{б}}{L_{Д}} - \frac{d_{б} (0) + d_{c} (0) + d_{б} (0)}{l_{п} (0)}, \\ q_{Д} (l) = \frac{D_{Д} + Σ D_{c} + D_{б}}{L_{Д}} - \frac{d_{б} (l) + d_{c} (l) + d_{б} (l)}{l_{п} (l)}, \end{array}\} Ф о р м . 22

где q_д, q_c, q₆ — веса дока, малых судов и балласта в пределах длин понтона или отсека l_п (0) и l_п (l) у концов килевой дорожки.

Последняя составляющая в выражении (Формула 21) показывает в развернутом виде величину температурного зазора между судном и доком Δ_t°.

Влияние зазора между судном и килевой дорожкой на реакции кильблоков и распределение усилий между судном и доком

Как было показано выше, дополнительный изгибающий момент на миделе дока от начального зазора между судном и килевой дорожкой Δ = Δ_c + Δ₀ + Δ_t° определяется приближенной формулой:

M_{∆} (\frac{l}{2}) = \frac{8 E I^{0} ∆}{l^{2}} [1 - φ_{1} (u)] = E_{Д} I_{Д}^{0} \cdot \frac{8 α}{1 + α} \cdot \frac{∆}{l^{2}} [1 - φ_{1} (u)] . Ф о р м . 23

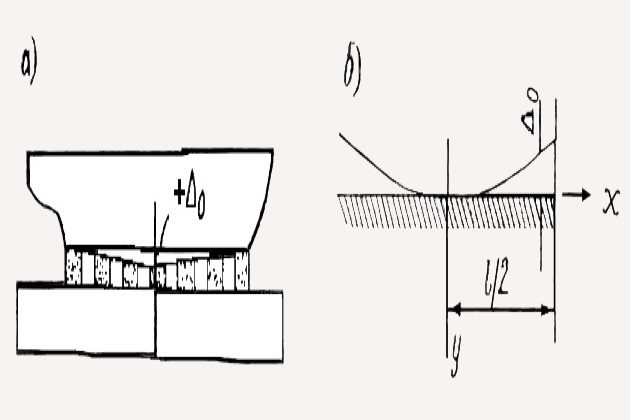
Рис. 2 Схема начального зазора между килевой линией судна и верхней кромкой килевой дорожки; а — при начальном изгибе верхней линии килевой дорожки; б — при деформации килевой линии судна

Величину Δ следует считать положительной, если она направлена от основной линии судна вниз (рис. 2, а). Величина дополнительных напряжений в доке определится формулой

σ_{Д ∆} (\frac{l}{2}) = \frac{M ∆ (\frac{l}{2})}{I_{Д}^{0}} Ζ_{Д m a x} = E_{Д} \frac{8 α}{1 + α} \cdot \frac{∆}{l^{2}} [1 - φ_{1} (u)] Ζ_{Д m a x} . Ф о р м . 24

Если док при постановке судна должен быть прогнут, а судно имеет начальный прогиб Δ_с (при принятом правиле знаков это дает отрицательную величину Δ, рис. 2, б), изгибающий момент в доке увеличивается, а в судне уменьшается на величину М_Δс. Это обстоятельство для дока наиболее опасно и должно учитываться при постановке деформированного судна в док. При известной начальной деформации судна килевой дорожке можно придать начальную стрелку погиби Δ₀ с тем, чтобы, суммарный зазор был близок к нулю:

∆ 0 - ∆ c = 0 . Ф о р м . *

Серьезное внимание должно быть обращено также на возможность изменения усилий в доке и судне при появлении температурного зазора Δ_t°.

Значительное влияние начального зазора между судном и килевой дорожкой на величину усилий в доке и судне приводит к возможности регулирования усилий с помощью преднамеренного создания начального зазора специальной выкладкой кильблоков. Таким приемом может воспользоваться лишь высококвалифицированный специалист и только в тех случаях, когда при приеме предельного (по грузоподъемности дока) судна прочность дока оказывается недостаточной и изменение усилий специальной балластировкой невозможно.

Рекомендуется к прочтению: Вопросы теории корабля и технические графики

Для определения необходимой начальной стрелки прогиба линии кильблоков (при параболическом законе изменения ее по длине килевой дорожки) с целью изменения изгибающего момента в доке на величину М_дΔ

\frac{l}{2}

следует пользоваться формулой (Формула 23). А. А. Курдюмов получил общую зависимость для построения начального зазора Δ₀ по длине килевой дорожки с целью получения заданной эпюры изгибающих моментов М (х) (при Δ_t° = 0):

{∆_{0}}_{μ}^{f} (x) = - ∆_{c} + f_{c} - f_{Д} - \frac{M''}{k} + \frac{M'' (x)}{k} + \int_{0}^{x} \int_{0}^{x} \frac{M (x)}{E I (x)} d_{x} d_{x} + α_{x} + b . Ф о р м . 25

Постоянные а и b определяются из граничных условий для Δ₀, например:

∆_{0} - 0 п р и x = 0 и x = l,

или

∆_{0} = 0, ∆_{0}^{'} - 0 п р и x = \frac{l}{2} .

Регулирование усилий подбором жесткости кильблоков

Изменение усилий в доке и судне в необходимом направлении можно получить соответствующим распределением по длине жесткости кильблоков. Этот метод, применявшийся с давних пор теоретически разработан А. А. Курдюмовым.

Покраска корпуса — Покраска надводной части корпуса круизного судна
Источник: pixabay.com

Подбор необходимого закона изменения жесткости килевой дорожки может быть осуществлен путем проб и проверочных расчетов или расчетным методом по схеме, разработанной А. Г. Архангородским, В. Г. Поповым и О. Л. Чернышевым.

Так как кривая реакций считается заданной, разыскание упругой линии балки сводится к решению уравнения

(E I (x) υ ″ (x)) ″ = q (x) - r (x) .

Представляя

υ

(х) в виде

υ (x) = f (x) + α + β x,

получим

f (x) = \int_{0}^{x} \int_{0}^{x} \frac{1}{E I (x)} \{M (0) + \int_{0}^{x} [P (0) + \int_{0}^{x} (q (x) - r (x)) d x] d x\} \times d x d x + C_{1} x + C_{0}, Ф о р м . 26

где

C₁ и С₀ определяются из условия

F (0) = f (l) = 0 .

Получив значения υ (х) при заданном r (х), можно из формулы (Формула 1) получить значения приведенного коэффициента жесткости k (x) и соответственно коэффициента жесткости кильблоков К₁ (х). Практические вычисления рекомендуется выполнять по упомянутой работе, учитывая, что при постановке судна в плавучий док все результаты относятся к элементам изгиба приведенной балки.

Полученный в результате такого решения закон распределения жесткости кильблоков по длине К₁(х) может быть достигнут различным сочетанием размеров стальной (в некоторых случаях бетонной), дубовой и сосновой части кильблоков по формулам (Формула 1) и (Формула 4).

Можно также заменять значение f (х) величиной

F (x) = f (x) + ∆_{с} .

При неизвестной величине строительного прогиба судна для снижения местных повышенных реакций применяют сминающиеся прокладки.

Предельную нагрузку прокладок выбирают на 10—15% выше величины расчетной реакции без учета начального прогиба судна, но не выше допустимой нагрузки для дока или судна. Изготовляют прокладки обычно из мягких пород дерева (ель, пихта, сосна).

Условия ремонта, достройки и подкрепления судов в плавучих доках

При ремонте, достройке и модернизации судов часто возникает необходимость замены отдельных связей корпуса или установки дополнительных подкреплений. Если при производстве этих работ изгибающий момент в соответствующем сечении корпуса судна не равен нулю, напряжения во вновь установленных связях при дальнейшей эксплуатации судна будут отличаться от напряжений в «старых» связях.

Так, если при ремонте суднаРемонт корпуса судна и судовых устройств изгибающий момент равен

M_{_{c}}^{(1)}

и момент сопротивления корпуса (с учетом уменьшения при снятии каких-либо связей) равен

W_{_{c}}^{(1)}

, напряжения в оставшихся связях корпуса равны

σ_{_{c}}^{(1)} = \frac{M_{c}^{(1)}}{W_{c}^{(1)}} .

Дополнительные напряжения в этих же связях после установки подкреплений и при действии изгибающего момента

M_{c}^{(2)}

равны

∆ σ_{c}^{1} = \frac{M_{c}^{(2)} - M_{c}^{(1)}}{W_{c}^{(2)}} .

Соответствующие суммарные напряжения в «старых» связях равны

σ_{c}^{(2)} = σ_{c}^{(1)} + ∆ σ_{c}^{(1)} = \frac{M_{c}^{(1)}}{W_{c}^{(1)}} + \frac{M_{c}^{(2)} - M_{c}^{(1)}}{W_{c}^{(2)}} =

\frac{M_{c}^{(2)}}{W_{c}^{(2)}} + M_{c}^{(1)} \frac{W_{c}^{(2)} - W_{c}^{(1)}}{W_{c}^{(1)} \cdot W_{c}^{(2)}},

при этом напряжения в «новых», или «замененных», связях равны

∆ σ_{с}^{1}

Если, как видно из приведенных формул, при установке новых связей изгибающий момент в корпусе судна не равен нулю

(M_{с}^{1} \neq 0)

, то при дальнейшей эксплуатации судна напряжения в старых связях больше определяемых по обычному расчету

(σ_{c}^{(2)} = \frac{M_{c}^{(2)}}{W_{c}^{(2)}})

на величину

M_{c}^{(1)} \cdot \frac{W_{c}^{(2)} - W_{c}^{(1)}}{W_{c}^{(1)} \cdot W_{c}^{(2)}}

, а в новых — меньше на величину

- \frac{M_{c}^{(1)}}{W_{c}^{(2)}}

Если же моменты

M_{c}^{(1)}

M_{c}^{(2)}

имеют разные знаки, напряжения в старых связях будут соответственно меньше расчетных, а в новых — больше.

При замене связей корпуса, в случаях, когда

M_{c}^{(1)} \neq 0

, возникает также концентрация напряжений в районах, прилегающих к удаляемым связям, оказывающая существенное отрицательное влияние на напряженное состояние корпуса при дальнейшей эксплуатации и снижающая фактический запас прочности.

Для получения суммарного нулевого момента в корпусе судна второй член М (х) в выражении для М_с (х) по формуле (Формула 6) должен быть равен первому члену

\frac{E_{c} I_{c}^{1} (x)}{E_{c} I_{c}^{1} (x) + E_{Д} I_{Д} (x)} M_{0} (x)

с обратным знаком (величина

I_{c}^{1} (x)

характеризует корпус в ослабленном сечении).

Для соединения двух частей судна необходимо так выровнять судно на кильблоках, чтобы угол поворота обеих половин корпуса судна в районе соединения был равен нулю:

υ_{c}^{'} (x) = 0 .

Это может быть достигнуто соответствующим подбором жесткости килевой дорожки, подклинкой кильблоков после установки судна в док или балластировкой дока.

Паром на реке Рейн
Источник: pixabay.com

При замене связей днища иногда требуется убрать кильблоки в районе ремонтируемого участка. Для приведения к нулю изгибающего момента в этом районе можно воспользоваться методом подбора жесткости кильблоков в оставшихся частях килевой дорожки.

Предлагается к прочтению: Некоторые вопросы по эксплуатации плавучих доков

При ремонте судна в доке иногда испытывают отсеки наливом воды. Влияние принятой в отсеки судна воды на величину реакций кильблоков и усилий в корпусах судна и дока можно оценить как изменением нагрузки судна q₀ (х), так и способом наложения, уравновешивая дополнительный вес судна ΔР_с дополнительными силами поддержания дока Δω_д и вычисляя дополнительные моменты ΔМ₀ (х) и ΔМ (х).

Для учета налива воды можно использовать также схему Б. Л. Николаи и А. А. Селиверстова.

Определение усилий при постановке нескольких судов в один док, одного судна в два дока, при неполном доковании судна

1 Если плавучий док поднимает несколько малых судов, располагающихся в доке по одной линии («в кильватер»), следует считать, что док воспринимает полный изгибающий момент, возникающий в системе док — судно, так как в промежутках между судами они не воспринимают свою долю момента, т. е.

M_{Д} = M_{0} .

2 Если в док ставится два или несколько судов параллельно друг другу и все они имеют соизмеримую длину, задача решается так, как указано в предыдущих материалах. В этом случае за момент инерции (или жесткость) комплекта судов принимается сумма их моментов инерции (или жесткостей)

E_{к о м п л} \cdot I_{к о м п л} (x) = \sum_{1}^{n} E_{c}^{(n)} I_{c}^{(n)} (x) .

Изгибающие моменты воспринимаются каждым из судов пропорционально их жесткостям:

M_{c}^{(n)} = M_{c} \cdot \frac{E_{c}^{(n)} \cdot I_{c}^{n}}{\sum_{1}^{n} E_{c}^{(n)} \cdot I_{c}^{(n)}} .

3 Если в док ставится комплект из одного большого судна (или двух больших судов) и несколько малых, вес малых судов следует включать в нагрузку дока, не учитывая их жесткости, а суммарные усилия распределять между доком и большим судном (или двумя большими судами) так, как указано выше.

4 При постановке одного судна в два дока величины суммарных моментов и усилий М₀(х) и N₀(х) следует определять обычным способом, считая за полную длину дока суммарную длину двух доков и исключая силы поддержания в промежутке между двумя доками (аналогично промежуткам между понтонами самодокующегося дока).

В промежутке между двумя доками изгибающий момент и перерезывающая сила воспринимаются только корпусом судна:

M_{c} = M_{0}; N_{c} - N_{0} .

Каждый док рассчитывают отдельно, причем за граничные условия в промежутке между доками принимают указанные величины М₀ и N₀ на границе между доками. Предполагается, что два дока не соединены шарниром (при шарнирном соединении двух доков следует определить также реакцию в шарнире).

5 При неполном всплытии дока с судном и осадке их «на ровный киль» нагрузка судна q’_c определяется как разность веса судна q_c и сил поддержания судна во всплывшем состоянии

γ ω_{с}

q_{c}^{'} = q_{c} - γ ω_{с}

Вес дока q_д должен учитывать вес оставшегося в отсеках балласта, а силы поддержания дока — объем понтонов и погруженной части башен.

Судно в доке — Ремонтный док в Гамбурге
Источник: pixabay.com

При подъеме одной из оконечностей судна нагрузка судна на длине килевой дорожки, вес свешивающейся оконечности и момент этого веса относительно конца килевой дорожки определяются с учетом сил поддержания судна. Вес дока определяется с учетом неравномерного распределения балласта в отсеках дока. Силы поддержания дока определяются с учетом его дифферента.

Сноски