Плавучий док представляет собой один или несколько соединенных между собой понтонов, разделенных на отсеки и поверху которых расположены башни. В материале представлены расчеты, с помощью которых возможно определить прочность плавучего дока.
Общая характеристика поперечного изгиба дока
Обеспечение поперечной прочности при проектировании доков является таким же важным условием, как и обеспечение общей продольной прочности. Поперечная нагрузка воспринимается поперечными связями. В связи с ограниченной высотой понтонов транспортных доков иногда не удается обеспечить поперечную прочность при постановке судна на одну диаметральную килевую дорожку и приходится предусматривать их две или три (рис. 1).
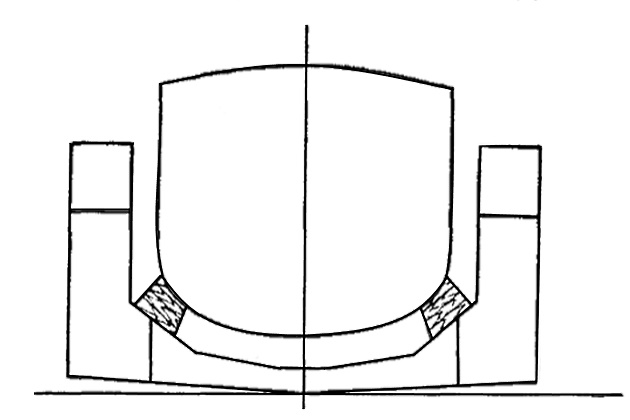
По принятой в практике расчетной схеме поперечные связи рассматриваются как изолированные «плавающие» балки1.
1При расчете прочности поперечных переборок на изгиб, особенно торцовых переборок понтонов самодокующихся доков, следует учитывать реакции от продольных переборок.
Уравновешенность действующих на поперечную связь нагрузок достигается приложением соответствующих сил в районе башен (реакций опор).
Определение внешних сил, вызывающих общий поперечный изгиб понтонов
Реакция кильблоков на поперечную связь определяется так:
- где r — интенсивность реакций кильблоков;
- S — расстояние между поперечными связями (шпация).
Для транспортных доков одним из расчетных случаев является положение дока с судном на подошве волны при минимальном погружении поперечных сечений.
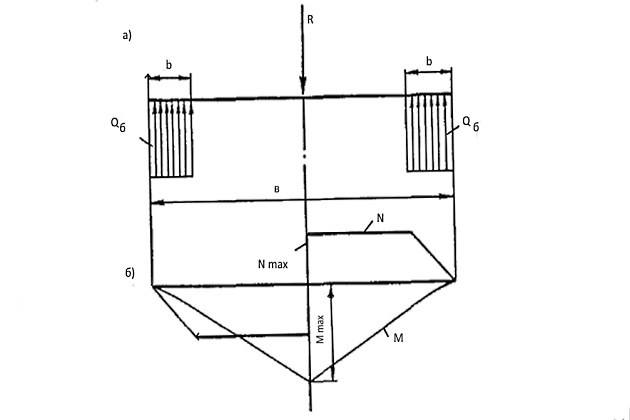
Рис. 2 Расчетная схема поперечного изгиба для транспортного дока при наибольшем прогибе (без учета сил поддержания): а — эпюра внешних нагрузок; R — сила давления кильблока;
— реакция башен; b — ширина башен; б — эпюры изгибающего момента M и перерезывающей силы N
В этом случае поперечные изгибающие моменты (М) и перерезывающие силы (N) от реакции кильблока могут определяться с ошибкой в безопасную сторону без учета сил поддержания. Для рассматриваемого случая
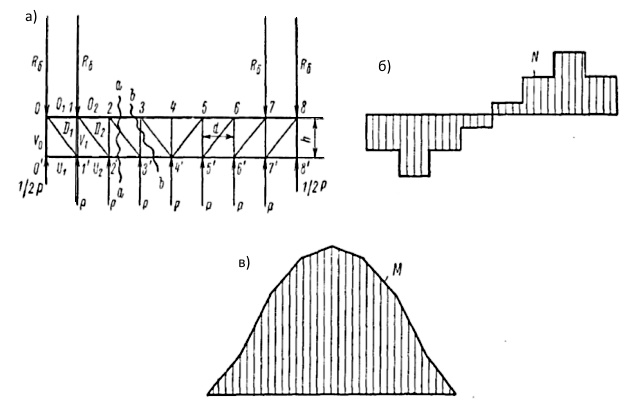
При погружении (всплытии) реакции кильблока изменяются в функции от осадки дока; характер изменения усилий при этом показан на рис. 3.
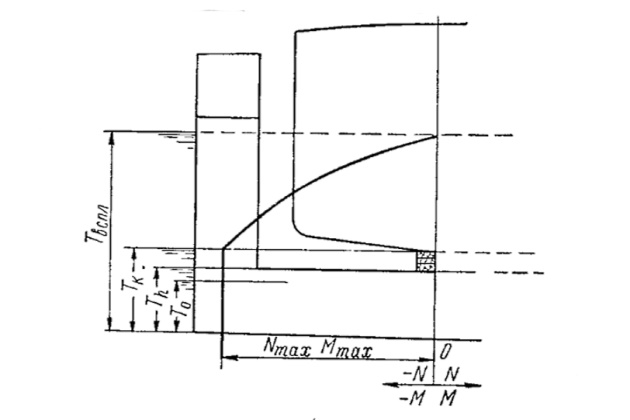
В поперечных связях дока без судна возникает перегиб, величина которого зависит от осадки дока при погружении — всплытии. Чтобы проанализировать изменения усилий при погружении – всплытии, рассмотрим несколько промежуточных положений дока. Составим для этих положений выражения максимальных значений поперечного изгибающего момента и поперечной перерезывающей силы. Будем считать, что балласт принимается равномерно по ширине и длине дока.
1-й случай. Положение полного всплытия по начальную осадку Т0 (рис. 4).
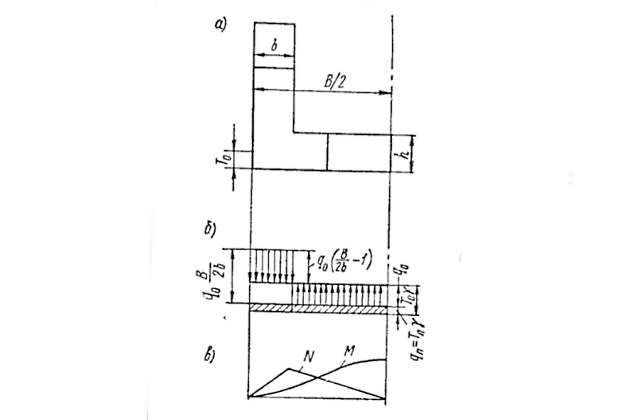
Для рассматриваемого случая
где
- γ — удельный вес воды;
- Qп — вес понтона дока.
Для «идеального» ремонтного дока
- Qб — вес башен дока.
2-й случай. Начало погружения Тн (рис. 5).
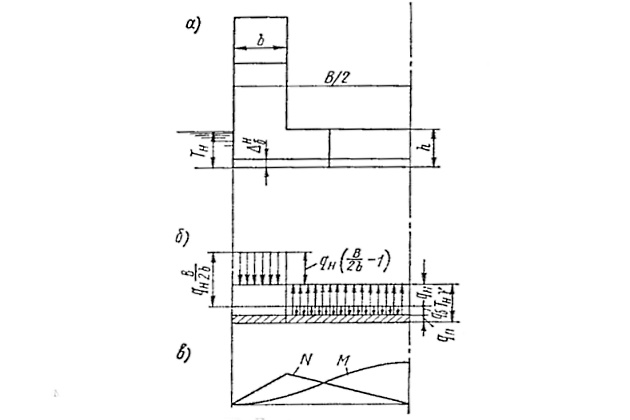
Рис. 5 Расчетная схема поперечного изгиба при осадке Тн, соответствующей началу погружения дока (
— Уровень принятого балласта): а — положение дока по осадку Тн; б — эпюра поперечной нагрузки; в — эпюры поперечных усилий (изгибающего момента М и перерезывающей силы N)
Для рассматриваемого случая
где
При равномерном погружении порожнего дока можно полагать, что
Тогда
т. е. величина усилий не изменяется при начальном погружении. Это положение остается справедливым до осадки Th = h (h — высота понтона, см. рис. 4, 5), когда начинает заливаться стапель-палуба.
Предлагается к прочтению: Конструкции и проектирование корпусов плавучих доков
В общем виде выражения для Nmax и Мmax в диапазоне осадок Т0 ≤ Ti ≤ Th будут иметь вид
Чтобы учесть при осадках Тi >Th влияние вливающейся на стапель-палубу воды, рассмотрим отдельно усилия, возникающие от ее веса (рис. 6).
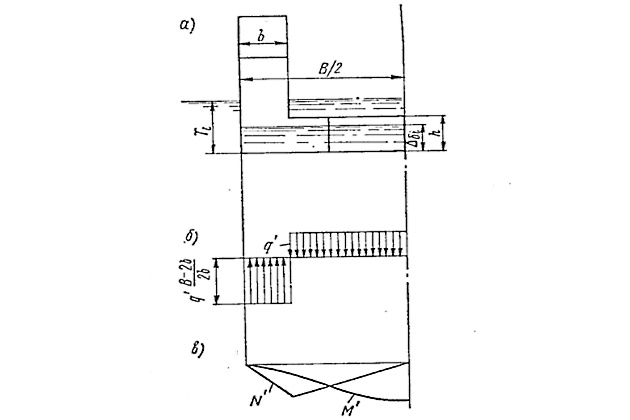
Для рассматриваемой системы дополнительных сил
Просуммировав (Формула 5) с (Формула 4), получим общее выражение максимальных, поперечных усилий для диапазона осадок Т0 ≤ Тi ≤ TΔ, где TΔ — осадка, соответствующая уровню балласта в понтоне Δб = h:
Только для осадок h ≤ Тi ≤ TΔ выражения (Формула 6) принимают вид
Из выражения (Формула 7) видно, что при осадке
, когда
то
Обычно для ремонтных доков h < Т0 < TΔ.
При запрессовке понтона балластом, т. е. при осадке TΔ, когда Δб = h,
Возникший прогиб понтона остается постоянным и при дальнейшем погружении.
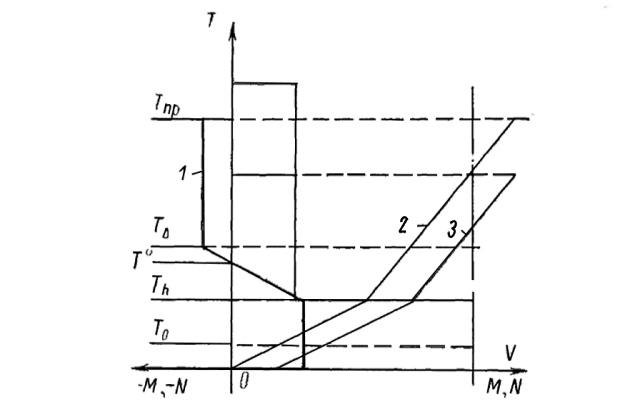
Усилия порожнего дока от гидростатического напора при погружении — всплытии имеют вид, представленный на рис. 7
Изменения суммарных усилий при погружении — всплытии дока с судном показаны на рис. 8.
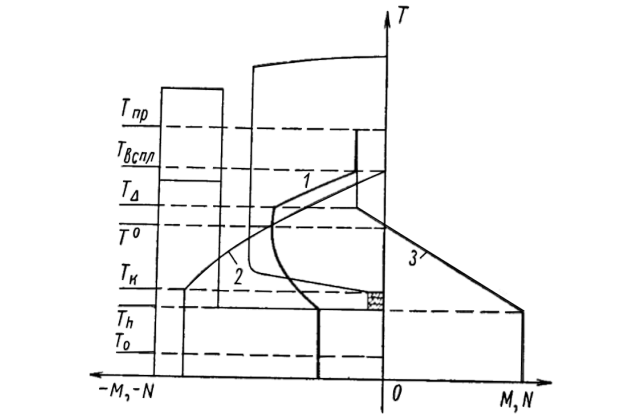
Формулы для Mmax, Nmax и графики их зависимости от осадки при погружении — всплытии не учитывают неравномерность приема (откачки) балласта по длине дока. Для учета этого явления при определении перегиба перепад давлений
рекомендуется увеличивать на 20% (см. Определение размеров продольных связей корпусаНекоторые вопросы проектирования и постройки корпусов доков).
В табл. 1 приведены выражения для определения расчетных значений изгибающих моментов и перерезывающих сил, соответствующих определенным случаям эксплуатации доков.
| Таблица 1. Формулы для расчета поперечных изгибающих моментов и перерезывающих сил | |||
|---|---|---|---|
| Тип дока | Положение дока (расчетное) | Формулы для расчетных M и N | Примечания |
| Прогиб | |||
| Транспортный | Док с судном на подошве волны | Предполагается, что днище понтона оголено | |
| Ремонтный | Док с судном в рабочем положении | ||
| Перегиб | |||
| Транспортный | Док без судна на вершине волны | r – полувысота расчетной волны. Вес понтона (в запас) не учитывается | |
| Ремонтный | Док без судна при погружении (всплытии) | Максимум определяется по диаграмме затопления. | |
Наличие сухого отсека в понтоне может оказаться благоприятным (с точки зрения поперечной прочности дока с судном) в диапазоне осадок Т0÷ТΔ. Так, сухой отсек в середине понтона для осадок То < Тi < ТΔ дает следующий дополнительный перегибающий момент:
При осадках Тi > ТΔ
- где bс.о — ширина сухого отсека.
Характерным для понтонов дока является применение ферм редко используемых в конструкции корпуса судна.
Расчеты ферм отличаются некоторыми особенностями.
Расчет раскосных ферм
Раскосная ферма это система, сохраняющая геометрическую неизменность и в том случае, если предположить, что все ее узлы шарнирны. На этом предположении основаны применяемые методы определения усилий в конструктивных элементах ферм. Основные методы расчета приведены ниже.
Будет интересно: Расчет общей продольной прочности дока
Способ Максвелла-Кремоны для расчета усилий в статически определимых фермах. Усилия в стержнях фермы определяются при помощи диаграмм усилий от нагрузки, приведенной к узлам верхнего или нижнего с обозначения полей фермы (рис. 9) и силового многоугольника внешних сил Р, включающего уравновешивающие силы — реакции башен Rб. Силовой многоугольник строится в последовательности получающейся при обходе фермы, например, по часовой стрелке. Затем, начиная с узла, в котором сходится не более двух стержней, с последующим переходом к узлам, где сходится не более двух новых стержней, строятся замкнутые силовые многоугольники. Отрезки прямых диаграммы, замеренные в масштабе многоугольника внешних сил, определяют значения усилий Si в стержнях фермы.
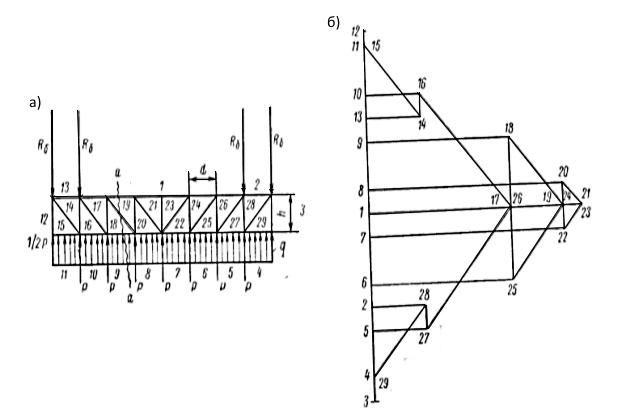
Знак усилия (сжатие или растяжение) определяется его направлением относительно узла фермы при обходе соответствующего силового многоугольника. Усилие, направленное к узлу, вызывает сжатие стержня; усилие, направленное от узла — растяжение. Направление обхода определяется направлением известной внешней силы в рассматриваемом узле.
Диаграмма Максвелла-Кремоны обладает следующими свойствами, могущими служить для проверки правильности ее построения:
- усилия в стержнях фермы, перерезанных сквозным сечением, вместе с внешними силами, расположенными по одну сторону от сечения, образуют на диаграмме замкнутый силовой многоугольник (например, сечение a — a на рис. 9, a соответствует многоугольнику 12—13—1—19—18—9—10—11—12 на рис. 9, б);
- усилия в стержнях, ограничивающих поле фермы, сходятся на диаграмме в одной точке, одноименной полю фермы, и, наоборот, вершины силового многоугольника, соответствующего усилиям определенного узла фермы, имеют номера полей, примыкающих к этому узлу;
- симметричной ферме с симметричной нагрузкой соответствует симметричная диаграмма усилий; оси симметрий фермы и диаграммы усилий повернуты относительно друг друга на 90°;
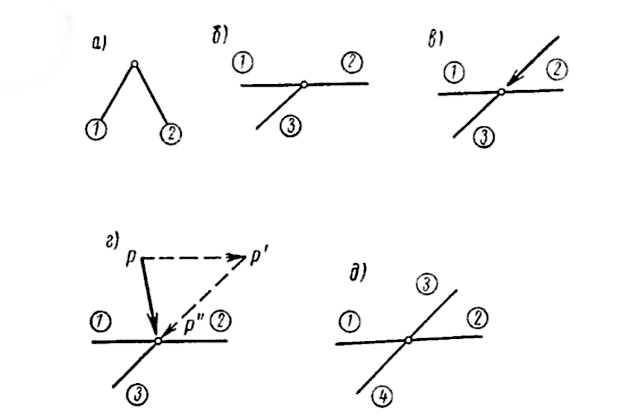
- узлы фермы должны быть статически уравновешены (частные случаи даны на рис. 10).
Способ сечений имеет то преимущество перед графическим способом Максвелла-Кремоны, что позволяет сразу определять усилия в любом сечении фермы. Это преимущество возрастает при определении усилия только в одном стержне или в небольшой группе стержней.
Способ сечения заключается в следующем. Ферму рассекают на две части так, чтобы в сечение попало не более трех стержней с неизвестными усилиями. Одну из частей фермы удаляют, а действие ее на оставшуюся часть заменяют неизвестными усилиями. Условия равновесия оставшейся части фермы можно записать в форме трех уравнений моментов всех действующих сил. Моментные точки следует выбирать в точках парного взаимного пересечения рассеченных стержней, тогда каждое уравнение равновесия будет содержать одну неизвестную. Выбранные таким способом моментные точки получили название «точки Риттера».
Усилия в стержнях определяются из уравнения
- где М — момент всех сил, приложенных к рассматриваемой отсеченной части фермы, относительно моментной точки;
- ρ — плечо усилия.
Если моментная точка находится в пределах пролета фермы, то М является изгибающим моментом балки того же пролета, что и ферма в сечении под моментной точкой. Такая балка называется «заменяющей».
Чтобы определить усилия в поясах и раскосах фермы с параллельными поясами, следует проводить разрезы типа a — a, а в стойках — типа b — b (рис. 1). Моментные точки (точки Риттера) для определения усилий в поясах фермы расположены в пределах пролета фермы. Для усилий любого стержня верхнего пояса моментной точкой является нижний узел той же панели, где пересекаются рассеченные раскос и стержень нижнего пояса (узел 3′ для усилия стержня 2—3); для стержней нижнего пояса моментной точкой является соответствующий верхний узел той же панели (узел 2 для усилия стержня 2′ — 3′).
Пользуясь эпюрой изгибающих моментов «заменяющей» балки (рис. 11, в), можно вычислить усилия в обоих поясах:
Точки Риттера для определения усилий в раскосах рассматриваемой фермы с параллельными поясами удалены по горизонтальному направлению в бесконечность. Соответствующее уравнение моментов превращается в уравнение проекций сил на вертикальную ось, которое можно рассматривать как уравнение моментов относительно бесконечно далекой моментной точки. Так, уравнение равновесия для раскосов левой половины фермы (рис. 12) имеет вид
откуда
- где N — перерезывающая сила в рассматриваемом сечении «заменяющей» балки.
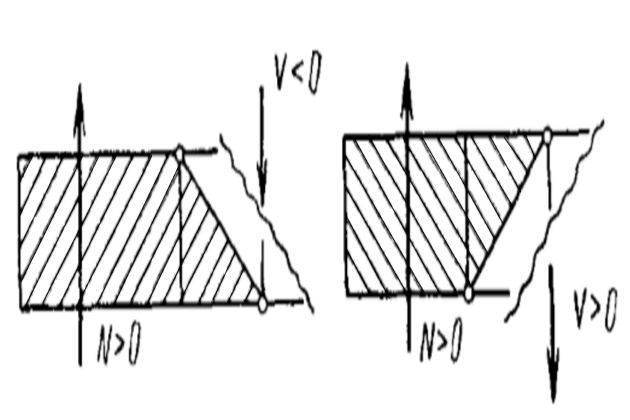
Знак усилия в раскосе (растяжение или сжатие) определяется в зависимости от знака перерезывающей силы и направления наклона раскоса относительно действия внешней нагрузки (нисходящий к середине фермы или восходящий). Правило определения знака усилия в раскосе видно из рис. 12.
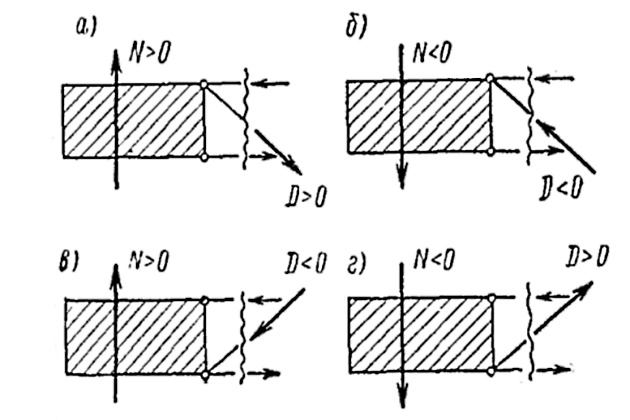
В раскосной ферме с параллельными поясами при действии равномерно распределенной нагрузки нисходящие раскосы всегда растянуты, восходящие — сжаты. Если нагрузка распределена неравномерно, то в одной или нескольких средних панелях возможно отступление от этого правила.
Усилия V в стойках фермы определяются по выражению
- где знак «минус» относится к левой схеме рис. 13, а «плюс» — к правой.
Если равнодействующая внешних сил в отсеченной части фермы направлена вверх, то усилие V направлено вниз, и наоборот. При равномерно распределенной нагрузке все стойки фермы с нисходящими раскосами сжаты, а с восходящими — растянуты.
Определение напряжений в стержнях ферм. По найденным усилиям определяются напряжения.
Для днищевых ригелей фермы и ригелей стапель-палубы напряжения определяются с учетом их изгиба (см. Расчеты местной прочности металлических плавучих доковРасчеты местной прочности металлических плавучих доков):
- где М — изгибающий момент от пролетной нагрузки ригеля;
- Wmin — момент сопротивления профиля стержня;
- Fi — площадь сечения стержня.
Сжатые элементы фермы должны быть проверены на устойчивость.
1 Определение деформации ферм. Перемещение vip любого из узлов статически определимой фермы от нагрузки вычисляется по формуле Максвелла-Мора
где
i — усилия в стержнях фермы от единичной силы, приложенной в рассматриваемом узле по искомому направлению;
- Sp — усилия в стержнях фермы от внешней нагрузки.
Знак суммы в формуле (Формула 13) распространяется на все стержни фермы. Расчет перемещений узлов по приведенной формуле удобно производить в форме таблицы (табл. 2). Усилия Si и
p определяются одним из изложенных выше способов.
| Таблица 2. Расчет деформаций фермы от нагрузки | ||||||
|---|---|---|---|---|---|---|
| № стержня | Длина стержня см | Площадь стержня см2 | Усилие от единичной нагрузки кг | Усилие от внешней нагрузки Р кг | ||
| 1 | l1 | F1 | ||||
| 2 | l2 | F2 | ||||
| 3 | l3 | F3 | ||||
| · | · | · | · | · | · | · |
| · | · | · | · | · | · | · |
| · | · | · | · | · | · | · |
| n | ln | Fn | ||||
2 Температурные перемещения
в статически определимой ферме могут быть вычислены по формуле
- где t — изменение температуры стержня по сравнению с начальной;
- α — коэффициент линейного расширения материала стержня (для стали а = 11,0×10-6в).
Остальные обозначения прежние.
Существующие графические способы (диаграммы Вилио и способ построения веревочного многоугольника «упругих сил») наглядно иллюстрируют перемещения узлов фермы при ее деформации.
Расчет статически неопределимых ферм
Конструкция понтонной фермы может иметь так называемые «лишние» стержни (рис. 14, а), превращающие ее в статически неопределимую систему.
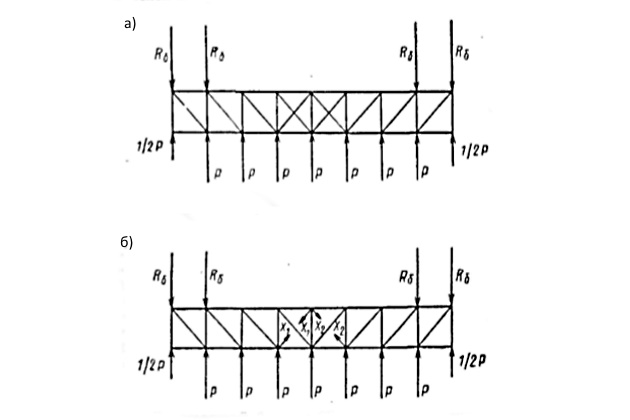
Решение статически неопределимых ферм состоит из следующих этапов:
1 лишние связи из системы исключаются и их действие заменяется неизвестными силами (рис. 14, б);
2 для так называемой основной фермы (без лишних стержней) составляются канонические уравнения равновесия деформаций. Так, для фермы с одним лишним стержнем (ввиду симметрии Х1 = Х2).
Количество уравнений должно соответствовать числу лишних неизвестных. При n лишних стержнях уравнения имеют вид:
причем, как всегда, в канонических уравнениях δik =bki;
3 определяются коэффициенты при неизвестных и свободные члены канонических уравнений по формулам
где усилия
в стержнях основной фермы, вызванные силой X = 1 и Sp от внешней нагрузки, определяются одним из изложенных выше способов;
4 из канонического уравнения (Формула 11) определяются неизвестные:
5 определяются окончательные значения усилий в любом стержне фермы по формуле
Вычисления формулы (Формула 17) рекомендуется вести в табличной форме, причем для вычисления δ11 и υ1p можно использовать форму табл. 2.
Если необходимо определить n неизвестных усилий, расчет коэффициентов и свободных членов системы уравнений может быть также произведен в табличной форме (по типу табл. 2).
При расчете статически неопределимой фермы на заданное воздействие температуры порядок решения сохраняется. Каноническое уравнение (Формула 11) принимает вид
Свободный член vit определяется по формуле
Усилие в любом стержне фермы
При вычислении прогибов статически неопределимой фермы от поперечной нагрузки следует также использовать формулу Максвелла-Мора. Усилия Sp для этой формулы вычисляются в заданной статически неопределимой ферме (Формула 18), a
в основной ферме, полученной из статически неопределимой отбрасыванием лишних стержней.
Рекомендуется к прочтению: Некоторые вопросы по эксплуатации плавучих доков
Температурные перемещения υit в статически неопределимых фермах вычисляются по формуле
- где St — усилия в стержнях заданной фермы, вызванные изменением температуры, вычисленные по формуле (Формула 20).
Расчет безраскосных ферм
Безраскосная ферма или жесткая рама это такая стержневая система, геометрическая неизменяемость которой достигается за счет жесткости узловых соединений стержней стоек и поясов фермы.
Раскрытие статической неопределимости фермы приводит к определению лишних неизвестных из системы канонических уравнений, число которых, равное числу лишних неизвестных, должно быть 3m, где m — число панелей фермы.
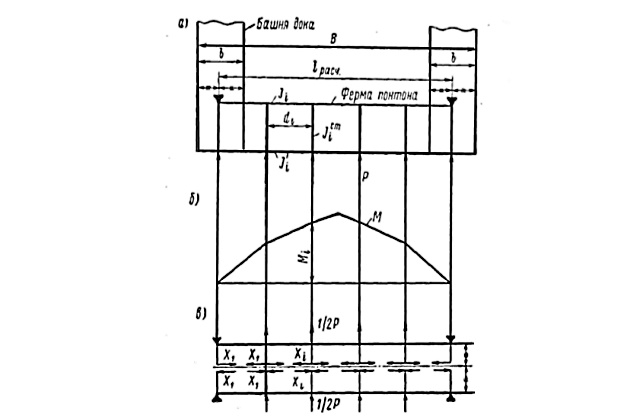
Для фермы с параллельными поясами (рис. 15, а) лишние неизвестные определяются из уравнения
где
— средний момент инерции поясов i-й панели;
— моменты инерции стоек;
— ординаты эпюры изгибающих моментов «заменяющей» балки (рис. 15, б).
Остальные обозначения видны из приведенной на рис. 15 схемы фермы.
Уравнение (Формула 22) представляется в виде системы канонических уравнений, первое и последнее из которых имеют, двухчленный вид, а промежуточные — трехчленный:
где
- I0 — произвольно выбранное значение момента инерции.
Так, для фермы с пятью панелями уравнения (Формула 23) будут иметь следующий окончательный вид2:
2Развертывание уравнения Галеркина (Формула 22) в форме системы канонических уравнений вида (Формула 23) заимствовано из работы А. С. Малиева, Расчет безраскосной фермы.
Изгибающий момент
в произвольном сечении i-й панели, имеющей абсциссу xi равен:
Максимальное значение изгибающего момента для стоек равно: для верхней точки
для нижней точки
Продольные усилия в стойках равны:
- где Рi — значение нагрузки в узле фермы.
Знак усилия Scт в стойке зависит от приложения внешней нагрузки. Если нагрузка приложена снизу, то стойка растянута, Scт имеет знак (+); если нагрузка приложена сверху, стойка сжата, Scт имеет знак (—).
Перерезывающая сила в поясах фермы равна половине перерезывающей силы «заменяющей» балки. В стойках перерезывающая сила равна
При определении перемещений узлов безраскосной фермы следует пользоваться обобщенной формулой Максвелла-Мора:
- где k — коэффициент неравномерности распределения касательных напряжений;
— усилия в стержнях от внешней нагрузки Р;
— усилия от нагрузки Р = 1, приложенной в рассматриваемом узле в искомом направлении.
Значения интегралов в формуле Максвелла-Мора определяются перемножением эпюр соответствующих усилий для определенного стержня фермы по правилу Верещагина. Усилие от внешней нагрузки (Мр, Sр, Nр) находятся из решения заданной статически неопределимой фермы; усилия
от Р = 1 могут быть найдены из статически определимой схемы заданной фермы (образующейся включением шарниров в середине пролетов всех ригелей фермы и стоек, кроме одной средней).
Читайте также: Металлические плавучие доки — общие сведения и классификация
Достаточно удобный способ расчета безраскосных ферм предложен В. В. Козляковым (способ основан на выводах теории составных стержней А. Р. Ржаницына). Прогиб безраскосной фермы по В. В. Козлякову определяется следующим образом:
- где I0 — момент инерции монолитной балки, составленной из поясов фермы;
- R — коэффициент (больший единицы), учитывающий особенности конструкции фермы.
Наиболее близко представляет работу днищевых понтонных ферм дока свободно опертая равномерно загруженная балка (с несдвигающимися, по А. Р. Ржаницыну, торцами) (см. рис. 16).

Выражение максимального прогиба будет иметь вид
где
— коэффициент, график которого приведен на рис. 17;
— моменты инерции поясов фермы;
— средние значения площади и момента инерции поясов фермы;
— площадь и момент инерции сечения стойки фермы.
Напряжения в какой-либо точке А поперечного сечения пояса фермы определяются по формуле
где
— напряжения в точке А в балке, составленной из поясов фермы, но без стоек;
- М° — изгибающий момент монолитной балки;
- ZА — расстояние от точки А до нейтральной оси стержня пояса фермы;
— напряжения в точке А, как в монолитной балке;
- UА — отстояние от точки А до нейтральной оси монолитной балки;
- ψ — коэффициент, учитывающий «сдвиговую» жесткость фермы по отношению к монолитной балке. Значения ψ = f (λl) приведены на рис. 17.
Дополнительные напряжения в поясах фермы от узловых моментов определяются по формуле
где
— среднее значение касательных напряжений в стойке;
— интенсивность касательных напряжений;
- х1 — координата рассматриваемой стойки;
— абсцисса максимального сдвигающего напряжения;
- S — статический момент площади верхнего или нижнего пояса.
Графики функций
и
приведены на рис. 17.
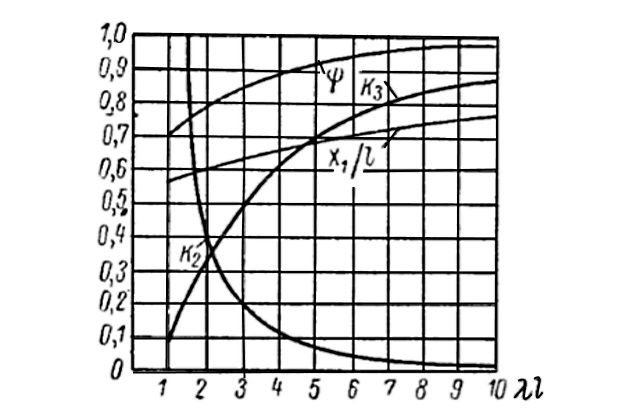
Рис. 17 Графики функций k2, ψ; k3 и
Максимальные нормальные напряжения в стойке определяются по формуле
- где Wmin — минимальный момент сопротивления профиля стойки.
