Условия управляемости судна и расчеты производятся по технике, изложенной ниже для безопасного управления малотоннажным плавательным средством.
Частные случаи расчета управляемости судна
Расчет поворотливости при кавитации руля
В случае возникновения кавитации на руле судна расчет поворотливости может быть произведен по формулам, приведенным в статье “Маневренность судна и расчеты крена на циркуляции”Способы вычисления маневренности судна на криволинейной траектории. Только в этом случае производная коэффициента подъемной силы изолированного руля
, на основании которой вычисляется боковая сила на руле, определяется не по формуле 18 в статье Управляемость малого судна“Гидродинамические характеристики изолированного руля”, а по данным атласа для соответствующего значения κ.
Для использования формулы 1 графики зависимости CYR = f(δR) приводятся к условному виду, показанному на рис. 1.
В формуле 1:
– угол перекладки изолированного руля, при котором кривая зависимости
, соответствующая кавитационному режиму, „отваливается” от кривой
при отсутствии кавитации (см. рис. 1, б);
– производная коэффициента подъемной силы (тангенс угла наклона) на участке
(см. рис. 1, б), для случая
определяется так же, как для кривой, исходящей из начала координат (рис. 1, a);
– определяется по формуле 18 в статье Управляемость малого судна“Гидродинамические характеристики изолированного руля”;
δR – углы перекладки руля, для которых производился расчет
без учета кавитации;
при δR ≠ 0 в формулу Способы вычисления маневренности судна на криволинейной траектории“Определение приемлемой эксплуатационной устойчивости” подставляются значения
- κE определяется по формуле 30 в статье Управляемость малого судна“Влияние ГВ и корпуса на ГДX руля”.
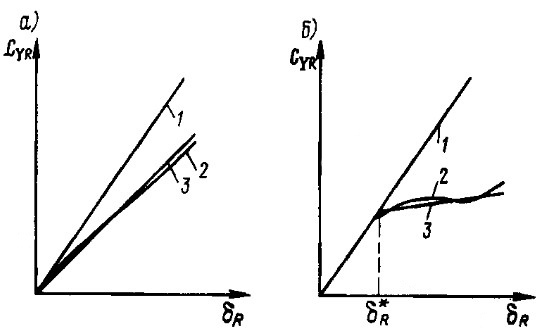
Рис. 1 К расчету управляемости судна с учетом кавитации руля:
а, б – различный вид зависимостей CYR=f(δR) кавитирующих рулей.
1 – зависимость CYR=f(δR) некавитирующего руля; 2 — зависимость CYR=f(δR) кавитирующего руля; 3 — условная зависимость CYR=f(δR) кавитирующего руля, по которой определяется
По результатам расчета
строят зависимости
и
а также перестраивают зависимость угла крена на установившейся циркуляции
, которая приводится к виду
Управляемость на заднем ходу и при движении по инерции
Суда, оборудованные подвесным мотором (поворотной колонкой) или РРУ водометного движителя, управляются на заднем ходу, т. е. судно способно входить в циркуляцию и выходить из нее при соответствующих перекладках рулевого органа, а прямолинейное движение обеспечивается даже при наличии неустойчивости на курсе.
Суда, оборудованные рулевым устройством, как правило, на заднем ходу не управляются. При этом могут встретиться несколько случаев:
- одновинтовое судно циркулирует только в сторону, противоположную направлению вращения ГВ (например, влево при винте правого вращения), прямолинейное движение поддерживать невозможно;
- судно входит в циркуляцию любого борта при перекладке руля (рулей) на соответствующий борт, однако вывести его из циркуляции с помощью перекладок не удается, прямолинейное движение поддерживать невозможно; это свойство судна называется частичной управляемостью;
- судно входит и выходит из циркуляции, однако прямолинейное движение поддерживать затруднительно из-за необходимости перекладывать руль на большие углы;
- судно входит (выходит) в циркуляцию при перекладке рулей на борт, противоположный направлению циркуляции, это свойство судна называется обратной управляемостью;
- судно (как правило, двухвинтовое) обнаруживает тенденцию к входу в циркуляцию с очень большим диаметром, прямолинейное движение обеспечивается.
Наиболее часто на практике встречается случай частичной Основные понятия об управляемости суднауправляемости судов на заднем ходу.
При движении по инерции (с выключенным движителем) управляемостью обладают суда, оборудованные рулями. Суда с водометами и подвесными моторами (поворотными колонками) таким свойством не обладают. Именно с целью улучшения управляемости при движении по инерции предложены конструкции, аналогичные показанной на рис. Определение корпусных характеристик в момент взаимодействия судна с водной поверхностью“Съемный руль подвесного мотора”.
Влияние ветра на управляемость судна
Управляемость судна при действии ветра оценивается по его способности сохранять прямолинейное движение на заданном курсе.
Действие ветра на надводную часть судна приводит к появлению аэродинамической силы и момента, которые определяются по следующим формулам:
где:
- CYa, Cma — аэродинамические коэффициенты нормальной силы и момента относительно миделя, определяемые соответственно следующими выражениями:
- — угол кажущегося ветра Применительно к парусным судам кажущийся ветер называют вымпельным, скорость обозначают vB, а курсовой угол – β.x, т. е. угол между вектором результирующей скорости обтекания надводной части νк и ДП судна (рис. 2) (вектор скорости кажущегося ветра νк образуется в результате сложения вектора скорости истинного ветра νи, определяемого в осях, связанных с Землей (угол ϒи), и скорости судна ν);
- — безразмерное отстояние центра парусности от мидель-шпангоута;
- , если центр парусности расположен к носу от миделя;
- — если центр парусности расположен к корме от миделя;
- QY — площадь парусности надводной части судна в проекции на ДП;
- ρ1 — плотность воздуха.
Из решения системы уравнений, включающей аэродинамические компоненты, а также гидродинамические силы на корпусе и органах управления, определяются угол перекладки рулевого органа, необходимый для поддержания прямолинейного движения, и угол дрейфа судна.
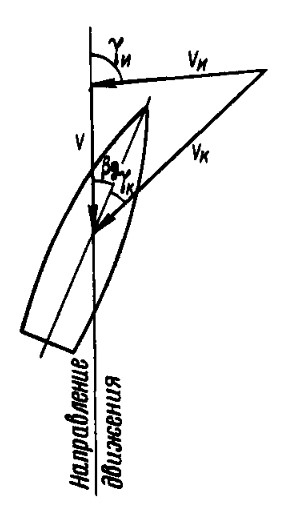
Анализ сил, действующих на судно, показывает, что наиболее опасный ветер, для компенсации которого требуется максимальная боковая сила рулевого органа, соответствует направлению ϒк = 120÷130°. Максимальный угол дрейфа судна наблюдается при ϒк = 50÷60°.
Ниже приведены формулы для судна с водометом, позволяющие определить угол дрейфа, возникающий при движении судна:
где:
и потребную боковую силу РРУ:
На основании расчета боковой силы Y0п может быть произведен выбор конструкции РРУ с учетом того, что:
Угол перекладки РРУ δR в формуле 10 не должен превышать половины от максимального. Расчет выполняется для ϒк = 130° при варьировании соотношения νк/ν, коэффициент q3 1 для судна с водометом определяется по формуле 18 в статье Способы вычисления маневренности судна на криволинейной траектории“Водоизмещающий режим”, а
— по табл. Управляемость малого судна“Производная подъемная сила РРУ”. Переход от значения кажущейся к истинной скорости ветра осуществляется по формуле:
При выполнении расчетов с использованием шкалы Бофорта (табл. 1) необходимо брать значение скорости, соответствующее верхней границе для данной балльности.
| Таблица 1. Шкала Бофорта | |||||
|---|---|---|---|---|---|
| Балл | Характер ветра | Средняя скорость, м/с | Балл | Характер ветра | Средняя скорость, м/с |
| 0 | Штиль | 0-0,5 | 7 | Крепкий | 12,5-15,2 |
| 1 | Тихий | 0,6-1,7 | 8 | Очень крепкий | 15,3-18,2 |
| 2 | Легкий | 1,8-3,3 | 9 | ||
| 3 | Слабый | 3,4-5,2 | 10 | Шторм | 18,3-21,5 |
| 4 | Умеренный | 5,3-7,4 | 11 | Сильный шторм | 21,6-25,1 |
| 5 | Свежий | 7,5-9,8 | 12 | Жестокий | 25,2-29 |
| 6 | Сильный | 9,9-12,4 | Ураган | 29,0 и более | |
Влияние волнения на управляемость судна
При движении малых судов на попутном волнении часто наблюдается явление захвата, при котором судно, увлекаемое попутной волной теряет устойчивость прямолинейного движения, разворачивается, становясь лагом к волне, и получает значительный крен, в результате которого оно может опрокинуться. Перекладка рулевого органа, даже на максимальный угол не выравнивает зарыскнувшее судно; т. е. происходит потеря управляемости.
Захват судна волной происходит при углах набегания волн к ДП 0—30°, при отношении длины волны и длины судна λв/L = 1÷2. При этом скорость судна на тихой воде близка к фазовой скорости волны Со. Соотношение между ними в соответствии с работами:
где:
- χ — угол набегания фронта волны по отношению ДП.
Кроме того, захват судна волной возможен при указанном выше соотношении длин волны и судна и при условии, что скорости судна в узлах определяется из соотношения:
Чтобы избежать захвата скорость судна должны быть меньше величины, подсчитанной по формуле 13.
Явление захвата и возможного опрокидывания у глиссирующих судов усугубляется резким сужением носовой части и возникающей в связи с этим дифферентовкой на нос. Конструктивные меры, способствующие нейтрализации действия попутного волнения, в этом случае сводятся, как правило, к приполнению Конструкция носовой и кормовой оконечностей суднаносовой оконечности или созданию специальных форм обводов, обладающих стабилизирующим свойством при ходе на волнении. К последним относятся обводы типа „морские сани”.
Влияние течения на управляемость судна
При движении судна на прямолинейном участке реки влияние течения сводится к сносу судна, т. е. к изменению его траектории при совершении циркуляции.
Характеристики управляемости (угол дрейфа, безразмерная угловая скорость) в относительном движении остаются такими же, как и на спокойной воде. Однако изменение скорости относительно воды (уменьшение при ходе вниз по течению и увеличение при ходе вверх) приводит к тому, что при движении вниз судно хуже слушается рулевого органа и более подвержено влиянию ветра. Кроме того, рост абсолютной скорости движения (относительно берега) при движении вниз увеличивает площадь, ометаемую судном при повороте. Вследствие этого маневры, связанные с подходом к причалу и швартовкой, выполняются против течения.
При движении на повороте реки изменяется характер силового взаимодействия между жидкостью и судном, в результате чего изменяются величины βg и
, а в случае необходимости совершения циркуляции с той же
, что и на спокойной воде, изменяется величина угла перекладки рулевого органа δR. Это изменение особенно заметно, если скорость течения соизмерима со скоростью судна в относительном движении.
При движении по повороту реки наибольшую сложность представляет движение вверх, поскольку при этом возрастает потребный угол перекладки рулевого органа и уменьшается угол дрейфа по сравнению со спокойной водой. При движении вниз по течению, наоборот, возрастает угол дрейфа и уменьшается угол перекладки рулевого органа (последний может быть даже переложен на сдерживание).
Примеры расчета управляемости малых судов
Расчет характеристик управляемости круглоскулого судна с рулем, установленным за гребным винтом.
1 Главные размерения и характеристики: L = 15,1 м, B = 3,14 м, T = 0,78 м, V = 24,0 м³, D = 24 600 кг, δ = 0,65, φ = 0,72, h = 0,5 м, xg = 0, zg = 1,15 м, ψ1 = 0. Эскиз кормовой оконечности приведен на рис. 3.
2 Максимальная скорость ν = 20 км/ч (5,56 м/с).
3 Данные по рулю:
- AR = 0,216 м², hR = 0,57 м, bR = 0,38 м, λ = 1,5;
профиль NASA,
tmax = 0,057 м, nR = 1, по чертежу расположения руля относительно винта определяются ARDp = 0,172 м, AR0 = 0,044 м, hв = 0,47 м, zp = 0,45 м и отстояние оси баллера от миделя судна lR = 7,24 м.
4 Данные по ходкости (берутся либо из расчета ходкости, либо из эксперимента) при Dp = 0,6 м (Rp = 0,3) м для скоростей 20 и 10 км/ч (5,56 и 2,78 м/с):
| Данные по ходкости | ||
|---|---|---|
| 20 (5,56) | 10 (2,78) | |
| FrL | 0,456 | 0,228 |
| CTν | 2 | 2,5 |
| ψp | 0,14 | 0,17 |
5 Определение средней скорости обтекания руля по формулам 32, 33 в статье Управляемость малого судна“Влияние ГВ и корпуса на ГДX руля”
- при ν = 20 км/ч:
- при ν = 10 км/ч:
6 Проверка руля на аэрацию при ν = 20 км/ч и δR = 30°. По формуле Управляемость малого судна“Определение условного поперечного размера руля” находим dR = 0,057+0,38sin 30° = 0,247;
Для заглубления нижнего торца руля hт = 0,65 м по рис. Управляемость малого судна“Зависимость Р1 отношения hТ/dR“ находим значение коэффициента P1 = 0,85.

Значение числа
при котором наступает аэрация, определяем по формуле:
Поскольку
аэрация на руле отсутствует.
7 Проверка руля на кавитацию:
находим число кавитации
Поскольку κ > 2,5 то руль не кавитирует.
8 Определение гидродинамических характеристик корпуса.
По чертежу кормовой оконечности (рис. 3) определяем площадь Fп = 0,57 м², шпангоут с номером i = 15,5. По формуле Определение корпусных характеристик в момент взаимодействия судна с водной поверхностью“Определение величины угла ходового дифферента” находим угол ходового дифферента при ν = 20 км/ч:
Приведенный коэффициент погруженной части ДП для случая ψ1 = 0 (см. формулу 12 в статье Определение корпусных характеристик в момент взаимодействия судна с водной поверхностью“ГДХ корпуса судна, движущегося в водоизмещающем режиме”):
- при ν = 10 км/ч:
- при ν0 = 20 км/ч:
Безразмерные ГДХ корпуса определяем по формулам 7-11 в статье Определение корпусных характеристик в момент взаимодействия судна с водной поверхностью“ГДХ корпуса судна, движущегося в водоизмещающем режиме”:
Приведенная площадь ДП:
Значения
и FD определяют для скоростей 10 и 20 км/ч:
| Определение безразмерных ГДХ корпуса | |||||
|---|---|---|---|---|---|
| 10 | 20 | 10 | 20 | ||
| 0,968 | 0,983 | 0,28 | 0,276 | ||
| 0,125 | 0,14 | 0,094 | 0,079 | ||
| 0,618 | 0,637 | 0,0452 | 0,0481 | ||
| 11,4 | 11,58 | ||||
9 Определение боковой силы на руле.
Производная коэффициента подъемной силы изолированного руля по формуле 18 в статье Управляемость малого судна“Гидродинамические характеристики изолированного руля” для подвесного руля:
Определяем по чертежу a1/Rр = 0,17/0,3 ≈ 0,567; hR/Rp = 0,57/0,3 = 1,9 и находим по рис. Управляемость малого судна“Зависимость коэффициента n1 от взаимного расположения и соотношения руля и гребного винта” n1 = 0,465.
Удлинение части руля, расположенной в струе ГВ:
Коэффициент индукции по формуле Управляемость малого судна“Определение коэффициента индукции ГВ” составит:
- при ν = 20 км/ч:
- при ν = 10 км/ч:
Производная коэффициента подъемной силы руля с учетом влияния гребного винта определится по формуле Управляемость малого судна“Производная коэффициента подъемной силы руля”:
- при ν = 20 км/ч:
- при ν = 10 км/ч:
Коэффициент влияния корпуса и винта на руль при κк = 1 по формулам 30 и 31 в статье Управляемость малого судна“Влияние ГВ и корпуса на ГДX руля” составит:
- при ν = 20 км/ч:
- при ν = 10 км/ч:
10 Расчет коэффициентов вида qij, rij, sij производится по формулам 3-8 в статье Способы вычисления маневренности судна на криволинейной траектории“Водоизмещающий режим”:
- при ν = 20 км/ч:
- при ν = 10 км/ч:
- при ν = 20 км/ч:
- при ν = 10 км/ч:
- при ν = 20 км/ч:
- при ν = 10 км/ч:
- при ν = 20 км/ч:
- при ν = 10 км/ч:
- при ν = 20 км/ч:
- при ν = 10 км/ч:
- при ν = 20 км/ч:
- при ν = 10 км/ч:
11 Расчет поворотливости.
При определении зависимостей
полагается, что судно одинаково поворачивается на правый и левый борта, поэтому расчет ведется только при перекладке рулевого органа на один борт при δR > 0.
Для неустойчивого судна значения δR < 0 означают перекладку рулевого органа на борт, противоположный направлению циркуляции.
Расчет коэффициентов q и s осуществляется по формулам 21 и 22 в статье Способы вычисления маневренности судна на криволинейной траектории“Маневренность судна и расчеты крена на циркуляции”:
- при ν = 20 км/ч:
- при ν = 10 км/ч:
- при ν = 20 км/ч:
- при ν = 10 км/ч:
Результаты расчета параметров βg по формуле Способы вычисления маневренности судна на криволинейной траектории“Угол дрейфа судна на установившейся циркуляции”,
по формуле 2 в статье Способы вычисления маневренности судна на криволинейной траектории“Маневренность судна и расчет крена на циркуляции”, а также
и
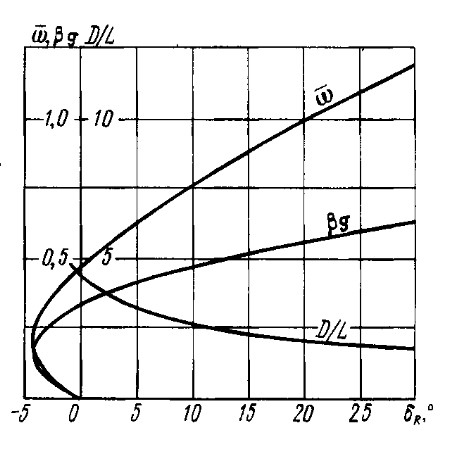
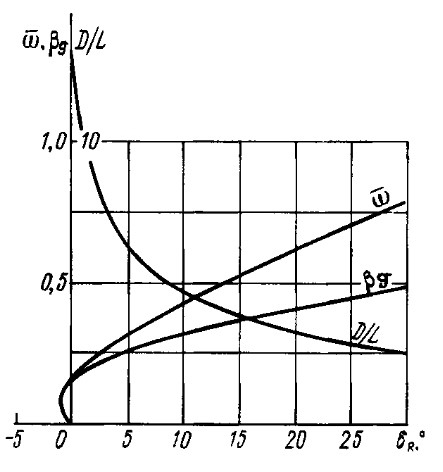
в зависимости от δR приведены в табл. 2 и представлены графически на рис. 4, 5.
| Таблица 2. Расчет поворотливости судна, движущегося в водоизмещающем режиме | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| ν0, км/ч | Элемент поворотливости | Угол перекладки руля, град/рад | |||||||
| 0/0 | 5/0,0873 | 10/0,174 | 15/0,262 | 20/0,349 | 25/0,436 | 30/0,523 | 35/0,611 | ||
| 10 | β | 0,343 | 0,418 | 0,475 | 0,524 | 0,566 | 0,604 | 0,639 | 0,671 |
| ω | 0,488 | 0,647 | 0,779 | 0,901 | 1,012 | 1,118 | 1,22 | 1,316 | |
| R | 2,05 | 1,54 | 1,28 | 1,11 | 0,99 | 0,9 | 0,82 | 0,76 | |
| D/L | 4,1 | 3,08 | 2,56 | 2,22 | 1,98 | 1,8 | 1,64 | 1,52 | |
| 20 | β | 0,151 | 0,257 | 0,321 | 0,372 | 0,415 | 0,453 | 0,488 | 0,52 |
| ω | 0,16 | 0,319 | 0,433 | 0,534 | 0,626 | 0,712 | 0,796 | 0,876 | |
| R | 6,25 | 3,14 | 2,31 | 1,87 | 1,6 | 1,4 | 1,26 | 1,14 | |
| D/L | 12,5 | 6,28 | 4,62 | 3,74 | 3,2 | 2,8 | 2,52 | 2,28 | |
| ν, м/с | 5,3 | 4,66 | 4,1 | 3,6 | 3,2 | 2,82 | 2,53 | 2,26 | |
| Y0, кг | -145,4 | -131,75 | -93,04 | -58,55 | -33,35 | -14,46 | -1,85 | 7,1 | |
| Θ, ° | 3,64 | 5,8 | 6,19 | 5,94 | 5,55 | 4,93 | 4,5 | 3,94 | |
12 Определение характеристик устойчивости.
Поскольку q < 0, производится расчет δR кр, βg кр,
по формулам 40-42 в статье Способы вычисления маневренности судна на криволинейной траектории“Устойчивость прямолинейного движения судна”:
- при ν = 20 км/ч:
- при ν = 10 км/ч;
- при ν = 20 км/ч:
- при ν = 10 км/ч:
- при v = 20 км/ч;
- при ν = 10 км/ч;
Соответствующие значения показаны на рис. 4, 5.
13 Оценка устойчивости прямолинейного движения и поворотливости.
По результатам расчета можно сделать вывод, что спроектированное судно имеет хорошую поворотливость, характеризующуюся минимальным диаметром (2,5 длин корпуса) при ν0 = 20 км/ч. Устойчивость прямолинейного движения, определяемая по формуле Управляемость малого судна“Соотношение составляющих гидродинамических сил”, при ν = 20 км/ч близка к требуемой:
и хуже при ν = 10 км/ч:
.
С целью улучшения устойчивости можно рекомендовать либо увеличить площадь дейдвуда, либо дать судну незначительный, в пределах 0,5°, дифферент на корму.
14 Расчёт крена на циркуляции при максимальной скорости ν = 20 км/ч.
Скорость на циркуляции вычисляют по формуле Способы вычисления маневренности судна на криволинейной траектории“Связь между циркуляцией и скоростью судна”:
Боковая сила руля:
По рис. Определение корпусных характеристик в момент взаимодействия судна с водной поверхностью“К определению точки приложения боковой силы корпуса по высоте для круглоскулых судов” определяется точка приложения боковой силы на корпусе В/Т = 3,14/0,78 ≈ 4; zr ≈ 0 и по формуле Способы вычисления маневренности судна на криволинейной траектории“Определение наружного крена по отношению круга циркуляции” рассчитывается зависимость Θ = f(δR):
Результаты расчета приведены в табл. 2 и на рис. 6.
Расчет характеристик управляемости остроскулого судна с двумя подвесными моторами (поворотными колонками).
1 Главные размерения и характеристики: L = 6 м, Bт = 2 м, T = 0,25 м, V = 1,5 м3, D0 = 1 501 кг, δR = 0,5, φ = 0,77, h = 0,55 м, xт = -3 м (xg = 0), zg = 0,7 м, ψ1 = -1°, β = 12°.

Эскиз кормовой оконечности соответствует рис. Определение корпусных характеристик в момент взаимодействия судна с водной поверхностью“К описанию управляемости глиссирующих судов”
2 Максимальная скорость ν = 35 км/ч.
3
Данные по подвесным моторам и ходкости при nв = 2, Dp = 0,25 м, zp = -0,2,
для скоростей 8, 14, 35 км/ч (2,22; 3,89; 9,72 м/с):
| Данные по подвесным моторам и ходкости | |||
|---|---|---|---|
| 8 (2,22) | 14 (3,89) | 35 (9,72) | |
| FrL | 0,29 | 0,51 | 1,27 |
| FrV | 0,66 | 1,16 | 2,9 |
| CTν | 1,2 | 0,9 | 0,6 |
| ψp | 0 | 0 | 0 |
4 Определение характеристик переложенного подвесного мотора. По рис. Управляемость малого судна“Зависимость Kc от CTv“ определяют коэффициент Кс:
| Определение характеристик переложенного подвесного мотора | |||
|---|---|---|---|
| CTν | 1,2 | 0,9 | 0,6 |
| Kc | 0,73 | 0,78 | 0,85 |
По формулам 42 и 43 в статье Управляемость малого судна“Подвесной мотор (поворотная колонка)” находят параметры
:
- при ν = 8 км/ч:
- при ν = 14 км/ч:
- при ν = 35 км/ч:
5 Определение характеристик управляемости при движении в водоизмещающем (ν0 = 8 и 14 км/ч) режиме Расчет характеристик управляемости при ν0 = 14 км/ч представляет интерес, поскольку соответствует движению судна, физически близкому к переходному режиму.x.
Этот расчет принципиально ничем не отличается от примера расчета, изложенного ранее, только вместо формул, относящихся к случаю расположения на судне руля, нужно использовать выражения, соответствующие установке подвесных моторов.
При этом приведенный коэффициент полноты диаметрали σD определяется по формуле:
- при ν = 8 км/ч:
- при ν = 14 км/ч:
(ψ2 — угол ходового дифферента, при FrL = 0,51, ψ2 = 0,0204).
Результаты расчета в виде зависимостей
при ν = 8 км/ч и ν = 14 км/ч приведены на рис. 7, 8.
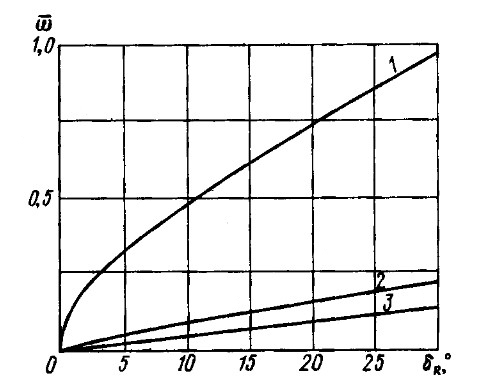
1 – водоизмещающий режим (ν = 8 км/ч); 2 – то же (ν = 14 км/ч); 3 – глиссирующий режим (ν = 35 км/ч)
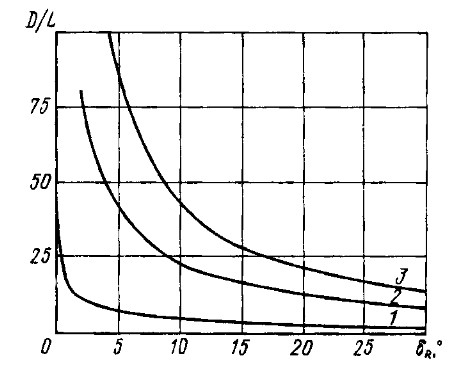
1 – водоизмещающий режим (v = 8 км/ч); 2 – то же (v = 14 км/ч); 3 – глиссирующий режим (v = 35 км/ч)
6 Определение исходных данных для расчета характеристик управляемости в глиссирующем режиме (ν = 35 км/ч):
- по рис. Определение корпусных характеристик в момент взаимодействия судна с водной поверхностью“Зависимость коэффициентов nv, mv, qv от угла килеватости” для (β = 12° nν = 1,22, mν = 0,91, qν = 39;
- по данным ходкости для ν = 35 км/ч ψ2 = 2,5° (0,0436), смоченная длина lсм = 4,1 м, осадка на транце Tтр = lсмψ2 = 4,1·0,0436 = 0,178 м;
- число Fr по ширине на транце:
приведенная производная боковой силы подвесных моторов по формуле Способы вычисления маневренности судна на криволинейной траектории“Производная коэффициента боковой силы для подвесного мотора”:
7 Расчет составляющих ГДХ корпуса при движении в режиме глиссирования по формулам 18-23 в статье Определение корпусных характеристик в момент взаимодействия судна с водной поверхностью“ГДХ корпуса судна, движущегося в режиме глиссирования”:
| Таблица 3. Расчет поворотливости судна, движущегося в глиссирующем режиме | |||||||
|---|---|---|---|---|---|---|---|
| Элемент поворотливости | Угол перекладки руля, град | ||||||
| 0 | 5 | 10 | 15 | 20 | 25 | 30 | |
| δR | 0 | 0,0873 | 0,174 | 0,262 | 0,349 | 0,436 | 0,523 |
| ωB | 0 | 0,00779 | 0,0155 | 0,0234 | 0,0311 | 0,0389 | 0,0466 |
| ω | 0 | 0,0234 | 0,0465 | 0,0702 | 0,0933 | 0,117 | 0,14 |
| D/L | 0 | 85,5 | 43 | 28,5 | 21,4 | 17,1 | 14,3 |
| θ | 0 | -1,91 | -3,82 | -5,73 | -7,64 | -9,55 | -11,46 |
8 Расчет поворотливости и определение крена на циркуляции при движении в глиссирующем режиме по формулам 26 и 27 в статье Способы вычисления маневренности судна на криволинейной траектории“Глиссирующий режим”:
Результаты расчета приведены в табл. 3 и на рис. 7-9 в виде зависимостей ωB = f(δR), Θ = f(δR), ω = f(δR), D/L = f(δR).
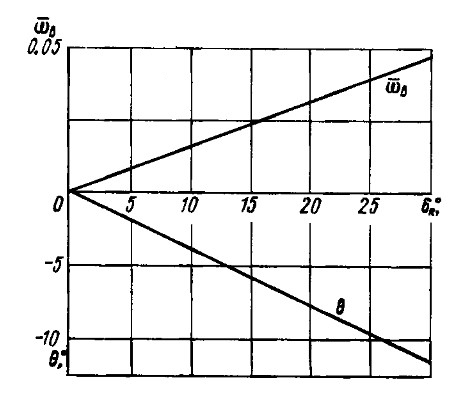
Из результатов расчета следует очевидный вывод о том, что для совершения крутой циркуляции необходимо перед перекладкой рулевого органа снизить скорость, т. е. перейти из глиссирующего режима движения в переходный или водоизмещающий.
🤝 Поддержите нашу работу
Нашли опечатку? Выделите и нажмите CTRL+Enter
