Автоматические системы судна, классификация элементов

Элементы регуляторов и устройств управления можно подразделить на: чувствительные или измерительные, преобразовательные, усилительные, исполнительные, логические, элементы обратных связей.

СодержаниеСвернуть

Классификация элементов. Требования к элементам
Измерительные (чувствительные), преобразовательные элементы и датчики
Усилительные и исполнительные элементы

Классификация элементов. Требования к элементам

Несмотря на различие в назначении перечисленных элементов, к их конструкции предъявляются ряд общих требований: малый вес и габариты, надежность работы — одно из важнейших требований, относительная простота устройства, удобство обслуживания, малая инерционность и линейность статических характеристик (для линейных САР).

Все элементы систем автоматики по своему конструктивному выполнению могут быть подразделены на механические, пневматические, гидравлические и электрические.

Ниже рассматриваются лишь общие вопросы, связанные с их назначением и классификацией.

Измерительные (чувствительные), преобразовательные элементы и датчики

Назначение измерительных элементов — измерение регулируемых величин с целью передачи сигналов на преобразовательные, усилительные и исполнительные Интегрированные системы управления судоходствомэлементы системы. Поэтому очень важно, чтобы такие элементы обеспечивали заданную точность измерения. Измерительный элемент должен создавать сигнал, достаточный по величине для передачи его на звенья, следующие за измерительным элементом.

В ряде случаев перед измерительным элементом ставится задача не измерять регулируемую величину, а лишь выдавать сигнал, свидетельствующий о том, что контролируемая величина превосходит или не превосходит определенное значение. Такие элементы принято называть чувствительными (ЧЭ). В целях упрощения под чувствительным элементом в дальнейшем будем подразумевать и измерительный элемент. Одним из показателей ЧЭ является его чувствительность. Чувствительностью k называют отношение изменения выходной величины Δx₂ элемента к его входной Δx₁:

$k = (Δ x_{2} / Δ x_{1}) или k = (d x_{2} / d x_{1}) .$

Величина k может быть получена, как тангенс угла наклона статической характеристики ЧЭ к оси абсцисс. Под чувствительностью элемента понимают также отношение изменения выходной и входной величин в их относительных значениях:

$K = Δ x_{2} / x_{2 н о м};$

$Δ x_{1} / x_{1 н о м}, Ф о р м . 1$

где:

x_1ном и x_2ном — выбранные номинальные или базовые значения входной и выходной величин.

Понятие чувствительности эквивалентно понятию коэффициента усиления ЧЭ. Одним из важных требований к ЧЭ является прямолинейность статической характеристики, которая снимается путем последовательного измерения входной величины и измерений Δx₁ и Δx₂ на статических режимах.

Величины непрямолинейности и нечувствительности (о которых говорилось в “Классификация систем автоматики. Основы теории взаимодействия дизеля и устройств автоматического регулирования“) должны быть минимальными. Величину чувствительности желательно иметь максимальной, чтобы уменьшить габариты и стоимость усилительных механизмов всей системы. При анализе конструкций ЧЭ должны быть также выявлены их динамические качества, влияющие на процесс регулирования на переходных режимах.

Как правило, динамика ЧЭ или датчика в результате линеаризации нелинейностей описывается дифференциальным уравнением 1-го порядка вида:

$T d x_{2} / d t + x_{2} = k x_{1},$

где:

T — постоянная величина ЧЭ, имеющая размерность времени (с, мин.);
K — коэффициент усиления.

При ступенчатом изменении x₂ на величину x₁₀ получим

$x_{2} = k x_{10} (1 - e^{- t / T}),$

когда

$t = T, x_{2} ≅ 0, 63 k x_{10} .$

Экспериментальное определение величины T может быть произведено путем ступенчатого изменения x₁ и осциллографирования x₂. Отрезок времени от момента начала переходного процесса до момента, когда x₂ = 0,63 kx₁₀ будет равен величине T.

В качестве примера приведем вывод дифференциального уравнения ЧЭ температуры. Изменение температуры контролируемой среды обозначим Δt_ж, а перемещение выходного элемента или изменение сигнала на выходе Δх. Обычно устройство ЧЭ температуры таково, что величина Δх пропорциональна температуре ЧЭ — t_чэ, на нагрев которого требуется время, т. к. количество переданной ему теплоты dQ = α F (tx – tчэ) dt, где α — коэффициент теплопередачи, F — площадь стенки.

Предлагается к прочтению: Требования и процесс регулирования судовой автоматики

В то же время dQ = MC dt_чэ, где:

M — масса;
C — его теплоемкость.

Используя метод малых отклонений, приведем эти уравнения к уравнению 1-го порядка.

$T d Δ t_{ч э} / d τ + Δ t_{ч э} = Δ t_{ж}, Ф о р м . 2$

где:

T — постоянная времени элемента, мин, с;
τ — время.

Для ряда датчиков значениями T можно пренебречь, если они малы по сравнению с другими постоянными времени.

Динамика ЧЭ, основанных на применении упругих элементов, описывается уравнением 2-го порядка. В качестве примера приведем приближенный вывод уравнения динамики ЧЭ частоты вращения (рис. 1), включающего грузы, которые качаются в шарнирах и одновременно вращаются с частотой ω, муфту, на которую действует с одной стороны приведенная центробежная сила грузов, с другой — сила E_пр сжимаемой пружины, с жесткостью с, другой конец которой может перемещаться под действием сигнала управления g.

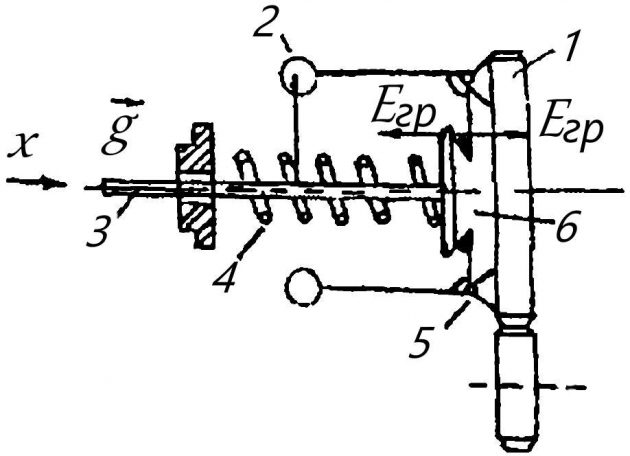
Частоты вращения элемента — Рис. 1 Схема чувствительного элемента частоты вращения.
1 – шестерня, 2 – грузы, 3 – тяга, 4 – пружина, 5 – шарнир, 6 – муфта

Выходная величина ЧЭ — перемещение тяги, x. На установившемся режиме:

$F_{п р} = E_{г р} = c x_{0} .$

На неустановившемся режиме, если пренебречь изменением радиуса вращения грузов и линеаризовать зависимость x от ω:

$M d^{2} Δ x / d t^{2} + K_{г} d Δ x / d t + c Δ x = - K_{1} Δ ω + K_{2} g,$

где:

M — масса поступательно движущихся частей, приведенных к муфте;
K_г — коэффициент гидравлического трения;
K₁ и K₂ — коэффициенты передачи от возмущающего Δω и управляющего g воздействий.

Это уравнение может быть представлено и в относительных координатах:

${T_{г}}^{2} d^{2} η / d t^{2} + T_{k} d η / d t + δ η = φ + δ, Ф о р м . 3$

${T_{г}}^{2} = M x_{н о м} / E_{п р}$
— квадрат времени поступательного движущихся масс, с2;
T_k —
«время» вязкого трения, с
$(T_{k} = K_{г} x_{н о м} E_{п р о})$
;
δ —
степень неравномерности ЧЭ скорости вращения
$(δ = C x_{н о м} / E_{п р о})$
.

Для ЧЭ прямого действия значение x эквивалентно перемещению хода Насосы двигателей Вяртсилярейки топливных насосов дизеля, а последнее — изменению эффективного (крутящего) момента.

Обычно для дизель-генераторов принимается, что при изменении нагрузки от 0 до 100 % частота тока не должна упасть более, чем на 2-3 %. Следовательно, при изменении φ на 0,02-0,03, величина η должна измениться на 1. Таким образом, если за величину η принять η = Δh_p/h_{p ном}, то δ = 0,02/0,03.

Для дизелей, работающих на винт, значение δ = 0,1- 0,15.

Величины масс поступательно движущихся частей и гидравлического трения относительно не велики и T_η² и T_k могут лежать в пределах(для регуляторов непрямого действия):

${T_{г}}^{2} = 10^{- 4} / 10^{- 3} c^{2}, T_{k} = 10^{- 3} / 10^{- 2} c .$

Для регуляторов скорости непрямого действия перемещение муфты ЧЭ приводит к перемещению золотника, открывающего окна для поступления масла под давлением к сервопоршню. Поэтому абсолютные значения перемещения муфты принимаются небольшими (0,1-0,5 мм), размеры и массы поступательно движущихся частей, так же как и величины гидравлического трения — относительно невелики.

Поэтому для ЧЭ регуляторов скорости вращения не-прямого действия значениями T_η² и T_k обычно пренебрегают. Уравнение (3) принимает вид:

$δ η = φ + δ g Ф о р м . 3, а$

При выводе уравнения чувствительного элемента в качестве направления координаты x принимают направление, соответствующее увеличению частоты вращения грузов. Если все постоянные в уравнении (3) разделить на δ, то уравнение (3) может быть представлено в виде:

${T_{r}^{‘}}^{2} \frac{d^{2} η}{d t^{2}} + T_{k}^{‘} \frac{d η}{d t} + η = k_{p} φ + G^{‘},$

где:

$k_{p} = \frac{1}{δ}$
— коэффициент усиления регулотора.

Широкое применение в системах автоматики находят датчики, представляющие собой единую конструкцию ЧЭ и преобразовательного элемента, преобразующего сигнал в электрический Основные свойства объектов автоматических систем суднавыходной сигнал.

По конструктивному устройству датчики делятся на контактные и бесконтактные. В контактных датчиках применяются ЧЭ с механической выходной величиной, в бесконтактных — с электрической. Контактные и бесконтактные датчики могут быть дискретными и непрерывными (пропорциональными). В дискретных датчиках имеются преобразователи релейного типа. В датчиках непрерывного действия ЧЭ соединен с преобразовательным, на выходе которого сигнал пропорционален изменению регулируемой величины. Так, например, в омических преобразовательных элементах сигнал перемещения преобразуется в изменение активного сопротивления, в индуктивных преобразовательных элементах перемещение сердечника приводит к изменению реактивного со-противления.

К числу ЧЭ и датчиков САР и САУ технических систем водного транспорта можно отнести ЧЭ и датчики: давления, температуры, уровня, частоты вращения, консистенции (плотности), расхода, угловых перемещений, состава газов и др., конструкции которых изложены в литературе, упомянутой выше.

Усилительные и исполнительные элементы

Усилительные элементы предназначены для усиления сигналов, идущих от датчиков к исполнительным механизмам. Как уже ранее отмечалось, усилители используются в системах непрямого регулирования, т.е. в тех случаях, когда для работы исполнительного механизма нужна большая мощность. Отказ от усилителей мог бы привести к существенному увеличению габаритов чувствительного элемента и ухудшению динамики системы.

Усилительные элементы подразделяются на гидравлические, пневматические и электрические. Энергетические возможности гидравлических, пневматических и электрических усилителей характеризуются коэффициентами усиления по мощности K_N = N/N_y где N — мощность потока рабочей жидкости или электрическая мощность на выходе усилителя, N_y — мощность, затрачиваемая на управление усилителем, или коэффициентом усиления по напряжению К_u = U_вых/U_вх, где U_вых и U_вх — напряжение на выходе и входе усилителя.

К исполнительным элементам (механизмам) относятся: гидравлические сервопоршни, изменяющие подачу топлива, воздуха и воды, электромагнитные устройства для подачи воздуха на пуск, стоп-устройство и пневмопрокачку дизеля маслом, электромагнитные выключатели автоматов, пускателей электронасосов и другие устройства. По роду используемой энергии исполнительные механизмы можно подразделить на следующие группы:

а) гидравлические;
б) пневматические;
в) электрические.

Для настройки или проектирования САР и САУ необходимо знать динамические характеристики усилительных и исполнительных элементов, которые можно получить, составляя дифференциальные уравнения этих элементов.

В качестве примера рассмотрим упрощенный вывод дифференциального уравнения гидравлической системы: усилитель с золотником — поршневой исполнительный механизм (сервомотор), схема которого представлена на рис. 2. Обозначим:

x — отклонение золотника от среднего положения (Топливные насосы золотникового типазолотник без перекрытий);
P — давление рабочей жидкости;
y — отклонение сервопоршня от положения, соответствующего перекрытым окнам;
F — площадь сервопоршня.

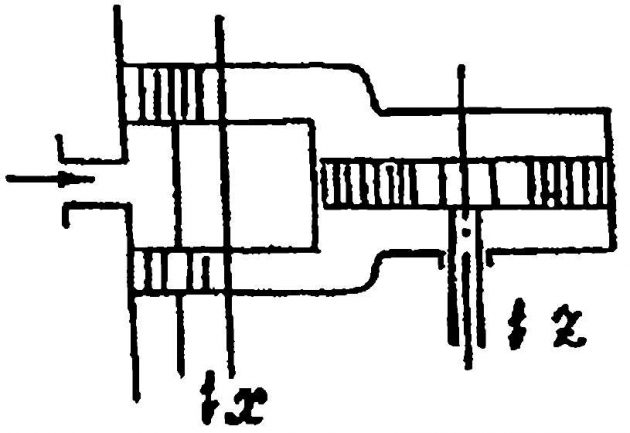
Сервомотор — Рис. 2 Схема системы: золотник — сервопоршень

Давление рабочей жидкости выбирается обычно таким, чтобы сила, развиваемая сервопоршнем, была значительно выше, чем силы инерции присоединенных к нему масс и силы трения. Поэтому последними при выводе пренебрегается. Полагая, в силу симметрии окон, открываемых золотником, потери давления рабочей жидкости при дросселировании ее потока через оба окна, открываемых золотником, одинаковыми и равными P/2 (суммарный перепад давления от P до P = 0 при сливе равен P).

Это интересно: Методология проектирования конструкций ледовых усилений по критерию предельной прочности

Получим выражение для расхода жидкости при движении сервопоршня

$Q = x K_{1} {(P / ρ)}^{1 / 2},$

где:

ρ — плотность жидкости;
К₁ — постоянная.

С другой стороны Q = Fdy/dt. Откуда получим:

$F d y / d t = χ μ b {(P / ρ)}^{1 / 2}$

μ — коэффициент истечения;
b — ширина окна.

Выбирая базовые значения уном и хном для y_ном и x_ном и переходя к относительным переменным z = (y/y_ном) и η = x/x_ном получим:

$T_{s} d z / d t = η, Ф о р м . 4$

где:

$T_{s} = {(P / ρ)}^{1 / 2} F (y_{н о м} / x_{н о м}) μ b,$

— постоянная времени сервомотора, которая тем меньше, чем больше давление рабочей жидкости и ширина окна T_s лежит в пределах 0,01-0,02 сек.

Сноски

Элементы автоматических систем судна

Классификация элементов. Требования к элементам

Измерительные (чувствительные), преобразовательные элементы и датчики

Усилительные и исполнительные элементы