В соответствии с результатами разд. см. “Анализ повреждаемости и обоснование критериев прочности корпусов судов ледового плавания и ледоколовКритерии и методы оценки прочности. Расчётные ледовые нагрузки. Принципы регламентации режимов движения во льдах” в Настоящей главе разрабатывается набор расчетных методик, обеспечивающих практическое внедрение критерия предельной прочности в практику проектирования корпусов судов ледового плавания.
Методики охватывают основные типы конструкций ледовых усилений – балки основного набора и балочные системы (перекрытия), пластины наружной обшивки, листовые конструкции, и, по существу, определяют методологию проектирования конструкций ледовых усилений по критерию предельной прочности, ориентированную на использование в требованиях Правил Регистра к судам ледового плавания и ледоколам.
Проектирование балок основного набора и балочных систем (бортовых перекрытий)
Иерархический принцип построения расчетных моделей бортовых перекрытий
Конструктивные схемы бортовых перекрытий
Задача проектирования (определения требуемых размеров связей) бортовых перекрытий, испытывающих Корпусные конструкции транспортных судов ледового плаваниявоздействие ледовых нагрузок, традиционно занимает одно из центральных мест в общей проблеме обеспечения ледовой прочности корпусов судов и ледоколов. Недостаточная прочность бортового перекрытия может привести к серьезным повреждениям корпуса, представляющим опасность для судна в целом. Наличие избыточных запасов прочности связано не только с необоснованным увеличением веса ледовых усилений, но и с появлением значительных технологических трудностей, возрастающих по мере увеличения класса.
Существующая практика проектирования бортовых перекрытий судов ледового плавания сводится к регламентации следующих типов балок:
- обыкновенные шпангоуты, подразделяемые на основные (расположенные в плоскости флоров или скуловых бракет) и промежуточные;
- рамные шпангоуты;
- продольные балки;
- стрингеры (несущие или разносящие).
В дальнейшем анализе принимаются следующие, как правило, выполняемые на практике допущения:
- пересекающиеся балки взаимно перпендикулярны;
- балки одного типа имеют одинаковые поперечные сечения, расположены на одинаковых расстояниях и одинаково закреплены на конструкциях образующих опорный контур перекрытия; исключением могут являться основные и промежуточные шпангоуты, для которых учитывается различие в условиях закрепления на опорном контуре.
В различных сочетаниях перечисленные балки могут образовывать следующие схемы бортовых перекрытий.
(i) Перекрытие с монотонной системой набора. Состоит из обыкновенных (основных и промежуточных) шпангоутов, опирающихся на палубы (платформы) или днище. Наличие промежуточных шпангоутов необязательно. Может включать разносящие (интеркостельные) стрингеры, выполняющие функцию разнесения локальных ледовых нагрузок на большое число шпангоутов (рис. 1).
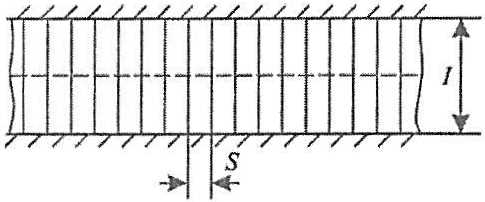
Конструкция судовых перекрытийГеометрия данного перекрытия описывается путем задания следующих параметров:
- S – расстояние между соседними шпангоутами;
- l – длина пролета шпангоута (процедура определения при l различных условиях закрепления концов основных и промежуточных шпангоутов будет описана ниже);
- m1 – число разносящих стрингеров.
(ii) Перекрытие с рамными шпангоутами при поперечной системе набора. Состоит из обыкновенных шпангоутов, несущих стрингеров и рамных шпангоутов. Между несущими стрингерами могут устанавливаться разносящие стрингеры (рис. 2).
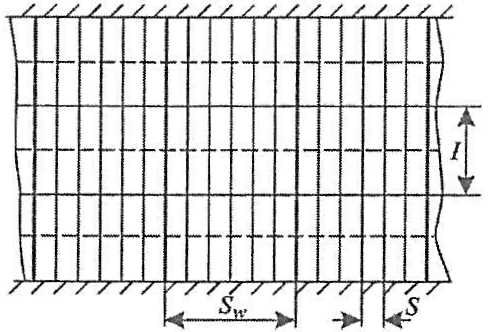
Геометрия перекрытия описывается путем задания следующих параметров:
- S – расстояние между соседними обыкновенными шпангоутами;
- mi – число обыкновенных шпангоутов между соседними рамными шпангоутами;
- l – расстояние между несущими стрингерами;
- mi – число несущих стрингеров;
- mi – число разносящих стрингеров;
- Sw = S (n + 1) – расстояние между рамными шпангоутами.
(iii) Общие вопросы проектирования судовых конструкцийПерекрытие с рамными шпангоутами при продольной системе набора. Состоит из продольных балок и рамных шпангоутов. Между рамными шпангоутами могут устанавливаться дополнительные шпангоуты (рис. 3).
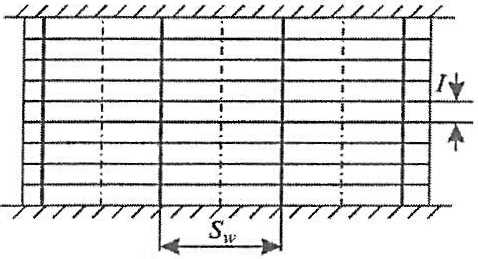
Геометрия перекрытия описывается путем задания следующих параметров:
- S – расстояние между соседними продольными балками;
- k – число продольных балок в пролете рамного шпангоута;
- Sw – расстояние между соседними рамными шпангоутами;
- j – число дополнительных шпангоутов между соседними рамными шпангоутами.
Иерархия уровней балок и типов пластических механизмов
Согласно изложенному бортовое перекрытие в общем случае включает балки нескольких иерархических уровней (типов). Каждый уровень реагирует на ледовые нагрузки различной степени локализации и вступает в силовое взаимодействие с балками более высокой иерархии. При этом в соответствии с процедурой расчета предельной прочности сложных балочных систем должно иметь место иерархическое соответствие между уровнями балок и типами пластических механизмов, описывающих переход в предельное состояние систем балок различных уровней, а также расчётной эпюры ледовой нагрузки для каждого типа пластического механизма.
Концепцию построения такого рода иерархической классификации целесообразно изложить применительно к наиболее общему случаю перекрытия, имеющего балки трех иерархических уровней, на практике соответствующего наиболее сложному варианту перекрытия с рамными шпангоутами при поперечной системе набора. Данная концепция, ориентированная на задачу регламентации размеров составляющих перекрытие балок на основании Общий продольный изгиб и общая продольная прочность корпусных конструкций суднакритерия предельной прочности, основывается на следующих представлениях.
(i) Перекрытие рассматривается как система пересекающихся балок трех иерархических уровней:
- 1- й уровень (i = 1) – обыкновенные шпангоуты, непосредственно воспринимающие ледовую нагрузку и передающие реакции на несущие стрингеры;
- 2- й уровень (i = 2) – несущие стрингеры, поддерживающие обыкновенные шпангоуты и передающие реакции на рамные шпангоуты;
- 3- й уровень (i = 3) – рамные шпангоуты, поддерживающие несущие стрингеры.
(ii) Множество пластических механизмов перехода перекрытия в предельное состояние также разделяется на три типа – по числу уровней балок. Таким образом, каждому i-му уровню балок ставится в соответствие i-й тип пластических механизмов, являющийся ключевым при определении требований к размерам балок i-го уровня. В результате реализуется следующая процедура регламентации предельной прочности балок перекрытия на основании ключевых типов пластических механизмов:
- 1-й тип (балочный) описывает переход в предельное состояние балок 1-го уровня (обыкновенных шпангоутов), как изолированных балок, разрушающихся между балками 2-го уровня. Соответственно балки 2-го и 3-го уровней остаются недеформированными. В результате устанавливаются требования к размерам балок 1-го уровня, зависящие только от параметров расчетной нагрузки и критериев прочности.
- 2-й тип (рамная шпация) описывает совместный переход в предельное состояние балок 1-го и 2-го уровней (обыкновенных шпангоутов и несущих стрингеров) в пределах одной рамной шпации, то есть при условии, что балки 3-го уровня (рамные шпангоуты) остаются недеформированными. Поскольку размеры балок 1-го уровня уже определены, рассмотрение пластических механизмов 2-го типа позволяет установить требования к размерам балок 2-го уровня, которые оказываются зависящими не только от параметров расчетной нагрузки и геометрии перекрытия, но и от размеров балок 1-го уровня.
- 3-й тип (перекрытие) описывает переход в предельное состояние перекрытия в целом. В результате рассмотрения пластических механизмов 3-го типа устанавливаются требования к размерам балок 3-го уровня (рамных шпангоутов) в зависимости от параметров расчетной нагрузки и геометрии перекрытия, а также уже определенных размеров балок 1-го и 2-го уровней.
Расчётные нагрузки и упрощающие допущения
Расчетная нагрузка согласно принятому в российской практике подходу (см. “Анализ повреждаемости и обоснование критериев прочности корпусов судов ледового плавания и ледоколовОтдельные и массовые повреждения и ледовые нагрузки“) считается распределённой в соответствии с эпюрой трапецеидальной формы (см. рис. 8 Расчетная эпюра ледовой нагрузки) и характеризуется тремя параметрами: максимальным давлением р, высотой распределения b и длиной эпюры 1. Для механизма 1-го типа в общем случае может учитываться ещё и возможность увеличения давления за счёт эффекта пиковости ледовой нагрузки.
Данная эпюра в большей степени ориентирована на выполнение проверочных расчетов предельной прочности перекрытия. При разработке метода проектирования перекрытий на основании гибкой процедуры необходимо введение дополнительных упрощающих допущений, позволяющих конкретизировать положение центра эпюры нагрузки для каждого типа механизма и упростить форму эпюры. С целью формирования упрощающей системы допущений проводился специальный расчётный анализ. На основании его результатов были предложены следующие допущения.
Для всех типов пластических механизмов расчетным (соответствующим минимальному значению предельной нагрузки) является симметричное положение эпюры нагрузки относительно вертикальной и горизонтальной осей пластического механизма.
Зона деформирования конструкции при реализации пластического механизма 3-го типа не выходит за пределы двух рамных шпаций, т.е. в предельное состояние переходит только одна балка 3-го уровня (рамный шпангоут). Расчётная нагрузка на механизм i-го типа характеризуется величиной давления pi, равномерно распределённого на прямоугольном пятне контакта с размерами (b х li), где li, – продольный размер деформированной зоны пластического механизма i-го типа,
где:
- S, Sw – расстояния между балками 1-го и 3-го уровней.
Представленная система допущений внутренне сбалансирована, поскольку ограничение на продольный размер пластического механизма согласно экстремальным принципам ТПР способствует некоторому завышению предельной нагрузки, а допущение о равномерном распределении давлений – её занижению.
Величина давления pi связана с максимальным давлением расчётной эпюры р соотношением
где:
- KLi – коэффициент локализации ледовой нагрузки.
Дня механизмов 2-го и 3-го типов коэффициент локализации определяется из очевидных соображений, отражающих редуцирование расчётного давления в случае, когда длина li, превышает длину эпюры нагрузки l:
Для механизма 1-го типа с помощью коэффициента локализации могут учитываться особенности предельного состояния балок первого уровня (шпангоутов) и их взаимодействие с наружной обшивкой при воздействии высоко интенсивных нагрузок, возникающих на малых площадях контакта (2Sb). В рамках настоящего анализа принимается
Обобщённый метод гибкого проектирования сложных бортовых перекрытий
Требования к методу гибкого проектирования
При разработке метода проектирования бортовых перекрытий по критерию предельной прочности на основании сформированной иерархической расчетной модели необходимо учитывать следующие обстоятельства. Высокая интенсивность и Восприятие корпусными конструкциями внешних нагрузок, действующих на суднолокальный характер ледовых нагрузок определяют повышенную жёсткость балочных конструкций и значительное влияние сдвиговых компонентов на общий характер напряжённого состояния, однако степень данного влияния претерпевает заметные количественные изменения при переходе от судов низших к высшим ледовым категориям. Соответственно изменяется и соотношение между требуемыми запасами сдвиговой и изгибной прочности балок перекрытия.
Наряду с этим наличие дополнительных конструктивно-технологических ограничений приводит к появлению у некоторых типов балок избыточных запасов прочности. Поэтому перспективы получения рациональных решений связаны с разработкой нового метода гибкого проектирования бортовых перекрытий, ориентированного на исключение избыточных запасов прочности и представляющего проектанту следующие возможности:
- Учёт различий в величинах расчётных ледовых нагрузок, используемых при проектировании балок разных иерархических уровней.
- Вариацию соотношения между изгибной и сдвиговой геометрическими характеристиками при проектировании поперечного сечения балки.
- Учёт избыточных запасов материала, образующихся при проектировании поперечных сечений при выполнении дополнительных расчетных требований к устойчивости и предельной прочности отдельных элементов сечений, а также конструктивно-технологических ограничений.
- Перераспределение материала межу балками различных иерархических уровней с целью оптимизации размеров перекрытия.
Формулировка критерия предельной прочности, прямой и обратной задач
Сформированная расчётная модель позволяет рассматривать сложное бортовое перекрытие как балочную систему, включающую в общем случае балки 3-х иерархических уровней. Применительно к данной модели критерий предельной прочности может быть сформулирован в следующем, удобном для последующей разработки алгоритма гибкого проектирования перекрытия, виде:
где:
- pui – предельная нагрузка для i-го типа пластических механизмов.
Физически критерием (Формула 5) устанавливается принцип равнопрочности балок всех уровней в отношении в отношении воздействия расчетной ледовой нагрузки.
Предлагается к прочтению: Эксплуатация плавучей буровой установки
Согласно экстремальным принципам ТПР pui определяется как минимальная из предельных нагрузок механизмов i-го типа:
где:
- n – число возможных пластических механизмов i-го типа.
Величина pui является функцией вектора геометрических размеров перекрытия и эпюры ледовой нагрузки {gi}, предела текучести материала σт, векторов фактических геометрических характеристик поперечных сечений балок, образующих пластические механизмы рассматриваемых трех типов – площадей стенок {SAfi} и предельных моментов сопротивления {PMfi}:
Однако определение pui и последующая проверка выполнимости критерия (Формула 5), составляющие обычную процедуру проверочного расчета прочности конкретной конструкции, не являются целью настоящего исследования. Поэтому нет необходимости в построении зависимостей (Формула 7). Вместо этого требуется решение обратной задачи: определить геометрические характеристики поперечных сечений балок, при которых обеспечивается удовлетворение критерия предельной прочности (Формула 5) для всех типов пластических механизмов, возникающих в процессе перехода перекрытия в предельное состояние.
В отличие от проверочного расчёта, называемого часто прямой задачей, формулировка обратной задачи, как задачи проектирования, более сложна, поскольку распадается на совокупность связанных задач по числу уровней балок в перекрытии и типов пластических механизмов. Для лучшего понимания общего алгоритма проектирования перекрытия целесообразно последовательно рассмотреть решение обратной Конструкция судовых перекрытийзадачи проектирования балок 1-го, 2-го и 3-го уровней применительно к наиболее сложному случаю перекрытия с рамными шпангоутами при поперечной системе набора (см. рис. 2)
Оценка предельной прочности и проектирование балок 1-го уровня (обыкновенных шпангоутов)
При регламентации прочности балок 1-го уровня рассматривается предельное состояние изолированной балки, загруженной согласно схеме рис. 4, а.
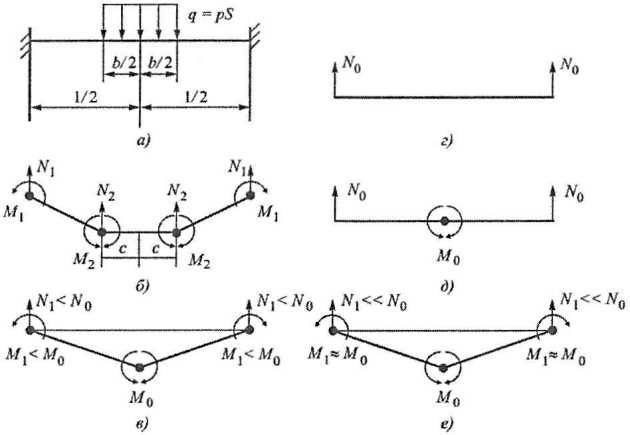
Условие образования в сечении, испытвающем в общем случае воздействие изгибающего момента М и перерезывающей силы N, изгибно-сдвигового пластического шарнира описывается уравнением предельной кривой (условием пластичности) следующего вида:
где:
- M0 = σт PM – предельный изгибающий момент поперечного сечения при чистом изгибе;
- N0 = σт SA/√3 – предельная перерезывающая сила поперечного сечения при чистом сдвиге;
- σт – Принципы проектирования конструкций корпуса суднапредел текучести материала;
- PM, SA – предельный момент сопротивления и площадь стенки поперечного сечения.
Применительно к частным случаям напряженно-деформированного состояния, реализуемым в балочных конструкциях, имеют место следующие формы уравнения (Формула 8):
- чистый изгиб (изгибный пластический шарнир):
- чистый сдвиг (сдвиговой пластический шарнир)
Точное решение ТПР для рассматриваемой балки приводит к схеме 4-шарнирного изгибно-сдвигового пластического механизма, представленной на рис. 4, б. Полученная в разд. “Методы расчета прочности конструкций ледовых усилений при глубоком пластическом деформированииМетоды расчета прочности конструкций из жесткопластического материала в геометрически нелинейной постановке” система уравнений (Формула 2, 5) для описания предельного состояния балочных систем в этом случае примет вид
где:
- M1, N1, M2, N2 – абсолютные значения изгибающих моментов и перерезывающих сил, действующих соответственно в опорном (индекс «1») и пролетном (индекс «2») изгибно-сдвиговых пластических шарнирах;
- l – длина пролета балки;
- b – высота распределения нагрузки (при b > l следует принимать b = l);
- с – отстояние пролетного изгибно-сдвигового шарнира от середины пролета;
- – предельная нагрузка пластического механизма при произвольном значении с;
- pи – истинная величина предельной нагрузки балки.
Решение (Формула 11) может быть получено только численно. Поэтому его использование в дальнейшем анализе нецелесообразно. Приемлемое по точности приближённое решение в аналитической форме может быть получено из рассмотрения двух пластических механизмов: 3-шарнирного изгибно-сдвигового (см. рис. 4, в) и чистого сдвига (см. рис. 4, г). Отметим, что 3-шарнирный механизм вытекает из решения (Формула 11) при c =0, N2 = 0, M2 = M0. Дня приближенного решения имеет место следующая система уравнений:
- изгибно-сдвиговой пластический механизм
- пластический механизм чистого сдвига
где:
- pи1, p и2 – Дополнительные или усиленные конструкции корпуса суднапредельные нагрузки изгибно-сдвигового и чисто сдвигового механизмов.
Решение (Формула 12) имеет вид
где:
Соотношение (Формула 13) позволяет проверить выполнение критерия предельной прочности (Формула 5) для балки 1-го уровня (прямая задача). Решение обратной задачи на основании (Формула 12, 5) приводит к следующим требованиям к геометрическим характеристикам поперечного сечения балки 1-го уровня:
где:
- – фактическая площадь стенки поперечного сечения балки 1-го уровня;
- γ1 ≥ 1 – независимый варьируемый параметр.
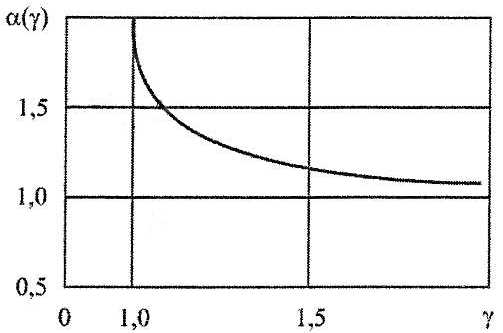
Особенность расчетных зависимостей (Формула 14) состоит в возможности изменять соотношение между величинами геометрических характеристик за счёт увеличения фактической площади стенки SA1f – по сравнению с минимальной площадью стенки SA1. Происходящее при этом увеличение параметра γ1 приводит к уменьшению функции а (γ) (рис. 5) и соответственно требуемого значения PM1. Имеют место два крайних случая.
При
в балке реализуется напряженное состояние, представленное на рис. 4, д: сдвиговые пластические шарниры на опорах и предельный изгибающий момент в пролете. Этому состоянию соответствует минимальная площадь стенки и Справочные показатели для проектирования судового мидель-шпангоута. Приложениемаксимальный требуемый момент сопротивления. Если бы отсутствовали какие-либо дополнительные расчетные или конструктивно-технологические требования к элементам поперечного сечения шпангоута, то данному случаю однозначно соответствовал бы минимум площади поперечного сечения, поскольку при минимальной площади стенки достижение требуемого предельного момента сопротивления осуществляется за счет простого увеличения высоты поперечного сечения. На практике данный случай реализуется в конструкциях судов высших ледовых категорий при относительно малых длинах пролётов балок.
При
Т.е. в балке возникает состояние, близкое к чистому изгибу и фактически реализуется традиционная трехшарнирная схема перехода в предельное состояние (рис. 4, е). За счет существенного увеличения площади стенки по сравнению с требуемой момент сопротивления снижается вдвое по сравнению со случаем SA1f = SA1. Данный случай характерен для конструкций судов низших ледовых категорий при относительно больших длинах пролётов балок, испытывающих слабое влияние сдвига.
Реально для большинства встречающихся конфигураций бортовых перекрытий реализуется совокупность промежуточных между указанными крайними случаев, при которых
и в балке реализуются изгибно-сдвиговые шарниры на опорах и изгибный шарнир в пролете (рис. 4, в). В этих случаях увеличение фактической площади стенки по сравнению с требуемой минимальной SA1 может производиться из-за наличия дополнительных требований и ограничений (например, к минимальной толщине стенки, максимальной высоте сечения и т.п.). Зависимости (Формула 14) обеспечивают возможность использования дополнительного запаса материала в стенке для снижения требуемого момента сопротивления сечения. Важно подчеркнуть, что при выполнении (Формула 17) строго удовлетворяется условие pи = pи2, т.е. не происходит изменения уровня предельной прочности балки.
Дополнительный резерв предельной прочности появляется, если наряду с запасом по площади стенки SA1f > SA1 при проектировании балки вносится запас и по моменту сопротивления PM1f > PM1 (такая ситуация реализуется, например, при использовании катанных профилей). Способ учета данного резерва на стадии проектирования балок более высоких уровней будет изложен в следующем пункте.
Преимущества предложенного гибкого подхода к регламентации требуемых геометрических характеристик в соответствии с зависимостями (Формула 14) при практическом проектировании балочных конструкций ледовых усилений очевидны. Поэтому этот подход следует использовать и при решении обратной задачи для балок более высоких уровней.
Проектирование балок 2-го уровня (несущих стрингеров)
Согласно обоснованной в п. “Иерархический принцип построения расчетных моделей бортовых перекрытий” расчётной модели перекрытия при регламентации прочности балок 2-го уровня рассматривается предельное состояние пластического механизма 2-го типа, загруженного согласно схеме рис. 6, а.
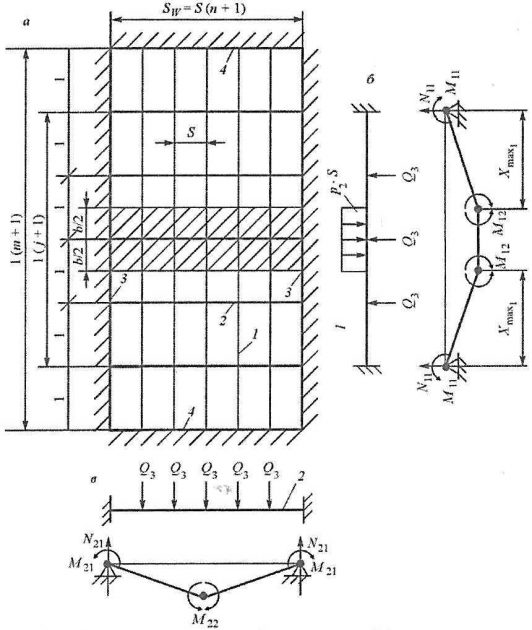
1 – обыкновенные шпангоуты;
2 – несущие стрингеры;
3 – рамные шпангоуты;
4 – опорные конструкции;
▨ – область приложения ледовой нагрузки P2;
• – пластические шарниры
Рамные шпангоуты, ограничивающие с двух сторон пластический механизм, остаются недеформированными. Ледовая нагрузка в пределах рамной шпации полагается равномерно распределенной на полосе высотой b и длиной Sw (рамная шпация). Равномерное давление на полосе b x Sw определяется согласно (Формула 2). Горизонтальная ось симметрии эпюры нагрузки совпадает с горизонтальной ось симметрии пластического механизма.
При рассмотрении пластических механизмов 2-го типа принимается следующее традиционное предположение о характере силового взаимодействия составляющих его балок;
- ледовая нагрузка непосредственно воспринимается балками 1-го уровня (обыкновенными шпангоутами);
- балки 2-го уровня (несущие стрингеры) загружены только реакциями в узлах их пересечения со шпангоутами.
Поскольку рассматриваемый механизм состоит из одинаковых обыкновенных шпангоутов и одинаковых несущих стрингеров, все узловые реакции должны быть одинаковы.
Из-за локального характера ледовой нагрузки заранее неизвестно число несущих стрингеров, переходящих в предельное состояние совместно j = 1,…, m со шпангоутами. Поэтому в соответствии с кинематической теоремой ТПР истинная предельная нагрузка конструкции определяется из условия:
где:
- m – число несущих стрингеров в перекрытии;
- j = 1,…, m – индекс j-го пластического механизма 2-го типа, равный числу несущих стрингеров, перешедших в предельное состояние;
- pи2j – предельная нагрузка j-го пластического механизма 2-го типа;
- pи2 – истинная предельная нагрузка для всех пластических механизмов 2-го типа.
Схемы перехода в предельное состояние обыкновенного шпангоута и несущего стрингера для j-го пластического механизма (при j = 3) представлены на рис. 6, б, в. Расчетная схема несущего стрингера сводится к изолированной жестко заделанной балке под действием равномерно распределенной на длине S х n (n – число обыкновенных шпангоутов в рамной шпации) погонной нагрузки:
где:
- Qj — реакция, передаваемая обыкновенным шпангоутом на несущий стрингер.
Применяя для несущего стрингера решения разд. см. “Методы расчета прочности конструкций ледовых усилений при глубоком пластическом деформированииДеформирование локально загруженной пластины наружной обшивки при образовании бухтины” в совокупности с критерием предельной прочности (Формула 1), легко получить аналогичные представленным в п. “Оценка предельной прочности и проектирование балок 1-го уровня (обыкновенных шпангоутов)” выражения для требуемых геометрических характеристик поперечного сечения несущего стрингера:
где:
- Q – величина узловой реакции, соответветствующая истиному пластическому механизму с предельной нагрузкой pи2f;
- SA2f – фактическая площадь стенки поперечного сечения несущего стрингера.
Поскольку безразмерная реакция Q обратно пропорциональна ри2, из (Формула 18) вытекает следующее экстремальное условие:
Таким образом, для определения требуемых геометрических характеристик несущих стрингеров необходимо на основании анализа предельного состояния всех пластических механизмов 2-го типа получить выражения для безразмерных реакций
и найти максимальное значение Q. Как уже отмечалось выше, при этом не возникает необходимости в непосредственном отыскании предельных нагрузок и истинной предельной нагрузки.
Как будет показано ниже, для определения параметра Q оказывается достаточным проанализировать пластические механизмы, включающие не более трех несущих стрингеров. При таком ограничении система уравнений (Формула 2, 5), включающая уравнения равновесия, уравнения предельных кривых, а также дополнительное условие для отыскания положения изгибных пластических шарниров в пролете обыкновенного шпангоута, может быть записана в общем виде (обозначения соответствуют принятым на рис. 6):
где:
– абсолютные значения изгибающих моментов и перерезывающей силы, действующих в опорных сечениях (индекс «11») и в пролете (индекс «12») (в сечении Xmax1) обыкновенного шпангоута;
- Xmax1 – координата сечения, в котором образуется изгибный пластический шарнир;
- Mf1, Nf1 – момент и перерезывающая сила, соответствующие фактическим размерам поперечного сечения обыкновенного шпангоута, определенным на основании требований п. см. “Оценка предельной прочности и проектирование балок 1-го уровня (обыкновенных шпангоутов)“.
Разрешающая система (Формула 22) получена в предположении, что уже осуществлено Общие вопросы проектирования судовых конструкцийпроектирование балок первого уровня и известны фактические величины геометрических характеристик их поперечных сечений. Тогда на основании (Формула 8, 14) выражения для Mf1, Nf1 могут быть представлены в виде
где:
- ψ1, φ1 – функции, определяемые на основании следующих соотношений:
Рассмотрение (Формула 24) показывает, что коэффициенты ψ1 и φ1 позволяют учесть при проектировании балок 2-го уровня два важных фактора:
- разницу между требуемыми и фактическими характеристиками поперечного сечения балок 1-го уровня;
- различие в величинах расчётных нагрузок на балки 1-го уровня при их работе в составе пластических механизмов 1-го и 2-го типов.
Поэтому можно заключить, что введение коэффициентов ψ1 и φ1 отражает принятую ориентацию на разработку гибкой процедуры проектирования. Совместное решение (Формула 22, 23 и 20) позволяет получить следующее нелинейное уравнение для определения безразмерных реакций Qj:
где:
На основании анализа, выполненного автором и подробно описанного в, получено следующее аппроксимационное решение уравнения (Формула 25)
где:
- сjk – коэффициенты, представленные в табл. 1 (k -1,…,5, j -1,2,3).
Достоверность полученного решения в широком диапазоне изменения параметров β, φ1 и производного от ψ параметра
подтверждена представленными в результатами массовых расчётов, выполнявшихся с помощью аппроксимации (Формула 26) и на основании численного решения уравнения (Формула 25).
Читайте также: Расчет судовой электроэнергетической системы
Следует обратить внимание, что при j = 3 из-за увеличения длины пролета шпангоута влияние перерезывающих сил в опорных сечениях практически нивелируется. Поэтому для Q3 вместо (Формула 26) может быть предложена более простая зависимость, обеспечивающая необходимый уровень точности:
Величина реакции Q, определяющая требования в размерам несущего стрингера, находится из условия (Формула 21).
Естественно, что при одном несущем стрингере в перекрытии m = 1 и Q = Q1.
При m = 2 для раскрытия соотношения (Формула 21) выполняется сравнение значений параметров Q1 и Q2 при вариации параметров ψ1 и φ1. Результаты данного анализа показаны на рис. 7 системой графиков
где:
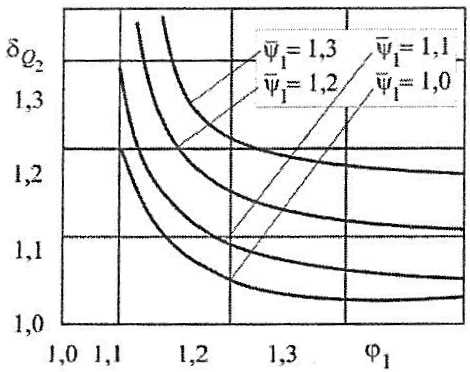
Графики на рис. 7 позволяют однозначно установить, что в перекрытии с m = 2 всегда выполняется условие δQ2 > 1 и, следовательно, Q1 = Q2. Выполнение аналогичной процедуры при m = 3 (рис. 8) дает δQ2 < 1 и, следовательно, Q1 = Q2 при m > 2.

Таким образом, для безразмерной реакции Q:
где:
- j – индекс, определяемый в зависимости от числа стрингеров, j = m при m ≤ 2, j = 2 при m > 2;
- Qj – функция, задаваемая с помощью соотношения (Формула 26) и табл. 1.
Таким образом, на основании выполненного анализа установлена важная особенность предельного состояния пластического механизма 2- го типа, обусловленная локальным характером ледовой нагрузки. Если Листовые конструкции корпуса суднабалки 1-го уровня спроектированы на основании требований (Формула 14), то в механизм вовлекается не более двух балок 2-го уровня.
Естественно, что полученное решение для определения реакций взаимодействия Q справедливо в рамках принятой при разработке модели перекрытия иерархии, согласно которой балки 1-го уровня (шпангоуты) нуждаются в поддержке балок 2-го уровня (стрингеров).
Однако в отдельных случаях, когда коэффициенты φ1 и ψ1, существенно больше единицы, предельная прочность обыкновенных шпангоутов оказывается настолько высокой, что они способны воспринять ледовую нагрузку р2 без дополнительной поддержки несущих стрингеров. Формально в этих случаях из решения уравнения системы (Формула 25) будет следовать Qj ≤ 0, что не позволяет предъявить расчетные требования к размерам несущих стрингеров.
Корректное уточнение решения для указанных случаев состоит в рассмотрении предельного состояния пластического механизма 2-го типа, в который под действием переменной ледовой нагрузки вовлекается только часть (n1) наиболее нагруженных обыкновенных шпангоутов, а остальные (n – n1) остаются недеформированными (рис. 9).
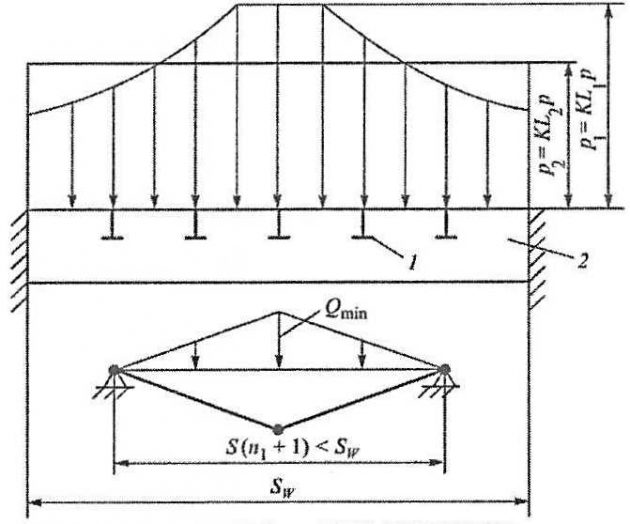
1 – обыкновенные шпангоуты;
2 – несущий стрингер
Из рассмотрения данного механизма в установлено минимальное значение Qmin реакций Qj:
где:
- с0 = 0,3 – верхняя граница реального диапазона изменения функций c (φ1, ψ1).
С учетом полученных соотношений для Q и Qmin зависимости (Формула 20) для определения требуемых геометрических характеристик несущего стрингера примут вид:
где:
Проектирование балок 3-го уровня (рамных шпангоутов)
Требования к размерам балок 3-го уровня (рамных шпангоутов) определяются из рассмотрения пластических механизмов 3-го типа, описывающих Общий продольный изгиб и общая продольная прочность корпусных конструкций суднапредельное состояние конструкции в пределах двух рамных шпаций под действием ледовой нагрузки интенсивностью p3 согласно (Формула 2), равномерно распределенной на полосе 2Sw x b.
Сформулированные в п. “Проектирование балок 2-го уровня (несущих стрингеров)” для пластических механизмов 2-го типа допущения о характере восприятия нагрузки и силовом взаимодействии балок различных уровней применительно к пластическим механизмам 3-го типа в отношении обыкновенных шпангоутов остаются неизменными, а для несущих стрингеров и рамных шпангоутов приобретают вид:
- каждый из несущих стрингеров на длине пролета в две рамные шпации загружен 2n реакциями Q, передаваемыми со стороны обыкновенных шпангоутов и одной поддерживающей реакцией G, приложенной в узле пересечения с рамным шпангоутом;
- рамный шпангоут загружен погонной ледовой нагрузкой p3S, а также реакциями G в узловых точках пересечения с несущими стрингерами, перешедшими в предельное состояние.
Как и в случае пластических механизмов 2-го типа, число несущих стрингеров j, вовлекаемых в перемещения пластического механизма, заранее неизвестно и определяется из условия минимума истинной предельной нагрузки:
где:
- pи3j – предельная нагрузка пластического механизма с j несущими стрингерами.
Согласно результатам, полученным в п. “Проектирование балок 2-го уровня (несущих стрингеров)“, в пластических механизмах 2-го типа в предельное состояние переходит не более двух несущих стрингеров. Как показывают предварительные оценки, для пластических механизмов 3-го типа истинным является пластический механизм, включающий все m несущих стрингеров. Поэтому условие (Формула 38) приобретает вид
Справедливость (Формула 34) в указанном диапазоне изменения числа несущих стрингеров в перекрытии (m ≤ 6) будет продемонстрирована ниже на основании анализа итоговых результатов. В области m > 6 в принципе не исключено отклонение от (Формула 34), однако, Конструкция и расчет бортовых перекрытийбортовые перекрытия с таким большим количеством несущих стрингеров на практике не встречаются.
Расчетная схема пластического механизма 3-го типа (при m = 3) представлена на рис. 10.
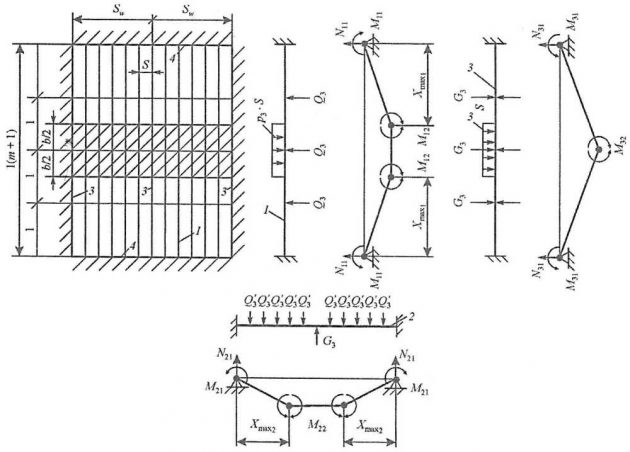
1 – обыкновенные шпангоуты;
2 – несущие стрингеры;
3 – рамные шпангоуты;
4 – опорные конструкции
Применительно к данной схеме система уравнений равновесия и предельных кривых (Формула 2, 5) после подстановки в них критерия предельной прочности (Формула 5) примет вид:
где:
– реакции в точках пересечения обыкновенных шпангоутов и несущих стрингеров, возникающие в пластическом механизме 3-го типа и, в общем случае, отличающиеся от определенных в п. “Проектирование балок 2-го уровня (несущих стрингеров)” реакций Qj;
- Mi1, Mi2, Ni1 – абсолютные значения изгибающих моментов и перерезывающих сил, действующих в опорном (индекс «1») и пролетном (индекс «2») шарнирах балки i-го уровня;
- Gm – реакции взаимодействия между несущими стрингерами и рамными шпангоутами;
- Mfi, Nfi – предельный изгибающий момент и перерезывающая сила, соответствующие фактическим размерам поперечного сечения балки i-го уровня;
- хmaxi – координата шарнира в пролете балки i-го уровня;
- ym, zm, tm – коэффициенты, определяемые согласно табл. 2 для перекрытий с m ≤ 6.
Решение системы (Формула 35) осуществляется в три последовательных этапа.
Первоначально рассматривается решение подсистемы (Формула 35, а) в отношении реакций Qm. Величины Mfi и Nfi, входящие в нее, известны, поскольку обыкновенный шпангоут уже спроектирован. Отличие Сущность и системы управления морским транспортомподсистемы от представленной в п. “Проектирование балок 2-го уровня (несущих стрингеров)” системы (Формула 22) состоит в следующем:
- рассматриваются пластические механизмы с большим числом несущих стрингеров (m ≤ 6 вместо j ≤ 3 );
- используется нагрузка p3 = KL3p вместо p2 = KL2p.
Данные отличия не приводят к необходимости внесения изменений в выражения для безразмерных реакций Q1, Q2, Q3 (Формула 26, 28).
Вывод зависимостей для безразмерных реакций Qm в диапазоне m = 4, 5, 6 не представляет затруднений. Исходя из соображений, отмеченных в п. “Проектирование балок 2-го уровня (несущих стрингеров)” при построении соотношения (Формула 28), можно аналогичным путем получить соотношения для m = 4, 5, 6:
где:
- сmk – коэффициенты, представленные в табл.3.
С учетом различия в нагрузках решение (Формула 40, а) должно быть представлено в виде
где:
- – коэффициенты, определяемые согласно табл. 1 (при m = j = 1, 2) или табл. 3 (при m = 3, 4, 5, 6 ).
Учитывая, однако, что некоторое различие в коэффициентах KL2 и KL3 проявляется только в нетрадиционных случаях (перекрытия с увеличенной рамной шпацией), в практических расчетах допустимо полагать:
На втором этапе рассматривается подсистема (Формула 35, б), в которой считаются известными величины
, а также Mf2 и Nf2, поскольку несущий стрингер уже спроектирован. Дня дальнейшего анализа выражения для Mf2 и Nf2 по аналогии с процедурой п. см. “Проектирование балок 2-го уровня (несущих стрингеров)” удобно преобразовать к следующему виду:
где:
- PM2f, SA2f – фактические предельный момент сопротивления и площадь стенки поперечного сечения несущего стрингера.
Подставляя соотношения (Формула 37, 39) в подсистему (Формула 35, б), можно получить следующее решение относительно неизвестной реакции взаимодействия в точках пересечения несущих стрингеров с рамным шпангоутом:
где:
- – безразмерный параметр, определяемый из решения следующего нелинейного уравнения:
На основании численного анализа получено приближенное решение уравнения (Формула 41):
Достоверность (Формула 42) в реальной области изменения параметров n, φ2, а также вводимого по аналогии с (Формула 27) параметра ψ2:
подтверждена представленными в результатами сопоставлений с точным численным решением уравнения (Формула 41).
Это интересно: Автоматизированные системы плазовых работ
Полученное решение для реакции Gm используется на последнем этапе анализа общей системы (Формула 35) — определении требуемых значений геометрических характеристик поперечного сечения рамного шпангоута из решения подсистемы (Формула 35, в). Подстановка в (Формула 35, в) выражений (Формула 40, 42) после некоторых преобразований дает:
где:
- lw – пролет рамного шпангоута, равный расстоянию между его опорными сечениями на опорных конструкциях;
- SA3f – фактическая площадь стенки поперечного сечения рамного шпангоута.
На основании соотношений (Формула 44) легко доказать достоверность принятого выше допущения о замене общего условия минимума предельной нагрузки (Формула 33) упрощенным соотношением (Формула 34). Анализ показывает, что геометрические характеристики поперечного сечения рамного шпангоута в диапазоне m ≤ 6 оказываются возрастающими функциями m (рис. 11), т.е. выполняются условия:
где:
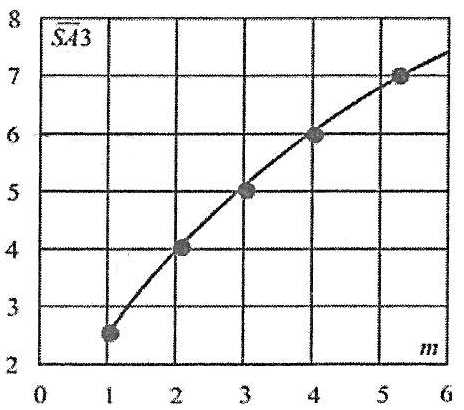
Поскольку задача определения геометрических характеристик по критерию предельной прочности обратна задаче нахождения предельной нагрузки, то выполнение (Формула 45) доказывает справедливость замены условия (Формула 33) при определении истинной (минимальной) нагрузки на упрощенное условие (Формула 34).
Следует обратить внимание, что геометрические характеристики рамного шпангоута зависят от параметров φ1, ψ1, φ2, ψ2 (они входят в соотношения (Формула 44) через функции Gm (Qm R), Q (φ1, ψ1).
Таким образом, при проектировании балки 3-го уровня учитывается вся система проектных решений, принимавшихся на стадии проектирования балок более низких уровней. Этим обеспечиваются широкие возможности для гибкого проектирования как перекрытия в целом, так и составляющих его балок.
Общий алгоритм гибкого проектирования бортовых перекрытий, включающих балки трех уровней
Представленные в п. “Оценка предельной прочности и проектирование балок 1-го уровня (обыкновенных шпангоутов)“-“Проектирование балок 3-го уровня (рамных шпангоутов)” результаты применимы для проектирования наиболее сложного и, в то же время, распространенного типа бортовых перекрытий – с рамными шпангоутами при поперечной системе набора. Следует отметить, что процедура гибкого проектирования разработана и для двух других отмеченных в п. “Конструктивные схемы бортовых перекрытий” типов перекрытий, однако, подробного описания этих исследований не приводится.
Выполненные исследования могут быть обобщены в виде алгоритма гибкого проектирования бортового перекрытия по критерию предельной прочности.
Пусть рассматриваемое перекрытие включает балки трех уровней. Задан набор геометрических размеров, однозначно определяющих взаимное расположение балок в перекрытии и параметры расчетной ледовой нагрузки. Для удобства дальнейшего изложения вводится следующая система обозначений:
- i – индекс типа пластического механизма и уровня балки;
- p,b – параметры расчетной ледовой нагрузки;
- pi = KLip – расчетное давление, используемое при анализе предельного равновесия пластических механизмов i-гo типа;
- KL1 — коэффициенты локализации расчетной нагрузки;
- (SAf, PMf) – требуемые и фактические площадь стенки и предельный момент сопротивления поперечного сечения балки i-го уровня;
- {gi} – вектор геометрических размеров перекрытия и эпюры ледовой нагрузки, используемых при рассмотрении пластических механизмов i-го типа.
На первом этапе осуществляется проектирование балок 1-го уровня.
Из рассмотрения пластических механизмов 1-го типа устанавливаются требования к геометрическим характеристикам поперечного сечения балок 1-го уровня:
где:
- – функции, определяемые из решения задачи о предельном равновесии пластических механизмов 1-го типа.
Подбор профиля на основании (Формула 46) осуществляется путем варьирования параметра ϒ1. После Конструкция поперечных и продольных переборокопределения размеров поперечного сечения вычисляются коэффициенты φ1 и ψ1, характеризующие фактические Материалы конструкций корпуса, активно используемые в судостроениизапасы материала балки по сравнению с требуемыми по (Формула 46), а также различие между давлениями p1 и p2, обусловленное фактором локализации нагрузки:
(ii) На втором этапе осуществляется проектирование балок 2-го уровня.
Из рассмотрения пластических механизмов 2-го типа устанавливаются требования к геометрическим характеристикам поперечного сечения балок 2-го уровня:
где:
- – функции, определяемые из решения задачи о предельном равновесии пластических механизмов 2-го типа.
Главное отличие (Формула 48) от (Формула 46) состоит в том, что требуемые геометрические характеристики балок 2-го уровня зависят еще и от фактических размеров поперечного сечения балок 1-го уровня.
Подбор профиля на основании (Формула 48) осуществляется путем варьирования параметра ϒ2. После определения размеров поперечного сечения вычисляются коэффициенты φ2 и ψ2, характеризующие фактические запасы материала балки по сравнению с требуемыми по (Формула 48), а также различие между давлениями р1 и р2, обусловленное фактором локализации нагрузки:
На третьем этапе осуществляется проектирование балок 3-го уровня.
Из рассмотрения пластических механизмов 3-го типа устанавливаются требования к геометрическим характеристикам поперечного сечения балок 3-го уровня:
где:
- – функции, определяемые из решения задачи о предельном равновесии пластических механизмов 3-го типа.
Соотношения (Формула 50) зависят уже от фактических размеров балок 1-го и 2-го уровней.
В целом изложенный алгоритм (Формула 46-50) позволяет не только снижать размеры балок 2-го и 3-го типа уровней за счет наличия избыточных запасов материала в балках 1-го и 2-го уровней. На его основе непосредственно осуществляется учет различий в величинах расчетных нагрузок для балок различных уровней, а также может производиться целенаправленное перераспределение материала между балками различных уровней для оптимизации размеров перекрытия. Наконец, в него включены возможности изменения в широких пределах соотношений между изгибными и сдвиговыми характеристиками поперечного сечения путем варьирования параметров ϒ1, что в значительной степени облегчает процедуру проектирования поперечного сечения.
Поскольку в разработанном обобщенном методе проектирования бортовых перекрытий по критерию предельной прочности используется ряд упрощающих допущений и аппроксимационных зависимостей была осуществлена независимая проверка его достоверности. Алгоритм данной проверки, предложенный автором и осуществленной в рамках процедуры подготовки Унифицированных правил Международной ассоциации классификационных обществ (МАКО) для полярных судов, состоял в следующем. Были согласованны две конструктивные схемы бортовых перекрытий (с рамными шпангоутами, Конструкция судового наборапоперечная система набора), одна из которых представляла типичную канадскую конфигурацию (три несущих стрингера, три обыкновенных шпангоута в рамной шпации), другая – типичную российскую (два несущих стрингера, семь обыкновенных шпангоутов в рамной шпации).
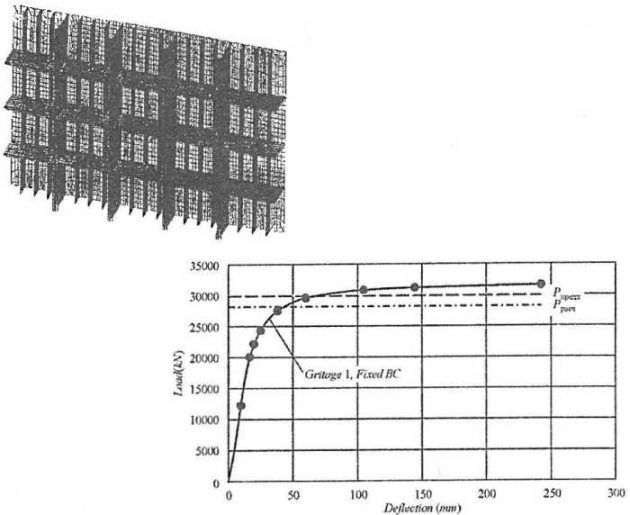
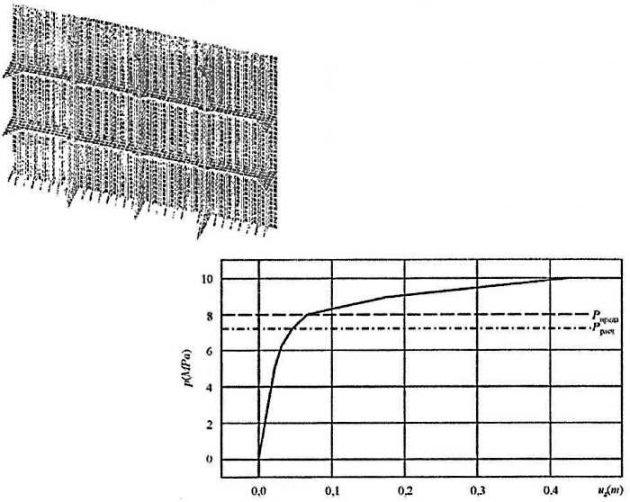
Для согласованных схем с помощью обобщенного метода были определены размеры связей на заданную расчетную нагрузку pрасч. Для спроектированных перекрытий выполнялись прямые расчеты упругопластического изгиба перекрытий на основании универсальной конечноэлементной программы ANSYS. В результате расчета определялась величина нагрузки, соответствующей моменту начала интенсивного нарастания прогибов перекрытия. Данная нагрузка трактовалась как предельная нагрузка перекрытия pпред. Она сравнивалась с расчетной нагрузкой, на которую проектировалось перекрытие. В зависимости от степени согласования значений нагрузок pрасч и pпред оценивалась достоверность обобщенного метода.
Результаты конечно-элементных расчетов, представленные на рис. 12 и 13, продемонстрировали практически идеальное согласование предельных и расчетных нагрузок. Наблюдаемое превышение предельной нагрузки над расчетной (соответственно 7 % и 10 %) объясняется влиянием фактора упрочнения материала, учитываемого в конечно- элементных расчетах и сознательно игнорируемого в обобщенном методе в связи с традиционными требованиями к консервативности расчетных процедур, используемых в Правилах классификационных обществ. Таким образом, получено полноценное подтверждение достоверности разработанного обобщенного метода проектирования бортовых перекрытий по критерию предельной прочности.