Основные свойства объектов автоматических систем судна

В теории автоматического регулирования рассматриваются общие закономерности, характеризующие влияние различных элементов САР на устойчивость и точность регулирования, методы проектирования и расчета параметров и настройки регуляторов для удовлетворения требований заданной точности САР. Используемые для этих целей методы исследования в теории автоматики основаны на анализе дифференциальных уравнений САР и ее отдельных элементов.

Основные понятия

Методы, применяемые для Технико-эксплуатационные характеристики морских судов и плавучих сооруженийисследования судовых САР, можно разделить на 2 группы: методы исследования линейных САР, т. е. систем, динамика которых описывается линейными дифференциальными уравнениями, и методы исследования нелинейных САР, т. е. систем, динамика которых описывается нелинейными дифференциальными уравнениями.

С целью упрощения анализа стремятся линеаризовать нелинейности, для чего используют метод малых отклонений. Пусть, например, F (x, у) носит нелинейный характер. Используя метод малых отклонений от состояния системы, принятого за исходное, в данном случае F (х₀, у₀), получаем:

члены высшего порядка малости, отбросив которые, получим

Графическая трактовка линеаризации заключается в том, что нелинейные зависимости заменяются касательными в соответствующей точке кривой. Вместе с тем такая линеаризация не всегда возможна (см. ниже).

Объектами регулирования называются агрегаты и установки, оборудованные регуляторами. Под объектом подразумевается собственно агрегат (без регулятора), точнее те его элементы, которые влияют на процесс регулирования.

Если в установке регулируется несколько величин, то ее можно рассматривать как объект регулирования раз-личных величин. Так, например, котельная установка является объектом регулирования давления пара и уровня воды. Свойства котельной установки как объекта регулирования давления пара зависят от свойств тех эле-ментов котла, в которых происходит преобразование тепловой энергии в энергию давления пара, например, от тепловой емкости пароводяной смеси и металлических частей котла. Этот же котел является объектом уровня воды в барабане. Главные и вспомогательные паровые котлыХарактеристики котла как объекта регулирования уровня воды в барабане зависят от объема, занимаемого водой, площади поверхности зеркала воды и, естественно, отличаются от предыдущих.

Свойства объекта, влияющие на процесс регулирования и выбор регулятора, могут быть установлены на основании дифференциального уравнения объекта. Последнее позволяет получить зависимость изменения выходной величины объекта — регулируемой величины — от входных: нагрузки и регулирующего воздействия.

В качестве примера рассмотрим вывод дифференциального уравнения изменения уровня воды в емкости. На основании проведенного ранее анализа

где:

• F — площадь зеркала воды в баке.

Величина F характеризует емкость, или аккумулирующую способность, объекта регулирования. Чем больше емкость, тем меньше скорость dH/dt и, следовательно, склонность регулируемой величины к изменению.

Приток воды Q_пр связан с ходом h клапана 7 зависимостью Q_пр ~ K₁h, где К₁ — постоянная. Расход воды из бака при постоянном открытии клапана 1 нелинейно зависит от уровня: Q_расх = AH^1/2, где A — величина, пропорциональная открытию выпускного клапана. Эта зависимость представлена на рис. 1.

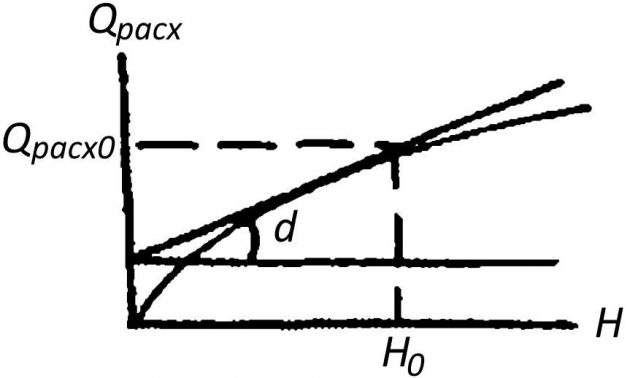
Линеаризуем нелинейную зависимость расхода от уровня в районе точки, соответствующей заданному уровню Н₀. Эта линеаризация равноценна замене кривой Q_расх (H) на рис. 1 отрезком касательной в точке (H₀, Q_расх0). Тогда дифференциальное управление изменения уровня воды получим в виде:

где:

• $K_1{h}_0=Q_{расх}; K_2={(d{Q}_{расх}/dH)}_0$

Перейдем к относительным единицам, для чего выберем так называемые базовые или номинальные значения величин: уровня H_ном расхода Q_ном и хода клапана h_ном (Q_ном = K₁h_ном). Дифференциальное уравнение емкости, как объекта регулирования уровня воды, получим в виде:

где:

• $x=z–\lambda , z=\Delta h/hном, \lambda =\Delta A/Aном, y=\Delta H/Hном, Ta=FHном/Qном$

  — так называемое время разгона объекта с, за которое регулируемая величина у изменится на относительную единицу, если в этот период;

• $x=1=const,\beta =0,\beta =K_2{H}_{ном}/Q_{ном}$

  — самовыравнивание объекта, характеризующее склонность регулируемой величины у к восстановлению установившегося значения.

Пусть в момент

Предагается к прочтению: Управление флотом судовой компании

Решение уравнения (формула 1) примет вид:

т. е. чем больше величина T_a, тем меньше отличие между новым и прежним (до изменения х) значениями регулируемой величины.

График переходного процесса, соответствующий решению уравнения (формула 1) при х₀ = 1 представлен на рис. 2. При β > 0 самовыравнивание положительное, а процесс изменения регулируемой величины устойчивый: величина у при t = ∞ принимает новое установившееся значение

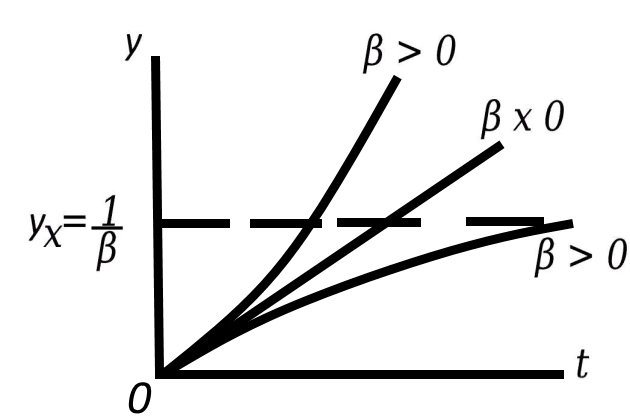
В рассмотренном примере увеличение расхода воды приводит к снижению уровня, что в свою очередь снижает расход воды Q_расх и стабилизирует регулируемую величину.

Таким образом, самовыравнивание определяет свойства объекта стабилизировать регулируемую величину самостоятельно, без помощи регулятора. Чем больше величина β, тем легче регулятору справиться с задачами поддержания регулируемой величины в заданных пределах. В некоторых случаях необходимость в регуляторе может вообще отпасть.

Очень часто для математического описания ряда объектов регулирования можно использовать дифференциальное уравнение 1-го порядка (формула 1). В правой части этого уравнения выражение (z-λ) соответствует случаю, когда действие нагрузки обуславливает отвод энергии или питающей жидкости от объекта. Если же действие нагрузки обуславливает Средства автоматизации главных энергетических установокподвод энергии (питающей жидкости) к объекту, то уравнение (формула 1) принимает вид:

Время разгона T_a характеризует инерционные свойства объекта. Чем больше T_a, тем больше инерционность объектов. Для большинства объектов самовыравнивание положительно β > 0, однако, в отдельных случаях β < 0 или β = о.

Если β < 0, т. е. самовыравнивание отрицательное, то при t → ∞ и z = const (регулятор отсутствует или не действует) у → ∞ и процесс регулирования неустойчив.

Если β = о, то самовыравнивание отсутствует, а регулируемая величина изменяется с постоянной скоростью:

Формула (формула 1) может быть приведена к виду:

где:

• $T_{об}=T_a/\beta$

  — так называемая постоянная времени объекта;

• $K_{об}=1/\beta$

  — коэффициент усиления объекта.

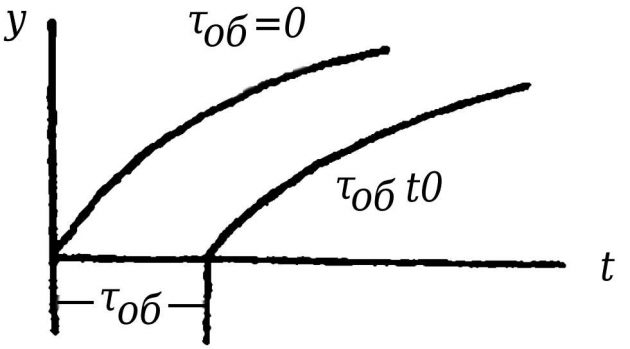
Требования и процесс регулирования судовой автоматикиОбъект регулирования может иметь элементы с «чистым» запаздыванием. Такие элементы задерживают прохождение сигнала на величину τ_об т. е. выходная величина копирует входную с запаздыванием на τ_об. Уравнение объекта из последовательно соединенных элементов с «чистым» запаздыванием и элементом, описываемым уравнением 1-го порядка, имеет вид:

Переходная характеристика объекта при τ_об ≠ 0 и τ_об = 0 представлена на рис. 3.

Уравнение объекта в общем случае может иметь не только первый, но второй, третий и более высокий порядок. В соответствии с порядком уравнения объект называется «одноемкостным», «двухемкостным» и т. д.

В рассмотренных случаях воздействия нагрузки и регулятора на регулируемую величину имеют одинаковый характер. В соответствии с уравнением (формула 1) при изменении z и λ регулируемая величина изменяется по одному и тому же закону. В общем случае воздействие нагрузки и регулятора на объект может быть различно и проходить по разным элементам объекта, что должно учитываться при составлении уравнения динамики объекта.

Экспериментальное определение постоянных уравнений динамики объектов регулирования

Ремонт электрооборудования и систем автоматики суднаВыбор параметров регуляторов при их проектировании или настройке основан на том, что постоянные уравнений динамики объектов T_a, β и (или T_об, K_об и τ_об) заданы. Вместе с тем определение расчетным путем перечисленных постоянных может быть либо затруднительным из-за отсутствия данных для расчета, либо сопряжено со значительными погрешностями из-за допущений, принятых при выводе уравнений. Поэтому широкое применение нашел экспериментальный способ определения величин T_a, β и τ_об.

Для этой цели на действующем объекте искусственным путем изменяется нагрузка или регулирующие воздействие, которые в дальнейшем поддерживаются постоянными, и производится регистрация регулируемой величины, т. е. получается разгонная характеристика объекта (рис. 4). Для определения величины τ_об и T_об к кривой переходного процесса проводится касательная в точке ее наибольшего наклона.

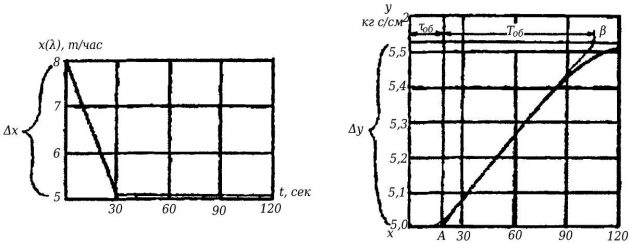
Отрезок времени от начала переходного процесса до точки A пересечения касательной с прямой, соответствующей начальному значению регулируемой величины у₀, равен ≅ τ_об. Отрезок времени от точки A до точки B пересечения касательной с прямой, соответствующей конечному значению регулируемой величины, равен T_об, величина получается как частное от деления изменения регулируемой величины на изменение нагрузки: К_об = Δу/Δх.

Величины β и T_a могут быть найдены в этом случае по формулам:

Уравнение дизеля, как объекта регулирования частоты вращения

Уравнение может быть получено из анализа динамики вращающихся масс:

где:

• J — момент инерции вращающихся масс, кг·м²;
• ω — частота вращения, с^-1.

μ_e (ω, h_e) Влияние моментов топливоподачи на индикаторный процесс двигателейэффективный момент дизеля, н.м., являющийся функцией частоты вращения ω и положения рейки топливных насосов h_p, μ_нагр (ω, h_e) — нагрузочный момент, н.м., зависящий от ω и положения h_н органа, изменяю-щего нагрузку.

Используя метод линеаризации при малых отклонениях ω, h_p и h_н от установившихся значений ω₀, h_ро и h_но. Получим на установившемся режиме:

и на неустановившемся режиме:

В качестве исходного обычно выбирается режим номинальной мощности.

Переходя к относительным единицам, введем обозначения:

• $T_{а}=J{\omega }_{ном}/{\mu }_{е ном}$

  — время разгона объекта, с;

• $\beta =\left[{\left(\partial {\mu }_{нагр}/\partial \omega \right)}_{ном}–{(\partial {\mu }_{е}/\partial \omega )}_{ном}\right]{\omega }_{ном}/{\mu }_{е ном}$

  — самовыравнивание объекта;

• $\phi =\Delta \omega /{\omega }_{ном}$

  — относительное изменение частоты вращения.

• $K_z={(\partial {\mu }_{е}/\partial h_{р})}_{ном}{h}_{р ном}/{\mu }_{е ном}$

  — передаточный коэффициент регулирующего воздействия.

При постоянном значении ш изменение хода рейки топливных насосов примерно пропорционально изменение эффективного момента дизеля, поэтому:

• $z=\Delta h_{р}/h_{р ном}$

  — регулирующее воздействие;

• $\lambda =K\Delta h_{н}/h_{н ном}$

  — нагрузка.

Получим:

На рис. 5 представлен вид скоростной Внешние характеристики дизеляхарактеристики дизеля (h_р = const, ω = Var).

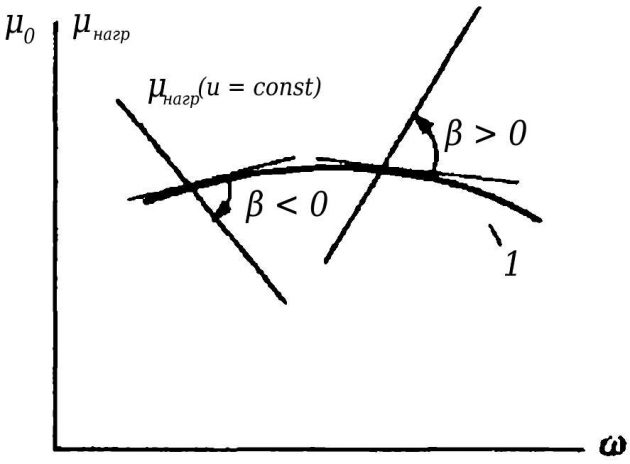
Эффективный момент μ_е, развиваемый дизелем при работе по скоростной характеристике μ_е (ω) примерно постоянен, несколько уменьшаясь в зоне больших чисел оборотов вследствие снижения механического КПД и падения коэффициента наполнения и в зоне малых чисел оборотов вследствие ухудшения рабочего процесса. При работе дизеля на винт μ_нагр ≅ сω2, (dμ_нагр/dω) 0 > 0 поэтому значение β > 0.

При работе дизеля на генератор, имеющий быстро-действующий регулятор напряжения, который обеспечивает стабильность напряжения U = const по крайней мере в малом диапазоне изменения чисел оборотов, электрическая мощность сохраняется постоянной P_эл = u²/R = const, а момент нагрузки изменяется по гиперболе (см. рис .61).

Поэтому (dμ_нагр/dω)₀ < 0 и β < 0.

Следовательно, задачи обеспечения устойчивости и точности регулирования чисел оборотов дизель-генератора, имеющего отрицательное самовыравнивание, значительно сложнее, чем дизеля, работающего на винт, когда β > 0. САР дизель-генератора должна иметь более сложные и дорогостоящие регуляторы скорости, в то время как судовой дизель в принципе может работать устойчиво, за исключением режимов холостого хода с отсоединенным винтом, без регулятора скорости.

Уравнение дизеля, как объекта регулирования температуры охлаждающей воды

Из статьи «Сборка судовых двигателей внутреннего сгоранияСудовые ДВС» известно, что к точности поддержания температуры охлаждающей воды на выходе из дизеля предъявляются строгие требования, выполнение которых позволяет обеспечить оптимальный режим его работы с уменьшением потерь в охлаждающую среду и механических. ГОСТ 12709-67 определяет зону статической неравномерности Δt_р = 10-12 °C, а температуру на выходе t_р при замкнутых системах охлаждения 75-85 °С. Выбор и настройка регуляторов температуры должна производиться с учетом свойств дизеля, как объекта регулирования температуры.

Приведем упрощенный вывод дифференциального уравнения дизеля, как объекта регулирования температуры охлаждающей воды. К охлаждающей воде зарубашечного пространства и омываемым ею поверхностям остова дизеля подводится теплота от рабочего тела дизеля Q_подв (t_р λ), величина которой при постоянной нагрузке дизеля λ зависит от температуры воды в зарубашечном пространстве: чем больше эта температура, тем перепад между температурой рабочего тела и температурой охлаждающей воды и количество отведенного тепла в нее меньше. Температура воды на выходе — регулируемая величина t_р — прямо-пропорциональна средней температуре охлаждающей воды в зарубашечном пространстве и поэтому логическая связь между t_р и Q_подв — подобна описанной выше. Количество теплоты, уносимой из зарубашечного пространства с потоком охлаждающей жидкости Q_подв (t_р, t_вх) зависит от t_р и температуры воды на входе t_вх. Последняя изменяется путем изменения положения регулирующего органа, делящего поток на две части: на перепуск и холодильник.

На установившемся режиме:

На неустановившемся режиме:

Вводя определенные допущения, можно принять, что:

где:

• M и C — масса деталей и воды, на нагрев которых затрачивается теплота и их условная средняя теплоемкость.

Используя метод линеаризации и вводя обозначения:

• $T_{а}=MC{t}_{р0}/Q_{подв.0}$

  — время разгона дизеля, как объекта регулирования температуры воды, с;

• $\beta =\left[{\left(\partial Q_{отв}/\partial t_{р}\right)}_0–{(\partial Q_{подв}/\partial t_{р})}_0\right]T_{р0}/Q_{подв.0}$

  — самовыравнивание;

• ${\theta }_{р}=\Delta t_{р0}/t_{р0}$

  — регулируемая величина;

• $\Delta t_{вх}/t_{вх0}=z$

  — регулирующее воздействие;

• $K_{\lambda }=(\partial Q_{подв}/\partial \lambda ){\lambda }_0/Q_{подв.0}$

  — передаточный коэффициент возмущающего действия;

• $K_z={(\partial Q_{отв}/\partial t_{вх})}_0{t}_{вх0}/Q_{отв0}$

  — передаточный коэффициент регулирующего воздействия.

Получим упрощенное уравнение дизель как объекта регулирования температуры воды:

Дизель, как объект регулирования температуры охлаждающей воды имеет положительное самовыравнивание, что облегчает решение задач обеспечения устойчивости и статической точности.

Читайте также: Гидродинамические характеристики гребных винтов и технология построения паспортных диаграмм

Постоянная времени T_а, может быть определена экспериментально и для среднеоборотных судовых ДВС составляет 2-5 мин. Значения К_λ и К_z могут быть определены расчетом и экспериментально Более точный вывод, с учетом процессов в теплообменнике и запаздывания в переносе теплоты по трубопроводам приводит к уравнению 2-х емкостного звена с запаздыванием. Теория регуляторов температуры изложена в трудах проф. М.И. Левина.x.

Уравнения динамики парового котла

Вывод уравнения динамики парового котла, как объекта регулирования давления пара. На рис. 6 представлена схема системы регулирования, обеспечивающая стабильность давления пара в котле.

На установившемся режиме количество теплоты, идущей на парообразование, и количество теплоты, выделяемой за счет сжигания топлива, соответствуют нагрузке. При увеличении нагрузки Ремонт вспомогательных паровых котлов и теплообменных аппаратовдавление пара уменьшается и исполнительный механизм ИМ воздействует на регулирующий клапан РК, увеличивая количество подаваемого топлива B. В соответствии с общим анализом процессов, происходящих в котле, структурную схему котла как объекта регулирования давления пара при некоторых допущениях можно представить в виде следующих последовательно соединенных элементов:

• регулирующего органа, входной величиной которого является отклонение Δh положения штока РК, а выходной — изменение количества поданного топлива ΔВ;
• звеньев, соответствующих тепловым емкостям газовоздушного тракта, металлических частей котла и пароводяной смеси под зеркалом испарения;
• звена, соответствующего емкости над зеркалом испарения, образованной паровым пространством, в которое поступает образующийся пар в количестве D_обр при давлении p и откуда происходит потребление пара количеством D.

Если ΔDобр > 0, ΔD = 0, то давление пара р будет возрастать, а если ΔDобр = 0 ΔD > 0, то оно будет падать.

Таким образом, предварительный анализ показывает, что котел как объект регулирования давления пара является многоемкостным. Ниже рассматривается упрощенный вывод уравнения динамики котла.

В основу упрощенного вывода положены следующие допущения:

• тепловая инерционность газовоздушного тракта мала, и ею можно пренебречь;
• при регулировании уровня воды в котле отклонения его от установившегося значения малы и влиянием их на процесс парообразования можно пренебречь. Количество поданной в котел воды равно количеству образовавшегося пара;
• котел не имеет пароперегревателя или его аккумулирующей способностью можно пренебречь;
• благодаря регулированию коэффициента избытка воздуха а его изменение в процессе горения не настолько велико, чтобы существенно повлиять на к.п.д. котла, поэтому зависимостью энтальпии сухого насыщенного пара i″ от можно пренебречь;
• регулирующий орган можно принять безынерционным, так как ТНВД клапанного типа с регулированием по началу подачи дизельного топливаизменение подачи топлива В практически мгновенно следует за изменением положения штока регулирующего клапана h;
• давление во всех точках пароводяного тракта одинаково и равно p;
• величиной разности температуры питательной воды и температуры насыщения можно пренебречь.

Изменение давления пара Δp в котле определяется материальным балансом парового объема:

где:

• V — общий паровой объем котла.
• γ – удельный вес сухого насыщенного пара.

Количество образующегося в котле пара определяется тепловым балансом участка котла, заполненного кипящей водой:

где:

• i″ — энтальпия пара, дж/н *;
• i_пв — энтальпия питательной воды, дж/н;
• i′ — энтальпия воды при температуре кипения, дж/н;
• τ′ — температура кипения воды при давлении р;
• G_в — масса воды при температуре кипения;
• G_ж — масса металла котла, ограничивающего кипящую воду);
• C_жобр — удельная теплоемкость стали, дж/н °С.

При установившемся режиме уравнения теплового баланса котла будут иметь вид:

где:

• D₀, D_{обр 0}, Q₀, i₀ — параметры котла на установившихся режимах работы.

Так как:

то на переходном режиме

Исключив из уравнений промежуточный расход D_обр, получим уравнение динамики давления пара в виде

Заметим, что γ, t′, i″ как параметры воды и сухого насыщенного пара являются функциями давления: γ = γ (р); t′ = t′ (p); i″= i″ (p), а приращения ΔQ и Δi″ определяются как

$\Delta Q=k_qВ и \Delta i″=\frac{di″}{dp}\Delta p.$

На основании сделанных допущений: V = const; G_ж = const; G_в = const; c_ж = const, после некоторых преобразований получим:

Переходя к относительным величинам, уравнение динамики котла как объекта регулирования давления пара запишем в виде:

где:

• T_р — Монтаж вспомогательных паровых машин и паровых насосоввремя разгона парового котла по давлению:

• φ_к — относительное изменение давления пара:

• β — коэффициент самовыравнивания:

• μ — относительное изменение расхода топлива:

• λ — относительное изменение расхода пара:

На рис. 7 представлена зависимость изменения расхода жидкости ζ, протекающей через РК, от положения штока клапана z.

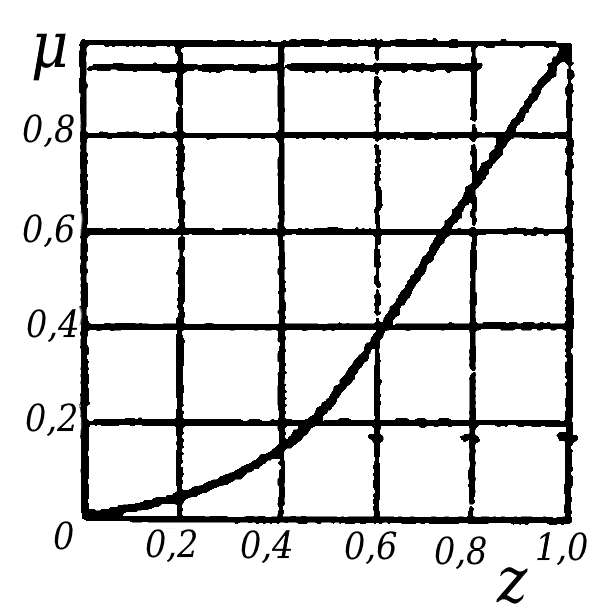
На основании этой зависимости, полагая, что для небольших отклонений от положения равновесия ζ = kz, получаем:

где:

• z — относительное перемещение органов подачи топлива,

  $z=\frac{\Delta H}{H_{ном}};$
• k — коэффициент пропорциональности, близкий к единице.

Таким образом, при сделанных допущениях котел как объект регулирования давления пара описывается уравнением 1-го порядка.

Это инетерсно: Изменение технологии грузовых работ и перевозки грузов — определяющий фактор в развитии конструктивных типов судов

Особенности котла как объекта регулирования давления пара. Из выражения для коэффициента T_p видно, что он прямо пропорционален массе металла котла G_ж, массе воды в котле на данном статическом режиме G_в, массе пара или объему парового пространства V. Величина T_p тем больше, чем массивнее металлические части котла и больше емкость пароводяного тракта.

С увеличением нагрузки котла масса воды в нем уменьшается за счет увеличения содержания пара в котловой воде. Поэтому постоянная времени T_p с увеличением нагрузки также несколько уменьшается, значения β всегда положительны, так как

Величины T_p и β определяют динамические свойства котла как объекта регулирования давления пара, и на основании этих величин производится выбор настроечных параметров регуляторов давления.

Эксперименты показывают, что динамика котла как объекта регулирования пара с большей точностью описывается уравнениями двух последовательно соединенных звеньев: звена 1-го порядка и звена с чистым запаздыванием τ_обр. Уравнение котла при этом будет иметь вид

Время разгона современных паровых котлов составляет:

• отопительных 250-400 сек;
• энергетических среднего давления 100-200 сек;
• форсированных судовых 50-100 сек.

Коэффициент самовыравнивания β относительно мал; так, для судовых котлов β = 0,3-0,8.

Значение времени запаздывания τ_об для отопительно-производственных котельных может достигать нескольких десятков секунд.

Так как увеличение давления пара недопустимо, а коэффициент самовыравнивания котла относительно невелик, то необходима установка регуляторов давления пара.

Вывод уравнения динамики парового котла как объекта регулирования уровня воды. Главные паровые машины на судахПаровые котлы оборудуют системой автоматического регулирования питания, которая обеспечивает поддержание уровня воды в барабане котла в заданных пределах. Рассмотрим статические и динамические характеристики котла как объекта регулирования уровня воды. Схема котла объекта регулирования уровня воды представлена на рис. 8.

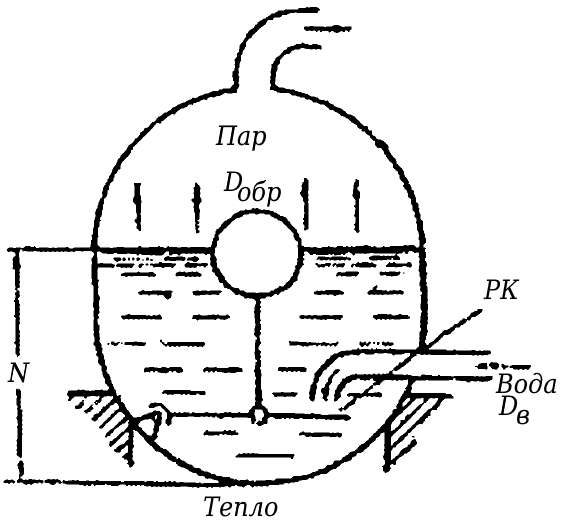
На установившемся режиме количество образующегося пара D_обр компенсируется подачей в котел такого же количества питательной воды D_в. В случае уменьшения или увеличения нагрузки (D_в ≠ D_обр) уровень воды в котле будет меняться. Поплавковый регулятор уровня действует на регулирующий орган — клапан РК, который изменяет величину проходного сечения таким образом, чтобы при увеличении уровня количество подаваемой воды D_в, уменьшалось, при понижении — увеличивалось.

Помимо нагрузки на уровень воды в котле влияют количество теплоты Q, идущего на парообразование, и давление пара p. Характер воздействия Q и р поясняется ниже.

Возмущающим воздействием объекта является изменение расхода пара D. При этом давление пара p в барабане котла в период переходного процесса является функцией D_обр и времени t: p = f (D_обр, t).

На установившихся режимах уравнение материального баланса котла имеет вид:

В динамике:

Или, в приращениях:

где:

• G_см = мacca воды и пара, аккумулированных под зеркалом испарения котла.

Для G_см получим: G_см = V_см p_см, где V_см — объем пароводяного тракта под зеркалом испарения; p_см — плотность пароводяной смеси в объеме V_см.

Величина V_см является переменной и определяется уровнем воды в котле.

Имеется различие в подходе к выводу уравнения динамики уровня воды в котле и уравнения давления пара. При выводе уравнения динамики давления пара величина V_см принимается постоянной, что вполне естественно, так как изменение V_см и G_см практически не влияет на изменение p.

Линеаризуя функцию G_см, получим:

После дифференцирования уравнения:

Учтем зависимости:

где:

• F_{з н} — площадь зеркала испарения, м³;
• H — уровень воды в котле и

где:

• m_в — положение штока питательного клапана.

Величина p_см в настоящем выводе принимается функционально зависящей от давления пара p: чем Средства автоматизации главных энергетических установокбольше давление пара, тем больший удельная масса пароводяной смеси p_см. В действительности величина p_см зависит также и от тепловой нагрузки котла Q, уменьшаясь с увеличением Q. Однако в целях упрощения динамику процесса изменения уровня воды будем рассматривать при условии постоянства тепловой нагрузки Q на данном исходном установившемся режиме.

Подставив вышеописанные зависимости в левую и правую части уравнения материального баланса котла в приращениях, получим:

Перейдем к относительным величинам. В качестве базового (номинального) значения принимается некоторое значение уровня H_ном. Введем следующие обозначения:

• $\frac{\Delta H}{H_{ном}}={\phi }_{у}$

  — относительное приращение уровня;

• $\frac{H_{ном}{\rho }_{см0}{F}_{зи}}{{\displaystyle \frac{d{D}_{в}}{d{m}_{в}}}{m}_{вном}}=T_H$

  — постоянная времени котла по уровню, сек;

• $\frac{\Delta m_{в}}{m_{вном}}=z$

  — относительное перемещение координаты регулирующего органа;

• $\frac{\Delta D_{обр}}{D_{обр.ном}}=\lambda$

  — относительное значение нагрузки;

Получим упрощенное уравнение динамики котла по уровню воды.

где:

• $T_H=30–100c, b_2\approx 1$

Первоначально при набросе нагрузки, когда давление пара уменьшается (dφ_k/dt < 0), уровень в барабане котла повышается. Самовыравнивание по уровню отсутствует.

Особенности судна как объекта регулирования курса

Авторулевой Аист, общие характеристикиАвтоматический регулятор курса предназначен для поддержания судном заданного курса. Он включает чувствительный элемент для измерения курса, элементы для измерения рассогласования курса с заданным и усиления этого рассогласования, рулевую машину, воздействующую на исполнительный орган объекта — руль.

За регулируемую величину примем Δα — отклонение курса судна от заданного значения α₀. Регулирующее воздействие Δβ — отклонение пера руля от значения, соответствующего заданному курсу.

На установившемся режиме совокупность действия сил ветра, волны, течения должна компенсироваться действием сил со стороны руля, а значения α и β должны быть постоянны.

Возмущающие воздействия ветра, волны и течения λ = f(t) приводят к изменению α. Компенсация достигается поворотом руля. В результате возникает дополнительная сила, действующая на руль, и момент, поворачивающий судно, который можно приближенно принять пропорциональным величине Δβ. При повороте судна энергия затрачивается на создание углового ускорения поворота d² Δα/dt², которое будет тем больше, чем меньше момент инерции судна. Повороту судна будут препятствовать силы сопротивления воды, пропорциональные скорости вращения и которые поэтому равны K₂ dΔα/dt, где K₂ — коэффициент гидравлического сопротивления, зависящий от типа судна. Исходя из изложенного, можно упрощенно записать уравнение моментов, действующих на судно или уравнение судна, как управляемого объекта движения по заданному курсу в виде:

Переходя к относительным единицам получим:

где:

• I — момент инерции судна во вращательном движении в плоскости поворота.
• T₀ — постоянная времени, определенная экспериментально, лежит в пределах 10-60 с, и K₀ = 2 х 10^-2/8 х 10^-2 градус курса/градус руля х с.

Из уравнения (формула 4) следует, что Крупнотоннажное судно как объект управлениясудно, как управляемый объект, не имеет самовыравнивания и поэтому не обладает устойчивостью движения по курсу. В связи с тем требуется постоянное воздействие со стороны руля для поддержания судна на курсе.

Особенности объекта автоматического регулирования насыщения пульпы — гидроперегружателя

На рис. 9 показана принципиальная схема САР насыщения пульпы гидроперегружателя. На схеме обозначены:

• 1 — баржа с грузом;
• 2 — грунтовый насос;
• 3 — регулятор насыщения пульпы;
• 4 — клапан регулирования подачи размывочной воды.

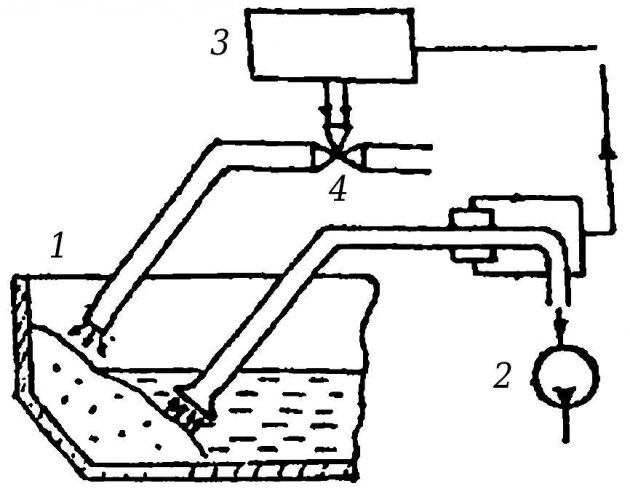
Объект регулирования — емкость с перерабатываемым сыпучим грузом. Регулируемая величина — плотность ρ₀ пульпы, определяемая отношением количества твердого и жидкого компонентов, регулирующее воздействие — ход h клапана 4, изменяющего подачу размывочной воды, возмущающее воздействие — со стороны неравномерно поступающего к насосу перерабатываемого груза.

Основное назначение САР — обеспечение устойчивой работы системы при поддержании постоянства плотности пульпы в заданных пределах.

Проведем приближенный анализ свойств объекта регулирования. Увеличение количества размывочной воды в месте забора пульпы будет приводить к уменьшению значения p_n и отклонению от заданного p_mp а уменьшение количества размывочной воды приведет к тому, что P_n > P_mp. Определим взаимосвязь между изменением плотности пульпы p_n и изменением хода клапана h, регулирующего подачу размывочной воды. Введем обозначения: p_в и p_г — плотности воды и груза, V_в и V_г — объемы количеств воды и груза, смешивающихся в месте забора пульпы сосуном.

Тогда:

При изменении количества воды в месте смешения на величину p_в x ΔV_в изменится величина p_n

С изменением V_в изменяется уровень H в месте смешения, между которым и значением V_в имеется прямая зависимость, в общем случае линеаризуемая. Поэтому ΔV = с₁ΔН, где с₁ — коэффициент пропорциональности.

Следовательно:

где:

В относительных единицах

Взаимосвязь между уровнем воды в емкости и ходом клапана, открывающего подачу воды в емкость, была получена ранее в виде (формула 1). Подставив в (формула 1) ΔН = -1/с₃ х Δр₂ получим уравнения объекта

где:

• $z=(\Delta h/hном).$

Значения T_об и K_об наиболее целесообразно получить экспериментальным путем.

Предлагается к прочтению: Управление судном при выполнении буксировочных операций

Полученное уравнение следует дополнить запаздыванием τ_об между изменением плотности пульпы у зева сосуна и этим же изменением у датчика, помещенного на грунтопроводе, в том случае если величина τ_об значительна.