Маневренные качества судов, решение задач судовождения

Анализ столкновений судов показывает, что причиной многих из них являлись запоздалые действия судоводителей, т. е. маневры, направленные на предотвращение столкновений судов, предпринимались слишком поздно. Это означает, что дистанция между судами начала маневра оценивалась судоводителем не совсем правильно. В качестве примера использования инерционных качеств крупнотоннажных судов для решения практических задач навигации рассмотрим математическую модель расхождения судов на пересекающихся курсах, когда требуется произвести маневр скоростью.

При расхождении судов на пересекающихся курсах, например, при наличии в районе маневрирующего судна помех в виде отмелей или других судов, идущих в том же направлении и не позволяющих изменить курс в правую сторону, маневр скоростью может оказаться единственно возможным маневром. В рассматриваемых случаях судоводителю приходится решать одновременно две задачи: уступить дорогу судну, идущему пересекающимся курсом и не допустить опасного отклонения своего судна в правую сторону, т. е. сохранить управляемость своего судна.

Положение уступающего дорогу судна может еще более усложниться при ветре со стороны правого борта. В этом случае недопустима не только работа движителя (винта правого вращения) на задний ход, но и его остановка, так как и в том и в другом случае судно будет уклоняться в правую по ходу опасную сторону. Необходимость сохранить управляемость уступающего дорогу судна и невозможность применять маневр вправо определяют в данных случаях вид маневра скоростью, т. е. наиболее быстрое ее снижение от исходной до скорости малого или самого малого хода. Для этой сложной ситуации расхождения дистанция, с которой нужно начинать уменьшение скорости, может быть определена следующим образом.

В соответствии с правилами 15 и 16 МППСС-72 маневр скоростью при встрече двух судов на пересекающихся курсах, когда пеленг на встречное судно не меняется, должно производить судно Б (рис. 1).

Рис. 1 Схема расхождения судов на пересекающихся курсах при маневре скоростью (S_А – путь, пройденный судном А на постоянной скорости; S_Б – путь, пройденный судном Б на переменной скорости; D₀ – дистанция, с которой начинается снижение скорости судном 5; в – относительный курс; φ_А1, φ_А2, φ_А0 – курсовые углы на судно Б; φ_Б1, φ_Б2, φ_Б0 курсовые углы на судно A; D₁, D₂ – дистанция до судна А, определяемая до снижения скорости судном Б; х₀у₀ – подвижная система координат; х₀у₀ – начальные координаты судна Б)

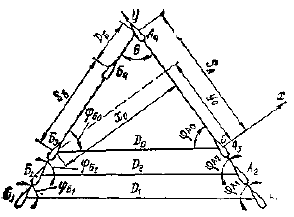
Примем, что расстояние между крупнотоннажными судами в момент окончания расхождения D_B равно 2 мили. Для решения задачи о расхождении на заданном расстоянии D_в когда скорость уступающего дорогу судна изменяется, необходимо определить время расхождения судов t₀, т. е. время от начала маневра скоростью до момента, когда встречное судно пересечет линию курса уступающего дорогу судна на расстоянии от него, равном D₀. Время t₀ можно определить графически, с помощью ЭВМ или аналитически по приближенным формулам.

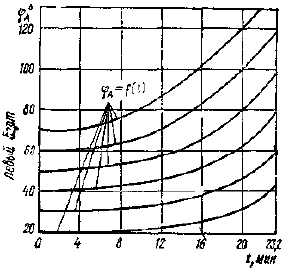
При графическом способе определения нужно построить, как показано на рис. 2, три графика, график пройденного пути при постоянной начальной скорости v_Б, с которой судно Б шло до начала маневра, т. е. S = V_Б t; график пройденного пути при снижении скорости судном Б, т. е. S_Б (t), определяемый по формуле 53, и график разности этих пройденных путей для каждого момента времени D(t) = S – S_Б (t).

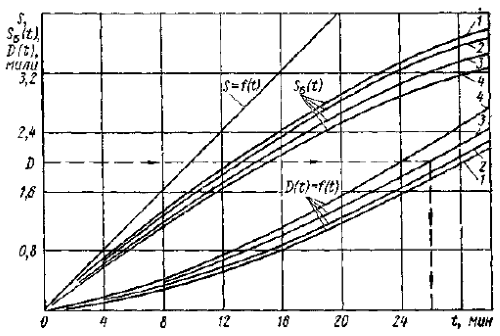
Пользование графиком для определения t_о поясним на примере. Определим время расхождения t_о для танкера типа «Маршал Жуков», идущего со скоростью v_Б = 12 уз, при работе двигателя в маневренном режиме, если обороты двигателя снижены до малого переднего хода, при которых скорость установившегося движения равна v = 4 уз, а дистанция в момент окончания расхождения D_Б должна равняться 2 милям.

Проведем из точки на оси ординат D_Б – 2 милям линию, параллельную оси абсцисс до пересечения с кривой D(t) = f(t), обозначенной цифрой 3 (кривая для теплохода «Маршал Жуков») и, опустив перпендикуляр на ось абсцисс, находим t₀, равное 26 мин.

Время расхождения t_о для крупнотоннажных судов можно определять и по приближенной формуле:

t_{0} = \frac{1, 1 D_{Б}}{v_{Б} - u_{у с т}} (1 + \sqrt{1 + b_{1} (\frac{2 α_{1}}{D_{Б}} - 1)}) . Ф о р м . 1

Погрешность при расчете t₀ не превышает 3-5 %. Зная время t₀, дистанцию между судами для начала маневра скоростью можно определить по формуле:

D_{0} = t_{0} \sqrt{v_{Б}^{2} + v_{А}^{2} - 2 v_{Б} v_{А} \cos θ,} Ф о р м . 2

где:

v_Б — скорость хода судна Б до начала маневра;
v_А — скорость встречного судна А;
Θ — относительный курс.

Скорость встречного судна А может быть определена графически с помощью РЛС, автоматически (снята с экрана РЛС) с помощью САРПИспользование радиолокатора для расхождения или по формуле:

v_{A} = \sqrt{v \begin{matrix} 2 \\ Б \end{matrix} + (\frac{D_{1} - D_{2}}{Δ t})^{2} - 2 \frac{D_{1} - D_{2}}{Δ t} v_{Б} \cos φ_{Б}}, Ф о р м . 3

где:

D₁, D₂ – дистанции до встречного судна А, измеренные с помощью РЛС в промежутке времени Δt не менее 6 мин;
φ_Б – курсовой угол на судно А.

Для практического применения на мостике судна расчеты по приведенной методике по определению D₀ удобно представить в виде номограммы, приведенной на рис. 3.

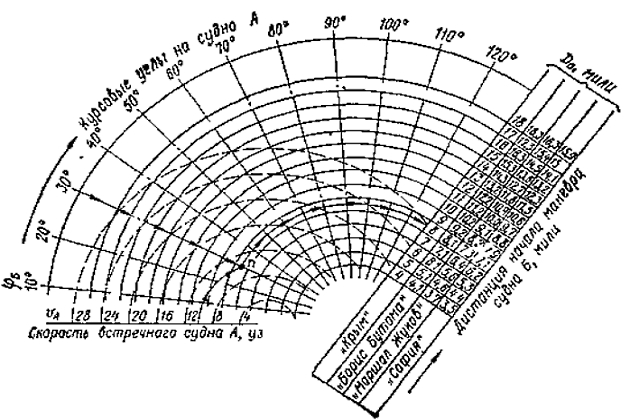
Номограмма для определения дистанции судна — Рис. 3 Номограмма для определения дистанции D₀ для начала маневра скоростью при движении маневрирующего судна Б с начальной скоростью 12 уз

Номограмма построена для изменения скоростей хода крупнотоннажных судов с 12 до 4 уз. При маневре обеспечивается дистанция в конце расхождения D Б = 2 милям.

На номограмме штрихпунктирными радиальными линиями обозначены курсовые углы на встречное судно от 10 до 110° (шкала равномерная), штриховыми линиями в виде окружностей обозначены скорости встречного судна, идущего на пересечение курса (шкала линейная), сплошными линиями в виде окружностей обозначены искомые дистанции начала маневра скоростью для судов типа «Крым» «Борис Бутома», «Маршал Жуков» и «София» (шкала линейная).

Пользование номограммой производится следующим образом: по известным величинам курсового угла φ_Б и скорости встречного судна v_А определяется точка пересечения радиальной штрихпунктирной линии с штриховой линией окружности, а затем по сплошной линии окружности, проходящей через эту точку при пересечении ее со шкалой, обозначенной DO с правой стороны номограммы, определяется дистанция начала маневра в милях.

Пример. Танкер типа «Маршал Жуков» идет со скоростью 12 уз. На курсовом угле 30° правого борта обнаружено встречное судно А, идущее со скоростью 110° уз, пеленг на которое не меняется. Определим дистанцию начала маневра скоростью. Как показано стрелками на рис. 3, находим точку n пересечения радиальной линии, обозначающей курсовой угол 30°, с линией штриховой окружности, обозначающей скорость встречного судна А, равную 10 уз. Из точки n проводим вправо линию, как показано стрелками, параллельную окружности, обозначенной сплошной линией, и на шкале DO справа номограммы для танкера типа «Маршал Жуков» определяем дистанцию начала маневра скоростью, равную D₀ = 7,8 мили. Таким образом, если на расстоянии между судами, равном 7,8 мили, режим работы двигателя будет изменен с маневренного полного переднего хода до самого малого переднего хода, то суда разойдутся на безопасном расстоянии в конце маневра не менее 2 миль.

Исследования показали, что дистанции начала маневра скоростью при расхождении крупнотоннажных судов велики, а время маневра составляет 20-30 мин. В течение этого времени судоводителям необходимо производить постоянный контроль за ходом процесса расхождения. Контроль можно производить по изменению пеленга, курсового угла, дистанции между судами D.

Для обеспечения безопасности расхождения большое значение приобретает знание закономерностей изменения этих величин. С этой целью нами была разработана математическая модель этого процесса расхождения, которая для системы координат, указанной на рис. 1, имеет следующий вид:

d x / d t = v_{Б} (t) \sin Θ;

d y / d t = v_{Б} (t) \cos Θ - v_{A}, Ф о р м . 4

где:

х, у – координаты маневрирующего судна Б, м;
v_Б (t) – скорость судна Б в момент времени t, м/с.

Скорость судна v_Б (t) можно определить по формуле “Определение закона изменения скоростиДвижение судна постоянным курсом“. Подставив значение v_Б (t) в систему уравнений (формула 4) и интегрируя уравнения, получим законы изменения координат x(t) и y(t), имеющие вид:

$x (t) = x_{0} + (v_{у с т} t + α_{1} \ln \frac{h_{1} - e^{- 2 v_{у с т} t α_{1}}}{b_{1} - 1}) \sin Θ;$

y (t) = y_{0} + (v_{у с т} t + α_{1} \ln \frac{h_{1} - e^{- 2 v_{у с т} t / α_{1}}}{b_{1} - l}) \cos Θ - v_{A} t . Ф о р м . 5

где:

x₀ и y₀ – координаты в начале маневра, определяемые известным способом по дистанции DO.

Расстояние между судами в любой момент времени в процессе сближения судов при маневре скоростью можно определить по формуле:

D_{t} = \sqrt{{[x (t)]}^{2} + {[y (t)]}^{2}} . Ф о р м . 6

Курсовой угол на судно Б в любой момент времени в процессе сближения судов при маневре скоростью можно определить по формуле:

ϕ_{_{} A} = 90^{0} + a r c t g \frac{y (t)}{x (t)} (7)

Курсовой угол на судно А в любой момент времени можно определить по формуле:

φ_{Б} = 180 ° - Θ - φ_{A} (t) Ф о р м . 8

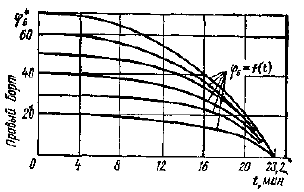
По формулам 6 и 8 были проведены расчеты по определению изменения расстояния между судами и курсовых углов для танкеров типа «Крым». Результаты расчетов представлены на графиках рис. 4, 5, 6.

График дистанции между судами — Рис. 4 Изменение дистанции между судами при начальных скоростях хода обоих судов 15 уз (`D_t` — при маневре скоростью судна Б; `v_0t` — если судно Б идет с постоянной скоростью)

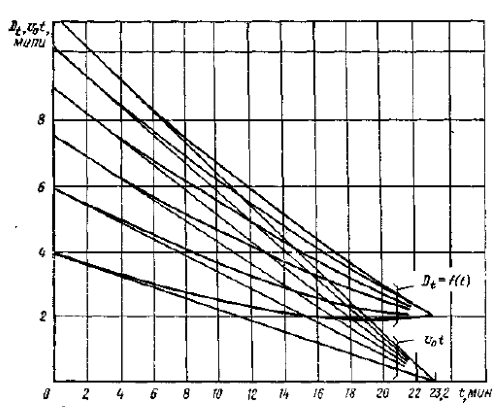
Анализируя результаты проведенных исследований и расчетов, можно отметить следующие закономерности, которые необходимо учитывать при контроле за ходом расхождения крупнотоннажных судов при маневре скоростью.

График изменения курсового угла — Рис. 5 Изменение курсового угла на маневрирующее скоростью судно типа «Крым» (начальная скорость обоих судов 15 уз)

При курсовых углах на встречное судно (Φ_Б) 10-30° изменение курсового угла (φ_Б(t)) практически можно обнаружить спустя 12-14 мин после начала снижения скорости (см. рис. 5, 6). Постоянство угла (φ_Б (t)) или пеленга в данное время свидетельствует о том, что встречное судно курс и скорость не меняет, и процесс расхождения происходит нормально.

Диаграмма курса судна — Рис. 6 Изменение курсового угла с маневрирующего судна типа «Крым» (начальная скорость обоих судов 15 уз)

Как показано на рис. 4, в этом случае закономерность изменения дистанции за счет изменения скорости может быть обнаружена с помощью РЛС уже спустя 6 мин после начала маневра скоростью, т. е., как показано на рис. 4, при t = 6 мин изменение дистанции превосходит 3-5 % дистанции, которая была бы в случае, если скорость и курсы обоих судов не изменялись. Поэтому судоводители обоих судов должны проявлять особую бдительность.

При курсовых углах на встречное судно φ_Б более 50° изменение курсового угла (пеленга) на встречное судно после начала маневра скоростью может быть обнаружено уже спустя 6 мин (см. рис. 5, 6). В течение этого периода изменение дистанции может быть обнаружено только при малых скоростях хода встречного судна (5-7 уз).

Приведенные графики на рисунках по значению φ_А(t), φ_Б(t) и D_t позволяют судоводителям осуществлять контроль за правильностью хода процесса расхождения и его безопасность.

В результате проведенных исследований процесса расхождения судов на пересекающихся курсах, когда пеленг на встречное судно не меняется и крупнотоннажное судно для предотвращения столкновения применяет маневр скоростью, можно сделать следующие выводы.

Дистанции между судами, с которых должен начинаться маневр, иногда достигают 16 миль и более, т. е. сопоставимы с дальностью обнаружения судов с помощью РЛС. Максимальные дистанции начала маневра скоростью соответствуют случаям расхождения с быстроходными судами (контейнеровозами и пассажирскими лайнерами) на курсах, пересекающихся под острыми углами.
Процесс расхождения крупнотоннажных судов при маневре скоростью иногда происходит в течение 20-30 мин, поэтому требуется заранее разработанный метод контроля процесса расхождения.
Для обеспечения безопасности расхождений при маневре скоростью крупнотоннажных судов необходимо принимать решения на мостике на основании расчетного метода динамики процесса расхождения, используя номограммы, аналогичные рис. 3, а для контроля за процессом расхождения – графики изменения курсовых углов и дистанций между судами, аналогичные приведенным на рис. 4, 5, 6.
Маневр скоростью малоэффективен и его следует применять лишь в исключительных случаях. Если при расхождении на пересекающихся курсах судно, уступающее дорогу другому судну, предпринимает маневр путем остановки двигателя (движителя), то при отсутствии ветра и течения для определения времени расхождения судов о необходимо построить графики пройденного пути на постоянной скорости S (t) =v_Бt, график пройденного пути при остановке двигателя (движителя) S _Б(t), определяемый по формуле “Интегрирование неоднородного дифференциального уравненияЗакономерности движения крупнотоннажных судов при перекладке руля“, и график разности этих пройденных путей для каждого момента времени D(t) = S(t)-S_Б(t) аналогично тому, как это показано на рис. 2.

После определения t₀ дистанция между судами, с которой необходимо остановить двигатель (движитель) на судне Б, чтобы безопасно разойтись на заданном расстоянии D_Б, определяется по формуле 6.

Закон изменения координат x(t) и y(t) для данного случая можно определить, подставив в систему (формула 4) значение скорости v_Б (t), определяемое по формуле “Закон изменения скорости пассивного торможения”Оптимальные способы торможения судов. После интегрирования получим

x (t) = X_{0} + \frac{m (1 + λ_{11}) v_{S}^{2} \sin Θ}{R_{0}} \ln (1 + \frac{R_{3} t}{m (1 + λ_{11}) v_{0}}); Ф о р м . 9

y (t) = y_{0} + \frac{m (1 + λ_{11}) v_{S}^{2} \cos Θ}{R_{0}} \ln (1 - \frac{R_{1} t}{m (1 + λ_{11}) u_{0}}) - v_{A} t

Расстояния между судами и курсовые углы в любой момент времени можно определить, подставив полученные значения х(t) и y(t) в формулы 6, 7, 8.

Аналогично можно определить и все параметры расхождения.

В качестве примера использования поворотливости для решения задач судовождения рассмотрим математическую модель движения двух судов на встречных курсах при экстремальных условиях расхождения, когда для предупреждения столкновения судов применяется маневр последнего момента, выполняемый путем перекладок руля на правый борт обоими судоводителями.

Под минимальной дистанцией l_ВСТР будем понимать расстояние между судами, позволяющее избежать столкновения судов при маневре отворотом вправо. Под временем t будем понимать промежуток времени от начала перекладки руля до окончания расхождения, когда кормовые части судов будут находиться друг против друга на расстоянии, которое мы примем равным 1 кб.

Рис. 7 Схема маневров судов по предупреждению столкновения на встречных курсах

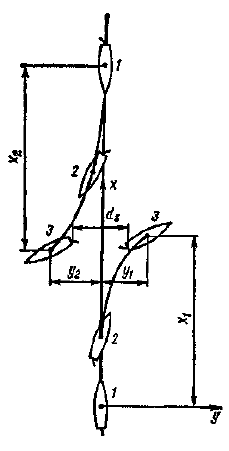
Как видно из рис. 7, дистанция расхождения двух судов с длинами L₁ и L₂ будет равна:

d_{б} = y_{1} - \frac{1}{2} L_{i} \sin (φ_{1} - β_{1}) + y_{2} - \frac{L_{2}}{2} \sin (φ_{2} - β_{2}) Ф о р м . 10

Для однотипных судов можно положить, что L₁ 0 = L₂, φ₁ = φ₂; β₁ = β₂, у₁ = y₂. Тогда индексы можно опустить:

d_{0} - 2 i - L \sin (φ - β) . Ф о р м . 11

Подставляя значение в формулу 11, получим интегральное уравнение

y = \int_{0}^{t}, \sin (φ_{t} - β_{t}) d t . Ф о р м . 12

Полагая известным d_б из уравнения (формула 12), можно определить время t, за которое встречные суда после перекладок рулей вправо на борт расходятся на безопасное расстояние (d_б = 1 кб). Затем, подставив значение t в формулу для определения абсциссы центра тяжести судна при перекладке руля

x (t) = \int_{0}^{t} v_{t} \cos (φ_{t} - β_{t}) d t,

можно определить искомую дистанцию между судами l_ВСТР

t_{B С Т Р} = x_{1} (t) + x_{2} (t) - L 2 - L_{2} 2 . Ф о р м . 13

При однотипных судах очевидно будем иметь

Ι_{В С Т Р} = 2 \int_{0}^{t} v_{i} \cos (φ_{t} - β_{t}) d t - L . Ф о р м . 14

Как показывают расчеты по формуле 14, для крупнотоннажных танкеров l_ВСТР достигает 800-1 000 м.

В результате исследований установлено, что с уменьшением скорости движения крупнотоннажного судна поворотливость судна ухудшается и на очень малых скоростях хода судно перестает слушаться руля. Кинетическая энергия судна уменьшается пропорционально квадрату скорости, поэтому тормозной путь резко сокращается. При скоростях хода около 5 уз выбег на циркуляции приблизительно равен тормозному пути, а при меньших скоростях превышает его.

Предлагается к прочтению: Методы определения маневренных элементов крупнотоннажных судов

При скоростях хода 5 уз и менее минимальная дистанция между судами, с которой можно предотвратить столкновение, будет наблюдаться при применении маневра торможения (работа двигателя) на полный задний ход с одновременной перекладкой руля на правый борт.

Сноски

Использование маневренных качеств судов для решения конкретных задач судовождения