В данной статье рассматриваются вопросы, связанные с прочностью корпуса судна при общем продольном изгибе в вертикальной плоскости. Особое внимание уделяется определению расчетных величин изгибающих моментов и перерезывающих сил, а также построению эпюр этих величин по длине судна. Общий продольный изгиб судна при сильном волнении в открытых водах рассчитывают при проектировании судовой корпусной конструкции.
- Общий продольный изгиб в вертикальной плоскости
- Определение расчетных величин изгибающих моментов и перерезывающих сил
- Кривая сил поддержания
- Кривая нагрузки
- Кривая изгибающих моментов и перерезывающих сил по длине судна (построение эпюр)
- Определение расчетных волновых изгибающих моментов вероятностными методами
- Энергетический спектр
- Амплитудно-частотные характеристики
- Функции распределения волновых изгибающих моментов
- Эффективная и эквивалентная высоты волн
Для анализа продольного изгиба судна необходимо учитывать кривые сил поддержания и нагрузки, которые позволяют определить распределение веса и плавучести по длине судна. На основе этих кривых строится кривая изгибающих моментов и перерезывающих сил, которая является основой для оценки прочности корпуса.
Общий продольный изгиб в вертикальной плоскости
Корпус судна во время плавания в морских условиях испытывает разного характера внешние воздействия, или внешние усилия. Большую часть времени корпус судна в море находится под воздействием больших динамических нагрузок на волнении, которое почти не прекращается, поскольку море редко бывает спокойным. На стоянках в портах при проведении грузовых операций судно находится на спокойной воде. Таким образом, при расчетах общей и местной прочности рассматриваются силы, возникающие при плавании на тихой воде (спокойная поверхность) и на морском волнении. Последние иногда рассматриваются как дополнительные к усилиям на тихой воде. Дополнительные усилия могут возникнуть при постановке на ремонт в док, при швартовках на волнении и при движении во льдах.
Усилия, действующие на корпус судна при нахождении на тихой воде, определены довольно точно, чего нельзя сказать о дополнительных усилиях, действующих на волнении, так как до сих пор остается недостаточно изученным поведение судна на волнах-убийцах, вызывающих серьезные повреждения и даже приводящих к гибели судов. Тем не менее в настоящее время накоплен материал для расчетов качки на реальном нерегулярном волнении. Считается, что это позволяет получить удовлетворительные результаты при определении волновых изгибающих моментов и перерезывающих сил. Это делается с использованием спектральной теории волнения и статистико-вероятностных методов, как и при разработке требований Правил классификационных обществ и Норм прочности.
Хотя поведение судна на волнах-убийцах остаётся недостаточно изученным, современные требования классификационных обществ к продольной прочности, основанные на спектральной теории волнения и статистико-вероятностных методах, позволяют получать удовлетворительные результаты при определении волновых изгибающих моментов и перерезывающих сил.
В расчетные схемы при определении напряжений в Элементы конструкции корпуса суднакорпусных конструкциях судна вносят некоторые упрощения, идеализирующие как весь корпус, так и отдельные его конструкции, свойства материала и способы изготовления конструкций.
Корпусные конструкции судна подвержены напряженному состоянию, которое определяется:
- суммой напряжений от общей деформации всего корпуса, от изгиба его в вертикальной и горизонтальной плоскостях и общего скручивания;
- а также от местного изгиба элементов перекрытий, образующих корпус.
При этом считается, что при общих деформациях корпуса его поперечные сечения, плоские до деформации, остаются такими же и после деформации. В расчетах исходят из предположения, что при местных деформациях опорный контур отдельных перекрытий и отдельных балок его набора не деформируется.
Расчет местной и общей прочности судна рассматривает только наибольшие номинальные (средние по сечению) напряжения (от действия изгибающих моментов и перерезывающих сил), характеризующие напряженность и нагруженность достаточно больших объемов материала конструкций. Однако во всех конструкциях возникают еще дополнительные местные напряжения от изменения поперечных сечений балок набора и обшивки, от обработки материала, его сварки и резки.

Источник: Foter.com
До недавнего времени все расчеты по определению номинальных напряжений выполнялись на базе гипотез, которыми пользуются в сопротивлении материалов. Появление же судов с необычными обводами и конструкциями требует проверки допустимости их применения.
Расчет общей продольной прочности корпуса судна включает в себя следующие задачи:
- определение внешних усилий (нагрузки), действующих на корпус на тихой воде, и усилий от суммарного волнового воздействия при плавании на волнении. Такое суммарное воздействие традиционно представляется в форме волнового изгибающего момента судна, действующего в вертикальной плоскости, при статической постановке судна на волну длиной, равной длине судна;
- вычисление момента сопротивления для принятых за расчетные поперечных сечений корпуса;
- определение нормальных и касательных напряжений, возникающих в нескольких поперечных сечениях корпуса-балки, для характерных условий загрузки судна (расчет эквивалентного бруса);
- оценку прочности, или нормирование прочности путем сравнения действующих (расчетных) напряжений с допускаемыми, которые берутся по нормативным документам (Правилам Регистра или Нормам прочности).
За критерии прочности принимается появление опасных состояний корпуса в виде потери устойчивости, пластических деформаций, хрупкого разрушения и усталости материала, из которого он изготовлен.
Предельная прочность судна при нормировании общей продольной прочности определяется двумя основными критериями:
- предотвращение пластических деформаций;
- предотвращение появления массовых трещин усталости под действием знакопеременных нагрузок при качке.
Критерий предотвращения появления хрупких трещин определяет требования к материалу корпуса, а критерий устойчивости – к оформлению конструкций.
При определении моментов сопротивления поперечных сечений корпуса невозможно учесть все индивидуальные особенности судов, и при расчетах общей прочности принимаются во внимание только важнейшие составляющие внешних усилий, действующих на судно. При расчете общих деформаций корпуса судна используется балочная теория, и нормальные напряжения в поясках эквивалентного бруса принимаются равномерно распределенными, а по стенке – по линейному закону.
Для определения размеров и формы конструкций широко используются расчетные методы, а современные Правила позволяют выбирать размеры связей корпуса по формулам, содержащим расчетные нагрузки в явном виде.
Основными нагрузками на корпус считаются нагрузки на тихой воде, а дополнительными — нагрузки, вызываемые волнением.
Внешние нагрузки на тихой воде находят в соответствии с законом Архимеда для плавающего тела (судна), которое погружается в воду тем больше, чем больше его масса, и тем больше это тело испытывает давление воды. В условиях равновесия плавающее тело представляет как бы невесомую балку, находящуюся под действием собственной массы и давления воды. Из-за неуравновешенности на отдельных участках длины судна массы и сил поддержания судно на тихой воде изгибается.
При плавании на волнении возникают дополнительные нагрузки. Если внешние нагрузки на тихой воде определить довольно просто, то значительно сложнее это сделать для судна на волнении. Масса судна в обоих случаях не меняется (меняется за длительный промежуток времени), в то время как силы давления воды изменяются быстро в зависимости от изменения формы волны, положения судна на волне и инерционных сил, действующих на судно при качке.
Читайте также: Восприятие корпусными конструкциями внешних нагрузок, действующих на судно
При нахождении судна на тихой воде его масса и силы поддержания распределяются неодинаково, однако в сумме по всей длине корпуса они уравновешиваются. Строевая по шпангоутам для данной осадки судна характеризует распределение его водоизмещения по длине или распределение вертикальных составляющих давления воды, действующих на корпус (силы поддержания). Равнодействующая этих сил равна водоизмещению судна, действует также вертикально вверх и совпадает с равнодействующей масс, направленной вниз. В результате изгиба в поперечных сечениях корпуса-балки возникают перерезывающие силы и изгибающие моменты, которые могут быть определены для каждого сечения корпуса.
Величина этих сил и моментов зависит от взаимного распределения массы и сил поддержания по длине судна. В зависимости от этого в одном случае судно получит перегиб, когда середина судна будет располагаться выше носа и кормы, или прогиб, когда нос и корма, наоборот, погрузятся в воду меньше, чем средняя часть судна (рис. 1). На рис. 2 показано распределение изгибающих моментов и перерезывающих сил для контейнеровоза на тихой воде перед выходом его в море. Судно загружено равномерно и имеет на палубе два яруса контейнеров.
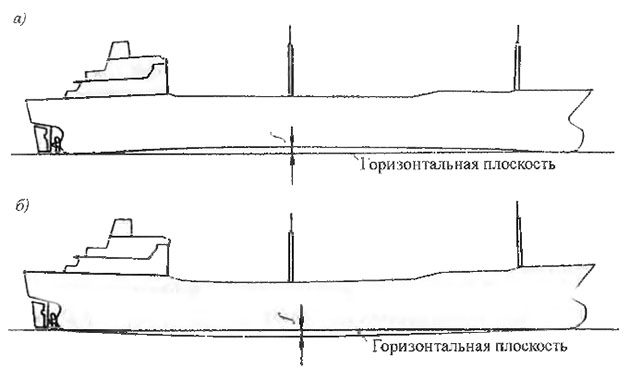
а – перегиб; б – прогиб; f – максимальная стрелка прогиба
Водоизмещение контейнеровоза 28 330 т. Максимальный изгибающий момент при растянутой палубе (перегиб) составляет 113 000 тм. При прогибе судна оно должно быть загружено так, чтобы палуба на тихой воде у него была сжата, а днище растянуто. Перерезывающие силы судна и изгибающие моменты соответственно обозначаются NТВ и MТВ. Чем ближе распределение массы судна по его длине на тихой воде соответствует распределению сил поддержания, тем меньше максимальные величины изгибающих моментов и перерезывающих сил, действующих в поперечных сечениях корпуса.
Часто одно и то же судно с грузом и порожнее на тихой воде изгибается по-разному. Действительно, контейнеровоз, который загружен равномерно и машинное отделение в котором расположено близко к средней части, имеет перегиб, а это же порожнее судно на тихой воде будет иметь прогиб, поскольку при такой загрузке в средней части судна преобладают силы тяжести. Если машинное отделение расположено в корме, перегибающий момент на тихой воде при ходе порожнего судна обычно больше, чем перегибающий момент судна с грузом.
При проектировании судов разных конструктивных типов важно знать, как меняется величина расчетного изгибающего момента на тихой воде посредине длины корпуса в зависимости от изменения его обводов и размещения машинного отделения и грузов.
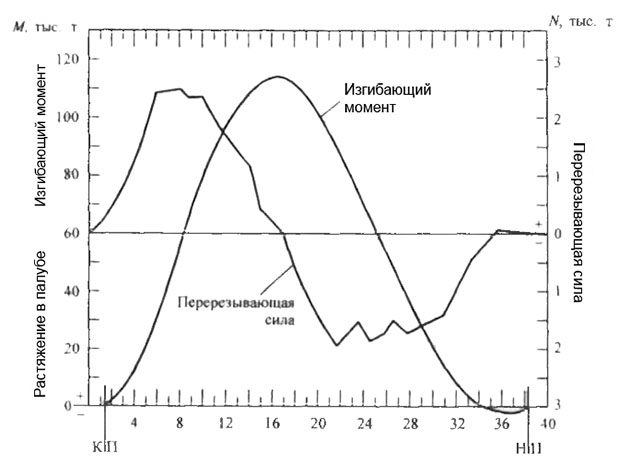
КП – кормовой перпендикуляр; НП – носовой перпендикуляр
При расчетах прочности корпуса судна определяют целесообразные способы загрузки судна в данных условиях эксплуатации на определенных линиях и устанавливают величину изгибающего момента. В некоторых условиях возникают непредвиденные неблагоприятные обстоятельства, когда изгибающий момент может значительно увеличиваться.
Например, это бывает, когда суда-снабженцы у борта базы в открытом море из-за внезапного шторма вынуждены прекратить передачу грузов на базу и с неблагоприятным расположением грузов уйти штормовать.
Важно установить основные факторы, которые обязательно должны быть рассмотрены при проектировании из-за их значительного влияния на значение максимального изгибающего момента на тихой воде.
К таким факторам относятся:
- распределение массы отдельных элементов, составляющих водоизмещение;
- форма и размеры трюмов;
- положение центра тяжести отдельных тяжеловесных грузов;
- размещение запасов, устройств и специального тяжелого оборудования (рампы, грузовые мачты и стрелы тяжеловесов, надстройки).
При проектировании обычно рассматриваются два основных случая загрузки судна:
- порожнее судно в балластном переходе;
- и судно, полностью загруженное при максимальной допустимой осадке по летнюю грузовую марку (см. статью “Архитектурные и конструктивные формы морских судов”Конструктивные типы транспортных судов и особенности проектирования их конструкций).
Изменение максимального момента на тихой воде при ходе порожнего судна в одном направлении и с грузом в обратном изменяет характер работы корпусных конструкций и особенно продольных связей, резко меняющих поперечное сечение (прерывистые связи). При изменении знака изгибающего момента на тихой воде происходит изменение среднего уровня напряжений, к которым добавляются напряжения на волнении. В результате этого возможно резкое возрастание размаха деформаций продольных связей корпуса от максимального сжатия до максимального растяжения. В районах высокой концентрации напряжений это может привести к возникновению знакопеременных пластических деформаций и к малоцикловой усталости.
Используемые для грубой оценки величины максимального изгибающего момента в миделевом сечении на тихой воде для судна длиной L и водоизмещением D с машинным отделением в средней части при коэффициенте общей полноты δ≈0,70 определяют по формулам: MТ.В ≈ DL/10 (для судна с полным грузом и с полными запасами); MТ.В ≈ DL/100 (для судна с полным грузом и 10 % запасов).
Несколько подробнее рассмотрим влияние изменения некоторых характеристик судна на изгибающий момент на миделе на тихой воде.
Предлагается к прочтению: Спасение людей с терпящего бедствие судна
При увеличении длины машинного отделения, если оно находится в середине длины судна, а величина грузов постоянная, перегибающий момент возрастает по причине увеличения отстояния от миделя масс грузов в трюмах. Перемещение машинного отделения в корму от миделя и уменьшение его размеров приводит к изменению распределения массы грузов, запасов, надстроек и главных механизмов, в результате чего максимальный изгибающий момент судна с полным грузом уменьшается. Однако это сопровождается увеличением перегибающего момента порожнего судна, так как с целью удифферентовки необходимо в носовой оконечности размещать балласт.
При изменении коэффициента общей полноты δ максимальные моменты изменяются от массы грузов, от массы корпуса и от сил поддержания. С увеличением δ составляющая момента от сил поддержания увеличивается быстрее, чем составляющая от грузов, а в результате на миделе изгибающий момент уменьшается.
Из приведенных соображений очевидно, что на тихой воде сухогрузные суда с машинным отделением в середине длины судна при ходе с полным грузом имеют на миделе перегибающий момент. В случае расположения машинного отделения в корме момент на миделе будет прогибающий. Промежуточное положение машинного отделения в пределах 1/3-1/4L от кормового перпендикуляра вызывает на миделе момент, близкий к нулю.

В последнее время большинство сухогрузных судов, так же как все танкеры, имеют машинное отделение в корме, однако на танкерах жидкий груз занимает все свободные объемы, а на крупных танкерах после загрузки по разрешенную максимальную осадку в грузовых танках остаются свободные избыточные объемы. Меняя их расположение по длине судна, можно значительно уменьшить величину максимальных изгибающих моментов на миделе. Этого можно добиться и путем изменения положения по длине насосных отделений. В пустые отсеки жидкие грузы никогда не принимаются, а избыточные объемы (кроме насосных отделений) заполняются только водой, когда нужно увеличить осадку при ходе порожнего судна с целью улучшения работы винтов и мореходных качеств на волнении. Эти танки называются танками чистого балласта.
Максимальный изгибающий момент на миделе при полной загрузке судов на тихой воде характерен для танкеров, у которых танки чистого балласта из-за малых размеров судов создать не удается. Корпус судна при этом имеет прогиб.
При нормировании общей продольной прочности транспортных судов расчетные изгибающие моменты определяются как сумма максимального или некоторого среднего момента на тихой воде MТ.В и волнового изгибающего момента MВ.
Во время плавания по мере расхода топлива и воды момент на тихой воде как на сухогрузных судах, так и на танкерах постепенно увеличивается. На тихой воде максимальный изгибающий момент обычно наблюдается на судах с полным грузом после израсходования 10 % запасов. Среднее же значение момента отмечается при израсходовании 50 % запасов, и его можно рассматривать как математическое ожидание изгибающего момента на тихой воде за весь рейс судна.
Во время погрузки часто нарушается равномерная загрузка судна (пропорционально кубатуре трюмов). Это может происходить и при выгрузке части груза в одном из портов. Подобные явления приводят к значительному увеличению максимального изгибающего момента MТ.В.
Особенно большие изменения величины максимального изгибающего момента могут происходить при плавании на волнении, когда в дополнение к внешним силам на тихой воде корпус подвергается действию волновых нагрузок и инерционных усилий, которые дополнительно изгибают корпус судна в вертикальной продольной и горизонтальной плоскостях, а также вызывают его кручение. Последнее может наблюдаться и на тихой воде, если масса груза по ширине распределяется неравномерно.
Во время плавания на волнении судно качается, наклоняясь и перемещаясь под действием изменения сил поддержания по длине и ширине судна, а также в результате ударов волн.
При этом судно испытывает:
- килевую качку (периодически судно получает дифферент то на нос, то на корму);
- бортовую качку (периодически судно накреняется то на правый борт, то на левый);
- вертикальную качку (периодически судно то поднимается вверх, то опускается вниз);
- горизонтальную качку (судно отклоняется по горизонтали от курса и задерживается или, наоборот, увеличивает скорость движения).
В поперечных сечениях корпуса в дополнение к перерезывающим силам и изгибающим моментам, возникающим на тихой воде, появляются перерезывающие силы и изгибающие моменты, вызванные качкой. Килевая и бортовая качка вызывается угловыми перемещениями корпуса вокруг поперечной оси (килевая качка в диаметральной плоскости) и вокруг продольной оси (бортовая качка в плоскости шпангоутов). Остальные виды качки вызываются поступательными перемещениями по вертикали и по горизонтали.
Амплитуды качки зависят от размеров судна, высоты и длины волн, направления движения судна относительно волн и от его скорости. Качка судна сопровождается возникновением дополнительных инерционных усилий и изменением сопротивления воды колебательным движениям, так как меняются величины гидродинамических сил, действующих на корпус.
На величину этих сил оказывают значительное влияние формы образований корпуса.
На хаотической волновой поверхности моря часто возникают отдельные высокие гребни и впадины. Гребни внезапно обрушиваются на судно, и в момент их разрушения выделяется громадная энергия, которая часто являлась причиной многочисленных повреждений оконечностей и надпалубных конструкций. При смешанной качке в самый неблагоприятный момент, когда нос зарывается глубоко в воду и судно имеет большой дифферент на нос, на него накатывается громадная одиночная волна, значительно отличающаяся от всех окружающих судно волн. Расчет внешних усилий, действующих на судно в таких обстоятельствах, создает определенные трудности.
Описывая общий продольный изгиб корпуса в вертикальной плоскости и определяя волновые воздействия, раньше принимали за регулярное волнение, представляющее собой гладкие, в виде параллельных рядов, одинаковые по форме, длине и высоте волны с бесконечной протяженностью вдоль их гребней. Профиль волн принимался трохоидальньм или синусоидальным.
Рекомендуется к прочтению: Предупреждение столкновений судов
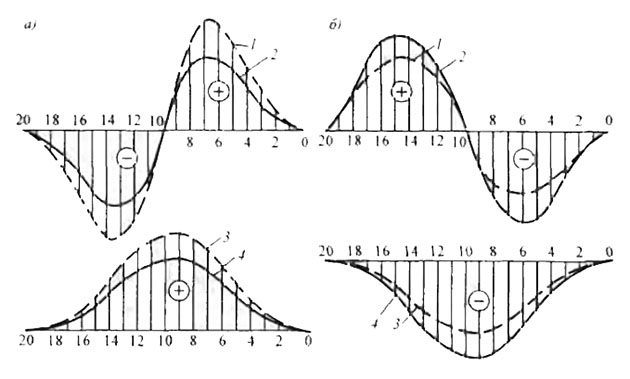
При плавании в штормовом море судно находится то на вершине волны, то на ее подошве или в любом промежуточном положении. При положении судна на вершине регулярной волны по сравнению с положением на тихой воде силы поддержания в средней части длины корпуса резко увеличиваются, а в оконечностях они резко уменьшаются (рис. 3, а). В результате этого судно получает дополнительные деформации в виде перегиба и, если корпус имел уже перегиб на тихой воде, деформации перегиба будут суммироваться. Если же на тихой воде судно имело прогиб, то деформации корпуса на волне уменьшают его.
При нахождении судна на подошве волны, наоборот, произойдет резкое уменьшение сил поддержания в средней части корпуса по его длине и увеличение в оконечностях (рис. 3, б). При этом корпус получит дополнительный прогиб, и если на тихой воде у судна был прогиб, то общие деформации на тихой воде и на вершине волны будут суммироваться. Изменение распределения сил поддержания в результате перемещения водного профиля вдоль судна приводит к периодическому изменению сил поддержания, что вызывает изменение общих деформаций корпуса по сравнению с тем, что было на тихой воде, значительному изменению суммарных перерезывающих сил и изгибающих моментов.
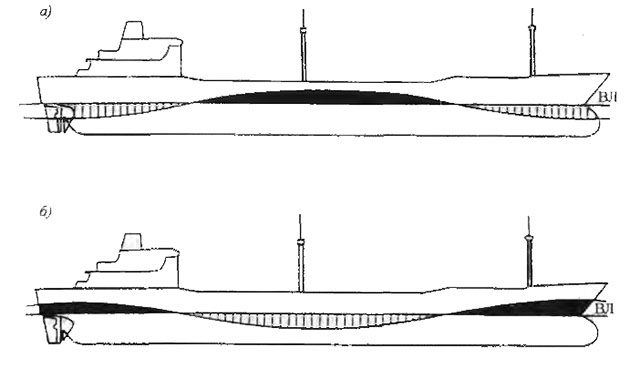
а – судно на вершине волны; б – судно на подошве волны.
ВЛ – ватерлиния на тихой воде (залитые участки – объемы, вошедшие в воду; заштрихованные – вышедшие)
Та часть дополнительного изгибающего момента, который возникает в результате нахождения судна на волне MВ, изменяется как по величине, так и по знаку с периодом килевой качки, который равен кажущемуся периоду волн, встречаемых судном при его движении. Воздействие волнового момента принимается за статически переменное, так как при длинах волн, близких к длине судна, эти периоды в несколько раз больше периода собственных упругих колебаний корпуса первого тона. Это дает возможность волновую составляющую изгибающего момента объединить с составляющей изгибающего момента на тихой воде. Сумма этих двух моментов называется расчетным изгибающим моментом Mp на регулярном волнении, который получается равным Mp = MТ.В + MВ.
Для любого отдельного случая загрузки, когда известны величина и распределение масс судна по его длине, MТ.В будет для данного судна величиной постоянной, а величина MВ при перемещении судна в разрез волнам имеет два максимальных значения на вершине и на подошве волны:
Поэтому и суммарная величина Mp имеет два максимальных значения. Его волновая составляющая изменяется в зависимости от длины и высоты волны.
Регулярное циклическое изменение изгибающего момента, характерное для плавания судов на волнении, изменяет характер работы корпуса судна и прежде всего продольных его связей. Возрастает размах их деформаций от максимального сжатия до максимального растяжения, и в районах с повышенной концентрацией напряжений возможно возникновение знакопеременных пластических деформаций и, как результат этого, появление усталости, даже при небольшом количестве циклов.
Установлено, что число циклов волновых напряжений за весь срок плавания судна до его вывода из эксплуатации приблизительно равняется 10-8—10-9. Обеспеченность волновых напряжений, которые приняты во вновь разработанных Правилах Регистра 1999 г. в качестве расчетных, составляет 10-5. Это значит, что возможное их превышение за весь срок эксплуатации судна может быть в 10-4 случаях. Допустим, что если судно делает в год 10 рейсов и за 20 лет — 200 рейсов, то неоднократно будет меняться знак напряжений на тихой воде (судно то загружено, то порожнее). На судно при этом попеременно действуют прогибающий и перегибающий моменты. Эти моменты по-разному суммируются с изгибающими моментами на вершине и на подошве волны для случаев плавания судна с грузом и без груза.
Идеализированное представление волнения регулярным при расчетах силовых воздействий на корпус судна, которым пользовались еще совсем недавно, основывалось на теории качки акад. А. Н. Крылова и давало удовлетворительные результаты только при плавании на морской зыби, но в условиях хаотического штормового волнения (нерегулярного волнения) результаты значительно расходились с фактическими. В то же время рассмотрение поведения судна на регулярном волнении позволяет при изучении курса конструкции судов лучше представить силовые воздействия при плавании судна и на нерегулярном волнении. Расчеты прочности судна на регулярном волнении имеют большое практическое значение, так как судам часто приходится плавать в условиях регулярного волнения или в условиях, близких к ним. Поэтому представляется целесообразным изучать характеристики и свойства регулярных волн и условия плавания на них судов.
Будет интересно: Успокоители качки судна
Предполагается, что судно находится в состоянии статического равновесия, будучи зафиксировано в определенном положении, например на вершине или подошве волны. Эти два положения судна соответствуют наибольшим силовым воздействиям при длине волны, равной длине судна, и при высоте волны, равной 1/20 ее длины. Такие соотношения размеров волн обычно наблюдаются при мертвой зыби. Этот приближенный метод называется статической постановкой судна на волну по Риду – по имени английского ученого Э. Рида.
Считается, что судно остановилось на воде, принявшей форму волны, на ее вершине или на ее подошве. Явление постепенного перемещения профиля волны от положения, когда на миделе судна располагается самая верхняя часть волны, до положения, когда на миделе располагается самая нижняя ее часть, сопровождается изменением сил поддержания по длине судна и вертикальными и вращательными перемещениями. При рассмотрении любого фиксированного положения судна по длине волны считается, что оно удифферентовано, т. е. находится в таких же условиях, как и на тихой воде, однако тихая вода не находится в горизонтальном положении, а имеет волновую форму.
Практикой установлено, что величина перерезывающих сил и изгибающих моментов в поперечных сечениях корпуса тем больше, чем больше высота волн, на которую ставится судно. Многолетнее изучение регулярного волнения дало основание принимать расчетную высоту волны h, равной 1/20 ее длины L, и она получила название стандартной высоты волны, при статической постановке судна на волну.
Нормы прочности 1958 г. расчетную высоту волны принимали
Позже Нормы прочности 1962 г. рекомендовали расчетную высоту волны
В обоих документах статическая постановка осуществлялась на волну, длина которой равнялась длине судна.
Так как статическая постановка на волну не дает возможности учесть трехмерности волнения и своеобразного поведения судна во время качки на таком волнении, а также скорости движения, в связи с постройкой крупнотоннажных судов с большими скоростями потребовалось уточнение условного метода расчета внешних сил. Сначала это делалось для установления погрешности метода путем использования новых теоретических и экспериментальных исследований качки судов на волнении, влияния динамических воздействий на корпус судна при качке и заливаемости палубы.
Открылись новые возможности для определения волновых составляющих изгибающих моментов и перерезывающих сил с использованием расчетов качки, а также приближенных формул, полученных статистическими методами при плавании судов на реальном, нерегулярном, трехмерном волнении.
В настоящее время большинство Правил классификационных обществ в той или иной степени учитывают волновые воздействия, применяя при этом вероятностные методы с целью уточнения расчетных элементов волнения и величины наибольших изгибающих моментов, возникающих в поперечных сечениях корпуса судна при плавании на волнении. Эти методы дают возможность установить повторяемость изгибающих моментов различной величины (спектр нагрузок). Волновые нагрузки на судно учитываются, но существующие методы не в полной мере отражают влияние индивидуальных особенностей судов, что может привести к неточностям в расчетах. В Правилах Норске Веритас введены дополнительные требования, учитывающие изменение расчетных нагрузок по длине судна в зависимости от формы носовых обводов и скорости. Английский Ллойд ввел требования с целью контроля составляющей изгибающих моментов в поперечных сечениях от удара в развал борта в зависимости от скорости судна и формы носовой оконечности.
При составлении Правил принята зависимость, характеризующая расчетную стандартную высоту волны:
Эта стандартная высота волны для малых длин Lм> судов корректируется введением коэффициента Кc:
| Kc | 0,82 | 0,93 | 0,98 | 1,00 |
| Lм | 80 | 120 | 160 | 200 и больше |
Постоянство суммарных напряжений для корпусов новых судов разной длины достигается соответствующим назначением расчетного волнового момента, т. е. выбором расчетной высоты волны.
Изучение повреждений судов показывает, что часто повреждения судов происходят в результате распространения появившихся трещин. Однако причиной появления начальных трещин может быть как усталость, так и хрупкое разрушение материала корпуса. Вполне возможен и другой вид разрушений конструкций, когда отмечается единичное превышение напряжений до опасной величины.
Использование в течение многих лет для расчета общей продольной прочности статической постановки судна на регулярные волны, имеющие форму трохоидального профиля (см. рис. 11), несмотря на существенное отличие от реальностей волновой поверхности позволяло получать определенное представление о прочности корпуса судна. В действительных условиях плавание на волнах сопровождается динамическими воздействиями в виде сильных ударов о корпус судна (днище, борта, верхняя палуба), которые всегда воспринимаются конструкциями в виде импульсов, вызывающих вибрацию всего судна и отдельных его частей. Кроме этого вибрация вызывается работой механизмов и винтов, особенно в кормовой оконечности (см. рис. 17).
Сам процесс волнообразования на поверхности моря является вероятностным, подчиняющимся законам теории вероятности, и форма волновой поверхности представляет собой случайную функцию координат и времени. Для оценки нагрузок, вызываемых в корпусе судна на волнении, и расчетов прочности используются обобщенные их оценки, получаемые вероятностными методами.

Источник: Foter.com
С целью физического представления и изучения явления воздействия внешних сил на корпус судна при плавании его на взволнованном море и определении волновых изгибающих моментов очень удобно использовать старый прием статической постановки судна на волну. Позже этот процесс будет представлен.
Конструкции корпуса в штормовом море часто разрушаются в результате усталости материала, а также по причине возникновения местного хрупкого состояния в напряженных конструкциях. В обоих случаях это происходит прежде всего при местных напряжениях. В первом случае за расчетный изгибающий момент принимается среднестатистический момент:
(средняя амплитуда волнового момента), а во втором — возможный наибольший предельный изгибающий момент
Последний представляет собой предельную нагрузку, которая приводит корпус судна в предельное состояние. При этом хотя бы в одной точке поперечного сечения корпуса (эквивалентного бруса) нормальные напряжения достигают величины, достаточной для начала разрушения. Таким образом, предельная прочность корпуса судна оценивается двумя способами: по методу допускаемых напряжений и по методу предельного момента.
Обеспеченность
принимается равной 10-4 или 10-5, а
10-8.
Действие моментов
и
делится на постоянные составляющие (Mст.в) и (Mпт.в).
Они меняются только с изменением нагрузки. Переменные же величины – волновые моменты (Mсв и Mпв), вызываемые качкой на волнении с частотой килевой качки.
По Нормам прочности, волновые моменты определяются при условии, что высоты расчетных волн для
и
берутся равными h1 и h2 по диаграмме (рис. 4) для судов разной длины.
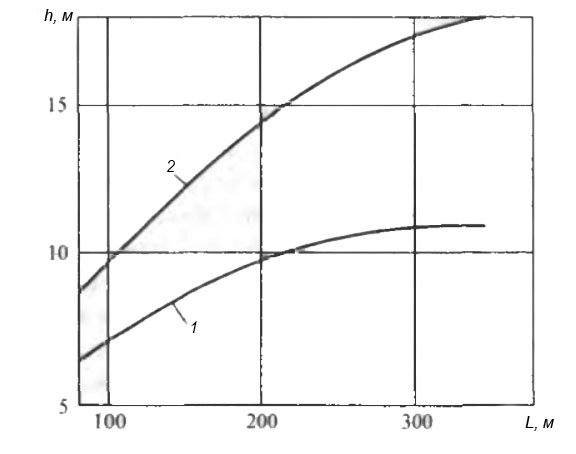
(1) и для наибольшего возможного волнового момента
(2):
h – высота волны; L – длина волны
Исследования, выполненные с помощью вероятностных методов, дали возможность уточнить элементы волнения и наибольшие изгибающие моменты в сечениях корпуса на волнении. Методы определения волновых изгибающих моментов судна позволили установить повторяемость изгибающих моментов различной величины.
Кроме изгибающих моментов на тихой воде и волнении в статическом их представлении корпус судна на нерегулярном волнении испытывает еще ударные нагрузки в результате ударов о воду носовой оконечностью и ударов о воду при продольной качке в случае заливаемости. Удары в днище (слеминг) появляются как результат оголения днища при смешанной качке. Удары в развал борта в носу вызываются необходимостью создавать такую форму надводной часта носа, чтобы на палубу попадало возможно меньше воды, и чтобы судно во время качки глубоко не зарывалось носом в воду.
Три перечисленных вида динамических нагрузок вызывают в поперечных сечениях корпуса-балки при общем продольном изгибе в вертикальной плоскости дополнительные изгибающие моменты, которые должны суммироваться с моментами на тихой воде и волне. Эти динамические нагрузки растут с увеличением скорости судна на волнении и зависят от курса судна по отношению к бегу волн, от обводов носовой оконечности в подводной и надводной ее частях, от осадки, дифферента и волнения.
В моменты заливаемости палубы, ударов в днище и развал борта корпус судна совершает затухающие упругие колебательные движения, и, следовательно, величина перерезывающих сил и изгибающих моментов после ударов постепенно уменьшается. Эти перерезывающие силы и изгибающие моменты называются ударными или динамическими и обозначаются Ny и My. Волновые изгибающие моменты Mв при использовании вероятностных методов для их определения также носят характер динамических, и поэтому моменты от заливаемости, слеминга и ударов в развал борта лучше называть ударными. Раньше же волновые моменты определялись в условиях статической постановки на волну.
Читайте также: Корпус судна и предъявляемые к нему требования
Рассмотренные ударные нагрузки характерны для судна во время его плавания на волнении как в загруженном состоянии, так и без груза. Чем больше осадка судна, тем меньше сила ударов в днище в носовой оконечности, но тем больше ударные нагрузки в развал борта и на палубные конструкции от заливаемости верхней палубы. Наибольшие ударные нагрузки наблюдаются на судах при попытках двигаться на волнении с повышенной скоростью и прежде всего на судах с полными образованиями (с большим коэффициентом общей полноты), с большим развалом шпангоутов и плоской частью днища, расположенной близко к форпику.
Во время сильного волнения капитаны всех судов стремятся значительно уменьшить скорость и стараются иметь ее возможно максимальной при безударном плавании. Однако желание иметь максимальную при данных условиях скорость приводит к ударам и заливаемости, которые вызывают опасные повреждения.
Так, рефрижератор «Профессор Попов» с полным грузом на пути во Владивосток, двигаясь с большой скоростью на крупном встречном волнении зимой 1983 г., испытывал сильные удары в развал бортов, в результате которых палуба и верхняя часть бортов на расстоянии около 1/3 от носового перпендикуляра потеряла устойчивость.
Подобная же авария произошла с судном «Ономичи мару» в декабре 1980 г. При подходе к Японии судно с полным грузом потеряло носовую оконечность и затонуло. Подобные же аварии отличались еще на ряде судов. На современных сухогрузных судах при движении против волны во время сильного шторма скорость обычно уменьшается до 1,5-1,8 уз в балластном переходе и до 2-2,5 уз при ходе с полным грузом Такие скорости наблюдались в плавании на судах “Дальстрой”, “Джурма”, “Советская Латвия”, “Магадан”, “Орехов” (типа Омск), “Балтийский-64”, “Кунгур” и “Электросталь” (типа “Беломорсклес”), на контейнеровозе “Пестово” типа (“Варнемюнде”), “Пионер России” типа (“Пионер Москвы”, “Серпухов” и “Кулунда” типа “Сибирьлес”) “Белгород” (танкер типа “Либерти”)*. При большей скорости суда получают повреждения, что и произошло с судном «Профессор Попов», которое на крупном волнении плыло со скоростью около 9 уз.
Повышенные скорости при сильных ударах допускаются только при необходимости оторваться от берега при опасности, что судно будет выброшено на мель или на камни, особенно при проходе проливов при внезапно развившемся крупном волнении. В таких условиях получил повреждения днища теплоход «Орехов» в 1965 г. при проходе Сангарского пролива и переломился пароход «Чкалов» при экстренном отходе от побережья Камчатки в 1946 г. Опытные капитаны во избежание аварии допускают увеличение скорости при ударах только в крайних случаях. Однако известны примеры переломов судов, когда капитаны нарушали это правило. В 1946 г. танкер типа Т-2 «Донбасс» по этой причине разломился на две части. Обе половины судна остались на плаву и были прибуксированы в порт. Капитан и еще несколько человек при аварии погибли.
Большие повреждения днища наблюдались на многих судах разных лет постройки. Особенно большие повреждения произошли на теплоходе «Оренбург», на котором перекрытие в трюме №1 деформировалось с максимальной стрелкой 150 мм. После значительного ужесточения требований Правил Регистра к конструкции днищевых перекрытий количество повреждений значительно сократилось.
Неоднократно наблюдались повреждения носовых шпангоутов и фальшбортов в районе развала у бака, местная прочность которых оказывалась недостаточной. Во время испытаний, проводившихся на теплоходе «Пестово» (типа «Варнемюнде»), при плавании через Тихий океан при волнении 8 баллов шпангоуты от ударов в развал бортов потеряли устойчивость плоской формы изгиба (рис. 5).
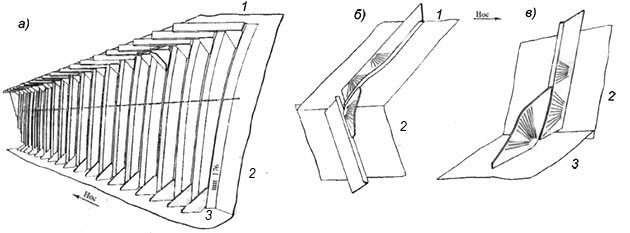
а – общий вид конструкции в районе развала борта; б – повреждение подпалубного узла; в – повреждение узла пересечения борта с палубой.
1 – палуба бака; 2 – борт; 3 – главная палуба
Особенно часто повреждаются фальшборты, которые крепятся к палубе только стойками. На рис. 6, а можно видеть судно, палуба которого испытывает динамические нагрузки при заливаемости.
Такая же картина наблюдается при заливаемости с носа, когда после удара от влившейся воды палуба бака и фальшборт испытывают динамические нагрузки, и удар вызывает вибрацию всего судна (рис. 6, б).


Расчетная величина максимального изгибающего момента и момента в любом поперечном сечении корпуса-балки должна быть дополнена суммарным ударным моментом от слеминга, от удара в развал бортов и от заливаемости, который обозначается My: M = Mт.в + Mв + My (у Mв – низкая частота, а у My – высокая, что при суммировании должно учитываться).
По аналогии с волновой составляющей изгибающего момента суммарная величина ударного момента, вызывающего перегиб, обозначается
, а вызывающего прогиб –
.
При всех трех ударных явлениях (удар в днище, удар в развал бортов и удар при заливаемости о палубу бака и его фальшборт) мгновенно возникают колебания всего корпуса, которые постепенно затухают, но в момент удара My в поперечном сечении на миделе может достигать значительной величины. В других поперечных сечениях корпуса могут также возникать значительные моменты, которые обычно в расчет не принимаются. Ударный момент может существенно увеличивать суммарный максимальный момент на тихой воде и на волне.
Сразу после удара величины дополнительного ударного изгибающего момента на вершине и подошве волны почти одинаковы. Действительно, после появления максимального ударного момента на вершине волны сразу же начинается затухание и возникает почти такой же момент на подошве волны. Это затухание идет очень быстро, однако в какой-то момент времени максимальные моменты, вызванные ударами, могут достигать значительной величины и давать существенную добавку к волновым моментам и моментам на тихой воде для каждого данного поперечного сечения.
Во время продольной качки судна на стационарный случайный процесс волновых изгибающих моментов при общем продольном изгибе корпуса в вертикальной плоскости накладываются дополнительные нестационарные затухающие случайные процессы ударных моментов (рис. 7). Удары обычно возникают через значительные промежутки времени, и вызванные ими колебания (вибрация) корпуса задолго до следующего удара могут постепенно затухать. Установлено, что продолжительность действия ударной нагрузки составляет 0,02-0,05 с, т. е. за это время давление успевает достичь максимального значения и возвратиться к нулю.
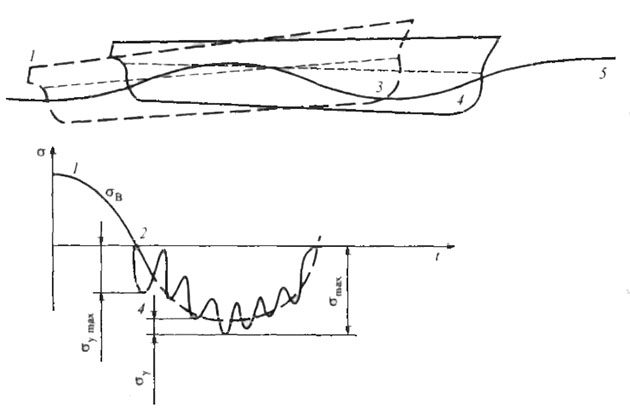
1 – перегиб на вершине волны; 2 – начало изменения деформаций корпуса изгиба на волне; 3 – район оголения днища; 4 – момент максимума гидродинамического (ударного) давления на днище; 5 – волновой профиль;
σв – волновые напряжения; σу max – наибольшие ударные напряжения; σу – амплитуда ударных напряжений, суммирующихся с волновыми напряжениями σв
Длительность же колебаний первого тона всего корпуса (см. статью Конструкция надстроек и рубок“Надстройки и рубки судна в корпусной конструкции”) измеряется секундами. Она значительно больше времени действия ударной нагрузки. На рис. 8 представлена запись волновых напряжений, намеренных в одной точке у миделя последовательно для вершины и подошвы волны. В некоторый период времени возникает удар, в результате которого к волновым напряжениям, например в точке А, добавляются напряжения от удара σу того же знака, что и волновые напряжения.
Напряжения от удара в начальный период затухания на рисунке сохраняют почти постоянную величину и то добавляют, то уменьшают волновые напряжения. Размах же суммарных напряжений в некоторый момент будет больше, чем размах волновых напряжений, что видно из рисунка. Суммарные напряжения, замеренные в точке А, вызваны изгибающим моментом и имеют большую величину, чем напряжения волнового изгибающего момента.
Определение расчетных величин изгибающих моментов и перерезывающих сил
От прочности корпуса зависит безопасность плавания судна, в том числе в наиболее тяжелых условиях волнения на море. Особенно большие нагрузки и, как результат их действия, напряжения возникают в судовых корпусных конструкциях во время сильных штормов и при форсировании льдов в зимних условиях, когда прочность ледового покрова становится при низких температурах наибольшей. Внешние воздействия, воспринимаемые корпусами судов, проявляются в виде изменения распределения сил поддержания (давление воды) по поверхности обшивки корпуса, грузов, размещенных в корпусе вместе с весом самого корпуса судна, динамических воздействий при ударах о воду во время качки и при форсировании льдов. Динамические воздействия вызывают вибрацию всего корпуса и отдельных его конструкций: особенно при оголении винтов во время шторма и воздействия работающих механизмов (см. рис. “Источники судовой вибрации (а) и общая вибрация разных тонов корпуса как балки (б)Восприятие корпусными конструкциями внешних нагрузок, действующих на судно“).
Читайте также: Обозначение и расшифровка всех составляющих корпуса судна
Необходимо учитывать, что уровень напряжений в корпусе, вызванных внешними воздействиями, может значительно увеличиваться за счет внутренних, остаточных, реактивных и местных напряжений, возникающих в процессе изготовления конструкций, а также температурных напряжений, которые особенно опасны в арктических районах при выходе судов из льдов на чистую воду во время сильного волнения при низких температурах воздуха. Все перечисленные здесь напряжения трудно учесть и невозможно использовать при прогнозировании. Это основная причина существования неопределенности в оценке прочности конструкций, поэтому накопление данных результатов эксплуатации разных судов в различных условиях является источником оценки прочностных возможностей корпусных конструкций, дополняющим результаты условных методов расчета их прочности.
На рис. 8 приведены напряжения от общего продольного изгиба на волнении, замеренные в одной точке корпуса во время жестокого шторма в Тихом океане на теплоходе «Орехов». Данные, полученные расчетным путем, отличаются от фактических, хотя рассчитывают напряжения при проектировании с использованием самых современных подходов. Обычно вначале строят кривую нагрузки, действующую на корпус при его общем продольном изгибе и вызывающую в поперечных сечениях балки-корпуса: нормальные и касательные напряжения в любой точке. Для этого предварительно необходимо рассчитать перерезывающие силы и изгибающие моменты, действующие в этих поперечных сечениях, последовательно проинтегрировав эпюру нагрузки один и два раза.
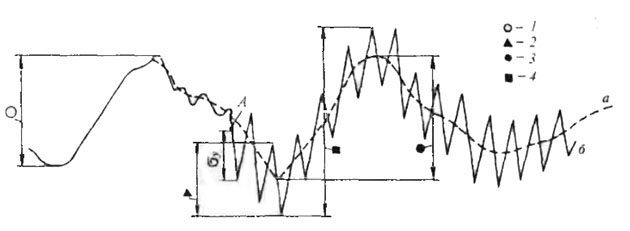
а – положение судна по отношению к волне; б – график изменения напряжений во времени.
1 – размах волновых напряжений; 2 – размах ударных напряжений; 3 – размах наибольших волновых напряжений за весь режим; 4 – размах суммарных напряжений;
σу – напряжения в момент удара А
Изгибающие моменты и перерезывающие силы на тихой воде при плавании порожнем и в грузу регулярно меняются. При изменении знака изгибающего момента средний уровень напряжений меняется, а на него накладывается та часть напряжений, которая возникает на волнении. Это приводит к резкому росту размаха напряжений от максимального сжатия до максимального растяжения. В результате могут возникнуть знакопеременные пластические деформации в районах с повышенными местными напряжениями и малоцикловая усталость конструкций.
Определять изгибающие моменты и перерезывающие силы на тихой воде целесообразно, используя приближенные зависимости, позволяющие оценить максимальные перерезывающие силы и изгибающие моменты (например, таблицы и графики, разработанные А. И. Максимаджи и А. М. Мельниковым).
Рассчитанные нагрузки, определяющие продольную прочность судна, включают кроме изгибающих моментов и перерезывающих сил на тихой воде также волновые перерезывающие силы и изгибающие моменты, а для судов с большим развалом бортов еще и вызванные ударом волн в развал борта.
Дополнительные расчетные волновые и ударные нагрузки можно определять по формулам Правил и по методике с учетом качки на волнении, долговременного распределения волновых ресурсов в районах плавания.
Таким образом, воздействие внешней среды на корпус судна проявляется в виде постоянных гидростатических нагрузок, а также в виде переменных волновых и гидродинамических (ударных) нагрузок.
При плавании волновые нагрузки меняются с периодом, близким к периоду движущихся волн, а гидродинамические – со значительно большей скоростью и динамически действуют на корпус.
Изгибающие моменты и перерезывающие силы на тихой воде следует рассчитывать для всех реально возможных в эксплуатации случаев распределения весовой нагрузки по длине судна, включая состояние нагрузки в полном грузу и балласте в начале и в конце рейса. Для отдельных типов судов Регистр требует дополнительное рассмотрение некоторых вариантов загрузки в грузу для любого сечения по длине судна как при его прогибе, так и при перегибе. Эти величины принимают в качестве расчетных для данного сечения.
Каждый конструктивный тип судна имеет свои особенности в зависимости от рода перевозимого груза, условий плавания и эксплуатационного назначения. Поэтому даже одинаковые по типу суда во время эксплуатации в разных условиях по-разному загружают и разгружают в портах назначения. В результате различно распределяются и переменные составляющие массы судна. При проектировании судна требуется внимательно исследовать возможности появления наиболее неблагоприятных случаев его загрузки. Важной задачей при этом является разработка руководства для капитана по загрузке или, как говорят, по составлению каргоплана, позволяющего минимизировать нагрузки на тихой воде. То же самое делают и для случая приема балласта при плавании судна без груза.

Источник: Foter.com
Одним из возможных способов уменьшения максимальных изгибающих моментов и перерезывающих сил и, следовательно, уменьшения действующих в конструкциях напряжений при общем продольном изгибе корпуса является правильное размещение груза, топлива, балласта, запасов по длине судна. Как уже было установлено, чем точнее соответствует размещение груза эпюре емкости помещений, тем меньше на каждом участке длины разница между массой и силами давления воды, тем меньше результирующие нагрузки на корпус и, следовательно, тем меньше перерезывающие силы и изгибающие моменты.
Общую продольную прочность корпуса при проектировании проверяют по следующим параметрам:
- по критерию усталости от многократного изгиба корпуса на волнении под действием волнового составляющего изгибающего момента Mв и изгибающего момента на тихой воде Mт.в;
- по предельному состоянию, когда на судно одновременно действует сумма трех максимально возможных составляющих полного изгибающего момента на тихой воде при перегибе и прогибе судна, волновой составляющей изгибающего момента и составляющей от удара о волну днищем и в развал носовой оконечности;
- по предельному состоянию на срез под действием максимально возможной суммы расчетных значений перерезывающих сил, которые соответствуют составляющим изгибающего момента.
Общую прочность по приведенным критериям следует рассчитывать для всех наиболее неблагоприятных случаев загрузки судна, при которых в проверяемых поперечных сечениях корпуса возможны наименьшие запасы прочности. Расчетные схемы, используемые в настоящее время, позволяют достаточно точно (+5 %) определять изгибающие моменты и перерезывающие силы для случая судна на тихой воде. Точность же определения волновых и ударных составляющих изгибающих моментов и перерезывающих сил значительно меньше.
Как очевидно из предыдущих рассуждений, изгибающие моменты и перерезывающие силы корпуса на тихой воде вычисляют для возможных случаев загрузки, при которых в условиях перегиба или прогиба полный изгибающий момент (Mт.в+Mв+My) будет наибольшим.
Максимальный изгибающий момент, который возникает на тихой воде от общего продольного изгиба корпуса, иногда называют постоянной составляющей полного расчетного изгибающего момента в отличие от дополнительных волнового Mв и ударного Mу моментов.
Величина изгибающего момента определяется кривой распределения масс, составляющих водоизмещение судна. Масса судна включает в себя отдельные массы, составляющие водоизмещение судна, такие, как масса корпуса, механизмов, устройств, топлива, смазочных масел, снабжения, воды и всех перевозимых грузов. В процессе эксплуатации отдельные массы могут по мере частичного их расходования меняться (топливо, масло, продовольствие, вода и т. п.). Поэтому кривая распределения масс по длине судна для разных случаев загрузки будет также меняться.
Кривая распределения масс для каждого эксплуатационного случая будет своя. Она получается как сумма распределения отдельных ее составляющих по длине судна. С целью практических расчетов при проектировании судна составляют подробную таблицу нагрузки, в которой приводят отдельные компоненты массы судна и положения центра тяжести каждого компонента. Используют также чертежи общего расположения судна, по которым определяют район, занимаемый каждым отдельным компонентом массы.
Если построить кривую распределения масс, точно следуя таблице нагрузок, то эпюра нагрузки будет представлена сложной кривой. Эту кривую желательно привести к более простой, не уменьшая точности последующих вычислений перерезывающих сил и изгибающих моментов корпуса на тихой воде, что достигается заменой сложной кривой ступенчатой. Длину судна между перпендикулярами разбивают на 20 равных участков (теоретических шпаций) и принимают, что масса на длине каждого участка распределена равномерно (рис. 9). Такой метод построения кривой распределения массы по длине судна предложил в 1916 г. академик Ю. А. Шиманский. В российском судостроении этот метод используется до сих пор.
Массу транспортного судна при построении ступенчатой кривой разбивают на следующие отдельные статьи:
- масса корпуса вместе с оборудованием;
- масса главной механической установки вместе с валопроводом, винтом и вспомогательными механизмами;
- масса надстроек с оборудованием;
- масса топлива, воды и смазочных материалов;
- масса перевозимого на судне груза;
- масса принимаемого балласта.
После разбивки отдельных составляющих массы судна по 20 теоретическим шпациям необходимо убедиться, что общая их сумма равна водоизмещению судна, а положение центра тяжести (ЦТ) по длине остается в прежнем положении. Для этого пользуются чертежом продольного разреза судна с указанием местоположения отдельных составляющих масс и их ЦТ по длине судна.
Различаются массы судна по характеру распределения по длине корпуса:
- массы, распределенные по всей длине судна (обшивка, набор, настилы палубы и т. п.);
- массы, распределенные на части длины (надстройки, платформы, механизмы, устройства, валопроводы и т. п.); к таким массам относятся все массы, находящиеся на участке длиной больше 0,02L;
- сосредоточенные массы, расположенные на коротких участках длины судна (мачты, поперечные переборки и т. п.).
Используя чертеж общего расположения судна и таблицу нагрузки, определяют часть водоизмещения, приходящуюся на каждую теоретическую шпацию (масса шпации). Ординаты кривой распределения массы получаются как результат деления массы шпации на ее длину (размерность – тонна на метр).
Распределение масс по теоретическим шпациям выполняют в табличной форме, которая приводится в справочниках по строительной механике корабля.
В практике проектирования судов используют различные способы построения кривой массы судна. Наибольшие трудности возникают при разбивке массы корпуса на 20 шпаций. Существует несколько приближенных способов построения этой кривой. В российской и иностранной практике широко применяют прием построения кривой масс основного корпуса для судов с цилиндрической вставкой, т. е. для всех грузовых транспортных судов, когда эпюры сил веса удобно представить в виде прямоугольника посередине и двух трапеций по концам (рис. 10).
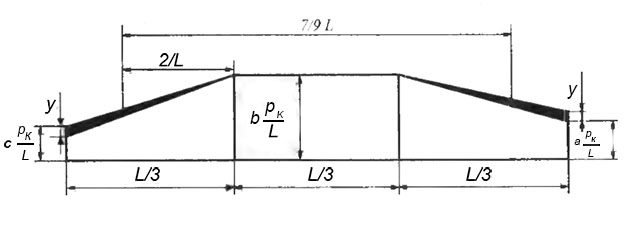
Построение эпюры начинают с разделения длины судна на три равные части L/3. Ординату среднего прямоугольника назначают по данным статистики, а крайние ординаты трапеции определяют так, чтобы сохранялась общая масса корпуса и расположение его ЦТ по длине. Крайние ординаты имеют разную величину, если ЦТ корпуса расположен не по середине длины судна.
Площадь, ограниченная на рис. 10 сплошными линиями, должна равняться массе всего корпуса:
При положении центра тяжести площади pк по середине длины судна a = c. Если положение ЦТ корпуса по длине судна хg не совпадает с ЦТ по длине построенной площади хк, то необходима корректировка концевых ординат для обеспечения совпадения хg и хк. Нужного смещения ЦТ по длине можно добиться, перемещая треугольные элементы площади эпюры от одной трапеции к другой (см. залитые треугольники на рис. 10).
Плечо переноса центра тяжести залитого треугольника из одного положения в другое х = (7/9)L, а площадь треугольника:
где:
- y – основание треугольника.
Статический момент перемещаемой площади треугольника из одного положения в другое:
Центр тяжести всей площади сместится на величину:
Зная Δхк, можно определить y.
Необходимо учесть, что длина цилиндрической вставки на многих современных грузовых судах значительно больше 1/3. Поэтому на диаграмме длина средней части должна приниматься равной фактической ее длине на судне и соответствующим образом должны подбираться ординаты диаграммы.
Другой способ распределения массы корпуса по длине судна, предложенный А. А. Курдюмовым, предполагает использование ступенчатой кривой Ю. А. Шиманского для целей дальнейших расчетов. Этот способ дает возможность построения ступенчатых кривых для двух типов судов, отличающихся остротой своих образований. Для построения ступенчатой кривой для судна с полными образованиями с длинной цилиндрической вставкой принимается равномерное распределение масс корпуса по его длине в пределах восьми средних теоретических шпаций. В соответствии с этим способом цилиндрическая вставка делается больше 1/3 длины судна, однако в последнее время построено большое количество крупнотоннажных судов, у которых цилиндрическая вставка имеет еще большие размеры.
Предлагается к прочтению: Обеспечение непотопляемости судна
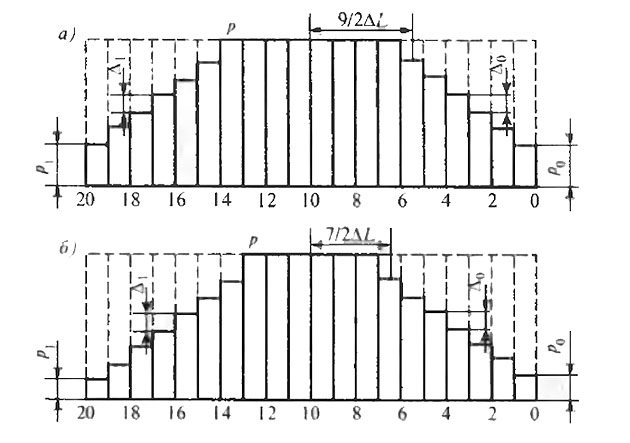
Для судов с небольшой цилиндрической вставкой, к которым относятся прежде всего пассажирские суда и контейнеровозы с очень большой скоростью, может быть использована другая ступенчатая кривая (рис. 9, б), при использовании которой масса принимается равномерно распределенной только в пределах шести средних шпаций (что составляет длину цилиндрической вставки).
Допустим, что масса корпуса, находящаяся в пределах одной средней шпации, p = m(pк/20), а в крайних носовых и кормовых оконечностях соответственно p0= m0(pк/20) и p1 = m1(pк/20), где:
- m, m0, m1 – некоторые коэффициенты пропорциональности.
Если, как рекомендовано А. А. Курдюмовым, m = 1,18, два других коэффициента пропорциональности для кривой на рис. 9, а будут равны m0 = 0,667 + 0,365ξк; m1 = 0,667 – 0,365ξк и для кривой на рис. 9, б m0 = 0,730 + 0,ЗЗЗξк; m1 = 0,730 – 0,333ξк; ξк = xк/ΔL, где:
- xк – отстояние центра тяжести массы корпуса от миделя (положительное направление – в нос).
В описанном методе можно сразу найти значения ординат ступенчатой кривой для всех теоретических шпаций. Сопоставление результатов, получаемых по методике А. А. Курдюмова, дает близкое совпадение с результатами расчета по рабочим чертежам корпуса судна.
Суммарное значение распределения масс на длине судна можно вычислить, если к массам корпуса добавить все другие массы, распределяя их равномерно в пределах той теоретической шпации, на длине которой располагается данная масса, а центр тяжести площади совпадает по длине с ЦТ массы. При таком распределении масс погрешность в моментах не должна превышать 2 %.
Кривая сил поддержания
Данную кривую строят с использованием строевой по шпангоутам для ватерлинии, соответствующей данной осадке судна, по масштабу Бонжана. На диаграмму наносят ватерлинию и для каждого теоретического шпангоута снимают площади погруженных частей шпангоутов. Эти площади и будут ординатами строевой по шпангоутам в масштабе площадей погруженных шпангоутов. Ординаты строевой по шпангоутам представляют собой объем вытесненной корпусом воды на 1 м длины судна. Умножением этого объема на плотность воды получают силы поддержания. Ординаты сил поддержания имеют размерность «тонна на метр». Разница между кривой распределения по длине судна объемного водоизмещения – строевой по шпангоутам – и кривой распределения сил поддержания заключается только в разнице масштабов их ординат.
Для случая нахождения судна на тихой воде кривую сил поддержания определяют по известной массе судна – по водоизмещению и соответствующему ему объемному водоизмещению. По кривым элементов теоретического чертежа находят среднюю осадку, отстояние ЦТ ватерлинии, соответствующей данной осадке, от миделя, отстояние центра величины ЦВ от миделя и продольный метацентрический радиус. Эти данные позволяют определить осадку судна носом и кормой, по которым на масштабе Бонжана проводят ватерлинию и вычисляют погруженные площади шпангоутов. Если ватерлиния нанесена правильно, то ЦТ и ЦВ должны находиться на одной вертикали. Это положение соответствует удифферентованному судну.
После умножения всех 21 ординат строевой по шпангоутам на плотность воды концы их соединяют плавной кривой. В результате получают новую кривую, напоминающую по форме строевую на тихой воде (рис. 11).
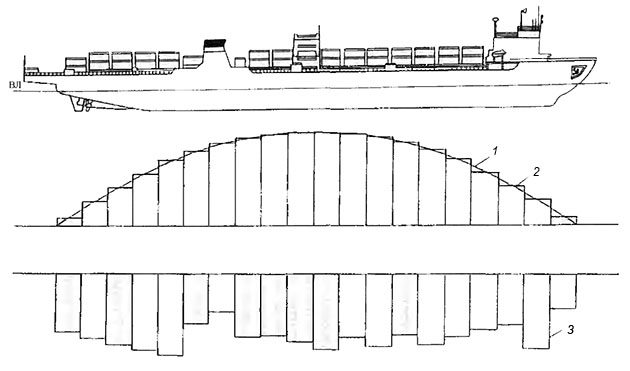
1 – кривая сил поддержания; 2 – ступенчатая кривая сил поддержания; 3 – ступенчатая кривая распределения масс
С целью упрощения расчетов по нахождению нагрузки, действующей на судно-балку, кривую сил поддержания в российской практике заменяют на ступенчатую линию, но так, чтобы площади, ограниченные плавной кривой и ступенчатой линией, были одинаковы, а положения ЦТ обеих этих площадей по длине совпадали. Каждая ступенька должна располагаться на длине одной теоретической шпации ΔL. Допуская, что на этой длине силы поддержания распределены так же, как и массы, равномерно, для сил поддержания на участке одной шпации можно получить выражение:
где:
- ωi, ωi+1 – погруженные площади (до ватерлинии) соседних теоретических шпангоутов, снятые с масштаба Бонжана;
- p – плотность воды.
Кривая сил поддержания для судна на волнении отличается от кривой для судна на тихой воде, так как форма ватерлинии изменяется. В данном случае судно будет находиться не на плоской поверхности воды, а на вершине или подошве волны, или же в любом промежуточном положении. Каждое положение судна при статическом рассмотрении вопроса, т. е. когда волна и судно как бы застывают в определенном положении, должно иметь в соответствии с законом Архимеда, так же как и на тихой воде, силы поддержания, уравновешиваемые массой судна, т. е. новая кривая сил поддержания и кривая массы должны иметь одинаковые площади, и их ЦТ по длине должны совпадать.
Рассматриваемая здесь статическая постановка на волну как бы соответствует случаю движения судна без качки со скоростью, равной скорости распространения волн, когда судно принимает то или иное положение на волнении. Обычно в расчет берут два экстремальных случая – на вершине и на подошве волны, принимая на волнении ватерлинию, имеющую форму и размеры расчетной волны. В этих двух положениях самая верхняя и самая нижняя части волн находятся на миделе. В таких двух положениях судна обычно в поперечных сечениях корпуса возникают максимальные изгибающие моменты и перерезывающие силы, когда судно расположено на волне длиной, равной длине судна, перпендикулярно к бегу волн.
Если же судно находится перпендикулярно к волнам и расстояние между гребнями значительно больше длины судна, то силы поддержания изменяются незначительно по сравнению со случаем движения судна на тихой воде (рис. 12, а). При небольших длинах волн, когда расстояние между гребнями волн очень мало (рис. 12, б), изменение сил поддержания также незначительно.
Таким образом, дополнительный изгиб при положении судна на волнах большей длины по сравнению с длиной судна и при положении на волнах, длина которых меньше длины судна, всегда меньше изгиба, возникающего при изгибе судна на волне, равной длине судна. Точными исследованиями, однако, установлено, что наибольшая величина изгибающего момента на миделе отмечается при длине волн, немного превышающей длину судна.
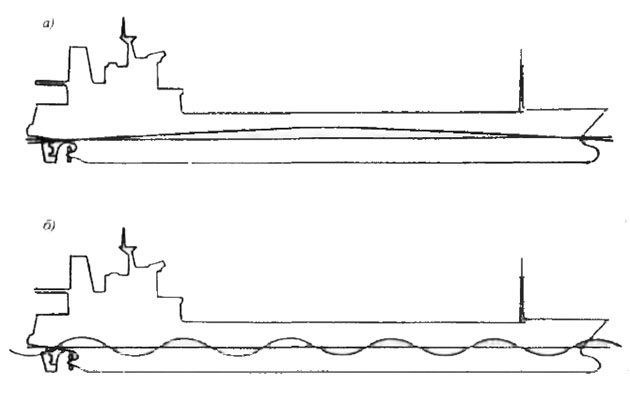
Поэтому при статической постановке на волну ее длину λ принимают всегда равной длине судна (λ = L). Когда самая верхняя или самая нижняя точка волны смещается от миделя к оконечностям, величина изгибающего момента на участке 0,4-0,5L судна меняется очень мало, т. е. моменты в поперечных сечениях корпуса на этом участке мало отличаются от максимальной величины изгибающего момента на вершине или подошве волны, когда экстремальные их точки совпадают с миделем.
Характеристики расчетной волны при статической постановке судна определены на основании многолетних наблюдений и записей волнения в море. Между высотой волны и ее длиной аналитической зависимости не существует, так как имеется сложная взаимосвязь параметров волнения от силы и продолжительности ветра, размеров водного бассейна, расстояния от берегов, состояния атмосферы, глубины, вихревых образований в глубине воды и в воздухе. Однако длительные многолетние наблюдения за волнением при различных условиях волнообразования позволили установить зависимость между высотой и длиной наиболее опасных для прочности судов регулярных волн. Как установлено в последние годы, при взаимодействии корпуса судна и движущихся волн возникают своеобразные гидродинамические условия, которые влияют на уменьшение максимальных изгибающих моментов по сравнению с тем, что получается при статической постановке на волну.
Как показывают наблюдения и замеры в море, форма двухмерных регулярных волн типа морской зыби напоминает трохоиду (см. рис. 11). Действительно, вершины у регулярных волн более крутые, чем их подошвы. Трохоидальный профиль волны строят следующим образом. За ось трохоиды принимают горизонтальный отрезок, равный длине волны λ. Один конец этого отрезка помещают в центр круга, на котором имеются две окружности: внешняя окружность I радиусом R ограничивает катящийся по плоскости АВ круг; внутренняя окружность имеет диаметр, равный высоте волны h (рис. 13). Если на окружности II наметить какую-нибудь точку и затем катить круг I по плоскости АВ, то эта точка опишет кривую, которая и будет трохоидой. За полный оборот круга I получится вся волна.
Профиль трохоидальной волны можно построить и по заранее вычисленным ординатам, которые приведены в справочниках по строительной механике корабля. На рис. 13 показано построение только части длины волны с вершиной в точке 10 и с подошвой в точке 0. Чтобы построить всю длину волны, необходимо кривую для вершины волны продлить влево, а для подошвы волны — вправо. На рисунке можно видеть, что подошва трохоидальной волны более плавная, чем ее вершина.
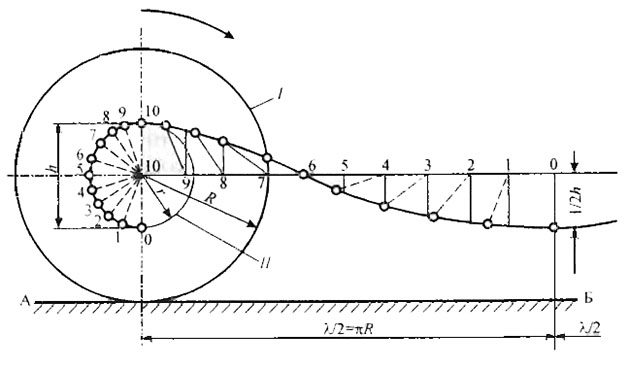
Расчет общей продольной прочности корпуса судна при его изгибе в продольной вертикальной плоскости на волне выполняется в такой последовательности:
- выполняют удифферентовку судна на волне, т. е. находят равновесное состояние судна, при котором объемы корпуса судна, вышедшие из воды и вошедшие в воду, одинаковы (алгебраическая сумма моментов этих объемов относительно миделя равняется нулю);
- вычисляют дополнительные силы поддержания, появляющиеся как результат того, что по сравнению со случаем положения судна на тихой воде изменяется осадка всех поперечных сечений корпуса и водоизмещение вошедших в воду объемов корпуса рассматривается как появление дополнительных сил, направленных вверх, а вышедших из воды объемов – как сил, направленных вниз. Интегрируя два раза кривую дополнительных сил поддержания, можно найти дополнительные перерезывающие силы и изгибающие моменты.
При удифферентовке судна на волне совершенно так же, как это делалось для случая на тихой воде, пользуются масштабом Бонжана. Волновой профиль наносят на кальку в виде вершины или подошвы волны, и наложением кальки на масштаб Бонжана добиваются равенства входящих и выходящих объемов при совпадении по длине в одной поперечной плоскости ЦТ и ЦВ судна.
Кривая нагрузки
Построение этой кривой предполагает предварительное построение ступенчатой кривой распределения масс и ступенчатой кривой распределения сил поддержания на тихой воде. При положении судна на вершине или подошве волны дополнительные силы поддержания разных знаков возникают в результате увеличения объемов подводной части в одних местах по длине корпуса и уменьшения в других (см. рис. 21).
Рекомендуется к прочтению: Безопасность эксплуатации судна
Рассматривая ступенчатые кривые сил тяжести и сил поддержания, вычерченные в одинаковом масштабе, можно видеть, что по отдельным теоретическим шпациям наблюдается их неравенство. В одних шпациях имеется избыток сил тяжести, а в других – сил поддержания. Накладывая обе площади, ограниченные двумя ступенчатыми кривыми, одну на другую, произведем алгебраическое суммирование площадей. Если при распределении масс и сил поддержания все действия выполнены правильно, то общий избыток сил тяжести (масса) и избыток сил поддержания должны быть равны, а общая площадь, ограниченная новой ступенчатой кривой, должна иметь ЦТ на одной вертикали с ЦТ и ЦВ судна.
Кривая, ограничивающая площадь результирующей ступенчатой кривой, называется кривой нагрузки, а площадь, ограниченная этой кривой, – эпюрой нагрузки (рис. 14). Для каждой теоретической шпации ординаты ступенчатой кривой нагрузки вычисляются как разность ординат ступенчатой кривой распределения сил тяжести и ступенчатой кривой сил поддержания:
где:
- px – ордината интенсивности сил тяжести, кН/м;
- pgw – ординаты ступенчатой кривой сил поддержания, кН/м.

Естественно, что разной загрузке одного и того же судна будет соответствовать своя кривая нагрузки, так же как и для судна, находящегося в том или ином месте по длине волны. Когда на кривой нагрузки отмечается избыток сил тяжести в средней части длины судна, а избыток сил поддержания наблюдается по его концам, судно получает общую деформацию прогиба. В случае же избытка сил поддержания в средней части и избытка сил тяжести в оконечностях судно будет иметь общую деформацию перегиба корпуса.
Кривая изгибающих моментов и перерезывающих сил по длине судна (построение эпюр)
Построение этих кривых выполняют по кривой нагрузки, ординаты которой обозначаются qx. Для любого случая загрузки судна, а также и порожнего на тихой воде и на волне для каждого поперечного сечения корпуса можно определить величины перерезывающей силы Nx и изгибающего момента Mx и установить, в каком поперечном сечении действуют максимальные Nx и Mx. Это достигается для каждого случая загрузки судна последовательным интегрированием предварительно построенных кривых нагрузки (рис. 15):
При распределенной по длине судна нагрузке перерезывающие силы для любого сечения находят как алгебраическую сумму всех внешних сил, которые представлены площадью эпюры нагрузки, ограниченной ступенчатой кривой нагрузки, и расположены с одной стороны от рассматриваемого сечения. Изгибающий момент – это сумма моментов всех сил, действующих с одной стороны от рассматриваемого сечения относительно этого сечения. Изгибающие моменты для любого сечения корпуса-балки определяют как алгебраическую сумму площадей эпюры перерезывающих сил, ограниченной кривой перерезывающих сил.
При этом площади эпюры перерезывающих сил, расположенные с разных сторон (выше и ниже) оси, имеют разные знаки. Ординаты полученных эпюр перерезывающих сил и изгибающих моментов являются расчетными для данного поперечного сечения.
При этом:
- максимальный изгибающий момент обычно отмечается на миделе;
- максимальная перерезывающая сила обычно имеет максимальное значение в сечениях, расположенных на 1/4L, от оконечностей;
- там, где кривая изгибающих моментов имеет максимум, кривая перерезывающих сил пересекает ось (т. е. равна нулю);
- там, где перерезывающая сила имеет максимальное значение, кривая изгибающих моментов имеет перегиб.
Когда судно попадает на вершину волны по сравнению со случаем на тихой воде в средней части, силы поддержания увеличиваются, а в оконечностях уменьшаются. В этом положении судна в его середине действуют дополнительные силы вверх, а в оконечностях силы поддержания как бы имеют отрицательную величину (направлены вниз). Дополнительные положительные и отрицательные силы на вершине волны вызывают дополнительный изгиб корпуса.
В случае нахождения судна на подошве волны дополнительные силы поддержания возникают в оконечностях и действуют вверх, а в средней части они направлены вниз и имеют как бы отрицательный знак. Такое состояние судна также сопровождается дополнительным изгибом всего корпуса. Для статического равновесия судна на вершине и подошве волны необходимо равенство дополнительных сил поддержания, имеющих разные знаки, поэтому вышедшие и вошедшие объемы должны быть одинаковыми (см. рис. 3).
При определении полной величины перерезывающих сил и изгибающих моментов для случаев нахождения судна на вершине и подошве волны следует суммировать ординаты эпюр перерезывающих сил и изгибающих моментов на тихой воде с ординатами эпюр дополнительных перерезывающих сил и изгибающих моментов на вершине и подошве волны. Эпюры силовых факторов, определяющих общий продольный изгиб судна, приведены на рис. 15 для случая его нахождения на тихой воде, а на рис. 16 – суммарные кривые перерезывающих сил и изгибающих моментов, полученные путем добавления к перерезывающим силам и изгибающим моментам на тихой воде дополнительных волновых компонентов.
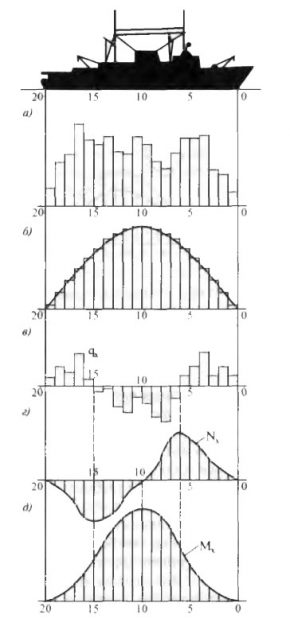
а – кривая распределения массы судна по длине; б – кривая сил поддержания; в – кривая нагрузки; г – кривая перерезывающих сил; д – кривая изгибающих моментов
Метод статической постановки судна на вершину и подошву волны длительное время использовался для расчета общего продольного изгиба корпуса. Однако этот метод, так же как метод расчета для случая на тихой воде, является приближенным условным методом, который мог удовлетворять кораблестроителей, пока строились лишь суда, хорошо зарекомендовавшие себя многолетней практикой эксплуатации. С появлением судов новых конструктивных типов и судов очень больших размеров в последние годы были разработаны более надежные способы определения перерезывающих сил и изгибающих моментов при общем изгибе путем определения внешних нагрузок, возникающих при качке, с использованием вероятностных методов, позволяющих учесть случайный характер воздействия волн и связать величину нагрузки с вероятностью ее возникновения.
1 – суммарная перерезывающая сила; 2 -дополнительная перерезывающая сила; 3 – суммарный изгибающий момент; 4 – дополнительный изгибающий момент
Современная наука о нагрузках, действующих на корпус судна на волновой поверхности моря, основывается на теории регулярных волн малой высоты по сравнению с длиной. Предполагается, что профиль волны имеет установившуюся синусоидальную форму и частицы жидкости движутся по круговым орбитам, радиусы которых с увеличением глубины уменьшаются. Крутизна морской волны для открытого моря обычно меняется от 1/30 до 1/50 (h/λ).
Волны разной длины распространяются с разной скоростью. Чем длиннее волна, тем больше ее скорость, и поэтому длинные волны в море обгоняют короткие. Система регулярных волн разной высоты, длины и направления при их взаимодействии образует нерегулярное волнение, в каждое мгновение состоящее, из беспорядочно расположенных вершин (бугров) и впадин, являющихся результатом случайного суммирования (наложения) многочисленных регулярных волн.
Такое беспорядочное состояние моря может быть описано только статистическими методами. Особенность этих методов заключается в том, что с их помощью можно получить не точный, а только ожидаемый с некоторой достоверностью результат. Реальное нерегулярное волнение характеризуется высотой отдельных волн на поверхности моря баллами. То или иное волнение оценивается по специальной шкале. Самое крупное волнение называют девятибалльным. Таким образом, характеристиками волнения являются высоты волн.
Приближенные формулы для определения суммарных изгибающих моментов и перерезывающих сил на миделе позволяют быстро получить приближенные величины, которые могут потребоваться кораблестроителям и судоводителям при необходимости.
Максимальный изгибающий момент в средней части судна длиной L может быть определен по приближенной формуле:
где:
- D – водоизмещение судна;
- k – коэффициент, принимаемый по прототипу (среднее значение коэффициента k для некоторых типов судов приведено в справочниках по строительной механике корабля).
Для вычисления максимального значения изгибающего момента на миделе можно воспользоваться другим способом. Для этого нужно знать равнодействующую нагрузки для одной половины судна по длине и ее отстояние от миделя. Как известно, для удифферентованного судна:
где:
- xg и xc – соответственно отстояния ЦТ и ЦВ от миделя.
Алгебраическая сумма моментов масс относительно плоскости миделя Mм.к, Mм.н и сил поддержания Mс.п.к, Mс.п.н корпуса, находящихся только в кормовой или только в носовой части судна, одинакова:
- Mмид = Mм.к – Mс.п.к
- Mмид = Mм.н – Mс.п.н.
Сложив правые и левые части этих двух выражений, получим:
Следовательно, изгибающий момент на миделе можно определить по средним значениям плеч нагрузок, расположенных в корму и в нос от миделя.
При статической постановке судна на вершину и подошву регулярной волны для случая его полной загрузки можно воспользоваться формулой А. Манделли:
где:
- D0 – водоизмещение судна с полным грузом;
- α – коэффициент для вершины волны αв.в = a – (h/T)bв.в и для подошвы волны αп.в = a + (h/T)bп.в;
- b – коэффициент полноты поперечного сечения;
- a — безразмерный коэффициент (рис. 11);
- bв.в и bп.в – коэффициенты, указанные в Нормах прочности.
В местах формирования гидродинамических сил ударные изгибающие моменты можно разделить на вызванные ударом волн в днище и в развал бортов носовой оконечности. До сих пор эти удары вызывают местные повреждения конструкций во время плавания судов на волнении, а также значительно увеличивают максимальный изгибающий момент от общего изгиба как на миделе, так и в поперечных сечениях носовой оконечности.
Изгибающие моменты, вызываемые ударами в днище и скулы, характерны для судов, имеющих не только плоские участки днища близко к форштевню, но и острые образования. В последнем случае удары возникают в нижней части борта при большом крене во время смешанной качки. Удары в плоскую часть днища чаще наблюдаются у судов в балластном переходе, а в скуловые части носовой оконечности – у судов с полным грузом. Дополнительные изгибающие моменты от ударов в развал бортов возникают у судов с грузом, способных двигаться на волнении с повышенной скоростью.
При плавании судна в штормовых условиях величина изгибающих моментов от ударов в днище и борта ограничивается в результате снижения скорости из-за опасности повреждения днища и бортов, которую в штормовых условиях контролирует капитан, основываясь на опыте, так как приборов, которые могли бы предупреждать судоводителей об опасности, пока нет. Коэффициент корреляции между ударными изгибающими моментами и волновыми – 0,7-0,8.
Ударные моменты представляют собой вибрационные изгибающие моменты, и только часть их увеличивает максимальный волновой изгибающий момент на миделе. Однако эти моменты все же следует учитывать, так как в носовых сечениях наблюдались потеря устойчивости листов обшивки и набора и даже полный отрыв носовой оконечности. При очень сильном беспорядочном волнении удары в днище и борта, хотя и редко, но наблюдаются и при попутном волнении.
При ударах в развал бортов нагрузки быстро нарастают, но действуют короткий промежуток времени. Такие нагрузки называются импульсными. Они воспринимаются как удар и являются кратковременными. При расчете балок (модель С. П. Тимошенко) на действие импульса с учетом сдвига, инерции вращения и внутреннего трения выявлено, что кратковременный импульс можно заменить мгновенным, если его продолжительность меньше 0,01 периода колебаний балки первого тона.
О механических характеристиках материала при ударном нагружении дает представление рис. 17.
Механические характеристики стали при ударном нагружении улучшаются. Это связано с высокой скоростью деформации конструкций. У высокопрочных сталей предел прочности и предел текучести не зависят от скорости деформации конструкций.
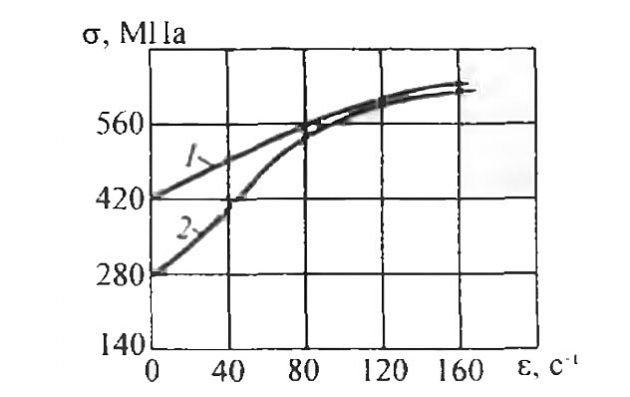
При слеминге и ударах в развал бортов скорость нагружения меняется от 10² до 105 МПа/с, а скорость деформации – от 10-5 до 1,0 с-1.
Величина гидродинамических ударных воздействий на носовую оконечность корпуса зависит от относительной осадки T/L, дифферента судна, обводов носовой оконечности (надводной и подводной), характера волнения и направления движения судна по отношению к господствующему волнению. Иногда господствующее волнение наблюдается с разных направлений.
Следствием ударов в днище и развал бортов является общая вибрация корпуса, которая постепенно затухает. Вызванные ударами колебания имеют частоту первого тона и накладываются на более медленный общий продольный изгиб судна на волнении (см. рис. 8). В результате вибрации в корпусных конструкциях возникают знакопеременные напряжения, и при больших амплитудах они могут вызвать их повреждения в результате усталости материала. Трещины усталости прежде всего появляются в местах высокой концентрации напряжений (прерывистые связи, технологические дефекты, жесткие точки).
Осмотры многочисленных судов в доках свидетельствуют о том, что зона ударов днищем при слеминге располагается от носового перпендикуляра до (0,25-0,3)L. Натурные замеры давлений на днище, проведенные во время штормовых плаваний, показывают, что эпюры местных нагрузок при ударах имеют конический вид, и для разных судов максимальная величина наблюдается в разных местах по длине зоны повреждений. Однако Нормы прочности 1991 г. распределение расчетной нагрузки на днище принимают в виде колокола с синусоидальной формой образующей и с диаметром основания, равным одной теоретической шпации L/20.
Эксперименты, проведенные в море на американском судне типа «Маринер», обладавшем большой скоростью, позволили получить зависимости давлений при ударе днищем о воду от скорости для второго теоретического шпангоута. Давление в момент касания обшивки корпуса поверхности воды зависит от формы сечения шпангоутов (рис. 18). При острых образованиях носовой оконечности усилия при ударе меньше, чем при более полных. Они пропорциональны скорости перемещения сечений в носовой оконечности:
где:
- k – коэффициент, зависящий от формы сечений шпангоутов;
- v – скорость судна в момент касания, м/с.
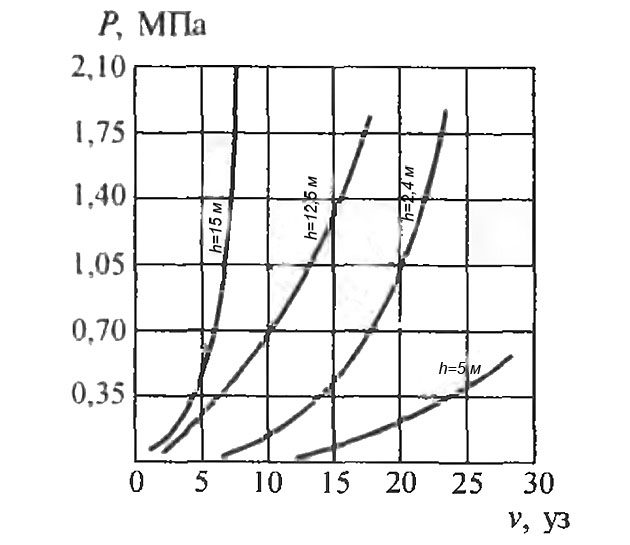
h – высота волны 3 %-й обеспеченности; v – скорость судна, узлов; р – давление на днище при ударе, МПа
Как видно из рисунка, чем больше волнение, тем меньше скорость судна и тем больше давление на днище при ударах. При 3 % волн высотой более 16 м судно, скорость которого на тихой воде достигает 22 уз, может двигаться со скоростью только 7 уз, испытывая давление на днище при ударах о воду 2,1 МПа.
Общая прочность судов при кручении корпуса должна проверяться для большинства современных судов, имеющих большие вырезы в палубе и малое число поперечных переборок внутри корпуса. При этом корпус судна в пределах грузовых трюмов рассматривается как тонкостенная призматическая оболочка закрытого профиля, подвергающаяся скручиванию при плавании на волнении как целая балка. На нерегулярном волнении кручение корпуса-балки носит весьма сложный характер и является результатом своеобразного размещения по длине и ширине корпуса сил поддержания при хаотическом движении волн в штормовом море. Кручение корпуса может наблюдаться и на тихой воде при несимметричном расположении грузов по длине судна относительно ДП.
Наиболее опасным с точки зрения скручивания корпуса является плавание судна на регулярном волнении при его движении под углом к бегу встречных или попутных волн (рис. 19). Для судов с небольшими по ширине и длине люками проверка прочности корпуса на кручение не делается. Для судов новых конструктивных типов с большим раскрытием палуб (большие вырезы) проверка прочности на общее кручение корпуса обязательна, так как в их корпусе дополнительные нормальные и касательные напряжения от скручивания оказывают влияние на общую прочность. Возникает опасность перекоса люков, что может привести к нарушению плотности их закрытия и попаданию воды в грузовые трюмы.
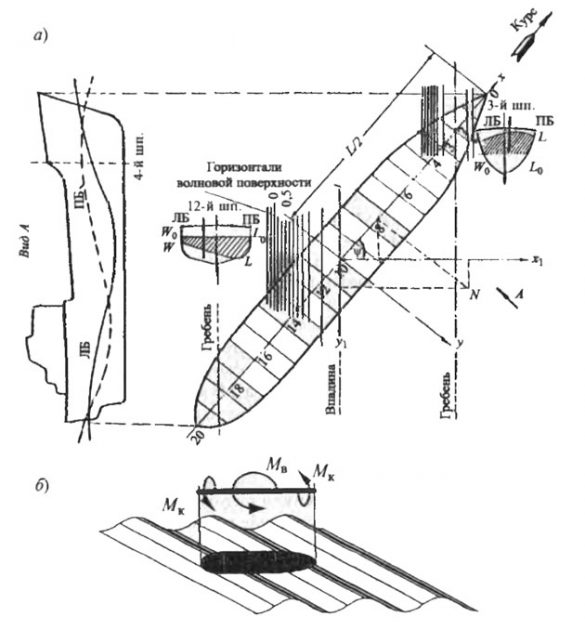
Впервые вопрос о кручении судов был поставлен известным норвежским кораблестроителем Г. Веделером в 1924 г. Он рассчитал скручивающий момент при статической постановке судна на косую регулярную волну, когда оно движется под углом к направлению движения волн. Судно принималось остановившимся на остановившейся волне в определенном положении.
В России кручение судна было рассмотрено в 1948 г. акад. Ю. А. Шиманским в связи с определением сдвигающих усилий в районе прямоугольных палубных вырезов при опасной концентрации напряжений в их углах.
Постройка в нашей стране речных судов с широким раскрытием палуб давно уже стала обычной практикой, однако создание крупных водохранилищ на реках и выход речных судов в морские прибрежные районы потребовали проверки их на скручивание корпуса. В 1951 г. был разработан нормативный документ, в котором на основании многочисленных исследований проф. В. В. Давыдова свободного и стесненного кручения тонкостенных конструкций применительно к судовому корпусу давались рекомендации по расчету речных судов на кручение.
В 1961 г. на Международном конгрессе в Глазго было предложено с целью увеличения крутильной жесткости корпуса создавать дополнительные замкнутые контуры в виде двойных бортов, двойного дна, а также устанавливать прочные поперечные перемычки между люками. Еще раньше двойные борта на речных судах с широким раскрытием палуб широко использовались для увеличения жесткости на кручение советскими судостроителями.
Российские исследователи предложили новые конструктивные решения, обеспечивающие прочность корпуса на кручение: вместо двойных бортов предлагалось устройство только подпалубных и скуловых цистерн. Были разработаны простые расчетные методы, основанные на теориях В. З. Власова, А. А. Уманского и В. В. Давыдова. Однако для судов новых типов мы до сих пор не располагаем достаточными данными о влиянии отдельных сложных конструкций на прочность корпуса при кручении. Правда, в последнее время делаются попытки уточнить роль отдельных связей при кручении нетрадиционных судов и проводятся исследования в этом направлении.
В результате модельных и натурных испытаний судов установлено, что при общем кручении корпуса скручивающий момент достигает максимальной величины на волнах длиной 0,2-0,4L. Величина этого момента меняется с изменением курса судна относительно направления движения волн. Длина волны, при которой крутящий момент имеет наибольшую величину, меняется с изменением отношения ширины судна к его длине.
Наибольшие изгибающие моменты от общего кручения и от общего продольного изгиба, таким образом, возникают при разных длинах волн. Напряжения, вызываемые крутящим моментом, должны добавляться к напряжениям от общего продольного изгиба в вертикальной плоскости.
Для каждого теоретического шпангоута при движении судна под углом к направлению бега волн на регулярном волнении можно построить след пересечения любого теоретического шпангоута с волновой поверхностью и определить вошедшие в воду и вышедшие из нее площади (по сравнению с тем, что было на тихой воде).
При большой скорости судна на крупном волнении в результате ударов волн то с одной стороны борта, то с другой могут возникать дополнительные скручивающие моменты, достигающие порой большой величины.
Бортовая качка при кручении всего корпуса также вызывает дополнительные инерционные и демпфирующие усилия, в результате которых происходит перераспределение сил поддержания. Все это приводит к изменению крутящих моментов, действующих на корпус судна. Если крутящий момент достигает максимальной величины, крена у судна почти нет, поэтому усилиями, которые вызываются бортовой качкой, можно пренебречь. Этот момент возникает при движении судна на регулярном волнении под некоторым углом к бегу волн.
При движении судна на регулярном волнении под некоторым углом к бегу волн появляется горизонтальный изгиб корпуса. В поперечных сечениях корпуса судна кроме изгибающих волновых моментов в вертикальной плоскости возникают еще и волновые моменты в горизонтальной плоскости. Многочисленные эксперименты на моделях и плавающих в море судах, а также расчеты свидетельствуют о том, что наибольшие горизонтальные моменты в корпусе судна возникают при курсовых углах Ψ = 60 °, при длинах волн λ = 0,45÷0,50L, и по величине они соизмеримы с волновыми моментами при общем продольном изгибе в вертикальной продольной плоскости.
Горизонтальные моменты почти не меняются с изменением коэффициента общей полноты δ.
Между вертикальными и горизонтальными моментами имеется сдвиг фаз, т. е. эти моменты достигают максимальной величины в разное время. При одновременном действии обоих моментов наибольшие напряжения от изгиба корпуса будут суммироваться в месте соединения палубного стрингера верхней палубы и ширстрека. Установлено, что угол сдвига фаз изменяется в широком диапазоне в зависимости от 1/L, возрастая с увеличением длины волны. Этот угол находится в пределах от 0 до 90 °.
Суммарные напряжения от вертикального и горизонтального изгибов могут превышать наибольшие напряжения при общем вертикальном изгибе, и их величина зависит также от соотношения между моментами сопротивления эквивалентного бруса относительно горизонтальной нейтральной оси W при изгибе в ДП и момента сопротивления относительно вертикальной нейтральной оси W1 при изгибе в горизонтальной плоскости.
Расчеты показывают, что суммарные напряжения могут превышать напряжения при движении в разрез волны, если отношение W/W1 >0,5. Такое соотношение моментов сопротивления может быть у танкеров.
Для всех судов с большим раскрытием палуб требуется определение деформаций корпуса при его кручении, так как деформации палубных перекрытий могут привести к искажению формы прямоугольных вырезов люков и в результате этого к нарушению плотности закрытия грузовых люков крышками. Такая оценка деформаций возможна, если известны величины и закономерности изменения углов закручивания корпуса по его длине. Чем больше степень раскрытия верхней палубы судна, тем больше снижается жесткость корпуса при общем кручении. Напряжения от кручения увеличивают также и общий уровень напряженности связей корпуса.
Для определения напряженного и деформированного состояния корпуса при кручении используются основные положения теории стесненного кручения, сформулированной В. 3. Власовым и А. А. Уманским. Практические методы для расчета корпусов судов разработаны В. В. Давыдовым и Г. О. Таубиным. Последние уточнили влияние отдельных конструкций и их размеров на жесткость корпуса при кручении. Было установлено положительное влияние двойных бортов на напряжения и деформации корпуса. Определена роль перемычек между соседними люками.
При использовании теории стесненного кручения корпус судна рассматривается как тонкостенная вытянутая оболочка, которая по всей длине палубы раскрыта, а межлюковые перемычки как бы разрезаны, однако их влияние при расчете прочности судна учитывается. Нормальные напряжения в корпусе судна при его кручении складываются из напряжений, вызываемых силовым воздействием перемычек, а также действием напряжений, вызываемых непосредственно скручивающим моментом. Чем больше раскрытие палуб, тем меньше напряжения в перемычках и тем больше дополнительные нормальные напряжения в палубном стрингере и в концевых поперечных сечениях открытой части палубы, которые требуют подкрепления и из-за уменьшения поперечных сечений по концам выреза в результате сужения корпуса в оконечностях.
Межлюковые перемычки уменьшают углы закручивания до 1,5 раза. Другие конструктивные мероприятия, например такие, как устройство подпалубных и скуловых цистерн, оказывают умеренное влияние на общие деформации и напряжения от скручивания. Эти меры не являются единственными способами обеспечения жесткости корпуса при кручении.
На величины перерезывающих сил и изгибающих моментов в поперечных сечениях корпуса-балки при общем ее изгибе на тихой воде и взволнованной поверхности оказывает некоторое влияние скорость судна.
Экспериментальные исследования показывают, что на регулярном двухмерном волнении при λ = L наибольшее увеличение волновых моментов из-за высокой скорости составляет около 20 %. Такое увеличение изгибающих моментов может наблюдаться только при высоких скоростях судна навстречу волнам. Однако во время шторма движение судна с высокой скоростью невозможно из-за опасности его поломки. В этих случаях судоводители уменьшают скорость до минимальной, при которой судно еще слушается руля.
Дополнительные моменты большой величины создает волновая вибрация от ударов корпуса о воду, когда нарушается хорошая морская практика или возникает необходимость выполнения судном во время шторма сложных маневров.
Существенное влияние на величину изгибающего момента оказывает форма изгиба корпуса на тихой воде. Для судов, имеющих перегиб, волновые моменты при реальных скоростях возрастают немного, а для судов с прогибом – значительно.
Определение расчетных волновых изгибающих моментов вероятностными методами
Необходимость применения вероятностных методов для исследования волновых нагрузок и особенности этих методов. Волны в морях и океанах могут быть вызваны различными причинами:
- ветрами;
- приливами;
- землетрясениями;
- извержениями вулканов.
Главная из всех этих причин — ветер. Он представляет собой ту внешнюю силу, действие которой на водную поверхность постоянно вызывает нарушение ее равновесия и ведет к появлению волновых колебаний.
Ветер обычно изменяется по силе, скорости и направлению, вследствие чего волны на поверхности моря различаются по форме и элементам, а чередование их оказывается случайным. Естественно, что реакции корпуса, в том числе и волновые изгибающие моменты, возникающие в результате воздействия на судно случайной системы волн, оказываются также случайными, и для их описания и численной оценки необходимо применять методы теории вероятностей и математической статистики.
Особенностью методов теории вероятностей и математической статистики является то, что исследования, выполненные с их помощью, позволяют получить не окончательный (точный), а только ожидаемый с определенной достоверностью результат, скажем с достоверностью 90 или 99 %. Поэтому расчетные значения любых величин, полученных такими методами, должны определяться двумя параметрами: значением величины и ее статистической характеристикой, например вероятностью превышения этой величины (обеспеченностью).
В настоящее время для оценки расчетных волновых нагрузок статистические методы применяются в форме полновероятностной схемы, согласно которой процесс волнения отображается энергетическим спектром, свойства судна как динамической системы, преобразующей волновое воздействие в выходные процессы качки, изгибающих моментов и т. п., – амплитудно-частотными характеристиками (передаточными функциями), а сами выходные процессы (реакции) представляются в виде функций распределения, позволяющих связать любое численное значение реакции с вероятностью ее превышения.
Комбинация функций распределения реакций, отвечающих различным волновым режимам и условиям движения судна, с учетом вероятности появления каждого возможного их сочетания дает суммарный закон распределения. Этот закон носит название долговременного распределения исследуемого выходного процесса, а метод определения закона, учитывающий вероятностные характеристики всех участвующих в формировании реакций случайных процессов, называют полновероятностной схемой.
Важным допущением в таком математическом описании случайных реакций становится предположение о том, что судно является линейной динамической системой, и поэтому существует линейная зависимость между высотой волны и реакцией судна. Составляющие элементы полновероятностной схемы сведены в табл. 2. Рассмотрим эти элементы более подробно.
Энергетический спектр
Любую волновую поверхность можно описать как состоящую из большого числа наложенных одна на другую регулярных волн различных высот, периодов и направлений (рис. 20).
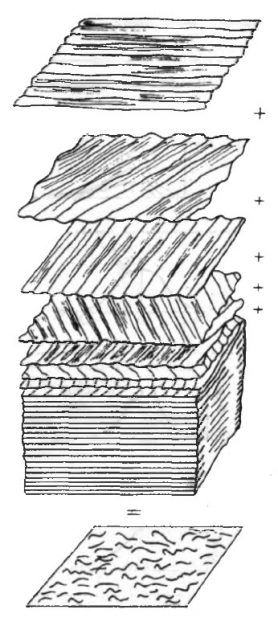
Если в данном волновом режиме все волны сгруппировать по интервалам значений периодов τ или частот ω = 2π/τ и для каждой группы установить приходящуюся на нее среднюю волновую энергию, отнесенную к единице площади поверхности моря, то получается гистограмма распределения энергии волн по периодам (частотам) волн. Так как между τ, ω и λ (длиной регулярной волны) существует прямая связь
аналогичную гистограмму можно построить и в функции от длины регулярных волн. Чаще всего такие гистограммы строят в зависимости от частоты волны, а отображающую их математическую функцию называют энергетическим спектром волнового режима. Таким образом, энергетический спектр волнового режима является функцией, характеризующей распределение энергии единицы поверхности взволнованного моря по частотам регулярных волн.
Каждая элементарная площадь под кривой спектра S(ω)Δω представляет долю энергии ΔE в элементарной полосе частот Δω:
| Определение волновых изгибающих моментов вероятностными методами (полновероятная схема) | |
|---|---|
| Физическое явление | Форма представления |
| Нерегулярное двумерное волнение | Энергетический волновой спектр |
| Трехмерность волнения | Функция распределения энергии по направлениям ψ |
| Свойства судна как динамической системы Реакция линейной системы на регулярную волну единичной амплитуды | Амплитудно-частотная характеристика (передаточная функция) |
| Изгибающие моменты при движении судна на нерегулярном трехмерном волнении данного режима с различными курсовыми углами | Функция обеспеченности (вероятности превышения) Mв на данном режиме |
| Распределение волновых режимов | Функции плотности вероятности характеристик волновых спектров |
| Долговременное распределение волновых изгибающих моментов на всей рассматриваемой совокупности режимов | Долговременная функция обеспеченности Mв |
| Математическое выражение | Графическое преставление |
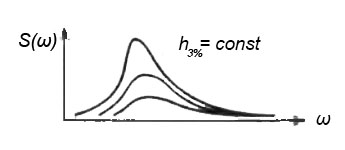 | |
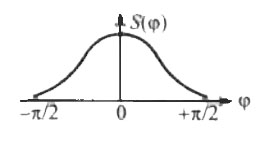 | |
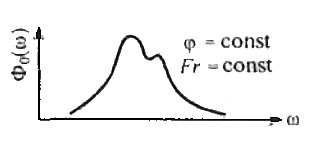 | |
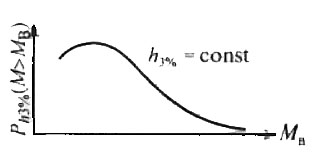 | |
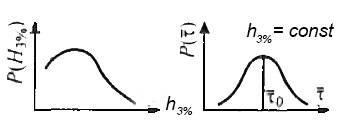 | |
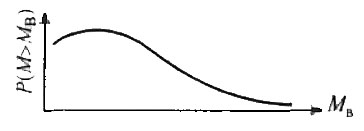 | |
Поскольку энергия каждой волны пропорциональна также квадрату ее высоты,
Принимая это во внимание и учитывая, что площадь под кривой энергетического спектра определяет дисперсию волновых ординат
, дифференциальное распределение высот волн представляют в виде закона Рэлея:
Во время плавания судов в море им приходится попадать на очень большие волны разной формы.
Обычно реальное нерегулярное морское волнение характеризуют условными измерителями – баллами, а в качестве численного измерителя балла принимают характерную высоту волны, в российской практике – высоту волны 3 %-ной обеспеченности (больше этой высоты могут быть только 3 % всех волн системы) (табл. 3).
| Таблица 3. Шкала балльности морского волнения | ||
|---|---|---|
| Степень волнения, баллы | Характер волнения | Высота волны h, м |
| 0 | Отсутствует | 0 |
| 1 | Слабое | 0-0,24 |
| 2 | Умеренное | 0,25-0,74 |
| 3 | Значительное | 0,75-1,24 |
| 4 | Значительное | 1,25-1,9 |
| 5 | Сильное | 2,0-3,4 |
| 6 | Сильное | 3,5-5,9 |
| 7 | Очень сильное | 6,0-8,4 |
| 8 | Очень сильное | 8,5-10,9 |
| 9 | Исключительное | 11,0 и более |
Распределение энергии волн по поверхности моря зависит не только от характерности высоты волны, но также от характерного периода, например среднего периода волнового режима
и направления распространения волн, которое определяется углом φ. Возможны различные комбинации этих параметров и, следовательно, бесчисленное множество различных волновых спектров. Поэтому для отображения двумерного энергетического волнового спектра предлагались различные аналитические зависимости, большинство из которых являются различными модификациями формулы Барминга. При оценке волновых нагрузок наиболее часто используется двухпараметрическая формула, рекомендованная II конгрессом по конструкции и прочности судов:
где:
— средний период волнения;
— его средняя частота.
Одним из частых математических представлений распределения энергии волн по направлениям является функция:
где:
- φ – угол расчетного направления, изменяющийся от -π/2 до π/2.
В ряде случаев удобно представлять S(φ) в функции только одного параметра — h3 %. Это можно сделать, если в качестве τ применять некоторое среднее его значение, характерное для фиксированного:
где:
- a = 3,3÷4,0;
- b = 0,4÷0,5.
Такое аналитическое выражение для S(w) с одним пиком удовлетворительно отображает спектр развитого ветрового волнения, возникающего в результате достаточно продолжительного действия ветра постоянных направления и силы. В случае волнения, вызванного ветром недостаточной длительности или находящегося в стадии затухания, а также при наложении систем волн разных направлений и возраста реальный спектр может существенно отличаться от аналитического: иметь, например, форму в виде одного узкого, двух или нескольких выраженных пиков.
Амплитудно-частотные характеристики
При движении судна на волнении оно может иметь шесть типов перемещений (рис. 21), являющихся реакциями на действие волн. Многие реакции судна на действие волн, в том числе волновые изгибающие моменты, могут рассматриваться как «выходные» случайные процессы, вызванные «входным» случайным процессом морского волнения. Обычно считается, что судно является линейной динамической системой, и поэтому его реакция на регулярную волну имеет частоту самой волны и пропорциональна ее высоте.
Функция, отражающая изменения амплитуды реакции в зависимости от частоты регулярных волн единичной амплитуды, носит название амплитудно-частотной характеристики реакции (АЧХ). Так как при изменении курсового угла и скорости судна изменяется кажущаяся частота волн, ординаты АЧХ оказываются зависящими не только от частоты волн ω, но и от скорости Fr и курсового угла судна к основному направлению волн Ψ, а также от особенностей распределения грузов на судне и его формы обводов, которые определяют собственную частоту колебаний судна ωс. От соотношения частот ω и ωс зависит ордината АЧХ (см. табл. 3).
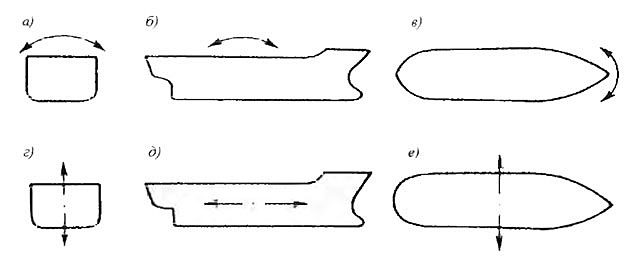
а – бортовая качка; б – килевая качка; в – рыскание; г – вертикальная качка; д – горизонтально продольные колебания; е – горизонтально-поперечные колебания
АЧХ обычно получают теоретически или экспериментально. В первом случае используется расчет качки на регулярном волнении, во втором – испытания моделей в опытовом бассейне на серии регулярных волн. Влияние курсового угла на величины некоторых реакций корпуса танкера приведено в табл. 4.
| Таблица 4. Среднее влияние курсового угла на некоторые реакции корпуса при постоянной скорости танкера типа “Великий Октябрь” | |||||
|---|---|---|---|---|---|
| Реакция корпуса | φ0 | ||||
| 0 (против волны) | 45 | 90 | 135 | 180 (за волной | |
| Изгибающий момент в вертикальной плоскости на миделе | 1 | 0,89 | 0,78 | 0,94 | 1,06 |
| Относительное перемещение | 1 | 0,89 | 0,74 | 0,69 | 0,72 |
| Бортовая качка | 1 | 1,75 | 2,50 | 2,70 | 2,50 |
| Ускорение на носовом перпендикуляре | 1 | 1,02 | 0,97 | 0,63 | 0,44 |
Функции распределения волновых изгибающих моментов
Экспериментально установлено, что гистограммы амплитуд и размахов волновых изгибающих моментов (так же как амплитуд и высот волн), возникающих в корпусе судна, движущегося на нерегулярном волнении с постоянными статистическими характеристиками (h3 %, τ) Режим, статистические характеристики которого не изменяются во времени, носит название стационарногоx, соответствуют некоторому образцу или по специальной терминологии подчиняются закону распределения Рэлея.
В случае справедливости закона Рэлея и предположения, что τ = f(h3 %), вероятность превышения (обеспеченность) волнового момента на стационарном режиме, характеризуемом высотой волны будет определяться выражением:
где:
– спектральная плотность волнения;
- S(φ/Ψ) – условная плотность распределения энергии волн по направлениям φ при курсовом угле Ψ;
– АЧХ.
Если обозначить плотность вероятности встречи судна с волновыми режимами, характеризуемыми h3 %i и τi, функциями p(h3 %) и p(τi/h3%), то долговременное распределение Мв можно представить в виде:
где:
- p(Ψ/h3 %) – условная плотность распределения курсовых углов Ψ на режиме h3 %;
- p(τ/h3 %) – условная плотность распределения средних периодов τ на режиме h3 %.
В результате расчетного анализа установлено, что долговременные распределения Mв в большинстве случаев подчиняются двухпараметрическому закону Вейбулла с показателем степени, близким к единице. Последнее для грубых оценок при исследованиях долговременных распределений позволяет использовать экспоненциальный закон.
Эффективная и эквивалентная высоты волн
Удобно, сохраняя преемственность с методом статической постановки судна на вершину или подошву волны, представлять расчетный волновой момент Mв данной обеспеченности p в виде:
Mв(p) = pgkв[h(p)/2]BL²,
где:
- kв – волновой коэффициент;
- h(p) – расчетная высота волны функции обеспеченности p.
В зависимости от метода назначения волнового коэффициента различают эффективную hе(p) и эквивалентную hэ(p) высоты волн. Первая отвечает kв, вычисленному при статической постановке на волну, вторая – kв, вычисленному как ордината максимума передаточной функции Ф0 волнового момента. В первом случае hе(p) оказывается зависящей от длины судна, а также и ряда других его характеристик (коэффициента полноты, продольного радиуса инерции масс, изгибающего момента на тихой воде и т. д.), так как закономерность изменения от этих параметров при статической постановке судна на волну отличается от зависимостей, вытекающих из динамического расчета. Во втором случае h3(p) зависит только от длины судна, так как прочие его особенности учитываются непосредственно в kв через передаточную функцию Ф0.
Расчетные высоты волн h(p) должны различаться также в зависимости от вида функций p(h3 %), характеризующих проектный район плавания.
Для судов неограниченного района плавания p(h3 %) принимается по результатам измерения волновых режимов в Северной Атлантике, штормовые условия в которой считаются наиболее тяжелыми. Такой подход оправдан, так как даже кратковременный выход судна в океан приводит к долговременным распределениям Mв, мало отличающимся от тех, которые отвечают условиям постоянного плавания в океане.
В Правилах постройки судов Регистра различаются следующие районы эксплуатации:
- неограниченный,
- открытые моря,
- закрытые моря.
Перечень морей, относящихся к каждому району, с учетом соответствующих им функций повторяемости p(h3 %) указывается в Правилах.
Расчетные волновые изгибающие моменты в российских нормативных документах (Правилах постройки, Нормах прочности) выражаются в форме, отвечающей эквивалентным высотам волн. В зависимости от расчетной обеспеченности в этих нормативных документах различают две группы расчетных нагрузок: экстремальные и эксплуатационные.
Расчетную обеспеченность выбирают исходя из следующих соображений. Считается, что судно эксплуатируется примерно 300 дней в году при сроке эксплуатации 24 года. Тогда, принимая средний период изменения волновой нагрузки порядка 7 с, получают общее число ее перемен, близкое к 108 циклам.
В качестве экстремальной расчетной нагрузки – волнового изгибающего момента – принимается его значение, имеющее обеспеченность 10-8, т. е. такое, которое может быть превышено не более одного раза за весь срок службы судна.
В качестве эксплуатационного расчетного волнового момента принимается его величина с обеспеченностью 10-5, т. е. такая, которая во время эксплуатации может быть превышена примерно в тысячу раз.
Экстремальные значения нагрузок используются при контроле предельной прочности, эксплуатационные – при контроле по критерию усталости.
Значения эквивалентных высот волн, принятые в российской расчетной практике, приведены на рис. 4.
Сноски🤝 Поддержите нашу работу
Чтобы продолжить проекту существовать нам нужна ваша помощь!👥 Нас поддерживают:Геннадий, safebridge, Capt Mohee, Dim, Tika, Anto Serviceи ещё 26 человекТакже есть переводы на карту • Спасибо каждому!Нашли опечатку? Выделите и нажмите CTRL+Enter
Сентябрь, 05, 2020 10630 1Пометки

Полезные подсказки для вычислений, формулы всегда актуальны, хороший материал.