Основные положения гидравлики и движение жидкости по трубопроводам судна

Судовая гидравлика является важным аспектом в судостроении, так как она относится к передаче энергии и управлению движением жидкости (обычно масла) для привода различных систем на судне.

Гидравлические системы судна разработаны с учетом безопасности, надежности и эффективности, чтобы обеспечивать безаварийное управление судном и его системами.

Физические свойства жидкости

Гидравлика изучает законы равновесия и движения жидкостей. В основу изучения и установления важнейших законов гидравлики положено понятие идеальной жидкости. В отличие от реальной она считается абсолютно несжимаемой, не изменяющей свой объем под воздействием температуры и не обладающей вязкостью. Это понятие вводится в гидравлике для того, чтобы легче было применять законы механики и физики к жидкостям.

Основные физические понятия, употребляемые в гидравлике, – масса, плотность, удельный объем и другие – не отличаются от понятий, принятых в:

• физике,
• термодинамике,
• технической механике.

Жидкостью называется физическое тело, весьма мало изменяющее свой объем при изменении давления или температуры и обладающее текучестью, благодаря чему она не имеет собственной формы и принимает форму того сосуда, в котором находится.

Рассмотрим физические свойства реальной жидкости.

Сцепление – свойство жидкости сопротивляться растягивающим и разрывающим усилиям. Это свойство у разных жидкостей различно и зависит от величины сил, «связывающих» молекулы этих жидкостей. Сцеплением объясняется поверхностное натяжение в жидкостях, возможность образования капель и т. д.

Читайте также: Расчет элементов систем трубопроводов на судне

Смачивание – способность жидкости прилипать к твердым телам. Это явление обусловлено силами сцепления между жидкостью и твердым телом, причем эти силы должны быть больше сил сцепления между молекулами самой жидкости, в противном случае смачивания не будет.

Вязкость – свойство жидкости сопротивляться внутренним перемещениям частиц при ее движении.

Сжимаемость – свойство жидкости уменьшаться в своем объеме под действием внешних сил.

Различают следующие виды движения жидкости:

• турбулентное – частицы жидкости беспорядочно перемешиваются;
• ламинарное – частицы жидкости не перемешиваются (это движение называется также слоистым или трубчатым);
• установившееся – при котором скорость и давление в каждой точке занятого жидкостью пространства остаются неизменными с течением времени;
• неустановившееся – скорость и давление во всем занятом жидкостью объеме или в его части со временем изменяются;
• одноразмерное – величина скорости и давления жидкости изменяется только в одном направлении (величиной изменения их в других направлениях пренебрегают).

Средняя скорость потока – это скорость, с которой должны были бы двигаться все частицы жидкости через живое сечение потока так, чтобы расход был равен расходу, проходящему через это сечение при действительном распределении скоростей.

Расход жидкости – весовое или объемное ее количество, протекающее через поперечное сечение потока в единицу времени.

Живое сечение потока жидкости представляет собой поверхность поперечного сечения потока, расположенную перпендикулярно средней скорости.

Свободная поверхность жидкости – это поверхность раздела между жидкостью и газообразной средой.

Сплошностью потока в гидравлике называют неразрывное перемещение частиц жидкости, движущихся сплошной массой. Во всех сечениях таких потоков расход их будет одинаков. Если сечения потока (рис. 1) обозначены f₁, f₂, f₃, а скорость в этих сечениях v₁, v₂, v₃, то расход:

т. е. там, где сечение трубопровода меньше при установившемся непрерывном потоке, скорость жидкости будет больше.

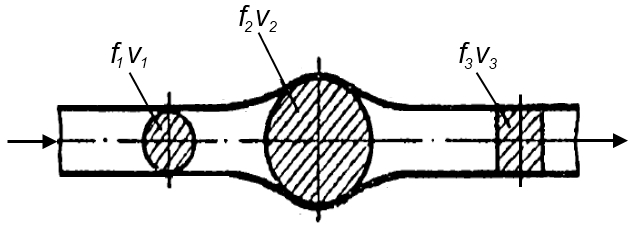
Это уравнение называется уравнением постоянства расхода, или уравнением сплошности.

Гидродинамическое давление жидкости – это сила, действующая на единицу площади поверхности. Гидродинамическое давление относится к жидкости, которая находится в движении. Если речь идет о жидкости, находящейся в состоянии покоя, то давление в этом случае называется гидростатическим. Давление измеряется отношением единицы силы к единице площади и высотой столба жидкости, выраженной в линейных единицах (м, см, мм). Если давление измеряется высотой столба жидкости, то термин «давление» заменяется терминами «напор» или «пьезометрическая высота» Пьезометрическая высота h = p/γ измеряется пьезометром, которым можно измерить также гидростатическое давление в любом сечении потока жидкости.x.

Рассмотрим наиболее часто встречающиеся в гидравлике соотношения между единицами измерения. Если из трубки, закрытой с одного конца, выкачать воздух и, наполнив водой, опустить ее открытый конец в чашу с водой, то высота столба воды в трубке от уровня жидкости в чаше будет составлять 10,33 м вод. ст. Указанная высота столба жидкости уравновешивается нормальным давлением атмосферы (наружного воздуха) на свободную поверхность жидкости в открытой чаше.

Таким образом, атмосферное давление равно гидростатическому напору или пьезометрической высоте, равной 10,33 м вод. ст., т. е. физ. атм = 1,033 кгс/см². Техническая атмосфера соответствует пьезометрической высоте или гидростатическому напору водяного столба высотой в 10 м.

Если трубку вместо воды наполнить ртутью, то давление атмосферы будет уравновешиваться высотой столба ртути.

Разрежением (вакуумом) называют недостачу давления до атмосферного.

Уравнение Д. Бернулли и движение жидкости по трубопроводам

Движение жидкостей имеет много общего с движением твердых тел под действием приложенной к ним силы, например с падением тела под действием силы тяжести (собственной массы).

Кроме силы тяжести, на движение жидкости влияют также силы трения и гидродинамическое давление. Рассмотрим процесс вытекания жидкости из сосуда А (рис. 2) с постоянным напором H = h + z, выделив в трубке сосуда центральную струйку mm.

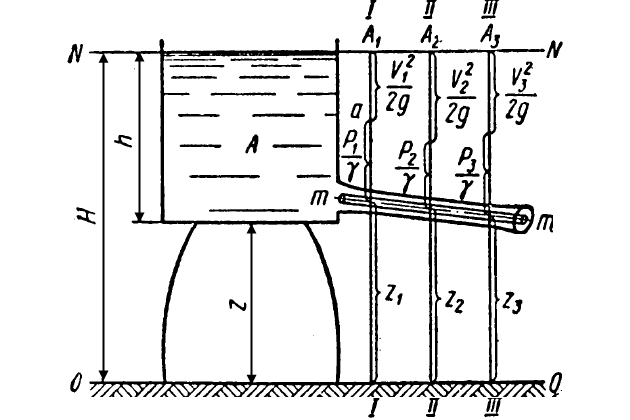
Жидкость изменяет свою форму в зависимости от формы трубки, через которую она протекает. Причем количество жидкости, которое протекает через каждое сечение трубки, соответствующее на рисунке отметкам I-I, II-II, III-III, за одно и то же время вследствие неразрывности массы и постоянства расхода остается неизменным. При переходе жидкости от одного сечения (I-I) к другому (II-II) и т. д. изменяются скорость ее вытекания, энергия положения частиц жидкости (принимая последовательно значения z₂ и z₃) и удельная энергия давления, или пьезометрическая высота (от значения

$\frac{p_1}{\gamma }$

к значениям

$\frac{p_2}{\gamma }, \frac{p_3}{\gamma }$

).

По уравнению Д. Бернулли Д. Бернулли (1700-1782 гг.) – выдающийся ученый математик и механик. Работал в Петербургской Академии Наук.x, при установившемся движении идеальной Жидкость, не имеющая трения между своими частичками, а также о стенки ограничивающего ее сосуда (трубопровода).x жидкости сумма потенциальной

$\left(z + \frac{p}{\gamma }\right)$

и кинетической

$\left(\frac{v^2}{2g}\right)$

энергии в любом сечении неизменна:

Для обозначений, принятых на рис. 2, можно записать:

Уравнение Д. Бернулли называется также уравнением энергии жидкости.

В теории и расчетах насосов широко применяется уравнение Д. Бернулли, содержащее, кроме всех членов рассмотренного уравнения для идеальной жидкости, член h_w, который учитывает потерянную энергию от гидравлических сопротивлений и называется потерянным напором. Таким образом, для реальной жидкости уравнение Д. Бернулли имеет следующий вид:

В гидравлике это уравнение формулируют так:

при установившемся течении жидкости энергия жидкости плюс потерянный напор в любом поперечном сечении потока есть величина постоянная.

Движение жидкости по Общие сведения о судовых системах, эксплуатация трубопроводовтрубопроводам судна неизбежно связано с потерей напора (энергии жидкости) на преодоление сопротивлений по длине трубопровода h_{д. т} и местных сопротивлений h_{м. с}. Тогда формула 3 примет вид:

Потери по длине трубопровода возникают вследствие трения жидкости о стенки труб и внутреннего трения между частицами движущейся жидкости. Трение о стенки зависит от степени шероховатости труб и свойств жидкости.

Практикой установлено, что на величину сопротивления течению жидкости в шероховатых трубах решающее влияние оказывают не размеры выступов, а отношение средней высоты выступов l к радиусу трубы r. Это отношение

$\epsilon =\frac{l}{r}$

называется относительной геометрической шероховатостью и является величиной, характеризующей шероховатость стенок трубы. Среднюю высоту выступов называют абсолютной геометрической шероховатостью.

 
Гидравлическая шероховатость обусловливается не только высотой неровностей внутренней поверхности труб и взаимным расположением их, но также толщиной пограничного ламинарного слоя и значением числа Рейнольдса (Re), или критерием Рейнольдса, которое характеризует ламинарное или турбулентное течение жидкости:

где:

• v – скорость течения жидкости, м/с;
• d – диаметр трубы, м;
• $\nu =\frac{\mu g}{{\gamma }_0}$

  – кинематический коэффициент вязкости жидкости;

• μ Размерности величин μ и γ₀ справедливы при g = 981 см/с².x – динамический коэффициент вязкости жидкости, кгс/с·м²;
• γ₀ – объемная масса жидкости, кг/м³.

При определении необходимой подачи насосов необходимо принимать во внимание степень совершенства всасывающего трубопровода. При достаточно больших значениях чисел Рейнольдса толщина пограничного ламинарного слоя в трубопроводе уменьшается.

Другими словами, в установившемся потоке жидкости действует закон сплошности, из которого вытекает, что скорости обратно пропорциональны площадям сечений. Эта связь скоростей с площадями сечений позволяет управлять скоростями путем варьирования конфигурации трубы. Со скоростями движения жидкости связаны давления в потоке.

Для жидкости, движущейся по трубопроводам, ее турбулентный режим наступает при Re > 2 320. Таким образом, труба, гидравлически гладкая, при увеличении числа Рейнольдса становится гидравлически шероховатой. Гидравлически гладкими считают трубы с относительной геометрической шероховатостью:

Потери по длине трубопроводов (м вод. ст.), кроме того, зависят от рода текущей жидкости и могут быть определены по формуле:

где:

• λ – безразмерный коэффициент, характеризующий потери от трения по длине труб;
• l – длина труб, м;
• d – внутренний диаметр трубы, м;
• g – ускорение силы земного притяжения (g = 9,81 м/с²).

Безразмерный коэффициент λ зависит от условий трения, т. е. шероховатости внутренней поверхности трубы, вязкости перекачиваемой жидкости и др. Его можно определить по следующим формулам.

1. При Re < 2 320, т. е. когда значения λ не зависят от шероховатости труб,

   $\lambda =\frac{60}{Re}.$

   Этой формулой пользуются при определении λ для темных нефтепродуктов при любых трубах.

2. При ламинарном движении жидкости Re < 2 320 применяют формулу Блязиуса:

   $\lambda =\frac{0,3164}{Re}.$

   Эта формула справедлива для известных пределов, определяемых относительной геометрической шероховатостью труб ε. Ею пользуются при определении λ для воды и светлых нефтепродуктов, перекачиваемых по цельнотянутым трубам из цветного металла (красномедным, латунным), а также по резиновым и прорезиненным рукавам. При больших диаметрах труб эта формула справедлива и для темных нефтепродуктов.

3. При

   $Re=\epsilon \frac{59,5}{1,143}$

   рекомендуется пользоваться формулой

   $\lambda =0,093\sqrt{\epsilon }.$

   Эта формула пригодна для воды и светлых нефтепродуктов, перекачиваемых по стальным трубам и пеньковым рукавам.

4. При Re > 10⁵ пользуются формулой Окорского λ = 0,1387Re ^-0,18. Она применяется для воды и светлых нефтепродуктов, перекачиваемых по цветным трубам с большими скоростями.

Для приближенных расчетов значение λ для воды можно принимать 0,03-0,04.

Кинематический коэффициент вязкости ν, входящий в формулу определения числа Рейнольдса, для различных жидкостей находят по специальным справочным таблицам, где он приводится в зависимости от температуры перекачиваемой жидкости.

Значения абсолютной геометрической шероховатости l, необходимые для определения относительной геометрической шероховатости ε, могут быть приняты для:

• резиновых рукавов 0,1 мм;
• стальных труб 0,2 мм;
• прорезиненных рукавов 0,3-0,4 мм;
• пеньковых рукавов 1 мм.

Потери напора от местных сопротивлений возникают при проходе жидкостью Ремонт систем трубопроводов и арматуры суднаразличной арматуры, а также колен, крестовин, тройников и пр., т. е. участков, где изменяют скорость и направление движения жидкости. Вследствие однотипности явлений, происходящих при движении жидкости, потери напора от местных сопротивлений определяют по формуле:

где:

• ξ – безразмерный коэффициент местного сопротивления, зависящий от характера сопротивления; определяется на основании опыта. Значения этого коэффициента могут быть взяты из таблиц, приводимых в справочниках по гидравлике;
• v – скорость жидкости, м/с.

Автор статьи

Виктор Свиридов

Судовой механик

Список литературы

1. Александров А. В. Судовые системы. Л., «Судостроение». 1966. 200 с.
2. Богомольный А. Е. Судовые вспомогательные и рыбопромысловые механизмы. Л., «Судостроение», 1971. 384 с.
3. Валдаев М. М. Гидравлические приводы судовых палубных механизмов. Л., «Судостроение», 1973. 295 с.
4. Гурович А. Н. и др. Судовые устройства. Справочник. Л., «Судостроение», 1967. 412 с.
5. Дубровский О. Н., Руфин Б. А., Артамонов М. Н. Гидравлические приводы судовых механизмов. Л., «Судостроение», 1969. 383 с.
6. Ермилов В. Г. Эксплуатация испарительных установок теплоходов. М., «Транспорт», 1969. 92 с.
7. Епифанов Б. С. Судовые системы. Л., «Судостроение», 1973. 136 с.
8. Завиша В. В., Декин Б. Г. Судовые вспомогательные механизмы. М., «Транспорт», 1974. 392 с.
9. Инструкция по химической очистке судовых испарителей. ММФ, 1968.
10. Коваленко В. Ф. и др. Водоопреснительные установки морских судов. М., «Транспорт», 1964. 304 с.
11. Кравченко В. С. Монтаж судовых вспомогательных механизмов. Л., «Судостроение», 1968. 219 с.
12. Михайлов С. С., Мартынов Б. М. Пневматические приводы судовых механизмов и устройств. Л., «Судостроение», 1974. 190 с.
13. Петрина Н. П. Судовые насосы. Л., Судпромгиз, 1962, 376 с.
14. Плявин Н. И. Эксплуатация морского танкера. М., «Транспорт», 1968. 336 с.
15. Правила классификации и постройки морских судов. Регистр СССР. Л., «Транспорт», 1967. 311 с.
16. Правила классификации и постройки морских судов. Регистр СССР. Л., «Транспорт», 1970. 855 с.
17. Правила техники безопасности на судах морского флота. М., Реклам-бюро ММФ, 1970.
18. Правила технической эксплуатации судовых вспомогательных механизмов и оборудования. М., «Транспорт», 1975.
19. Правила технической эксплуатации корпуса, помещений, устройств и систем судна. М., «Транспорт», 1965. 164 с.
20. Положение о технической эксплуатации морского флота. М., Реклам-бюро, 1973. 151 с.
21. Справочник судового механика. Т. 2. Под ред. Л. Л. Грицая. М., «Транспорт», 1974. 697 с.
22. Шмаков М. Г. Рулевые устройства судов. Л., «Судостроение», 1968. 364 с.
23. Ясинский А. С. Судовые паросиловые установки. М., «Транспорт», 1969. 192 с.
24. Судовые центробежные насосы, Каталог-справочник. М., ЦИНТИХИМНЕФТЕМАШ, 1968. 64 с.