Сопротивление движению судна может быть серьезным препятствием, особенно для облегченного корпуса, поэтому ниже приведены все виды сопротивлений и способы расчета всех показателей для комфортного плавания.
- Основные понятия и определения
- Составляющие сопротивления движению судна
- Безразмерные коэффициенты сопротивления
- Сопротивление трения
- Сопротивление формы
- Волновое сопротивление
- Сопротивление выступающих частей
- Воздушное сопротивление
- Сопротивление водоизмещающих судов
- Изменение сопротивления при движении на волнении
- Влияние основных характеристик корпуса на сопротивление
- Отношение ширины к осадке судна В/Т
- Коэффициенты полноты судна
- Форма корпуса судна
- Способы снижения сопротивления движению судна
Основные понятия и определения
Ходкостью называется способность судна двигаться с заданной скоростью при определенной затрате энергии.
Ходкость и движителиХодкость зависит от главных размерений, обводов и состояния наружной поверхности судна, а также от условий движения. Оценку ходкости принято производить применительно к случаю, когда судно движется вперед равномерно и прямолинейно со скоростью v. Поскольку судно симметрично относительно его ДП, то действие аэро- и гидродинамических сил в этом случае может быть сведено к результирующей Q и моменту М, действующим в ДП (рис. 1).
Сопротивлением воды движению судна R называется проекция результирующей аэро- и гидродинамических сил на направление движения.
Гидродинамической силой поддержания Y называется вертикальная проекция результирующей аэро- и гидродинамических сил.
Дифферентующим моментом называется момент аэро- и гидродинамических сил М.
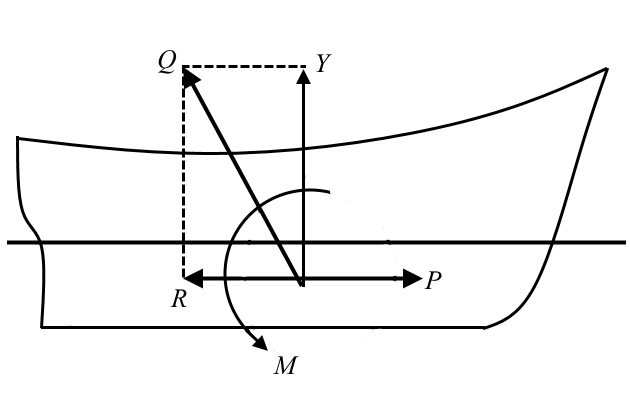
Действие силы Y и момента М вызывает при движении судна изменение его осадки и дифферента, причем с увеличением скорости влияние этих факторов возрастает.
Для поддержания движения к судну необходимо приложить в направлении движения силу. Эта движущая сила создается у самоходных судов движителями и называется упором движителей Р. В случае равномерного прямолинейного движения P = R.
Буксировочной мощностью NR называется наименьшая мощность, необходимая для преодоления силы сопротивления движению судна со скоростью v,
При описании физических процессов, обусловливающих сопротивление воды движению судна, и в практических расчетах ходкости, основанных на результатах испытаний моделей и натурных судов, возникает необходимость использования критериев подобия. Для обеспечения механического подобия Теория судна — Методические указаниясудна и его модели необходимо выполнение трех видов подобия — геометрического, кинематического и динамического.
Геометрическое подобие соблюдается, когда соответствующие линейные размеры модели (Lм, Bм, Tм) и натурного судна (Lн, Bн, Tн) находятся в постоянном соотношении:
Lн/Lм = Bн/Bм = Tн/Tм = k, Форм. 2
где:
- k — геометрический масштаб.
Для соответствующих площадей натуры и модели отношение равно квадрату масштаба, а для соответствующих объемов — кубу масштаба:
Кинематическое подобие соблюдается в том случае, когда сходственные точки геометрически подобных судна и модели проходят подобные отрезки траекторий в течение промежутков времени Δt, находящихся в постоянном отношении
Δtн/Δtм = τ, Форм. 4
где:
- τ — масштаб времени.
Соотношение скоростей в сходственных точках при кинематическом подобии постоянно:
vн/vм = k/τ. Форм. 5
Динамическое подобие соблюдается, когда при наличии кинематического подобия отношение масс сходственных объемов постоянно:
Для описания основных закономерностей сопротивления воды движению судов используются безразмерные критерии динамического подобия потоков жидкости — число Фруда Fr и число Рейнольдса Re.
Число Фруда характеризует отношение инерционных сил к силам тяжести. В динамически подобных случаях движения числа Фруда равны между собой. Это означает, что картины волнообразования двух судов при равных числах Фруда будут геометрически подобны, силы, вызванные волнообразованием, будут относиться как k³, а моменты, как k4. Число Фруда является также мерой относительной скорости судна, которая выражается соотношением скорости v набегающего потока на значительном удалении впереди тела или скорости движения тела и одного из характерных размеров судна.
Для водоизмещающих судов таким размером является длина по ватерлинии; для судов с динамическим поддержанием, у которых в процессе движения длина по ватерлинии изменяется, используют значение ширины В (преимущественно для глиссеров) и, в наиболее универсальной форме, корень кубический из объемного водоизмещения
Число Рейнольдса характеризует отношение инерционных сил к силам вязкостной природы:
Re = vL/v, Форм. 8
где:
- v — скорость судна, м/с;
- L — длина, м;
- v — кинематическая вязкость жидкости, м²/с.
В динамически подобных системах числа Рейнольдса равны между собой. При этом картины вихреобразования и пограничные слои будут геометрически подобны. Вместе с тем необходимо учитывать, что в реальных условиях помимо числа Рейнольдса на картине обтекания существенно сказываются шероховатость поверхности тела и начальная турбулентность потока. Полное динамическое подобие явлений ходкости достигается для рассматриваемых надводных судов при условии одновременного равенства чисел Фруда и чисел Рейнольдса.
Однако это достижимо только в случае полного равенства модели и натуры, т. е. k=1. Поэтому обычно ограничиваются частичным подобием — по числу Фруда или по числу Рейнольдса. Первое обеспечивают при определении Виды парящих судов на подводных крыльяхходкости надводных судов, второе — при изучении движения глубоко под поверхностью воды рулей, выступающих частей и других тел. По числу Рейнольдса обеспечивают также подобие для судов, движущихся с малыми скоростями — в доволновых режимах.
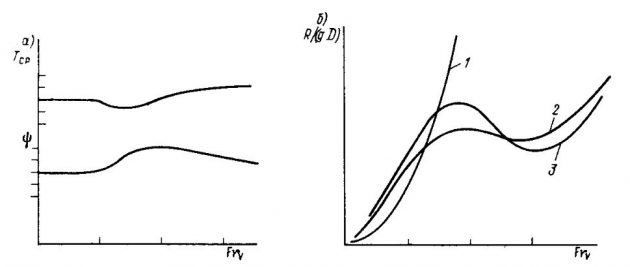
В зависимости от характера действия гидродинамических сил различают следующие характерные режимы движения судов:
- плавание;
- переходный режим;
- режим динамического поддержания.
Режим плавания судов наблюдается при относительной скорости FrV ≤ 1,0. В этом режиме гидродинамическая сила поддержания Y и дифферентующий момент М малы по абсолютной величине, и приводят к некоторому увеличению осадки судна на ходу и появлению небольшого дифферента на нос. Поддержание судна обеспечивают силы гидростатической природы:
gD=γV. Форм. 9
Суда, движущиеся в режиме плавания, принято называть водоизмещающими. В зависимости от значения числа Фруда они подразделяются на тихоходные (FrL < 0,22), среднескоростные (FrL = 0,23—0,35) и быстроходные (FrL > 0,35).
Переходный режим движения наблюдается в диапазоне относительной скорости 1,0 ≤ FrV≤3,0. Его характерной особенностью является перераспределение сил поддержания за счет увеличения динамической составляющей Y, а также появление дифферентующего момента М на корму. В результате совместного действия этих факторов, как правило, уменьшается осадка судна и возрастает дифферент на корму:
gD = γVi+Y, Форм. 10
где:
- Vi — величина погруженного объема судна (Vi < Vo).
Режим динамического поддержания наступает при относительных скоростях движения FrV > 3,0. При этом поддержание судна обеспечивается в основном динамическими силами:
Для глиссирующего судна гидростатическая составляющая поддержания практически исчезает при FrV > 5. Режим движения с динамическим поддержанием является основным для глиссеров, судов на воздушной подушке (СВП), судов на подводных крыльях (СПК), экранопланов (ЭП). Характер действия гидродинамических сил при этом существенно зависит от величины относительной скорости (рис. 2).
Составляющие сопротивления движению судна
В теории корабля сопротивление воды движению судна рассматривают как сумму составляющих:
R = Rм+Rф+Rв, Форм. 12
где:
- Rт — сопротивление трения;
- Rф — сопротивление формы (неточное название — вихревое сопротивление);
- Rв — волновое сопротивление.
Составляющие Rт и Rф обусловлены силами вязкостной природы, а Rв — волнообразованием судна. Основной гипотезой при изучении сопротивления является предположение о независимости вязкостной и волновой составляющих. На самом деле наблюдается их некоторое взаимовлияние. Оно чрезвычайно мало, поэтому на практике успешно используют методы отдельного расчета вязкостного и волнового сопротивлений.
Расчет сопротивления реального судна включает в себя также учет влияния рулей, кронштейнов, гребных валов, скуловых килей, которые создают так называемое сопротивление выступающих частей Rв.ч. Часть силы сопротивления при движении судна определяется также его надводной частью и учитывается как аэродинамическое сопротивление Ra. У водоизмещающих малотоннажных судов величина Ra составляет весьма небольшую часть полного сопротивления и в ряде случаев ее можно не учитывать. Для судов в переходном режиме и глиссирующих воздушное сопротивление составляет уже заметную долю. Особенно важен учет Ra для скоростных глиссеров, СВП, СПК и ЭП. Таким образом, полное сопротивление:
R = Rт+Rф+Rв+Rв.ч+Rа. Форм. 13
Для практического расчета полного сопротивления судов сумму составляющих Rт, Rф и Rв часто представляют как:
где:
- — сопротивление трения прямоугольной гладкой пластины, имеющей площадь и длину, равные соответственно площади и длине смоченной поверхности судна (такую пластину принято называть эквивалентной);
- Ro — остаточное сопротивление.
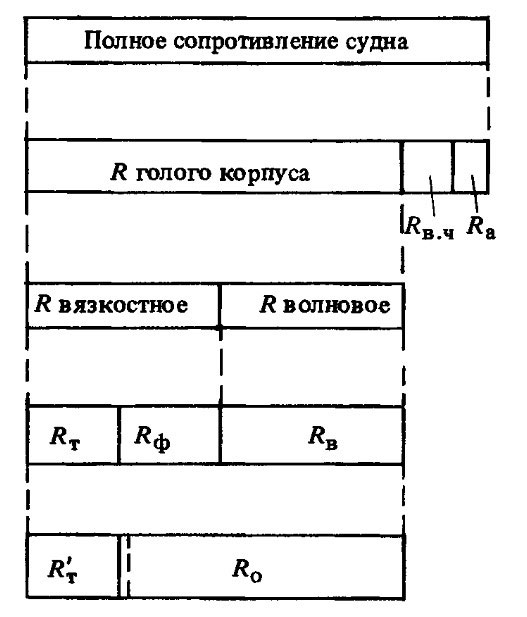
Оно включает в себя сопротивление формы, волновое, а также ту часть сопротивления трения, которая обусловлена отличием плоской эквивалентной пластины от реальной Конструкция корпуса морских деревянных судовформы корпуса судна. Такой подход, несмотря на некоторую некорректность, позволяет удовлетворить условиям гидродинамического подобия. При этом используемые зависимости Rт = f1(Re); Ro = f2(Fr) соответствуют реальным Rт ~ f1(Re); Rв + Rф ~ f2(Fr) и обеспечивают достаточную точность расчета. Указанный метод получил широкое распространение также вследствие удобства расчета сопротивления трения судна как сопротивления эквивалентной пластины по хорошо известным зависимостям и остаточного сопротивления на основе модельных испытаний. На рис. 3 показана схема разделения полного сопротивления судна на составляющие.
Величина прямоугольников иллюстрирует взаимное соответствие величин составляющих, характерное для переходного режима движения.
Безразмерные коэффициенты сопротивления
Для расчета сопротивления используют формулы, структура которых соответствует принципам гидромеханического подобия. Принимая в качестве характерного размера величину смоченной поверхности Ω, получаем общую формулу:
где:
- ζ — безразмерный коэффициент полного сопротивления, который является функцией чисел Фруда и Рейнольдса и представляет собой сумму сопротивления коэффициентов трения, формы и волнового:
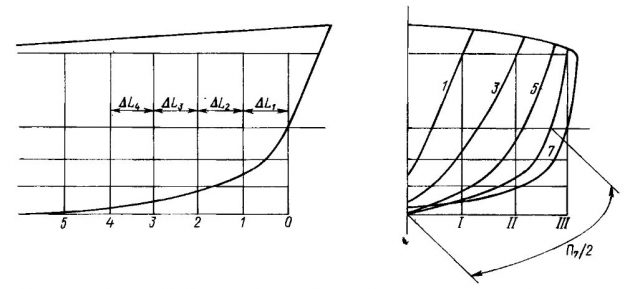
Для того чтобы определить смоченную поверхность судна Ω, используют теоретический чертеж. На проекции “корпус” теоретического чертежа измеряют половины периметров смоченной части шпангоутов судна. Схема замеров показана на рис. 4. Удобнее всего указанную операцию производить с помощью курвиметра. Дальнейшие вычисления производят согласно табл. 1.
В большинстве случаев можно также использовать приближенные формулы.
1 Формула Тейлора
где:
- с = 2,52 для круглых обводов;
- с = 2,75 — для эллиптической формы погруженной части;
- с = 3,00 для U-образных обводов.
2 Формула Мумфорда при δ ≈ 0,7; В/Т = 2÷3:
3 Формула Бенге:
4 Формула Мурагина при δ = 0,4÷0,5; В/Т = 2,5÷3,5:
5 Формула для транцевых судов (А = 0,85) и судов с острой кормой (А = 0,75÷0,78):
Примеры.
1 Вычислить смоченную поверхность моторного бота с L = 6,00 м, В = 1,8 м, Т = 0,5 м. Выбираем формулу (Формула 21) с коэффициентом А = 0,85 для транцевых судов:
Ω = 6,0(0,85·1,8+0,25·0,5) ≈ 9,9 м².
2 Вычислить смоченную поверхность катера с L = 9,2 м; V = 4,6 м² и U-образными обводами. Применяем формулу Тейлора с коэффициентом с = 3,0:
Сопротивление трения
Сцепление отдельных частиц вязкой жидкости между собой и обшивкой судна приводит к возникновению сил, проекция которых на направление движения называется сопротивлением трения Rт.
Применяемая схема расчета основана на следующих допущениях:
сопротивление трения гладкого корпуса Rт равно сопротивлению трения эквивалентной пластины
- обшивка судна считается гидродинамически гладкой, а влияние ее шероховатости учитывается путем надбавки на шероховатость.
При обтекании тела на начальном участке пограничного слоя устанавливается ламинарный режим, который затем теряет устойчивость и переходит в турбулентный. С увеличением скорости протяженность ламинарного участка уменьшается и при больших числах Re становится пренебрежимо малой. Для практических целей можно считать, что начиная с величины числа Re = 1·107 пограничный Окраска корпуса суднаслой на корпусе судна турбулентный. Для подавляющего большинства малотоннажных судов с механическим двигателем это соответствует практически всем режимам эксплуатации.
| Таблица 1. Определение смоченной поверхности корпуса судна | ||||||
|---|---|---|---|---|---|---|
| № шп. | Замер курвиметра Пn/2 | Масштаб чертежа | Смоченные полупериметры шпангоутов Pi/2, м | Сумма смоченных полупериметров двух соседних шпангоутов Pi/2+Pi+1/2, м | Шпация ΔLi, м | Смоченная поверхность одной шпации |
| 0 | ||||||
| 1 | ||||||
| 2 | ||||||
| 3 | ||||||
| … 10 | ||||||
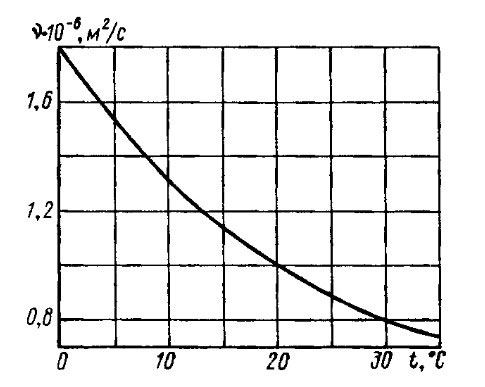
Для определения числа Рейнольдса необходимо знать смоченную длину судна и скорость движения. Затем, задавшись значением температуры t° воды (пусть даже ориентировочно), определить по графику (рис. 5) величину коэффициента кинематической вязкости v, м²/с, и вычислить Re по формуле (Формула 8). При этом необходимо следить за соблюдением размерности.
Примеры.
1 Судно имеет смоченною длину 6 м и скорость v = 2 м/с; температура воды 13 °C По рис. 5 v = 1,2·10-6 м²/с. Тогда:
2 Катер имеет длину по ватерлинии L = 9,2 м, v = 6,9 м/с, температура воды 4 °C; v = 1,6·10-6 м²/с. Тогда:
Величина сопротивления трения эквивалентной пластины определяется формулой:
где:
где:
- ζт0 — коэффициент трения гидродинамически гладкой поверхности;
- △ζт — надбавка на шероховатость.
Функции зависимости коэффициента ζт0 от числа Рейнольдса называют экстраполяторами турбулентного трения. Наиболее употребительной в отечественной практике является формула Прандтля—Шлихтинга:
В графической форме указанная зависимость представлена на рис. 6.
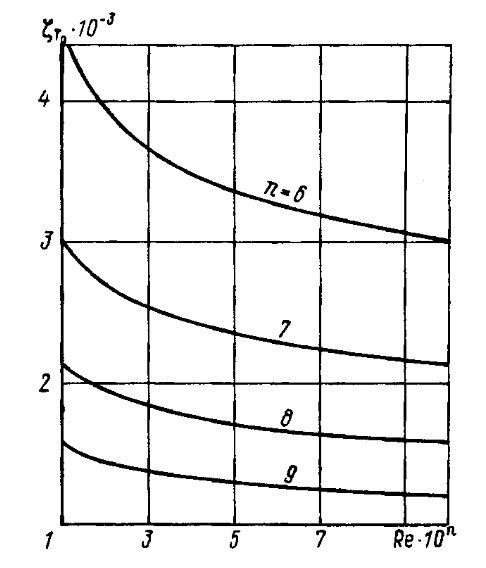
Влияние продольной и поперечной кривизны поверхности судна на сопротивление трения сравнительно невелико.
Предлагается к прочтению: Конструктивные и архитектурные типы морских деревянных судов
Суда с отношением L/В=5 имеют Rт на 8 %, а с L/В=10 — на 2 % больше, чем эквивалентная пластина. Обычно эта разница учитывается при расчете других составляющих сопротивления. Весьма существенным фактором оказывается отличие степени шероховатости корпуса судна от гидродинамически гладкой пластины. На практике дополнительное сопротивление, вызванное шероховатостью поверхности судна, учитывают надбавкой △ζт к величине ζт0 для эквивалентной гладкой пластины. Основная часть надбавки △ζт обусловлена влиянием шероховатости наружной обшивки (40—60 %), а также наличием вырезов и ниш (20—30 %). Эксперименты показывают, что величина △ζт может быть принята постоянной при всех числах Re для данного судна. Численные значения △ζт зависят от конструктивных и технологических особенностей корпуса, состояния наружной обшивки.
Значения надбавки на шероховатость △ζт:
- для судов со сварной обшивкой — (0,3÷0,5)·10-3;
- для судов с клепаной обшивкой либо со сварной обшивкой при наличии ниш и вырезов — (0,7÷1,0)·10-3;
- для судов с деревянной обшивкой — (1,8÷2,3)·10-3;
- для железобетонных судов — (1,3÷1,9)·103;
- для судов с пластмассовым корпусом, полученным методом формования в матрице – (0,1÷0,3)·10-3.
Для судов с меньшими размерами рекомендуется принимать бóльшие значения △ζт.
Для некоторых типов малотоннажных судов, которые в процессе эксплуатации подвергаются обрастанию, надбавка на шероховатость должна приниматься по верхнему значению △ζт.
Примеры.
1 Моторный бот имеет L = 6 м, В = 1,8 м, Т = 0,5 м, деревянную обшивку, v = 2 м/с; Re =1·107, Ω = 9,9 м², ρ = 1 000кг/м³.
По графику на рис. 6
. Надбавка на шероховатость с учетом обрастания △ζт = 2,3-10-3. Тогда:
2 Разъездной катер имеет L=9,2 м, стальную сварную обшивку с противообрастающим покрытием; Re=4,0·107, Ω=19,5 м², ρ = 1 000
кг/м³.
По графику на рис. 6 ζТ0 = 2,4·10-3. Надбавку на шероховатость принимаем △ζт = 0,4·10-3. Тогда
Основные пути снижения сопротивления трения приведены ниже.
При проектировании судна:
- все имеющиеся в корпусе вырезы должны быть закрыты решетками или крышками;
- отдельные выступы на обшивке должны быть размещены как можно дальше от носа судна или в гидродинамической тени от других выступов.
При постройке судна:
- нельзя допускать волнистости наружной обшивки, грубых сварных швов;
- головки болтов и заклепок выполнять по возможности впотай;
- следует тщательно удалять ржавчину и окалину перед окраской корпуса;
- следует применять краску с высокими антикоррозионными свойствами, препятствующую обрастанию.
В процессе эксплуатации необходимо периодически очищать подводную часть судна от водорослей и ракушек. Все эти мероприятия дают возможность снизить сопротивление трения судна на 10-20 %.
Сопротивление формы
Сопротивление формы возникает вследствие влияния вязкости на распределение давлений по поверхности тела. Приближенно можно считать, что волнообразование не влияет на вязкостное сопротивление, в том числе и на сопротивление формы. Поэтому для расчета используют общую формулу:
где:
- ζф — коэффициент сопротивления формы, который для данного тела является функцией числа Re.
При экспериментальном измерении полного сопротивления модели пользуются способом разделения его на
эквивалентной пластины и остаточное Ro. Сопротивление формы входит в остаточное вместе с волновым сопротивлением Rв и той частью сопротивления, трения, которая обусловлена разницей между Rт криволинейного корпуса судна и эквивалентной пластины. Разность между Rт и
для судов традиционных обводов невелика. Поэтому для скоростей, на которых Как устроено судно на воздушной подушкесудно не вызывает волнообразования, Ro ≈ Rф.
Результаты теоретических и экспериментальных исследований позволяют считать, что при увеличении скорости хорошо обтекаемых тел сопротивление формы возрастает по тому же закону, что и сопротивление эквивалентной пластины. Это означает, что сопротивление формы для этих тел можно рассчитать по формуле:
где:
- коэффициент kф не зависит от числа Рейнольдса и является постоянным для данной формы корпуса.
Все тела можно разделить на хорошообтекаемые и плохообтекаемые. К хорошообтекаемым можно отнести водоизмещающие суда, имеющие отношение L/В > 6. Суда с отношением L/В < 6, к которым относятся буксиры, баржи, суда других назначений, обтекаются менее благоприятно и обычно предназначены для движения с небольшими значениями числа Фруда. В практике малотоннажного судостроения формы корпуса с L/В < 6 встречаются наиболее часто. Из этого следует, что отработке обводов малого судна должно быть уделено особенно серьезное внимание.
Для снижения Rф водоизмещающего судна наряду с определением рациональных значений L/В и
необходимо правильно выбрать величину кормового заострения Lк, отсчитываемого от кормового конца цилиндрической вставки. Наиболее благоприятное обтекание обеспечивается при
(ωмид — площадь погруженной части миделевого сечения).
Следует отметить некоторые особенности сопротивления формы глиссирующих судов. При движении в водоизмещающем режиме остроскулый корпус обтекается потоком с отрывом у скул и на транце. Сопротивление формы в этом случае очень велико. Оно гораздо больше, чем у судна тех же размеров, но рассчитанного на водоизмещающий режим движения. Именно по этой причине эксплуатация глиссирующего судна в водоизмещающем режиме нецелесообразна.
При движении глиссирующего судна с относительной скоростью FrV > 3 составляющая сопротивления формы отсутствует. В этом случае остаточное сопротивление судна полностью состоит из волновой составляющей.
Для расчета сопротивления формы необходимо знать величину ζф, которую определяют путем испытаний моделей в опытовом бассейне. Возможно также использование ζф, взятого по близкому прототипу или вычисленного по приближенной формуле. При этом следует помнить, что незначительные отклонения Принципы проектирования конструкций корпуса суднаформы корпуса, шероховатости обшивки, конфигурации выступающих частей могут вызвать существенное изменение величины ζф.
Коэффициент сопротивления формы приближенно определяют:
по формуле Палмеля
из уравнения (Формула 26)
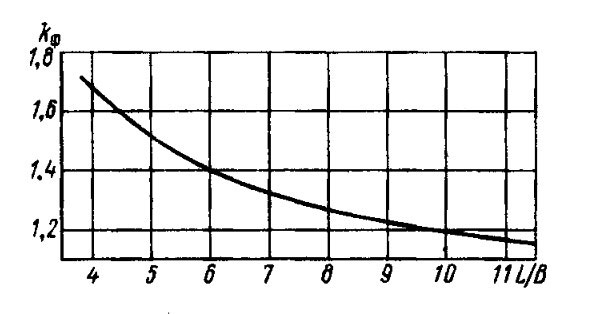
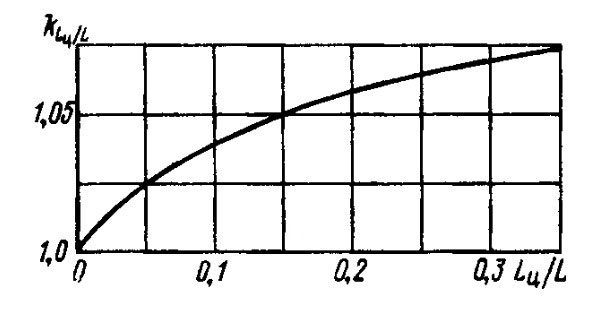
коэффициент kф при числах Фруда FrL ≤ 0,15 находят по графику (рис. 7) в зависимости от L/B судна;
наиболее точно влияние главных размерений и особенностей формы корпуса учитывает определенная методика. По ней определяется вязкостное сопротивление судна, т. е. Rт+Rф:
где:
- η — множитель коэффициента вязкостного сопротивления;
ηо — составляющая множителя, зависящая от относительного удлинения судна
и коэффициента продольной полноты φ;
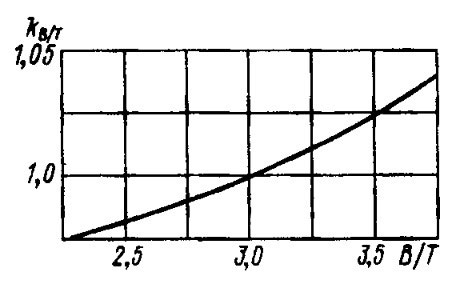
- kB/T — коэффициент, учитывающий влияние отношения В/Т; kLц/L – коэффициент, учитывающий влияние относительной протяженности цилиндрической вставки.
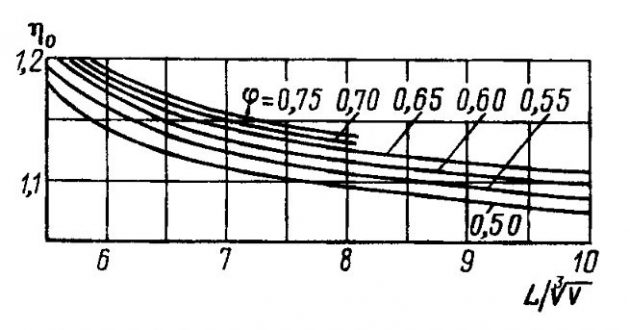
На рис. 8 приведены значения η0, построенные для судов без цилиндрической вставки (Lц/L=0) с отношением В/Т = 3; рис. 9, 10 дают значения поправочных коэффициентов kB/T и kLц/L.
Примеры.
1 Моторный бот имеет L = 6 м, В = 1,8 м, Т = 0,5 м, v = 2 м/с, ωмид = 0,72 м², Ω = 9,9 м², Lк = 2 м.
Используя формулу 27, получим:
По общей формуле 25 получим:
2 Катер без цилиндрической вставки имеет L = 9,2 м, В = 2,2 м, T = 0,6 м, v = 6,9 м/с, V = 4,6 м³, ωмид = 1,06 м². Вычисляем:
- δ = V/(LBT) = 0,38;
- β = ωмид/(ВТ) = 0,80;
- φ = δ/β = 0,48;
- В/Т = 3,67;
.
По формуле 31 и графикам (рис. 8-10) находим:
- ηо = 1,17;
- kB/T = 1,03;
- kLц/L = 1,0;
- η = 1,17·1,03·1,0 ≈ 1,21.
По формуле 29
Основные способы снижения сопротивления формы в процессе проектирования судна:
- увеличение отношения L/В;
- уменьшение углов притыкания батоксов или ватерлиний в корме (желательно, чтобы эти углы не превышали значений 18—20°);
- размещение сломов обшивки, скуловых килей и прочего вдоль линий тока жидкости.
Волновое сопротивление
Волновое сопротивление является частью сопротивления давления, которая возникает вследствие волнообразования при движении судна. При отсутствии волнообразования волновое сопротивление равно нулю. Это наблюдается у надводных судов при движении с малыми скоростями и у подводных лодок, движущихся глубоко под водой.
Для расчета волнового сопротивления пользуются общей формулой
где:
- ζв — коэффициент волнового сопротивления, который является функцией числа Фруда.
У геометрически подобных судов 1 и 2 при равных числах Фруда коэффициенты волнового сопротивления равны.
Следствием этого является соотношение:
Характер изменения волнового сопротивления в зависимости от Портативные лодки малого типаскорости судна тесно связан с картиной волнообразования. Основными волнообразующими участками являются нос и корма судна, вызывающие при движении появление резко выраженных пиков гидродинамического давления. В носовой и кормовой группах волн можно выделить расходящиеся и поперечные волны. Изменение скорости движения судна незначительно сказывается на структуре расходящихся волн, так как между носовой и кормовой группами этих волн практически не происходит взаимодействия.
В противоположность этому характер интерференции поперечных волн носовой и кормовой групп существенно зависит от скорости судна. Результатом этого является наличие местных горбов и впадин на кривой волнового сопротивления по скорости. Характер зависимости коэффициента волнового сопротивления от числа Фруда показан на рис. 11. У водоизмещающих судов ζв имеет максимумы при значениях FrL ≈ 0,22; 0,25; 0,30; 0,50.
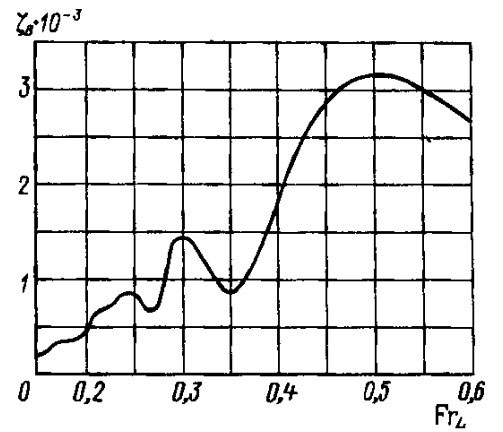
У судов с острыми обводами корпуса местные горбы и впадины на кривой сопротивления сглажены, заметно выделяется лишь один максимум при FrL = 0,50. При малых значениях числа Фруда волновое сопротивление очень невелико. Его практически можно считать равным нулю для полных тихоходных судов при FrL ≤ 0,10÷0,15, а для быстроходных — при FrL ≤ 0,15÷0,20.

Абсолютные значения коэффициента ζв в большей степени зависят от Конструктивные типы транспортных судов и особенности проектирования их конструкцийформы обводов судна, поэтому для практических целей его определение производят экспериментально. Приближенно величину Rв можно вычислить по формулам Папмеля. Для этого определяют скорости:
где:
- L* = xL.
Коэффициент х находят в зависимости от характеристики судна:
| к | 0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 |
| x | 1,100 | 1,100 | 1,095 | 1,090 | 1,063 | 1,000 | 0,920 | 0,840 |
| к | 0,8 | 0,9 | 1,0 | 1,1 | 1,2 | 1,3 | 1,4 | 1,5 |
| x | 0,790 | 0,750 | 0,730 | 0,715 | 0,710 | 0,700 | 0,700 | 0,700 |
Если скорость судна меньше v1, то Rв = 0; если v1 < v < v2, то:
где:
- Св — коэффициент, определяемый в зависимости от числа FrL (рис. 12).
Если скорость судна больше v2, то:
Изложенный способ применим только для судов, движущихся в водоизмещающем режиме или в самом начале переходного режима движения. Расчеты волнового сопротивления быстроходных катеров на таких скоростях не производят, а в случае необходимости определяют экспериментально. Существуют и широко используются также различные методики, в которых определяется сразу сумма составляющих сопротивления: Rф, Rв и
(остаточное сопротивление Rо).
Читайте также: Транспортные суда ледового плавания
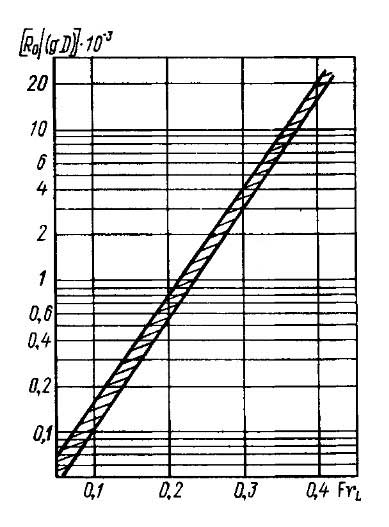
Обычно такие материалы обобщают результаты систематических испытаний серии моделей. Одним из примеров может служить диаграмма Неймана для буксиров и траулеров (рис. 13). Этот график позволяет приближенно определить значение остаточного сопротивления для судов с соотношениями:
Примеры.
1 Моторный бот имеет L = 6 м, В = 1,8 м, Т = 0,50 м, v = 2 м/с, δ = 0,50.
Используя способ Палмеля, получаем:
Находим х = 0,7.
Вычисляем:
Для v1 < v < v2 по рис. 12 находим Св = 2. Тогда:
2 Катер имеет L = 9,2 м, В = 2,2 м, T = 0,6 м, v = 6,9 м/с, V = 4,6 м3, δ = 0,42 при:
Находим х = 0,73, v1 = 1,6 м/с, v2 = 4,15 м/с, v > v2. Определяем:
При выборе главных размерений и формы корпуса судна следует учитывать следующие особенности волнового сопротивления:
- существует ряд значений относительной скорости FrL, благоприятных в отношении волнообразования;
- величина волнового сопротивления уменьшается при увеличении L/B
,
и при уменьшении В/Т, δ;
- положение наибольшей ширины судна по длине, относительная величина цилиндрической вставки, форма и углы притыкания носовых ветвей ватерлиний должны соответствовать относительной скорости FrL.
Сопротивление выступающих частей
К выступающим частям относят Балластные кили парусного суднаскуловые кили, рули, кронштейны гребных валов, гребные валы и т. д. Сопротивление движителей учитывается в расчете их характеристик и в состав сопротивления выступающих частей не входит.
Сопротивление выступающих частей состоит в основном из вязкостных составляющих — сопротивления трения и формы; обтекание корпуса влияет на характер обтекания выступающих частей. В свою очередь, наличие выступающих частей может существенно изменить сопротивление самого корпуса судна.
Сопротивление выступающих частей можно определять либо экспериментально, либо расчетным путем. При испытании моделей судов в опытовом бассейне обычно сопоставляют модель судна с выступающими частями и без них (голый корпус). Коэффициент сопротивления выступающих частей:
При этом ζв.ч по сути представляет собой условную надбавку к величине сопротивления голого корпуса Rг.к. В зависимости от числа и расположения выступающих частей обычно ζв.ч = (0,25÷0,3)·10-3. Для судов с сильно развитыми выступающими частями ζв.ч = (0,4÷0,5)·10-3. Для быстроходных катеров сопротивление выступающих частей можно учитывать как надбавку к сопротивлению голого корпуса, определяемую по экспериментальным данным: Rв.ч=kв.чRг.к.
Величины коэффициента для учета сопротивления выступающих частей kв.ч приведены в табл. 2.
| Таблица 2. Надбавка на сопротивление выступающих частей kв.ч | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Число гребных валов | Круглоскулые суда при FrL | Остроскулые суда при FrV | |||||||
| до 0,5 | 0,5-1,0 | 1,0 | 1,5 | 2,0 | 2,5 | 3,0 | 3,5 | 4,0 | |
| 1 | 0,03-0,05 | 0,06-0,08 | 0,02 | 0,03 | 0,04 | 0,07 | 0,11 | 0,15 | 0,19 |
| 2 | 0,08-1,0 | 0,10-0,12 | – | – | – | – | – | – | – |
| 3 | 0,12-0,15 | 0,15-0,20 | 0,02 | 0,06 | 0,08 | 0,10 | 0,12 | 0,18 | 0,20 |
Наряду с указанными способами учета Rв.ч применяют расчетный метод определения величины сопротивления выступающих частей. Этот метод сводится к вычислению сопротивления каждой из таких частей и отдельности на основании экспериментальных данных для геометрических тел соответствующей формы и последующему суммированию результатов.
Для определения Rв.ч, Н, судов с угловыми колонками или подвесными моторами рекомендуются данные, полученные экспериментально:
Коэффициенты rв.ч = ζв.ч·Sмнд принимаются для подвесных моторов (при заглублении антикавитационной плиты на 20 мм ниже среза транца):
- “Ветерок” — 14·10-4;
- “Москва-25” и “Москва-30” – 20·10-4;
- “Нептун” – 21·10-4;
- “Нептун-23” – 20,5·10-4;
- “Привет-22” – 17,5·10-4;
- “Вихрь-М” – 22,5·10-4.
Для угловой колонки катера “Амур-2” Rв.ч = 0,93v2, Н.
Необходимо помнить, что значения упора винтов подвесных моторов по скорости, приводимые в справочных изданиях, учитывают также и влияние сопротивления их подводной части. Поэтому при использовании этих данных сопротивление выступающих частей моторов добавлять к сопротивлению корпуса судна не нужно.
Примеры.
1 Моторный бот имеет L = 6 м, v = 2 м/с, Ω = 9,9 м² . Принимаем ζв.ч = 0,25·10-3, тогда:
2 Разъездной катер с L=9,2 м, v=6,9 м/с, Ω= 19,5 м² имеет открытый наклонный гребной вал с кронштейном и подвесной руль за винтом, FrL = 0,73. Для этого случая принимаем по табл. 2 kв.ч = 0,07. Тогда:
Rв.ч = kв.ч(Rт+Rф+Rв) = 0,07·(1 573 + 2 712) ≈ 300 H (∼ 30 кгс)
3 Глиссирующая лодка с подвесным мотором “Вихрь-М” имеет v = 9,4 м/с. Получаем:
Для снижения Rв.ч рекомендуется:
- уменьшение числа выступающих частей путем объединения конструктивно совместимых элементов;
- придание выступающим частям хорошообтекаемой формы;
- расположение выступающих частей по направлениям линий тока и в тех местах судна, где они не вызывают возрастания сопротивления голого корпуса и сами имеют минимальное сопротивление;
- установка однолапого кронштейна вместо двухлапого;
- крепление двухлапых кронштейнов таким образом, чтобы оси следа их притыкания к корпусу были параллельны;
- Центровка и монтаж валопроводаустановка гребного вала с наклоном не более 10-12°.
Воздушное сопротивление
Сопротивление надводной части судна имеет вязкостный характер, т. е. само состоит из сопротивлений трения и формы. Надводная часть многих судов является плохообтекаемым телом, поэтому основную роль в ее воздушном сопротивлении играет сопротивление формы.
Величина воздушного сопротивления вычисляется по формуле:
где:
- СА — безразмерный коэффициент воздушного сопротивления;
- ρв — плотность воздуха, кг/м³;
- vв — скорость воздуха, обтекающего судно, м/с;
- Sмид — проекция надводной части судна на плоскость мидель-шпангоута, м².
Вычисление vв производится с учетом скорости истинного ветра vи. При этом следует принимать наиболее неблагоприятный встречный ветер: vв = v + vи.
Значения коэффициента СА определяют экспериментальным путём. Его величина для судов с малыми L/В и плохообтекаемыми надстройками может доходить до >СА = 1. Обычно СА = 0,6÷0,9; для судов, при проектировании которых приняты меры по снижению аэродинамического сопротивления, СА = 0,4+0,6. Следует отметить, что создание хорошообтекаемых надстроек часто нерационально из-за удорожания постройки и ухудшения эксплуатационных условий на судне, однако устранение угловатых форм, особенно углов передних стенок, размещение надстроек и рубок с учетом их взаимного экранирования полезны.
Примеры.
1 Моторный бот имеет L = 6 м, v = 2 м/с, В = 1,8 м, Sмид = 1,5 м², ρ = 1,293 кг/м³. Учитывая отсутствие надстроек, принимаем СА = 0,6. Считаем vи ≈ 5 м/с, следовательно:
2 Катер имеет L = 9,2 м, В = 2,2 м, v = 6,9 м/с, Sмид = 5,5 м² и хорошо обтекаемые надстройки vи = 8 м/с.
Принимаем СА = 0,5, тогда:
Основываясь на выполненных расчетах, получим значения полного сопротивления для рассматриваемых судов.
Примеры.
1 Моторный бот имеет L = 6 м, В = 1,8 м, Т = 0,5 м, δ = 0,5, Ω = 9,9 м², v = 2 м/с.
2 Катер имеет L = 9,2 м, В = 2,2 м, T = 0,6 м, δ = 0,42, V = 4,6 м³, Ω = 19,5 м², ωмид = 1,06 м², v = 6,9 м/с.
Отсюда:
Сопротивление водоизмещающих судов
Для правильного выбора формы корпуса необходимо учитывать весомость каждой из составляющих полного сопротивления воды движению судна. У разных типов водоизмещающих судов соотношение этих составляющих различно. Оно зависит прежде всего от относительной скорости и главных элементов судна.
На рис. 14 представлены кривые, хорошо отражающие качественную сторону этого явления. Здесь составляющие сопротивления трения и остаточного сопротивления выражены в долях от полного.
Кривая 1 характерна для пассажирских судов
и водоизмещающих катеров (FrL > 0,5);
кривая 2 — для грузовых судов
;
кривая 3 — для буксирных, ледокольных, рыбопромысловых судов
.
Изменение сопротивления при движении на волнении
.
При движении судна на волнении скорость снижается вследствие увеличения сопротивления воды, нарушения режима работы движителей и увеличения рыскливости судна. Наибольшее влияние оказывает изменение сопротивления воды движению судна.
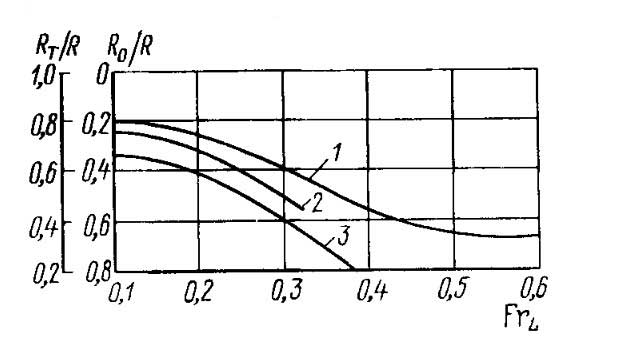
1 – пассажирские суда и водоизмещающие катера; 2 – транспортные суда; 3 – буксирные, ледокольные, промысловые суда
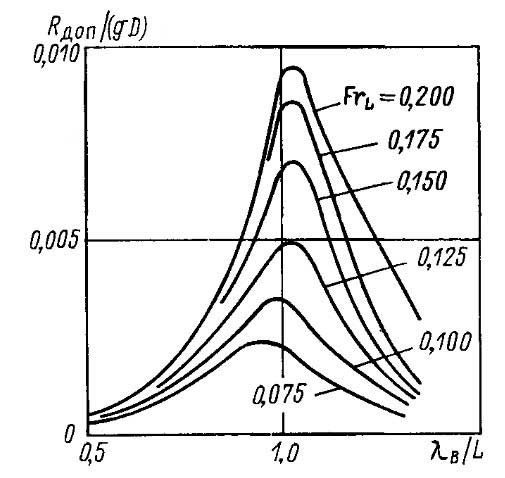
Результаты исследований позволяют установить несколько общих свойств дополнительного сопротивления Rдоп. На встречном волнении при постоянных значениях числа Фруда и относительной высоты волны hв/λв наблюдается зависимость дополнительного сопротивления от отношения длины волны к длине судна λв/L. Максимум Rдоп соответствует значениям λв/L, близким к единице (рис. 15). При движении судна на попутном волнении значение имеет отношение Главная энергетическая установка буксирного суднаскорости судна к скорости распространения волн св. При v/св < 1 сопротивление судна близко к своему значению на тихой воде. При v/св, близких к единице, когда судно оказывается неподвижным относительно системы волн, оно “захватывается” волной и устойчиво движется во впадине между гребнями.
В этом случае сопротивление существенно уменьшается. При дальнейшем увеличении скорости движения судна сопротивление резко возрастает (рис. 16). Помимо указанных соотношений на величину Rдоп серьезное влияние оказывают элементы теоретического чертежа и форма обводов судна. Опыт показывает, что увеличение коэффициента общей полноты δ свыше 0,7 приводит к возрастанию сопротивления на волнении. Неблагоприятно также сказывается чрезмерная величина В/Т. При разработке проекта можно рекомендовать выполнение шпангоутов в носовой части с достаточным развалом, а ватерлиний – острыми по всей высоте форштевня. Это достигается применением наклонного форштевня с плавным подрезом. Целесообразно также предусмотреть достаточный запас мощности.
Вместе с тем следует помнить, что “ограничителем” скорости на волнении зачастую является не повышенное сопротивление движению, а неблагоприятные перегрузки, действующие на экипаж при ударах и качке, а также прочность корпуса судна.
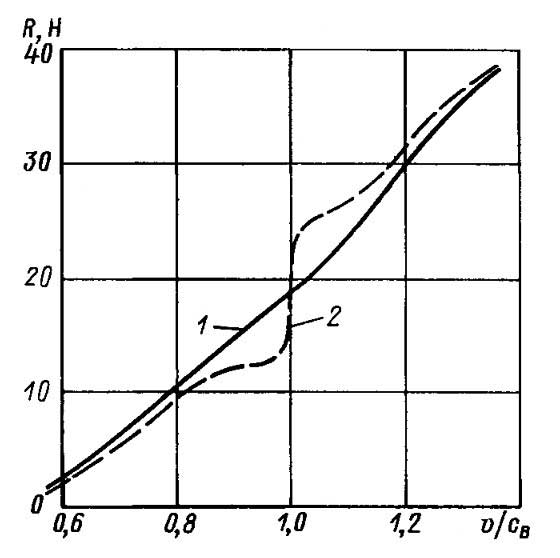
1 – тихая вода; 2 – волнение (А/L=1)
Влияние основных характеристик корпуса на сопротивление
На величину сопротивления воды движению судна влияет очень большое число параметров, характеризующих форму его корпуса. Можно однако, выделить наиболее характерные зависимости ходкости и соотношений теоретического чертежа судна. Удлинение судна и относительное удлинение. Увеличение относительного удлинения
приводит к уменьшению составляющей остаточного сопротивления. При этом с увеличением относительной скорости — числа Фруда — это явление становится более выраженным. Одновременно с уменьшением Rо происходит возрастание составляющей трения Rт. При этом для каждого значения Fr существует величина
, при которой полное сопротивление судна будет минимальным. Рекомендуемые значения
приведены на рис. 17.
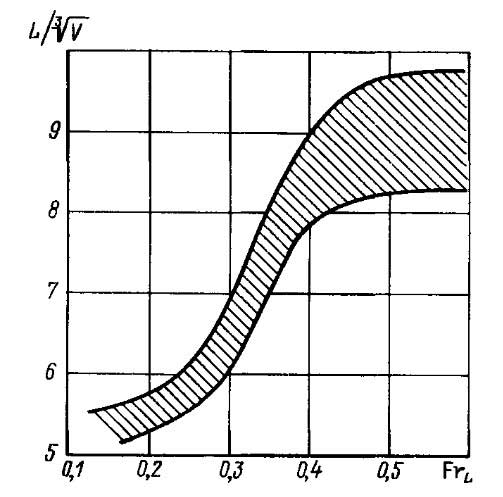
Для однокорпусных судов эти оптимальные с точки зрения обеспечения ходкости значения
часто оказываются неприемлемыми по соображениям остойчивости, общего расположения и т. п. Однако для многокорпусных судов целесообразно ориентироваться на рекомендуемые значения. Удлинение судна L/В менее точно характеризует остроту обводов судна, но с качественной стороны влияет на величину основных составляющих сопротивления так же, как и относительное удлинение
.
Отношение ширины к осадке судна В/Т
Существует общая тенденция возрастания волновой составляющей сопротивления судна с увеличением В/Т при постоянных значениях T.
Смоченная поверхность, а следовательно, и составляющая трения, при этом также возрастает. Однако в пределах значений В/Т, характерных для каждого типа судна, полное сопротивление воды R и его основные составляющие изменяются мало. Поэтому при разработке проекта величину В/Т выбирают из условий обеспечения остойчивости судна и ограничений по осадке.
Коэффициенты полноты судна
Коэффициенты полноты, форма корпуса и мореходные качества буксировУвеличение коэффициента общей полноты δ незначительно влияет на сопротивление трения Rт, но приводит к возрастанию остаточного сопротивления Ro. Это особенно сказывается при FrL > 0,3. Поэтому для судов, рассчитанных на скорости FrL > 0,3, желательно уменьшение δ до значений, при которых увеличение массы корпуса еще не очень существенно. Ориентиром могут служить значения δ, рекомендованные Эйром:
| FrL | 0,300 | 0,325 | 0,350 | 0,375 | 0,400 | 0,500 | 0,600 |
| δ | 0,575 | 0,560 | 0,545 | 0,538 | 0,533 | 0,516 | 0,500 |
Изменение коэффициента продольной полноты φ оказывает существенное влияние на величину волнового сопротивления Rв. Выбор рационального значения φ особенно важен для быстроходных судов, у которых волновая составляющая сопротивления относительно велика. При FrL > 0,45 рекомендуется принимать величины в пределах 0,6-0,65, причем большие значения относятся к более высоким числам Фруда.
Изменение коэффициента полноты мидель-шпангоута β в широких пределах не оказывают значительного влияния ни на волновое сопротивление, ни на сопротивление формы. Величину β можно принимать равной 0,75—0,85 для FrL > 0,45.
Форма корпуса судна
Характер обтекания судовой поверхности потоком жидкости, определяющий величину остаточного сопротивления Ro, зависит от формы корпуса. Для носовой оконечнсти важна форма ватерлиний. В основном она определяется величиной угла носового заострения αн, который составляет ветвь ватерлинии с ДП. Для судов с относительной скоростью FrL > 0,32 рекомендуется принимать прямые ветви ватерлиний с углами αн = 10÷14°. В целях обеспечения малых значений αн рационально некоторое смещение максимального поперечного сечения судна в корму от миделя.
Качество кормовых обводов в значительной мере определяется тем, насколько обеспечиваются безотрывное обтекание и равномерность поля скоростей в районе расположения движителей. С этой точки зрения стремятся к уменьшению углов притыкания ватерлиний в корме αк до величин меньше 20°. Для судов с относительными скоростями FrL > 0,4 целесообразно применение транцевой кормы. Такое решение позволяет получить наиболее пологие ветви батоксов. При этом допустимо увеличить до 35—45°.
Формование судового рангоута из стеклопластикаФорма шпангоутов судна в ряду параметров, определяющих сопротивление воды, имеет второстепенное значение. Гораздо более существенное влияние она оказывает на работу движителей и мореходность судна.
Способы снижения сопротивления движению судна
Все способы снижения сопротивления движению судна разделяются на способы снижения вязкостного сопротивления и способы снижения волнового сопротивления.
Снижение вязкостного сопротивления возможно путем управления пограничным слоем тела. К этим способам относятся:
- применение ламинаризованных тел;
- отсасывание жидкости из пограничного слоя;
- применение демпфирующих покрытий;
- использование слабых растворов полимеров;
- применение воздушных пленок.
В настоящее время большинство указанных методов снижения вязкостного сопротивления разработано только на лабораторном уровне. Это не позволяет дать конкретных рекомендаций по их применению на натурном судне.
Наиболее реальным способом следует считать применение воздушных пленок, создаваемых при помощи подачи воздуха под днище. Результаты модельных и натурных испытаний показывают, что это позволяет снизить сопротивление движению речного транспортного судна на 12—20 % при затратах мощности на подачу воздуха, не превышающих 1—1,5 % мощности энергетической установки. Однако для малотоннажных судов трудно рассчитывать на серьезный эффект от применения воздушной смазки. Прежде всего это связано с тем, что корпус малого судна либо вовсе не имеет плоского участка днища, либо этот участок относительно мал, и создание воздушной прослойки под ним весьма сложно.
Вторым и наиболее важным обстоятельством является то, что режимы движения малых судов, как правило, характеризуются высокими значениями относительной скорости Fr. Это определяет превалирование волновой составляющей в общей величине сопротивления. Отсюда и снижение полного сопротивления в результате применения указанных мер будет существенно меньше (вероятнее всего, единицы процентов).
Вместе с тем практическое применение способов снижения вязкостного сопротивления неизбежно вызывает усложнение конструкции судна и удорожание его эксплуатации. Поэтому целесообразно использовать для уменьшения вязкостной составляющей сопротивления малотоннажного судна те возможности, которые дает грамотный выбор формы корпуса и расположения его выступающих частей.
Снижение волнового сопротивления достигается следующими основными способами:
- переходом к движению судов со скоростями, при которых волновое сопротивление снижается (малые и большие числа Фруда);
- использованием благоприятной зоны скоростей (FrL < 0,35) со впадинами на кривой волнового сопротивления;
- приданием корпусу обводов и соотношений главных размерений, соответствующих минимуму волнового сопротивления;
- применением устройств для гашения волновых систем;
- созданием судов с уменьшенной площадью ватерлинии;
- созданием многокорпусных судов;
- переходом от водоизмещающего режима к динамическим принципам поддержания.
Первые три способа относятся к методам оптимизации формы судов традиционных форм. Последние четыре способа являются новыми направлениями в развитии судостроения.
Под устройствами для гашения волновых систем подразумеваются:
- носовые наделки;
- носовые крылья;
- бортовые були.
При рациональном выборе формы, размеров и расположения бульба можно получить благоприятное взаимодействие волновых систем корпуса и бульба, приводящее к уменьшению волновой составляющей сопротивления.
Однако нужно иметь в виду, что при изменении посадки судна эффект от применения бульба снижается и даже может быть отрицательным. Этот эффект уменьшается также при пониженных эксплуатационных скоростях. Поэтому в каждом отдельном случае решение о применении указанных форм обводов должно приниматься на основе анализа всех составляющих сопротивления, весовых и прочностных характеристик судна.
Суда с малой площадью ватерлинии (СМПВ) привлекают все большее внимание судостроителей. В настоящее время в мире эксплуатируется уже ряд судов подобного типа.
Уменьшение волнового сопротивления достигается за счет того, что подводная часть судна состоит из двух торпедообразных корпусов, заглубленных под поверхность воды и вертикальных стоек, соединяющих их с подводным корпусом. Стойки, пересекающие поверхность воды, имеют минимальное сечение, определяемое соображениями продольной и поперечной остойчивости. Это и определяет эффект снижения волновой составляющей сопротивления. При этом нельзя забывать, что вязкостные составляющие полного сопротивления такого судна возрастают.
Необходимо учитывать также и то, что главные элементы и характеристики СМПВ существенно отличаются от таковых у традиционных судов. Например, при сравнении с обычным судном одинакового водоизмещения у СМПВ осадка будет больше на 70-100 %, масса корпуса — на 60—150 %; СМПВ будет иметь также пониженную продольную и поперечную остойчивость. При всем этом преимущества СМПВ по ходкости проявятся только при числах Фруда FrL > 0,5.
Значительного эффекта от применения указанного принципа можно достичь в том случае, если стоит задача создания судна с большой площадью палубы, большой вместимостью или особо высокой мореходностью. Однако, учитывая сложность и непроработанность ряда вопросов проектирования таких судов, можно рекомендовать создание СМПВ только после тщательного общепроектного анализа, детальной гидродинамической и конструктивной проработки.
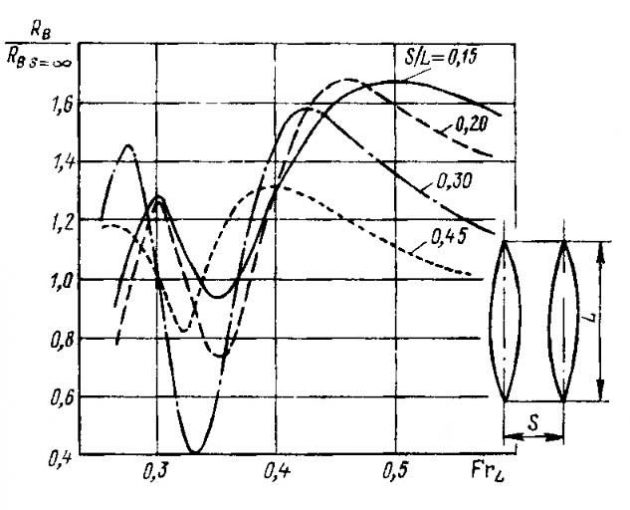
Многокорпусные суда уже завоевали широкую популярность. Основное достоинство гидродинамики такого судна состоит в возможности придания каждому из корпусов большого (до 12—15) удлинения, что ограничено у обычных однокорпусных судов требованиями остойчивости. Кроме того, результаты исследований показывают, что при некоторых числах Фруда и значениях отстояния корпусов у катамарана возможны благоприятная интерференция волновых систем и выигрыш в волновом сопротивлении. При больших числах Фруда взаимное влияние корпусов катамаранов неблагоприятно сказывается на сопротивлении воды движению. На рис. 18 показаны схема двухкорпусного судна и кривые зависимости его волнового сопротивления от относительного отстояния корпусов. Перспективными можно считать трехкорпусные суда, у которых средний Формование малотоннажного суднакорпус выдвинут вперед относительно двух других.
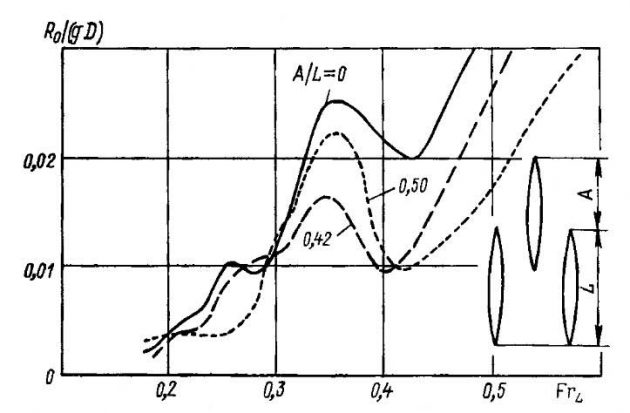
Испытания моделей показывают, что величина выдвига существенно влияет на сопротивление. Это позволяет при помощи правильного выбора взаимного расположения корпусов тримарана обеспечить на расчетной скорости или в выбранном диапазоне скоростей минимальное сопротивление. На рис. 19 показаны схема трехкорпусного судна и кривые его остаточного сопротивления
в зависимости от относительного выдвига среднего корпуса.
Суда с динамическим поддержанием — это быстроразвивающиеся группы судов, к которым относятся глиссеры, суда на подводных крыльях, суда на воздушной подушке, суда-экранопланы и их возможные модификации. Разделы теории и проектирования каждого из этих типов судов весьма специфичны. Общей характерной чертой является то, что они могут двигаться при высоких значениях относительной скорости (числа Фруда), недостижимой для водоизмещающих судов.

Для яхтсмена очень полезная информация!