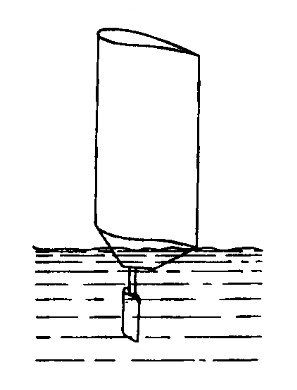
Современное описание физической картины движения судна под парусом строится на основе теории крыла. Принципиальная схема (рис. 1) представляется в виде системы вертикальных гидро- и аэродинамических крыльев. Воздушное (парус) и подводное (киль, шверт) крылья преобразуют энергию ветра в силу, движущую судно. На практике для уравновешивания направленной вниз силы тяжести необходима эквивалентная сила поддержания — плавучесть. Водоизмещающий корпус, обладающий необходимой плавучестью сам по себе практически не имеет значения для преобразования силы ветра.
Основные понятия и определения
Скорость воздушного потока, действующего на парус (вымпельный ветер vв), определяется суммой векторов истинного vи и индуцированного движением судна встречного ветра v, что в геометрической форме выражается парусным треугольником (рис. 2). Согласно теореме синусов, отношение стороны треугольника к синусу противолежащего угла является постоянной величиной:
Для отношения величин скорости индуцированного ветра, или, что то же самое, скорости судна, к скорости истинного ветра, получаем:
Скорость судна v и направление истинного ветра γ могут быть определены, поэтому скорость движения судна зависит от β. Чтобы выявить физический смысл угла β, вернемся к рассмотрению принципа движения парусного судна. Поток воды, обтекающий подводное крыло со скоростью v, и воздушный поток, движущийся относительно паруса со скоростью vв, создают гидродинамическую силу R и силу давления P ветра на парус соответственно. При равномерном (без ускорения) движении R = P.
Гидродинамическую силу R можно разложить на силу лобового сопротивления Rx, направленную противоположно движению судна, и перпендикулярную к ней подъемную силу Ry (рис. 3).

Отношение этих составляющих представляет собой гидродинамическое качество Kг = Ry/Rx и может быть выражено через угол гидродинамического сопротивления єг = arctg Ry/Rx. Аэродинамическую силу P можно разложить на пару составляющих — параллельную и перпендикулярную направлению движения судна: силу тяги T и силу дрейфа Д. Вторую пару составляющих силы P, параллельной и перпендикулярной направлению вымпельного ветра vв, представляют собой сила лобового сопротивления X и аэродинамическая подъемная сила Y. Отношение этих последних характеризует аэродинамическое качество K = Y/X, или угол аэродинамического сопротивления єa = arcctg Y/X.
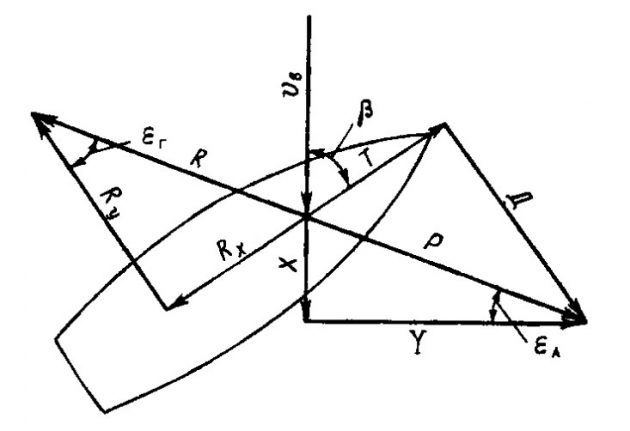
В связи с тем, что гидродинамическое сопротивление Rx равно силе тяги T, а Rv = Д, угол между P и Д равен єr, а вследствие перпендикулярности Y к vв и Д к v можно записать:
Это выражение известно под названием теоремы курсов, а равенства:
являются математическим описанием парусного судна.
Из формулы 2 видно, что для значений угла γ, не слишком близких к 180, ctg β должен иметь возможно большую величину, чтобы обеспечить возможно большее отношение v/vн. Иными словами, для быстроходного судна характерны малые значения угла β, что достигается при высоких значениях отношения подъемной силы к сопротивлению.
На рис. 4 и 5 представлены графики изменения углов гидро- и аэродинамического сопротивления в зависимости от курсового угла относительно истинного ветра для отдельных типов парусных судов и буеров с жесткими парусами.
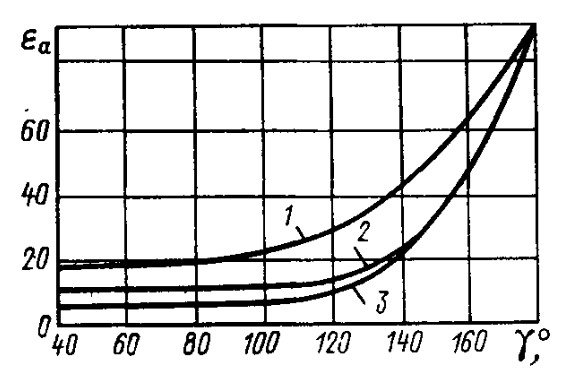
1 – швертбот; 2 – яхта; 3 – буер
Они дают наглядное представление о ходовом преимуществе, которое обеспечивается высокоэффективным парусным вооружением и минимальной величиной сопротивления движению, характерных для ледовой яхты.

1 – швертбот; 2 – яхта; 3 – катамаран; 4 – буер
Суммируя значения єг и єa можно построить график (рис. 6) зависимости непосредственно β от γ, а затем, используя формулу 2, рассчитать полярную диаграмму скоростей (рис. 7).

1 – швертбот; 2 – яхта; 3 – катамаран; 4 – буер
Как видно, ни швертбот, ни Малые суда парусного типакилевая яхта не могут превзойти скорости истинного ветра (v/vи < 1). Полярные диаграммы свидетельствуют о неоспоримых преимуществах в скорости, которыми обладают многокорпусные парусники и о фантастических возможностях буеров, способных при истинном ветре vи = 5 м/с развивать скоростью v = 40 м/с.
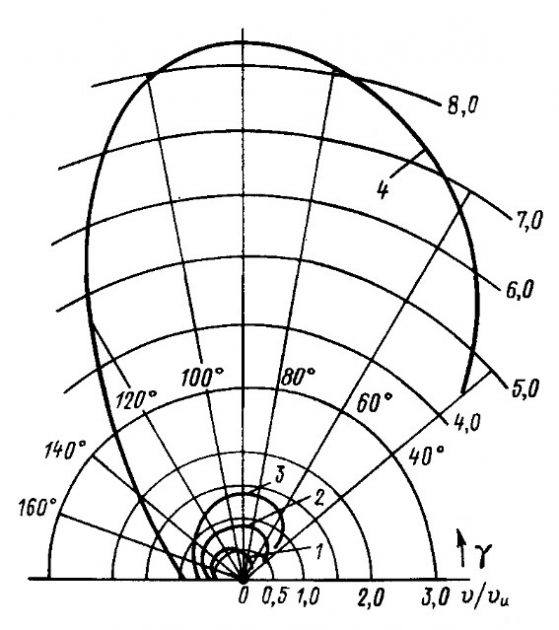
1 – швертбот; 2 – яхта; 3 – катамаран; 4 – буер
Аэродинамика паруса
Составляющие силы давления P ветра на парус — подъемная сила Y и сила сопротивления X, ориентированные вдоль и поперек воздушного потока, — определяются по формулам:
где:
- Cy и Cx — коэффициенты подъемной силы и лобового сопротивления;
- ρв = 1,293 кг/м³ — плотность воздуха;
- S — площадь паруса;
- vв — скорость вымпельного ветра, м/с.
Аналогичный вид имеют формулы для сил тяги и дрейфа:
где:
- Cт и Cд — коэффициенты сил тяги и дрейфа.
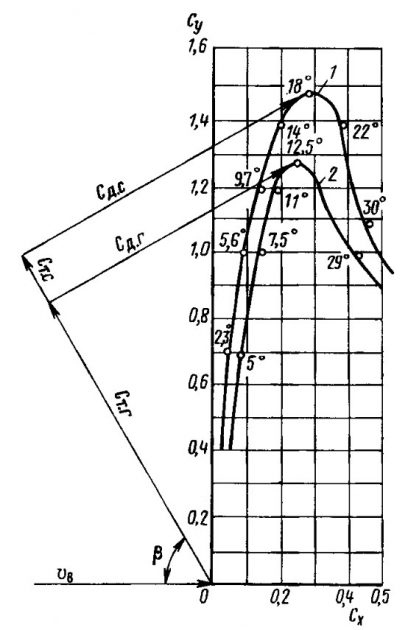
Коэффициент силы сопротивления и подъемной силы паруса определяются его профилем, формой в плане, соотношением высоты и ширины и задаются полярами (рис. 8), на которых они представляются в функции от угла атаки a. С увеличением a значения этих коэффициентов изменяются неодинаково. Cy достигает наибольшей величины при некотором критическом угле атаки aкр, который для бермудских парусов лежит в пределах 12—20°. Cx возрастает сравнительно равномерно и достигает максимума при a = 90°.
Коэффициенты Cт и Cд можно также определить с помощью поляры паруса. Для этого нужно проложить из начала координат под углом к направлению вымпельного ветра (ось абсцисс) курс яхты, затем разложить относительно него коэффициент Cр полного давления ветра на парус на составляющие тяги Cт и дрейфа Cд. Можно определить угол атаки a, при котором на данном курсе величина тяги Cт будет максимальной. Этот угол, очевидно, укажет составляющая Cд, проведенная по касательной к кривой поляры.
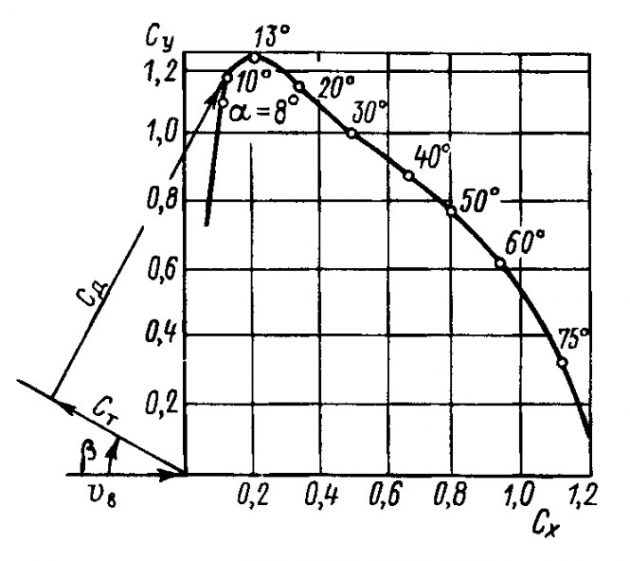
На острых к ветру курсах, включая галфвинд, сила тяги T создается исключительно подъемной силой Y. На попутных курсах начинает играть роль и сила сопротивления. В полный бакштаг сила тяги, примерно в равной мере создается силами Y и X. Естественно, при чисто кормовом ветре движущая сила на парусе полностью создается его сопротивлением. Для установки паруса полезно использовать зависимость:
ψ = β – α,
где:
- ψ — угол установки паруса к ДП судна.
Более 2/3 суммарной силы давления ветра на парус создается за счет разрежения на его подветренной стороне.
Величина разрежения в основном определяется полнотой профиля, или “пузом”, паруса, которое измеряется в долях или процентах стрелки погиби от хорды. Наименьшее аэродинамическое качество имеет плоский парус — пластина. Даже при минимальном угле атаки воздушный поток срывается с его подветренной стороны. Здесь образуется вихревая полость, давление в которой в 2—2,5 раза больше, чем при безотрывном обтекании паруса, имеющего аэродинамический профиль.
С увеличением “пуза” подъемная сила паруса увеличивается, однако при этом растет и его сопротивление. На лавировке предпочтение отдается более плоским парусам, которые создают меньший кренящий момент и могут устанавливаться под более острым углом атаки, чем полные.
Например, парус 2 (рис. 9) на курсе β = 30° лишь немного проигрывает по силе тяги T парусу 3, но при этом создает значительно меньшие дрейф и крен и может быть установлен под меньшим углом атаки.
Однако в слабый (2—3 балла) ветер, когда абсолютная величина силы дрейфа невелика и не создает заметного крена, пузатые паруса благодаря значительной подъемной силе обеспечивают яхте наибольшую скорость. При этом они устанавливаются под меньшим углом атаки, чем плоские, чтобы, по возможности, уменьшить лобовое сопротивление. В совсем слабый, до штилевого, ветер вновь становятся предпочтительными более плоские паруса, так как слабый воздушный поток оказывается не в силах обогнуть профиль с большим “пузом” и срывается с подветренной стороны паруса.
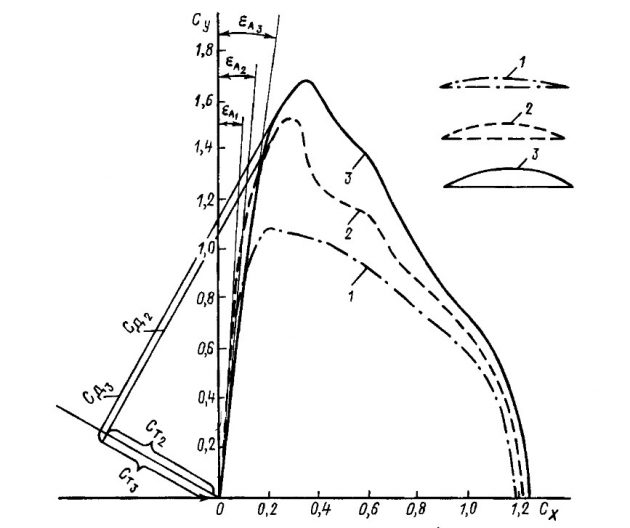
1 – 0,05; 2 – 0,1; 3 – 0,14
Лавировочные паруса на ветер:
- 2-3 балла обычно имеют “пузо” 8-10 %;
- для 4-5-балльного — 6-8 %;
- и для более сильного — 4-6 %.
На современных яхтах величина “пуза” одного и того же паруса может изменяться с помощью такелажа и рангоута. Например, чтобы сделать более плоским грот, мачте придают изгиб, увеличивая натяжение ахтерштага (при оснастке 3/4 или 7/8) либо регулируя натяжение промежуточного штага и бакштагов (при топовой оснастке). Излишек “пуза” при этом убирается в образующийся у передней шкаторины серп.
Для полных курсов, начиная с пологого бейденвинда, применяются паруса с “пузом” до 25 %. Особенно эффективно они работают в слабый и умеренный ветер, в полной мере используя свои высокие тяговые характеристики при практическом отсутствии крена.
На гонках в таких ситуациях прибегают к установке легких передних парусов:
- дрифтер-генуи;
- блупера;
- спинакера.
В свежий ветер, когда яхта гидродинамически исчерпывает свои ходовые возможности, применение полных парусов не дает такого эффекта. Однако если судно способно выходить на режим серфинга, спинакер и блупер несут и в 5—6-балльный ветер.
Помимо глубины “пуза” имеет значение его положение по ширине паруса. На лавировочных парусах наибольшая выпуклость обычно находится на расстоянии 40 % хорды профиля от передней шкаторины. Практика, однако, свидетельствует, что для каждых силы ветра и курса существует положение “пуза”, при котором парус работает с наибольшей отдачей. Так, в слабый и умеренный ветер парус с “пузом” посредине хорды обеспечивает движение с минимальным лавировочным углом. В сильный ветер для лавировки предпочтительнее парус с максимумом прогиба на 1/3 ширины от мачты. Это обеспечивает оптимальное распределение сил разрежения, максимум которых при этом имеет наклон от перпендикуляра к хорде паруса в сторону движения судна.
Парус со сдвинутым к задней шкаторине на 2/3 ширины “пузом” имеет благоприятную форму для безотрывного обтекания подветренной стороны, однако на лавировке при таком расположении “пуза” максимум разрежения сдвигается к задней шкаторине, где его вектор имеет наклон против движения яхты. Такие паруса применяются только на галфвинде и более полных курсах.
Аэродинамическое качество паруса в значительной мере зависит от его удлинения:
- для прямоугольного паруса удлинение равно отношению его сторон λ = l/b;
- для треугольного — удвоенному отношению передней и нижней шкаторин λ = 2l/b;
- для парусов более сложной формы λ = l²/S (S — площадь паруса).
Паруса с большим удлинением наиболее эффективны при лавировке. Благодаря большой длине передней шкаторины, у которой расположена зона максимального давления ветра на парус, они создают большую подъемную силу при высоком аэродинамическом качестве. За счет относительно небольшой ширины снижается индуктивное сопротивление, вызываемое перетеканием воздуха с наветренной стороны на подветренную через верх и низ паруса.
Из всех типов парусного вооружения наиболее эффектными являются бермудские паруса. Они имеют наименьший критический угол атаки и создают наибольшую тягу при курсовых углах β ≤ 70°. Бермудскими парусами с удлинением λ = 3÷6 вооружаются все современные гоночные и крейсерско-гоночные парусные суда. На более полных курсах эффективнее работают гафельные или рейковые паруса. При удлинении, близком к единице, они имеют критический угол атаки aкр = 35÷40° и не могут конкурировать с бермудскими в качестве лавировочных, но в галфвинд и бакштаг нередко превосходят их.
Теоретическая форма паруса, заданная его профилем, удлинением и конфигурацией в плане, под действием ветра искажается. Выбирая шкоты, регулируют по сути дела только положение нижней трети паруса; верхняя его часть выгибается под ветер, за счет чего уменьшается угол атаки и полотнище начинает заполаскивать.
При добирании шкотов возможен срыв потока на нижней части паруса, установленной с избыточным углом атаки.
Скручивание паруса по высоте особенно заметно проявляется в свежий ветер на полных курсах, когда шкоты потравлены и нок гика задирается вверх. В связи с этим паруса, в частности гафельные, у которых скручивание проявляется наиболее интенсивно, утрачивают свои преимущества на этом курсе перед бермудскими. Для уменьшения скручивания применяются оттяжки гика, проводка гика-шкотов с поперечными погонами от борта до борта. В известных пределах скручивание дает положительный эффект, компенсируя изменение угла атаки за счет увеличения скорости ветра по мере удаления от поверхности воды (рис. 10) и отклонения воздушного потока вихрями, образующимися при перетекании воздуха через верх паруса. В зависимости от высоты паруса и силы ветра эта разность углов атаки по высоте паруса составляет 3-5° в бейдевинд и до 10-12° на курсе бакштаг.
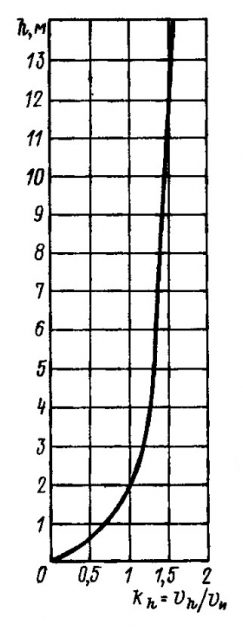
Значительным резервом повышения эффективности парусного вооружения, особенно его лавировочных качеств, может служить снижение лобового сопротивления рангоута и такелажа. С этой целью практикуются проводка фалов внутри мачты, применение цельнонатянутых стальных струн вместо тросов для вант, установка обтекателей на штагах. Наибольшие потери аэродинамического качества вызывает мачта. Ее влияние тем более чувствительно, что искажение обтекающего парус воздушного потока она создает у передней шкаторины, где находится максимум эпюры давления.
Вихревой след мачты уменьшает разрежение, вследствие чего существенно снижается подъемная сила. При слишком большом удлинении бермудские паруса теряют эффективность, когда диаметр мачты становится сопоставимым с глубиной “пуза”. Чтобы уменьшить влияние мачты, ее сечению придают овальный или крыловидный профиль, имеющий меньшее лобовое сопротивление и более высокое аэродинамическое качество.
Эффект, однако, достигается только на вращающейся мачте (рис. 11), причем наименьшее завихрение создает не самонастраивающаяся по ветру мачта, а та, которую можно принудительно установить под действительным углом набегания воздушного потока на парус. Резко увеличивает сопротивление щель между шкаториной и мачтой, поэтому на современных яхтах грот поднимают не по рельсу, а в ликпазе. На небольших яхтах и швертботах хороший результат дает способ крепления паруса, применяемый на винд-серферах — мачта вставляется в карман, прошитый у передней шкаторины.
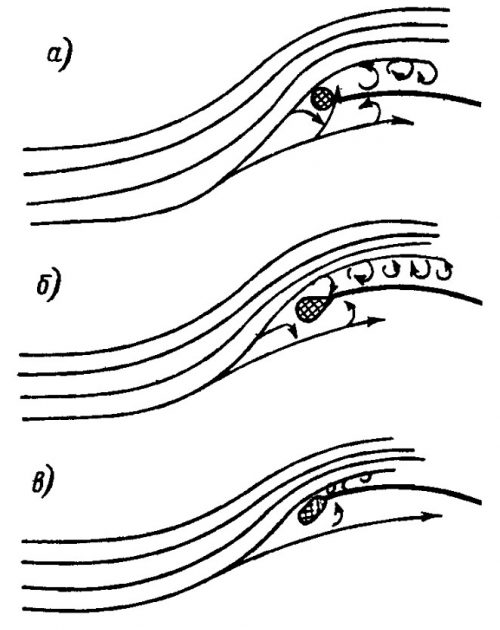
а, б – круглая и профилированная мачта с креплением паруса на ползунах; в – профилированная мачта с принудительно устанавливаемым углом атаки и креплением паруса ликтросом
На наиболее быстроходных парусных судах — катамаранах и тримаранах — находят применение двухслойные паруса, полотнища которых огибают парус и образуют несимметричный крыловидный профиль, с высоким аэродинамическим качеством. Еще более эффективно работают жесткие паруса, устанавливаемые на буерах. Парусное вооружение подобных конструкций позволяет развивать скорости, в несколько раз превышающие скорость истинного ветра.
Как видно на полярной диаграмме (см. рис. 7), такие скорости достигаются при направлении истинного ветра γ = 90÷120°, когда значение курсового угла к вымпельному ветру составляют от β = 45° при v/vи = 1 до β = 7° при v/vи = 8. Любой выигрыш в сопротивлении или величине подъемной силы в таких условиях приобретает огромное значение. Условия обтекания грота воздушным потоком могут улучшиться при его совместной работе со стакселем.
Механизм взаимодействия парусов объясняется по-разному:
- и как действие щели — сопла между гротом и стакселем;
- и как результат циркуляции потоков вокруг парусов.
В наиболее общей форме его можно представить как устранение вихрей и соответственно увеличение разрежения на подветренной стороне парусов благодаря проходящему между гротом и стакселем с увеличенной скоростью воздушному потоку (рис. 12). Получаемый эффект зависит от формы и размеров парусов, их взаимного расположения, курса яхты относительно ветра.
Например, излишне выбранный или со слишком большим “пузом” стаксель будет “задувать” в грот.
Вектор скоростей проходящего между парусами потока получит составляющую, направленную перпендикулярно к полотнищу грота. Ее действие может снизить разрежение настолько, что давление с обеих сторон паруса уравняется, и профиль его деформируется. Эффективная совместная работа парусов обеспечивается только в том случае, когда воздушный поток, проходящий в щель между ними, направлен по касательной к поверхности грота. Это условие в большинстве случаев выполняется за счет увеличения угла установки стакселя, т. е. уменьшения угла его атаки. Необходимо также, чтобы форма щели выдерживалась по всем сечениям парусов от нижней шкаторины до верха. В частности, следует учитывать возможность скручивания парусов, уменьшающего угол их атаки в верхней части до 20°. На форму грота в нижней части оказывает влияние гик.
Чтобы уменьшить вызываемое им искажение профиля, применяют независимую проводку нижней шкаторины. Известна конструкция гика типа так называемого “парк-авеню”, который предоставляет возможность поперечных перемещений нижней шкаторины и служит аэродинамической шайбой, уменьшающей перетекание воздуха с наветренной стороны на подветренную. В последнее время получила распространение конструкция гика-уишбона, который с парусных досок перешел на яхты.
По среднестатистическим данным принимается, как правило, и значение центровки — расстояния по горизонтали между центрами парусности (ЦП) и бокового сопротивления судна (ЦБС). Положения ЦП и ЦБС могут быть определены геометрически соответственно как центры тяжести площади паруса и проекции погруженной части судна на его ДП.
Геометрические ЦП и ЦБС, однако, далеко не всегда совпадают точками приложения аэро- и гидродинамических сил. Центровка изменяется в зависимости от курсового угла и ходового крена.
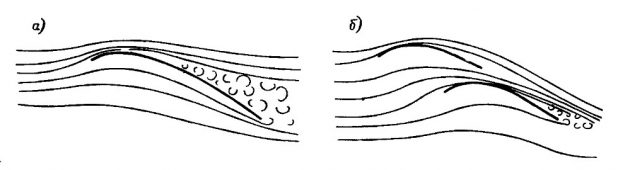
По данным продувки изолированного паруса центр давления (ЦД) ветра в зависимости от угла атаки располагается при a = 15÷25° на расстоянии 34—38 % хорды от передней шкаторины, а при a = 90° посередине хорды. На шлюпе можно принимать, что ЦД находится на линии, соединяющей геометрические ЦП грота и стакселя, и смещен в нос от суммарного геометрического ЦП на величину
, равную в зависимости от соотношения площадей стакселя и грота от 0,1 при Sc/Sr = 0,5 до 0,05 при Sc/Sr = 2,5.
Положение гидродинамического ЦД определяется в основном площадью и расположением плавника и руля, создающих главную долю поперечной силы. Исходная величина суммарной площади плавника и руля, которая может быть принята при эскизном проектировании, для яхт с отдельно стоящим рулем составляет 5—7 % максимальной площади лавировочных парусов, а для яхт с рулем на ахтерштевне — 8—11 %. Площадь руля принимается 24 ± 5 % суммарной площади руля и плавника и не менее 1,2—1,5 % парусности. Гидродинамический ЦД плавника у яхт с отдельно стоящим рулем должен находиться на расстоянии 43 ± 3 % Lквл от носа по КВЛ, а у яхт с рулем на ахтерштевне — на 48 ± 1 % Lквл.
Приближенно центровка может быть определена по формуле, полученной путем обработки данных по хорошо отцентрованным яхтам:
где:
— горизонтальное расстояние между геометрическими ЦП и ЦБС, % Lквл;
- Hп — габаритная высота парусов над КВЛ, м;
- S — фактическая площадь парусности, для которой определяется положение ЦП, м²;
- kц — коэффициент центровки;
- Sпл, Sp – площади плавника (шверта) и руля, м².
Для катамаранов расчет можно выполнить по формуле:
где:
- S — расстояние между ДП корпусов, м.
В зависимости от типа вооружения и компоновки подводной части яхты рекомендуются следующие значения коэффициента центровки kц:
| Значения коэффициента центровки kц | ||
|---|---|---|
| Шлюпы | швертботы | +0,06 ± 0,01 |
| яхты с рулем на ахтерштевне | +0,25 ± 0,03 | |
| яхты с отдельно стоящим рулем | +0,21 ± 0,03 | |
| Кечи и иолы | с рулем на ахтерштевне | +0,03 ± 0,01 |
| с отдельно стоящим рулем | -0,03 ± 0,01 | |
Гидродинамика парусного судна
Парусные суда эксплуатируются в основном в водоизмещающем режиме. Только при благоприятных сочетаниях силы и направления ветра некоторые из них способны выходить на частичное глиссирование. Соответственно основными составляющими сопротивления воды, как и у других судов, рассчитанных на подобные скорости, для парусников будут сопротивление трения, формы и волновое. Характер зависимости этих составляющих от скорости, размерений и обводов судна изложен в статье Сопротивление движению малого судна“Сопротивление движению судна – виды и понятия”. Специфика движения парусников вызывает два дополнительных вида сопротивления, создаваемых дрейфом и креном.
При вызванном дрейфом косом обтекании корпуса судна встречным потоком воды возникает гидродинамическая сила R. Ее составляющая, ориентированная поперек направления движения судна, представляет собой поперечную силу Ry, противодействующую дрейфу. При увеличении угла дрейфа δ величина Ry возрастает, но одновременно растет и сила сопротивления Rx за счет возникающего при поперечном перетекании потока воды под корпусом судна индуктивного сопротивления Ri (рис. 13).
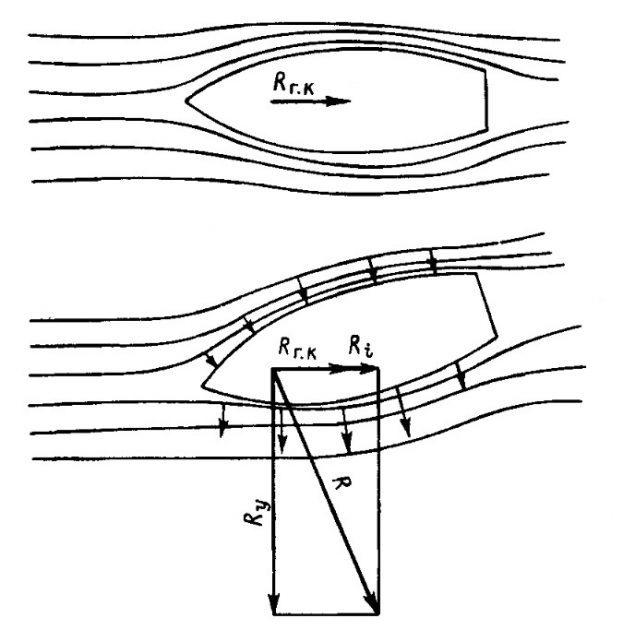
Голый корпус современных яхт и швертботов с плоским днищем лишь в малой мере участвует в создании поперечной силы Ry, являясь в то же время как гидрокрыло малого удлинения основным источником индуктивного сопротивления. Поперечную силу создают главным образом плавниковый киль (или шверт) и перо руля, имеющие для этой цели наиболее подходящие характеристики. Вместе с тем следует учитывать, что, не проявляя активности в создании Ry, корпус способствует повышению ее величины на киле, играя роль шайбы, исключающей перетекание потока воды через верхнюю кромку.
По этой причине в гидродинамических расчетах для киля используется так называемое эффективное удлинение, равное удвоенному геометрическому удлинению, λк = 2T ² Aк (Aк – площадь проекции киля на ДП). Для пера руля в зависимости от способа его установки λк = 0,8÷1,25T ² Aк.
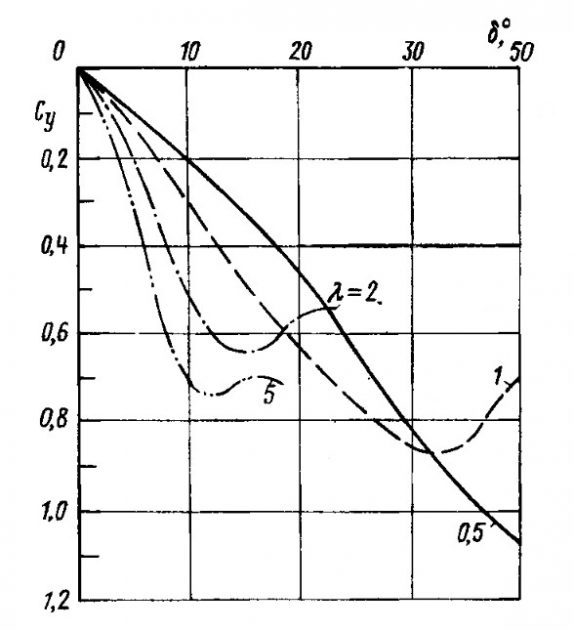
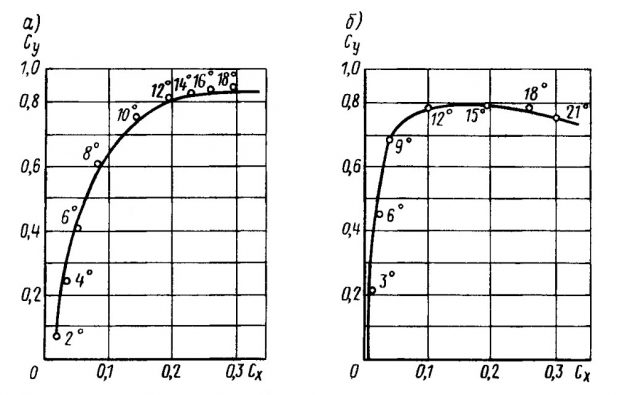
Увеличивая удлинение киля, можно получить требующуюся Ry при меньшем угле дрейфа (рис. 14) и за счет этого снизить индуктивное сопротивление. Дополнительное преимущество дает обтекаемый профиль, который при равной с плоским для одинаковых углов дрейфа величине Ry имеет заметно меньшее сопротивление (рис. 15).
На многокорпусных судах, а иногда и на швертботах, применяют парные шверты несимметричного профиля, либо устанавливаемые под углом к ДП, которые работают поочередно с подветренной стороны. Поперечная сила в этом случае создается при нулевом угле атаки, т. е. и при отсутствии дрейфа, что обеспечивает выигрыш в сопротивлении. Несимметричный в плане профиль придается иногда корпусам катамаранов и тримаранов. Расчет при этом основывается на том, что при лавировке подветренный корпус привсплывает или даже отрывается от воды, а подветренный, притапливаясь, создает поперечную силу при нулевом дрейфе. С этой же целью на тримаранах боковые поплавки устанавливают под углом к ДП среднего корпуса.
Прирост индуктивного сопротивления происходит в основном на острых курсах и усугубляется в свежий ветер Крен судна при поперечном перемещении грузакреном судна. Заметную долю в общем сопротивлении (до 15 %) эта добавка проявляется при крене порядка 30°.
Ходкость парусного судна
В отличие от судов с механическими двигателями о Ходкость и движителиходкости парусника нельзя судить по его экстремальным возможностям. Хорошая яхта должна обладать высокими ходовыми качествами при любом ветре и на любом курсе, чтобы выиграть гонку или хотя бы выдержать приемлемую среднюю скорость в дальнем плавании. Соответственно поставленной цели формулируются и задачи, например:
- определить при заданной парусности S и силе истинного ветра vи скорость судна v на всех возможных курсовых углах;
- определить оптимальную площадь парусов при заданных курсе и скорости истинного ветра;
- найти предельную скорость ветра, которую может выдержать яхта с заданной парусностью и т. п.
Рассмотрим решение первой из названных задач, имеющей наиболее широкий интерес.
1 Задавшись несколькими значениями скорости судна v по возможности, наиболее близкими к реальным для известной скорости истинного ветра vи, находим скорости вымпельного ветра vв при курсовых углах β от 30 до 180°.
Расчеты выполняются графически — построением для каждой скорости v и каждого курсового угла β парусного треугольника (см. рис. 2) или по зависимостям, выведенным из формулы 1:
Пример. Яхта 1/4-тонного класса (см. рис. 2 и таблицу 3 в статье “Характеристики яхт четвертьтонного класса”Малые суда парусного типа) имеет вооружение шлюпа; площадь грота Sr = 10 м², площадь стакселя Sc = 17 м²; удлинение обоих парусов λ = 4; скорость истинного ветра vи = 6,5 м/с.
Коэффициенты сил тяги Cт и дрейфа Cд снимаем по рис. 16 отдельно для грота и стакселя. Расчетные значения скоростей v = 1, 2, 3, 4 м/с; курсовых углов β = 30, 60, 90, 120, 180°.
Для β = 30°;
Последующие вычисления производятся аналогично, результаты записываются в табличной форме (табл. 1).
| Таблица 1. Скорость вымпельного ветра vв, сила тяги Т и сила дрейфа Д в зависимости от курсового угла β и скорости судна v | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| v, м/с | β = 30° | β = 60° | β = 90° | β = 120° | β = 180° | ||||||||
| vв, м/с | Т, Н | Д, Н | vв, м/с | Т, Н | Д, Н | vв, м/с | Т, Н | Д, Н | vв, м/с | Т, Н | vв, м/с | Т, Н | |
| 1 | 7,3 | 452 | 1 215 | 6,9 | 897 | 828 | 6,4 | 1 008 | 201 | 5,9 | 770 | 5,5 | 655 |
| 2 | 8,2 | 569 | 1 536 | 7,3 | 990 | 915 | 6,2 | 934 | 187 | 5,2 | 594 | 4,5 | 437 |
| 3 | 8,8 | 654 | 1 765 | 7,4 | 1 028 | 950 | 5,8 | 836 | 173 | 4,5 | 440 | 3,5 | 262 |
| 4 | 9,4 | 748 | 2 017 | 7,5 | 1 047 | 967 | 5,1 | 639 | 167 | 3,5 | 264 | 2,5 | 131 |
2 Сопротивление воды движению яхты в положении на ровный киль без дрейфа определяется как для любого водоизмещающего судна. Раздельно находятся сопротивление трения Rт и остаточное сопротивление R0 с помощью формул и графиков в статье Сопротивление движению малого судна“Сопротивление движению судна – виды и понятия”.
Пример. Рассматривавшаяся в предыдущем примере яхта 1/4-тонного класса имеет длину по КВЛ Lвл = 6,0 м, водоизмещение D = ϒV = 1,77 т, площадь смоченной поверхности Ω = 11,6 м². Расчет приведен в табл. 2.
3 Поперечная сила Ry, создаваемая голым корпусом, определяется по формуле:
где:
- Aг.к — погруженная площадь ДП голого корпуса.
Значение коэффициента подъемной силы Cy г.к корпуса как крыла малого удлинения можно найти по приближенной формуле К. К. Федяевского:
где:
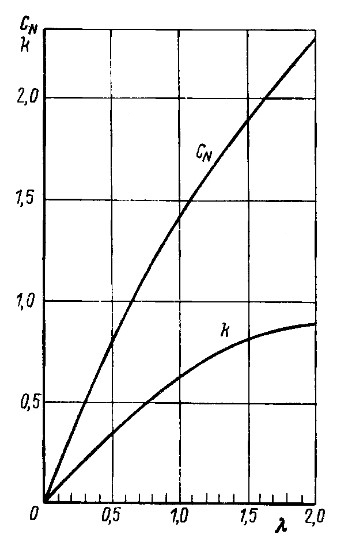
- CN – определяется по графику на рис. 17;
- CD = 2 при λ = 2(T ²/A) ≤ 0,15.
| Таблица 2. Расчет сопротивления корпуса яхты в положении на ровный киль | ||||
|---|---|---|---|---|
| Рассчитываемая величина | v, м/с | |||
| 1 | 2 | 3 | 4 | |
| 5 | 10 | 15 | 20 | |
| (по рис. “Коэффициенты турбулентного трения гидродинамически гладкой пластины”) | 3,35 | 3,0 | 2,8 | 2,7 |
| (см. статью “Составляющие сопротивления движению судна”) | 3,65 | 3,3 | 3,1 | 3,0 |
| 21 | 77 | 162 | 278 | |
| FrL | 0,13 | 0,26 | 0,39 | 0,52 |
| FrV | 0,29 | 0,58 | 0,87 | 1,16 |
| Ro/(gD) (по рисункам “График для определения остаточного сопротивления буксиров и траулеров (диаграмма Неймана)” и “Коэффициент учета взаимодействия корпусов катамарана: а — в диапазоне FrV = 0,8÷1,6″) | 0,15 | 1,6 | 16 | 65 |
| Ro = [Ro/gD]gD | 2 | 27 | 279 | 1 128 |
| Rг.к = Rт+Ro | 23 | 104 | 441 | 1 406 |
Индуктивное сопротивление, возникающее в результате перетекания потока воды под корпусом судна, выразится формулой:
где:
- Ci г.к = Cy г.к tg δ — коэффициент индуктивного сопротивления.
Пример. У рассматриваемой яхты Tг.к = 0,4 м; Aг.к = 2,08 м². Таким образом:
Результаты расчета Ry г.к, и Ri г.к приведены в табл. 3.
| Таблица 3. Поперечная сила Rу г.к, Н, и индуктивное сопротивление Ri г.к, Н корпуса яхты 1/4-тонного класса | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| δ, ° | tg δ | Cу г.к | Ci г.к | v, м/с | |||||||
| 1 | 2 | 3 | 4 | ||||||||
| Ry | Ri | Ry | Ri | Ry | Ri | Ry | Ri | ||||
| 4 | 0,07 | 0,021 | 0,0015 | 22 | 2 | 88 | 8 | 198 | 18 | 352 | 32 |
| 6 | 0,105 | 0,039 | 0,0041 | 41 | 4 | 164 | 16 | 369 | 36 | 656 | 64 |
| 8 | 0,14 | 0,062 | 0,0087 | 64 | 9 | 256 | 36 | 576 | 81 | 1 024 | 144 |
| 10 | 0,18 | 0,089 | 0,0160 | 93 | 17 | 372 | 68 | 837 | 153 | 1 488 | 272 |
4 Гидродинамические характеристики плавникового киля и пера руля определяются так же, как для гидрокрыла, обтекаемого потоком воды под углом атаки, равным углу дрейфа. Для определения коэффициента подъемной силы Cy и сопротивления Cx используются подходящие поляры, приведенные в справочнике либо других изданиях.
Пример. Для рассматриваемой яхты удлинение киля
, пера руля
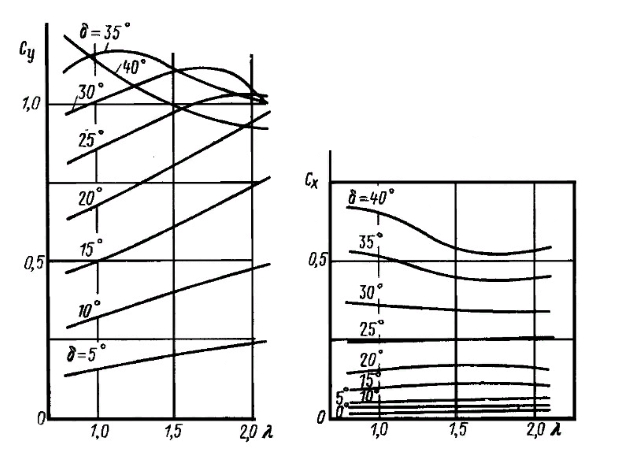
Результаты расчета приведены в табл. 4. Коэффициенты Cy и Cx находим по рис. 18 для λ = 1 и δ = 4, 6, 8, 10°.
| Таблица 4. Подъемная сила и сопротивление киля и руля яхты, Н | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| δ, ° | Cy | Cx | v, м/с | |||||||
| 1 | 2 | 3 | 4 | |||||||
| Ry | Rx | Ry | Rx | Ry | Rx | Ry | Rx | |||
| 4 | 0,13 | 0,030 | 114 | 26 | 456 | 104 | 1 026 | 234 | 1 824 | 416 |
| 6 | 0,19 | 0,035 | 166 | 31 | 664 | 124 | 1 494 | 279 | 2 656 | 496 |
| 8 | 0,26 | 0,042 | 227 | 37 | 908 | 148 | 2 043 | 333 | 3 632 | 592 |
| 10 | 0,30 | 0,050 | 280 | 43 | 1 120 | 172 | 2 520 | 387 | 4 480 | 688 |
5 Определяя скорость и дрейф яхты при заданной силе ветра, можно вычислить ожидаемый крен. Для этого находят кренящий момент:
где:
- Д — сила дрейфа;
- lкр — плечо кренящего момента, равное расстоянию от ЦП до ЦБС.
По метацентрической формуле остойчивости восстанавливающий момент:
где:
- D — водоизмещение судна;
- h — Определение поперечной метацентрической высоты судна путем выполнения опыта кренованияметацентрическая высота, равная для крейсерско-гоночных яхт 0,75—1,2 м.
Величина крена:
Пример. Для рассматриваемой яхты lкр = 4 м; h = 0,8 м; D = 1,77 т.
Определим углы крена на курсе β = 30°:
| v, м/с | 1 | 2 | 3 | 4 |
| Д, Н | 1 215 | 1 536 | 1 765 | 2 017 |
| θ, град. | 20 | 26 | 31 | 35 |
Заметного увеличения сопротивления, следовательно, на этом курсе можно ожидать при v ≥ 3 м/с. Принимаем его равным 0,37Ri.
6 Полное сопротивление яхты:
Полная поперечная сила определится суммой Ry корпуса, киля и руля.
Пример. Полное сопротивление и поперечная сила яхты, полученные суммированием составляющих, вычисленных в предыдущих примерах, приведены в табл. 5 и 6.
| Таблица 5. Полное сопротивление яхты Rп, Н | ||||
|---|---|---|---|---|
| δ, ° | v, м/с | |||
| 1 | 2 | 3 | 4 | |
| 4 | 51 | 216 | 693 | 1 854 |
| 6 | 57 | 240 | 756 | 1 966 |
| 8 | 70 | 293 | 866 | 2 162 |
| 10 | 86 | 357 | 1 010 | 2 428 |
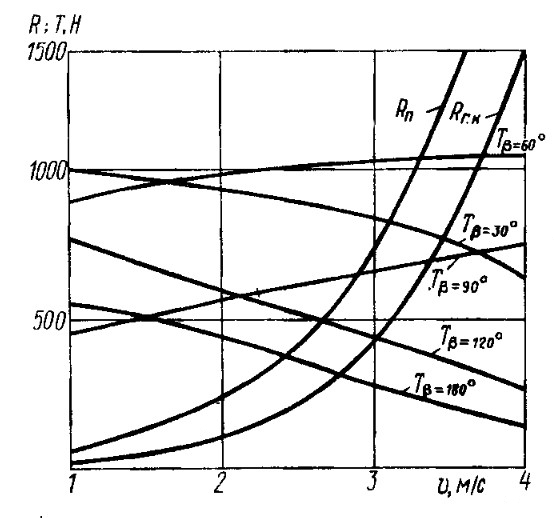
7 Для определения скорости строится график сопротивления, на который наносятся кривые силы тяги для заданных курсовых углов β.
| Таблица 6. Полное сопротивление яхты Ry, Н | ||||
|---|---|---|---|---|
| δ, ° | v, м/с | |||
| 1 | 2 | 3 | 4 | |
| 4 | 136 | 544 | 1 224 | 2 176 |
| 6 | 207 | 828 | 1 863 | 3 312 |
| 8 | 291 | 1 164 | 2 619 | 4 656 |
| 10 | 373 | 1 492 | 3 357 | 5 968 |
В связи с тем, что на попутных курсах, начиная от галфвинда, крен и дрейф практически отсутствуют, на графике строится также кривая сопротивления голого корпуса. Величина дрейфа для найденной скорости определится из условия Ry ≥ Д.
8 Наглядное представление о ходовых качествах яхты дает полярная диаграмма скоростей. Для ее построения определяют курсовые углы γ к истинному ветру и откладывают на них векторы скорости v.
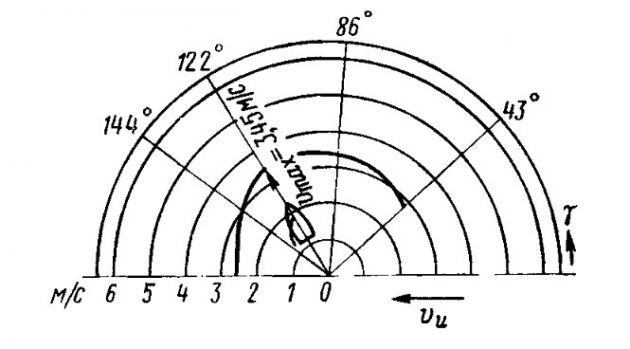
Пример. Для рассматриваемой яхты на курсе β = 30° условие Ry > Д выполняется при v = 3 м/с, δ = 6°. Строим графики сопротивления для δ = 6° и δ = 0 (рис. 19). Наносим на график кривые тяги по табл. 2. Для полученных значений скорости яхты определяем курсовые углы γ к направлению истинного ветра и строим полярную диаграмму скоростей (рис. 20).
🤝 Поддержите нашу работу
Нашли опечатку? Выделите и нажмите CTRL+Enter
