Глиссирующие катамараны обычно представляют собой систему из двух остроскулых корпусов и соединительного моста. С гидродинамической точки зрения глиссирующими катамаранами являются и суда на гидролыжах.
- Сопротивление глиссирующих судов
- Силы и моменты, действующие на глиссирующую пластину
- Приближенные способы расчета сопротивления движению малого судна
- Расчет сопротивления водоизмещающего судна
- Расчет сопротивления судна, движущегося в переходном режиме
- Расчет сопротивления судна, движущегося в режиме чистого глиссирования
Сопротивление глиссирующих судов
Силы и моменты, действующие на глиссирующую пластину
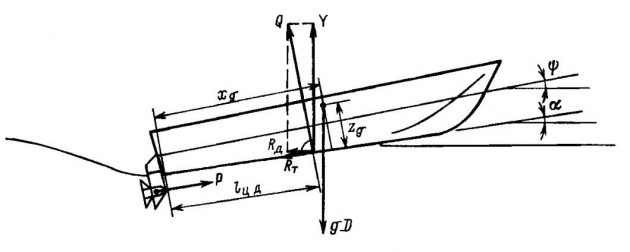
Сила поддержания создается при движении глиссера в результате взаимодействия днища с набегающим потоком жидкости. На всех режимах установившегося движения она равна весу судна:
В общем случае величина силы поддержания слагается из гидростатической и гидродинамической составляющих. При относительных скоростях движения глиссера FrV ≥ 3 гидростатическая составляющая для глиссеров невелика.
Сила сопротивления R движению глиссера слагается из касательных и нормальных составляющих. Касательные силы при чистом глиссировании создаются сопротивлением трения Rт. Сопротивление от нормальных сил Rд (его часто называют сопротивлением нормальных давлений) представляет собой проекцию результирующего вектора гидродинамических давлений Q на направление движения. Следует оговориться, что равнодействующая касательных сил в общем случае не совпадает с направлением движения, однако в расчетах ходкости этим пренебрегают.
Гидродинамическим моментом М называют момент сил поддержания относительно нижней кромки транца (плечо этих сил определяется положением центра давления и обозначается lц.д)
Моментом сил веса Mg называют момент от сил веса судна на плече, равном расстоянию от центра масс судна до транца, которое обозначается xg. Момент сил веса Mg изменяется при изменении дифферента судна, а также зависит от положения центра масс по высоте zg:
Поскольку при движении глиссеров углы дифферента невелики, без особого ущерба для точности расчетов полагают:
Момент Мp от упора движителя Р определяется относительно нижней кромки транца. В ряде случаев его величина мала и может не учитываться при определении посадки судна. Это относится к глиссерам малой и средней быстроходности. Для высокоскоростных, в том числе спортивных, Глиссирующие суда в малотоннажном судостроенииглиссирующих судов Мp имеет очень большое значение.
При всех режимах установившегося движения глиссирующих судов:
Угол дифферента ψ глиссера определяют относительно его расчетного положения на плаву. При этом угол атаки α несущей поверхности в общем случае не совпадает с углом дифферента судна.
Это интересно: Вант-путенсы и такелаж на судах из стеклопластика
Схема сил, действующих на глиссер, приведена на рис. 1.
В литературе по глиссированию встречаются также термины волновое сопротивление и брызговое сопротивление. По своей природе волно- и брызгообразование является следствием действия системы давлений на днище судна. В режиме чистого глиссирования волновое и брызговое сопротивления представляют собой составные части сопротивления нормальных давлений (как уже говорилось, сопротивление формы у глиссирующей пластины отсутствует). Поэтому о брызговом сопротивлении можно говорить лишь в том смысле, в каком замыв частей корпуса брызговой струей увеличивает (или уменьшает) сопротивление трения.
В расчетах ходкости глиссеров используют безразмерные характеристики:
- удлинение корпуса судна l = Lck/B;
- смоченное удлинение λ = lсм/B;
относительное удлинение
;
относительная центровка
;
коэффициент момента m△ = M/(gDB); m△ ≈ xg/B, или строго
- коэффициент статической нагрузки С△ = V/B³;
- коэффициент динамической нагрузки
- гидродинамическое качество К = Y/R;
- коэффициент глиссирования, или обратное качество, ∈ = 1/К.
Для удобства пользования материалами, в которых употреблены различные формы выражения числа Фруда, приводим формулы перевода:
В режиме чистого глиссирования сопротивление воды движению судна складывается из сопротивления трения и сопротивления нормальных давлений.
Сопротивление трения глиссера Rт прямо зависит от величины смоченной поверхности, которая меняется с изменением v, m△, С△. Величину смоченной поверхности определяют либо по графикам, полученным в результате испытания систематических серий моделей, либо экспериментально. Для катеров, имеющих сложную форму корпуса, определение величины Ω возможно только экспериментально. То же самое следует сказать относительно глиссеров, рассчитанных на переходный режим движения. Для плоской пластины:
Полный коэффициент трения определяют по формуле (Формула 23).
Основная его часть
зависит помимо числа Рейнольдса еще от угла атаки α. Режим пограничного слоя у глиссеров практически всегда турбулентный. Экспериментальные исследования подтверждают справедливость использования формулы Прандтля—Шлихтинга (Формула 24) для определения
.
При углах α < 3° результаты расчета и эксперимента совпадают. При 3° < α < 6° происходит небольшая ошибка в безопасную сторону.
Для α > 6° формула (Формула 24) дает большое завышение
.
Большинство глиссеров имеют оптимальные углы атаки α = 5÷6°. В этом случае для Re~107 можно принимать
.
Величина полного коэффициента трения включает в себя также надбавку на шероховатость
(Формула 23). Для стальных судов рекомендуют принимать
, для деревянных
.
Рассмотрим величину
для глиссирующих катеров, предназначенных для разъездных и туристических целей. Диапазон водоизмещений этих судов колеблется в пределах 0,6—6 т. Скорость полного хода — 10—15 м/с. Диапазон чисел Рейнольдса при этом составляет (1,3÷3,2)·106.
Соответствующие им значения
равны (2,9÷2,6)·10-3 (бóльшие величины
— у судов меньшего водоизмещения, меньшие — у больших катеров). При этом для малых глиссеров, имеющих, как правило, высококачественную поверхность днища, надбавка на шероховатость составляет
. Для судов большего водоизмещения рекомендуемые значения надбавки
. В результате суммарный коэффициент
колеблется для катеров разного водоизмещения в небольших пределах. На практике в расчетах ходкости разъездных и туристских катеров с относительной скоростью FrV = 3÷3,5 можно принимать величину
. Приборы для контроля тел каченияПогрешность при этом составляет не более 5 % и лежит в пределах точности определения смоченной поверхности.
Существенное влияние на величину сопротивления трения глиссера оказывают направление и интенсивность брызговой струи, возникающей на передней кромке смоченной поверхности. Замыв этой струей части днища приводит к образованию силы вязкостной природы, которая может приводить и к увеличению, и к уменьшению вязкостной составляющей сопротивления. Результаты экспериментального исследования позволяют сделать следующие выводы:
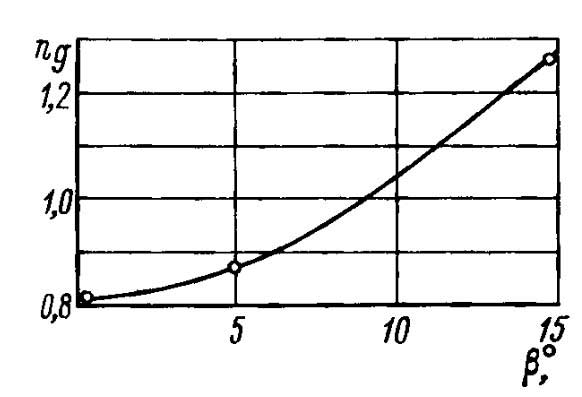
- при углах килеватости β > 12° практически для всех углов ходового дифферента сопротивление трения в зоне брызговой струи приводит к увеличению сопротивления трения плоскокилеватой пластины;
- при β < 7° эта составляющая уменьшает сопротивление трения пластины;
- в диапазоне 7° < β < 12° при углах ходового дифферента 3—6° влияние брызговой струи на сопротивление плоскокилеватой пластины незначительно.
Сопротивление нормальных давлений представляет собой по существу остаточное сопротивление. Для режима чистого глиссирования:
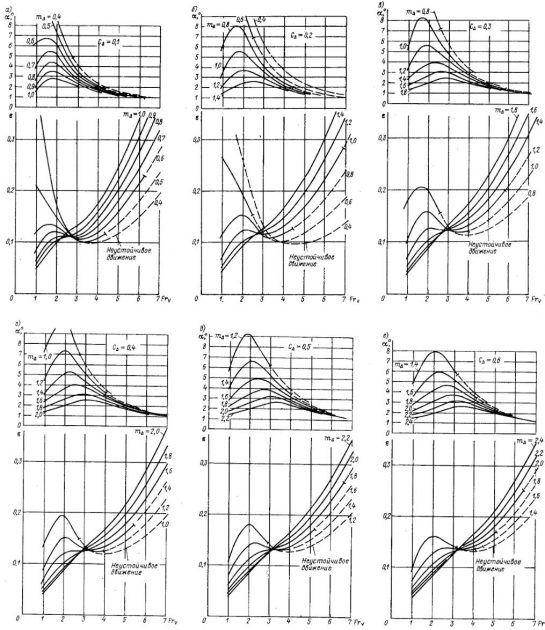
Величина угла атаки несущей поверхности глиссера (в режиме чистого глиссирования) является функцией числа Фруда и коэффициентов нагрузки С△ и момента m△. Взаимосвязь этих характеристик можно определить экспериментально. Для глиссеров, имеющих несложные плоскокилеватые обводы, с успехом используют результаты испытаний систематических серий схематизированных моделей. В отечественном судостроении наиболее широко применяют материалы Л. И. Седова и А. С. Перельмутра. Эти материалы представляют собой эмпирические зависимости для гидродинамических характеристик плоских пластин.
Ниже приведены формулы, справедливые при λ > 0,3÷0,4:
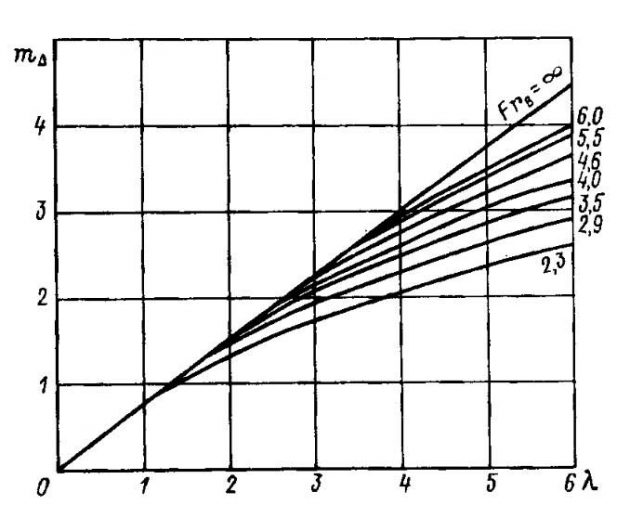
В графической форме эти зависимости представлены на рис. 2 и 3.
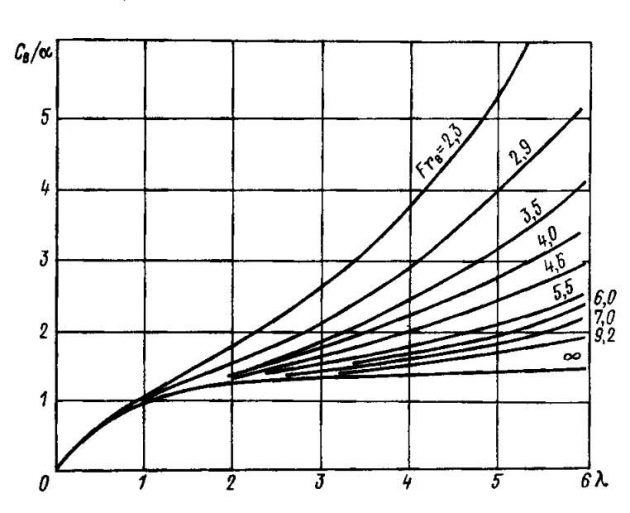
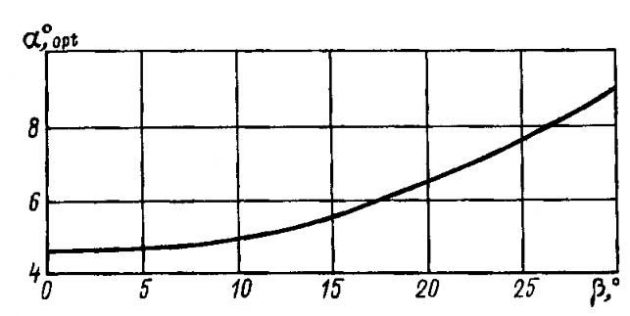
Сопротивление глиссера зависит от угла атаки несущей поверхности. У каждой пластины существует для данных С△, FrB такой угол aopt при котором ее сопротивление минимально. С увеличением a > aopt быстро растет составляющая сопротивления Rд; при уменьшении a < aopt существенно возрастает Rт. Величина aopt меняется в зависимости от коэффициента нагрузки СB, связанной с величинами С△ и Fr (Формула 46). Величина aopt также существенно зависит от килеватости днища (рис. 4). На величину aopt влияет шероховатость поверхности пластины.
Если увеличить
, возрастет вязкостная составляющая и aopt переместится в область больших значений.
Именно вследствие этого явления оптимальный угол дифферента модели судна в общем случае не равен оптимальному углу дифферента самого натурного судна, что нужно всегда учитывать. Для отыскания aopt натуры следует на расчетных числах Фруда измерить зависимость полного сопротивления модели от угла атаки вблизи его оптимального значения. Затем, пересчитав сопротивление на натурное Основные материалы применяемые в морском деревянном судостроениисудно по законам подобия, нужно построить кривую его полного сопротивления от угла атаки днища; aopt определится в точке Rmin.
Сопротивление движению глиссирующего судна зависит от Сопротивление движению малого судначисла Фруда и коэффициента статической нагрузки. Однако если для каждого случая движения выбрана наилучшая центровка, увеличение коэффициента глиссирования с ростом С△ невелико. Значение же коэффициента момента при этом изменяется весьма значительно. Существует также зависимость безразмерного коэффициента ∈ от удлинения смоченной поверхности глиссера. Однако само удлинение является функцией нагрузки, центровки и числа Фруда, и в оптимальных режимах (m△opt) увеличение удлинения однозначно соответствует увеличению коэффициента С△.
Влияние килеватости пластин на гидродинамическое качество показано на рис. 5.
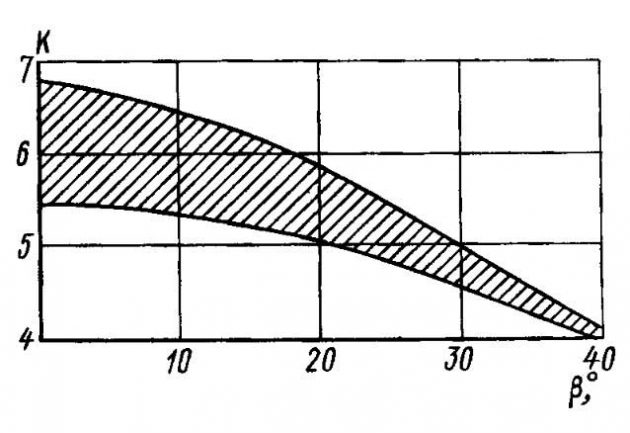
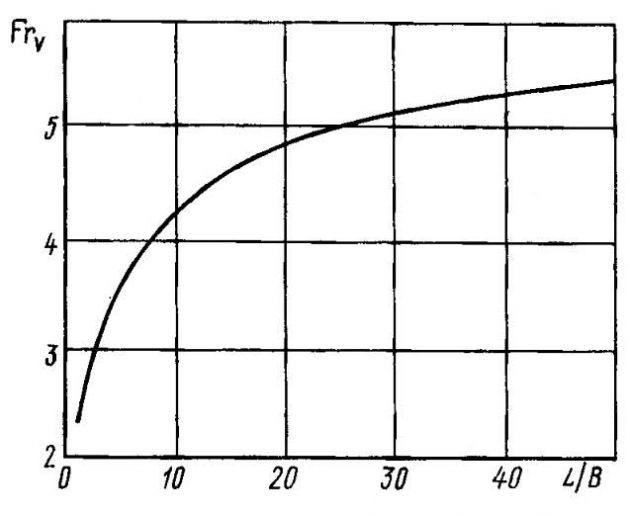
При расчетах ходкости глиссирующих судов важно также знать момент наступления режима чистого глиссирования. Для центровок, близких к оптимальным, может быть использована зависимость скорости начала чистого глиссирования от величины удлинения днища (рис. 6). Весьма важным вопросом ходкости глиссеров является нахождение границ устойчивости движения.
Известно, что неустойчивость движения судна наблюдается при определенных сочетаниях скорости и углов атаки несущей поверхности. Положение зон устойчивости обычно описывают для какого-либо конкретного случая в координатах a, v, а в обобщенном виде — в координатах a, CB (рис. 7, а, б). Первая граница зоны неустойчивости характерна возникновением преимущественно вертикальных колебаний. Для плоской пластины ее положение определяют по формуле:
aI = RICB Форм. 15
где:
- RI — коэффициент пропорциональности для границы I;
- aI — угол атаки, соответствующий границе I, рад.
Значение RI при изменении продольного момента инерции масс относительно центра масс судна меняется незначительно.
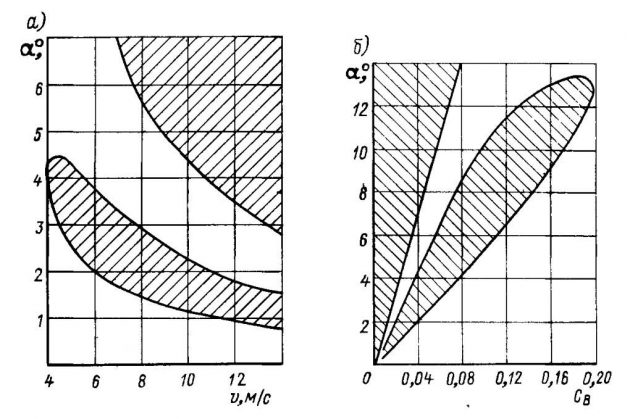
При С△ > 0,2:
В диапазоне С△ = 0,02+0,2:
Однако можно полагать RI постоянным для всех С△. В этом случае ошибка при расчете режимов устойчивости произойдет в безопасную сторону, т. е. образует некоторый запас устойчивости.
Область устойчивого глиссирования между границами I и II относится к режимам движения реданных глиссеров, экранопланов и гидросамолетов.
Вторая граница зоны неустойчивости характеризуется возникновением в основном угловых колебаний. Величина коэффициента пропорциональности для границы II RII зависит от угла поперечной килеватости корпуса. Влиянием нагрузки и массы судна можно пренебречь:
где
- β — угол килеватости, рад.
В соответствии с этим участки границы II с движением на полной ширине описываются формулой:
Третья граница характеризует пределы устойчивости движения безреданных глиссирующих судов. На положение границы устойчивости III влияют число Фруда, килеватость несущей поверхности и безразмерные коэффициенты массы и продольного момента инерции. Безразмерным коэффициентом массы в общем случае (глиссер без разгрузки) является коэффициент статической нагрузки С△. Для вычисления коэффициента продольного момента инерции сначала определяют сам момент инерции масс судна относительно поперечной оси, проходящей через центр масс. На практике пользуются формулой:
где:
- △L — величина шпации, принятой при построении кривой распределения масс;
- xi — абсцисса центра масс каждой шпации относительно общего центра масс;
- mi — ордината кривой распределения масс по длине судна.
Далее вычисляют безразмерный коэффициент продольного момента инерции I по формуле:
Формула для границы III:
При использовании этой формулы в случае FrB > 3 влиянием относительной скорости следует пренебречь, тогда:
Для практических целей целесообразно использовать эмпирическую формулу, полученную в результате испытания серии моделей Клемента и Блаунта:
В более удобном виде эта формула может быть представлена следующим образом:
Указанные зависимости получены для остроскулых катеров с плоскокилеватыми обводами, скорости которых в процессе испытаний не превышали FrV ~ 7. Решение вопроса об устойчивости глиссеров других форм и с другими скоростями движения (FrV > 7) требует специального исследования.
Особенности гидродинамики таких судов определяются наличием взаимовлияния корпусов в процессе движения, а также существенно большим, нежели у однокорпусных глиссеров, удлинением несущих поверхностей.
Взаимодействие двух корпусов приводит к изменению картины волно- и брызгообразования. Оно начинает проявляться, как только поперечное отстояние корпусов с становится меньше удвоенной ширины одного корпуса (с < 2В или
, где с — относительное отстояние корпусов).
По мере сближения корпусов между ними образуется волновой “петух”, который при
может начать замывать соединительную конструкцию. При с = 0,5 брызговые усы от несущих поверхностей могут начать замывать борта судна. В этих случаях сопротивление катамарана превышает удвоенное сопротивление одного изолированного корпуса. Если же при проектировании формы глиссирующего катамарана приняты меры против замывания корпуса и моста, сопротивление судна по сравнению с удвоенным сопротивлением одного изолированного корпуса снижается (рис. 8). Величина оптимального угла атаки с уменьшением
также уменьшается. Однако величина коэффициента момента m△ при этом остается такой же, как и для одного изолированного корпуса.

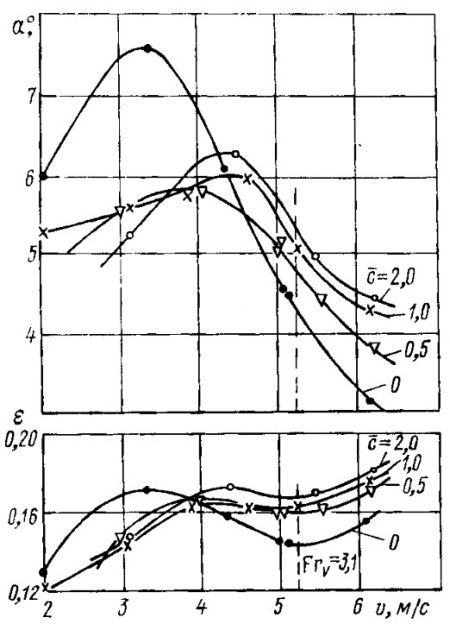
Килеватость несущих поверхностей при отсутствии замывов на изменение сопротивления не влияет (см. рис. 8). Указанная зависимость получена для серии остроскулых катамаранов с постоянной килеватостью по длине (моногедрон), имеющих углы килеватости β от 0 до 15°, С△ ~ 0,8, на скорости FrV = 3,1 при наивыгоднейших углах атаки (~5°). Характер изменения кривой сопротивления от скорости в зависимости от относительного отстояния корпусов показан на рис. 10 для модели с β = 0° и на рис. 3 для модели с 0 = 15°.
Сопоставление кривых сопротивления катамарана и однокорпусного глиссера, рассчитанных на одинаковые скорости движения, показывает заметное преимущество двухкорпусного судна по сопротивлению в районе горба. Это объясняется значительным влиянием на переходном режиме сопротивления формы, которое имеет меньшие значения для корпусов с большим удлинением.
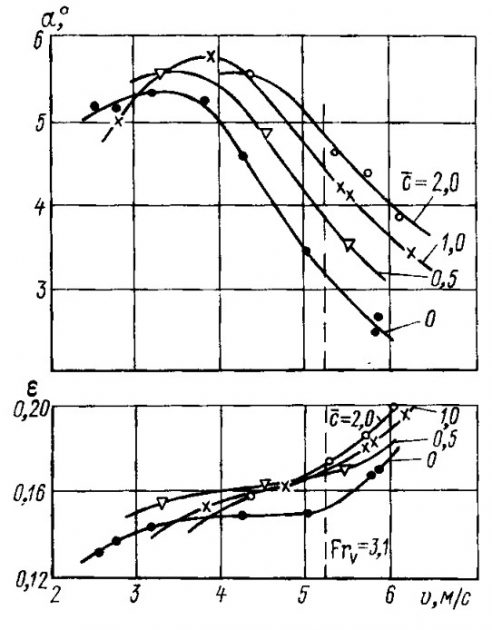
Поэтому можно считать целесообразным применение двухкорпусных компоновок при проектировании судов переходного режима движения. На высоких скоростях применение катамаранной схемы также дает известные преимущества. Они обусловлены тем, что однокорпусные глиссеры при больших числах Фруда движутся с углами дифферента, существенно меньшими (1—2°) оптимальных. Увеличение углов до ~5° возможно без потери устойчивости лишь за счет сужения несущей поверхности и зачастую неприемлемо по соображениям остойчивости. Поэтому скоростной глиссер-катамаран может оказаться быстроходнее однокорпусного глиссера.
Читайте также: Малые суда парусного типа
На рис. 11 показаны кривые сопротивления моделей с однотипными обводами, имеющими симметричную и асимметричную формы корпусов.
К Определение корпусных характеристик в момент взаимодействия судна с водной поверхностьюособенностям гидродинамики катамаранов следует отнести также их повышенные мореходные качества. Сравнительное экспериментальное исследование остроскулых одно- и двухкорпусной модели одинаковой килеватости на регулярном волнении показало существенное преимущество катамарана по величинам вертикальных ускорений.
Так, на скорости FrV = 3 перегрузки катамарана были меньше в 1,44 раза в носу и в 1,2 раза в центре масс. При скоростях FrV = 3,8 соотношение перегрузок достигает 1,74 в носу и 1,68 в центре масс.
Следует отметить, что отстояние корпусов влияет на величины максимальных перегрузок катамарана. Если вертикальные ускорения двухкорпусной модели с
принять за единицу, то для случая с
они составят 1,15, а для
. Весьма своеобразно на величины перегрузок катамарана влияет килеватость корпусов. Если сравнивать модели с разной килеватостью, но имеющие одинаковое сопротивление на тихой воде, то килеватые корпуса должны будут иметь большую ширину. Вследствие этого на волнении, несмотря на благоприятное влияние килеватости, перегрузки моделей с большой килеватостью оказываются большими, чем у более узких плоских пластин.
В качестве примера на рис. 12 приведен график изменения величин максимальных перегрузок призматических моделей при оптимальных центровках. Практика подтверждает целесообразность принятия для глиссирующих катамаранов минимальных значений килеватости на транце и на миделе.
Все сказанное относится к судам с коэффициентами статической нагрузки 0,6—0,8 и более, рассчитанными на скорости переходного режима и начала чистого глиссирования.
Приближенные способы расчета сопротивления движению малого судна
Применяемые методы приближенного расчета сопротивления движению судов можно разделить на следующие группы.
- Методы непосредственного расчета полного сопротивления R или буксировочной мощности NR по обобщенным эмпирическим зависимостям, а также средней достижимой скорости движения v в функции энерговооруженности судна N/D по статистическим данным для данного типа судна.
- Методы пересчета остаточного сопротивления по данному прототипу.
- Методы расчета остаточного сопротивления Ro по результатам буксировочных испытаний систематических серий моделей судов в опытовом бассейне.
Наименее точны методы первой группы из-за несоблюдения геометрического подобия и из-за ошибок, связанных с неточным определением сопротивления трения Rт, составляющего обычно значительную часть полного сопротивления.
Неточность методов второй и третьей группы определяется невозможностью обеспечения полного геометрического соответствия элементов судна либо прототипу, либо моделям систематической серии. Частично эта неточность может быть скорректирована в расчете применением ряда поправочных коэффициентов.
Если определены составляющие полного сопротивления движению судна, то буксировочная мощность:
При этом потребная эффективная мощность двигателя:
где:
- η = 0,50÷0,70 — коэффициент полезного действия движителя;
- ηв = 0,95÷0,98 — коэффициент полезного действия валопровода;
- ηp — коэффициент полезного действия редуктора.
Его можно принимать равным 0,97—0,98 при одной паре шестерен; 0,96—0,97 — при цепной передаче и 0,95—0,97 — при клиноременной передаче. При выборе метода следует исходить из условия предпочтительности использования материалов, полученных для судов или моделей, наиболее близких к рассматриваемому.
Наиболее обоснованным следует считать применение зависимостей, структура которых соответствует законам гидродинамического подобия, например Волновое сопротивлениеформула расчета волнового сопротивления. При этом роль характерной площади может играть смоченная поверхность судна Ω или его объемное водоизмещение в степени (2/3)—V2/3.
Для получения большей достоверности целесообразно использовать зависимости для пересчета только величины остаточного сопротивление Ro, а сопротивление трения Rт рассчитывать по методике, приведенной в статье Сопротивление движению малого судна“Сопротивление водоизмещающих судов”.
Расчет сопротивления водоизмещающего судна
При предварительной оценке скорости и полной мощности малых судов допустимо использовать обобщенные эмпирические зависимости, связывающие скорость, мощность и размеры судна.
При этом нужно помнить о статистической природе формул, приводящей к заметным погрешностям (формулы первой группы). Для малых водоизмещающих судов с удельной энерговооруженностью Nэ/D ≤ 10 кВт/т используют формулу:
где:
- Nэ — эффективная мощность двигателя, т. е. формула включает в себя и среднее значение общего пропульсивного коэффициента.
Результат расчета скорости для судов длиной L = 3-5 м может оказаться заниженным на 15—20 %, при L > 6 м скорость завышается на ~10 %.
Если у проектируемого судна есть близкий прототип, можно применить формулу адмиралтейских коэффициентов (вторая группа методов). Выражение имеет вид:
где:
- Се — адмиралтейский коэффициент.
Вычисления производят следующим образом:
- по данным прототипа вычисляют значение Се;
- подставляя найденный адмиралтейский коэффициент в формулу для проектируемого судна, находят NR.
При использовании метода адмиралтейских коэффициентов необходимо обеспечить равенство чисел Фруда и соответствие углов дифферента одного и другого судна. Формула адмиралтейских коэффициентов имеет следствием зависимость, которая позволяет найти для судна, имеющего скорость vo и мощность двигателя No, новую скорость v с другим двигателем N при том же водоизмещении V:
Формула (5) справедлива в том случае, когда изменение мощности не приводит к изменению режима движения судна.
Более точные результаты получают при определении сопротивления корпуса судна по отдельным составляющим (третья группа методов). Сопротивление трения определяют как сопротивление трения эквивалентной пластины, а остаточное сопротивление находят по результатам экспериментальных исследований.
Форма представления этих результатов может быть графической или аналитической в виде аппроксимирующей формулы). При этом в качестве аргументов обычно фигурируют число Фруда и относительное удлинение. В некоторых случаях, когда испытывались суда близкой или геометрически подобной формы, ограничиваются одним аргументом — числом Фруда. Расчет сопротивления голого корпуса производят в указанной ниже последовательности.
По заданным D, L, В, Т, δ, v, t° воды определяют:
- FrL (см. формулу Сопротивление движению малого судна“записи числа Фруда”);
- gD;
- Ro/gD (см. формулы Сопротивление движению малого судна“Сопротивление формы”, “формула Палмеля”Сопротивление движению малого судна, формулы 34—37 в статье Сопротивление движению малого судна“Волновое сопротивление”, формула 6 или графики на рис. Сопротивление движению малого судна“График для определения остаточного сопротивления буксиров и траулеров (диаграмма Неймана)”, и рисунки 6, 7);
- Ro = (3)·(2) Н;
- v (см. рис. Сопротивление движению малого судна“Зависимость коэффициента кинематической вязкости воды от температуры”);
- Re (см. формулу Сопротивление движению малого судна“Отношение инерционных сил к силам вязкостной природы”);
(см. Сопротивление движению малого суднаформулу Прандтля—Шлихтинга, рис. Сопротивление движению малого судна“Коэффициенты турбулентного трения гидродинамически гладкой пластины”);
(см. Сопротивление движению малого судна“Значения надбавки на шероховатость △ζт“);
(см. формулу Сопротивление движению малого судна“Величина сопротивления трения эквивалентной пластины”);
- Ω (см. формулы 17-21 в статье Сопротивление движению малого судна“Составляющие сопротивления движению судна”);
(см. формулу Сопротивление движению малого судна“Определение величины сопротивления трения эквивалентной пластины”);
.
Полученное значение сопротивления голого корпуса используют с учетом добавок на сопротивление выступающих частей и аэродинамическое сопротивление в расчете буксировочной мощности. Ниже приведены материалы, которые можно использовать в расчетах по приведенной методике.
Формула остаточного сопротивления шлюпок. Для спасательных шлюпок, имеющих вместимость 20—99 чел., скорость FrL ≤ 0,4, L/B = 2,25÷3,2, В/T = 3,3÷5,0, δ = 0,485÷0,570 и симметричных относительно миделя, получена формула остаточного сопротивления на единицу веса судна:
При расчете Rт смоченная поверхность может быть подсчитана по формуле С. П. Мурагина. Надбавка на шероховатость и сопротивление выступающих частей для деревянных шлюпок с обшивкой внакрой составляет (1,0÷1,2)·10-3, для шлюпок с металлической обшивкой и деревянной вгладь (0,7÷0,8)·10-3.
Диаграмма Неймана может быть использована для определения величины остаточного сопротивления буксиров, рыболовных или близких к ним по форме судов (см. рис. Сопротивление движению малого судна“График для определения остаточного сопротивления буксиров и траулеров (диаграмма Неймана)”). На вертикальной оси диаграммы отложены значения отношения Ro, Н, к весовому водоизмещению судна gD<, кг.
Формулы Папмеля позволяют определить остаточное сопротивление как сумму сопротивления формы и волнового сопротивления. Для этого нужно дополнительно вычислить площадь погруженной части мидель-шпангоута, длину кормового заострения, а также произвести промежуточные вычисления по формулам Сопротивление движению малого судна“Вычисление скорости”, Сопротивление движению малого судна“Коэффициент х в зависимости от характеристики судна”. Сопротивление формы рассчитывают с использованием формул 25, 27 в статье Сопротивление движению малого судна“Сопротивление формы”, а волновое — по формуле Сопротивление движению малого судна“Волновое сопротивление формы” или Сопротивление движению малого судна“Вариант волнового сопротивления формы”. Полученные результаты суммируют и используют как значение Ro. Дальнейший расчет производится как и в предыдущих случаях по приведенной схеме.
Методика В. А. Дубровского может быть использована для расчета остаточного сопротивления водоизмещающих катамаранов. Она основана на применении коэффициентов, учитывающих взаимодействие корпусов.
Исходной величиной для расчета коэффициента остаточного сопротивления катамарана с отстоянием корпусов с является коэффициент остаточного сопротивления
одного изолированного корпуса.
Он может быть найден экспериментально или, например, по графику (рис. 13), где построены кривые удельного остаточного сопротивления судов с большим относительным удлинением l в зависимости от числа Фруда.
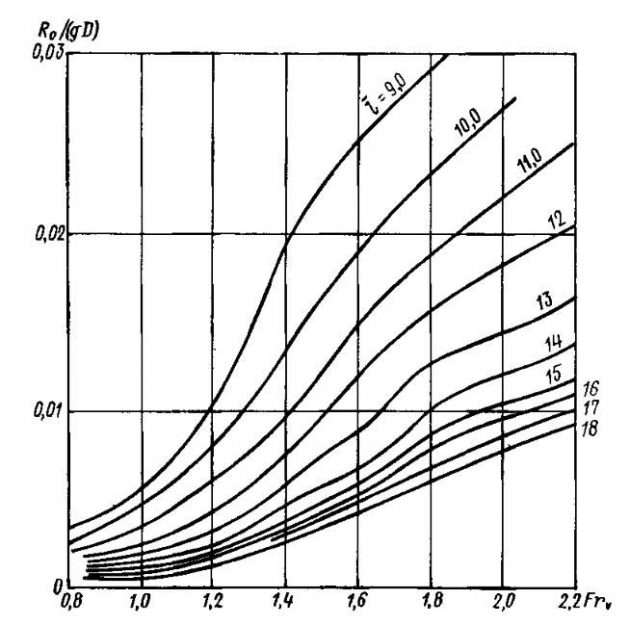
Для расчета предварительно определяют относительное удлинение одного корпуса и число Фруда по объемному водоизмещению FrV. Затем используя график (рис. 13), определяют Ro одного корпуса. Остаточное сопротивление катамарана Rо.кат находят по формуле:
где:
- k — коэффициент, учитывающий взаимовлияние корпусов (рис. 14).
Расчет сопротивления судна, движущегося в переходном режиме
Для предварительной оценки скорости судов в переходном режиме можно использовать формулу, пригодную в диапазоне относительной энерговооруженности Nэ/D = 10÷30 кВт/т:
Скорость более легких судов с V-образными плоскокилеватыми обводами водоизмещением до 5 т в конце переходного режима и начале глиссирования (при FrL = 0,8÷2,7) можно вычислить по формуле Ю. В. Емельянова:
Точность формулы ± 10%.
Формула адмиралтейских коэффициентов для малого судна, движущегося в конце переходного режима и начале глиссирования, имеет вид (2-я группа методов):
Последовательность вычислений та же, что и для формулы 4.
При использовании метода адмиралтейских коэффициентов следует особое внимание уделить помимо равенства чисел Фруда соответствию центровки прототипа и проектируемого судна. При этом для судов указанного режима движения ходовой дифферент определяется не столько отношением xg/L, сколько величиной m△.
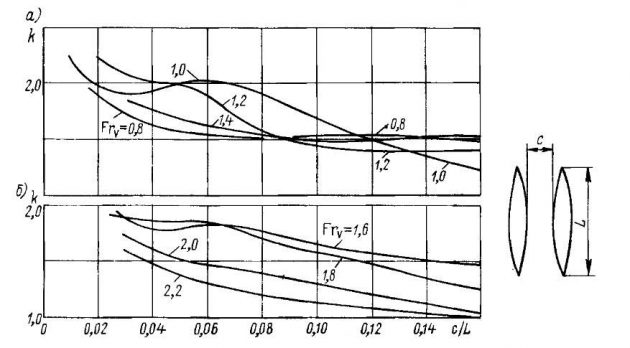
а — в диапазоне FrV = 0,8÷1,6; б – в диапазоне FrV = 1,6÷2,2
Справедливость указанного выражения обеспечивается только при равенстве углов дифферента судна на скоростях v и vo.
В тех случаях, когда необходимо пересчитать cкорость данного судна при изменении мощности или вычислить мощность для другого значения скорости при условии постоянства водоизмещения, применяют формулу:
Поэтому для новой скорости движения должно быть найдено соответствующее значение m△.
Указанные методы могут быть употреблены только для получения результата в первом приближении. Более точные способы основаны на определении сопротивления судна по составляющим с использованием экспериментальных данных (по остаточному сопротивлению). Расчет производят в указанной ниже последовательности.
По данным D, V, L, B, T, δ, v, t° воды определяют:
- FrV;
- gD;
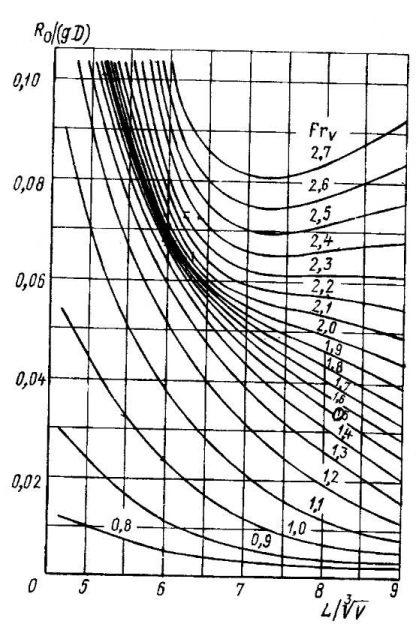
- Ro/(gD) (см. рис. 8—16);
- v (см. рис. Сопротивление движению малого судна“Зависимость коэффициента кинематической вязкости воды от температуры”);
- Re (см. формулу для определения Сопротивление движению малого судначисла Рейнольдса);
- (см. рис. Сопротивление движению малого судна“Коэффициенты турбулентного трения гидродинамически гладкой пластины”);
- (см. Сопротивление движению малого судна“Значения надбавки на шероховатость △ζт“ и Способы расчета управляемости маломерного судна“Примеры расчета управляемости малых судов”);
- Ω [по теоретическому чертежу, таблица Сопротивление движению малого судна“Определение смоченной поверхности корпуса судна” или по формулам 17-21 в статье Сопротивление движению малого судна“Составляющие сопротивления движению судна”];
(см. формулу Сопротивление движению малого судна“Определение величины сопротивления трения эквивалентной пластины”);
.
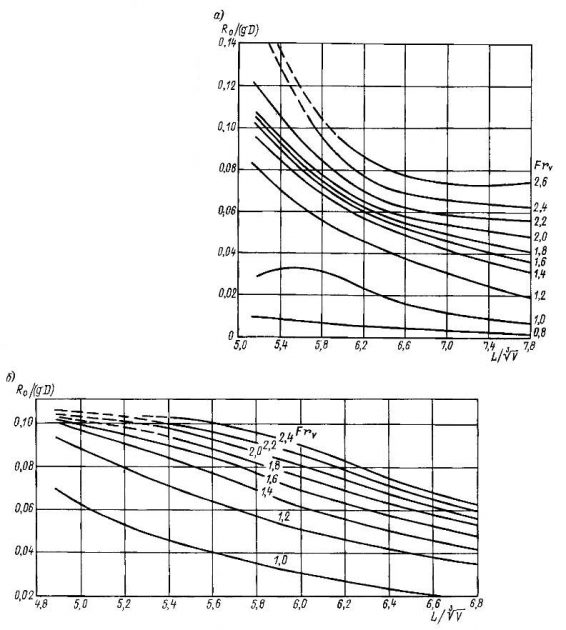
Далее к сопротивлению голого корпуса добавляют сопротивление выступающих частей и аэродинамическое сопротивление.
В расчетах по данной методике можно с успехом использовать приведенные ниже материалы.

Диаграммы Брауна применяют для определения остаточного сопротивления судов, имеющих L/B = 3,5÷7,4, В/Т = 3,1÷4,4, δ = 0,29÷0,54 и движущихся в конце режима плавания и переходном режиме. На рис. 15 приведены диаграммы для судов с U и V-образными обводами. Для использования кривых необходимо предварительно вычислить величины
и FrV. На каждой кривой обозначено соответствующее ей значение числа Фруда; промежуточные величины получают методами графической интерполяции. Вдоль вертикальной оси диаграмм отложены значения относительного остаточного сопротивления Ro на единицу весового водоизмещения.
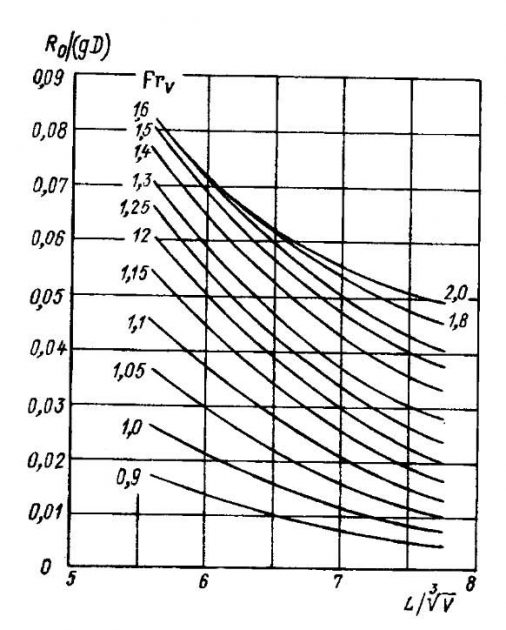
Диаграмма Н. С. Володина, построенная на основании большого экспериментального материала, позволяет определить остаточное сопротивление круглоскулых быстроходных катеров в зависимости от
для ряда значений FrV (рис. 16). Величина Ro, отнесенная к весу судна gD, т·м/с², отложена вдоль вертикальной оси диаграммы. Для промежуточных величин числа Фруда результат получают методом графической интерполяции. Расчет сопротивления трения производят по смоченной поверхности корпуса, соответствующей статическому положению судна.
Систематическая серия Нордстрема опубликована автором в 1936 г. по результатам испытаний 14 круглоскулых моделей, характеристики которых имели следующие значения:
- L/B = 4,83÷6,94;
- B/T = 3,16÷3,57;
- δ = 0,373÷0,410;
- φ = 0,576÷0,599;
- хc = -1,79÷2,88 %;
- aн = 15,1÷22,5°.
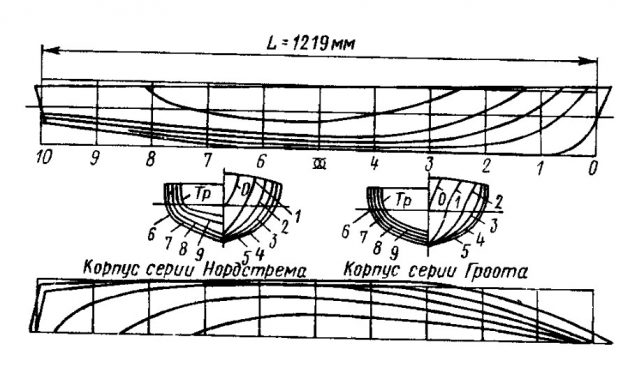
Значения безразмерного коэффициента Ro/(Dg) в зависимости от относительного удлинения и числа Фруда по объемному водоизмещению представлены на рис. 10 (см. примечание 1). В настоящее время результаты серии Нордстрема применяются в основном для катеров водоизмещением 10—30 т. Теоретический чертеж модели Нордстрема показан на рис. 18.
Систематическая серия Гроота опубликована в 1951 г. по данным испытаний 31 модели круглоскулых быстроходных катеров. Геометрические характеристики корпусов следующие:
- L/B = 3,53÷10,09;
- B/T = 2,72÷6,58;
- δ = 0,293÷0,560;
- φ = 0,463÷0,791;
- хc = -11,5÷3,09 %;
Материалы испытаний Гроота (рис. 19) широко используются в настоящее время как образцовые при разработке новых форм быстроходных катеров. Теоретический чертеж модели Гроота приведен на рис. 18 (см. примечание 1).
Серия 63. Результаты испытаний пяти моделей 15-метрового катера многоцелевого назначения были опубликованы в 1963 г. Это систематическая серия, в которой у теоретических чертежей всех моделей проекции “корпус” геометрически подобны. Модели имеют расчетные значения L/B = 2,5; 3,0; 4,0; 5,0; 6,0 (рис. 20). Поскольку каждая модель испытывалась с разными значениями нагрузки, величины L/B, B/T, δ и φ в процессе опытов несколько изменялись (табл. 1).
Будет интересно: Маломерные суда с механическим двигателем
Данные серии 63 наглядно иллюстрируют влияние основных характеристик корпуса на сопротивление и поэтому могут быть с пользой применены при выборе главных размерений судна.
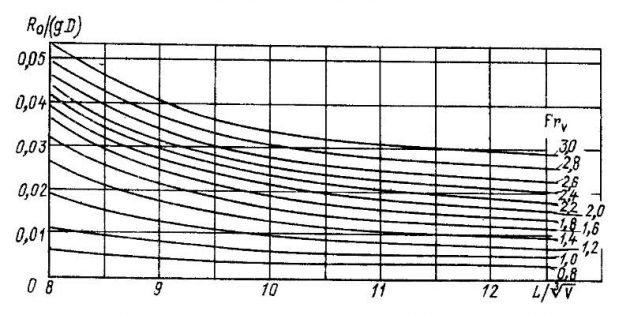
Серия 64. Результаты испытаний 27 моделей быстроходных круглоскулых катеров в Тейлоровском бассейне опубликованы в 1965 г. Это систематическая серия моделей, в процессе испытаний которой варьировались относительное удлинение, отношение ширины к осадке и коэффициент общей полноты.
Модели имеют:
- L/B = 8,454÷18,264;
- В/Т = 2,0÷4,0;
- δ = 0,35÷0,55;
- φ = 0,63;
- αн = 3,7÷7,8;
Кривые коэффициента остаточного сопротивления в функции от числа Фруда и относительного удлинения представлены на рис. 21 (см. примечание 1).
Данные по серии 64 часто используют для целей проектного исследования. Они также с успехом могут быть применены в расчетах ходкости двухкорпусного судна. При этом необходимо дополнительно учесть взаимодействия корпусов по методике, изложенной в статье Гидроаэродинамика парусного судна“Аэродинамика и гидродинамика парусного судна”.
Серия Шведского опытового бассейна (SSPA). В 1968 г. Линдгрен и Вильямс получили результаты систематической серии из девяти моделей быстроходных круглоскулых катеров.
Параметры формы корпуса имели следующие значения:
- L/V1/3 = 6, 7, 8;
- B/T = 3,0; 3,5; 4,0;
- δ ∼ 0,4;
- φ = 0,68;
- хg = 4,15;
- aн = 8,2÷14,4°;
Результирующие значения L/В составляли от 4,62 до 8,20 в зависимости от номера модели и ее загрузки. Кривые безразмерного коэффициента остаточного сопротивления приведены на рис. 15 (см. примечание 2).
Серия Британской национальной физической лаборатории (NPL). Данные, опубликованные Мэрвудом и Бэйли в 1969 г. и Бэйли в 1976 г., представляют собой результаты испытаний систематической серии из 22 моделей с различными значениями L/B и B/T.
Величины L/B составляли:
- 3,33;
- 4,54;
- 5,41;
- 6,25;
- 7,50.
Значения B/T изменялись от 1,72 до 6,87.
Все остальные параметры формы корпуса поддерживались постоянными: δ = 0,397, φ = 0,693, хc = —6,4%. Результаты приведены на рис. 16 (см. примечание 2). Помимо приведенных материалов существуют широко известные графики Хеншке. Они представляют собой диаграммы изменения буксировочной мощности в функции скорости для разных значений относительного удлинения.
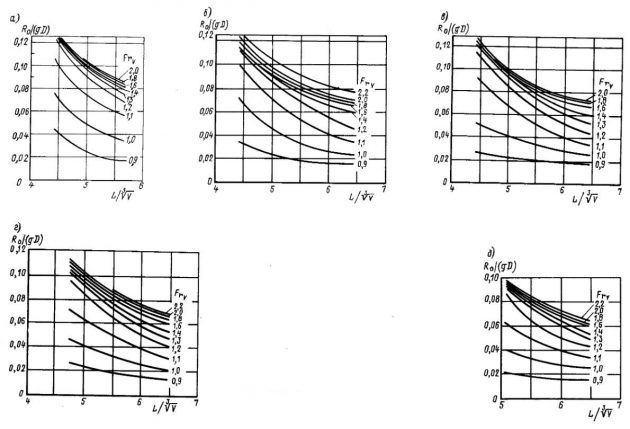
a – 2,5; б – 3,0; в – 4,0; г – 5,0; д – 6,0
Графики построены на основании анализа большого числа судов и отображают средние значения буксировочной мощности хорошо выполненных судов. Поскольку эти данные относятся к судам с устаревшими формами обводов, графики Хеншке здесь не приводятся. Результаты, полученные по данным Хеншке, нужно рассматривать только как ориентировочные.
Предлагается к прочтению: Управляемость малого судна
Примечание 1. Экспериментальные данные обработаны с применением принятой в американском судостроении кривой Шенхерра, которая может быть выражена формулой вида:
Коэффициенты
, полученные по формуле Шенхерра незначительно отличаются от принятой в отечественном судостроении формулы Прандтля—Шлихтинга.
Примечание 2. Экспериментальные данные обработаны с применением формулы коэффициента турбулентного трения, рекомендованного Международной конференцией опытовых бассейнов (Мадрид, 1957 г.):
Расчет сопротивления судна, движущегося в режиме чистого глиссирования
Для предварительной оценки скорости глиссирующих остроскулых катеров с плоскокилеватыми обводами, имеющими L/B = 2,8÷3,5, С△ = 0,10÷0,25 и энерговооруженность N/D = 15÷90 кВт/т, можно пользоваться формулой, разработанной Л. Л. Романенко и Л. С. Щербаковым на основании статистических данных:
Хорошие результаты можно получить при использовании формулы Л. М. Кривоносова:
где:
- сk — коэффициент:
- для малых безреданных глиссеров сk = 1,7;
- для однореданных глиссеров сk = 2,0;
- для трехточечных гоночных глиссеров сk = 2,3.
Скорость реданных глиссеров при FrV > 3 можно оценить по формуле А. И. Мартынова:
Формула адмиралтейских коэффициентов для глиссеров, движущихся с большими числами Фруда (FrV > 4), имеет следующий вид:
Если известны vo и No глиссера, то новая скорость v с другим двигателем N при том же водоизмещении может быть определена по формуле:
Формулы адмиралтейских коэффициентов с повышением скорости судна дают все менее надежный результат, так как при этом возрастает влияние неучитываемых моментов гидродинамических и аэродинамических сил, аэродинамической составляющей сил сопротивления и поддержания, а также изменения сопротивления выступающих частей. Поэтому для получения более достоверных значений сопротивления следует использовать методы третьей группы — расчеты по данным испытаний систематических серий схематизированных моделей.
При расчете гидродинамических характеристик и сопротивления возможны две основных схемы решения задачи:
- первый — когда для выбранных водоизмещения, ширины, центровки и скорости требуется определить сопротивление движению;
- и второй — когда для выбранного режима движения нужно вычислить необходимое значение центровки.
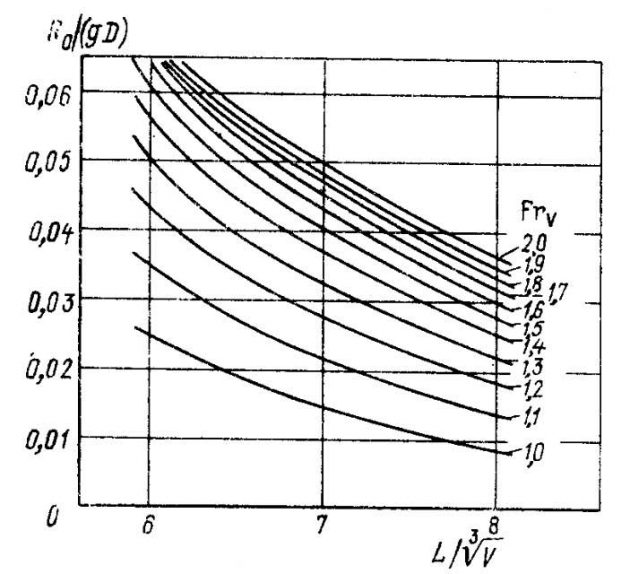
Схема I. Известны D, В, xg судна и скорость v. Требуется определить углы дифферента и сопротивление движению.
Находят FrB по формуле Сопротивление движению малого судна“форма записи числа Фруда”, m△ по формуле 6, λ по графику на рисунке 3. По найденному значению λ с учетом FrB определяют по графику на рисунке 2 величину CB/a. Находят CB, вычисляют a.
| Таблица 1. Характеристики моделей серии 63 | |||||||
|---|---|---|---|---|---|---|---|
| Модель (см. рис. 13) | L/B | B/T | δ | φ | xg | aH,° | |
| а | 2,52-2,70 | 6,64-9,20 | 0,383-0,464 | 0,577-0,642 | 0,30-3,4 | 22,6-27,9 | 3,21-3,65 |
| б | 2,95-3,31 | 5,44-9,50 | 0,393-0,520 | 0,591-0,690 | 0,0-4,63 | 18,8-27,5 | 2,91-3,81 |
| в | 3,76-4,10 | 3,76-7,14 | 0,462-0,586 | 0,647-0,734 | 3,11-4,95 | 17,2-28,6 | 2,64-3,25 |
| г | 4,62-4,92 | 3,21-5,59 | 0,512-0,623 | 0,690-0,764 | 3,55-4,94 | 16,9-27,7 | 2,57-2,93 |
| д | 5,48-5,75 | 2,89-4,34 | 0,549-0,636 | 0,740-0,744 | 5,33-5,80 | 17,4-25,3 | 2,57-2,77 |
Далее определяют сопротивление нормальных давлений Rд (Формула 51) и сопротивление трения Rт [см. формулу Сопротивление движению малого судна“Определение величины сопротивления трения эквивалентной пластины”] (точнее, сопротивление трения эквивалентной пластины
). При этом число Re вычисляют по смоченной длине l см = λВ, смоченную поверхность судна — по формуле (Формула 50). Надбавки на шероховатость принимают с учетом рекомендаций в статье Сопротивление движению малого судна“Сопротивление движению судна – виды и понятия”. Полное сопротивление голого корпуса глиссера составит:
К нему необходимо прибавить аэродинамическое сопротивление и добавки на сопротивление выступающих частей согласно соответствующим рекомендациям.
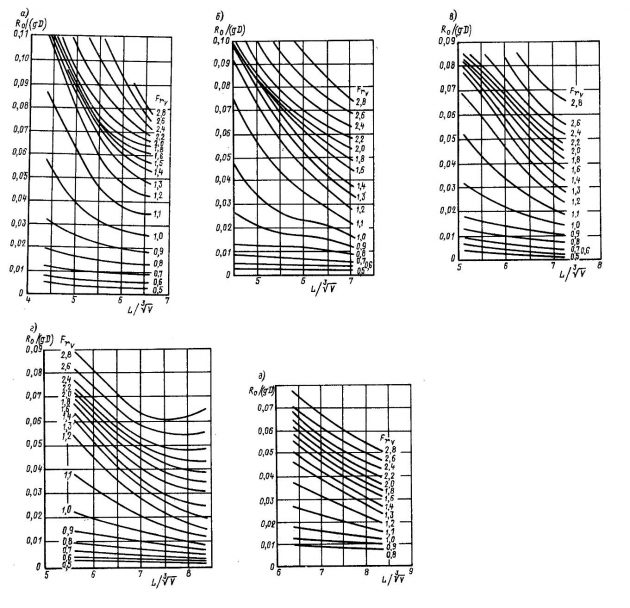
a – L/B = 3,3; B/T = 3,19÷10,21; б – L/B = 4,54; B/T = 1,72÷6,87; в – L/B = 5,41; B/T = 1,94÷4,86; г – L/B = 6,25; B/T = 1,93÷5,80; д – L/B = 7,50; B/T = 2,01÷4,02
В случае если судно имеет несущую поверхность, значительно отличающуюся от плоской пластины, в процессе расчета величин λ и α необходимо ввести поправки на килеватость по формулам И. П. Любомирова:
Схема II. Известны D, B, скорость v и принятое проектантом значение α. Требуется определить необходимое для этого xg.
Находят FrB по формуле Сопротивление движению малого судна“форма записи числа Фруда”, СB по формуле 46. Вычисляют СB/α. По графику на рис. 2 находят смоченное удлинение λ. По графику на рисунке 3 для известных λ и FrB определяют m△. Вычисляют xg по формуле 6.
В процессе проектирования судна часто ставится задача нахождения гидродинамически наивыгоднейших значений ширины и относительной центровки. В этом случае расчет производят по схеме I для ряда значений В и xg. По результатам расчета строят график ∈ = f(В, xg) и определяют искомые величины методами графической интерполяции. Однако такой подход требует большого объема вычислений.
Графики на рис. 24, построенные на основе формул 13 и 14 в безразмерном виде, позволяют не только найти нужные сочетания ширины и центровки, но и выбрать желаемый характер изменения сопротивления по скорости судна. Эти графики наглядно иллюстрируют влияние коэффициентов момента и статической нагрузки, а также числа Фруда на углы атаки и сопротивление глиссирующих пластин. В случае непосредственного использования предлагаемых кривых для определения сопротивления глиссера следует учитывать, что при их построении принят суммарный коэффициент трения:
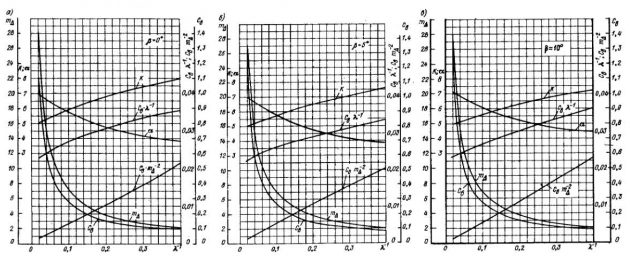
За рубежом при проектировании глиссеров широко используются материалы Е. П. Клемента. Наиболее интересны графики, построенные им для определения параметров глиссирования в гидродинамически наивыгоднейших режимах. Кривая гидродинамического качества на этих графиках — огибающая максимумов гидродинамического качества пластин с систематически изменяющимися параметрами (рис. 25, 26).
Рекомендуется к прочтению: Портативные лодки малого типа
Материалы получены численным расчетом по эмпирическим формулам для судна водоизмещением 4 т. Пренебрегая незначительными погрешностями, их можно использовать на стадии эскизного проектирования для судов водоизмещением от 0,4 до 40 т.
В некоторых случаях удобно пользоваться аппроксимирующими формулами, построенными по данным Клемента для наивыгоднейших режимов.
Предлагаем уравнение оптимальных центровок:
и уравнения гидродинамического качества:
- для β = 0°:
- для β = 5÷10° (осредненная кривая, ± 2 %):
При проектировании глиссирующего судна, имеющего сложные обводы, а также в тех случаях, когда по скорости судно не достигает режима чистого глиссирования, использование представленных материалов приведет к большим погрешностям. Поэтому в указанной ситуации неизбежны испытания модели судна в опытовом бассейне. Перенос результатов эксперимента на натурное судно производят по законам гидродинамического подобия.

Следует помнить, что характер обтекания моделей небольших размеров определяется дополнительно еще и силами поверхностного натяжения. Это не только увеличивает масштабный эффект, но и меняет картину волно- и брызгообразования. Поэтому рекомендуется испытывать модели шириной не менее 0,3 м.

При обработке результатов эксперимента иногда трудно бывает выделить составляющую трения из полного сопротивления модели судна. Это происходит, когда модель имеет сложную конфигурацию днища, либо когда в процессе замеров невозможно точно зафиксировать площадь смоченной поверхности. В этих случаях при равенстве чисел Фруда модели и натуры пересчитывают полное сопротивление по кубу масштаба. Возникающая при этом неточность часто бывает вполне допустима, тем более что она направлена в безопасную сторону.
Помимо приведенных материалов полезно также использовать графики Клемента, позволяющие определить сопротивление глиссера при любых углах дифферента. В этой монографии также приводится основное содержание методики по расчету сопротивления глиссеров, разработанной на основе испытания серии моделей больших (БК) и малых (МБК) глиссирующих катеров. Данную методику можно использовать в тех случаях, когда проектируемое судно имеет коэффициенты нагрузки и центровки, не выходящие за границы, оговоренные в работе, а также весьма близко по конфигурации корпуса к испытанным моделям. При применении указанных материалов необходимо помнить, что параметры движения моделей серии определялись рядом заранее заданных значений нагрузки и центровки и только в отдельных случаях близки к оптимальным.
