Исследования прочности плавучих доков проводятся модельным и экспериментальным путем для определения упругой линии корпуса дока и других технических данных.
Определение упругой линии корпуса дока
Полная стрелка прогиба корпуса дока от изгиба складывается из стрелки прогиба от действия изгибающего момента v1 и стрелки прогиба от действия перерезывающей силы v2 (таблица):
Стрелка прогиба от продольного изгиба определяется уравнением
где:
- M0 и I0 — величины, введенные для приведения подынтегральных выражений к безразмерному виду (например, изгибающий момент и момент инерции на миделе дока);
- Mх и Iх — соответственно изгибающий момент и момент инерции в сечении с координатой х, отсчитываемой от одной из оконечностей дока.
Стрелка прогиба от сдвига определяется уравнением
где:
- Nх — перерезывающие силы, действующие в корпусе дока;
- ωх — приведенная суммарная площадь стенок дока (бортов и внутренних стенок башен).
| Схема вычисления стрелок прогиба от изгиба и сдвига | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| № сечений i | Изгибающий момент Mx, тм | Момент инерции Ix м4 | Интегральная сумма(4) | Интегральная сумма(5) | (6)-(7),т/м3 | Nx,т | |||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 0 | 0 | 0 | 0 | 0 | 0 | ||||
| 2 | |||||||||
| 4 | |||||||||
| 6 | |||||||||
| 8 | |||||||||
| 10 | |||||||||
| 12 | |||||||||
| 14 | |||||||||
| 16 | |||||||||
| 18 | |||||||||
| 20 | (6)20 | (6)20 | 0 | 0 | |||||
| Схема вычисления стрелок прогиба от изгиба и сдвига (Продолжение) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| № сечений i | Sx,м3 | δx,м | Интегральная сумма(14) | (16)-(15),т/м2 | ||||||
| 1 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | ||||
| 2 | ||||||||||
| 4 | ||||||||||
| 6 | ||||||||||
| 8 | ||||||||||
| 10 | ||||||||||
| 12 | ||||||||||
| 14 | ||||||||||
| 16 | ||||||||||
| 18 | ||||||||||
| 20 | 15(20) | 15(20) | 0 | 0 | 0 | 0 | ||||
Для приближенного вычисления максимальной стрелки прогиба от изгиба можно пользоваться формулой акад. Ю. А. Шиманского:
Максимальное значение стрелки прогиба от сдвига для дока как для призматической балки (I = I0 = const) можно вычислить по формуле, получаемой из уравнения (Формула 3):
Таким образом, полная стрелка прогиба дока от продольного изгиба с учетом сдвига может приближенно определяться по формуле
Сказанное выше о вычислении стрелки прогиба от общего продольного изгиба может быть применено к вычислению стрелки прогиба от общего поперечного изгиба, если поперечный набор понтона дока представляет собой сплошные флоры (переборки).
О вычислении деформаций (в том числе температурных) ферм, рам, составных стержней см. Расчет общей поперечной прочности сухого дока
При учете влияния «гибкости» дока на силы поддержания (см. Расчет общей продольной прочности дока) стрелку прогиба можно вычислить по формуле
где:
для продольного изгиба:
«Гибкость» дока следует учесть при тарировании прогибомера и постановке на нем начального прогиба и тщательно вычислить изгибающие моменты и перерезывающие силы, действующие на док в момент установки прогибомера.
Читайте также: Некоторые вопросы по эксплуатации плавучих доков
При несимметричной относительно диаметральной плоскости нагрузке дока (см. Продольная прочность докаРасчет общей продольной прочности дока) прогиб рекомендуется вычислять для каждой башни отдельно, а наблюдение вести за прогибом наиболее загруженной башни.
Определение температурных напряжений и деформаций в корпусе дока
Способы определения температурных напряжений и деформаций при заданном распределении температур применительно к вопросам судостроения разработаны А. В. Масягиным и акад. Ю. А. Шиманским, а также изложены А. А. Курдюмовым.
Пусть:
- t° (х, у, z) — закон распределения температурного поля по корпусу дока;
- α — коэффициент линейного расширения материала корпуса (для стали α = 11,5 × 10-6 1/град.);
- ε’ — линейная температурная деформация, связанная с температурными напряжениями, законом Гука;
- ε — полная линейная температурная деформация, подчиняющаяся гипотезе плоских сечений.
Если закон распределения температурного поля по высоте и ширине корпуса является линейным, т.е:
температурные напряжения в корпусе равны нулю. Однако равенство нулю температурных напряжений не означает равенство нулю температурных деформаций. Если дополнительные деформации, вызывающие нормальные напряжения, равны нулю, т.е
полная относительная деформация топ-палубы будет равна
Полная относительная деформация днища соответственно будет равна
Полная относительная деформация нейтральной оси будет равна
Радиус кривизны дока определится из Соотношения (рисунок ниже):
откуда
Из определения радиуса кривизны балки известно, что
Таким образом, фиктивный момент Мy, определяющий температурный прогиб балки (дока), будет равен
Пользуясь приближенной формулой для прогиба дока под действием постоянного по длине фиктивного момента Мy (при параболической упругой линии), получим:
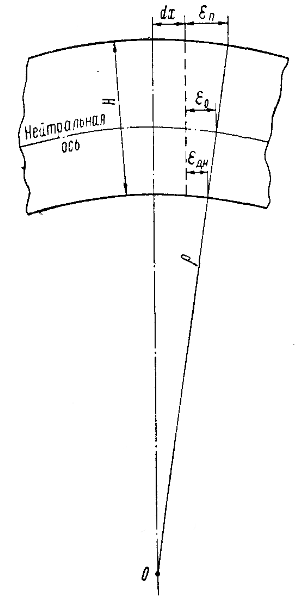
Следует обратить также внимание на температурные деформации при стоящем в доке судне. Если разность температур воздуха и воды обозначить через
а разность температур палубы и днища стоящего в доке судна через
где в обоих случаях под tп понимается температура палуб дока и судна на солнце, разность прогибов дока и судна выразится формулой
Во всех приведенных выше формулах не учитывается влияние на продольный температурный изгиб дока нагрева или охлаждения стапель-палубы, температура которой обычно равна температуре топ-палубы, т. е. принят линейный закон распределения температуры по высоте дока.
При определении поперечного температурного изгиба дока учитывается разность температур стапель-палубы и днища:
Наблюдение за прочностью плавучих доков
Для правильной оценки прочности дока по его прогибу необходимо прежде всего установить «нулевое» положение прогибомера на доке (см. выше Определение упругой линии корпуса дока), а также в любом положении правильно учесть наличие температурных деформаций (см. выше Определение температурных напряжений и деформаций в корпусе дока), которые следует учитывать также и в дальнейшем, при контроле прочности дока, так как температурные деформации корпуса могут завышать, либо (что наиболее опасно) занижать действительные упругие деформации дока.
Натурные испытания прочности плавучих доков
К числу наиболее интересных испытаний следует отнести испытания крупного металлического понтонного дока, проведенные группой сотрудников кафедры строительной механики ЛКИ под руководством В. В. Козлякова. Цель испытаний заключалась в определении истинного минимального момента сопротивления корпуса дока.
Предлагается к прочтению: Учет динамических факторов при определении дополнительных продольных усилий на волнении
Испытания показали, что действительные моменты сопротивления корпуса понтонного дока несколько выше вычисленных в предположении, что разрезные понтоны не участвуют в общем изгибе дока. По-видимому, имеют значение «юбки» по бортам дока.
Модельные испытания прочности корпусов плавучих доков
Работа по испытанию прочности моделей корпусов плавучих доков проведена кафедрой строительной механики корабля ЛКИ и Одесским институтом инженеров Морского флота.
Теоретические исследования и эксперименты на моделях показали наличие существенной гидродинамической поправки к величинам статических изгибающих и крутящих моментов на волнении (см. Прочность дока при скручиванииРасчет прочности корпуса дока при скручивании). Эксперименты проводились буксировкой на волнении моделей, снабженных специальной тензометрической установкой.
Представляют интерес испытания целлулоидной модели корпуса дока на кручение, проведенные в лаборатории строительной механики ЛКИ. Работа велась для проверки применимости теории кручения тонкостенных стержней замкнутого профиля, разработанной А. А. Уманским, к расчетам корпусов доков на кручение. Выявлена возможность замены многосвязного замкнутого контура (каким является поперечное сечение дока) одноконтурным (см. Прочность плавучих доковПрочность плавучих доков и общие характеристики внешних сил).
Исследования прочности доков должны быть продолжены, причем особое внимание рекомендуется обратить на следующие вопросы:
- взаимное влияние продольного и поперечного изгибов;
- взаимное влияние сечений при поперечном изгибе;
- совместная работа башен и понтонов при ударе волн в башни дока;
- экспериментальное исследование внешних усилий, действующих при ударе волн в башни и торцовые стенки;
- усилия взаимодействия между судном и доком и распределение внешних усилий между ними на тихой воде и на волнении при различном соотношении их размеров и жесткостей;
- определение концентрации нормальных и касательных напряжений в узле соединения понтона и башен;
- определение концентрации напряжений в башнях понтонных доков на участках между соседними понтонами;
- определение внешних усилий при ударе волн в оконечности дока;
- степень участия разрезных понтонов самодокующихся доков в общем изгибе и т. д.
