Реальные системы регулирования, как правило, нелинейны. Зачастую в нелинейных системах имеют место периодические колебания, не связанные с наличием каких-либо возмущающих сил и объясняющиеся только наличием нелинейностей.
Общие понятия. Метод гармонической линеаризации
Эти Методы исследования линейных систем автоматического регулирования. Структурные схемы и передаточные функцииколебания, имеющие постоянную амплитуду и частоту, носят название автоколебаний. Если их амплитуда настолько велика, что превышает установленные требования, то такую систему необходимо исследовать с поиском путей ликвидации или уменьшения этих колебаний. Для этих целей способ линеаризации нелинейностей разложением в ряд Тейлора неприменим. Кроме того, для анализа устойчивости нелинейной системы, в которой имеются такие нелинейности, как: типа реле, люфта, гистерезиса, нечувствительности, разложение в ряд Тейлора также — неприменимо.
Существуют 2 типа методов исследования нелинейных систем: точные и приближенные. К точным методам относятся метод фазовых траекторий, некоторые другие, и, как наиболее универсальный метод — решение нелинейной задачи с помощью ЭВМ. К приближенным методам относится метод гармонической линеаризации, сущность которого состоит в следующем.
Допустим, что в системе автоматического регулирования, схема которой представлена на рис. 1, имеется линейная часть ЛЧ с передаточной функцией Wл.ч(p) и нелинейный элемент НЭ, расположенный последовательно ЛЧ.
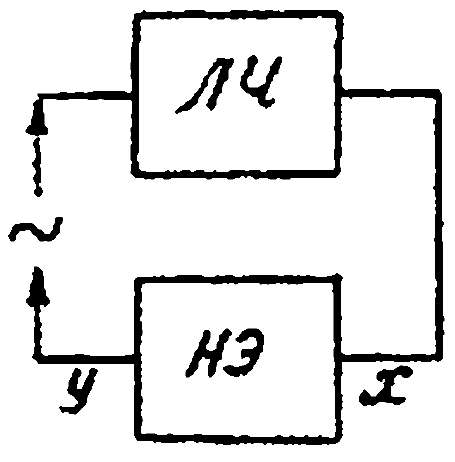
Допустим также, что наличие этой нелинейности в системе может привести к автоколебаниям или к тому, что процесс будет либо сходящимся, устойчивым, либо наконец, расходящимся — неустойчивым, однако во всех случаях кривая переходного процесса будет носить Исследование и способы улучшения качества регулирования линейных автоматических системколебательный характер. Такой случай характерен для многих систем, если например, в них имеются колебательные звенья с малым демпфированием.
Для дальнейшего анализа можно принять, что выходная величина линейной части, ЛЧ, изменяется по синусоидальному закону. Выходная величина нелинейного элемента НЭ будет изменяться периодически, но не синусоидально, так как в общем случае решение нелинейного уравнения при синусоидальном изменении в правой части дает гармонический ряд — сумму гармоник. Однако, если положить в основу принятое условие, что из суммы гармонических составляющих колебаний в линейной части усиливается только одна — наиболее низкая составляющая, или, что в линейной части более высокие гармонические составляющие отфильтровываются, то наличие этих составляющих на выходе нелинейного элемента НЭ не влияет на прохождение основного сигнала в замкнутой системе.
Это условие — необходимое для применения метода гармонической линеаризации, называется условием фильтра.
Такая система будет подобна линейной системе, так как в каждом ее элементе имеют место гармонические колебания одной и той же частоты — что характерно для линейной системы, и для ее анализа можно использовать методы автоматики, разработанные для линейных систем.
Предлагается к прочтению: Грузовые характеристики морских грузов
Остается найти выражение для передаточной функции НЭ, т.е. отношение выходного и входного сигналов НЭ и сдвиг фаз между ними. На рис. 2 показан вид входного x и выходного y сигналов НЭ. Для анализа автоколебаний используется лишь первая, т.е. низшая, гармоника (кривая yt, на рис. 2).
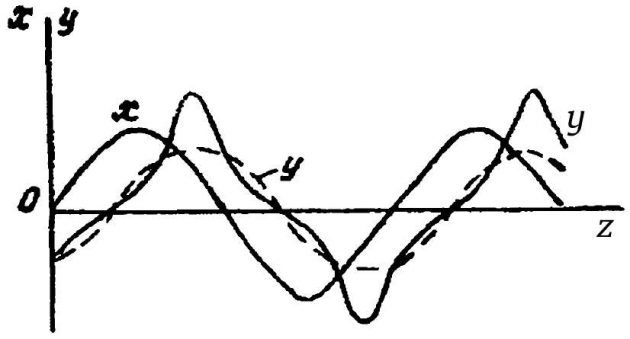
Выделить эту гармонику можно путем разложения нелинейной зависимости в ряд Фурье.
Допустим, что нелинейная зависимость имеет вид y = F(x) где x = asimψ, ψ = ωt, ω и a — частота и амплитуда колебаний.
В результате разложения в ряд Фурье получим:
Предположим, что нелинейность симметрична относительно оси x, т.е. колебания y имеют одинаковый характер, как вверх так и вниз от оси x, что наиболее часто встречается в системах.
Это означает, что;
— т.е. постоянная разложения отсутствует.
Так как
— окончательно получим:
высшие гармоники, где:
Если теперь допустить, что при дальнейшем исследовании высшие гармоники отброшены, то получим выражение:
или:
Выражение для частотной передаточной функции НЭ примет вид:
АФХ разомкнутой гармонически линеаризованной Исследование и способы улучшения качества регулирования линейных автоматических системСАР может быть определена по частотной передаточной функции
Так как q и q1 — функции от а, то передаточная функция гармонически линеаризованного НЭ и системы зависит от амплитуды колебаний, что отличает их от передаточных функций линейных колебаний, которые не зависят от амплитуды колебаний.
Дальнейшее исследование необходимо проводить пользуясь известными критериями устойчивости линейных систем. Например, если использовать критерий Найквиста, то необходимо построить АФХ разомкнутой системы. Такое построение следует выполнить, задаваясь тремя различными амплитудами (рис. 3).
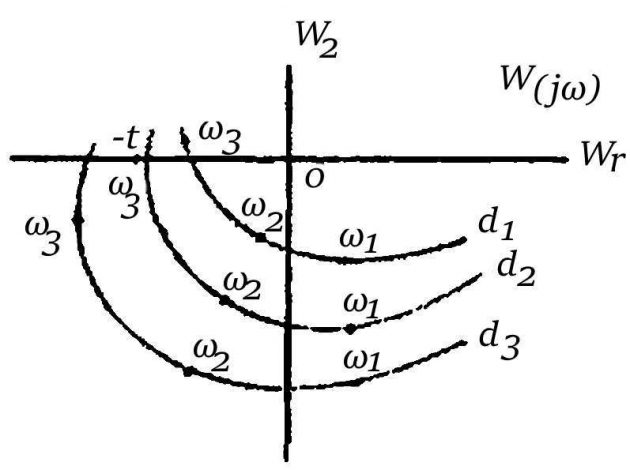
Допустим, что мы подобрали амплитуду колебаний а таким образом, что АФХ разомкнутой системы при a = a2, проходит через точку (-1, J0), соответствующая частота в этой точке < ω2. Изменим амплитуду: a1 > a2 и вновь построим АФХ. Если АФХ при амплитуде a1 > a2, не охватывает точку (-1, jO), то (в случае, если разомкнутая САР устойчива) замкнутая САР будет устойчива и в ней коле-бания должны проходить с уменьшающейся амплитудой. С течением времени a → а2. Вновь изменим амплитуду: a3 < a2 и построим АФХ для a = a3. Если АФХ при амплитуде a3 охватывает точку (-1, j0), то это свидетельствует о неустойчивости замкнутой САР. Основы взаимодействия дизеля и устройств автоматического регулированияАмплитуда колебаний в неустойчивой САР должна возрастать и a → a2.
Проведенный анализ показывает, что в системе должны возникнуть автоколебания с амплитудой a2 и частотой и они будут устойчивыми.
Допустим АФХ на (рис. 1 Схема чувствительного элемента частоты вращения) соответствуют случаю, когда a1 < a2 < a3.
Можно показать, что в такой системе должен произойти срыв автоколебаний: если амплитуда больше a2, то САР неустойчива и амплитуда будет все время возрастать и наоборот, если амплитуда меньше a2, то амплитуда автоколебаний будет уменьшаться до нуля.
Пример исследования нелинейной системы с нелинейностью релейного типа
Рассмотрим пример гармонической линеаризации нелинейности релейного типа (рис. 4) и применения описанного метода для одноконтурной системы 3-го порядка.
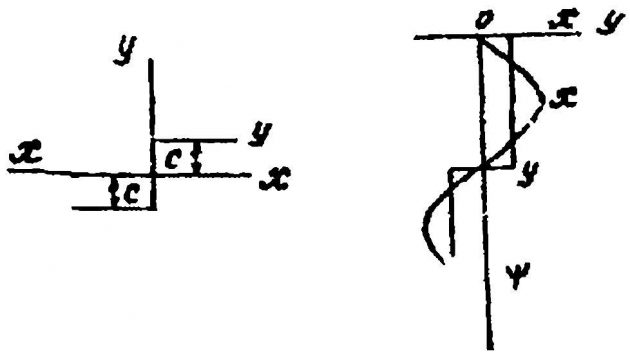
а – график нелинейности; b – графики изменения входной у и выходной величин
Уравнение нелинейного элемента — (идеального) реле;
- y = +C при x 0;
- y = -C при x 0.
где:
- C — параметр нелинейности.
Входная величина
Окончательно
Таким образом, гармоническая линеаризация нелинейности типа идеального реле приводит к весьма простому выражению, которое не содержит производной от х и частоты ω. Можно показать, что при гармонической линеаризации однозначных нелинейностей, например, типа реле с зоной нечувствительности, и типа ограничения, величина q1 при гармонической линеаризации будет обращаться в нуль.
При наличии гистерезисной петли коэффициент q1 отличен от нуля. Коэффициенты q1 и q для типовых нелинейных звеньев приведены.
Приведем теперь анализ системы, включающей последовательно соединенные линейные звенья, общий порядок которой равен трем, и последовательно включенный НЭ — «идеальное» реле.
На основании (Таблица 1. Передаточные и переходные функции динамических звеньев) можно установить, что АФХ разомкнутой системы, состоящей из трех последовательно соединенных звеньев 1-го порядка, или одно из которых имеет второй порядок, одно — первый, а одно — безынерционное, должна заканчиваться на комплексной плоскости АФХ в точке начала координат при суммарном угле поворота у = -270°. Пусть АФХ ЛЧ имеет вид 1 на рис. 5.
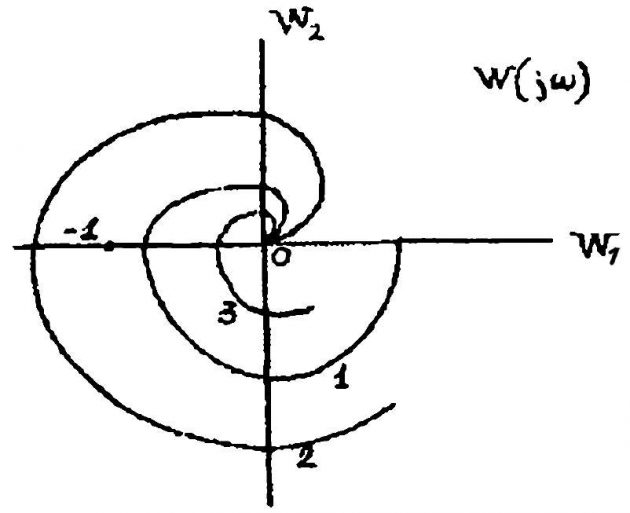
1 – АФХ ЛЧ; 2 – АФХ разомкнутой системы при a = a1 → 0; 3 – то же при a » a1
При анализе АФХ всей САР нужно Wл.ч. (jω) умножить на коэффициент передачи НЭ. Коэффициент передачи НЭ зависит от амплитуды колебаний: чем меньше амплитуда а, тем он больше. Поэтому при малых a АФХ разомкнутой системы будет охватывать точку (-1, j0) — кривая 2, а при больших значениях не охватывать ее — кривая 3 — что свидетельствует от устойчивости автоколебаний в рассматриваемой системе.
Амплитуда и частота автоколебаний может быть определена последовательным изменением a и расчетом АФХ.
Заметим, что амплитуда автоколебаний не зависит от начальных условий: с течением времени она становится постоянной, соответствующей точке (-1, J0) на комплексной плоскости АФХ — что является характерным свойством нелинейных систем.
Автоколебания вследствие упругости валопровода судовой энергоустановки
Реально смоделировать нелинейности для определения амплитуды автоколебаний достаточно сложно. Поэтому в ряде случаев ограничиваются лишь определением частоты, при которой возможно возникновение автоколебаний и определением зоны неустойчивой работы. В качестве примера ниже рассмотрены автоколебания в системе двигатель-валопровод — винт.
Напомним, что автоколебаниями называются периодические изменения параметров системы с определенными амплитудой и частотой при отсутствии возмущающих воздействий.
Ниже излагаются ограниченные сведения причин автоколебаний, прежде всего тех, которые приводят к неустановившемуся режиму дизеля.
Автоколебательный режим дизельной установки при постоянных нагрузках и положении органа управления затяжкой пружины регулятора скорости может возникнуть, если: частоты собственных крутильных колебаний одноузловой или двухузловой формы валопровода “пропускаются” регулятором скорости, т.е. отношение амплитуды колебаний рейки топливных насосов к амплитуде колебаний частоты вращения дизеля имеет значение, которое оказывает влияние на развитие колебаний; привод регулятора скорости расположен вне узла крутильной схемы, в котором колебаний частоты вращения вала дизеля не происходит.
Признаками того, что автоколебания возникают вследствие упругости валопровода, могут быть: малая зависимость частоты автоколебаний от частоты вращения вала дизельной установки; изменение частоты колебаний при изменении податливости валопровода или отсутствие этих колебаний при отсоединении упругих элементов; результаты осциллографирования частоты вращения вала дизеля и хода рейки топливных насосов при колебаниях, подтверждающие теоретические расчеты.
К одноузловой форме колебаний отнесем колебания в дизельных установках типа дизель-валопровод-винт и дизель-тормозная система. К двухузловой форме колебаний отнесем колебания, возникающие, когда к дизелю подсоединен через рессору турбокомпрессор.
Описываемые автоколебания теоретически могут иметь частоту, близкую частоте трехузловой формы колебаний крутильной схемы. Однако многоузловые формы колебаний имеют относительно высокую частоту, кото рую регулятор скорости из-за инерционности своих элементов пропустить не может.
Для расчетного анализа автоколебаний используются формулы передаточной функции объекта автоматического регулирования скорости дизельной установки Wоб (jΩ), под которой подразумеваются дизель с упругим валопроводом и присоединенными к нему инерционными массами, и передаточной функции регулятора.
Рассмотрим случай, когда одна J2 из присоединенных к валопроводу масс J1 значительно больше другой (см. рис. 5 Скоростная характеристика дизеля). Тогда уравнения для крутильных колебаний при средней частоте вращения валопровода ωs будет иметь вид:
- Mmp — момент трения;
- Ms0 — крутильная жесткость;
- Ta — время разгона;
- Δθ — отклонение угла при колебаниях с частотой Ω.
Условие устойчивости по Найквисту для рассматриваемой системы имеет вид
при
где:
— модуль частотной передаточной функции и сдвиг фаз в регуляторе скорости с учетом упругости муфты привода регулятора скорости;
— сдвиг фаз в дизельной установке с учетом запаздывания величины Ttq, по отношению к изменению хода рейки.
Поскольку величина γобe (Ω) с учетом производной pω меньше π/2, то возникновение автоколебаний возможно в случае, если сдвиг фаз значителен в других звеньях системы регулирования. Возникновение автоколебаний наиболее вероятно, если частота собственных колебаний регулятора скорости близка к частоте собственных колебаний крутильной схемы или когда имеется дополнительное запаздывание, обусловленное, например, зазорами в передаче регулирующего воздействия или обусловленное топливной аппаратурой.
Читайте также: Международные Правила морской перевозки опасных грузов
При высокой частоте колебаний следует учесть запаздывание между изменением цикловой подачи топлива и момента на валу дизеля (57° п.к.в.).
Исследования, проведенные предприятием-изготовителем, с дизелями типа 124 Н18/20, имеющими приводные турбокомпрессоры и регулятор скорости непрямого действия с упруго присоединенным катарактом, показали, что автоколебания возникли на: стендовой установке, дизель которой имел независимый турбокомпрессор и понижающий редуктор на выходе. Частота автоколебаний была близка частоте собственных одноузловых колебаний валопровода Ωe = 100с-1. Автоколебания наблюдались в широком диапазоне частоты вращения вала дизеля на холостом ходу и малых нагрузках, и сопровождались высокой вибрацией дизеля с амплитудой вибрации на головках блоков до 0,5 мм судовой установки с дизелем, имеющим приводной турбокомпрессор. Частота автоколебаний 122с-1 была близка частоте собственных колебаний двухузловой формы.
Колебания сопровождались высокими касательными напряжениями в рессоре привода агрегата наддува до 300 Мпа.
На рис. 6 приведены области устойчивости автоколебательных режимов для первой и второй установок и показаны амплитуды колебаний рейки топливных насосов (получены кандидатом технических наук М.Л. Ширяевым).
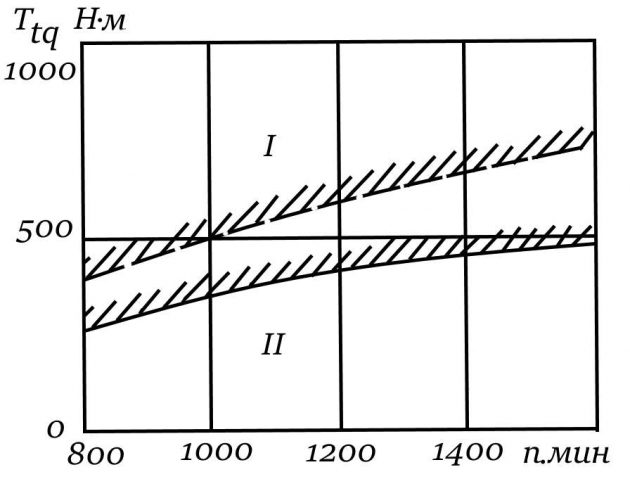
Автоколебания были значительно снижены путем применения более жестких основной пружины регулятора скорости, пружины упругого присоединенного катаракта и пружины упругой муфты привода регулятора, что уменьшило
Одной из причин низкой Расчет судового валопроводачастоты собственных колебаний валопровода на исследуемых установках является наличие понижающего редуктора, так как при этом увеличивается приведенная податливость валопровода за редуктором.
