Общие понятия. Задачи, решаемые при настройке регуляторов автоматических систем, или по их выбору или расчету сводятся в конечном счете к тому, чтобы для существующего объекта автоматического регулирования подобрать параметры регулятора таким образом, чтобы статическая характеристика САР и показатели переходных процессов удовлетворяли бы заданным требованиям.
- Задачи анализа и проектирования САР и пути их решения
- Передаточные функции, частотные и переходные характеристики линейных звеньев
- Структурные схемы и передаточные функции систем автоматического регулирования
- Методы исследования устойчивости линейных систем. Общие понятия. Необходимое условие устойчивости. Критерий Гурвица
- Критерий Михайлова и Найквиста
- Свойства одноконтурных систем
Задачи анализа и проектирования САР и пути их решения
Эта задача может быть решена, в частности, с помощью ЭВМ, для чего необходимо:
- составить уравнение объекта;
- составить уравнение регулятора.
Полученную систему уравнений необходимо дополнить уравнением основной обратной связи и получить, таким образом, систему дифференциальных уравнений замкнутой САР.
Эта система может решаться с помощью Системное программное обеспечение на судахЭВМ при введении различных возмущающих сигналов и изменений параметров регулятора с целью выбора оптимальных параметров и удовлетворения заданным требованиям. Такой путь решения задач является достаточно долгим и трудоемким, так как вопросы программирования, отладки программы и решения зачастую с помощью численных методов, требуют времени, а также затрат на дорогостоящее машинное время современных ЭВМ. Вместе с тем методы теории автоматического регулирования позволяют в ряде случаев относительно просто, без применения ЭВМ, ответить на вопросы: устойчива ли система или неустойчива, и определить по крайней мере порядок величин, характеризующих качество переходных процессов.
Если необходимая точность не может быть достигнута, то методы теории автоматического регулирования, по крайней мере, позволяют значительно сократить время, связанное с дальнейшим применением ЭВМ, и обеспечить уверенность в результатах. Большинство из этих методов основано на действиях над передаточными функциями и частотными характеристиками, которые поясняются ниже.
С целью исследования системы необходимо составить ее структурную схему в виде звеньев, связанных между собой. Каждое звено или несколько звеньев должны соответствовать определенному реальному элементу.
Динамика реальных элементов САР описывается линейными и нелинейными дифференциальными уравнениями, как правило, не выше 2-го порядка. В ряде случаев можно произвести линеаризацию нелинейностей. В связи с этим большинство элементов систем автоматики можно представить в виде типовых линейных динамических звеньев, которые описываются однотипными линейными дифференциальными уравнениями 1-го и 2-го порядка, например:
где:
- х1 — входная;
- х2 — выходная величины, причем порядок правой части, как правило, не выше, чем порядок левой части уравнения.
На установившемся режиме, когда производные в уравнении (1), равны нулю, получаем х2 = kх1 уравнение статической характеристики звена, где k = (b1/a2) — коэффициент усиления или статический коэффициент передачи звена.
Передаточная функция звена может быть получена с помощью операционного преобразования. С этой целью необходимо перейти от уравнения (1) к уравнению в изображениях. При нулевых начальных условиях:
где:
- p — оператор Лапласа;
- х1(p) и х2 (p) — изображения входной и выходной величин.
Передаточной функцией звена называется отношение изображения выходной величины к изображению входной величины звена при нулевых начальных условиях:
Заметим, что выражение (2) может быть получено непосредственно из уравнения (1), если принять, что W(p) = x2/x1 a p = d/dt — знак производной. Если в (2) вместо p подставить мнимую величину jω, где ω — произвольно изменяемая величина, называемая частотой, то получим величину W(jω), называемую частотной передаточной функцией.
Предлагается к прочтению: Гидротехнический расчет плавучей буровой установки и волновая нагрузка ПБУ
Поясним физическую сущность частотной передаточной функции на примере более простого уравнения вида:
или, разделив коэффициенты на а1,
где:
Допустим, что входная величина изменяется по синусоиде
Требуется найти решение уравнения (3), соответствующее вынужденным колебаниям, т. е. после определенного времени с момента начала переходного процесса и затухания отклонений, вызванных начальным возмущением. Как известно, решение для этого случая ищется в виде
где:
- B и ψ — постоянные, которые требуется определить.
Подставим (4) и (5) в уравнение (3), получим:
Равенство (6) может быть справедливо, если
Возводя в квадрат и складывая правые и левые части уравнений (7), получим:
С другой стороны, передаточная функция, соответствующая (3)
и частотная передаточная функция при p = jω.
- W(jω) = k/(Tjω + l) — комплексная величина. (8)
Модуль W(jω) равен отношению модулей числителя и знаменателя
Аргумент комплексного выражения (8) равен разности аргументов числителя и знаменателя, т. е. равен
На основании изложенного можно делать вывод: модуль частотной передаточной функции равен отношению амплитуды колебаний выходной величины к амплитуде входной, а аргумент — сдвигу фаз между входной и выходной величинами при условии, что выходная и входная величины изменяются по гармоническому закону.
Читайте также: Плазовые работы, подготовка и выполнение масштабирования
Хотя доказательство приведено для конкретного случая — дифференциального уравнения звена 1-го порядка, однако такое же доказательство может быть приведено для дифференциального уравнения любого порядка.
Если на комплексной плоскости вычертить кривую, соответствующую W(jω) при изменении ω от 0 до +∞, то такая кривая называется амплитудно-фазовой частотной характеристикой (АФХ). В частности, для (6) такая АФХ может быть построена, если последовательно изменяя ω находить значение ψ и на соответствующем направлении против часовой стрелки по отношению к положительной вещественной оси откладывать значение модуля |W(jω)|. В результате можно доказать, что получается полуокружность с диаметром, равным k.
Модуль АФХ при ω = 0 равен статическому коэффициенту усиления звена, т. е. отношению амплитуд гармонических сигналов выходной и входной величины, если период равен бесконечности, что соответствует установившемуся режиму.
Если входная величина звена изменяется ступенчато x1(t) = l(t) (в момент t = 0 x1 изменяется на единицу и в дальнейшем остается постоянной), то изменение выходной величины звена x2(t) называется его переходной функцией. Графическое изображение переходной функции называется переходной характеристикой. Получение переходных функций путем непосредственного интегрирования или использования операционного метода для уравнений 1-го и 2-го порядка не составляет труда.
Передаточные функции, частотные и переходные характеристики линейных звеньев
| Таблица 1. Передаточные и переходные функции динамических звеньев | |||
|---|---|---|---|
| № п/п | Наименование звена и уравнения | Передаточная функция | Переходная функция |
| 1 | Безынерционное звено | ||
| 2 | Инерционное звено 1-го порядка (апериодического 1-го порядка) | ||
| 3 | Инерционное звено 2-го порядка (апериодическое 2-го порядка) | ||
| 4 | Колебательное звено | ||
| 5 | Интегрирующее звено | ||
| 6 | Дифференцирующее звено | ||
| 7 | Звено с “чистым” запаздыванием | ||
Выше рассматриваются характеристики типовых линейных динамических звеньев систем автоматического регулирования. Так как выводы не представляют особого труда то в табл. 1 приведены характеристики звеньев без выводов.
Структурные схемы и передаточные функции систем автоматического регулирования
Для анализа устойчивости Элементы автоматических систем суднаСАР или получения ее переходной функции необходимо иметь передаточные функции или частотные характеристики всей системы.
Допустим, что разомкнутая САР состоит из 2-х последовательно соединенных звеньев, когда выходная величина 1-го звена является входной для 2-го (рис. 1).
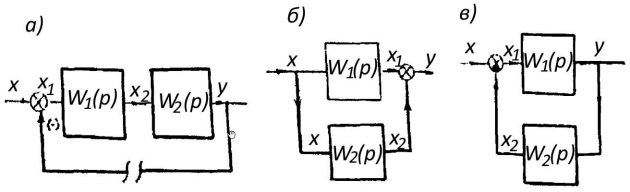
а – с последовательно соединенных; б – с параллельно соединенных дополнительной внутренней положительной прямой связью; в – то же отрицательной обратной связью
Входная величина 1-го звена является входной для САР, а выходная — 2-го звена является выходной для этой системы. Требуется определить передаточную функцию этой САР. По определению, передаточная функция системы равна отношению изображения выходной величины к входной, т. е.
Представим выражение (9) следующим образом:
Как видим, передаточная функция разомкнутой системы, состоящей из последовательно соединенных звеньев, равна произведению передаточных функций отдельных звеньев.
Определим передаточную функцию разомкнутой системы для параллельного соединения звеньев, когда направление сигнала в параллельно включенном звене такое же, как в первом звене.
В этом случае параллельная связь носит название дополнительной внутренней обратной связи. Связь при чрезвычайных и аварийных ситуацияхСвязь называется положительной, если проходящий по ней сигнал суммируется с основным, или отрицательной, если этот сигнал вычитается из основного.
На основании анализа схемы (рис. 1, б) получим:
Если параллельная обратная связь отрицательна, то
Передаточная функция замкнутой САР Ф(p), так же как и передаточная функция разомкнутой CAP W1(p) есть отношение изображения выходной величины к изображению ее входной величины. Особенность составления передаточной функции замкнутой САР состоит в необходимости учета действия основной обратной связи.
Определим Ф(p) для схемы на рис. 2. Входной величиной САР принята нагрузка λ. Выходной — регулирующее воздействие.
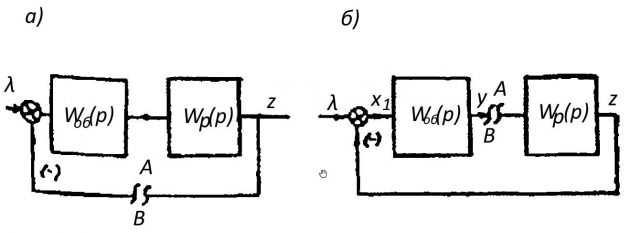
Система замкнута основной обратной связью. Поэтому x1 = λ-z. Передаточная функция замкнутой системы определится путем преобразований:
где:
Вид Ф(p) зависит от того, какая величина в САР принята за входную и какая — за выходную.
Это интересно: Основы взаимодействия дизеля и устройств автоматического регулирования
Пусть за входную величину принята y.
В этом случае регулятор входит в основную обратную связь САР. Поэтому
Обозначим Nоб(p); N(p) и Mоб(p), Мp(p) — полиномы числителей и знаменателей передаточных функций объекта и регулятора. По определению передаточной функции, если принять M(р) = 0, то получим характеристическое уравнение соответствующего звена, если за переменную характеристического уравнения принято p.
Из (11) следует:
Из (11, а) следует:
Таким образом, независимо от выбора входной и выходной величин замкнутой САР характеристическое уравнение замкнутой САР, определяемое полиномом знаменателя Ф(p), — одно и то же.
Покажем на примере схемы рис. 1, таким образом представить в виде структурной схемы САР, состоящую из типовых линейных звеньев. При составлении передаточных функций звеньев как правило, желательно переменные сигналы учитывать в относительных единицах, например z = Δh/hном φ = ΔH/Hном и т. п. Должны соблюдаться правила одинаковых масштабов переменных, выходящих из звеньев и входящих затем в последовательно или параллельно расположенные звенья.
Примем поплавковый измеритель уровня за безынерционное звено, входной величиной которого является φ = ΔH/Hном. Перемещение поплавка и точки A рычага 3 приведет к перемещению золотника на величину
За положительное направление ΔH, φ и Δx1 принимается направление вверх на рис. 1.
Топливные насосы золотникового типаПеремещение золотника вверх приведет к открытию окон и движению сервопоршня вниз. Примем за положительное направление движения сервопоршня — движение его вниз на величину Δh. При этом произойдет возврат золотника на линейную величину
Суммарное открытие золотника составляет Δx1 – Δx2.
Примем за базовые значения Ah – hном, Δx1,2 – хном.
Обозначим Z = Δh/hном, σ = (Δx1 – Δx2)/хном.
Уравнение внутренней отрицательной обратной связи примет вид:
где:
Уравнение сервомотора имеет вид согласно (9):
Уравнение объекта:
или разделив все постоянные на β получим
где:
- .
Уравнение основной обратной связи Z1 = -Z.
На рис. 18 представлена структурная схема САР уровня воды в емкости и передаточные функции ее звеньев.
Методы исследования устойчивости линейных систем. Общие понятия. Необходимое условие устойчивости. Критерий Гурвица
САР называется устойчивой, если регулируемая величина после отклонения, возникшего в результате внешнего воздействия, по истечении некоторого промежутка времени возвращается к заданному значению.
Если Элементы автоматических систем суднаСАР неустойчива, то возникают незатухающие или расходящиеся колебания, либо происходит монотонное изменение регулируемой величины и других параметров системы. Устойчивость системы может быть установлена на основании анализа корней характеристического уравнения.
Рассмотрим дифференциальное уравнение системы
Решение уравнения (12) включает общее решение yn(t) однородного уравнения и частное решение yв(t) неоднородного уравнения:
где:
- c1, …, cn — постоянные, зависящие от начальных условий.
Если x = const и t → ∞ y → bm/an х = yb.
Согласно проведенному выше определению, система будет устойчивой, когда выполняется условие при x = const и t → ∞ y → bm/an × x, (14). Последнее может быть выполнено, если при t → ∞ yn(t) → 0.
Из курса высшей математики известно, что, если λ1, …, λn вещественные отрицательные или комплексные сопряженные с отрицательной вещественной частью, то условие (14) выполняется и процесс регулирования устойчивый (рис. 3).
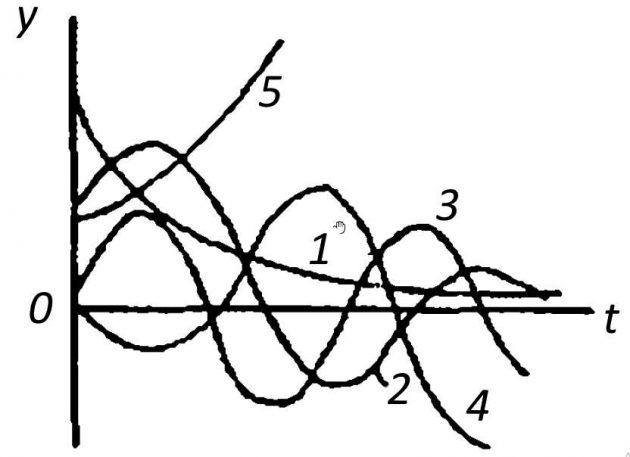
1 – вещественные отрицательные; 2 – комплексные, сопряженные с отрицательной вещественной частью; 3 – мнимые; 4- с положительной вещественной частью; 5 – вещественные положительные
Если корни чисто мнимые сопряженные, то этой паре λ1 = jβ и λ2 = jβ будут соответствовать слагаемые решения:
В этом случае система находится на границе устойчивости, т. к. благодаря наличию пары чисто мнимых корней величина будет изменяться по синусоиде (см. рис. 3, кривая 3). При наличии положительных вещественных корней или корней с положительной вещественной частью процесс будет расходящимся (см. рис. 3, кривые 5, 4) yn ≠ 0, а система — неустойчивой.
Следовательно, если известно расположение корней характеристического уравнения, то можно ответить на вопрос: устойчива или неустойчива система. Таким образом, вид правой части дифференциального уравнения САР не влияет на результаты анализа ее устойчивости. Изложенное справедливо для систем регулирования, описываемых линейными дифференциальными уравнениями. Реальные системы имеют нелинейности. В ряде случаев удается линеаризовать систему путем разложения функциональной зависимости в ряд Тэйлора и отбрасывая члены ряда, имеющие степень выше первой. Обоснование возможности линейного анализа для реальной системы с нелинейностями малой кривизны, которые могут быть разложены в ряд Тэйлора, дается в теоремах А.М. Ляпунова.
Определение корней характеристического уравнения линейной системы представляет собой более сложную задачу, если степень характеристического уравнения выше трех. В теории автоматического регулирования рассматриваются методы, которые позволяют судить об устойчивости лишь по значению коэффициентов характеристического уравнения, без определения его корней. Требования к предельной прочности и устойчивости элементов поперечных сечений балочных конструкций суднаКритерии устойчивости могут быть необходимыми и достаточными.
Необходимое условие устойчивости выполняется в том случае если коэффициенты характеристического уравнения имеют один и тот же знак.
Представим характеристическое уравнение в виде:
где:
- λ1, …, λn — корни характеристического уравнения.
Если все корни будут вещественными и отрицательными или комплексными с отрицательной вещественной частью, т. е. система регулирования устойчивости, то при перемножении сомножителей характеристического уравнения отрицательных коэффициентов быть не может.
Однако при выполнении условия равенства знаков коэффициентов характеристического уравнения система может быть также неустойчивой, так как при перемножении отрицательных чисел конечный результат может быть положительным и в конечном виде отрицательный знак не проявится.
Критерий устойчивости Гурвица. Широкое распространение нашли алгебраические критерии устойчивости (например, Гурвица, И. А. Вышнеградского) и графоаналитические (Михайлова, Найквиста).
Классификация систем автоматического регулированияСистема автоматического регулирования будет устойчива, если определитель Гурвица, составленный из коэффициентов характеристического уравнения, и все его миноры будут иметь один и тот же знак. Этот критерий является необходимым и достаточным (приводится без доказательства).
На основании алгебраических критериев, например, относительно просто исследовать устойчивость САР до 4-го порядка. Для системы n-го порядка, описываемой характеристическим уравнением, определитель Гурвица имеет вид:
Необходимое и достаточное условие устойчивости для системы 3-го порядка принимает вид:
Использование алгебраических критериев для систем с порядком уравнений выше 4-го затруднительно и для этих систем находят применение графо-аналитические методы.
Критерий Михайлова и Найквиста
Критерий Михайлова. В характеристическом уравнении (13) λ является в общем комплексной величиной λ = α ± jβ и может быть представлена на комплексной плоскости λ.
Любое значение λ, являющееся корнем уравнения (13) и расположенное на мнимой оси (λ = jω) или справа от нее, определяет неустойчивость системы. Граница устойчивости и неустойчивости – мнимая ось. Если двигаться вверх по этой оси от ω = -∞ до ω = +∞, то область неустойчивости находится от нее справа (заштрихована).
Рассмотрим теперь левую часть характеристического уравнения (13), в которой сделаем подстановку λ = α + jω, где α и ω произвольны. В результате получим:
Тогда М(λ) может быть представлена на комплексной плоскости в виде комплексных чисел, соответствующих различным значениям λ и ω. Плоскость М(λ) является конформным отображением плоскости корней: любым точкам плоскости λ соответствуют точки плоскости М(λ) и наоборот. Если же принять, что λ = jω и задавать значения ω от -∞ до +∞ то на плоскости М(λ) получим кривую (называемую кривой Михайлова)
которая отображает мнимую ось плоскости λ, причем область значений М(λ), соответствующих неустойчивым решениям дифференциального уравнения также должна быть справа (заштрихована).
Это интересно: Грузовые и грузопассажирские морские транспортные суда
Корни характеристического уравнения, отображаются точками плоскости λ и соответствуют началу координат плоскости М(λ). Если начало координат оказывается в заштрихованной области, то вещественная часть по крайней мере одного из корней положительна, а система регулирования — неустойчива. Если начало координат попадает на кривую M(jω), то это означает, что корни характеристического уравнения находятся на мнимой оси j и ω, а система — на границе устойчивости. Следовательно, необходимое и достаточное условие устойчивости формулируется как условие, при выполнении которого начало координат на плоскости M(jω) должно находиться в незаштрихованной области (критерий Михайлово). В приведенном на рис. 4 примере начало координат лежит в незаштрихованной области, поэтому система устойчива.
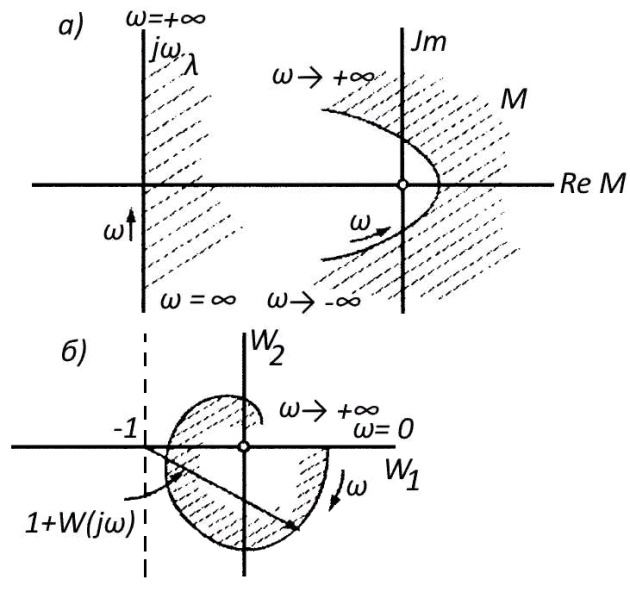
а – плоскость корней характеристического уравнения. Значения λ с положительной вещественной частью расположены в заштрихованной области; б – плоскость M
Сказанное относится к уравнениям как разомкнутых, так и замкнутых систем. Рассмотрим теперь случай, когда разомкнутая система устойчива и по виду АФХ мы хотим определить: будет ли устойчива Стационарные двигательные установки малотоннажных судовзамкнутая система.
Критерий Найквиста. На рис. 4 показано расположение корней и соответствующее им расположение точки М(λ) = 0 на плоскости М(λ), а также мнимой оси на плоскости корней и ее координатное отображение на плоскости М(λ) — кривая M(jω). Для устойчивой системы корни характеристического уравнения на плоскости корней, лежат слева от мнимой оси в не заштрихованной области, и отображение М(λ) = 0 — начало координат на плоскости, М(λ) — также слева от кривой M(jω), если двигаться по этой кривой от ω = -∞ до to = +∞. Для неустойчивой системы, если хотя бы один корень характеристического уравнения лежит справа от мнимой оси в заштрихованной области, то начало координат М(λ) — 0 на плоскости М(λ) также справа от кривой M(jω) в заштрихованной области плоскости М(λ). В приведенном на рис. 4 примере начало координат лежит в не заштрихованной области, поэтому система устойчива.
Пусть передаточная функция разомкнутой системы W(p) = N(p)/M(p), а ее характеристическое уравнение М(λ) = 0. Замкнем систему отрицательной (единичной) обратной связью. В соответствии с выражением (11) передаточная функция замкнутой системы:
Построим теперь на плоскости АФХ частотную характеристику разомкнутой CAP M(jω) и проведем из точки -1, j 0 вектор, опущенный своим концом на АФХ.
Величина этого вектора равна:
В числителе выражения (17) мы имеем левую часть характеристического уравнения САР, замкнутой единичной отрицательной обратной связью, в котором произведена замена λ = jω, а в знаменателе — то же для разомкнутой САР.
Разомкнутая САР по условию устойчива, поэтому M(jω) ≠ 0 и выражение (17) не может иметь значений, равных бесконечности (полюсов).
Следовательно, условие устойчивости замкнутой САР, равносильно тому, чтобы величина M(jω) + N(jω) ≠ 0 (или 1 + W(jω) ≠ 0), т. е. начало координат плоскости W(jω) находилось в незапггрихованной области.
Плоскость функции 1 + W(jω) может быть получена переносом начала координат на плоскости W(jω) влево на единицу. Тогда граничная кривая устойчивой и неустойчивой областей АФХ W(jω).
Строить эту кривую, в силу ее симметрии относительно вещественной оси достаточно только от значений jω = 0 до jω = +∞. Если точка (-1, j 0) на плоскости W(jω) попала в незаштрихованную область, то замкнутая САР устойчива.
Окончательно критерий Найквиста для рассматриваемого случая сформулируем таким образом: если разомкнутая САР устойчива, то для устойчивости замкнутой САР необходимо и достаточно, чтобы АФХ разомкнутой системы не охватывала точку (- 1, j 0).
Свойства одноконтурных систем
Пути обеспечения их устойчивости. Назовем одноконтурной систему, Основные свойства объектов автоматических систем суднаструктурная схема которой может быть представлена в виде последовательно соединенных звеньев, порядок каждого из которых не выше второго.
С помощью критерия Найквиста легко исследовать пути обеспечения устойчивости одноконтурных замкнутых САР.
Пусть АФХ разомкнутой САР имеет вид, показанный на рис. 5. Пусть известно также, что разомкнутая САР состоит из устойчивых звеньев и устойчива.
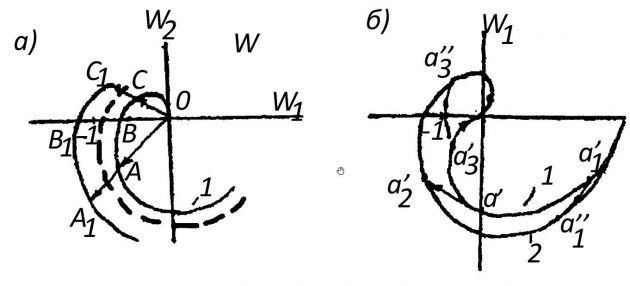
а – увеличение коэффициента усиления на величину K, 1 – АФХ устойчивой системы, 2 – АФХ неустойчивой системы; б – увеличения «чистого» запаздывания; 1 – АФХ системы при = 0; a’1, а’2, а’3 – точки АФХ; 2 – АФХ системы при τ ≠ 0; а”1, а”2, а”3 – точки АФХ, соответствующие точкам а1, … кривой 1
Согласно критерия Найквиста замкнутая САР для рассматриваемого случая (пунктирная линия) находится на границе устойчивости.
Проведем модернизацию системы таким образом, что уменьшим ее коэффициент усиления k. Это можно достичь путем уменьшения коэффициентов усиления одного или нескольких последовательно соединенных звеньев.
В этом случае АФХ разомкнутой системы переместится вправо и замкнутая САР станет устойчивой. Заметим, что уменьшение k приведет к увеличению наклона статической характеристики САР, т. е. к увеличению статической ошибки САР. Рассмотрим влияние «чистого» запаздывания на устойчивость замкнутой САР. Пусть САР содержит звено с «чистым» запаздыванием, а АФХ разомкнутой системы имеет вид, представленный на рис. 5 при условии, что разомкнутая САР устойчива, замкнутая САР также устойчива. Предположим, что запаздывание τ в силу каких-либо причин в звене с чистым запаздыванием, расположенным последовательно остальным звеньям, увеличивается. Тогда запаздывание в САР будет также увеличиваться, АФХ разомкнутой системы будет смещаться в сторону больших значений (рис. 5, б), в результате чего может охватить точку (- 1, j 0).
Читайте также: Классификация систем автоматического регулирования
Таким образом, замкнутая САР может стать неустойчивой. Следовательно, рассмотренными путями, обеспечивающими в ряде случаев устойчивость одноконтурной замкнутой САР могут быть: уменьшение коэффициента, усиления и «чистого» запаздывания в системе. Для САР, имеющих внутренние обратные связи, повышающие порядок последовательно соединенных в системе звеньев до 3-х и выше требуется более тщательное исследование устойчивости с помощью известных критериев. Полученные выводы для одноконтурных систем в ряде случаев для многоконтурных САР могут быть неверные. Однако в некоторых случаях нельзя сделать систему устойчивой, не изменив ее структуры. Такая система называется структурно неустойчивой. Например, если система содержит два последовательно соединенных интегрирующих звена или одно интегрирующее и одно неустойчивое звено.
Определение устойчивости по логарифмическим частотным характеристикам. Для анализа устойчивости системы по этому способу необходимо построить лога-рифмическую амплитудную характеристику ЛАХ) и логарифмическую фазовую характеристику ЛФХ разомкнутой системы.
Наиболее просто построить ЛАХ и ЛФХ системы, состоящей, из последовательно соединенных звеньев. В этом случае
где:
- Wi(jw) — частотная передаточная функция i-ro звена;
- n — число последовательно соединенных звеньев;
здесь φi(ω) — ЛФХ i-го звена.
Для более сложных систем, где имеются внутренние связи и параллельно включенные звенья, ЛАХ и ЛФХ вычисляют обычным способом по передаточной функции разомкнутой системы.
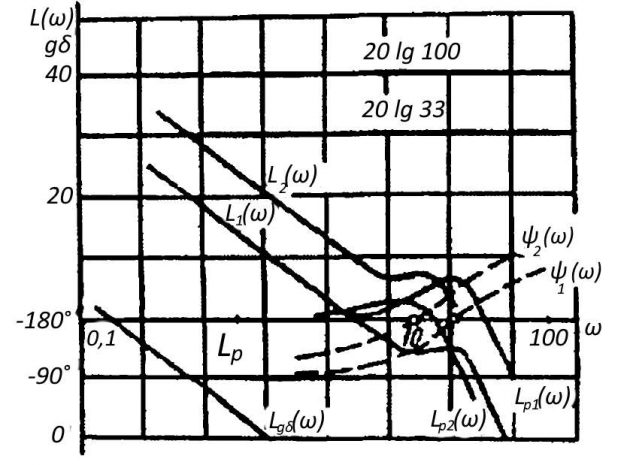
Устойчивость по ЛАХ и ЛФХ определяется следующим способом. Допустим, что разомкнутая система устойчива. Согласно критерию Найквиста, если замкнутая система абсолютно устойчива, то модуль АФХ разомкнутой системы должен быть меньше единицы при сдвиге фаз ψ = -180°. На рис. 6 представлены ЛАХ и ЛФХ разомкнутой системы (сплошные линии), которая по условию считается устойчивой.
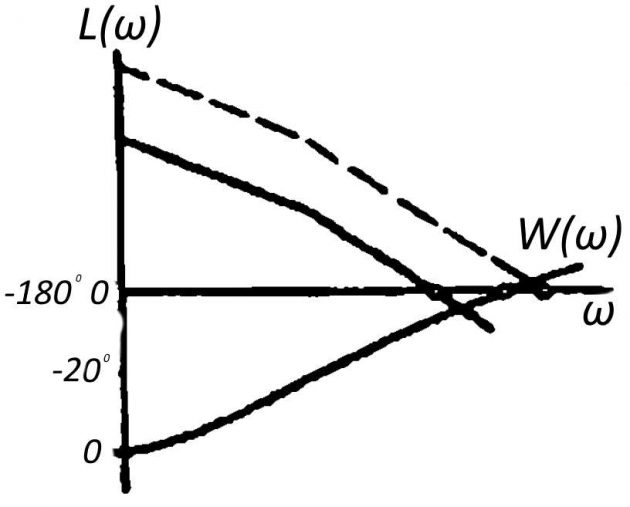
Как видно из рисунка, если ψ = -180° и L(ω) = 20lgA(ω) < 0, то следовательно, A(ω) = W(jω)| < 1 и замкнутая система устойчива.
Увеличение коэффициента усиления приводит к перемещению ЛАХ системы верх (пунктирная линия), что обусловливает неустойчивость САР. Если замкнутая система является условно устойчивой, то при ψ = -180° АФХ разомкнутой системы должна дважды пересекать левую полуось абсцисс.
На рис. 7 показан характер ЛАХ и ЛФХ условно устойчивой системы. Пунктирная линия соответствует ЛАХ неустойчивой САР.

Рассмотрим пример использования ЛАХ и ЛФХ для анализа устойчивости САР частоты Реверс дизельного двигателявращения дизель-генератора.
Уравнение регулятора скорости прямого действия, в котором чувствительный элемент передвигает рейку топливных насосов, имеет вид
где:
- z — изменение положения муфты регулятора.
Постоянные уравнения заданы и составляют
Степень неравномерности регулятора δ по условиям задачи может быть изменена в пределах от 0,03 до 0,01. На рис. 8 представлена структурная схема системы.
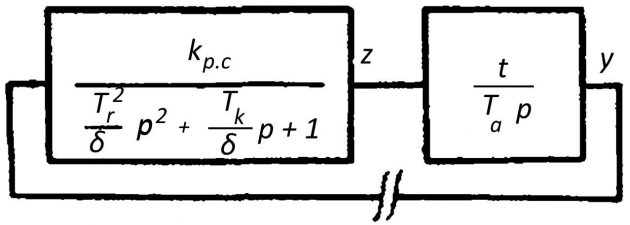
ЛАХ и ЛФХ системы строятся ω (обычно в логариф-мическом масштабе) и L(ω) и ψ(ω).
В данном случае
Суммарная ЛАХ системы L(ω) (см. рис. 6) при δ = 0,03 (Крc ≈ 33) и угле сдвига фаз ψ1 = -180° лежит ниже оси абсцисс. Следовательно, САР устойчива. При снижении степени неравномерности 8 до 0,01 и увеличении коэффициента усиления регулятора до 100 ЛАХ L2(ω) располагается выше L1(ω) И САР становится неустойчивой.