Качество регулирования характеризует способность устойчивой системы обеспечивать требуемую точность регулирования в установившихся и переходных режимах.
Общие понятия
К непосредственным показателям качества регулирования относятся:
- на установившихся режимах — величина статической ошибки регулирования;
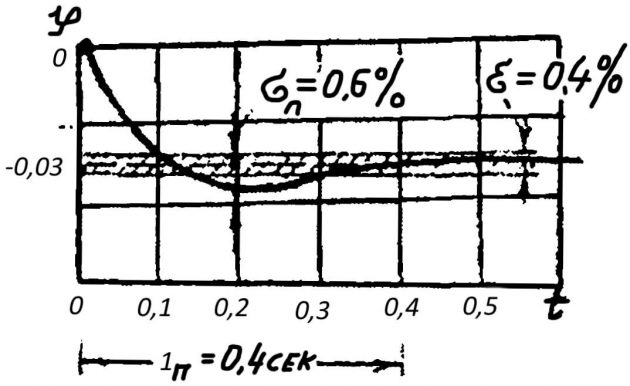
- на переходных режимах (см. рис. 1 Схема регулятора скорости и его характеристики) — показатели переходных процессов;
- максимальное отклонение регулируемой величины Δymax от прежнего установившегося значения, величина перерегулирования δn и длительность переходного процесса tn т.е. время до вхождения регулируемой величины в заданную зону. Для реальных систем такой зоной принимается зона нечувствительности.
Непосредственные показатели качества могут быть получены с помощью прямых методов исследования, т.е. непосредственно решением систем дифференциальных уравнений. Современные ЭЦВМ позволяют получить необходимую точность при решении нелинейных дифференциальных уравнений высокого порядка. На основании этого решения можно определить Δymax, δn и tn заданным требованиям. Однако точный ответ на вопросы качества регулирования требуется, как правило, при проектировании систем и, прежде всего, систем с высокими требованиями по качеству, осуществление выполнения которых зачастую сопряжено с конструктивными сложностями регулятора и специальных корректирующих устройств.
В ряде случаев, например, при настройке регуляторов, требуется знать способы изменения статизма, уменьшения или увеличения показателей Δymax, δn и tn по сравнению с имеемыми в системе. На этот вопрос можно ответить, изучая качество регулирования с помощью приближенных или косвенных методов оценки качества.
Оценка качества регулирования в установившихся режимах
Качество регулирования в установившихся режимах работы системы оценивается величиной статической ошибки υ:
где:
- у — текущее, уmp — заданное значение регулируемой величины.
Величина ошибки υ равна отклонению регулируемой величины от заданного значения и может быть обусловлена как принятым законом регулирования, так и особенностями структурной Методы исследования линейных систем автоматического регулирования. Структурные схемы и передаточные функциисхемы системы. При оценке величины ошибки линейных САР не учитываются нечувствительность и непрямолинейность статических характеристик реальных систем, обусловленных зазорами, сухим трением и другими нелинейностями.
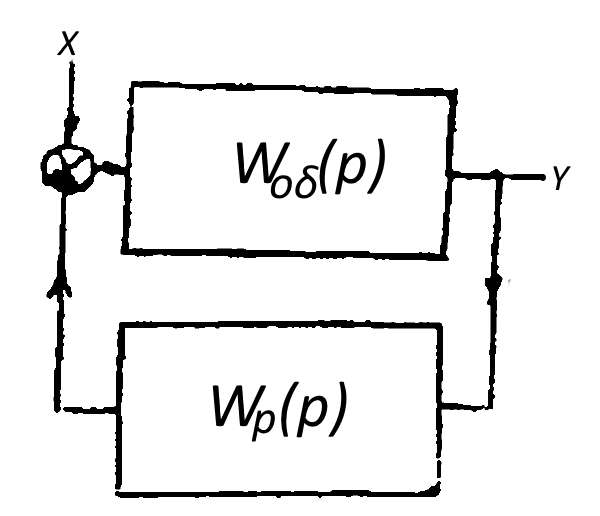
Для систем стабилизации, задача которых уменьшать отклонение регулируемой величины от заданного значения уmp, целесообразно в качестве выходной величины принимать это отклонение, считая уmp за ноль отсчета. Статическая ошибка системы будет υ = -у.
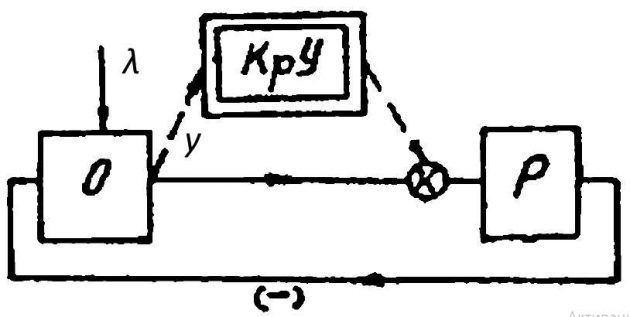
Если в качестве входной величины системы (рис. 1) принять нагрузку λ, то значение статической ошибки может быть получено из выражения для передаточной функции замкнутой системы Ф(p):
Максимальную статическую ошибку υmax получим, подставив λ = 1:
Таким образом, величина максимальной статической ошибки САР стабилизации численно равна наклону статической Методы исследования линейных систем автоматического регулирования. Структурные схемы и передаточные функциихарактеристики САР.
Допустим, что регулятор САР состоит из позиционных звеньев (П-регулятор).
Определим ошибку для этого случая:
где:
- kоб и kp — коэффициенты передачи объекта и регулятора.
Обычно kобkp » 1, поэтому υmax = ≈ 1/kp.
Таким образом, максимальная статическая ошибка САР, регулятор которой состоит из позиционных звеньев, обратно пропорциональна коэффициенту усиления регулятора.
Рассмотрим также случай, когда в числе звеньев регулятора имеется одно последовательно соединенное интегрирующее звено (рис. 2), которым может быть, например, сервомотор, не охваченный обратной связью (И — регулятор):
где:
- 1/p × Wp(p) — передаточная функция регулятора;
- Wp(p) — передаточная функция остальных звеньев.
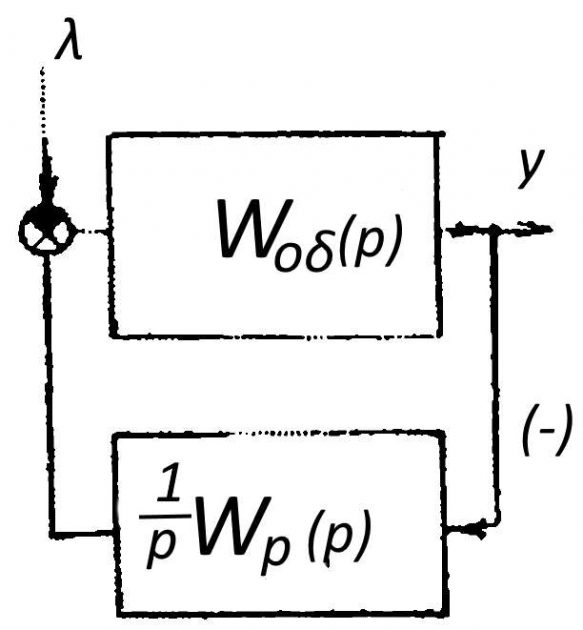
В этом случае коэффициент усиления регулятора равен бесконечности, а САР является астатической (δ = 0). Следовательно, повышение точности САР на установившихся режимах может быть достигнуто увеличением коэффициента усиления регулятора.
Предлагается к прочтению: Океанотехника прошлого
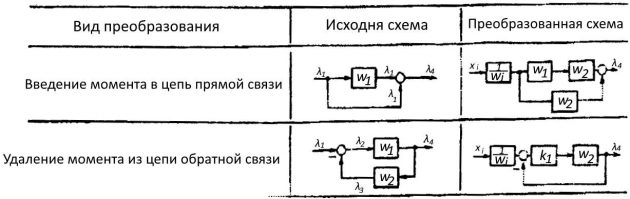
Для упрощения анализа влияния элементов на работу САР возможно произвести преобразование структурных схем.
Методы оценки качества в переходных режимах. Диаграмма Вышнеградского
Для оценки качества переходных процессов используются прямые оценки, определяемые путем расчета переходных процессов при стандартных входных воздействиях, и косвенные оценки. Различают ступенчатое (скачкообразное) воздействие — наиболее часто используемый метод для систем стабилизации, импульсное воздействие, гармоническое (синусоидальное) воздействие, случайное воздействие.
Случайное воздействие наиболее часто встречается в практике. Однако ступенчатое воздействие (единичный скачок) приводит к наибольшему отклонению выходной величины и поэтому является основным используемым методом оценки качества переходных процессов.
Разработаны различные методы позволяющие по прямым и косвенным признакам судить о качестве переходных процессов линейной САР.
Интегральные оценки качеств. Интегральной оценкой качества может служить площадь под кривой переходного процесса
где:
где:
- х — отклонение xp от ее значения в новом установившемся режиме.
В колебательных системах используется квадратичная интегральная оценка
,
которая не зависит от закона отклонений. Для улучшенной интегральной оценки
, где T — заранее заданная постоянная величина.
Приближенное построение переходной характеристики h(t) можно осуществить, если рассчитать вещественную часть АФХ замкнутой системы P(ω) = ReФ(ω). Заменяя кривую Р(ω) трапециями, путем несложных расчетов получают h(t) — метод, трапециедальных частотных характеристик, разработанный профессором Солодов-пиковым.
Можно доказать, что по виду Р(ω) можно судить о характере переходного процесса — h(t). Например, конечное Ремонт автоматики, регуляторов частоты вращения и систем регулированиязначение регулируемой величины будет соответствовать у = δ = Ф(jω)ω = 0. Так как Ф(ω) = P(ω) + jQ(ω), где Q(ω) — нечетная функция от ω, то при ω = 0 равном нулю,
Можно также доказать, что начальное значение регу-лируемой величины будет равно Р(ω) при ω → ∞.
О качестве переходных процессов можно судить по расположению корней характеристического уравнения на плоскости корней. Так, например, наличие комплексных корней, расположенных близко к мнимой оси, свидетельствует о колебательности системы.
Наглядное представление о качестве переходных процессов и устойчивости линейной системы 3-го порядка дает диаграмма И.А. Вышнеградского, построенная в координатах А и В, где А и В постоянные нормированного уравнения 3-го порядка вида:
На рис. 3 показаны 3 области, соответствующие устойчивому решению уравнения, однако характер переходных процессов во всех областях различный: III — со-ответствует затуханию процесса по экспоненте, в области II — на экспоненту накладываются колебания, а в области I — процесс носит затухающий колебательный характер. При АВ < 1 процесс неустойчив.
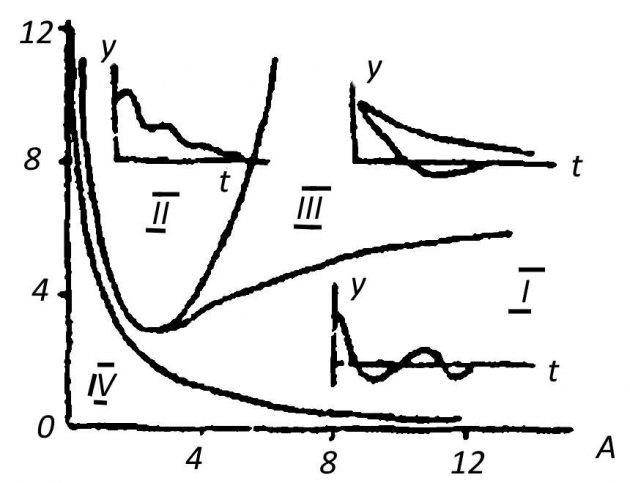
I, II, III – области устойчивости САР; IV – область неустойчивости САР
При исследовании систем регулирования с помощью АФХ разомкнутой системы удобно использовать частотные критерии качества: Расчет судовой электроэнергетической системызапас устойчивости по модулю (амплитуде) и запас устойчивости по фазе.
Запасом устойчивости по модулю называется величина, определяемая в общем случае для устойчивой САР по выражениям:
где:
- U1 и U2 — расстояния от начала координат до точек пересечения АФХ с отрицательной полуосью абсцисс (рис. 4).
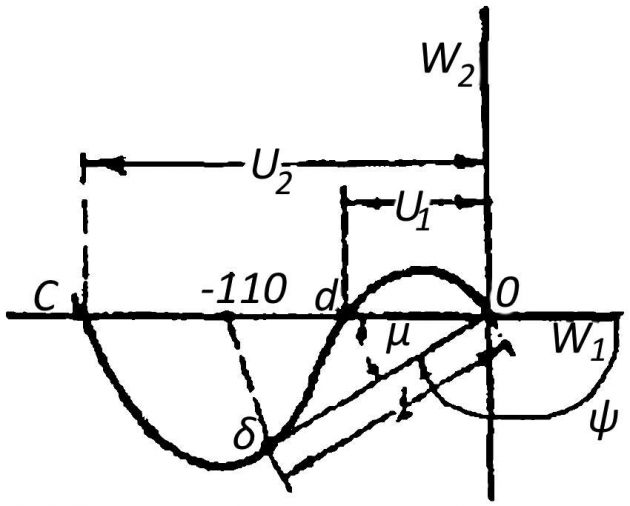
Запасом устойчивости по фазе называется вели-чина μ = 180 + ψ, где:
- ψ — аргумент передаточной функции при модуле, равном единице.
Запасы устойчивости по модулю и фазе могут быть косвенно связаны с видом переходного процесса. Так, например, уменьшение демпфирования в звеньях системы, приводящие к увеличению колебательности процесса, как правило, приводит к уменьшению запасов устойчивости по модулю и фазе. В хорошо демпфированных системах запас устойчивости по модулю составляет 6-20∂δ, а запас устойчивости по фазе 30-60°.
Системное программное обеспечение на судахЦифровые вычислительные машины имеют большие возможности в решении линейных и нелинейных дифференциальных уравнений высокого порядка. Этим, в известной степени, можно объяснить, что приближенные и косвенные методы исследования качества переходных процессов, разработанные для линеаризованных систем, в настоящее время не имеют широкого применения. ЭВМ позволяют легко решать те же задачи путем прямого интегрирования нелинейных уравнений, что более важно, т. к. в любой реальной САР имеют место нелинейности, оказывающие существенное влияние на качество регулирования.
Способы улучшения качества переходных процессов САР
Поясним вначале на примере конкретной САР влияние на показатели переходного процесса быстродействия регулятора, оцениваемое величиной, обратно пропорциональной его постоянной времени Тp, при описании регулятора дифференциальным уравнением 1-го порядка, принято, что Kp = 30. Объект регулирования принят также инерционным звеном 1-го порядка, Тоб = 5с.
На рис. 5 приведены результаты исследования рассматриваемой системы при изменении значения Тp. Уменьшение быстродействия регулятора путем увеличения Тp приводит к тому, что регулирующее воздействие Z принимает значение, компенсирующее набрасываемую нагрузку λ = 1, позже. К этому времени регулируемая величина y успевает отклониться от прежнего установившегося значения на большую величину Δymax. Новое установившееся значение при сохранении Kp = const остается неизменным. При уменьшении Тp, значения Δymax и δn снижаются. Заметим, что снижение Тp ниже определенных пределов может быть конструктивно сложной задачей.
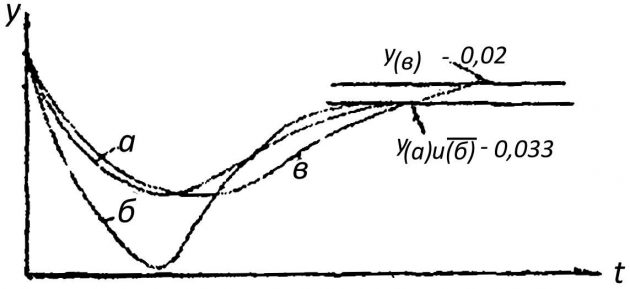
а) Kp = Kp1 = 30, Тp = Тp1 = 0,5 с; б) Kp2 = Kp1, Tp2 » Tp1, Тоб = 5с; в) Tp3 = Tp1, Kp3 = 50
В регуляторах прямого действия чувствительные элементы должны иметь работоспособность, достаточную для передвижения регулирующего органа, а это, как правило, приводит к увеличению Тp.
Эффект по уменьшению величины Δymax может быть достигнут путем увеличения Кp. Одновременно растет колебательность δn. Из предыдущего известно, что устойчивая САР с ростом Кp может стать неустойчивой.
Читайте также: Организация труда вахтенного ПКМ
Вместе с тем, имеются способы улучшения качества переходных процессов, которые позволяют решать задачи улучшения качества, без ухудшения устойчивости. К ним относится
Применение принципа комбинированного регулирования. Пусть имеется САР, включающая объект и регулятор, действующий по отклонению регулируемой величины (рис. 6). С целью повышения точности регулирования используем принцип комбинированного регулирования и введем устройство, осуществляющее регулирование по возмущению (нагрузке) с коэффициентом передачи Кк.
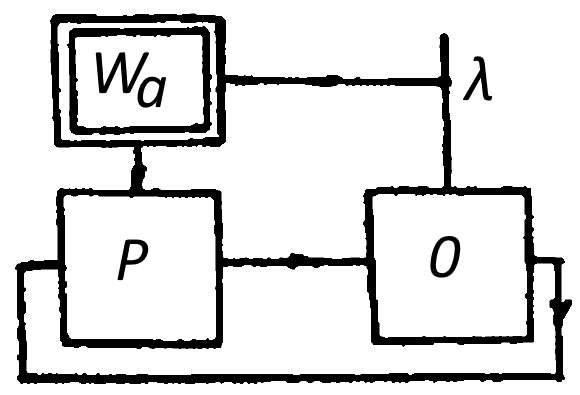
Будем считать, что все ПФ соответствуют позиционным звеньям.
Передаточная функция замкнутой системы, после решения системы алгебраических уравнений:
примет вид
при P = 0 наклон регуляторной характеристики определяется выражением:
Увеличивая Kк можно уменьшить наклон статической характеристики САР. На устойчивость системы и ее колебательность это влиять не будет, так как устойчивость определяется характеристическим уравнением, которое может быть получено, если полином знаменателя ПФ приравнять нулю. В полином знаменателя выражение Wк(p) не входит.
Коррекция введением производных. Для улучшения качества регулирования в систему могут быть введены дополнительные корректирующие звенья, например, по производным от возмущающего воздействия или регулируемой величины. SOS, Мэйдэй и другие международные сигналы о бедствииДействие сигнала производной по возмущению, если этот сигнал подавать с помощью специального устройства на регулирующий орган, в известной степени аналогично рассмотренному выше случаю. Отличие состоит в том, что сигнал по производной не действует на установившихся режимах и не изменяет статизма САР, но может повысить точность регулирования, снизив Δymax, в переходных режимах.
Рассмотрим действие коррекции по производной регулируемой величины, подаваемой на вход регулятора — (рис. 7), состоящего из позиционных звеньев, с помощью специального устройства, реализующего сигнал где:
- YK — выходная величина корректирующего устройства;
- K — его коэффициент передачи.
В переходном режиме, в первый момент переходного процесса, когда значение у еще мало, значение dy/dt может быть более существенно. Увеличивая коэффициент передачи, можно получить значение
В результате регулирующей орган будет передвигаться быстрее, восстанавливая требуемое значение регулируемой величины, значение Δymax — уменьшается. При значительном увеличении К колебательность может возрасти.
На рис. 8 представлена Элементы автоматических систем суднасхема чувствительного элемента регулятора скорости дизелей типа Д-6 и Д-12, в случае, если дизель используется для привода генераторов, когда к САР скорости вращения предъявляются высокие требования к показателям переходных процессов.
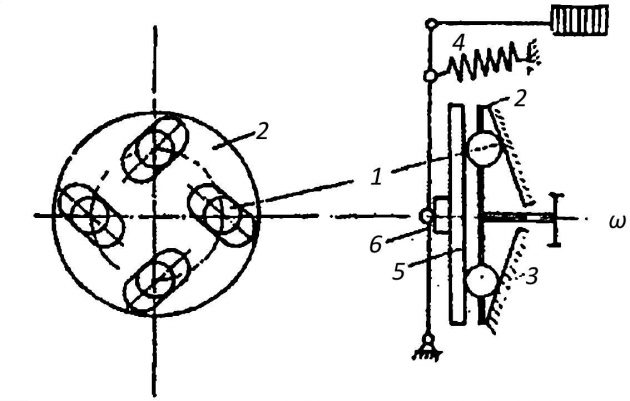
Чувствительный элемент частоты вращения — шаровые грузы 1, вращаются вместе с диском 2, приводимым во вращение от дизеля и имеющим продольные прорези, в которых могут передвигаться шары. При вращении диска шары перекатываются по неподвижной конусообразной поверхности 3 и под действием центробежных сил, приведенных к осевому направлению, преодолевают давление основной пружины 4 регулятора, воздействую-щей через рычаг 6 на тарельчатую муфту 5, прижимающую шары к неподвижной поверхности. При изменении частоты вращения баланс между центробежными силами грузов F и силой пружины изменяется и происходит передвижение муфты, вместе с ней рычага 6, передвигающего рейку топливных насосов. Прорези диска в модификации регулятора, предназначенного для ДГ, располагаются не радиально, как для варианта дизеля, работающего на винт, а под наклоном к радиусу. В этом случае при возникновении углового ускорения ε = dω/dt возникает противоположно направленная ему сила инерции шаров Fε = – mεε (где m — масса шара). Составляющая этой силы, направленная вдоль прорези — F1 вызывает передвижение шаров, также как и центробежная сила инерции F, но может действовать, опережая действие силы F, если ускорение возникнет, а изменение ω еще не произойдет.
Таким образом, передаточная функция такого чувствительного элемента (регулятора скорости прямого действия) будет иметь вид
При точном выводе уравнения можно показать, что стремление в приведенной конструкции к увеличению действия 2-го импульса регулятора — по ускорению, величина постоянной времени Т1 растет, что нежелательно, т.к. увеличивает инерционность регулятора скорости.
Введение внутренних жестких и гибких обратных связей. Рассмотрим влияние жесткой обратной связи на примере схемы регулирования уровня воды в емкости (см. рис. 1 Схема уровня воды).
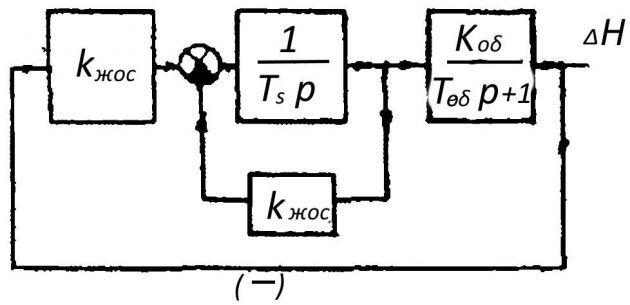
На рис. 9 представлена структурная схема этой системы. Интегрирующее звено — сервомотор, охвачен жесткой обратной связью с коэффициентом передачи kжос = АО/ОВ, где ОА и ОВ — плечи рычага 3 (на рис. 1 Схема уровня воды).
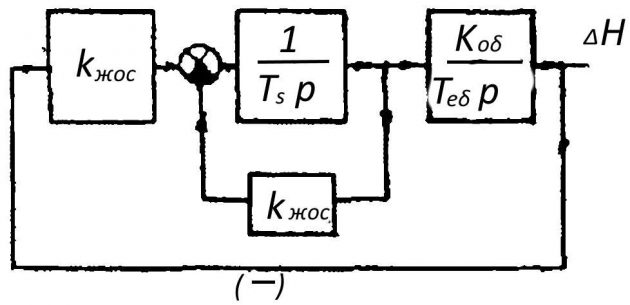
Передаточная функция сервомотора, охваченного отрицательной обратной связью примет вид:
Интегрирующее звено, охваченное ЖОС, превратилось в инерционное. Коэффициент передачи этого звена равен 1/Kжос.
Увеличивая Kжос можно уменьшить коэффициент усиления регулятора и увеличить наклон статической характеристики САР. Запас устойчивости такой системы по модулю и фазе возрастет. Жесткие обратные связи действуют в установившихся и переходных режимах.
В отличие от жестких гибкие или Процессы в судовых системах автоматического управления. Особенности настройки регуляторовизодромные обратные связи имеют передаточную функцию вида:
и действуют только в переходных режимах, так как при Р = 0
Для анализа влияния гибкой обратной на качество переходных процессов рассмотрим случай, когда величина Ti велика и поэтому в первый период переходного процесса
Очевидно, что передаточная функция гибкой обратной связи примет виц W(р ) = Кj; т.е. в первый период переходного процесса, гибкая обратная связь действует подобно жесткой обратной связи с коэффициентом усиления Kj.
Это интерсно: Мировой Океан и океанотехника. Характеристики морских льдов, течений и волн
Таким образом, коэффициент усиления звена, охваченного гибкой обратной связью, временно уменьшается. Этим можно достичь уменьшения колебательности системы, без влияния на ее статизм. Однако при больших Kj может увеличиться величина перерегулирования и возрасти длительность переходного процесса (см. рис. 10, кривая 3).
1 – при отсутствии обратной связи; 2 – при включении ГОС; 3 – при значительном увеличении коэффициента усиления обратной связи
Конструкции устройств гибких обратных связей
Гидравлические обратные связи. Устройство гидравлической обратной связи рассмотрим на примере изодрома — рис. 11, а. Изодром включает ведущий поршень А, ведомый поршень В, на который действует пружина, и иглу изодрома С, прикрывающую отверстие, ведущее в полость изодрома. Входной координатой xвх принимается относительное перемещение поршня А, выходной xвых — поршня В, который передает это движение последующим элементом регулятора. Очевидно, что характер движения поршня В зависит от скорости перемещения поршня А и положения иглы изодрома С. Если поршень А прекратит движение, то под действием избыточного давления или разрежения жидкость будет поступать в полость изодрома через отверстие, прикрываемое иглой С до тех пор, пока поршень В не займет положения, соответствующее разжатой пружине.
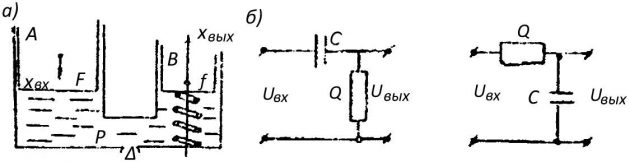
а) – гидравлической; б) – электрической, где F и f- площади поршней А и В, р – давление жидкости, а – коэффициент пропорциональности, Q – расход через отверстие
Таким образом, поршень В всегда занимает одно и то же установившееся положение.
Для случая ламинарного истечения жидкости через перепускное отверстие изодрома уравнение неразрывности имеет вид:
Если пренебречь силами гидравлического трения и передвигающихся частей, приложенных к ведомому поршеньку, которые малы по сравнению с силами давления масла, действующими на него, то уравнение его движения примет вид:
где:
- с — Основы взаимодействия дизеля и устройств автоматического регулированияжесткость пружины ведомого поршенька.
Опуская вывод и приводя эти уравнения к относи-тельным координатам, получим:
где:
Изменением положения иглы изодромной обратной связи можно изменять ее постоянную времени: при завинчивании иглы постоянная времени увеличивается. Кроме того Tj можно изменить за счет жесткости с пружины ведомого поршенька. Увеличение коэффициента передачи изодромной обратной связи достигается за счет увеличения F/f.
Электрические гибкие и жесткие обратные связи. Гибкие и жесткие обратные связи электрического типа широко используются, например, в системах регулирования напряжения генераторов. На рис. 11, б представлена электрическая схема, состоящая из емкости С и сопротивления R. Найдем uвых = RI, где I — ток в цепи uвх = Uc + RI, где uc — падение напряжения на емкости С;
Исключив из этих уравнений uc и I, получим дифференциальное уравнение
где:
- T = RC.
Полученному уравнению соответствует передаточная функция гибкой обратной связи.
Таким образом, для осуществления гибкой обратной связи необходимо последовательное включение емкости и сопротивления. Такого типа связи используются, на-пример, в регуляторах напряжения генераторов со статической системой возбуждения. Электрическая жесткая обратная связь включает в себя только активное сопротивление; изменяя величину этого сопротивления, можно изменять коэффициент усиления жесткой обратной связи.
На рис. 12 представлена Основы взаимодействия дизеля и устройств автоматического регулированиясхема регулятора скорости непрямого действия двигателей типа М-401-А и др. В варианте главного судового дизеля этот всережимный регулятор (ВРН) не имеет жесткой обратной связи. В период переходного процесса грузы измерителя 1 изменяют свое положение, перемещая золотник 2. Пружина катаракта 9 временно увеличивает степень неравномерности измерителя, обеспечивая устойчивость системы. Передвижение золотника 2 приводит к тому, что масло под давлением либо попадает под сервопоршень 3, либо через то же окно во втулке сервопоршня идет на слив, в результате чего сервопоршень передвигается, следуя за золотником и перемещая рейку топливных насосов.
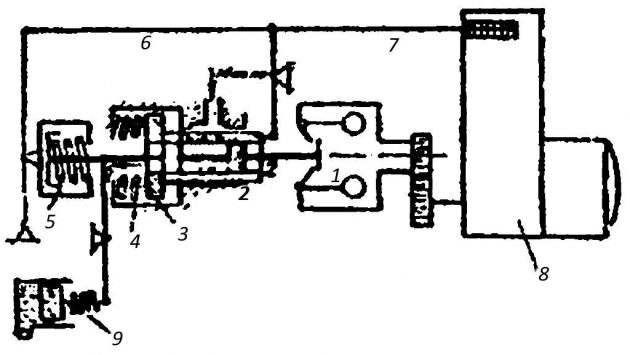
1 – грузы измерителя; 2 – золотник; 3 – сервомотор; 4 – пружина сервомотора; 5 – пружина измерителя; 6 – жесткая обратная связь; 7 — рычаг связи регулятора с рейкой; 8 – двигатель; 9 – пружина катаракта
При выводе передаточных функций звеньев можно ориентироваться на уже приведенном выше уравнении измерителя скорости, сервомотора, входной величиной которого является разность координат чувствительного элемента и сервомотора (η-z) и объекта регулирования — дизеля.
Передаточная функция упруго-присоединенного катаракта может быть получена из его дифференциального уравнения, которое приводится в п. VIII, 2. В передаточной функции чувствительного элемента пренебрегается влиянием T2ч и Тk из-за их малости. Кроме того, влиянием ЖОС на динамику из-за его малости также пренебрегаем.
Читайте также: Монтаж судовых двигателей внутреннего сгорания
Требуется определить показатели переходных процессов при набросе 100% нагрузки. Постоянные уравнений заданы: Система дифференциальных уравнений и передаточные функции регулятора (без ЖОС) примут вид:
- 1Уравнение и передаточная функция объекта:
- Уравнение чувствительного элемента
- Уравнение и передаточная функция упруго присоединенного катаракта:
- Уравнение и передаточная функция сервомотора:
- Уравнение основной обратной связи:
где:
- η, l, z — координаты чувствительного элемента, упруго присоединенного катаракта и сервомотора соответственно.
На рис. 13 показан график переходного процесса, полученный путем решения системы уравнений на ПЭВМ.