Общие положения
Единственным методом определения прочных размеров корпуса деревянных судовКонструктивные и архитектурные типы морских деревянных судов долгое время был метод сравнения проектируемого судна с судами, оправдавшими себя в эксплуатации. Естественно, что такой метод не является прогрессивным, потому что при этом, как правило, повторяются имеющиеся у прототипа конструктивные недостатки и проанализировать работу конструкции, чтобы выбрать оптимальные размеры отдельных связей, обеспечивающих корпусу необходимую прочность, не представляется возможным.
Основным методом проектирования корпусных конструкций до настоящего времени является конструирование на основании правил классификационных обществ. В некоторых случаях такой подход приводит к излишнему расходу материала и исключает учет особенностей проектируемого судна, а также рационализацию его конструкции.
За последние годы наметился уверенный переход к расчетному конструированию, что нашло отражение в ряде специальных работ, посвященных этому вопросу, а также в современных изданиях правил классификационных обществ.
Наиболее прогрессивными являются Правила Регистра России, в которых в наибольшей степени, по сравнению с зарубежными, применены методы расчетного проектирования при определении прочных размеров деталей корпуса судна. Это, однако, относится главным образом к правилам постройки стальных судов и не распространяется пока на правила постройки морских деревянных судов.
Одной из задач проектирования новых судов является создание корпуса, который при наименьшем весе и возможной простоте конструкции обладал бы достаточной прочностью, отвечающей всем условиям плавания судна. Наиболее правильным решением этой задачи следует признать непосредственный расчет прочности судна, основанный на положениях строительной механики корабля. При определении деталей корпуса расчетным путем для конструктора открываются более широкие возможности рационального использования материала и проявления инициативы. Начиная с 30-х годов, в Советском Союзе сделан ряд попыток дать более или менее обоснованные расчетные методы определения прочных размеров корпуса деревянных судов, представляющего сложную совокупность отдельных связей, совместная работа которых достигается различными способами их соединения.
Клееные швы, при условии их качественного исполнения, равнопрочны с основным материалом и склеенная деревянная конструкция ведет себя так, как если бы была выполнена из одного куска дерева.
Указания о проектировании клееных соединений и методах их расчета приведены в статье “Основные материалы и изделия, применяемые в морском деревянном судостроении. Соединения деталей корпусных конструкцийОсновные материалы применяемые в морском деревянном судостроении». Осуществить соединение на нагельных средствах крепления, равнопрочное основному материалу (доска, брус), практически не представляется возможным, поэтому расчет прочности деревянной конструкции на нагельных соединениях сводится к расчету прочности этих соединений. Ниже приводится описание некоторых методов расчета общей прочности деревянных судов, нашедших применение в практике проектных организаций.
Расчет прочности по допускаемым напряжениям (метод П. О. Зандина)
1. Схема расчета. Работа П. О. Зандина, выполненная в 1930 г., учитывает специфику расчета прочности деревянного судна, причем внешние нагрузки определяются теми же способами, что и для металлического судна, т. е. строятся эпюры нагрузок, изгибающих моментов и срезывающих сил, а при расчете изгибающих моментов рекомендуется учитывать прогиб судна, так как ввиду малой жесткости деревянного корпуса прогиб будет существенно влиять на величину максимального изгибающего момента. Это соображение относится главным образом к речным баржевым судам, имеющим большую длину и малую высоту борта, и значительно меньше к морским судам, обладающим большей жесткостью корпуса.
Сущность расчета по Зандину сводится к замене немонолитной конструкции эквивалентного бруса монолитной, путем введения в расчет соответствующих редукционных коэффициентов. Это необходимо вследствие ограниченных размеров отдельных штук брусьев, составляющих корпус судна, так как приходится допускать стыки по их длине; кроме того, как уже указывалось, существующие способы крепления отдельных штук между собой несовершенны и неэквивалентны прочности целой древесины.
Рассмотрим сложную деревянную конструкцию, находящуюся под действием растягивающих усилий (рис. 1).

При достаточно большой величине растягивающего усилия, вследствие слабости креплений, произойдет разрушение конструкции. При разрушении будет преодолеваться сумма усилий закрепления более слабых (более коротких, заштрихованных на рисунке) концов досок. Следовательно, определение усилия, допускаемого на данную конструкцию, сведется к определению суммарного усилия, допускаемого на крепежные деталиВосстановление и упрочнение деталей механизмов, расположенные на заштрихованной части.
Если Рi — усилие, удерживающее наиболее слабо закрепленную часть доски (бруса), то площадь эквивалентной монолитной связи:
где:
- [σ] — допускаемое напряжение для дерева.
Для нескольких связей площадь эквивалентной монолитной связи определится в случае растяжения формулой:
в случае сжатия формулой:
В этих формулах:
- k — коэффициент, учитывающий неодновременность работы разнородных соединений, принимаемый обычно равным 0,8;
- Ti — допускаемое усилие на единицу крепления;
- Т’i — допускаемое усилие на единицу смятия торца;
- ni— количество работающих креплений данного типа, в том числе и торцов;
- ki —коэффициент, учитывающий неодновременность работы креплений данного типа (для нагельных соединений принимается обычно равным 1,0);
- [σp] — допускаемое для дерева напряжение на растяжение;
- [σсж] — допускаемое для дерева напряжение на сжатие.
Редукционный коэффициент r для каждой связи определится как отношение площади эквивалентной монолитной связи ƒм к фактической площади поперечного сечения ƒi:
При подсчете эквивалентного бруса учитывается не вся площадь сечения продольных связей, а лишь часть ее, определяемая редукционным коэффициентом, и потому:
Редукционный коэффициент характеризует степень совершенства конструкции и степень использования материала в ней, а также показывает, насколько удачно спроектировано соединение отдельных штук досок (брусьев). Последующий расчет эквивалентного бруса, составленного из редуцированных связей, выполняется обычным путем — путем вычисления напряжения по формуле:
где:
- М — изгибающий момент, действующий в рассматриваемом сечении судна;
- I — момент инерции рассматриваемого сечения эквивалентного бруса;
- y — отстояние сечения рассматриваемой связи от нейтральной оси.
Следовательно, схема расчета по методу П. О. Зандина такова:
- определяются методом статической постановки на волну изгибающие моменты, действующие на судно на вершине и подошве волны;
- устанавливается система допускаемых напряжений с учетом определенных условий работы дерева;
- определяются допускаемые усилия для отдельных связей корпуса судна, причем нет необходимости проделывать это для каждой штуки дерева в отдельности. Обычно представляется возможным расчленить конструкцию на группы связей, одинаково устроенных в отношении расположения стыков и характера креплений, и уже для этих групп производить расчет допускаемых усилий и редукционных коэффициентов;
- производится расчет эквивалентного бруса, составленного из редуцированных связей. По формуле (12) определяют нормальные напряжения и сравнивают их с допускаемыми. Условие достаточной прочности выразится формулой.
2. Допускаемые напряжения и допускаемые усилия. При расчете по методу П. О. Зандина ранее пользовались допускаемыми напряжениями и допускаемыми усилиями на крепежные детали в соответствии с ОСТ 90001—38. В настоящее время вместо ОСТ 90001—38 действуют «Нормы и технические условия проектирования деревянных конструкций» (Н и ТУ 122—55), изданные в 1955 г. Государственным Комитетом Совета Министров по делам строительства.
Расчетные формулы и нормативы по ОСТ 90001—38, определяющие допускаемые усилия для различных крепежных средств, выведены из условий прочности и не учитывают величины деформаций соединений Н и ТУ 122-55 также не учитывают величины деформаций соединений.x. Поэтому П. О. Зандин предложил ввести в расчет учет деформаций конструкции, ограничив, по условиям водонепроницаемости, раскрытие каждого стыка обшивки величиной 1,5 мм.
В результате модельных испытаний были получены расчетные формулы Эти формулы были введены Г.В.Ефремовым.x, в которых допускаемое усилие на один срез нагеля выражено в зависимости от деформации соединения, а именно:
для соединения на деревянных нагелях:
для гвоздевого соединения:
для болтового соединения при действии усилия поперек волокон:
При действии усилия вдоль волокон величина Т может быть увеличена на 20—25%. В приведенных формулах:
- Т — допускаемое усилие на одно крепление, кг;
- d — диаметр крепежа, см;
- Δ — допускаемое смещение (деформация), мм, которое рекомендуется принимать равным 0,5—0,7 мм.
Достоверность приведенных формул вызывает, однако, сомнения, так как они базируются на отдельных разрозненных испытаниях ЦНИИВТ.
3. Некоторые замечания. Основным недостатком метода П. О. Зандина следует признать то обстоятельство, что деформации отдельных связей эквивалентного бруса не соответствуют действующим усилиям, предположенным при исчислении редукционных коэффициентов. В действительности усилия, развиваемые отдельными связями, зависят не только от вида и количества креплений, но и от величины деформации, которую данная связь получает в составе эквивалентного бруса.
Как это было показано А. С. Соколовой, приведение эквивалентного бруса к монолитному по прочности не равнозначно с приведением по жесткости, поэтому несомненного интереса заслуживает ее рекомендация об уточнении метода расчета эквивалентного бруса путем вычисления редукционных коэффициентов по формуле:
где:
- Е — модуль упругости редуцируемой связи;
- 105 — модуль упругости воздушно-сухой сосны при растяжении вдоль волокон, кг/см².
Модуль упругости редуцируемой связи, в свою очередь, определяется по зависимости:
где:
- Ел — модуль упругости древесины связи;
- δ — половина расхождения стыка при растяжении связи или местного обмятия при сжатии;
- Δl — абсолютное удлинение половины длины связи, для которого определено δ, при усилии в брусе, соответствующем величине δ.
Естественно, что эквивалентный брус, составленный с применением редукционных коэффициентов, исчисленных по методу А. С. Соколовой, можно рассматривать с точки зрения жесткости как однородную балку из цельной воздушно-сухой древесины.
Перечисленные недостатки показывают, что по ряду положений метод П. О. Зандина нельзя считать достаточно обоснованным, так как фактические условия работы связей в составе эквивалентного бруса отличаются от предусмотренных расчетной схемой: не соблюдена принятая гипотеза плоских сечений, что в какой-то мере искажает оценку участия отдельных связей в общем изгибе судна, вызывают сомнение и формулы для определения допускаемых усилий из условия водонепроницаемости для различных видов нагельных креплений. В то же время формулы по ОСТ 90001—38, являющиеся нормативами для промышленного и гражданского строительства и оправданные практикой эксплуатации наземных сооружений, не учитывают пределов возможных деформаций по условиям водонепроницаемости.
Несмотря на сказанное, проектными организациями были выполнены по этому методу расчеты прочности многих деревянных судов, в последующем проверенных в эксплуатации, а потому указанная схема расчета и теперь еще находит применение.
Расчет прочности по предельным состояниям (метод П. Н. Матвеева)
1. Схема расчета. Попытки дальнейшего развития методологии расчета прочности деревянных судов были сделаны П. Н. Матвеевым. В методологии П. Н. Матвеева заложено применение принципа расчета по предельным состояниям. Основным критерием прочности является выполнение условия, чтобы наибольшая возможная нагрузка (предельная возможная нагрузка), называемая «расчетной нагрузкой», не превосходила величины «несущей способности» конструкции в ее предельном состоянии, т. е. состоянии, при котором дальнейшая нормальная эксплуатация конструкции становится невозможной.
Предельное состояние конструкции корпуса деревянного суднаПалубные конструкции морских деревянных судов определяется двумя условиями:
- условием достаточной прочности конструкции и условием сохранения водонепроницаемости корпуса, что обеспечивается введением допускаемых относительных перемещений (деформаций) связей.
В рассматриваемом методе расчета по предельным состояниям при расчете общей прочности корпуса судна П. Н. Матвеевым были предположены следующие условия работы конструкции:
- элементы сечения корпуса, несущие нагрузку, подчиняются закону плоских сечений;
- усилия в связях, составных по длине и входящих в состав сечения, передаются только путем крепежных нагельных (податливых) средств;
- деформация основной массы древесины связей считается пренебрежимо малой по сравнению с деформациями в местах сопряжения составных по длине связей;
- момент внутренних сил в сечении судна получается суммированием моментов усилий относительно нейтральной оси, выдерживаемых связями при условии соблюдения по высоте сечения линейного закона распределения деформаций;
- деформация сжатых элементов, происходящая за счет обжатия стыков, пренебрежимо мала в сравнении с деформацией растянутых элементов, происходящей за счет податливости нагельных соединений; это позволяет считать нейтральную ось проходящей через верхнюю расчетную палубу в случае прогиба судна и через днище — в случае перегиба судна.
Предельное состояние конструкции корпуса деревянного судна будет достигнуто, когда одна из связей этой конструкции будет находиться в предельном положении, определенном указанными выше условиями: условием достаточной прочности и условием сохранения водонепроницаемости в местах стыкования отдельных штук брусьев. Следовательно, для определения несущей способности конструкции в целом необходимо определить несущие способности и соответствующие им относительные перемещения отдельных связей, входящих в состав корпуса судна. Так как прочность всех деревянных конструкций, за исключением клееных, определяется прочностью креплений, то несущая способность связи определяется несущей способностью входящих в нее соединений.
Подобно тому как предельное состояние всей конструкции определяется достижением предельного состояния какой-либо одной связи, входящей в состав конструкции, предельное состояние самой связи определяется прочностью входящих в ее состав соединений и считается достигнутым, если деформация, вызванная усилием, приложенным к связи, вызывает в каком-либо одном соединении (крепежной детали) напряжения, равные допускаемым.
В этом случае величина полной несущей способности связи выразится как сумма усилий всех видов креплений связи, вызываемых наименьшей деформацией, приводящей какой-либо вид крепления в предельное состояние, формула:
где:
- Р — несущая способность связи;
- Т1, Т2, …, Тn — несущая способность для каждого вида крепежных средств;
- Δ1, Δ2, …,Δm — деформации, соответствующие этим несущим способностям;
- при этом считается, что Δ1 < Δ2 < Δ3 <… < Δn.
Формула (13) позволяет вычислить несущие способности для всех групп связей, входящих в состав эквивалентного бруса (рис. 2).
Изображенные на рис. 2 несущие способности и лимитирующие деформации связей определены без учета их совместной работы. Для определения несущей способности конструкции корпуса необходимо подчинить деформации отдельных связей следующим условиям:
- условию совместной работы всех связей корпуса, что соответствует соблюдению по высоте сечения линейного закона распределения деформации хi;
- условию сохранения прочности конструкции, для чего необходимо, чтобы деформации связей хi по своей величине не превосходили деформаций Δi соответствующих несущим способностям Рi;
- условию сохранения водонепроницаемости обшивки, для чего необходимо, чтобы деформации связей xi по своей величине не превосходили некоторой допускаемой величины Δво1, обусловленной максимально допустимой величиной раскрытия стыка;
- условию достижения конструкцией ее предельного состояния, для чего необходимо, чтобы деформация одной из связей корпуса была равна предельно допустимой с точки зрения прочности связи или ее водонепроницаемости.
На рис. 2 деформации xi определены для случая перегиба судна, когда палуба растянута, а днище сжато.
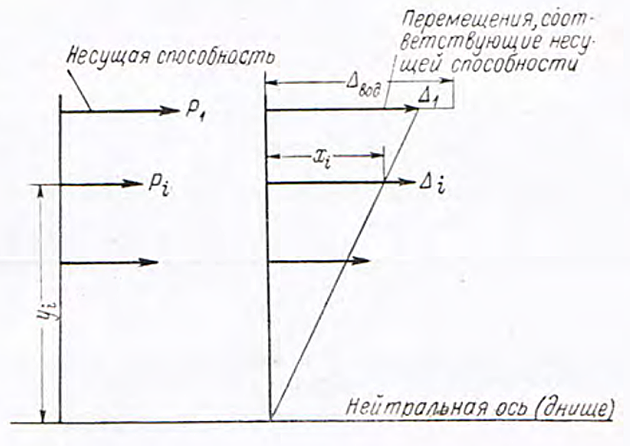
Принимая во внимание допущение о том, что деформации растянутых связей велики по сравнению с деформациями сжатия, и считая поэтому деформацию сжатых связей (днища) равной нулю, определяем деформации отдельных связей хi построением прямой с таким расчетом, чтобы:
В нашем случае, очевидно, предельное состояние конструкцииНадзор за состоянием судов определяется условием прочности верхней связи.
Деформации xi, определенные с учетом вышеприведенных условий, позволяют вычислить действующие усилия в связях при предельном состоянии конструкции корпуса судна. Усилия, действующие в любой связи при предельном состоянии конструкции, определяются как:
Несущий момент внутренних сил выразится формулой:
где:
- уi — отстояние i-и связи от нейтральной оси.
Прочность конструкции считается достаточной, если несущий момент внутренних сил будет превышать момент внешних нагрузок.
Кроме того, связи, работающие на сжатие, должны быть в состоянии уравновесить общее усилие растяжения, т.е. напряжение в сжатых связях должно быть:
где:
- Fсж — площадь сжатых связей.
Таким образом,схема расчета по методу П. Н. Матвеева следующая:
- определяется гибающий момент внешних нагрузок;
- определяются несущие способности и соответствующие им деформации связей корпуса судна;
- определяются деформации связей, соответствующие предельному состоянию конструкции корпуса судна при условии совместной работы связей;
- определяются усилия, действующие в связях при предельном состоянии конструкции, и вычисляется несущий момент внутренних сил.
Корпус судна считается достаточно прочным, если вычисленный несущий момент будет больше момента от внешних нагрузок.
2. Несущая способность нагельных креплений и их деформации. Несущая способность и относительные перемещения для различных связей корпуса определяются с учетом действующих нагрузок, которые по характеру действия подразделяются на кратковременные и длительные. Применительно к расчету общей прочности морских деревянных судов кратковременными нагрузками будут нагрузки при спуске судов на воду или подъеме. Изгибающие моменты и перерезывающие силы, возникающие в корпусе судна при волнении, следует отнести к длительным нагрузкам.
В табл. 1—5 приведены значения несущих способностей и относительных перемещений, вычисленных применительно к различным типам крепежа для наиболее употребительных размеров. При пользовании таблицами необходимо иметь в виду следующее:
- приведенные в таблицах значения Т и f должны быть умножены на коэффициент с, равный 0,65 при кратковременной нагрузке и 0,50 при длительной нагрузке;
- предполагается, что правый брус имеет величину несущей способности Т не менее левого бруса;
- при вычислении несущей способности деревянных нагельных соединений не принято во внимание трение стержня нагеля, усиливающее несущую способность, особенно древесины в мокром состоянии. Заотсутствием достоверных опытных данных можно принять это увеличение для состояния предельного насыщения до 50%.
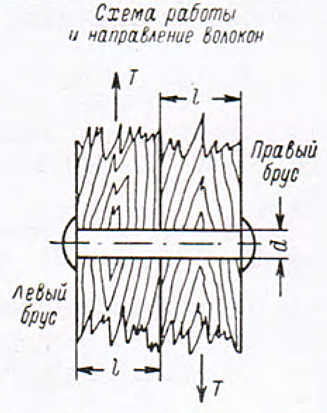
| Таблица 1. Несущая способность Т и относительное перемещение f болтовых соединений, работающих на одинарный срез вдоль волокон | ||||||||
|---|---|---|---|---|---|---|---|---|
 | ||||||||
| Несущая способность T, кг | Относительное перемещение f=2fo, мм | |||||||
| d, мм | Влажность W, % | l/d | ||||||
| 15 | 22,5 | 30 | 5,0 | 7,5 | 10,0 | 12,5 | 15,0 | |
| 13 | 1070 | 895 | 720 | 2×1,0 | 2×2,5 | 2×4,5 | 2×70 | 2×10,5 |
| 16 | 1630 | 1365 | 1100 | 2×1,5 | 2×3,0 | 2×5,5 | 2×9,0 | 2×13,0 |
| 19 | 2280 | 1905 | 1530 | 2×1,5 | 2×4,0 | 2×7,0 | 2×10,5 | 2×15,0 |
| 22 | 3050 | 2550 | 2050 | 2×2,0 | 2×4,5 | 2×8,0 | 2×12,0 | 2×17,5 |
| Таблица 2. Несущая способность Т и относительное перемещение f болтовых соединений, работающих на одинарный срез поперек волокон в радиальном направлении | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
 | ||||||||||||
| d, мм | Несушая способность Т, кг | Относительное перемещение f=2fo, мм | ||||||||||
| Влажность W, % | ||||||||||||
| 15 | 22,5 | 30 | ||||||||||
| l/d | ||||||||||||
| 5 | 10 | 5 | 10 | 5 | 10 | 2,5 | 5,0 | 7,5 | 10,0 | 12,5 | 15,0 | |
| 13 | 640 | 600 | 530 | 487 | 420 | 375 | 2х1,5 | 2х2,5 | 2х4,0 | 2х6,0 | 2х8,5 | 2х11,5 |
| 16 | 950 | 910 | 795 | 742 | 640 | 575 | 2х1,5 | 2х2,5 | 2х4,5 | 2х7,0 | 2х10 | 2х14,0 |
| 19 | 1350 | 1280 | 1130 | 1040 | 910 | 800 | 2х1,5 | 2х3,0 | 2х5,0 | 2х8,0 | 2х12 | 2х16,5 |
| 22 | 1800 | 1750 | 1505 | 1415 | 1210 | 1080 | 2х1,5 | 2х3,0 | 2х5,5 | 2х9,0 | 2х13,5 | 2х19,0 |
| Таблица 3. Несущая способность Т и относительное перемещение f болтовых соединений, работающих на одинарный срез поперек волокон в тангенциальном направлении | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
 | ||||||||||||
| d, мм | Несушая способность Т, кг | Относительное перемещение f=2fo, мм | ||||||||||
| Влажность W, % | l/d | |||||||||||
| 15 | 22,5 | 30 | ||||||||||
| l/d | 2,5 | 5,0 | 7,5 | 10 | 12,5 | 15 | ||||||
| 5 | 10 | 5 | 10 | 5 | 10 | |||||||
| 13 | 640 | 600 | 530 | 487 | 420 | 375 | 2х0,5 | 2х1,5 | 2х3,0 | 2х5,0 | 2х7,5 | 2х10,5 |
| 16 | 950 | 910 | 795 | 742 | 640 | 575 | 2х0,5 | 2х1,5 | 2х3,5 | 2х6,0 | 2х9,0 | 2х13,0 |
| 19 | 1350 | 1280 | 1130 | 1040 | 910 | 800 | 2х0,5 | 2х2,0 | 2х4,0 | 2х7,0 | 2х11,0 | 2х15,5 |
| 22 | 1800 | 1750 | 1505 | 1415 | 1210 | 1080 | 2х0,5 | 2х2,0 | 2х4,5 | 2х8,0 | 2х12,5 | 2х18,0 |
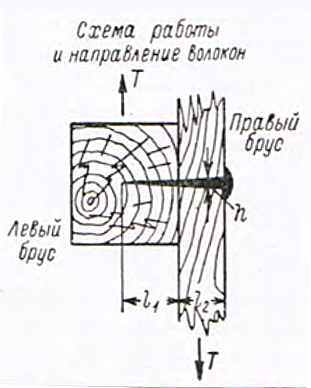
| Таблица 4. Несущая способность Т и относительное перемещение f гвоздевых соединений, работающих на одинарный срез (гвозди кованые) | ||||||
|---|---|---|---|---|---|---|
 | ||||||
| Несущая способность Т, кг | Полное относительное перемещение f, мм | |||||
| h, мм | Влажность W, % | |||||
| 30 | 22,5 | 15 | Влажность W, % | |||
| 30 | 22,5 | 15 | ||||
| 6 | 90 | 112 | 135 | 5 | 3 | 1,5 |
| 7 | 125 | 155 | 185 | 6 | 3,5 | 1,5 |
| 8 | 160 | 200 | 240 | 6,5 | 4 | 2 |
| 9 | 200 | 252 | 305 | 7 | 4 | 2 |
| 10 | 250 | 287 | 375 | 8 | 5 | 2,5 |
| 11 | 300 | 377 | 455 | 9 | 5 | 2,5 |
| 12 | 306 | 450 | 540 | 10 | 5,5 | 3 |
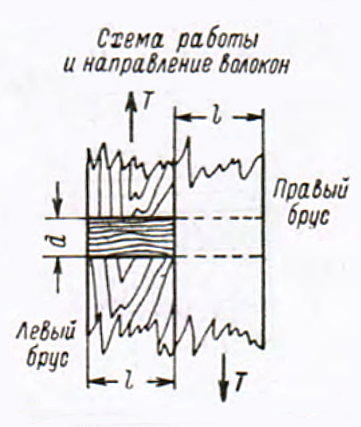
| Таблица 5. Несущая способность Т и относительное перемещение f нагельных (деревянные нагели) соединений, работающих на одинарный срез | |||||||||
|---|---|---|---|---|---|---|---|---|---|
 | |||||||||
| d, мм | Несущая способность Т, кг | Относительное перемещение f=2f0, мм | |||||||
| Влажность W, % | Влажность W=15% | ||||||||
| 15 | 22 | 30 | вдоль волокон | поперек волокон | |||||
| l/d | |||||||||
| 2 | 6 | 10 | 2 | 6 | 10 | ||||
| 24 | 485 | 360 | 240 | 2х0,5 | 2х4,0 | 2х11,5 | 2х2,0 | 2х6,0 | 2х13,0 |
| 27 | 620 | 465 | 310 | 2х0,5 | 2х4,5 | 2х12,6 | 2х2,0 | 2х6,5 | 2х14,5 |
| 30 | 760 | 570 | 380 | 2х0,5 | 2х5,0 | 2х14,0 | 2х2,5 | 2х7,0 | 2х16,0 |
| Продолжение | |||||||||
| d, мм | Несущая способность Т, кг | Относительное перемещение f=2f0, мм | |||||||
| Влажность W, % | Влажность W=30% | ||||||||
| 15 | 22 | 30 | вдоль волокон | поперек волокон | |||||
| Влажность l/d | |||||||||
| 2 | 6 | 10 | 2 | 6 | 10 | ||||
| 24 | 485 | 360 | 240 | 2х1,0 | 2х6,0 | 2х17,0 | 2х2,5 | 2х8,0 | 2х18,5 |
| 27 | 620 | 465 | 310 | 2х1,0 | 2х7,0 | 2х19,0 | 2х2,5 | 2х8,5 | 2х20,0 |
| 30 | 760 | 570 | 380 | 2х1,0 | 2х7,5 | 2х21,0 | 2х2,5 | 2х9,5 | 2х22,5 |
3. Замечания. По сделанным в методе П. Н. Матвеева допущениям следует высказать некоторые замечания.
В первую очередь, надо отметить, что принятая при определении несущих способностей связей, имеющих в своем составе крепеж различных типо-размеров, линейная зависимость между усилиями и перемещениями неполностью соответствует действительному напряженному состоянию, что не может не влиять на усилия, развиваемые отдельными креплениями во время их совместной работы. Кроме того, предположение о недеформируемости отдельных штук дерева вносит определенный элемент условности в расчеты по данной методологии.
Предлагается к прочтению: Тепловое состояние и охлаждение форсунок
Способ определения несущих способностей различных видов крепежных средств, принятый при составлении табл. 1—5, также имеет ряд спорных положений. Так, например, П. Н. Матвеевым учитывается сила трения между поверхностями соединяемых брусьев. Предположено, что эта сила может быть учтена для болтов — через величину силы затяжки болта, для гвоздей — через силу сопротивления вытаскиванию гвоздя из гнезда и для деревянного нагеля — через величину трения нагеля в гнезде. Однако очевидно, что наличие осевых сил в крепеже не может определить величины трения между соединяемыми брусьями, так как несмотря на наличие таких осевых сил брусья могут оказаться собранными с зазором и тогда сила трения будет отсутствовать. Также надо иметь в виду, что учет сил трения в деревянных конструкциях гражданских сооружений не допускается, так как влечет возможную ошибку в опасную сторону.
Обращают на себя внимание и абсолютные значения деформаций, приведенные П. Н. Матвеевым в его расчетных таблицах, которые для больших отношений l : d достигают 30—40 мм, что, очевидно, не реально. Наконец, по решению П. Н. Матвеева получается, что несущая способность нагеля практически не зависит от толщины соединяемых элементов, а жесткость соединений безгранично возрастает с уменьшением толщины сплачиваемых брусьев и, наоборот, безгранично уменьшается с увеличением их толщины.
Несмотря на высказанные замечания, не следует все же недооценивать сделанное П. Н. Матвеевым для дальнейшего развития строительной механики деревянных судов и попытки перейти к расчету деревянных судовых конструкций по их предельному состоянию. Наряду с этим необходимо отметить, что хотя этот метод и был применен в отдельных расчетах, он имеет ряд спорных, недостаточно обоснованных положений и без переработки не может быть рекомендован для практических целей.
Метод конструирования продольных связей морских деревянных судов на футоксовом наборе
1. Схема расчета. Методы П. О. Зандина и П. Н. Матвеева, как правило, применяются не с целью определения прочных размеров связей корпуса, а только (н то не всегда) для поверочных расчетов прочности судов, элементы которых определены по Правилам Морского Регистра России. Авторы этих расчетов вполне удовлетворены, если действующие напряжения оказываются ниже допускаемых, и не ставят задачей дальнейшее улучшение и облегчение проектируемой конструкции.
В настоящее время методы строительной механики корабля не позволяют определить прочные размеры набора деревянных судовКонструкция судового набора чисто расчетным путем. Поэтому наиболее правильными следует считать методы, построенные на натурном изучении судов в сочетании с экспериментальным и математическим исследованиями.
Попытки применить некоторые теоретические положения строительной механики для выявления обоснованных требований Правил Морского Регистра России при назначении прочных размеров конструктивных элементов морских деревянных судов можно отнести к 1953 г.
В частности, автор при составлении некоторых разделов проекта «Правил классификации и постройки морских деревянных судов» применил подобного рода обоснования для расчета продольных связей судов на корабельном (футоксовом) наборе.
В 1956 г. автором был предложен метод, ставящий целью не только проверку прочности спроектированного корпуса, но и наиболее рациональное назначение размеров прочных связей и прочности соединения отдельных элементов конструкции. В основу метода положен анализ конструкции морских деревянных судов на корабельном наборе, построенных за последнее двадцатилетие, а также анализ опытных данных по постройке и эксплуатации судов, обобщенный в Правилах Морского Регистра и других классификационных обществ.
Исследование прочности эквивалентного бруса выполнено при следующих основных допущениях:
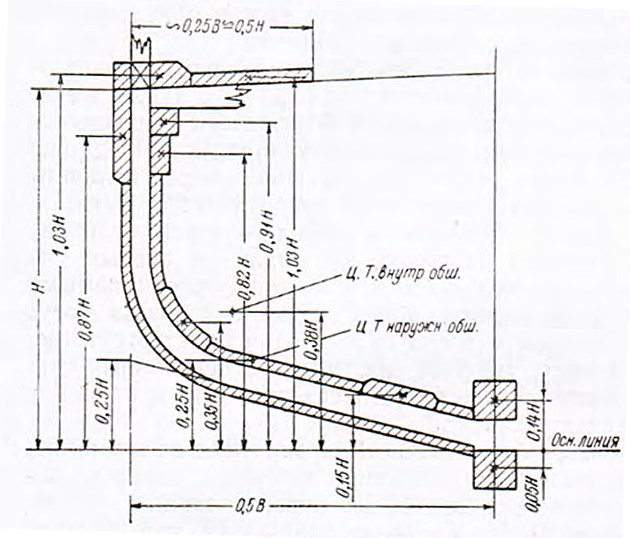
- установлена типовая схема основных продольных связей, работающих в составе эквивалентного бруса (рис. 3);
- предположено, что площадь каждой продольной связи может быть выражена аналитической зависимостью в функции от толщины наружной обшивки и главных размерений судна;
- центры тяжести поперечных сечений отдельных продольных связей приняты постоянными в долях высоты борта Н и независимыми от абсолютной величины высоты борта;
- несущие способности отдельных продольных связей и эквивалентного бруса в целом определены с учетом нижеследующего:
- деформации элементов эквивалентного бруса подчиняются закону плоских сечений (здесь под плоским сечением понимается шпангоутная рамка);
- деформациями считаются суммарные величины, слагающиеся из раскрытий стыков и абсолютных удлинений связей;
- несущая способность корпуса в целом выражена через момент внутренних сил всех связей, вычисленный относительно нейтральной оси;
- усилия в связях, составных по длине, при сжатии передаются только путем непосредственного контакта в стыках, при растяжении — только путем нагельных или других крепежных средств; при этом распределение усилий между нагелями но длине связи предполагается по линейному закону;
- раскрытие стыков в крайних связях эквивалентного бруса но условиям водонепроницаемости ограничено величиной 1,5 мм.
Сделанные допущения, естественно, вносят в расчет некоторую условность, тем не менее этот способ расчета приближает расчетную картину явлений к фактической в большей степени, чем приведенные выше.
На основании анализа существующей практики деревянного судостроения, Правил Морского Регистра России и других классификационных обществ, установлены следующие зависимости для определения прочных размеров отдельных элементов эквивалентного бруса в функции от главных размерений судна: наружная обшивка, внутренняя обшивка и настил палубИзготовление палубы судна из стеклопластикаы:
киль, кильсоны, ватервейс, бархоут, подбалочные и брусья под ними, скуловые и днищевые поясья:
где:
- F — площадь связи, см²;
- с и с1 — коэффициенты, значения которых для отдельных связей приводятся в-табл. 6;
- H — высота борта судна, м;
- L — длина судна, м;
- — расчетная толщина наружной обшивки, см.
| Таблица 6. Значения коэффициентов с и с1 | |||
|---|---|---|---|
| Наименование связей | Коэффициент с1 | Наименование связей | Коэффициент с |
| Киль | 4,1 | Скуловые поясья (L:H=8) | 8,7 |
| Кильсон | 7,5 | Днищевые поясья (L:H=11) | 6,7 |
| Ватервейс | 7,6 | Наружная обшивка | 276 |
| Бархоут | 8,8 | Внутренняя обшивка | 130 |
| Подбалочные брусья | 4,6 | Палуба | 78 |
| Брусья под подбалочными | 5,2 | ||
Формул (17) и (18) было бы достаточно для проектирования эквивалентного бруса морского деревянного судна только в том случае, если он представлял бы единую монолитную балку. В действительности же эквивалентный брус такого судна, вследствие несовершенства способов соединения отдельных связей между собой, а также наличия стыков по длине у отдельных штук, составляющих связи, нельзя рассматривать как единую монолитную конструкцию.
Очевидно, что с усилением крепежа несущая способность связей эквивалентного бруса возрастает, однако усиление крепежных средств ограничивается условиями их размещения, а также опасностью раскалывания древесины, вследствие чего выявление оптимальных размеров и количества крепежа является необходимым условием рационального конструирования. Очевидно также, что при размещении и назначении размеров крепежа следует стремиться к получению несущих способностей, близких к наибольшим из вычисленных для ряда судов, поскольку возможность такого насыщения крепежом может считаться проверенной и подтвержденной практикой эксплуатации многих судов.
Для выявления значений несущих способностей, которые могли бы считаться проверенными практикой и рекомендоваться в виде исходных норм при проектировании, вычислены удельные несущие способности всех связей, входящих в состав эквивалентного бруса. При этом за характеристики относительной величины несущей способности и относительной деформации связей приняты величины:
где:
- Р — несущая способность связи при растяжении;
- F — площадь поперечного сечения связи;
- v — половина раскрытия стыка;
- S — деформация, т. е. суммарная величина половины раскрытия стыка и абсолютного удлинения половины длины связи.
Абсолютные удлинения для всех видов связей при их растяжении рассчитаны в предположении действия усилий, вызывающих раскрытие половины стыка в 0,1 мм.
Величина абсолютного удлинения Δlраст мм определена для поле вины длины связи по формуле:
где:
- Sр — шпация, т. е. расстояние между шпангоутами в центрах, см;
- P — площадь связи, см;
- Р0, Р1, Р2, …, Рi — несущая способность единицы крепежа, кг, на 0, 1 и т. д. шпангоутах при раскрытии половины стыка в 0,1 мм;
- m0, m1, m2, …, mi — число единиц однотипных креплений на 0, 1 и т. д. шпангоутах;
- n — число шпаций от стыка до середины длины связи;
- Е—модуль упругости древесины, равный 0,7 – 105 кг/см².
Величина шпации в сантиметрах, в свою очередь, задана выражением:
где:
- L — длина судна, м
Приведенные в табл. 7 значения pраст и kраст приняты в последующем за расчетные величины.
| Таблица 7. Значения коэффициентов рраст и kраст | |||||
|---|---|---|---|---|---|
| Наименование связей | Несущая способность при растяжении рраст,кг/см2*мм | kраст | Наименование связей | Несущая способность при растяжении рраст, кг/см2*мм | kраст |
| Наружная обшивка | 11,5 | 0,36 | Подбалочные брусья и брусья под подбалочными | 5,5 | 0,45 |
| Бархоут | 10,5 | 0,37 | |||
| Скуловые и днищевые поясья | 9,0 | 0,38 | Ватервейс | 8,5 | 0,30 |
| Внутренняя обшивка | 11,5 | 0,34 | Киль и кильсон | 10,0 | 0,48 |
Несущие способности связей при сжатии рсж, кг, отнесенные к единице площади поперечного сечения связей, см², и к единице деформации этих связей в 0,1 мм, определены по формуле:
Предполагая, что длина всех связей равна минимально допускаемой по Регистру, т. е. 15 шпациям:
и считая Е = 0,7 • 105 кг/см², преобразуем формулу (27) к следующему виду:
где:
- kсж — коэффициент, учитывающий удельное значение абсолютной величины сжатия связи по отношению к величине всей деформации;
- L — длина судна, м.
Что касается значений коэффициента kсж,то если отнести упругие свойства крепежных средств и нагельных гнезд в запас прочности, величина его с достаточной степенью точности может быть оценена, как:
Такой способ определения коэффициента kсж оправдывается тем, что в обычных условиях эксплуатации судна одни и те же связи попеременно испытывают то сжатие, то растяжение, в связи с чем всегда можно считать, что стадии сжатия предшествовало растяжение, при котором стыки связей были раскрыты.
Для проверки принятых расчетных зависимостей у ряда судов подсчитана несущая способность эквивалентного бруса на вершине и на подошве волны, при этом сделаны ранее приведенные допущения и, в частности, из условий обеспечения водонепроницаемости корпуса раскрытие стыков для крайних растянутых связей ограничивается величиной 1,5 мм. Кроме того, величины раскрытий стыков ограничиваются значениями тех деформаций, при которых напряжение как в самом крепеже, так и в нагельных гнездах будет больше расчетных, принятых для определения предельно допускаемых несущих способностей крепежных средств.
Читайте также: Балластные кили парусного судна
На основании проделанных вычислений значение несущей способности эквивалентного бруса, выраженное через момент внутренних сил, в общем виде представлено следующей формулой:
где:
- А —численный коэффициент, кг/м • см;
- Н— высота борта судна, м;
- tр — расчетная толщина наружной обшивки.
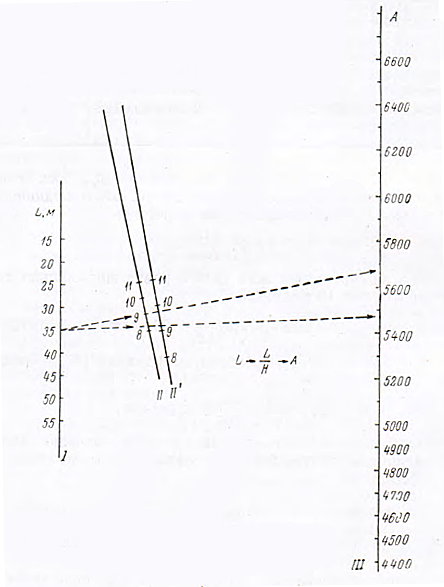
Для удобства определения коэффициента А на рис. 4 приведена номограмма, по которой коэффициент А находится в зависимости от длины судна L, отношения L : Н и положения судна на подошве (шкала II) или на вершине (шкала II’) волны. Значение коэффициента А читают на шкале III, соединяя точки шкалы I с соответствующей точкой на шкале II или II’.
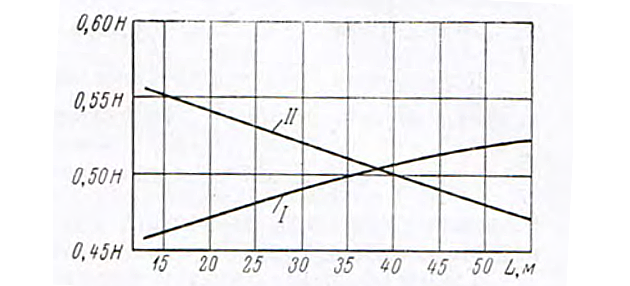
На рис. 5 представлено положение нейтральной оси в долях высоты борта Н.
Расчетный изгибающий момент от внешних сил, в свою очередь, выражен общеизвестной формулой:
где:
- D— водоизмещение судна;
- L — длина судна;
- k — статистический коэффициент.
Для определения коэффициента k сопоставлены значения этих коэффициентов для различных морских деревянных судов, полученные путем статических постановок их на волну. На основании этих данных, делая допущения в безопасную сторону, для судов длиной от 15 до 50 м величина k выражена следующей зависимостью:
Для определения минимально необходимой толщины наружной обшивки можно использовать равенство моментов внешних и внутренних сил, а именно:
или, подставляя значения формулы (29) и учитывая необходимость некоторого утолщения обшивки на износ, получим:
где:
- А — некоторый численный коэффициент, определяемый по номограмме рис. 4;
- Δt — утолщение наружной обшивки на износ, см;
- Мизг — максимальный изгибающий момент, кг • м.
Формула (27) для определения толщины наружной обшивки получена из предположения такого соотношения главных размерений судна: В : Н = 2; Т : Н = 0,70; коэффициент полноты водоизмещения судна δ = 0,50.
Так как в практике судостроения значения:
и δ могут отличаться от принятых выше, то необходимо учесть влияние изменения этих величин на толщину наружной обшивки.
Используя формулу (27) и заменяя в ней Мизг через:
представим tр в следующем виде:
Отсюда следует, что толщина наружной обшивки находится в линейной зависимости от значения коэффициента общей полноты δ и отношения
так как изменение значения
не влияет на величину момента внутренних сил, а изменение δ влияет незначительно, и им можно пренебречь. Что касается отношения
, то с изменением последнего момент внешних сил и момент внутренних сил меняются не в одинаковой зависимости.
Влияние значения отношения
на изменение момента внутренних сил выявлено сопоставлением величин моментов внутренних сил для ряда судов при различных
. Полученные результаты во всех случаях разнятся незначительно и могут характеризоваться следующими средними удельными значениями моментов внутренних сил:
- для
- для
- и для
Если учесть, что момент внешних сил находится в линейной зависимости от отношения
,
то окажется, что при изменении отношения
толщину наружной обшивки необходимо соответственно увеличивать или уменьшать из расчета 1% на каждую десятую долю изменения этого отношения Так, например, для отношения B/H=1,6 изменение момента внешних сил равно 1,6/2,0=0,8, а изменение момента внутренних сил – 0,84, что дает 1% на каждую десятую долю изменения этого отношения.x.
Таким образом, с учетом формулы (28) расчетная зависимость для толщины наружной обшивки в первом приближении может быть выражена следующей формулой Опыт эксплуатации морских деревянных судов показал, что для них, в отличие от речных, размеры продольных связей лимитируются условиями прочности, а не жесткости, обычно заведомо обеспеченной. Поэтому в расчетную формулу (29) введен поправочный коэффициент ζ=1,4-0,05 L/H, учитывающий зависимость между толщиной обшивки tp и отношением L/H из условия получения одинакового запаса прочности для судов одной и той же длины при различных значениях L/H. Выражение для величины поправочного коэффициента получено путем анализа конструкций морских деревянных судов. За критерий прочности принята прочность судна с отношением L/H=8.x:
Проведенный анализ и выведенные зависимости и соотношения позволяют рекомендовать следующую расчетную схему для определения прочных размеров основных продольных связей.
Предполагаются известными главные размерения судна:
- L — длина;
- В — ширина;
- Н — высота;
- Т — максимальная осадка в грузу;
- δ — коэффициент общей полноты;
- Мизг — величина расчетного изгибающего момента для худшего случая нагрузки.
За расчетный изгибающий момент принимается значение изгибающего момента, отношение которого к величине А, определенной по номограмме рис. 4 для случая прогиба или перегиба, дает максимальное значение. Расчет ведется в следующем порядке:
- по формуле (29) определяется минимальная толщина наружной обшивки t1 при этом значение запаса на износ Δt, входящее в расчетную формулу, если нет особых соображений, может быть принято для обычных грузовых и промысловых судов равным примерно 2 см:
- используя коэффициенты с и с1, приведенные в табл. 6, и зависимости (27) и (28), определяют необходимые площади основных продольных связей, входящих в состав эквивалентного бруса;
- задаются размещение, количество, размеры и тип крепежных средств, а также разгон стыков связен, которые в первом приближении могут назначаться в ориентации на прототип или существующую практику;
- производится подсчет несущих способностей отдельных связей и вычисление удельных несущих способностей; полученные значения удельных несущих способностей сопоставляются с данными, приведенными в табл. 7. В случае, если подсчитанные удельные несущие способности будут значительно отличаться от табличных, рекомендуется путем соответствующего изменения крепежа и разгона стыков получить значения, близкие к табличным;
- составляется схема эквивалентного бруса и подсчитывается момент внутренних силВзаимодействие плавучего дока и судна: усилия между ними и моменты изгиба, который сопоставляется с моментом внешних сил;
- если отношение расчетного изгибающего момента к моменту внутренних сил с учетом износа Δt будет отличаться от единицы, т. е.
то толщина наружной обшивки во втором приближении определяется формулой:
после чего весь расчет повторяется во втором приближении.
В заключение следует отметить, что в большинстве случаев достаточно первого приближения. Необходимость во втором приближении может возникнуть лишь в том случае, если действительная схема эквивалентного бруса будет значительно отличаться от типовой схемы, принятой при анализе, что для обычных грузовых и промысловых судов, как правило, не имеет места.
В приведенном методе конструирования элементы основных продольных связей определяются непосредственно в зависимости от действующего на судно расчетного изгибающего момента. Критерием достаточной прочности служит сравнение этого изгибающего момента с моментом внутренних сил.
При определении прочных размеров основных элементов набора корпуса, кроме значения изгибающего момента, учитывается также влияние соотношений главных размерений и коэффициента общей полноты судна.
Метод обоснован проведенным аналитическим исследованием, а также конкретными расчетными примерами для судов длиной от 15 до 50 м, выполненными автором. Во всех случаях полученные в результате проделанных расчетов сечения основных продольных связей конструктивны, и в то же время выгодно отличаются от размеров связей, определенных по Правилам Морского Регистра , так как в большинстве случаев оказываются несколько легче последних.
Не следует забывать, что приведенная схема расчета разработана применительно к судам на футоксовом наборе и к деревянным судам с иной системой набора данные значения коэффициентов применены быть не могут.
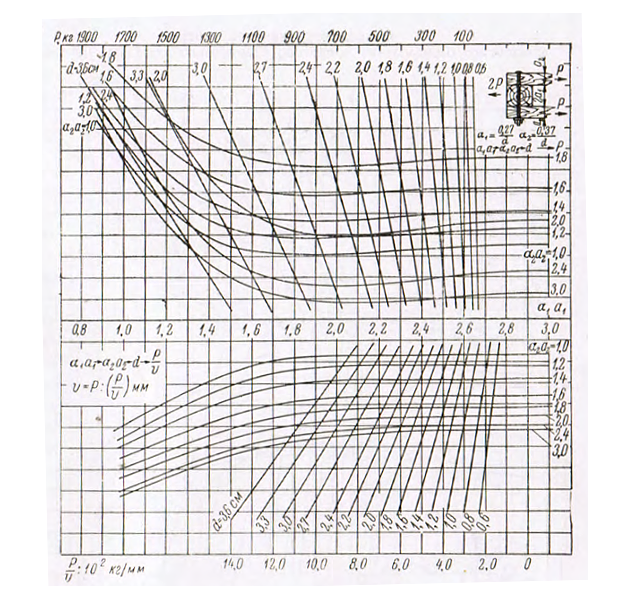
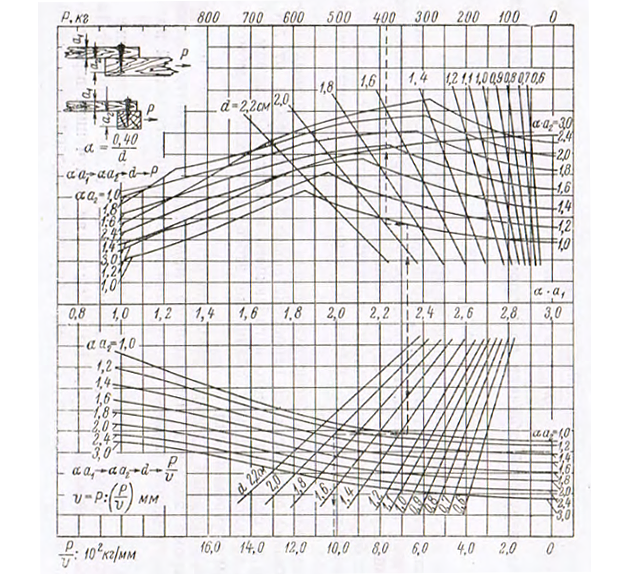
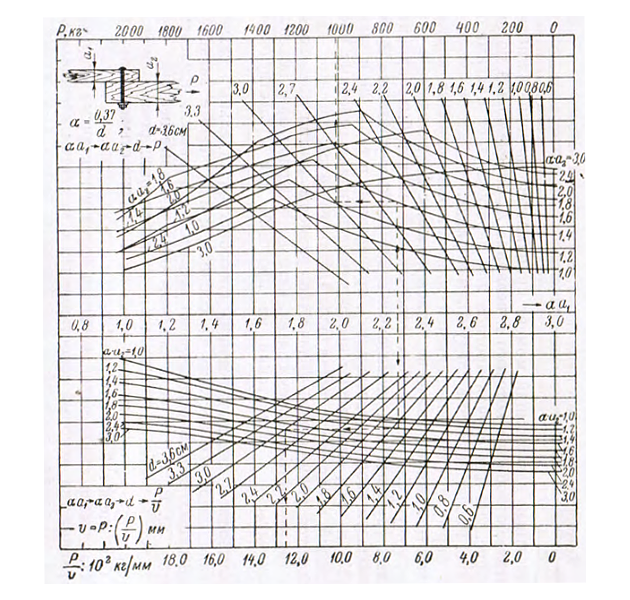
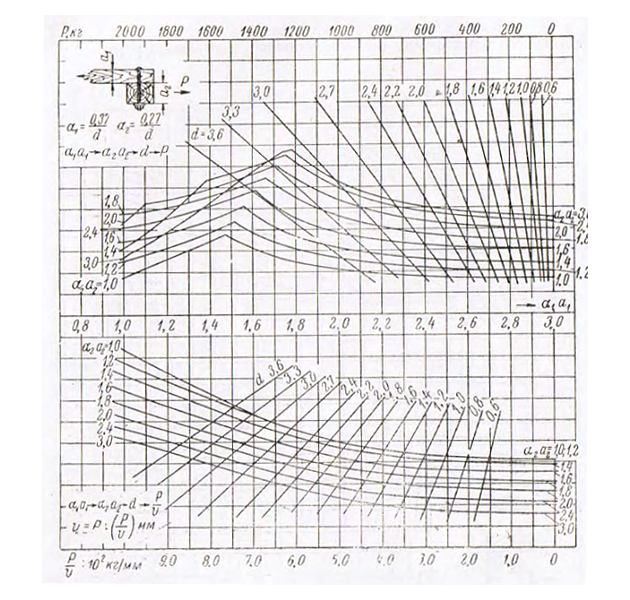
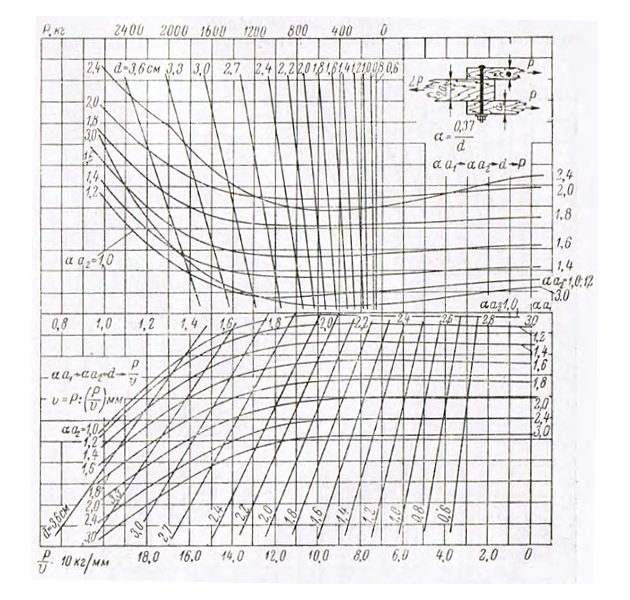
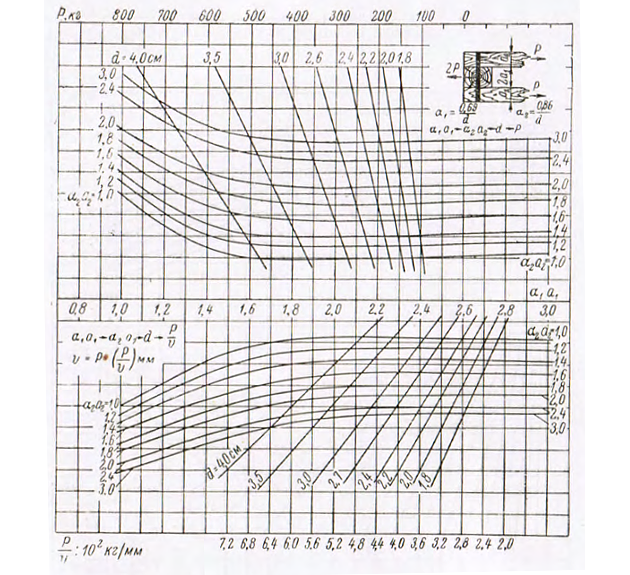
2. Номограммы для определения несущих способностей крепежных средств. Несущие способности и деформации различных видов нагельных креплений при определении размеров прочных связей корпуса по вышеприведенной схеме рассчитываются по номограммам, представленным на рис. 6—11.
В верхней части номограмм приводятся значения предельных несущих способностей Р для различных соединений при условии, что расчетные характеристики для дерева и стали не будут превышать приведенных значений. На нижней части приводятся значения усилий V при суммарном сдвиге соединения в 1 мм. Принцип пользования номограммами ясен из самих номограмм.
Несмотря, на кажущееся многообразие видов соединений в корпусе деревянных судов на футоксовом наборе, все они могут быть с достаточной степенью точности приравнены к одно- или двухсрезным соединениям. Для подтверждения последнего на рис. 12, а сопоставлены значения несущих способностей одно- и двухсрезных соединений при отношении толщин соединяемых брусьев 1:2, а на рис. 12, б значения одно, двух и многосрезных соединений, составленных из брусьев одинаковых размеров. Во всех случаях приведены несущие способности, приходящиеся на один срез при единичном перемещении. Указанные значения отнесены к несущей способности односрезного соединения, которая принята за 100%. Как видно из рис. 12, при значениях ad ≥ 1,5 расчет многосрезных, а также кбсосимметричных двухсрезных соединений может быть выполнен с достаточной для практических целей точностью по формулам для симметричного двухсрезного соединения.
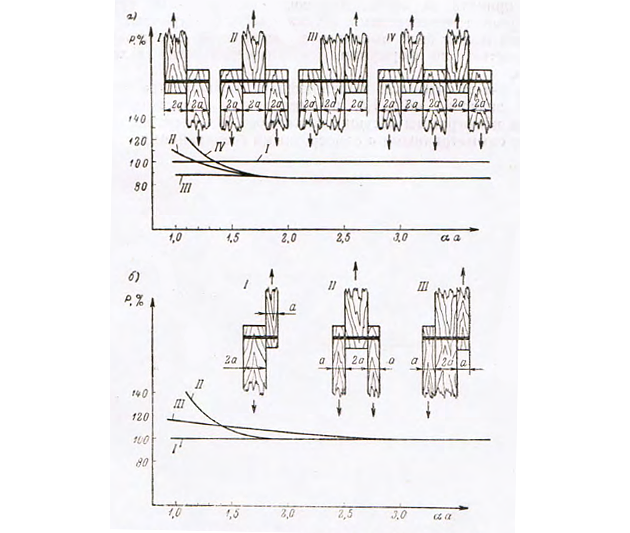
Если учесть, что для подавляющего большинства судовых конструкций значение ad ≥ 1,5, представляется возможным ограничить расчетные номограммы несущих способностей крепежных средств двухсрезными симметричными и односрезными соединениями.
