Центробежные судовые насосы являются ключевым элементом многих корабельных систем, обеспечивая перекачку жидкостей для балластировки, охлаждения и пожаротушения. Данный материал начинается с рассмотрения типов и общего устройства этих машин, чтобы заложить фундамент для понимания их работы. Далее мы подробно анализируем движение жидкости в рабочем колесе, что необходимо для построения треугольников скоростей – графического инструмента для оценки гидродинамики. Центральное место в теоретической части занимает основное уравнение центробежных насосов, которое связывает напор и скорость потока.
- Типы и общее устройство
- Движение жидкости в рабочем колесе
- Построение треугольников скоростей
- Основное уравнение центробежных насосов
- Влияние конечного числа лопастей рабочего колеса на напор
- Уравнения подобия для лопастных насосов
- Коэффициент быстроходности
- Коэффициент реакции и типы лопастей рабочего колеса
- Потери в центробежных насосах
- Гидравлические потери
- Объемные потери
- Механические потери
- Расчет рабочего колеса насоса
- Определение основных размеров колеса и построение его канала
- Профилирование лопасти
Однако на практике приходится учитывать влияние конечного числа лопастей и использовать уравнения подобия, а также коэффициент быстроходности для классификации насосов. Особое внимание уделяется коэффициенту реакции и типам лопастей, определяющим конструкцию рабочего колеса. Кроме того, детально рассматриваются потери – гидравлические, объемные и механические, которые влияют на общую эффективность агрегата. В завершение, мы представим методологию расчета рабочего колеса, включая определение его основных размеров и профилирование лопасти.
Типы и общее устройство
Судовые Основные параметры центробежных насосов и принцип действия на суднецентробежные насосы являются наиболее распространенным видом динамических насосов. Конструкция судового насоса приведена на рисунке 1.
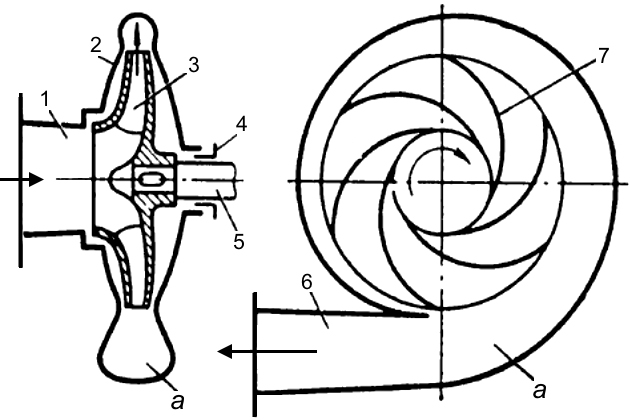
Основными деталями насоса являются:
- корпус 2;
- рабочее колесо 3, состоящее из двух дисков, между которыми находятся лопасти 7.
Рассмотрим принцип работы центробежного насоса. Рабочее колесо расположено на валу 5 консольно и закреплено на нем при помощи шпонки. При вращении рабочего колеса в центральной части его образуется пониженное давление, вследствие чего жидкость из приемного трубопровода непрерывно поступает в насос через подвод 1, выполненный в виде конического патрубка (конфузора) с прямолинейной осью. Лопасти рабочего колеса оказывают силовое воздействие на поток жидкости и передают ей механическую энергию. Повышение давления жидкости в колесе создается в основном под действием центробежных сил.
Обтекая лопасти, жидкость движется в радиальном направлении от центра колеса к его периферии. Здесь жидкость выбрасывается в спиральный отводящий канал а и направляется в диффузорный выходной патрубок 6, где скорость ее снижается и кинетическая энергия потока преобразуется в потенциальную энергию давления. Так как частота вращения колеса постоянна, то движение жидкости во всасывающей и нагнетательной трубах, присоединенных к насосу, совершается с постоянной скоростью. В месте выхода вала из корпуса насоса установлено уплотнение (сальник) 4, препятствующее вытеканию жидкости из насоса по зазору между корпусом и валом.
Изображенный на рис. 1 центробежный насос имеет одно рабочее колесо с односторонним входом жидкости. Применение нескольких рабочих колес в одном насосе позволяет значительно расширить область использования центробежных насосов и создает ряд конструктивных преимуществ. Центробежные судовые насосы выполняют с последовательным и параллельным соединениями колес (рис. 2).

Какие насосы являются многоступенчатыми?
Многоступенчатые насосы – это насосы с последовательным соединением рабочих колес (рис. 2, а). Напор такого насоса равен сумме напоров отдельных колес (ступеней), а подача равна подаче одного колеса. Все колеса многоступенчатого насоса насажены на общий вал и образуют единый ротор.
Насосы с параллельным соединением колес (рис. 2, б) называются многопоточными. Напор такого насоса равен напору одного колеса, а подача насоса равна сумме подач отдельных колес. Многопоточные насосы применяются для перекачивания больших количеств жидкости. Наибольшее распространение получили двухпоточные насосы с рабочим колесом двустороннего входа, которое представляет собой соединение в одной детали двух обычных колес (рис. 2, в).
Рассмотрим устройство четырехступенчатого насоса (рис. 3).
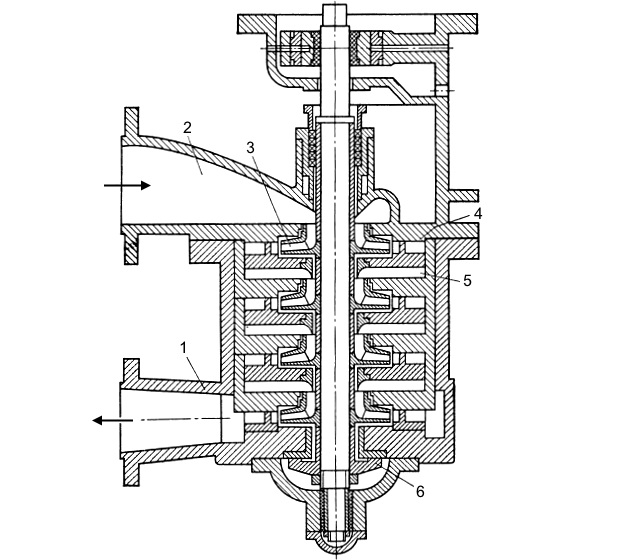
Из подвода 2 жидкость поступает в рабочее колесо 3 первой ступени, затем в лопаточный отвод 4 и далее по переводному каналу 5 подводится к рабочему колесу второй ступени и т. д. Пройдя все ступени, жидкость по отводу направляется в напорный патрубок 1, а из него в нагнетательный трубопровод. Как будет показано в дальнейшем, в насосах с односторонним подводом жидкости возникает осевая сила, действующая по оси ротора. В многоступенчатых насосах эту силу уравновешивают при помощи специального устройства – разгрузочного диска (пяты) 6. Центробежные судовые насосы бывают:
- вертикальные,
- горизонтальные.
Предпочтение следует отдавать вертикальным насосам, так как они занимают меньшую площадь.
По расположению опор насосы делятся на:
- консольные с опорами, расположенными по концам вала;
- моноблочные.
У моноблочных насосов рабочее колесо насаживают непосредственно на вал фланцевого электродвигателя; для крепления к электродвигателю насос имеет свой фланец.
Поскольку существуют различные типы центробежных насосов, они широко применяются в разнообразных Судовые системы и трубопроводысудовых системах:
- противопожарной,
- балластной,
- осушительной,
- водоотливной,
- санитарной.
Их используют в качестве охлаждающих в двигателях внутреннего сгорания, грузовых – на танкерах и т. д. Грузовые насосы танкеров выполняют одноступенчатыми с двусторонним входом жидкости.
Широкому распространению центробежных насосов на судах способствуют следующие их положительные качества:
- возможность непосредственного соединения с быстроходными двигателями (электродвигателем, турбиной);
- небольшие масса и габаритные размеры;
- простота конструкции, упрощающая обслуживание и ремонт насоса;
- быстрый пуск и простое регулирование во время работы;
- равномерная без пульсации подача жидкости;
- сравнительно малая чувствительность к загрязненной жидкости.
Существенным недостатком центробежных насосов является неспособность их к самовсасыванию или так называемому сухому всасыванию, когда в приемном трубопроводе находится воздух. Поэтому перед пуском центробежного насоса приемный трубопровод и насос должны быть заполнены жидкостью. С этой целью некоторые центробежные судовые насосы, такие, как осушительные, снабжают специальным самовсасывающим устройством.
Движение жидкости в рабочем колесе
В рабочем колесе центробежного насоса частицы жидкости движутся относительно самого колеса и, кроме того, они вместе с ним совершают переносное движение. Сумма относительного и переносного движений дает абсолютное движение жидкости, т. е. движение ее относительно неподвижного корпуса насоса. Скорость абсолютного движения v (абсолютная скорость) равна геометрической сумме скорости w жидкости относительно рабочего колеса (относительной скорости) и окружной скорости u рабочего колеса (переносной скорости):
Ввиду сложного характера движения жидкости в рабочем колесе это движение изучается на основе упрощенных теоретических представлений с последующей корректировкой полученных данных по результатам опыта. В основе исследований лежит элементарная струйная теория. По этой теории действительное движение жидкости в рабочем колесе с конечным числом лопастей заменяется движением в колесе с бесконечно большим числом бесконечно тонких лопастей. В таком колесе поток жидкости является симметричным относительно оси колеса. В осесимметричном потоке все частицы жидкости, находящиеся на одной окружности, имеют одинаковые относительные скорости, которые наклонены к этой окружности под одним и тем же углом (рис. 4, а).
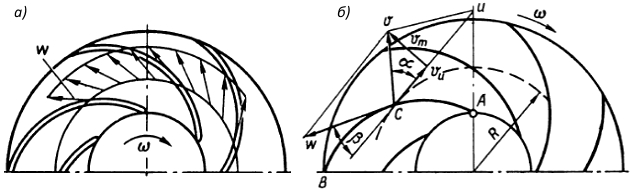
Относительная скорость w жидкости направлена по касательной к поверхности лопасти в рассматриваемой точке. Стрелка указывает направление вращения рабочего колеса с угловой скоростью ω.
Из формулы 1 следует, что векторы скоростей v, w и u образуют треугольник скоростей. На рис. 4, б изображено сложение векторов скоростей для произвольной точки C внутри колеса. Относительная скорость w направлена по касательной к лопасти. Окружная (переносная) скорость u направлена по касательной к окружности, на которой расположена рассматриваемая точка, в сторону вращения рабочего колеса. Для точки, расположенной на радиусе R, окружная скорость:
Вектор абсолютной скорости v замыкает треугольник скоростей, построенный при точке C (треугольник, образованный векторами скоростей u, w, v). Угол между векторами абсолютной и переносной скоростей обозначают через α, а угол между векторами относительной скорости и обратимым направлением переносной скорости – через β. Абсолютную скорость v можно разложить на две взаимно перпендикулярные составляющие:
- vu – окружную;
- vm – меридианную (радиальную).
Схема бесконечного числа лопастей создает элементарное представление о кинематике потока в области колеса и позволяет решить задачу по определению возмущения, вызываемого колесом в потоке, и, следовательно, напора колеса.
Построение треугольников скоростей
При расчете рабочего колеса строят треугольники скоростей насоса при входе и выходе жидкости из колеса. Рассмотрим, как построить треугольники скоростей центробежного насоса, исходя из схемы бесконечного числа лопастей.
Вход потока в колесо. При входе потока в межлопастные каналы находят скорости и строят треугольники скоростей до и после поступления потока на лопасти колеса (рис. 5, а).
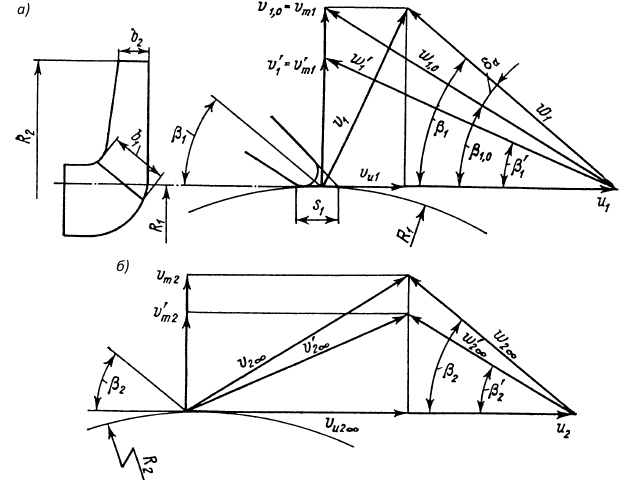
а – при входе в рабочее колесо; б – при выходе из рабочего колеса
Оба состояния потока относят к одному сечению у входных кромок лопастей.
Для определения абсолютной скорости жидкости до поступления на лопасти колеса найдем ее меридианную составляющую из уравнения неразрывности (сплошности):
где:
- Q′ – расчетная подача колеса;
- f – площадь сечения потока при поступлении на лопасти.
Сечение представляет собой поверхность вращения, которую приближенно можно заменить боковой поверхностью усеченного конуса с образующей b1, равной ширине колеса на входе:
где:
- R1 – радиус окружности, проходящей через средние точки входных кромок лопастей.
Окружная составляющая абсолютной скорости до колеса определяется устройством канала, подводящего поток к колесу. Так как наличие окружной составляющей снижает напор колеса, то подводящий канал обычно выполняют так, чтобы . Тогда абсолютная скорость потока при входе в колесо оказывается расположенной в меридианной плоскости и равной .
Переносная скорость жидкости при входе в колесо:
где:
- n – частота вращения колеса.
По скоростям и строят треугольник скоростей до поступления потока на лопасти колеса и из него находят относительную скорость w′ потока перед лопастями. Направление скорости определяется углом , который она составляет с переносной скоростью u1. После поступления потока в межлопастные каналы колеса строят 2 треугольника скоростей. Первый треугольник отражает только стеснение потока лопастями, второй характеризует полное воздействие лопасти на поток.
Рекомендуется к прочтению: Типовые конструкции судовых центробежных насосов
Меридианная составляющая абсолютной скорости при входе с учетом стеснения:
где:
- f1 – действительная площадь сечения потока;
- z – число лопастей рабочего колеса;
- s1 – толщина лопасти на входе в цилиндрическом сечении;
- k1 – коэффициент стеснения, равный отношению площади сечения потока, свободного от лопастей, к действительной площади сечения потока.
Коэффициент стеснения вычисляют по формуле:
где:
- – шаг лопастей на радиусе R1;
- δ1 – толщина лопасти на входе в нормальном сечении;
- β1 – угол установки лопасти при входе на радиусе R1.
Стеснение потока лопастями не изменяет момента количества движения жидкости . Поэтому и . Индекс 0 указывает, что скорости соответствуют условиям безударного поступления потока на лопасть.
По скоростям v1, 0 и u1 строят треугольник скоростей с учетом стеснения потока лопастями (см. рис. 5, а) и из него находят относительную скорость w1, 0 безударного поступления потока на лопасти. Угол безударного поступления потока на лопасти β1, 0 определяется из уравнения:
При безотрывном обтекании лопасти поток движется по касательной к ее поверхности. Относительная скорость w1 потока после поступления на лопасть направлена по касательной к лопасти при входе, которая составляет угол β1 с касательной к окружности входа R1, т. е. с направлением, обратным переносной скорости u1:
По скоростям w1 и u1 строят треугольник скоростей после поступления потока на лопасти и находят абсолютную скорость v1.
Возникновение окружной составляющей скорости vu1 при поступлении потока в колесо является следствием возмущающего действия лопастей на поток и поэтому не приводит к уменьшению создаваемого колесом напора. Угол поворота потока называется углом атаки. Для получения хороших гидравлических качеств на переменных режимах Классификация судовых насосов и принципы работыработы насоса лопасти колеса проектируют с углом атаки , а в отдельных случаях и более (до 15°) на расчетном режиме. Входную кромку лопасти закругляют для расширения диапазона углов атаки безотрывного обтекания лопасти.
Выход потока из колеса. При выходе жидкости из рабочего колеса строят 2 треугольника скоростей до и после выхода из колеса (рис. 5, б). Оба треугольника скоростей относят к сечению, проходящему через выходные кромки лопастей колеса.
До выхода из колеса относительная скорость жидкости направлена по касательной к средней линии профиля:
где:
- β2 – угол установки лопасти на выходе.
Меридианная составляющая скорости определяется из уравнения неразрывности:
где:
- R2 – выходной радиус рабочего колеса;
- b2 – ширина рабочего колеса на выходе;
- s2 – толщина лопасти на выходе в цилиндрическом сечении;
- – коэффициент стеснения (t2 – шаг лопасти на радиусе R2).
Переносная скорость u2 = R2ω.
По скоростям w2∞ и u2 строят треугольник скоростей до выхода потока из колеса и находят абсолютную скорость v2∞. Проектируя v2∞ на направление переносной скорости u2, получают окружную составляющую абсолютной скорости vu2∞.
После выхода потока из колеса меридианная составляющая скорости будет:
При выходе потока из колеса момент количества движения жидкости не изменяется:
Поэтому окружная составляющая после выхода потока из колеса:
По абсолютной скорости:
и переносной скорости u2 строят треугольник скоростей после выхода потока из колеса.
Индекс ∞ при скоростях указывает на то, что они определялись соответственно схеме бесконечного числа лопастей.
Основное уравнение центробежных насосов
Это уравнение устанавливает зависимость между энергией, сообщаемой потоку в рабочем колесе насоса, и скоростями потока на выходе и входе в колесо. При выводе основного уравнения пользуются теоремой о моменте количества движения и исходят из представления о среднем значении скорости по сечению потока. Имеется в виду, что движение жидкости в рабочем колесе установившееся.
Моменты количества движения жидкости у входного и выходного сечений рабочего колеса на радиусах R1 и R2 (рис. 6) соответственно будут:
где:
- – расчетная массовая подача колеса;
- v1 и v2 – абсолютные скорости потока на входе и выходе из колеса;
- l1 и l2 – соответствующие плечи моментов;
- α1 – угол между направлением абсолютной скорости v1 и окружной u1;
- α2 – угол между направлением абсолютной скорости v2 и окружной u2.

Момент внешних сил, действующих на жидкость:
где:
- vu2 и vu1 – средние окружные составляющие абсолютных скоростей.
Умножив левую и правую части этого уравнения на угловую скорость рабочего колеса ω, получим:
Так как R2ω = u2 и R1ω = u1 то:
Произведение Mω есть мощность, передаваемая потоку в межлопастных каналах колеса. С другой стороны эта мощность может быть представлена как работа в секунду, необходимая для подъема (кг/с) жидкости на высоту Hт (м), т. е.:
Подставляя в формулу 7 вместо члена Mω его значение согласно формуле 8 и решая относительно Hт, получим:
где:
- Hт – теоретический напор рабочего колеса.
Формула 9 является основным уравнением Лопастные насосы и их эксплуатация на суднелопастных насосов. Впервые оно было выведено Л. Эйлером. Данное уравнение применимо ко всем лопастным машинам (насосам, вентиляторам, компрессорам), принцип действия которых основан на силовом взаимодействии лопастей вращающегося рабочего колеса с потоком жидкости.
В центробежных насосах обычно жидкость поступает в колесо без закрутки, т. е. vu1 = 0, что делается с целью повышения напора и увеличения высоты всасывания. Тогда формула 9 принимает вид:
Формуле 9 можно придать иной вид. Из треугольников скоростей (см. рис. 6) следует:
Определив из этих уравнений произведения u2vu2 и u1vu1 и подставив их значения в основную формулу 9, получим:
Первое слагаемое формулы 11 выражает динамический напор, а второе и третье слагаемые представляют теоретический статический напор.
Теоретический напор Hт колеса по основному уравнению можно определить, если известны осредненные скорости потока. Вычисление этих скоростей связано с исследованием поля скоростей. Наиболее просто их можно определить, если принять число лопастей у колеса бесконечно большим. В этом случае формула 10 примет вид:
Напор H∞ называют напором рабочего колеса с бесконечным числом лопастей.
Влияние конечного числа лопастей рабочего колеса на напор
Напор H∞ рабочего колеса, рассчитанный по схеме бесконечного числа лопастей, превышает действительный теоретический напор Hт. Причина расхождения напора H∞ и Hт заключается в том, что основное положение струйной теории об осевой симметрии потока в каналах рабочего колеса (см. рис. 4, а) не соответствует действительности. Действительное распределение относительных скоростей в канале колеса конечных размеров не может быть осесимметричным вследствие силового взаимодействия между лопастью и потоком. Скорости с задней (тыльной) стороны лопасти должны быть больше, чем с передней, что можно видеть на рис. 7.
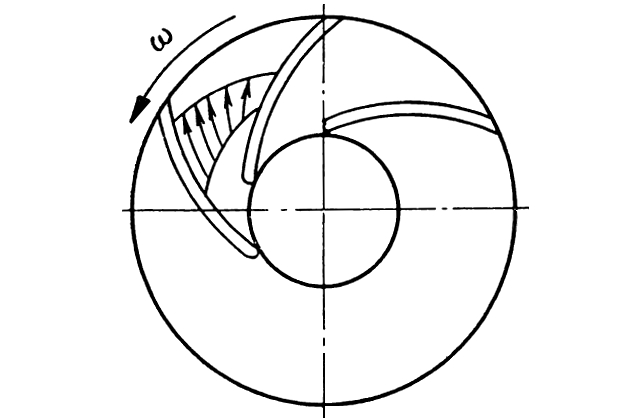
После выхода жидкости из колеса поле относительных скоростей выравнивается. При этом поток отклоняется от направления, касательного к лопасти, в сторону, обратную вращению колеса. Угол β2ср между средней относительной скоростью w2 выровненного потока и направлением, обратным переносной скорости u2, оказывается меньше угла β2 лопасти на выходе. Отклонение относительной скорости w2 в сторону уменьшения угла β2 приводит к уменьшению окружной составляющей vu2 абсолютной скорости по сравнению с vu2∞ (рис. 8).
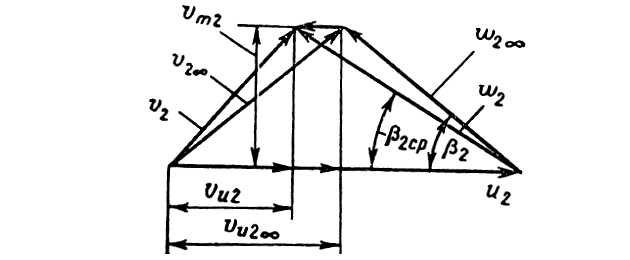
Из формул 10 и 12 следует, что при vu2<vu2∞ напор H∞ будет больше напора Hт.
Неравномерное распределение относительных скоростей потока по окружности в каналах колеса и отклонение относительного потока при выходе из колеса от направления, касательного к лопасти, можно объяснить воздействием на поток осевого вихря.
Покажем наглядно возникновение осевого вихря в относительном движении. Рассмотрим движение идеальной жидкости, заполняющей круглый закрытый сосуд, который в свою очередь движется по круговой траектории относительно точки О (рис. 9, а).

При движении сосуда абсолютное движение жидкости будет носить по инерции поступательный характер, что отмечено расположением стрелки N. Сосуд же, кроме поступательного движения, совершает поворот относительно своей оси, что видно из расположения отмеченной точки A. Сопоставляя положения конца стрелки N и точки A, видим, что жидкость получает в относительном к сосуду движении вращение, обратное его переносному движению. Таким образом, безвихревое (поступательное) абсолютное движение является вихревым (вращательным) в относительном движении.
При вращении рабочего колеса (рис. 9, б) осевой вихрь вызывает увеличение скорости движения жидкости на задней а – b стороне лопасти, замедление движения жидкости на передней c – d стороне лопасти и отклонение потока при выходе из колеса. При выходе из колеса скорость осевого вихря имеет направление, противоположное переносной скорости потока. Вследствие этого относительная скорость потока отклоняется в сторону, обратную вращению колеса.
Так как в центробежных насосах скорость vu1 = 0, то, используя формулы 10 и 12, можно написать:
Коэффициент kz учитывает влияние конечного числа лопастей на напор рабочего колеса. Значение его всегда меньше единицы и зависит от конструкции колеса и режима работы насоса.
Обычно для установления связи между напорами H∞ и Hт пользуются формулой Пфлейдерера:
Поправочный коэффициент p в формуле 14 для радиальных колес с числом лопастей z:
Входящий в эту формулу коэффициент ψ определяется по выражению:
Значение первого слагаемого зависит от шероховатости проточной части рабочего колеса. Для тщательно выполненных колес можно принимать нижний предел.
Теоретический напор колеса при конечном числе лопастей:
где:
Уравнения подобия для лопастных насосов
Как уже отмечалось, движение жидкости в каналах лопастных насосов имеет очень сложный характер и решение уравнений движения жидкости возможно только при определенных допущениях. В связи с этим при создании насосов наряду с теоретическими расчетами большое значение приобретают экспериментальные исследования и их обобщение. Научное обобщение результатов испытаний и распространение их на другие насосы проводятся на основании положения о механическом подобии потоков жидкости, которое требует соблюдения:
- геометрического,
- кинематического,
- динамического подобия.
Широкое применение на практике получили уравнения подобия, позволяющие выполнять пересчет параметров одного насоса на параметры другого, если проточные полости обоих насосов геометрически подобны, а также пересчитать параметры насоса с одной частоты вращения на другую. При проектировании насосов широко используется моделирование, причем модели изготовляют в соответствии с требованиями законов подобия.
Напишем выражения для условий подобия.
Если обозначить через lн, Dн и lм, Dм сходственные размеры натурного и модельного насосов, то условие геометрического подобия запишется так:
Коэффициент λ называется геометрическим масштабом, или масштабом длины.
Условие кинематического подобия имеет вид:
Коэффициент λ′ представляет собой масштаб скоростей.
Для выполнения условия динамического подобия необходимо равенство чисел Рейнольдса Re модели и натуры, т. е. Reм = Reн. Опыт показывает, что если Судовые насосы и их эксплуатационные характеристикисудовой насос и его модель перекачивают одну и ту же жидкость, то для их подобия достаточно соблюдения только условий, предусмотренных формулами 18 и 19. Независимость подобия от числа Re объясняется явлением автомодельности, наступающим при больших числах Re, при которых обычно работают лопастные машины.
Выведем уравнения подобия для насосов. Подача насоса пропорциональна площади поперечного сечения потока и скорости v, а так как площадь пропорциональна квадрату линейного размера l2, то отношение подачи колеса натуры к подаче колеса модели для подобных режимов будет:
Напор, создаваемый колесом, пропорционален квадрату скорости потока:
Мощность насоса пропорциональна произведению подачи на напор:
Уравнения подобия 20-22 являются приближенными. В целях уточнения этих уравнений им иногда придают следующий вид:
Отношение ηон/ηом учитывает изменение объемных потерь в связи с изменением относительного значения зазоров, обычно имеющих место при существенном изменении масштаба; ηгн/ηгм – изменение гидравлического КПД в функции числа Re и масштаба λ; ηмм/ηмн – изменение относительной величины внешних механических потерь (в подшипниках, сальниках).
Если уравнения подобия применяют к одному насосу, то λ = 1. В области режимов Re>Reкр КПД будут равны ηом = ηон и ηгм = ηгн и уравнения подобия примут следующий вид:
или приближенно:
Пользуясь этими формулами, можно определить подачу Q, напор H и мощность N насоса на режиме с частотой вращения n по опытным значениям Q1, H1 и N1 при частоте вращения n1.
Коэффициент быстроходности
Коэффициент быстроходности – это важная величина, определяющая рабочие характеристики центробежных насосов и их конструктивный тип. Численно он равен частоте вращения идеального (эталонного) насоса, который полностью геометрически подобен рассматриваемому, имеет тот же КПД, но при этом обеспечивает напор 1 м при полезной мощности 735,5 Вт. При этом предполагается, что эталонный насос работает на воде с плотностью ρ = 1 000 кг/м3.
Предположим, что насос имеет параметры:
- частоту вращения n;
- подачу Q;
- напор H;
- полезную мощность Nп.
Изменим частоту вращения так, чтобы насос стал давать напор H = 1 м. Остальные параметры соответственно будут n1, Q1 и Nп1.
Найдем Q1 и n1. Из формулы 26 следует, что:
поэтому:
Согласно формуле 27 отношение напоров или , следовательно:
Подставляя найденное значение для n1 в формулу 30, окончательно получим:
Будем менять размеры насоса, оставляя его подобным с таким расчетом, чтобы мощность Nп1 = 735,5 Вт. Остальные параметры следующие: ns, Q2 и H1 = 1 м.
Параметр Q2 найдем из выражения для мощности:
Получим:
Обозначим наружный диаметр рабочего колеса основного насоса через D2, а измененного – через . Из уравнения для теоретического напора следует, что равенство напоров у основного и измененного насосов возможно при одинаковой окружной скорости u2. Поэтому можно написать:
Отсюда:
Подачи основного и измененного насосов относятся как площади проходных сечений колес или как квадраты их наружных диаметров:
Отсюда:
Подставляя это значение в выражение для ns получим:
Заменяя в данном выражении значения n1 и Q1 согласно формулам 31 и 32, найдем окончательное выражение для коэффициента быстроходности, известное как формула коэффициента быстроходности для лопастных насосов:
Для колеса с двусторонним подводом жидкости в формулу 33 вместо Q следует подставлять Q/2.
Коэффициент быстроходности определяют для оптимального режима работы насоса, когда КПД его достигает наибольшего значения. Из формулы 33 видно, что коэффициент быстроходности при данных значениях Q и H пропорционален частоте вращения n насоса. Чем выше частота вращения, тем больше значение ns и тем меньше габаритные размеры и масса насоса.
Будет интересно: Виды лопастных насосов – устройство и принципы работы на судне
Коэффициент быстроходности насоса оказывает непосредственное влияние на форму рабочего колеса. Так как данному напору соответствует примерно определенная окружная скорость u2 на наружном диаметре рабочего колеса D2, то чем больше частота вращения, тем меньше D2. Вместе с тем диаметр отверстия входа потока в рабочее колесо D0 определяется главным образом значением Q и лишь незначительно уменьшается с возрастанием частоты вращения n. Отсюда следует, что увеличение n, а следовательно, и ns ведет к уменьшению отношения D2/D0. На рис. 10 показаны типы лопастных колес с односторонним подводом жидкости в зависимости от коэффициента быстроходности ns и указаны ориентировочные значения D2/D0.
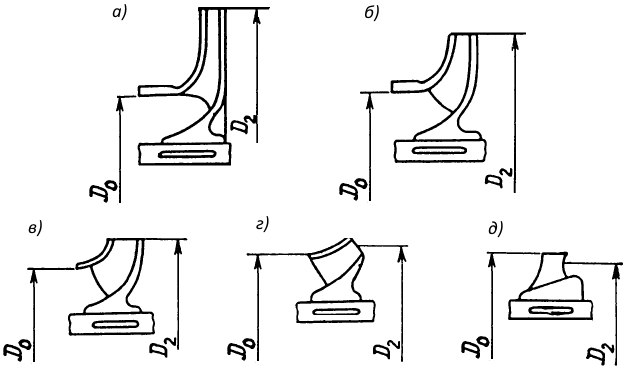
а – ns = 40-80 – центробежные тихоходные (D2/D0 = 3-2); б – ns = 80-150 – центробежные нормальные (D2/D0 = 2-1,6); в – ns = 150-300 – центробежные быстроходные (D2/D0 = 1,6-1,4); г – ns = 300-600 – диагональные (D2/D0 = 1,2-1,1); д – ns = 600-2 000 – осевые (D2/D0 = 0,8-0,6)
Как видно из формулы 33, при данной частоте вращения увеличение подачи и уменьшение напора приводят к увеличению коэффициента быстроходности и наоборот. Поэтому колеса большой быстроходности предназначены для создания малых напоров и больших подач, а колеса малой быстроходности используются для больших напоров и малых подач.
Коэффициент реакции и типы лопастей рабочего колеса
Отношение теоретического статического напора Hт. ст рабочего колеса к его полному теоретическому напору Hт называется коэффициентом реакции ρк колеса:
Так как:
то:
Динамический напор при условии, что vm1 = vm2 и vu1 = 0, будет (см. рис. 6):
Заменяя в формуле 35 значения Hдин и Hт по формулам 36 и 10, получим:
Лопасти центробежных колес можно разделить:
- по форме их поверхности на цилиндрические и двойной кривизны;
- по значению угла выхода лопасти (рис. 11) – на загнутые назад (β2<90°), с радиальным выходом (β2 = 90°) и загнутые вперед (β2>90°).
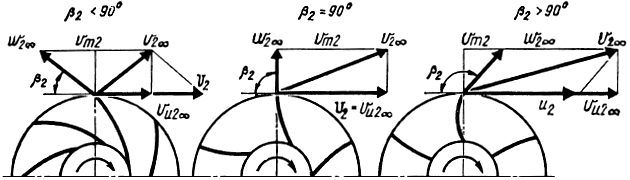
Цилиндрические лопасти имеют кривизну в плоскости, перпендикулярной оси вращения. Сечение поверхности цилиндрической лопасти плоскостью, проходящей через ось колеса, представляет собой прямую линию. Лопасти двойной кривизны имеют кривизну в радиальном и осевом направлениях.
Рассмотрим влияние угла β2 установки лопасти на выходе из рабочего колеса на его напор исходя из схемы бесконечного числа лопастей. Исследование выполним с помощью выходных треугольников скоростей (см. рис. 11). Напор и коэффициент реакции рабочего колеса определяются выражениями:
Увеличение угла β2 при постоянных значениях скоростей u2 и vm2 вызывает рост скорости v2∞ и ее окружной составляющей vu2∞. Возрастание скорости vu2∞ приводит к увеличению полного напора H∞ колеса и его динамической составляющей Hдин; коэффициент реакции ρ∞ колеса при этом уменьшается.
На рис. 12 представлен график зависимости напора H∞ и его составляющих Hст ∞ и Hдин ∞, а также коэффициента реакции ρ∞ колеса от отношения vu2∞/u2 для колес, у которых отличается только один параметр – угол β2.
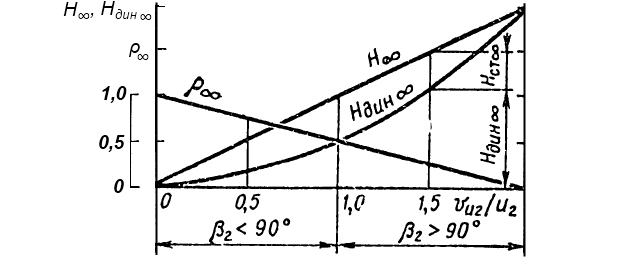
Из рисунка видно, что колеса с лопастями, загнутыми вперед, создают больший теоретический напор, чем колеса с лопастями, загнутыми назад. Однако отсюда не следует, что лопасти, загнутые вперед, являются наивыгоднейшими. Дело в том, что у колеса с лопастями, имеющими угол β2>90°, большую часть теоретического напора составляет динамический напор и жидкость выходит из колеса с большей скоростью v2. Уменьшение этой скорости до значения, допустимого для Расчет элементов систем трубопроводов на судненапорного трубопровода, происходит в диффузорных каналах корпуса насоса, что связано с гидравлическими потерями. Поэтому только часть кинетической энергии потока преобразуется в потенциальную энергию.
Гидравлический КПД таких насосов вследствие больших гидравлических потерь энергии в отводящих каналах корпуса насоса будет значительно ниже, чем гидравлический КПД насосов с колесами, лопасти которых загнуты назад. По этой причине в центробежных насосах применяют рабочие колеса с лопастями, загнутыми назад: β = 17-30° и ρк = 0,65-0,75. Колеса с лопастями, загнутыми вперед, находят применение в центробежных вентиляторах.
Потери в центробежных насосах
Различают гидравлические, объемные и механические потери, которые определяются соответствующими коэффициентами полезного действия. Труднее всего поддаются теоретическим исследованиям и экспериментальному определению гидравлические потери. Объемные и механические потери более доступны для изучения.
Гидравлические потери
Эти потери возникают на всем пути движения жидкости в насосе (в рабочем колесе, в проточных каналах корпуса насоса). Их можно разделить на три вида:
- путевые (по длине каналов);
- местные;
- профильные.
Путевые потери, вызываемые сопротивлением стенок каналов и турбулентным характером движения жидкости, определяют по формуле Дарси-Вейсбаха:
где:
- λ – коэффициент гидравлического трения;
- l и d – длина и диаметр канала;
- v – средняя скорость жидкости;
- a1 – постоянная для данного канала;
- Q – расход жидкости.
Местные потери, являющиеся следствием деформации поля скоростей потока, включают потери энергии в процессе преобразования скоростного напора в потенциальный, а также потери при изменениях направления потока и его сечений. Их можно подсчитать по формуле:
где:
- ζ – коэффициент местного сопротивления;
- a2 – постоянная для данного местного сопротивления.
Определение путевых и местных потерь в насосах связано с большими трудностями и базируется на экспериментальных исследованиях.
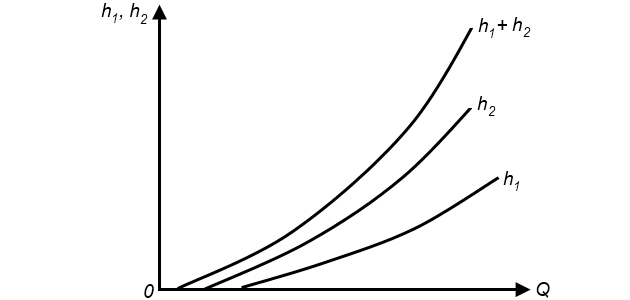
На рис. 13 показана зависимость h1 = f1(Q) для путевых потерь; график h2 = f2(Q) относится к диффузорным каналам и местным сопротивлениям, которые вызываются изменением направления потока и внезапным изменением сечения канала.
Профильные потери, которые часто называют потерями на удар, возникают при обтекании поверхностей лопастей рабочих колес и их можно вычислить по формуле:
где:
- Cx – коэффициент лобового сопротивления профиля;
- w – средняя геометрическая скорость из скоростей входа w1 и выхода w2 из рабочего колеса.
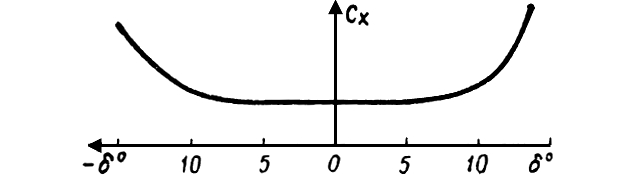
Коэффициент лобового сопротивления Cx ≈ 0,05-0,03 для многих профилей в области углов атаки δ = -10 – +10° почти не изменяется: заметное увеличение наблюдается вне указанной области углов атаки, как показано на рис. 14 для некоторых аэродинамических профилей.
Гидравлические потери оцениваются гидравлическим КПД ηг. Если известны гидравлические потери в насосе, то гидравлический КПД его можно определить по формуле «Общие сведения о судовых насосах и расчетные параметрыНахождение гидравлического КПД в насосе».
Достаточно совершенных методов расчета гидравлических потерь в центробежных насосах еще нет. При проектировании этих насосов для расчета гидравлического КПД обычно пользуются следующей эмпирической формулой:
где:
- D1пр – приведенный диаметр входа в колесо, мм;
Здесь:
- Q1 – подача колеса, м3/с;
- n – частота вращения колеса, об/мин.
При определении гидравлического КПД часто пользуются уравнениями подобия. Пересчет гидравлического КПД с модели (ηгм) на натуру (ηгн) можно выполнять по выражению:
Объемные потери
Внутри насоса через зазоры между ротором и корпусом (статором) всегда есть протечки жидкости. Они учитываются объемным КПД, определяемым по формуле «Общие сведения о судовых насосах и расчетные параметрыРасчет объемного КПД», в виде:
где:
- q0 – утечки жидкости (объемные потери);
- Q′ – расчетная подача насоса (колеса).
На рис. 15 показана схема утечек жидкости в одноступенчатом насосе.
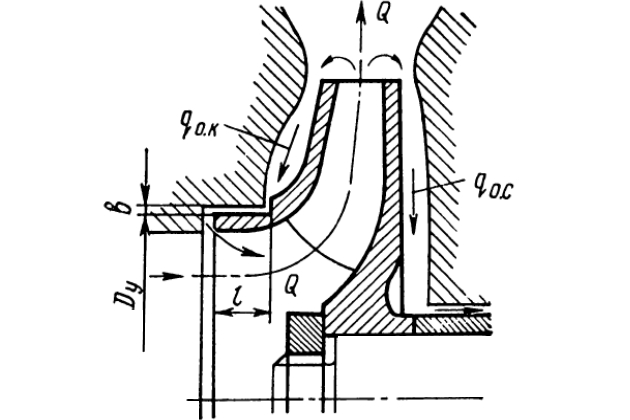
Жидкость поступает в рабочее колесо в количестве Q′, а выходит из насоса в меньшем количестве:
где:
- qок – часть жидкости, возвращающаяся в подвод через зазор между колесом и корпусом насоса;
- qос – утечка жидкости из насоса через сальник.
Утечки qос и qок обусловлены тем, что давление в отводе больше давления окружающей среды и давления в подводе.
Утечку жидкости через зазор в переднем уплотнении колеса можно определить по формуле:
где:
- μр – коэффициент расхода;
- Dу – диаметр уплотнения;
- b – радиальный зазор;
- Hук – напор, теряемый в уплотнении колеса.
Коэффициент расхода μр зависит от конструкции уплотнения. Для простого гладкого уплотнения:
где:
- λ – коэффициент гидравлического трения;
- l – длина щели уплотнения.
Радиальный зазор в уплотнении стремятся делать возможно меньше, однако при чрезмерно малом зазоре может произойти задевание уплотняющих поверхностей. Обычно принимают:
но не менее 0,25 мм.
Коэффициент гидравлического трения зависит от режима движения жидкости в зазоре и шероховатости стенок уплотнения, обычно
.
Напор Hук, теряемый в уплотнении колеса, для насосов с ns = 60-150 ориентировочно можно принимать равным 0,6 H.
Утечка через сальник qос незначительна и ею пренебрегают при расчете объемных потерь.
Для определения объемного КПД η0 одноступенчатых насосов можно пользоваться формулой:
Приведем значения η0 в функции ns, вычисленные по формуле 44:
| ns | 60 | 80 | 100 | 120 | 140 | 160 | 180 | 200 |
| η0 | 0,955 | 0,963 | 0,969 | 0,972 | 0,975 | 0,977 | 0,979 | 0,980 |
Механические потери
Механические потери представляют собой энергию, затраченную на преодоление механического трения внутри насоса. Общая мощность трения:
где:
- Nтрд – мощность дискового трения;
- Nтрп – мощность трения в подшипниках;
- Nтрс – мощность трения в сальнике.
Наиболее значительными являются потери дискового трения. Они обусловлены трением наружных поверхностей дисков колеса о воду. Мощность дискового трения при работе насоса на воде с t = 20 °C и характерным для центробежных насосов Re = 50 · 106:
Механические потери на трение в подшипниках и сальниках в приближенных расчетах оценивают суммарно по зависимости:
Механический КПД центробежного насоса согласно формуле:
Расчет рабочего колеса насоса
Определение основных размеров колеса и построение его канала
В данном пункте приведена конструкция и расчет рабочего колеса судового центробежного насоса. Расчет рабочего колеса насоса ведется по:
- заданным значениям подачи Q, напора H;
- принятой частоте вращения n насоса.
Подача колеса:
где:
- kп – число параллельных потоков, принимаемое для судовых насосов не более двух.
В двухпоточных насосах рабочее колесо обычно выполняют с двусторонним подводом жидкости. У однопоточного насоса Q1 = Q.
Напор колеса:
где:
- iс – число ступеней в насосе.
Исходя из найденных значений Q1, H1 и принятой частоты вращения n определяют коэффициент быстроходности ns и тем самым конструктивный тип насоса. Расчетную подачу колеса определяют по формуле:
Объемный КПД рассчитывают по формуле 44 или выбирают по прототипу.
Теоретический напор рабочего колеса:
Гидравлический КПД ηг вычисляют по формуле 41. Обычно он составляет 0,8-0,95.
Мощность насоса, кВт:
Механический КПД ηм для насосов с ns = 100-200 принимают равным 0,9-0,96.
Часто для приближенной оценки мощности насоса значение КПД η принимают на основе данных уже построенных и испытанных насосов.
Рассчитывают вал насоса на прочность от кручения и изгиба и проверяют на жесткость и критическую частоту вращения. В первом приближении диаметр вала находят из расчета на кручение:
где:
- [τ] – допускаемое напряжение на кручение для материала вала;
- Mкр – крутящий момент, приложенный к валу:
Диаметр втулки:
Для определения диаметра входа в колесо D0 (рис. 16) напишем уравнение расхода:
отсюда:
где:
- v0 – скорость входа жидкости в колесо.
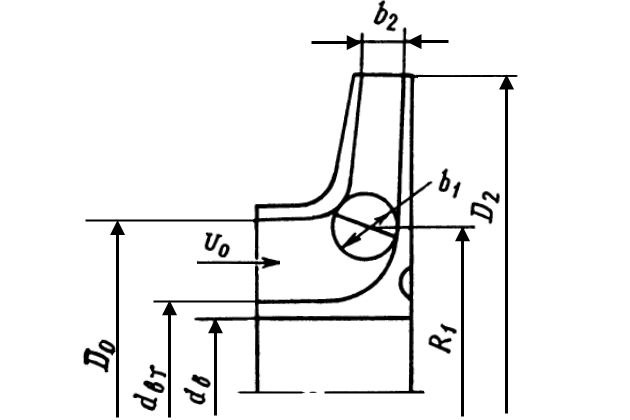
Для определения v0 обычно пользуются формулой b, n, m:
Ширина канала b1 на входе:
где:
- R1 – радиус средней точки входной кромки лопасти;
- – скорость жидкости до стеснения сечения лопастями, которая обычно выбирается равной скорости v0.
Входные кромки лопастей располагают по аналогии с имеющимися образцами колес наклонно под углом 15-30° к оси колеса. При этом определяют радиус средней точки R1, по которому рассчитывают угол входа β1. Для повышения антикавитационных качеств колеса его входную кромку выполняют криволинейной.
Выбрав предварительное значение коэффициента стеснения k = 1,1-1,15, определяют скорость vm1 при входе на лопасть по формуле 4 и окружную скорость u1 по формуле 3, а затем угол безударного поступления потока на лопасть β1, 0 по условию формулы 6.
Приняв угол атаки δа = 3-5°, находят входной угол лопасти:
Высокие значения гидравлического КПД обеспечиваются при угле β1 = 20-25°.
В дальнейшем после выбора числа лопастей z и толщины их при входе проверяют принятое значение коэффициента стеснения k1 и в случае необходимости исправляют расчет.
Читайте также: Основы гидравлики и насосы судовых систем
Выходной (наружный) диаметр D2 (см. рис. 16) колеса рассчитывают исходя из треугольника скоростей при выходе потока из колеса (см. рис. 8). Однако для определения влияния конечного числа лопастей на расчетный напор необходимо знать основные размеры колеса, влияющие на коэффициент p, входящий в формулу 14. Поэтому диаметр D2 определяется методом последовательного приближения.
Из основного уравнения лопастных насосов (формула 10), заменяя в нем:
найдем окружную скорость u2:
где:
- – коэффициент окружной составляющей абсолютной скорости при выходе потока из колеса, который для типовых конструкций центробежных колес с ns = 70-150 может быть принят равным 0,5;
- Hт1 – теоретический напор колеса.
Зная u2 можно определить диаметр D2 в первом приближении:
Полученное значение D2 используют для определения:
- угла β2;
- числа лопастей z;
- поправочного коэффициента p;
- для расчета D2 во втором приближении.
Скорость потока при выходе из колеса без учета стеснения сечения лопастями принимают обычно равной .
Если имеются специальные соображения, например необходимость получения на выходе более широкого колеса для облегчения отливки, то скорость выбирают меньшей – до 0,5 .
Угол выхода β2 лопасти определяют таким образом, чтобы получить отношение . Из треугольников скоростей (см. рис. 5) следует, что:
Из этих уравнений находим:
Коэффициент стеснения лопастями сечения на выходе k2 выбирается предварительно в пределах от 1,05 до 1,1.
Оптимальное число лопастей центробежного колеса:
По выбранному числу z и углу выхода лопастей β2 определяют из формул 15 и 16 коэффициенты ψ и p и по формуле 14 значение расчетного напора H∞.
Из основного уравнения и треугольника скоростей (см. рис. 8) следует, что:
Решая это уравнение относительно u2, получим:
По u2 находим D2 во втором приближении.
Ширину канала колеса на выходе (см. рис. 16) определяют по значению скорости :
Если предварительно принятые значения k1 и k2 и первое приближение u2 отличаются незначительно от значений, полученных во втором приближении, то расчет на этом заканчивается. В противном случае необходимо найти третье приближение.
Контур меридианного сечения колеса строят так, чтобы ширина канала изменялась плавно от входа к выходу (рис. 17).
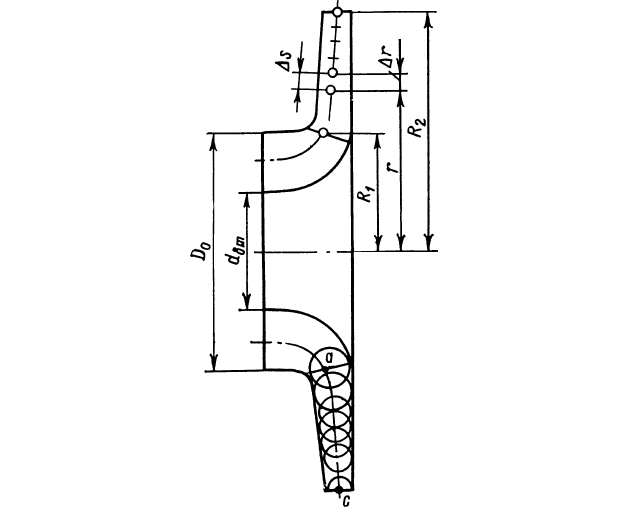
Для этого обычно задаются графиком изменения скорости в зависимости от радиуса r (рис. 18) или длины средней линии s канала от точки a до точки c (см. рис. 17).
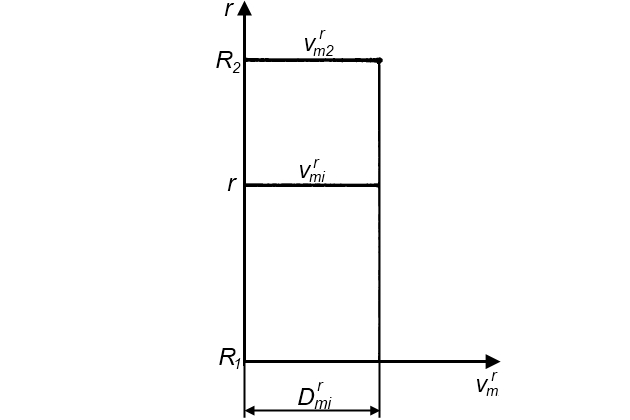
Имея для каждого значения s значение из графика, по уравнению неразрывности находят ширину канала:
Боковые стенки канала являются огибающими окружностей с диаметрами b и c центрами на средней линии. Форму контура канала в меридианном сечении рекомендуется выполнять подобной форме контура канала у колес, показавших высокие гидравлические свойства.
Профилирование лопасти
После построения канала колеса в меридианном сечении приступают к профилированию лопасти. Для обеспечения безотрывного обтекания контура лопасти потоком принимают плавное без минимумов и максимумов изменение относительной скорости w от начального значения w1 до конечного w2 в функции длины средней линии канала s. Имея функциональную зависимость w и от s, можно, задавшись значениями толщины лопасти δ в функции s, определить угол наклона лопасти β:
где:
- t – шаг лопастей.
Толщину лопасти δ выбирают или одинаковой по длине, или уменьшающейся к концам.
Для колес с почти радиальным направлением средней линии меридианного сечения канала ∆s ≈ ∆r (см. рис. 17) лопасть может быть запроектирована с цилиндрической поверхностью, образующая которой параллельна оси колеса. Координаты средней линии контура лопасти в плане (рис. 19, а) находят из уравнения:
Это уравнение получено исходя из условия, что при r = R1 угол ϑ1 = 0.

а – по точкам; б – по дугам круга
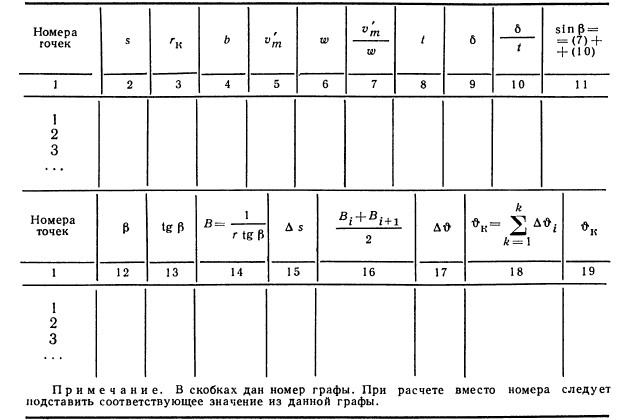
Формулу 48 интегрируют приближенно по правилу трапеций, так как угол β, толщина лопасти δ, скорости w и задают в функции радиуса в виде графика или таблицы.
Если обозначить подынтегральную функцию через , то приращение центрального угла ∆ϑi, соответствующее приращению радиуса ∆ri будет:
где:
- Bi и Bi + 1 – значения подынтегральной функции в начале и в конце рассматриваемого участка.
Для промежуточного радиуса rк получают:
Расчет координат rк и ϑк точек средней линии сечения лопасти в плане обычно сводится в таблицу (рис. 20).
По координатам rк и ϑк строят среднюю линию сечения лопасти в плане. Из точек на средней линии, как из центра, проводят окружности диаметром, равным толщине δ лопасти на данном радиусе. Огибающая окружностей будет контуром сечения лопасти в плане. Входную кромку лопасти закругляют по радиусу, равному половине толщины лопасти на входе.
Как известно, повышение частоты вращения насоса приводит к увеличению коэффициента быстроходности колеса ns и к уменьшению отношения D2/D0 (см. рис. 10). При D2/D0<1,6 поверхность лопасти, если расположить ее только в радиальной части колеса, значительно сокращается, что вызывает увеличение удельной нагрузки на лопасть и понижение антикавитационных качеств насоса. Чтобы увеличить поверхность лопастей, их располагают не только в радиальной части потока, но и в месте перехода потока из осевого в радиальный. Это приближает лопасть к оси насоса, благодаря чему уменьшаются окружные, а следовательно, и относительные скорости при входе потока в колесо, что снижает гидравлические потери и улучшает кавитационные свойства насоса. Входную кромку лопасти располагают наклонно к оси колеса, вследствие чего углы β1, 0 безударного поступления потока на лопасть получаются переменными и лопасть приобретает форму поверхности двойной кривизны.
Предлагается к прочтению: Поршневые насосы морских судов – классификация, устройство и принцип работы
Лопасти двойной кривизны строят по нескольким линиям тока, которые разделяют течение в колесе на ряд элементарных потоков. При этом на плане сначала строят проекции линий тока, являющихся вспомогательными линиями для построения модельных сечений лопасти.
Обычно эти построения выполняют методом конформных отображений.
Рассмотрим упрощенный способ построения профиля цилиндрической лопасти по дугам круга (рис. 19, б). Из центра О двух концентрических окружностей радиусов r1 и r2 проводят луч ОА в произвольном направлении и от этого направления откладывают угол β2 с вершиной в точке А и сумму углов β1 + β2 с вершиной в точке O. Сумма углов определяет положение точки В, через которую из точки А проводят прямую до пересечения с окружностью радиуса r1 в точке С. Линия АС делится пополам точкой D, из которой восстанавливают перпендикуляр до пересечения с линией АЕ в точке О1. Так находят положение точки О1, которая является центром при вычерчивании дуги АС радиусом О1A = О1C. Эта дуга описывает рабочую сторону профиля лопасти. Отложив толщину лопасти на входе e1 и на выходе e2, определяемые конструктивно, построение профиля лопасти завершается с тыльной стороны. Центр второй дуги, одинаковой с первой кривизны, находят обычными засечками. На рис. 19, б изображены в поперечном сечении колеса профили двух соседних лопастей. Все построение выполняют в масштабе.

