Целью контроля является обеспечение необходимого уровня качества выпускаемой продукции.
- Качество и надежность
- Посадки подшипников
- Основные метрологические понятия
- Классификация и метрологические показатели измерительных средств
- Погрешности измерений и обработка результатов ряда измерений
- Обработка ряда измерений
- Влияние погрешностей измерений на результаты контроля и выбор средств измерений
- Погрешности средств измерения
- Выбор измерительных средств
- Статистический контроль
- Определение экономической эффективности новых средств контроля
Качество и надежность
Под качеством изделия принято понимать совокупность свойств, определяющих степень пригодности изделия для использования его по назначению при определенных условиях эксплуатации и уровне себестоимости.
На производстве для упрощения оценки качества обычно руководствуются его формальным определением, согласно которому качеством называют степень соответствия изделий техническим требованиям. Понятие качества тесно связано с понятием надежности.
Надежностью называют свойство изделий выполнять заданные функции, сохраняя свои эксплуатационные показатели в заданных пределах в течение требуемого промежутка времени или требуемой наработки.
Другими словами, надежность изделияНадежность судовых технических средств в рыбной промышленности — это способность изделия сохранять качество при определенных условиях эксплуатации.
Дефектоскопический контроль, выявляя и отбраковывая дефектные детали, например, тела качения с трещинами, способствует существенному повышению надежности подшипников.
Под наработкой понимают продолжительность работы изделия в часах или объем его работы в каких-либо единицах.
Наработку изделия до предельного состояния, оговоренного в технической документации, называют ресурсом.
Продолжительность работы подшипников принято оценивать ресурсом, который имеют и превышают 9096 подшипников данного типа (90%-ный ресурс).
Ресурс зависит от качества деталей подшипников, например, повышение качества выполнения шариков в подшипнике с III степени точности до степени увеличивает ресурс подшипника на 30—3 596.
Состояние изделия, при котором оно способно выполнять заданные функции с параметрами, установленными требованиями технической документации, называют работоспособностью.
Изучением закономерностей отказов, их прогнозированием, разработкой методов расчета, способов повышения и сохранения надежности при конструировании, изготовлении и эксплуатации изделий занимается новая научная дисциплина — теория надежности.
Посадки подшипников
Допуски на наружный и внутренний диаметры колец подшипников установлены ГОСТом 520—71 и расположены в минус относительно номинальных диаметров колец (рис. 1).
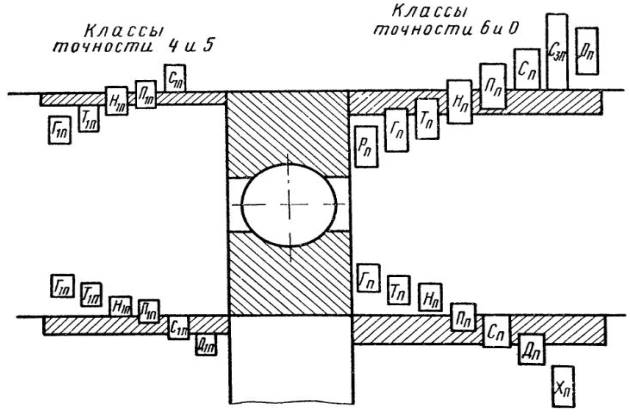
Посадку подшипников на вал осуществляют по системе отверстия, а в корпус — по системе вала.
Выбор посадки определяется величиной, направлением и характером действующих на подшипник нагрузок, а также конструктивными особенностями подшипникового узла.
Различают три следующих вида нагружения колец:
- местное нагружение — радиальная нагрузка неподвижна относи, тельно кольца и воспринимается ограниченным участком дорожки качения и посадочной поверхности;
- циркуляционное нагружение — нагрузка вращается относительно кольца и последовательно воспринимается всеми точками окружности дорожки качения и посадочной поверхности;
- колебательное нагружение — создается совместным воздействием неподвижной и вращающейся относительно кольца нагрузок, когда их равнодействующая не совершает полного оборота, а колеблется на определенном участке кольца.
Наиболее тяжелым видом нагружения является местное, а легким — циркуляционное.
Рекомендуемые посадки колец шарико и роликоподшипников, в зависимости от вида нагружения даны в табл. 1.
| Таблица 1. Рекомендуемые посадки колец радиальных шариков и роликоподшипников в зависимости от вида нагружения | ||
|---|---|---|
| Виды нагружения колец | Посадка внутреннего кольца на вал | Посадка нагруженного кольца в корпусе |
| Местное | П1n, Пn, С1n, Сn, Дn, Хn | П1n, Пn, С1n, Сn, Сэn, Дn |
| Циркуляционное | Г1n, Т1n, Н1n: П1n, Гn, Тn, Нn, Пn | Г1n, Т1n, Н1n, Гn, Р7, Тn |
| Колебательное | П1n, Пn | П1n, Пn |
Посадки 1-го класса точности применяют для подшипников классов точности 5, 4 и 2, а 2-го класса точности — для подшипников классов точности 0 и 6.
В сборочных чертежах стандартные посадки подшипников снабжают дополнительным индексом n.
К посадкам подшипников предъявляют дополнительное требование: отклонения формы валаЦентровка и монтаж валопровода и отверстия корпуса, предназначенных для посадки подшипников, не должны превышать ¹/2 допуска на диаметр при посадке подшипников классов точности 0 и 6 и ¹/3 допуска при посадке подшипников классов точности 5, 4 и 2.
Посадка Р7 заимствована из международной системы посадок ИСО и предназначена для посадок подшипников в тонкостенные корпусы.
Аналогичные посадки (за исключением посадки С3п) применяют при установке радиально-упорных подшипников.
Для тугих колец упорных подшипников используют посадки П1п и Пп.
Основные метрологические понятия
Измерение размеров в машиностроении основано на практическом приложении основных положений метрологии — науки об измерениях, методах и средствах обеспечения их единства и способах достижения требуемой точности.
Метрология занимается: установлением единиц измерений и воспроизведением их в виде эталонов, разработкой методов измерений, анализом точности методов измерений, исследованием и устранением причин, вызывающих погрешности измерений.
Измерением называют нахождение значения размера опытным путем с помощью средств измерения.
На производстве преимущественно приходится встречаться не с измерениями, а с контролем. Под контролем понимают определен не соответствия деталей техническим условием и заданному допуску, как правило, без определения числовых значений размера (например, контроль калибрами).
Различают следующие основные понятия:
- Номинальное значение размера — основной размер, определенный исходя из функционального назначения детали и служащий началом отсчета отклонений.
- Верное (истинное) значение размера — значение размера, свободное от погрешностей измерений.
- Действительное значение размера — значение, пол ученное в результате измерения с допускаемой погрешностью.
- Точное значение размера — значение, полученное с наивысшей практически достижимой точностью — метрологической точностью.
- Приближенное значение размера — это значение, полученное с погрешностью, большей допускаемой, и требующее уточнения.
- Погрешность измерения — отклонение результата измерения от истинного значения измеряемого размера. Так как истинное значение измеряемой величины остается неизвестным, на практике вместо него используют действительное значение измеряемой величины.
- Относительная погрешность измерения — отношение абсолютной погрешности измерения к истинному (или к действительному) значению измеряемой величины.
- Инструментальная погрешность — составляющая погрешность измерения, зависящая от погрешностей применяемых средств измерения.
- Поправка — значение величины, прибавляемое к полученному при измерении значению величины, с целью исключения систематической погрешности.
Численно поправка равна погрешности, взятой с обратным знаком.
Классификация и метрологические показатели измерительных средств
В зависимости от конкретных условий, применяемых измерительных средств и приемов их использования измерения могут производиться различными способами или методами. С точки зрения общих приемов получения результатов измерения различают измерения прямые и косвенные.
При прямых измерениях искомую величину определяют непосредственно по показаниям прибора.
При косвенных измерениях значение искомой величины (размер или отклонение) определяют по результатам прямых измерений одной или нескольких величин, связанных с искомой известной зависимостью.
Примером косвенных измерений могут служить тригонометрические измерения углов по двумя катетам, по катету и гипотенузе и др. Каждое измерение можно выполнять абсолютным или относительным методом.
При абсолютном измерении весь измеряемый размер определяют непосредственно по показаниям прибора.
Относительное (сравнительное) измерение непосредственно дает только отклонение размера от установочной меры или образца, по которым прибор был установлен на ноль. Определение размера в этом случае производят алгебраическим суммированием размера установочной меры и показаний прибора при измерении.
Кроме того, способы измерения делят на комплексные и дифференцированные.
Комплексный способ измерения заключается в сопоставлении действительного контура проверяемого объекта с его предельными контурами, определяемыми величинами и расположением полей допусков, отдельных элементов этого объекта. Комплексный метод измерения обеспечивает проверку накопленных погрешностей взаимосвязанных элементов объекта, ограниченных суммарным допуском.
Предлагается к прочтению: Перевозка опасных грузов в таре и навалом
Примером комплексного способа измерения может служить проверка комплексным калибром расположения отверстия под заклепки в полусепараторе.
Дифференцированный способ измерения сводится к независимой проверке каждого элемента отдельно.
Комплексный способ измерения применяют преимущественно при проверке изделий, а дифференцированный способ — при проверке инструментов и при выявлении причин размерного брака изделий.
Каждый из перечисленных выше способов измерения может осуществляться контактным или бесконтактным способом.
Контактный способ измерения осуществляют при непосредственном соприкосновении измерительных поверхностей прибора или инструмента с поверхностью контролируемого объекта.
Бесконтактный способ измерения характеризуется отсутствием измерительного контакта с проверяемым объектом (например, при проекционном или пневматическом принципе измерения).
Измерительные средства, применяемые в металлообрабатывающей промышленности, могут быть разбиты на три основные группы: меры, калибры, универсальные инструменты и приборы.
Мерами называют средства измерения, служащие для воспроизведения физической величины заданного размера.
Калибрами называют меры, служащие для проверки правильности размеров, форм и взаимного расположения частей изделия.
Универсальные инструменты и приборы служат для определения значений измеряемой величины. Они различаются по конструктивным признакам, по целевому назначению, по степени механизации, пределам измерения, цене деления и прочим показателям.
По конструктивным признакам универсальные инструменты и приборы делятся на следующие:
- штриховые инструменты, снабженные нониусом (штангенинструменты и универсальные угломеры);
- микрометрические инструменты, основанные на применении микропар (микрометры, микрометрические нутромеры, глубиномеры и др.);
Рычажно-механические приборы, которые подразделяются на следующие виды:
- собственно рычажные приборы (миниметры и др.);
- зубчатые приборы (индикаторы часового типа и др.);
- рычажно-зубчатые приборы (микромеры и др.);
- приборы с пружинной передачей (микрокаторы и др.);
- рычажно-оптические приборы (оптиметры и др.);
- оптические приборы (длиномеры, интерферометры, проекторы и др.);
- пневматические приборы с манометром и ротаметром;
- электрифидированные приборы (индуктивные, емкостные, фотоэлектрические и др.).
По числу одновременно проверяемых размеров приборы подразделят на одномерные и многомерные.
По установившейся на производстве терминологии простейшие измерительные средстваТехнические требования к деталям и собранным подшипникам — калибры, линейки, штангенинструмент и микрометрический инструмент — именуют измерительным инструментом.
Одним из основных конструктивных элементов приборов является шкала. Шкала — это совокупность ряда отметок (штрихов) и проставленных у некоторых из них чисел отсчета, соответствующих значениям или отклонениям измеряемой величины. В настоящее время созданы приборы с непосредственным цифровым отсчетом результатов измерений. У этих приборов шкала заменена цифровым табло, на котором появляется результат измерения.
Длина деления шкалы — это расстояние между серединами двух соседних отметок (штрихов) шкалы.
Длину делений шкал измерительных приборов выбирают в пределах 0,9—2,5 мм. При таких длинах делений обеспечивается наилучший результат глазомерной оценки долей деления при расположении стрелки (указателя) прибора между отметками шкалы.
Цена деления шкалы — разность значений величин, соответствующих двум соседним отметкам шкалы. Цена деления, как правило, не должна быть меньше погрешности показаний прибора.
Перемещение измерительного стержня прибора передается стрелке через увеличивающий передаточный механизм.
Передаточное отношение прибора — это отношение перемещения конца стрелки (указателя) к изменению размера, вызвавшему это перемещение. Оно численно равно отношению длины деления к цене деления шкалы.
Порог чувствительности или разрешающая способность прибора — это наименьшее изменение значения измеряемой величины, способное вызвать малейшее заметное изменение показаний прибора.
Порог чувствительности прибора является решающим фактором при выборе измерительных средств для, непрерывных измерений малых значений проверяемых величин (например, при проверке биения).
Расстояние между указателем и шкалой должно быть по возможности малым, чтобы при отсчете уменьшить погрешности, вызываемые параллаксом.
Параллакс — это кажущееся смещение указателя относительно отметок шкалы при наблюдении в направлении, не перпендикулярном плоскости шкалы.
По ГОСТу 5365—57 цена деления шкалы прибора должна быть кратной цифрам 1, 2 или 5.
Диапазон показаний — это значение измеряемой величины, соответствующее всей шкале прибора.
Пределы измерения прибора — это наибольшая и наименьшая величины, которые могут быть измерены прибором.
При многократном измерении одного размера вследствие несовершенства механизма прибора — наличия в нем зазоров, трения и деформаций — повторные показания прибора могут не совпадать.
Вариация показаний — наибольшая разность между показаниями прибора при многократном измерении одной и той же величины при неизменных внешних условиях.
Измерительное усилие — это сила, создаваемая прибором и действующая на измеряемую поверхность в направлении линии измерения.
Измерительное усилие обычно создается пружинами, деформации и усилия которых изменяются в зависимости от перемещения измерительного стержня прибора.
Колебание измерительного усилия — это разность между наибольшим и наименьшим значениями измерительного усилия при однонаправленном изменении значений измеряемой величины. Перепад измерительного усилия — это значение изменения измерительного усилия в момент перемены направления значений измеряемой величины.
Погрешности измерений и обработка результатов ряда измерений
Погрешности измеренийПравильное определение истинных ВМТ кривошипов на судах являются результатом суммарного действия составляющих погрешностей, вызываемых различными причинами.
В зависимости от причин элементарные ошибки делят на следующие группы:
- инструментальные погрешности, причиной которых являются погрешности изготовления и юстировки прибора, а также несовершенство его принципиальной схемы;
- погрешности схемы измерения являются результатом выбранной для измерения схемы базирования и условий проведения измерений, не позволяющих исключить влияние известных источников погрешностей (например, при измерении диаметра цилиндрической детали в двух взаимоперпендикулярных направлениях вместо непрерывного измерения при повороте детали на 1 800 погрешность может достигать половины овальности деталиКак, и где изготавливают составные детали корпусных конструкций?);
- внешние погрешности возникают от влияния внешней среды, в основном от изменения температуры;
- погрешности объекта определяются технической характеристикой объекта измерения — отклонениями формы, шероховатостью поверхности, деформациями объекта, изменением размеров в результате старения и т. п.;
- личные субъективные погрешности возникают в связи с ограниченными возможностями зрения контролера при отсчете по шкалам с оценкой долей деления при субъективных измерениях (например, оценки световой щели) и др.
Субъективные погрешности зависят от опытности и остроты зрения контролера, а также от нормы времени на контрольную операцию.
Составными частями суммарной погрешности метода измерения являются:
- погрешности показаний прибора;
- погрешности концевых мер или установочных образцов;
- погрешности, вызываемые отклонением температуры изделия и измерительного средства от нормальной температуры;
- погрешности, вызываемые измерительным усилием прибора.
Погрешности прибора объясняются неточным выполнением отдельных деталей его механизма, зазорами и силами трения в его кинематических парах и, в ряде случаев, несовершенством схемы прибора, приводящим к нарушению пропорциональности перемещения измерительного стержня и стрелки (например, у рычажно-зубчатых индикаторов). Погрешности прибора обычно определяют проверкой по концевым мерам. Для стандартизованных приборов предельные погрешности, при которых приборы могут быть допущены к эксплуатации, указаны в стандартах и инструкциях.
Погрешности концевых мер и установочных образцов входят в суммарную погрешность только в случае их применения при относительных измерениях.
Температурные погрешности пропорциональны измеряемым размерам, отклонениям температуры и разности коэффициентов линейного расширения материалов измерительных средств и проверяемых объектов.
Температурные погрешности могут быть уменьшены, если проводить измерения при температуре, близкой к нормальной, выравниванием температуры проверяемого изделия и прибора, внесением поправки в результаты измерения.
Температурную погрешность оценивают по формуле
где:
- △l — температурная погрешность измерения;
- l — номинальный размер;
- а1 и а2 — коэффициенты линейного расширения материалов измеряемого объекта и измерительного средства;
— температура измеряемого объекта и измерительного средства.
Температурные погрешности зависят не только от отклонения температуры от нормальной, но и от скорости изменения температуры. Быстрые колебания температуры, как правило, не могут быть компенсированы поднастройкой прибора или внесением поправки в результаты измерений.
Рекомендуемые температурные режимы измерения деталей при ведены в табл. 2.
| Таблица 2. Температурный режим контроля размеров стальных деталей | ||||||
|---|---|---|---|---|---|---|
| Диапазоны размеров в мм | Допуски измеряемых размеров в мкм | |||||
| От 1 до 3,0 | – | – | Св. 0,1 до 0,3 | Св. 0,3 до 1 | Св.1,0 до 3 | Св. 3 |
| Св. 3,2 до 10 | – | Св. 0,1 до 0,3 | Св. 0,3 до 1 | Св. 1 до 3 | Св. 3 до 10 | ” 10 |
| » 10 »32 | Св. 0,3 до 0,6 | Св. 0,6 до 1 | Св. 1 до 3 | Св. 3 до 10 | Св. 10 до 30 | » 30 |
| » 32 » 100 | Св. 1 до 3 | Св. 3 до 6 | Св. 6 до 10 | Св. 10 до 30 | Св. 30 до 100 | ” 100 |
| » 100 » 320 | Св. 3 до 10 | Св. 10 до 18 | Св. 18 до 30 | Св. 30 до 100 | Св. 100 до 300 | » 300 |
| » 320 » 1 000 | Св. 10 до 30 | Св. 30 до 60 | Св. 60 до 100 | Св. 100 до 300 | Св. 300 до 600 | » 600 |
| Допускаемые отклонения температуры от нормальной в °С | ±0,2 | ±0,5 | ±1 | ±2 | ±5 | ±10 |
| Допустимые колебания температуры в течении 1 ч в °С | 0,05 | 0,1 | 0,1 | 0,2 | 0,5 | 1 |
| Допускаемые колебания температуры течении 12 ч в °С | 0,2 | 0,5 | 1 | 2 | 3 | 5 |
| Допускаемая разность температур в двух точках пространства в °С | 0,05 | 0,2 | 0,2 | 0,2 | 0,5 | 1 |
Измерительное усилие может быть источником существенных погрешностей, если при измерении тонкостенных легкодеформируемых деталей настройку прибора на размер производить по концевым мерам длины. Для уменьшения погрешностей необходимо вносить поправку, определенную опытным путем, или настраивать прибор по аттестованной образцовой детали (в последнем случае деформации при настройке и измерении будут одинаковыми и взаимно компенсируются).
При измерении жестких деталей погрешности измерений возникают в основном из-за колебаний и перепада измерительного усилия, вызывающих изменение контактных деформаций и деформации стойки или скобы прибора.
Деформации поверхности изделийВосприятие корпусными конструкциями внешних нагрузок, действующих на судно зависят от формы измерительного наконечника (плоский или сферический), материала наконечника и проверяемой детали, величины измерительного усилия.
Величину контактной деформации в мкм находят по формуле
где:
- Р — измерительное усилие в н;
- r — радиус измерительного наконечника в мм;
- k — коэффициент, зависящий от материала измерительного наконечника: для наконечника из стали k = 1, из корунда k = 0,86, из твердого сплава k = 81.
Продифференцировав формулу и перейдя к конечным приращениям, получим зависимость погрешности измерения δк, вызываемой отклонением измерительного усилия на ΔР:
При:
- k = 1, P = 2 н, r = 1,5 мм и ΔР = 2,0 н получим
Для уменьшения погрешностей, связанных с деформациями под действием собственного веса горизонтально установленных больших концевых и штриховых мер и поверочных линеек, их опоры следует располагать на расстоянии 0,22 длины меры или линейки, считая от ее концов. При этом условии обеспечиваются наименьшие отклонения измерительных поверхностей от параллельности, наименьшее изменение расстояния между штрихами, нанесенными на нейтральной плоскости, и наименьшее отклонение линеек от прямолинейности.
Для уменьшения погрешностей, вызываемых перекосом, вследствие зазоров и непрямолинейности направляющих подвижных узлов прибора, передающих изменение размера, штриховые меры и измерительные наконечники приборов следует располагать на прододжении линии измерения.
По закономерности появления погрешности делят на систематические, случайные и грубые.
Систематическая погрешность измерения — составляющая погрешность измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же величины.
Примерами систематических погрешностей являются погрешности нанесения делений на точных шкалах, погрешности шага микрометрического винта микрометра и др. Систематические погрешности изучают опытным путем и записывают в виде поправок в аттестатах, прилагаемых к приборам или мерам. Для исключения систематической погрешности в результаты измерения необходимо внести поправку по аттестату.
Случайная погрешность измерения — составляющая погрешность измерения, изменяющаяся случайным образом при повторных измерениях одной и той же величины.
Случайные погрешности проявляются в различных показаниях (в пределах норм точности) прибора при многократном измерении одного и того же размера. Случайные погрешности вызываются зазорами и силами трения в соединениях деталей механизма прибора, погрешностями отсчета долей деления, отклонением объекта измерения от правильного положения и другими причинами.
Грубая погрешность измерения — погрешность измеренияТехнологические процессы разборки и сборки механизмов судна, существенно превышающая ожидаемую при данных условиях погрешность. Примерами грубых погрешностей могут служить неправильный отсчет по шкале прибора, ошибка в составлении блока мер, неправильная установка изделия при измерении и т. п. Результаты измерений с грубыми погрешностями подлежат безусловному исключению из ряда измерений, так как они дают неверное представление о размере.
Случайные погрешности подчиняются следующим правилам:
- большие по абсолютной величине погрешности встречаются реже малых погрешностей;
- равные по абсолютной величине положительные и отрицательные случайные погрешности равновероятны;
- с увеличением числа измерений среднее арифметическое из случайных погрешностей данного ряда стремится к нулю.
Из второго и третьего правил вытекает, что наиболее достоверное значение измеряемого размера при многократных измерениях есть среднее арифметическое из полученных результатов.
Основной характеристикой случайных погрешностей является средняя квадратичная погрешность (стандарт), определяемая по формуле
где:
- △i — погрешность отдельного измерения;
- n — число измерений данного ряда.
Погрешностью △ измерения называют разность между результатом измерения х и истинным значением хи размера:
Так как истинное значение размера нам, как правило, неизвестно, то вместо истинного значения размера используют действительное значение, а в случае многократных измерений — средний арифметический размер х, определяемый по формуле
За предельную погрешность данного метода измерения принимают погрешность, вероятность превышения которой равна 0,0027. Для обычно встречающегося в измерениях нормального закона распределения отклонений △lim = ± 3σ.
Предельная погрешность определяет область возможных значений случайных погрешностей.
Случайные погрешности превышающие предельную погрешность, относят к грубым погрешностям, и эти результаты измерений исключают из ряда.
Средняя квадратичная и предельная погрешности определяют точность отдельного измерения данного ряда.
Предельная погрешность Мlim среднего арифметического из ряда измерений определяется зависимостью
Предельная погрешность среднего арифметического является предельной погрешностью аттестации размера путем многократных измерений, к которым прибегают при недостаточной точности используемых средств измерения.
Погрешность определения средней квадратичной погрешности по результатам ограниченного числа измерений приближенно находят по формулам:
- при числе измерений п = 4 ÷ 40
- при числе измерений св. 40
Точную оценку погрешности определения средней квадратичной погрешности производят на основе использования х² распределения. Распределение случайных погрешностей, как правило, подчиняется нормальному закону (закону Гаусса):
где:
- е ≈ 2,7183 – основание натуральных логарифмов.
На рис. 2, а показаны две кривые нормального закона распределения с разными значениями параметра σ.
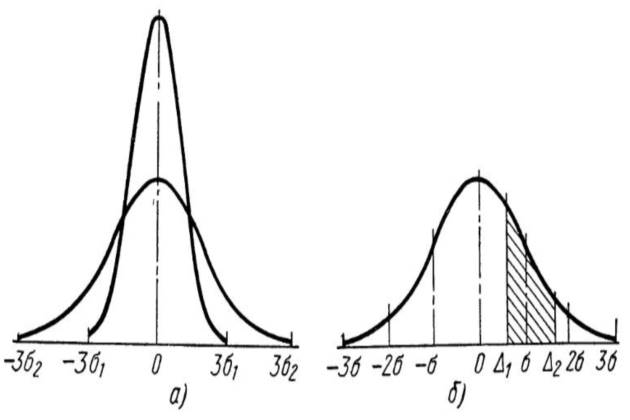
Вероятность получения отклонений в пределах интервала значений от △1 до △2 (рис. 2, б) определяется величиной площади ограниченной кривой в заданном интервале значений △ (заштрихованный участок).
Для вычисления этой вероятности составлены специальные таблицы Ф (z) — табл. 3 (функция Лапласа), в которых указана площадь кривой нормального распределения в интервале от нуля до любого практически возможного значения отклонения
.
| Таблица 3. Значение функций Гасса [φ (z)] и Лапласа [Φ (z)] | ||||||||
|---|---|---|---|---|---|---|---|---|
| z | φ (z) | Φ (z) | z | φ (z) | Φ (z) | z | φ (z) | Φ (z) |
| 0 | 0,3989 | 1,3 | 0,1714 | 0,4032 | 2,6 | 0,0136 | 0,4953 | |
| 0,1 | 0,3970 | 0,3989 | 1,4 | 0,1497 | 0,4192 | 2,7 | 0,0104 | 0,4965 |
| 0,2 | 0,3910 | 0,0793 | 1,5 | 0,1295 | 0,4332 | 2,8 | 0,0079 | 0,4974 |
| 0,3 | 0,3814 | 0,1179 | 1,6 | 0,1109 | 0,4452 | 2,9 | 0,0060 | 0,4981 |
| 0,4 | 0,3683 | 0,1554 | 1,7 | 0,0940 | 0,4554 | 3,0 | 0,0044 | 0,49865 |
| 0,5 | 0,3581 | 0,1915 | 1,8 | 0,0790 | 0,4641 | 3,1 | 0,0033 | 0,49903 |
| 0,6 | 0,3332 | 0,2257 | 1,9 | 0,0656 | 0,4713 | 3,2 | 0,0024 | 0,49931 |
| 0,7 | 0,3123 | 0,2580 | 2,0 | 0,0540 | 0,4772 | 3,3 | 0,0017 | 0,49952 |
| 0,8 | 0,2897 | 0,2881 | 2,1 | 0,0440 | 0,4821 | 3,4 | 0,0012 | 0,49966 |
| 0,9 | 0,2661 | 0,3169 | 2,2 | 0,0355 | 0,4861 | 3,5 | 0,0009 | 0,49977 |
| 1,0 | 0,2420 | 0,3413 | 2,3 | 0,0283 | 0,4893 | 4,0 | 0,00015 | 0,499968 |
| 1,1 | 0,2179 | 0,3643 | 2,4 | 0,0224 | 0,4918 | 4,5 | 0,00002 | 0,499997 |
| 1,2 | 0,1942 | 0,3849 | 2,5 | 0,0175 | 0,4938 | 5,0 | 0,000002 | 0,4999997 |
Площадь, ограниченная кривой в интервале от △1 до △2 определяется разностью табличных значений:
Погрешности измерений являются результатом суммарного воздействия случайных погрешностей, вызываемых разными причинами.
При независимых случайных погрешностях справедливо равенство
где:
- σсум — средняя квадратичная погрешность метода;
- σ1, σ2, …, σп — составляющие средние квадратичные погрешности собственно прибора, отклонений размеров установочной меры, от несоблюдения температурного режима и прочих причин.
Предельная суммарная погрешность метода измерения определяется формулой
- где Δ1 lim, Δ2 lim, …, Δn lim — составляющие предельные погрешности.
При косвенных измерениях, при анализе точности механизмов приборов и в других случаях искомый результат U является функцией x, y, z, …:
В этих случаях погрешности функции U приближенно определяют по формулам:
- систематическая погрешность
- средняя квадратичная случайная погрешность
- суммарная предельная случайная погрешность
суммарная предельная погрешность ∑ с учетом систематических и случайных составляющих
В формулах обозначено:
- θU, θx, θy и θz – систематические погрешности функции и ее аргументов (результатов измерений);
- σU, σx, σy и σz — средние квадратичные случайные погрешности функции и ее аргументов
- Δx lim, Δy lim , …, Δz lim – предельные случайные погрешности функции и ее аргументов;
— частные производные функции U (коэффициенты передачи).
Обработка ряда измерений
Ряд измерений обрабатывают для получения наиболее достоверного результата с оценкой его точности.
При обработке вычисляют средний арифметический размер, среднюю квадратичную погрешность, предельную погрешность одного измерения и предельную погрешность среднего арифметического. Эти параметры можно вычислять по приведенным выше формулам, однако вычисления могут быть значительно упрощены, если одинаковые результаты измерений сгруппировать и расположить в порядке возрастания (табл. 4), указав во второй графе число измерений с одинаковым результатом.
| Таблица 4. Математическая обработка ряда изменений | |||||
|---|---|---|---|---|---|
| Показания прибора хi в мкм | Число одинаковых показаний n | x0 = 70 xi – x0 | n (xi – x0) | (xi – x0)2 | n (xi – x0)2 |
| 65 | 2 | – 5 | – 10 | 25 | 50 |
| 67 | 6 | – 3 | – 18 | 9 | 54 |
| 68 | 12 | – 2 | – 24 | 4 | 48 |
| 69 | 16 | – 1 | – 16 | 1 | 16 |
| 70 | 23 | – | – | – | – |
| 71 | 18 | 1 | 18 | 1 | 18 |
| 72 | 12 | 2 | 24 | 4 | 48 |
| 73 | 8 | 3 | 24 | 9 | 72 |
| 74 | 3 | 4 | 12 | 16 | 48 |
| Сумма | 100 | – | 10 | – | 354 |
Затем выбирают произвольное число х0, близкое к предполагаемому значению х, и определяют среднее арифметическое по формуле
где:
- N — общее число измерений.
Среднюю квадратичную погрешность определяют по формуле
Предельные погрешности одного измерения и среднего арифметического определяют по приведенным выше формулам.
В табл. 4 дан числовой пример обработки ряда измерений. В данном случае σ ≈ 1,9 мкм; △lim = мкм.
Ни один результат измерения не должен отклоняться от среднего арифметического больше чем на предельную погрешность (проверяют только наибольшие отклонения ряда, т. е. верхние и нижние строчки таблицы). При обнаружении отклонений, превышающих ±△lim, эти результаты измерения вычеркивают, как имеющие грубые погрешности, и производят новый расчет среднего арифметического результата измерения и средней квадратичной погрешности.
В заключение определяют предельную погрешность среднего арифметического
Окончательным результатом математической обработки является наиболее достоверный результат х с предельной погрешностью ±Мlim т. е. 70,1±0,57 мкм.
При вычислении средней квадратичной погрешности результаты следует округлять, чтобы лишними десятичными знаками не создавать ложного впечатления о большой точности результата. При N ≤ 25 следует сохранять не более двух значащих цифр, а при N > 25 — не более трех.
Влияние погрешностей измерений на результаты контроля и выбор средств измерений
Погрешности средств измерения
Погрешности средств измерения приводят к тому, что результат измерения не соответствует истинному размеру детали. Для правильного выбора измерительных средств необходимо уметь оценивать влияние погрешностей измерения на результаты контроля, зависящие от вида контроля и распределения отклонений проверяемых деталей.
Это влияние будет разным для следующих типовых случаев измерений:
- измерение размера деталиВосстановление работоспособности и повышение долговечности судовых деталей и механизмов;
- контроль (разбраковка) деталей, отклонения которых подчиняются нормальному закону или закону существенно положительных величин (закону Релея);
- многодиапазонная рассортировка деталей.
Распределение погрешностей измерений принято считать следующим закону нормального распределения (закону Гаусса).
Влияние погрешностей измерений на результаты контроля определяется практически предельной погрешностью измерения и относительным количеством неправильных результатов измерений.
Погрешности при измерении (аттестации) размера детали. Предельная погрешность при измерении размеров, например, при аттестации образцовых деталей, равна предельной погрешности метода измерения △мет. Каждое отдельное измерение имеет случайное значение погрешности, распределяющееся в пределах ±△мет по нормальному закону.
Влияние погрешностей измерений на контроль деталей. Целью такого контроля является распортировка партии деталей на годные, действительные размеры которых лежат в пределах заданного допуска, и брак — с размерами, выходящими за пределы допуска.
Введем следующие обозначения:
- σмет и σтех — средние квадратичные отклонения метода измерения и технологического процесса соответственно;
- △мет = 3σмет — предельная погрешность метода измерения;
- △изд — допуск контролируемого параметра;
- △тех = 6σтех — область технологического рассеивания отклонений всех изготовленных деталей при нормальном законе распределения отклонений;
— относительная погрешность измерения (коэффициент точности метода измерения).
Для оценки влияния погрешностей измерений на результаты контроля (разбраковки) необходимо установить зависимость между погрешностью измерения, вероятностью неправильного принятия бракованных деталей т, вероятностью забракования годных деталей n и вероятной величиной предельного выхода размера за границу допуска с у неправильно принятых деталей. Эти зависимости будут разнымй для различных законов распределения отклонения размеров контролируемых деталей. Зависимости определяются по законам теории вероятностей и требуют трудоемких вычислений. Для практического применения составлены графики, по которым интересующие нас результаты могут быть получены при минимальных затратах времени.
На рис. 3, а дан график для определения процента неправильно принятых деталей (т%) с размерами, выходящими за пределы. поля допуска, на рис. 3, б — график для определения процента неправильно забракованных деталей (п%), а на рис. 3, в — график для определения относительной величины выхода размера за границу поля допуска
при различных значениях Амет
и при отклонениях контролируемых параметров и погрешностей измерительных средств, подчиняющихся закону нормального распределения.
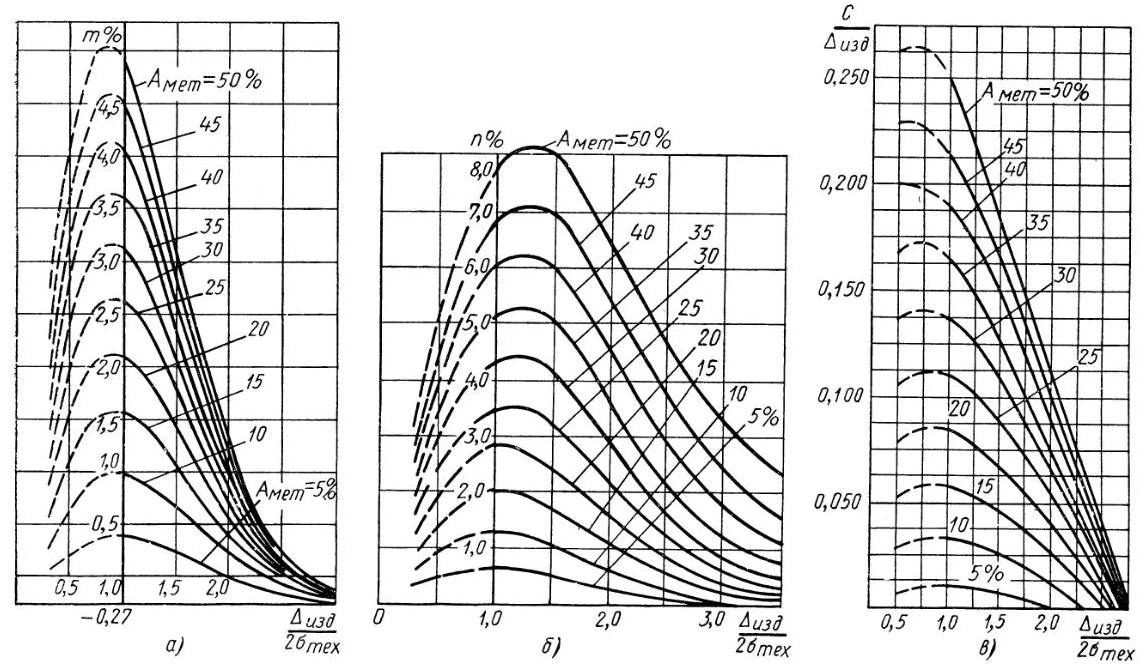
На рис. 4, а—в даны аналогичные графики для случая, когда отклонения контролируемых параметров подчиняются закону существенно положительных величин (закон Релея), а погрешность измерительных средств — закону нормального распределения (закон Гаусса). Закону существенно положительных величин подчиняются отклонения эксцентрицитета, биения, непараллельности плоскостей и приближенно овальности. Распределение отклонений при этом законе происходит в диапазоне(0 ÷ 5,25) σлин, среднее значение отклонений равно, 9 σлин (σлин — среднее квадратичное отклонение закона Релея).
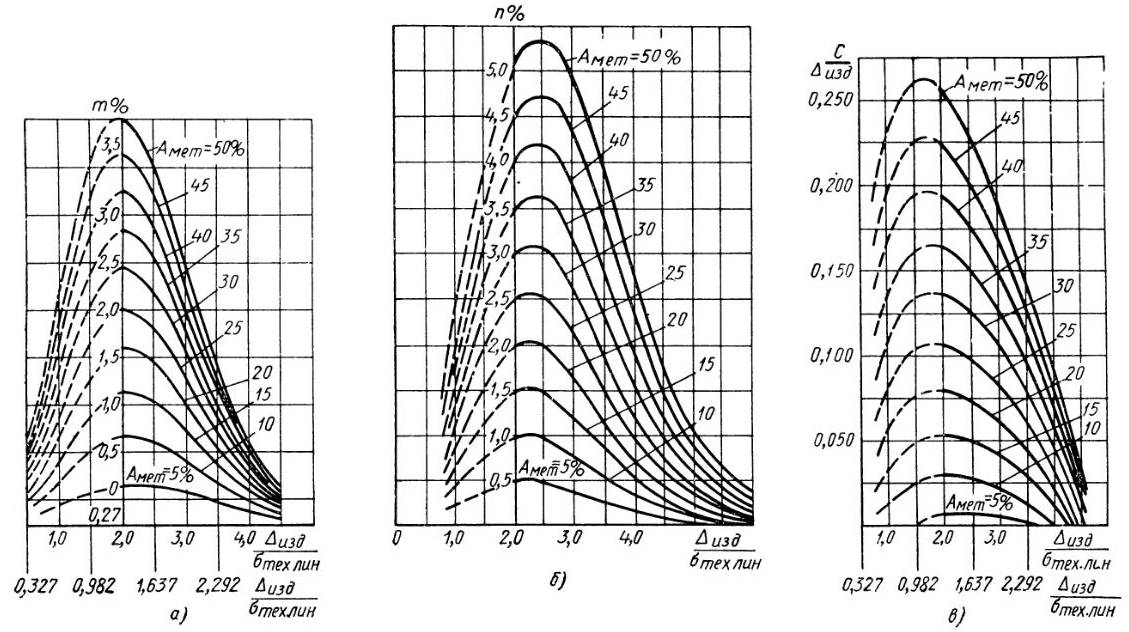
Следует учитывать; что значения т и п даются для общего количества проверенных деталей и одновременно для обеих границ поля допуска при симметричном выходе за эти границы.
Пользование графиком поясним конкретным примером. Пусть требуется определить результаты разбраковки при допуске △изд = 20 мкм, погрешности измерения △мет ± 6 мкм и разбросе размеров в пределах 30 мкм (6 σтех = 30 мкм).
Определяем
По графику рис. 3, а определяем, что количество неправильно принятых деталей т = 0,8%.
По графику рис. 3, б находим количество неправильно забракованных деталей п=3,0%.
По графику рис. 3, в определяем для неправильно принятых деталей предельную относительную величину выхода размера за границу допуска
Предельный выход размера за границу допуска будет
Графиками на рис. 4 для существенно положительных величин пользуются аналогичным образом.
При многодиапазонной рассортировке деталей распределение отклонений размеров в пределах отдельных групп принимают подчиняющимся закону равной вероятности, а погрешности измерений — нормальному закону.
В этом случае общее количество неправильно рассортированных деталей Р в % определяется формулой
(в данном случае под △изд понимают групповой допуск, причем △изд < σтех).
Предельное отклонение с размера неправильно рассортированных деталей от границ своей группы определяют решением уравнения
где:
- Ф (z) — функция Лапласа (площадь под кривой нормального распределения).
Решение этого уравнения производят по таблице интеграла функции Лапласа.
Выбор измерительных средств
Из всех возможных вариантов выбора измерительных средств наиболее целесообразным является тот, который обеспечивает наименьшую себестоимость контроля. При определении себестоимости контроля следует учитывать стоимость измерительных средств, стоимость их ремонта и эксплуатации, расходы на заработную плату контролера и потери из-за погрешностей измерений. Последние при относительной погрешности измерений >20% имеют первостепенное значение. Поэтому на практике выбор измерительных средств часто ограничивают подбором прибора с удовлетворительной точностью.
Порядок назначения измерительных средств и рекомендуемые допускаемые погрешности измерений установлены руководящими материалами «Выбор измерительных средств для линейных измерений от 1 до 500 мм в зависимости от точности изготовления» ОМТРМ-О466-001—65.
Читайте также: Технологические процессы разборки и сборки механизмов судна
По ГОСТу допуски устанавливают для действительных размеров, т. е. размеров, полученных в результате измерения с допускаемой погрешностью. Случаи, когда предельные размеры ограничивают действительные размеры с учетом погрешностей измерений, должны оговариваться особо в чертежах или технических условиях. Какую погрешность можно считать допустимой, ГОСТ 7713—62 не определяет.
Значение допускаемой погрешности зависит от ответственности механизма, в который входит деталь, от степени важности данного размера (его влияния на надежность механизма), от влияния погрешности измерения на искажение результатов контроля и от учета конструктором при назначении допусков возможных погрешностей измерений.
В тех случаях, когда в технической документации отсутствуют указания о допускаемой погрешности измерения или применении определенного типа прибора, можно руководствоваться следующими ориентировочными нормами:
- при аттестации размеров образцовых мер и деталей, погрешности не должны превышать 15—20% допуска;
- при контроле размеров деталей с рассортировкой на годные и брак погрешность не должна превышать 25—30% допуска;
- при контроле отклонений формы, положения и биений, погрешность не должна превышать 30—35% допуска;
- при многодиапазонной рассортировке погрешность не должна превышать 15—20% группового допуска. Если многодиапазонную рассортировку производят по результатам измерения случайного диаметра, то допускается увеличение погрешности измерения до 50% от влияния овальности деталей на результаты рассортировки.
После установления допустимой погрешности выбирают измерительные средства, погрешности которых не должны превышать допустимой.
В выборе измерительных средств должны участвовать конструкторы, технологи и метрологи.
Конструктор устанавливает допуск на изготовление детали по соответствующему стандарту, руководствуясь условиями работы детали (передаваемой нагрузкой, моментом или допустимым относительным смещением детали), и оценивает возможные последствия измерения детали с рекомендуемой РТМ погрешностью. Если рекомендуемая погрешность измерения признается допустимой, то конструктор оставляет принятый первоначально допуск. В противном случае, устанавливают допуск более высокого класса точности или вводят производственный допуск, уменьшенный на часть или всю величину с с каждого предела. В последнем случае на чертеже в примечаниях конструктор указывает производственный допуск.
Технолог осуществляет выбор конкретных измерительных средств на стадии подготовки производства, руководствуясь допустимой погрешностью и погрешностями применяемых на заводе измерительных средств. Выбирая технологический процесс, обеспечивающий необходимую точность, технолог должен оценить экономичность процесса, учитывая потери за счет неправильно забракованных деталей n. Если потери из-за неправильно забракованных деталей недопустимо велики, технолог принимает решение об улучшении технологического процесса или уменьшении погрешностей измерения. Первый вариант предпочтительней, так как позволяет уменьшить не только фиктивный, но и действительный брак.
Метрологи участвуют в выборе измерительных средств вместе с технологами или вместо них. Метрологи разрабатывают заводские инструкции для технологов по выбору измерительных средств и разрабатывают рекомендации по оснащению завода измерительными средствами.
Статистический контроль
Стоимость контроля составляет значительную часть себестоимости подшипников. Поэтому естественно стремление снизить стоимость контрольных операций путем повышения их производительности, в частности, их автоматизации, с одной стороны, и сокращения контроля, с другой стороны. Последнее достигают переходом со сплошного (100% -ного) контроля на выборочный.
Современные математико-статистические методы позволяют делать обоснованные заключения о состоянии технологического процесса или о качестве совокупности предъявленных к сдаче изделий по результатам проверки выборки.
Определение точностных характеристик и закономерностей протекания во времени технологического процесса статистическими методами называют статистическим анализом точности технологического процесса. Корректировка параметров технологического процесса в ходе производства с помощью выборочного контроля изготавливаемой продукции для технологического обеспечения требуемого качества и предупреждения брака называют статистическим регулированием технологического процесса.
Статистически управляемый процесс — это стабильный технологический процессТехнологические процессы повышения прочности и долговечности деталей судна, поддающийся статистическому регулированию и обеспечивающий заданные показатели качества продукции.
Статистическое регулирование технологического процесса может быть основано на разных методах оценки качества изготовляемой продукции. Наиболее распространены метод средних значений и средних квадратичных отклонений, метод средних значений и размахов, метод крайних значений, метод медиан и крайних значений, метод учета дефектов и метод группировок.
По результатам статистической оценки качества изготовляемой продукции принимается решение о необходимости произвести очередную настройку оборудования. При этом приходится считаться с возможностью незамеченной разладки или излишнего выполнения настройки.
Риск незамеченной разладки — это вероятность того, что по статистической оценке будет принято решение не производить настройку, в то время как в действительности она необходима.
Риск излишней настройки — это вероятность того, что по статистической оценке будет принято решение произвести очередную настройку, в то время как в действительности в ней нет необходимости.
Наибольший эффект в современном производстве дает сочетание статистического регулирования технологических процессов и статистического приемочного контроля качества.
Статистический приемочный контроль качества — это выборочный контроль качества готовой продукции, при котором используются статистические методы для обоснования плана контроля или корректировки этого плана по накопленной информации.
В основу статистического приемочного контроля качества кладется план контроля.
План контроля — это совокупность данных о виде контроля, объеме контролируемой партии продукции, выборок или проб, контрольных Нормативах и решающих правилах.
Решающие правила — это совокупность указаний для выбора варианта решения по результатам контроля.
План контроля устанавливает объем выборки n и приемочное число с (контрольный норматив, равный максимальному числу дефектных единиц продукции в выборке, при котором контролируемая партия продукции принимается) в зависимости от объема контролируемой партии. Эти параметры плана контроля определяются требованиями, предъявляемыми к качеству партии изделий.
Зависимость между вероятностью приемки партии продукции при определенном плане контроля и характеристикой уровня качества этой партии называют оперативной характеристикой плана приемочного контроля. Эта характеристика может быть выражена уравнением, таблицей или графиком. В последнем случае (рис. 5) по оси абсцисс оперативной характеристики откладывают процент q содержания бракованных изделий в партии, а по оси ординат — вероятность Р (q) приемки партии.

Статистический приемочный контроль не может обеспечить однозначный результат приемки партий изделий с одинаковым уровнем входного качества, так как число дефектных изделий в выборке подвержено случайным колебаниям. Чтобы уменьшить ошибки, вызываемые этим явлением, необходимо, чтобы выборка была представительной, т. е. как можно лучше отражала свойства партии.
Для этого выборка должна быть случайной, отобранной из разных мест перемешанной партии изделий.
В любом случае применения статистического приемочного контроля возможны ошибки в оценке уровня качества партии изделий, нарушающие интересы поставщика или потребителя.
Риск поставщика (а) — это вероятность забраковки партии продукции, обладающей приемочным уровнем качества.
Риск потребителя (β) — это вероятность приемки партии продукции, обладающей браковочным уровнем качества. Обычно принимают β = 0,05 ÷ 0,1. Зависимость риска поставщика a и риска потребителя β от приемочного q0 и браковочного qm уровней качества при принятом объеме выборки n и приемочном числе с наглядно показывает график оперативной характеристики плана приемочного контроля (рис. 5). На рис. 5 кривая 2 представляет оперативную характеристику плана статистического контроля при с ≠ 0 и кривая 3 — оперативную характеристику статистического контроля при с = 0. На этом же графике для сравнения нанесены отрезки прямых 1, представляющие оперативную характеристику сплошного контроля с предельным уровнем качества, равным qn.
Непосредственный расчет плана контроля весьма трудоемок. Поэтому на практике пользуются таблицами планов контроля, рассчитанными для различных значений указанных выше параметров.
На практике применяются десятки различных методов статистического приемочного контроля, отличающихся по виду контроля (одно, двух, многоступенчатые и последовательные) и по исходным условиям расчета норм контроля (объема выборки, приемочного числа). Эти условия в зависимости от степени ответственности изделия и его себестоимости задаются соответствующими гарантийными показателями (браковочный уровень качества и риск потребителя, приемочный уровень качества и риск поставщика, предел среднего уровня выходного качества и др.) и требованиями экономичности контроля.
Известные методы статистического контроля не учитывают информации о фактическом входном (до контроля) качестве изделий, что приводит к значительному завышению объема контроля, затрат на его осуществеление.
На предприятиях массовой и крупносерийной продукции со стабильным производством, на котором внедрена система бездефектного изготовления продукции и сдачи ее с первого предъявления целесообразно использовать специальные наборы планов статистического приемочного контроля, соответствующие одному и тому же гарантированному уровню качества продукции, но различным значениям процента партий, принятых с первого предъявления.
С увеличением этого процента уменьшается объем выборок.
Выбор программ контроля производят: по браковочному уровню качества qm и фактическому риску потребителя β = 0,05 или β = 0,10 или по пределу среднего уровня выходного качества q2.
Проект стандарта предусматривает выбор программ для Двух типов контроля, при которых по результатам контроля выборки, взятой из партии, принимают решение:
- при контроле типа Д1 — принять партию без дальнейшего контроля или подвергнуть ее 100%-ной разбраковке;
- при контроле типа Д2 — принять партию или отвергнуть ее без дальнейшего контроля.
Приемочное число для всех программ установлено равным с = 0. Планы контроля типа Д1 при с = 0 и β = 0,10 даны в табл. 5.
| Таблица 5. Таблица статистического приемочного контроля с учетом уровня (процента) сдачи партий с первого предъявления. Планы контроля с приемочным числом с = 0, риском потребителя β = 0,1 и сплошной проверкой забракованных партий. | ||||||||
|---|---|---|---|---|---|---|---|---|
| Браковочный уровень в % | Объем выборки и качество принятой продукции | Уровень сдачи партий с первого предъявления в % | ||||||
| неизвестен | 70 | 80 | 90 | 95 | 97,5 | 99 | ||
| 2,25 | n в шт. | 100 | 60 | 50 | 30 | 20 | 10 | 5 |
| q1 в % | 2,30 | 2,30 | 2,20 | 2,30 | 2,00 | 2,20 | 1,85 | |
| q2 в % | 0,35 | 0,40 | 0,35 | 0,30 | 0,25 | 0,25 | 0,20 | |
| 3 | n в шт. | 75 | 45 | 40 | 25 | 15 | 10 | 5 |
| q1 в % | 3,00 | 3,05 | 2,75 | 2,75 | 2,65 | 2,20 | 1,85 | |
| q2 в % | 0,50 | 0,55 | 0,45 | 0,40 | 0,30 | 0,25 | 0,20 | |
| 3,75 | n в шт. | 60 | 40 | 30 | 20 | 15 | 10 | 5 |
| q1 в % | 3,75 | 3,40 | 3,65 | 3,40 | 2,65 | 2,20 | 1,85 | |
| q2 в % | 0,60 | 0,60 | 0,60 | 0,50 | 0,30 | 0,25 | 0,20 | |
| 4,5 | n в шт. | 50 | 30 | 25 | 15 | 10 | 5 | 5 |
| q1 в % | 5,50 | 4,50 | 4,35 | 4,50 | 3,95 | 4,35 | 1,85 | |
| q2 в % | 0,75 | 0,80 | 0,70 | 0,65 | 0,50 | 0,50 | 0,20 | |
| 5,5 | n в шт. | 40 | 25 | 20 | 15 | 10 | 5 | 5 |
| q1 в % | 5,60 | 5,40 | 5,40 | 4,50 | 3,95 | 4,35 | 1,85 | |
| q2 в % | 0,90 | 1,00 | 0,90 | 0,65 | 0,50 | 0,50 | 0,20 | |
| 7,5 | n в шт. | 30 | 20 | 15 | 10 | 10 | 5 | – |
| q1 в % | 7,40 | 6,70 | 7,15 | 6,70 | 3,95 | 4,35 | ||
| q2 в % | 1,25 | 1,25 | 1,20 | 0,95 | 0,50 | 0,50 | ||
| 9 | n в шт. | 25 | 15 | 15 | 10 | 5 | 5 | – |
| q1 в % | 8,80 | 8,85 | 7,15 | 6,0 | 7,70 | 4,35 | ||
| q2 в % | 1,50 | 1,65 | 1,20 | 0,95 | 0,95 | 0,50 | ||
| Обозначения: q1 – максимально возможная доля дефективных изделий в отдельно принятых партиях; q2 – максимально возможная средняя доля дефектных изделий в ряде принятых партий | ||||||||
Таблица составлена для партий любого объема свыше n. Для получения экономического эффекта от выборочного контроля необходимо, чтобы объем партии был больше, чем 4n, где n — объем выборки, соответствующий неизвестному проценту принятых партий с первого предъявления.
Определение экономической эффективности новых средств контроля
Расчет экономической эффективностиТехнико-экономическая оценка эффективности технологических процессов в судоремонте имеет целью определение наиболее экономически эффективных направлений и вариантов мероприятий по развитию техники, а также годовой экономии от внедрения новой техники. Основными показателями для оценки экономической эффективности являются:
- капитальные вложения, необходимые для осуществления мероприятий;
- себестоимость контроля;
- сроки окупаемости капитальных вложений и коэффициент эффективности;
- производительность труда.
При определении экономической эффективности внедрения новой измерительной техники необходимо решить:
- насколько технически прогрессивно данное мероприятие по сравнению с лучшей внедренной или разработанной в проектах и апробированной техникой;
- каков экономический эффект в данных конкретных условиях по сравнению с заменяемыми измерительными средствами на данном предприятии или в отрасли, если новые средства намечаются к широкому внедрению.
Величину капитальных вложений используют при определении экономической эффективности для исчисления амортизационных отчислений, являющихся составной частью себестоимости продукции, и для определения сроков окупаемости. Эту величину рассчитывают отдельно по базовому и внедряемому вариантам.
Амортизационные отчисления производятся по первоначальной (или балансовой) стоимости основных фондов, в состав которых входят: затраты на проектирование, стоимость нового оборудования, включая его доставку и монтаж, затраты на модернизацию действующего оборудования и др.
Изменение себестоимости контроля в результате внедрения новой техники в общем случае определяют путем сравнения калькуляций себестоимости по базовому и внедряемому вариантам.
При определении экономии в результате внедрения контрольноизмерительной техники повышенной точности следует учитывать экономию, получаемую на смежных участках (например, на сборочном участке, в результате сокращения поступления бракованных деталей и связанных с этим переборок собранных узлов), экономию от сокращения потерь от фиктивного брака (т. е. из-за неправильно забракованных годных деталей) и эффект повышения качества продукции.
Экономическую эффективность от повышения качества продукции учитывают по эффекту, получаемому потребителем, а в случае невозможности этого — по повышению цены или увеличению срока службы продукции повышенного качества.
При внедрении высокоточных приборов взамен приборов с недостаточной точностью часто наблюдается уменьшение производительности контроля. В этом случае положительный экономический эффект получается за счет уменьшения потерь из-за неправильной разбраковки деталей, определяемых разностью стоимости неправильно забракоьанных деталей и разностью убытков на сборочном участке из-за пропуска бракованных деталей старым и новым приборами в объеме годовой продукции.
Эти потери определяют предварительно расчетным путем по графикам на рис. 3 и 4 и уточняют по отчетным данным после завершения внедрения новой техники.
Если из-за отсутствия данных о параметрах технологического процесса воспользоваться этими графиками не представляется возможным, то расчет ведут по трудоемкости контроля, приведенной к точности, обеспечиваемой более точным прибором.
При расчете исходят из формулы
где:
и
— предельные погрешности старого и нового приоора;
- n — число измерений, при котором погрешность среднего арифметического из результатов измерения старым прибором становится равной предельной погрешности нового прибора.
В расчете экономической эффективности трудоемкость измерения старым прибором увеличивают в n раз.
Срок окупаемости Т и коэффициент сравнительной экономической эффективности Е дополнительных капитальных вложений на внедрение новой техники определяется по формуле
где:
- К1 и К2 — капитальные вложения по базовому и внедряемому вариантам;
- С1 и С2 себестоимость годовой продукции по этим же вариантам.
Для машиностроения срок окупаемости капитальных вложений составляет 3—5 лет. Срок окупаемости измерительных средств обычно значительно меньше и колеблется в пределах года.
При определении роста производительности труда необходимо учитывать все факторы, влияющие на повышение производительности труда. Число высвобождаемых контролеров определяется разностью количества контролеров, занятых на производстве (на данном участке) при старом (базовом) и новом вариантах при выпуске продукции и объеме базового варианта.
При планировании внедрения новой техники возможны варианты, различающиеся объемом капитальных вложений и экономической эффективностью. Экономически наиболее эффективным следует считать тот вариант, внедрение которого требует наименьших капитальных затрат и обеспечивает одновременно наименьшую себестоимость контрольных операций. Если возможно дальнейшее снижение себестоимости контроля за счет дополнительных капитальных вложений, то эффективность такого варианта определяют исчислением сроков окупаемости дополнительных капитальных вложений по приведенной выше формуле.
Годовая экономия в руб. от внедрения новой техники
- где Ен — нормативный отраслевой коэффициент экономической эффективности (для машиностроения Ен 0,2+0,33).
