Изучение волновых процессов (формулы Мичелла, Хавелока и др.)

Понимание кинематики корабельных волн – это ключ к эффективному и безопасному судовождению. Изучение волновых процессов и то, как они влияют на маневренность судна и его остойчивость, позволяет судоводителю принимать обоснованные решения в различных морских условиях. Например, понимание кельвиновского угла поможет выбрать оптимальный курс для минимизации качки, а знание о волновом сопротивлении позволит оценить расход топлива и выбрать наиболее экономичный режим движения.

СодержаниеСвернуть

Основные обозначения и соотношения кинематики корабельных волн
Плоская модель поперечных волн
Теория волнового сопротивления Мичелла
Волнообразующий потенциал
Граничные условия и интегральное преобразование Фурье
Описание единичного волнообразующего источника
Описание корабельного волнообразования
Основные свойства волнового поля
Формула Мичелла для волнового сопротивления
Численная реализация расчетов волнового сопротивления
Интеграл по ватерлиниям
Интегрирование результатов расчета по ватерлиниям
Интеграл по волновому спектру, расчет сопротивления

В данной статье мы рассмотрим фундаментальные основы, на которых строится теория корабельных волн, уделив особое внимание таким аспектам, как теория Мичелла для расчета волнового сопротивления. Мы подробно остановимся на механизмах образования волн, на влиянии формы корпуса на волновое сопротивление судна и на современных методах численного моделирования волновых процессов. Будут рассмотрены как классические результаты теории Мичелла, так и современные ее развития, учитывающие влияние формы корпуса на волнообразование и нелинейные эффекты. Здесь также мы рассмотрим влияние формы корпуса на волнообразование, которое изучается с помощью экспериментов в бассейнах и численного моделирования.

Статья будет полезна как студентам морских учебных заведений, так и практикующим судоводителям, желающим углубить свои знания в области Определение корпусных характеристик в момент взаимодействия судна с водной поверхностьюгидродинамики судна. Полученные знания позволят более эффективно планировать рейсы, оптимизировать расход топлива и повысить безопасность плавания.

Что такое гидродинамика судна?

Гидродинамика судна – это раздел науки, изучающий взаимодействие судна с окружающей его водой. Другими словами, это исследование того, как вода влияет на движение судна и как судно влияет на воду.

Современные математические модели корабельного волнообразования и взаимодействия корпуса корабля с морским волнением не позволяют получить законченных численных решений об оптимальной форме корпуса, что связано со слабой разработанностью трехмерных моделей вычислительной гидромеханики. Построение многовариантных процессов оптимизации формы корпуса с использованием сложных численных схем для решения трехмерных задач гидромеханики со свободными поверхностями также затруднительно из-за ограниченных мощностей современных компьютеров.

Далее мы рассмотрим как рассчитать волновое сопротивление судна по теории Мичелла. Аналитическое изучение волнового сопротивления корабля берет свое начало от работ Джона Генри Мичелла, где был предложен вполне определенный интеграл, с указаниями на допущения о малости возмущений, вносимых движущимся узким корпусом корабля.

R_{χ} = \frac{ρ g^{2}}{{πV}_{0}^{2}} \cdot \int_{0}^{\frac{π}{2}} {| \int_{Ω} \frac{\partial f}{\partial χ} \cdot e^{k \cdot (- z + i x \cdot \cos ϑ)} d Ω |}^{2} \frac{d ϑ}{\cos^{3} ϑ} Ф о р м . 1

где:

f = f( x,z ) – ординаты формы корпуса;
V₀ – скорость корабля;
Ω – элементарная площадка на обшивке корпуса;
ϑ = arccos V/V₀ – фазовый угол Кельвина, задающий направление излучения (отражение) корабельных волн с частотой формы волны: k = g /( V₀²·cos²ϑ).

Физико-геометрическая интерпретация и анализ численных решений при моделировании гидродинамических процессов в интегралах Мичелла показывают, что уравнениями описывается процесс отражения от корпуса корабля внешних волн (рис. 1) в диапазоне длин: λ ∈ [0 ÷ ∧ = 2 · π · V₀²/g], что соответствует первой половине фазового угла: ϑ ∈ 0 ÷ π/2, в то время как недостающая для замыкания интеграла четверть горизонта: ϑ ∈ π/2 ÷ π определяет падающую на корпус «внешнюю волну». Следовательно, математическая оптимизация подводных обводов и надводной формы корпуса сводится к поиску технических решений, обеспечивающих прохождение штормовой волны через корпус с минимальными искажениями.

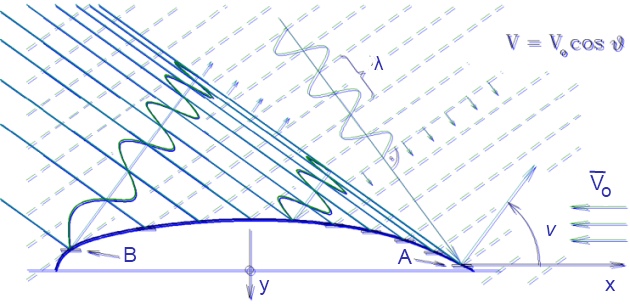
График интеграла Мичелла — Рис. 1 Геометрическая интерпретация классического *интеграла Мичелла* показывает процесс отражения внешних волн от диаметральной плоскости «*узкого*» корабля. На корпусе происходит существенное искажение фазовых и частотных свойств излучаемых волн. В оконечностях корпуса, вне интервала А-В, излучения волн не происходит.
ϑ – угол излучения корабельной волны; V₀ – скорость хода судна

То есть для недопущения отражения штормовой волны от Элементы конструкции корпуса суднабортовой обшивки корпуса и для ослабления передачи волновой энергии на опасное усиление рыскания и качки корабля необходимо оптимизировать волновое сопротивление на всех скоростях хода, включая высокоскоростные режимы с Сопротивление движению малого судначислами Фруда: Fn ⩾ 0,5, на которых происходит образование корабельных волн с такими же параметрами, как и внешнее морское волнение (аналогичные решения по оптимизации обводов корабля и его надводного облика способствуют скрытности в лучах гидро- и радиолокаторов).

Следовательно, справедлив вывод о том, что минимизация волнового сопротивления корабля на всех скоростях хода, включая закритически высокие, будет снижать силовое воздействие на корабль со стороны внешнего Практический разбор штормового мореплавания судовштормового волнения.

Рис. 1 показывает также, что аналитическое представление процесса «отражения» внешних волн от движущегося корпуса корабля не вполне адекватно учитывает реальную картину корабельного волнообразования, так как «теоретически» регулярные внешние волны при отражении от широкого корпуса корабля претерпевают очень сильные частотные (доплеровские) искажения, а в оконечностях корпуса происходит не отражение, а накопление волновой энергии. Соответственно, для корректного учета особенностей корабельного волнообразования снова необходимо искать инженерные (эвристические) подходы с использованием геометрической и динамической интерпретации потоков жидкости вблизи корпуса, особенно в его оконечностях.

Математическая оптимизация подводных обводов и Влияние формы корпуса на мореходные качества судна: ключевые факторы и характеристикинадводной формы корпуса и надстроек корабля, по сути, является поиском технических решений, обеспечивающих прохождение штормовой волны через корпус с минимальными искажениями. Аналогичные математические модели задают отражение от корпуса гидроакустических или радиолокационных волн, откуда следует дополнительное предположение, что оптимизация штормовой мореходности способствует скрытности корабля в море, а исторические корабли начала XX века удовлетворяли требованиям современных стеллс – технологий.

Основные обозначения и соотношения кинематики корабельных волн

$\{x, y, z\}$	Координаты в связанной с корпусом системе координат (СК);
$\{x_{0}, y_{0}, z_{0}\}$	Точка, лежащая на поверхности корпуса;
$\{ξ, η, ς\}$	Координаты в СК неподвижной относительно жидкости на бесконечности;
$\{ξ_{0}, η_{0}, ς_{0}\}$	Точки на свободной поверхности взволнованной жидкости;
`V₀`	Скорость набегающего потока (м/c);
$F n = V / \sqrt{g \cdot L}$	Число Фруда (скорость относительно продольной волны);
$λ / L = 2 π \cdot F n^{2}$	Отношение длины поперечной волны, излучаемой кораблем к длине его корпуса, выраженное с помощью числа Фруда;
$k \frac{g}{{V_{0}}^{2} \cdot \cos^{2} ϑ}$	Частота формы волны (1/м);
$C = V_{0} \cdot \cos^{2} ϑ$	Скорость волны, излучаемой в направлении `∠ϑ` (м/c);
$ϑ = a r c \cos V / V_{0}$	Фазовый угол Кельвина, задающий направление распространения “плоских” волн, образуемых корпусом корабля на частоте излучения параметра `ϑ`;
$V = V_{0} \cos ϑ$	Скорость распространения волны в направлении `ϑ`;
$σ = g / V = \sqrt{g \cdot k}$	Частота волновых колебаний (во Времени) (1/c);
$\vec{r}$	Отклонение частицы жидкости от невозмущенного состояния (м);
$ζ_{w} (\vec{r})$	Аппликаты волнового профиля (м);
$Q (\vec{r}) ≌ V_{0} \cdot q$	Интенсивность распределенных по поверхности корпуса особенностей, моделирующих движение в безграничной жидкости (м/c);
$σ^{2} = ω^{2} = g \cdot k$	Дисперсионное соотношение для волн на глубокой воде;
$λ = g \cdot T^{2} / 2 π = C^{2} \cdot 2 π / g$	Соотношение между длиной, периодом и скоростью движения гребней волн на глубокой воде (м).

Интеграл Мичелла далеко не исчерпал своих аналитических возможностей, и в случае углубленной физико-геометрической интерпретации его подынтегральных выражений, возможен не только уточненный расчет волнового сопротивления корабля, но и качественный анализ волнообразования в непосредственной близости к обшивке корпуса, в том числе с целью оптимизации формы судовых обводов.

Координаты судна по отношению к воде — Рис. 2 Система корабельных координат

Интеграл Мичелла содержит сложные сингулярные и осциллирующие подынтегральные выражения, которые без применения специальных аппроксимационных и асимптотических методов оказываются недоступными для уверенных вычислений на современных цифровых ЭВМ.

Существуют различные методы получения интеграла для расчета волнового сопротивления по Мичеллу с включением нелинейных моделей и особенностей волнообразования, которые пока не будут рассматриваться здесь. Основная цель рассмотрения линейной теории волнового сопротивления состоит в поиске наглядной геометрической и физической интерпретации вычислительных процессов, моделирующих корабельное волнообразование. Понимание основы и сути моделируемых явлений необходимо для построения уточненных полуэмпирических моделей и формул, учитывающих свойства реальных корабельных волн, что очень важно для практики, так как процессы волнообразования, равно как и процессы вихреобразования, относятся к фундаментальным и неосвоенным математическим моделям нестационарной гидромеханики.

Волнообразование за судном — Рис. 3 Характерная картина волнообразования при равномерном и прямолинейном движении судна по спокойной поверхности воды. (λ/L) = 0,5; V = 13 узлов. За кормой отчетливо просматривается система поперечных корабельных волн, ограниченная треугольником свободных расходящихся волн

Традиционно корабельные волны разделяются на поперечные и расходящиеся, что соответствует наблюдениям за внешним проявлением волнообразования при движении корабля. В непосредственной близости от корпуса корабля такое разделение корабельных волн на поперечные и расходящиеся весьма условно, однако оно вполне справедливо при рассмотрении особенностей распространения волн на большом удалении от корпуса, где поперечные волны ведут себя как вынужденные, а расходящиеся – как свободные, с ярким проявлением особенностей их групповой структуры.

В случае хорошо обтекаемого корпуса справедливо также допущение о стационарности формы волнового поля относительно движущегося корабля, что является ключевым упрощением особенностей реального корабельного волнообразования, используемого при теоретическом изучении волнового сопротивления его движению.

Плоская модель поперечных волн

Плоская модель корабельного волнообразования рассматривает интерференцию зарождающейся поперечной волны при прохождении потоков воды вдоль корпуса корабля и позволяет сделать самые первые оценки процессов зарождения корабельных волн.

Вне зависимости от формы корпуса за Корпус судна и предъявляемые к нему требованиякормой корабля образуется регулярная система поперечных корабельных волн, длина и период которых строго связаны со скоростью хода корабля:

λ_{w} = {V_{0}}^{2} \cdot 2 π / g;

τ_{w} = V_{0} \cdot 2 π / g .

Такое свойство системы поперечных волн позволяет довольно просто оценить реальную скорость хода корабля V, воспользовавшись визуальным соотношением расстояния между гребнями волн λ и длиной корабля

L \div (λ / L) = V^{2} / L \cdot 2 π / g,

откуда:

V \approx 1, 25 \cdot \sqrt{(λ / L) \cdot L} = 1, 25 \cdot \sqrt{λ} [m / c] .

В качестве безразмерного и независимого от длины корпуса параметра, характеризующего волнообразование на различных скоростях хода корабля, принято число Фруда:

F n = V / \sqrt{g \cdot L},

которое также связано с отношением длины поперечной волны к длине корпуса корабля:

(λ / L) = 2 π \cdot {Fn}^{2}

или

F n = \sqrt{\frac{λ}{2 π \cdot L}} \approx 0, 4 \cdot \sqrt{(λ / L)}

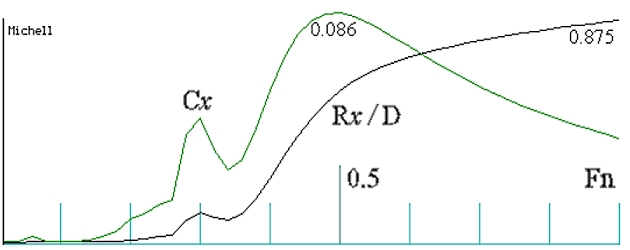
Теоретически получается, что при длине поперечной корабельной волны, строго равной длине корпуса, может ожидаться наиболее благоприятная интерференция носовой и кормовой систем волн. Однако, изучение волновых процессов на практике показывает, что реальная волнообразующая длина корпуса всегда меньше, отчего искомый минимум волнового сопротивления уменьшается со значения Fn ≈ 0,4 до Fn ≈ 0,32-0,36, соответствующий рост волнообразования на скорости хода при Fn ≥ 0,57 обычно соотносят с Fn ≥ 0,5.

Предлагается к прочтению: Эффект присасывания при маневрировании судна в узкостях

К сожалению, величину волнообразующей длины корпуса довольно трудно установить однозначно, так как она зависит от изменения скорости хода корабля. Рис. 4 иллюстрирует интерференцию корабельных волн, условно зарождающихся на форштевне и ахтерштевне. В реальности же носовая подпорная волна зарождается в районе скулы, а снижение уровня воды в кормовой части корпуса проявляется в районе кормовой раковины и винторулевого комплекса, что обязательно необходимо учитывать при проектировании обводов корпуса. Необходимо также отметить, что на больших скоростях хода, при Fn > 0,4, в кормовой части корпуса образуется довольно сильное разрежение, которое при совместном действии с носовой подпорной волной приводит к сильному ходовому дифференту корабля на корму.

График волнообразования от скорости судна — Рис. 4 Характерные режимы волнообразования при различных скоростях движения судна

При дальнейшем увеличении скорости судно как бы начинает толкать перед собой «гору» воды, отчего быстро растет как интенсивность корабельного волнообразования, так и волновое сопротивление движению корабля. Однако эффект столь неблагоприятной интерференции носовой и кормовой систем корабельных волн может быть частично скомпенсирован специальной формой корпуса, ключевым элементом которой должен являться завал бортов на уровне действующей ватерлинии в средней части корпуса.

Для оценки сопротивления воды движению корабля обычно пользуются величиной коэффициента сопротивления С_W, отнесенного к квадрату скорости и площади смоченной поверхности (подводной части) корпуса.

R_{W} = C_{W} \cdot \frac{ρ \cdot V^{2}}{2} \cdot S,

где:

R_W – волновое сопротивление (Н);
ρ – плотность жидкости (кг/м³);
V – скорость хода судна (м/с);
S – площадь смоченной поверхности корпуса (м²).

Для оценки формы корпуса и волнового сопротивления иногда удобно пользоваться размерной величиной удельного сопротивления, отнесенного к водоизмещению корабля: R_W/D, где D – водоизмещение (кг). Если тихоходное судно (Fn ≤ 0,2) обладает хорошо обтекаемым корпусом, то его волновое сопротивление будет пренебрежимо малым.

График оценки расчетных кривых волнового сопротивления — Рис. 5 Характерная форма и числовые оценки расчетных кривых волнового сопротивления для хорошо обтекаемого корпуса корабля. Сx – коэффициент сопротивления; Rx/D – удельное сопротивление. Хорошо видны экстремумы сопротивления при неблагоприятной интерференции носовой и кормовой систем поперечных волн, возникающей на скоростях хода при Fn ≈ 0,5 (0,57) и Fn ≈ 0,3 (0,33). Полного гашения волнового сопротивления при Fn ≈ 0,26 (0,28) и Fn ≈ 0,35 (0,4) не происходит, что объясняется затратами энергии на зарождение системы расходящихся волн

Расходящиеся от корпуса корабельные волны проявляются как свободные волны на глубокой воде, они обладают как ярко выраженными дисперсионными свойствами (увеличение длины и периода волны при ее свободном распространении), так и групповыми свойствами (скорость распространения волнового возмущения в два разе меньше скорости движения фронта каждой из волн, образующих волновой пакет).

Угол расхождения пакетов корабельных волн не зависит от скорости хода корабля и является ярким подтверждением того, что пакеты свободных расходящихся волн движутся со скоростью в два раза меньшей, чем гребни составляющих их волн. Этот угол составляет 20°42’. В 1887 Кельвином получено также решение для корабельных волн от точечного источника на поверхности воды, угол разворота гребней расходящихся волн составил 35°16’. Любопытно, что Кельвин также использовал эвристический аргумент, основанный на групповой скорости волн.

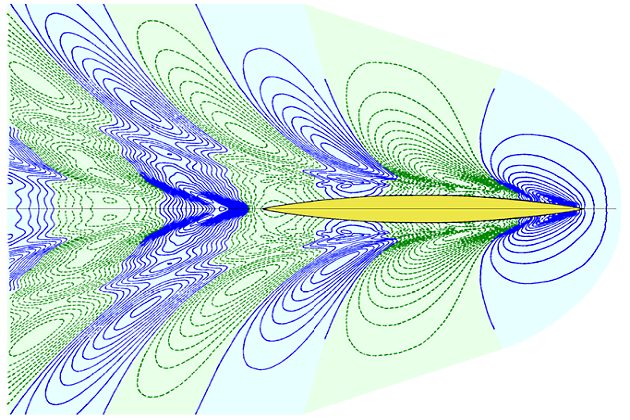
Схема корабельного волнообразования — Рис. 6 Картина корабельного волнообразования в непосредственной близости от обшивки корпуса. Скорость хода Fn = 0,316

К расходящейся корабельной волне неприменимы методы интерференционного анализа. Единственный способ минимизации энергии расходящейся волны – это построение таких обводов корпуса, которые способствовали бы ее гашению непосредственно в момент зарождения. Обычно это достигается «закручиванием» набегающего потока под днище корпуса в тот момент, когда вихрь зарождающейся волны начинает отрываться от корпуса. Привычные скуловые обводы в носовой и кормовой частях корпуса вполне успешно могут решить задачу минимизации таких расходящихся волн.

Предварительный обзор особенностей корабельного волнообразования можно закончить двумя заключениями, имеющими прямое отношение как к минимизации волнового сопротивления, так и к уменьшению интенсивности силового взаимодействия корпуса корабля с внешним морским волнением:

Минимизация интенсивности поперечных корабельных волн на всех скоростях хода, включая диапазон их длин, превышающих длину корпуса, выполненная на всех осадках, которые возникают при Качкавертикальной качке корабля, одновременно является условием снижения его килевой качки при движении на волнении.
Аналогичная минимизация интенсивности расходящихся корабельных волн будет способствовать снижению бортовой качки, возникающей под воздействием штормовых волн в широком диапазоне периодов.

Высказанные заключения являются всего лишь проектными условиями, выполнение которых безусловно необходимо, но отнюдь не достаточно для реального улучшения штормовой мореходности корабля. К примеру, в практике кораблестроения известны примеры использования судовых обводов в форме «двойного клина». «Двойной клин» раздвигает встречный поток в боковые стороны, а под широкий кормовой подзор поток воды поступает из-под днища корпуса. Такие обводы формально приводят к заострению оконечностей, что теоретически влияет на корабельное волнообразование как удвоение длины корпуса, что заметно снижает волновое сопротивление движению корабля. Однако в отличие от традиционного корабля с симметричным относительно мидель-шпангоута обводами, в штормовых условиях корпус в виде «двойного клина» может стать источником серьезнейшей опасности.

Рис. 7 Крейсер «Москва» имеет обводы в форме двойного клина и сильный развал бортов вдоль всего корпуса корабля

Попытка использовать интеграл Мичелла в качестве функционала для выбора оптимальной формы корпуса не приводит к сколь-нибудь однозначным решениям, так как при математической недостаточности внешних условий для формализации судовых обводов получается множество частных решений, иногда курьезных, дающих в качестве оптимальной формы корпуса как «двойной клин», так и различные пульсирующие формы ватерлиний с гиперболизованными размерами носовых бульбов.

Пройдите этот тест полностью на нашем сайте, по ссылке: Тренировочный Delta тест по должности матрос (квалифицированный)

Но все же решение Джона Генри Мичелла представляет не только исторический интерес. Детальный анализ промежуточных выкладок при получении интеграла Мичелла позволяет очень глубоко понять суть процессов, происходящих как при формировании корабельных волн, так и при воздействии штормовых волн на корпус корабля.

В настоящее время существуют и другие математические и вычислительные методы для получения результатов, аналогичных Мичелловским, но это уже тема других работ по гидромеханике корабля, в том числе требующих множества новых пионерских исследований.

Читайте также: Постановка судна на якорь

Мы проводим изучение волновых процессов в контексте конца XIX века. Наша цель – объединить математические методы того времени с современными численными методами для глубокого понимания физики волнообразования и точного расчета волнового сопротивления корабля.

Теория волнового сопротивления Мичелла

Основная цель рассмотрения линейной теории волнового сопротивления состоит в поиске наглядной геометрической и физической интерпретации вычислительных процессов, моделирующих корабельное волнообразование.

Это необходимо также для поиска аналитических решений, корректных асимптотических приближений и эмпирических экстраполяций при практическом моделировании процессов взаимодействия корабля и морского волнения.

Оригинальный интеграл Мичелла вполне пригоден для использования в областях разрывных или сильноосциллирующих численных решений, нежели любые его искусственные усложнения с помощью любых нелинейных добавок.

Волнообразующий потенциал

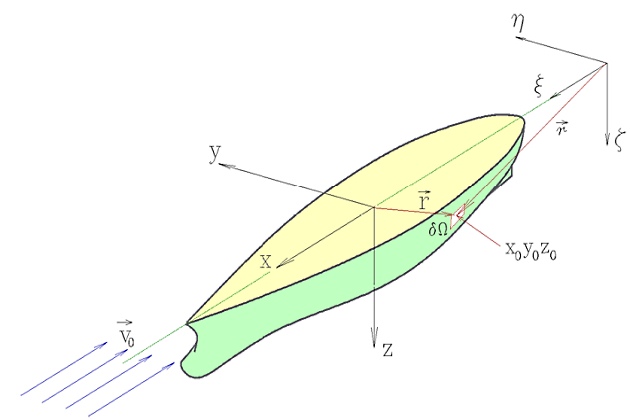
Вывод расчетных формул классической теории волнового сопротивления корабля основывается на анализе скалярных функций векторного аргумента или «теории потенциала»:

Ф (x, y, z) = Ф (r) .

Решение ищется в виде поля скалярного потенциала скорости:

\frac{\partial Ф}{\partial r} = V,

удовлетворяющего уравнению Лапласа:

(\frac{\partial}{\partial r} \frac{\partial Ф}{\partial r}) = 0 .

Принятые обозначения формулируются в курсе Физики А. В. Астахова и Ю. М. Широкова:

$(\frac{\partial \vec{φ}}{\partial \vec{r}}) \equiv d i v \vec{φ};$
$(\frac{\partial \vec{φ}}{\partial \vec{r}}) \equiv r o t \vec{φ};$
$(\frac{\partial φ}{\partial \vec{r}}) \equiv g r a d φ .$

С помощью стандартного аддитивного разложения потенциала мы проводим изучение волновых процессов, вызванных движением корабля, для более глубокого понимания этого явления:

Ф (\vec{r}) = - V_{0} x + φ_{0} (\vec{r}) + φ * (\vec{r}) [c^{- 1}]; Ф о р м . 2

где:

V₀x – потенциал набегающего потока (Форм. 2);

φ_{0} = \frac{1}{4 π} \int_{Ω} \frac{Q (\vec{r_{0}})}{|\vec{r}|} d Ω = \frac{V_{o}}{4 π} \int_{Ω} \frac{q (\vec{r_{0}})}{|\vec{r}|} d Ω Ф о р м . 3

*потенциал обтекания корпуса при отсутствии возмущения свободной поверхности;

φ * = \frac{V_{0}}{4 π} \int_{Ω} q \cdot G (\vec{r}) d Ω Ф о р м . 4

*потенциал, учитывающий взаимодействие корпуса со свободной поверхностью жидкости.

Образование волн от точечного источника — Рис. 8 Движение точечного источника (шарика) по поверхности воды.
Образуются расходящиеся корабельные волны, длина которых соизмерима с диаметром шарика. Поперечные же волны, скорость которых соответствует скорости движения источника возмущения, практически не образуются, и просматриваются только один раз в виде одиночного всплеска в следе за шариком. Расходящиеся гравитационные волны постоянно изменяют фазу своего переднего фронта, показывая, что волновое возмущение в целом движется в два раза медленнее, чем фронт одиночной трохоидальной волны. Впереди основных волн выстраиваются фронты коротковолновых капиллярных возмущений, скорость распространения которых выше, чем у гравитационных волн

Величина Q₀ = V₀ · q соответствует интенсивности распределенных по поверхности корпуса источников, моделирующих условие непротекания при движении корпуса корабля в безграничной жидкости.

Q = V_{0} \cdot \frac{\partial f}{\partial x} (м / с) Ф о р м . 5

где:

f(x, z) – ординаты корпуса.

Использование функции Q в интеграле (формула 4) накладывает условие малости искажений формы свободной поверхности вблизи корпуса.

Под функцией G будем понимать потенциал некоторого единичного возмущения свободной поверхности от источника, лежащего на элементарной площадке, расположенной на Принципы проектирования конструкций корпуса суднаповерхности корпуса корабля.

Тогда функция

V_{0} q (\vec{r_{0}}) \cdot G (\vec{r} \vec{r_{0}})

будет определять потенциал течения, обусловленного влиянием источников, распределенных по всей поверхности корпуса, на свободную поверхность пересекаемой им тяжелой жидкости.

Аддитивное разложение потенциала можно считать справедливым, если рассматриваются волновые движения, вызванные идущим кораблем, вдали от его корпуса, где потенциал φ₀ стремится к нулю и не оказывает влияния на динамические граничные условия на свободной поверхности. Соответственно влияние функции G должно быть настолько малым, чтобы ей можно было пренебречь при выполнении условий непротекания на поверхности корпуса в решении для потенциала φ₀.

Сформулируем исходные уравнения и граничные условия, чтобы произвести изучение волновых процессов:

Ф (x, y, z) = Ф (\vec{r}) Ф о р м . 6

потенциал течения в системе координат, связанной с корпусом:

\frac{\partial}{\partial \vec{r}} \frac{\partial Ф}{\partial \vec{r}} = 0 Ф о р м . 7

уравнение Лапласа, как условие существования потенциала и достаточное условие для обеспечения неразрывности жидкости;

{\vec{V}}_{n} = \frac{\partial Ф_{0}}{\partial \vec{n}} = 0 или (\frac{\partial Ф}{\partial \vec{r}} \cdot \vec{n}) = V_{0} \cdot \cos (\hat{n, x}) Ф о р м . 8

условие непротекания на поверхности корпуса для потенциала:

Ф_{0} = - V_{0} x + φ_{0}

\frac{\partial 2 φ *}{\partial x^{2}} + \frac{g}{{V_{0}}^{2}} \frac{\partial φ *}{\partial z} = 0, при z = 0 Ф о р м . 9

линейное динамическое граничное условие на свободной поверхности, которое получается из интеграла Эйлера по условию постоянства давления вдоль линии тока, лежащей на свободной поверхности:

ς_{w} = \frac{V}{g} \frac{\partial φ *}{\partial x}, при z = 0 Ф о р м . 10

описание профиля волны. Следует из формулы 9:

\begin{matrix} φ_{0} = 0 : x \to - \infty \\ φ_{0} = φ * = 0 : x \to + \infty \\ φ_{0} = φ * = 0 : z \to \infty \end{matrix} Ф о р м . 11

условия на бесконечности.

Волнообразующий потенциал G должен обеспечивать свойство симметрии относительно диаметральной плоскости корпуса, что может являться следствием определения распределенных источников Q(x, z) и считаться справедливым только для узкого корпуса. Такое же допущение делалось Мичеллом при выводе интеграла (формула 1).

Так же как Мичелл используем интенсивность распределенных источников в форме:

q ≅ \frac{\partial f}{\partial x},

а волнообразующий потенциал как:

φ * = \frac{V_{0}}{4 π} \cdot \int_{Ω} q G d Ω Ф о р м . 12

Граничные условия и интегральное преобразование Фурье

Предположим, что граничное условие на свободной поверхности удовлетворяется для каждого элемента свободной поверхности dΩ, содержащего волнообразующий потенциал q · G. Это будет означать также удовлетворение условий малости возмущений свободной поверхности от единичного волнообразующего потенциала G, действующего с элементарной площадки dΩ, в то время как суммарное влияние всего корпуса может быть достаточно большим.

Предлагается к прочтению: Центр вращения и его перемещение

Будем искать решение для G в форме отраженного через свободную поверхность стока, то есть в виде потенциала от зеркально отраженного источника с обратным знаком. Тогда функция G не имеет особенностей и непрерывна во всей области z ≥ 0, кроме случая, когда z = z₀ = 0, то есть на свободной поверхности и когда волнообразующий источник находится на этой же поверхности.

Пусть:

r^{'} = \frac{G = - \frac{1}{r^{'}};}{\sqrt{{(x - x_{0})}^{2} + {(y - y_{0})}^{2} + {(z - z_{0})}^{2} .}} Ф о р м . 13

Используем интегральное преобразование Фурье для функций трех переменных:

f (x, y, z) = \int \int \int_{0}^{\infty} A (P, Q, R) e^{P (x - x_{0}) + Q (y - y_{0}) + R (z - z_{0})} d P d Q d R . Ф о р м . 14

Удовлетворяя уравнение Лапласа (формула 7) для функции

$f (r^{'})$

, получим:

R = i \sqrt{P^{2} + Q^{2}} .

После введения обозначений:

P = k \cdot \cos ϑ;

Q = k \cdot \sin ϑ,

возможен переход к представлению источника 1/r^′ в виде интеграла Фурье, зависящего от двух параметров:

\begin{matrix} G = - \frac{1}{2 π} \int_{- π}^{π} \int_{0}^{\infty} e^{k \cdot (- z - z_{0} + i ω)} d k d ϑ; \\ ω = (x - x_{0}) \cdot \cos ϑ + (y - y_{0}) \cdot \sin ϑ + (σ - k v_{0} \cos ϑ) \cdot t . \end{matrix} Ф о р м . 15

В формуле 15 последнее слагаемое для ω взято из Дж. Ньюмена, и отвечает за волны нестационарные по отношению к корпусу.

По физическому смыслу – экспонента под интегралом в формуле 15 описывает некие плоские волны в связанной с корпусом системе координат {x, y, z}, эти волны стационарны относительно движущего корпуса и ориентированы в направлении угла λ.

Пусть:

G * = e^{k \cdot (- z - z_{0} - i w) .} Ф о р м . 16

Подставляя G* в динамическое граничное условие на свободной поверхности:

\frac{\partial^{2} G *}{\partial x^{2}} + \frac{g}{{V_{0}}^{2}} \frac{\partial G}{\partial z} = 0,

при z = 0.

Тогда:

{(i k \cos ϑ)}^{2} + k \cdot \frac{g}{V_{0}} = 0, и k = \frac{g}{{V_{0}}^{2} \cos ϑ} [m^{- 1}] . Ф о р м . 17

После установления зависимости между параметрами k и ϑ в интеграле (15), можно избавиться от одного параметра интегрирования.

С этой целью применим интегрирование по частям:

\int_{- π}^{π} \int_{0}^{\infty} G * d k d ϑ = \int_{- π}^{π} (G * k - \int_{- 0}^{k - \infty} k d G *) d ϑ .

При изменении порядка интегрирования во втором интеграле:

\int_{k - 0}^{k - \infty} \int_{- π}^{π} k d ϑ d G * = \int_{k = 0}^{k = \infty} \int_{- π}^{π} \frac{g d ϑ}{{V_{0}}^{2} \cos^{2} ϑ} d G *,

внутренний интеграл, по параметру ϑ обращается в нуль:

\int_{k = 0}^{k = \infty} \int_{- π}^{π} \frac{g d ϑ}{{V_{0}}^{2} \cos^{2} ϑ} d G * = \frac{g}{{V_{0}}^{2}} \tan ϑ \begin{matrix} π \\ - π \end{matrix} = 0 .

Тогда волнообразующий потенциал G может преобразуется к следующему виду:

G = \int_{- π}^{π} G * k d ϑ = - \frac{1}{2 π} \int_{- π}^{π} k \cdot e^{k \cdot (- z - z_{0} + i ω)} d ϑ, при z = 0, Ф о р м . 18

где:

$k = \frac{g}{{V_{0}}^{2} \cos^{2} ϑ};$
$ω = (x - x_{0}) \cdot \cos ϑ + (y - y_{0}) \cdot \sin ϑ + (σ - k V_{0} \cdot \cos ϑ) \cdot t .$

Описание единичного волнообразующего источника

Воспользуемся описанием профиля корабельной волны (формула 10) для получения общей волновой картины от движущегося источника, который описывается только что полученным интегралом (формула 18):

r_{w} = k \frac{V_{0}}{2 π \cdot g} \frac{\partial G *}{\partial x} = \frac{1}{2 {πV}_{0} \cos^{2} ϑ} \frac{\partial G *}{\partial x}; Ф о р м . 19

r_{w} = \frac{i g}{2 π {V_{0}}^{3} \cos^{3} ϑ} e^{k \cdot (- z_{0} + i ω)} . Ф о р м . 20

Аппликата свободной поверхности для заданной частоты формы:

ζ_{w} (ϑ, x, y) = R e ({\vec{r}}_{w}) = \frac{g}{2 {πV}_{0}^{3} \cos^{3} ϑ} e^{- k z_{0}} \sin (k ω) . Ф о р м . 21

Аппликата волновой поверхности от возмущения, вызванного элементарной площадкой Наружная обшивка и подкрепляющий ее наборсудовой обшивки:

r_{w} = i \frac{g}{2 {πV}_{0}^{3}} \int_{- π}^{π} e^{k (- z_{0} + i ω)} \frac{d ϑ}{\cos^{3} ϑ};

ζ_{w} = \frac{g}{2 {πV}_{0}^{3}} \int_{- π}^{π} e^{- k z_{0}} \sin (k ω) \frac{d ϑ}{\cos^{3} ϑ} .

Теперь необходимо воспользоваться требованием стационарности картины волнообразования относительно системы координат, связанной с корпусом корабля.

1 Если σ связана с k дисперсионным соотношением:

σ^{2} = g k;

σ = \frac{g}{V} = \frac{g}{V_{0} \cos ϑ}, Ф о р м . 22

то в функции G* пропадает величина:

2 Скорость движения излучаемой корпусом волны не может превышать скорости хода корабля: V ≤ V₀.

Тогда, если V = V₀ cos ϑ, что следует из (формула 17), то: V = 0 соответствует ϑ = ±π/2; V = V₀ – соответствует ϑ = 0 или ϑ = ±π.

Геометрическое толкование уравнения 21 изложено в книге Г. Е. Павленко, где показывается система трехмерных свободных волн, распространяющихся с фазовой скоростью V = V₀ cos ϑ в направлении угла ∠ ϑ.

Исходя из анализа рис. 8, будем считать возможным искусственное ограничение интервала интегрирования в определении волнообразующего потенциала (формула 18), до: ∠ ϑ∈[-π/2 ÷ -π], тогда:

G = \frac{1}{λ} \int_{- \frac{π}{2}}^{\frac{π}{2}} k \cdot e^{k \cdot (- z - z_{0} + i ω)} d ϑ, Ф о р м . 23

где:

$λ = \frac{2 π}{k},$
$k = \frac{g}{{V_{0}}^{2} \cos^{2} ϑ},$
$ω = (x - x_{0}) \cdot \cos ϑ + (y - y_{0}) \cdot \sin ϑ .$

Таким образом, из рассмотрения исключаются свободные волны, которые допускаются динамическим граничным условием (формула 9). Это именно те волны, которые можно интерпретировать как внешние и поглощаемые корпусом корабля при взаимодействии с морским волнением. Если корпус корабля способен поглощать внешние волны, то их энергия уходит на усиление качки и рыскания. Из указанных логических заключений следует вывод:

Изучение волновых процессов позволяет сделать вывод: если форма корпуса корабля не оптимизирована под различные скорости, то его мореходность в реальных морских условиях будет значительно снижена.

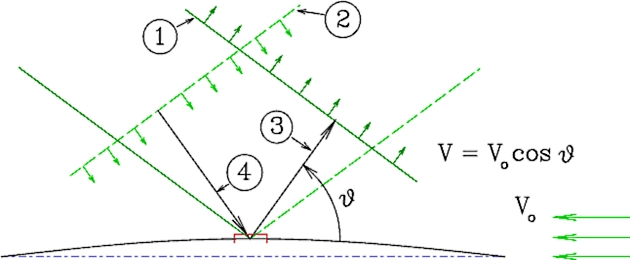
Схема отраженного излучения корабельных волн — Рис. 9 Полная схема отраженного излучения корабельных волн и положение их фронтов.
① – фронт расходящейся волны (излучаемой), движущейся со скоростью V = V₀cos ϑ; ② – положение фронта волны, приближающейся к корпусу корабля, которая также является стационарной в связанной системе координат, но не учитывается в наших динамических уравнениях; ③ – направление излучения расходящейся корабельной волны; ④ – направление подхода как бы внешней волны, у которой угол ∠ϑ лежит в диапазоне: ∠ϑ∈[-π/2 ÷ -π] или ∠ϑ∈[π ÷ π/2]

Описание корабельного волнообразования

По физическому смыслу функция:

G * \frac{k}{2 π} = \frac{1}{λ} e^{k (- z - z_{0} + i ω)} = G * * Ф о р м . 24

определяет потенциал плоской волны, которую мы можем наблюдать на некотором удалении от единичного источника. Так как амплитудным множителем перед G** стоит малая величина dΩ, то для подынтегральной функции эти волны можно считать малыми.

φ * (ϑ) = \frac{V_{0}}{4 π λ} \int_{Ω} q (x, z) \cdot e^{k (- z - z_{0} + i ω)} d Ω Ф о р м . 25

φ * = \int_{- \frac{π}{2}}^{\frac{π}{2}} φ * (ϑ) d ϑ .

Потенциал φ*(ϑ) описывает волны конечной амплитуды, его получения связано с интегрированием по всей поверхности корпуса (формула 25).

Рассмотрим механизм сложения корабельных волн, стационарных относительно движущегося корабля и имеющих заданную частоту формы.

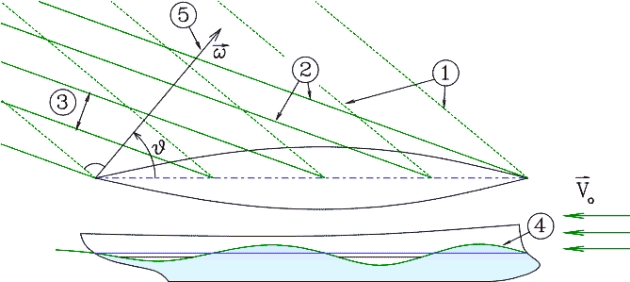
График расходящихся корабельных волн — Рис. 10 Две системы расходящихся от корпуса корабельных волн.
1-я имеет фазовые характеристики, с частотой формы k = f(ϑ); 2-я система волн формируется при их преобразовании к групповой структуре.
① – положение фронтов волн, имеющих фазовую структуру и движущихся со скоростью V = V₀ cosϑ; ② – положение фронтов расходящейся системы корабельных волн конечной амплитуды, полученных сложением элементарных волн от всех участков обшивки корпуса и распространяющихся с групповой скоростью для пакетов волн на глубокой воде; ③ – выделенные полосы на поверхности жидкости, в которых существуют пакеты волн с данной фазовой частотой формы; ④ – отметка волновой поверхности на диаметральной плоскости корпуса корабля; ⑤ – направление, по которому наблюдается распространение фазовых профилей волн

Для получения реальной картины корабельного волнообразования необходимо учитывать, что излучаемые корпусом корабля волны объединяются в пакеты, которые движутся с групповой скоростью V_g = 1/2V. При восстановлении волнового поля необходимо производить сложение пакетов волн во всем спектре частот:

k = \frac{g}{{V_{0}}^{2} \cos^{2} ϑ} + ϑ \in [0 \pm \frac{π}{2}] .

Рассмотрим поле скоростей в плоскости распространения фазовых волн. Пусть излучение ведется только с одной площадки на поверхности корпуса, тогда:

V_{z} = V_{0} q \cdot R e (\frac{\partial G * *}{\partial z}) = V_{0} q \cdot \frac{k}{λ} e^{- k (z + z_{0})} \cos (k ω); Ф о р м . 26

V_{ω} = V_{0} q \cdot R e (\frac{\partial G * *}{\partial ω}) = V_{0} q \cdot \frac{k}{λ} e^{- k (z + z_{0})} \sin (k ω); Ф о р м . 27

Аналогичный результат будет получен дифференцированием по времени положения частиц жидкости заданных формулами 19 и 20:

\vec{V} (ϑ) = \frac{\partial \vec{r_{w}}}{\partial \vec{r}} \frac{\partial \vec{r}}{\partial t} \cos ϑ = \frac{\partial r_{w}}{\partial \vec{r}} V_{0} \cos ϑ . *

*В соответствии с принятыми обозначениям:

$\frac{\partial r_{w}}{\partial \vec{r}} \equiv g r a d (r_{w});$
$[\frac{\partial \vec{V}}{\partial \vec{r}}] = r o t (\vec{V}) .$

Здесь учтено, что выражение (формула 19) определяет отклонение частиц жидкости от невозмущенного состояния, в проекции на плоскость {x : z}, в системе координат, связанной с подвижным корпусом.

Как известно, формулы для описания траекторий частиц жидкости (формулы 26, 29), являются также определениями для плоских трохоидальных волн конечной амплитуды, которые называют волнами Герстнера. Это справедливо, если считать V как локальную скорость частицы жидкости в Лагранжевом представлении течения.

Основные свойства волнового поля

Рассмотрим основные свойства корабельного волнообразования на основе полученного поля скорости.

1 Частицы жидкости участвуют в движении по круговым траекториям со скоростью, зависящей от аппликаты z:

V_{p} = V_{0} q \frac{k}{λ} e^{- k (z + z_{0})} . Ф о р м . 28

Угловая скорость:

ω = σ = \frac{g}{V_{0} \cos ϑ} .

Локальный радиус траектории:

r_{1} = \frac{V_{p}}{σ} = V_{0} \cdot V \cdot q \cdot \frac{k}{g λ} e^{- k (z + z_{0})} Ф о р м . 29

2 Пользуясь условием стационарности рассматриваемого потока жидкости, учтем, что линии тока и траектории частиц совпадают. При переходе же к Лагранжевым координатам, где всегда рассматриваются траектории частиц жидкости, ранее полученные уравнения (формулы 26-27) будут относиться также и к трохоидальным волнам Герстнера.

Подмена кинематической системы отсчета никак не отражается на использовании предположений о линейности волновых свойств потока, по крайней мере в пределах малых частиц жидкости, а сохраняя неизменным дисперсионное соотношение σ² = g · k, соответственно сохранится и большинство выводов из линейной теории волн (волн на свободной поверхности под действием сил гравитационной природы).

Как показано в работе А. Н. Шебалова, такое трактование поля скорости (формула 28) делает его вихревым:

|[\frac{\partial \vec{V}}{\partial \vec{r}}]| = - \frac{2 σ k^{2} R^{2} e^{2 k z_{0}^{'}}}{1 - k^{2} r^{2} e^{2 k z_{0}^{'}}};

R = V_{0} \cdot V \cdot q \cdot \frac{k}{g λ} .

Знак завихренности говорит о том, что в случае вязкой жидкости волны конечной амплитуды (волны Герстнера) будут угасать со скоростью, пропорциональной квадрату амплитуды.

Для получения волновой поверхности и поиска максимальной амплитуды волны в функции от ее «частоты формы» запишем выражение для радиусов траекторий частиц жидкости (формула 20) в следующем виде:

\vec{r_{w}} = \frac{1}{2} A \cdot e^{- k (z + z_{0})} .

В соответствии с трохоидальной теорией, локальная траектория частиц жидкости описывается дугой окружности с радиусом r_w, зависящим от текущей аппликаты: z, для данной частицы жидкости z_w и от амплитуды волны на поверхности:

A = \frac{2}{λ} \frac{q}{\cos ϑ} .

Скорость движения элементарных частиц определяется через произведение частоты колебаний и радиуса дуги траектории:

V_{r} = σ \cdot r = V_{0} q \frac{k}{λ} e^{- k (z + z_{0})} = \frac{q}{V} \frac{A}{2} e^{- k (z + z_{0})} .

Скорость движения частиц жидкости возрастает с уменьшением глубины z. На вершине волны эти частицы перемещаются с максимальной скоростью в направлении движения ее гребня.

Допустим, что скорость частиц жидкости не должна превышать скорости распространения корабельной волны, так как это является условием разрушения волнового гребня. В этом случае максимальная скорость V = V_r:

\frac{q}{{V_{0}}^{2}} \frac{A}{2} e^{- k z} = 1 = \frac{k A}{2} e^{- k z .}

В предельном случае трохоидальная теория, путем численного (приближенного) решения полученного соотношения, дает константу: A · k ≈ 1,134, при: z = A/2, или с учетом снижения амплитуды на подошве волны получается: λ/h ≈ 8,38, что соответствует прогрессивной волне с интенсивно разрушающимся гребнем.

Полученное соотношение определяет весьма важное свойство волн Герстнера, как реальных вихревых волн конечной амплитуды, и должно быть использовано при физической интерпретации характера волнообразования от всего корпуса корабля.

Формула Мичелла для волнового сопротивления

При построении формулы для волнового сопротивления корабля на основе линейной теории волн, которая подразумевает существование потенциалов (формула 26):

Ф = - V_{0} x + φ_{0} + φ *,

будем пользоваться потенциалом G** (23), который описывает малые возмущения, вносимые в поток с элементарной площадки на поверхности корпуса: dΩ. Основываясь на энергетических зависимостях линейной теории волн, определим энергию, распределенную по взволнованной поверхности моря, которая приходится на образование одной волны с длиной λ:

E = \frac{1}{2} ρ g A^{2} λ = {πρV}_{0}^{2} A^{2} \cos^{2} ϑ, (Н / м) Форм . 30

Далее учтем, что скорость переноса энергии определяется через групповую скорость пакета, состоящего из фазовых волн:

V_{g} = \frac{1}{2} V = \frac{1}{2} V_{0} \cos ϑ

(для глубокой воды). Излучение корабельных волн ведется в диапазоне:

λ \in [0 \div λ = 2 π \frac{{V_{0}}^{2}}{0}] .

Изучение волновых процессов в условиях стационарного движения корабля приводит к выводу о постоянстве длины волны на диаметральной плоскости. Это математически выражается в равенстве числа периодов волн любой частоты, укладывающихся на длину корпуса.

Вид корабельного волнообразования — Рис. 11 Картина корабельного волнообразования обладает свойством неподвижности относительно идущего с постоянной скоростью корабля, при этом поперечные волны в следе корабля обладают строгой регулярностью, а ограничивающие их расходящиеся волны имеют ярко выраженную групповую структуру с обрушающимися гребнями и частично стоячими фронтами одиночных волн

Мощность, затрачиваемая кораблем на образование волн, излучаемых в направлении ∠ϑ, выражается следующим уравнением:

P (ϑ) = \frac{π}{2} ρ {V_{0}}^{3} A^{3} \cos^{3} ϑ : (\times δ ϑ) Ф о р м . 31

Волновое сопротивление от всего спектра корабельных волн:

R_{x} = \frac{π}{2} ρ {V_{0}}^{2} \int_{- \frac{π}{2}}^{\frac{π}{2}} A^{2} (ϑ) \cos^{3} ϑ d ϑ . Ф о р м . 32

Полученный интеграл, известный как формула Хавелока, является основой для расчета волнового сопротивления корабля в рамках линейной теории волн. Амплитудную функцию A(ϑ) можно получить из линейного граничного условия на свободной поверхности жидкости (формула 10), применяя его к выражению для потенциала от всего корпуса (формула 25), подобно тому, как это делалось при получении формул для линий тока и аппликат частиц жидкости (формулы 20 и 21).

r_{w} = \frac{V_{0}}{g} \frac{φ * (ϑ)}{\partial x} : Ф о р м . 10 \Rightarrow 25

\begin{matrix} ζ_{w} (ϑ) = R e (r_{w}) \\ A (ϑ) = |r_{w}| \end{matrix}\} : Ф о р м . 20 \Rightarrow 21

r_{w} (ϑ) = \frac{i g}{2 {πV}_{0}^{2}} \int_{Ω} q \cdot e^{k (- z_{0} + i ω)} \cdot \frac{d Ω}{\cos^{3} ϑ} Ф о р м . 33

A (ϑ) = \frac{g}{2 {πV}_{0}^{2} \cos^{3} ϑ} | \int_{Ω} q \cdot e^{k (- z_{0} + i ω)} d Ω Ф о р м . 34

После подстановки амплитудной функции (формула 34) в формулу Хавелока (формула 32) может быть получен аналог интеграла Мичелла, который по сути является точной копией выражений, связанных с именем Н. Е. Кочина.

R_{x} = \frac{ρ g^{2}}{4 {πV}_{0}^{2}} \int_{0^{2}}^{π} | \int_{Ω} q e^{k (- z_{0} + i ω)} d Ω |^{2} \frac{d ϑ}{\cos^{3} ϑ}, Ф о р м . 35

$q (x, z) \approx \frac{\partial f (x, z)}{\partial x}; ω_{0} = x_{0} \cos ϑ (по Мичеллу);$
$ω_{0} = x_{0} \cos ϑ + y_{0} \sin ϑ (по Кочину);$

Переходя к физической и геометрической интерпретации полученных формул, сделаем повторение выкладок для получения амплитудной зависимости (формула 34), но уже с помощью геометрических построений на основе потенциала G**. Это позволит выявить области с нарушениями физических законов реального волнообразования, которые допускаются в случае прямого интегрирования формулы для вычисления волнового сопротивления корабля (формула 35).

Используем описание волнового поля в связанной с корпусом системе координат (формула 20):

r_{w} = \frac{i g}{2 {πV}_{0}^{3} \cos^{3} ϑ} e^{k \cdot (- z - z_{0} + i ω)} \cdot q \cdot V_{0} .

Амплитуда волны на свободной поверхности жидкости (z = 0), полученная в результате излучения с единичной площадки на обшивке корпуса, представляется как:

\begin{matrix} A (ϑ, x_{0}, y_{0}) = V_{0} q \cdot |r_{w}| \div d Ω = 1, \\ A (ϑ, x_{0}, y_{0}) = \frac{q (x_{0}, y_{0})}{λ \cos ϑ} e^{- k z} . \end{matrix} Ф о р м . 36

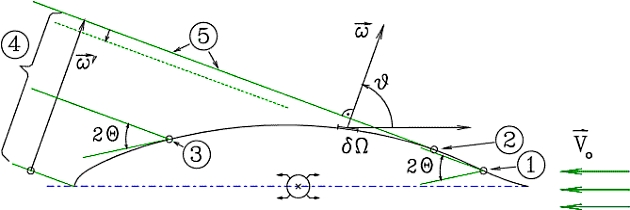
График фазовых волн — Рис. 12 Распространение и интерференция фазовых волн.
① – точка, в которой невозможно излучение носовой расходящейся волны с данной фазовой частотой; ② – точка, в которой корабельная волна отрывается от корпуса, до этой точки волны заданной частоты складываются в гребень; ③ – точка, в которой нарушается условие отхода кормовой расходящейся волны; ④ – линия, задающая направление распространения плоских фазовых волн, вдоль которой происходит интерференция этих волновых движений; ⑤ – фронт расходящейся корабельной волны с заданной фазовой частотой
$d Ω = d x_{0} d y_{0} \sqrt{1 + y_{x}^{2} + y_{z}^{2}}; Θ = \frac{π}{2} - ϑ - угол фронта$

Каждый элемент обшивки корпуса создает на свободной поверхности жидкости приращение амплитуды корабельной волны, фронт которой простирается вдоль линии, обозначенной на рис. 12 символом: ⑤ Цифры в кружочках, встречающиеся в тексте, означают позиции на рисунках.x, при этом фаза волны не меняется вдоль фронта, а амплитуда вычисляется по формуле 36. Поставим точки на линии

$ω^{'} : ④$

в соответствие с точками на поверхности корпуса:

ω^{'} = x_{0} \cos ϑ + y_{0} \sin ϑ, Ф о р м . 37

где учтено, что вектор

$ω^{'}$

может перемещаться вдоль фронта фазовой волны, а в формуле 37 он проведен из начала координат: (x = 0, y = 0).

Тогда, записывая результирующую амплитудную функцию для фазовых волн, как результат их интерференции на линии

$ω^{'}$

A (ϑ, z_{0}) = | \int_{ω Ⓒ} A (ϑ, x_{0,} y_{0}) \cdot e^{i k ω^{'}} d ω^{'} | . Ф о р м . 38

Интегрирование вдоль вектора

$ω^{'}$

усложняется тем, что направление

$ω^{'}$

задается фазовым углом ϑ. Воспользуемся тем свойством, что из условия стационарности картины волнообразования любая система фазовых волн единообразно проектируется на направление движения корабля. Можно изменить параметр интегрирования dω на dx, и при этом пересчет

$ω^{'}$

под экспонентой в формуле 37, будет правильно определять фазу волны в интерференционном интеграле (формула 38).

A (ϑ, z_{0}) = \frac{e^{- k z_{0}}}{λ \cos ϑ} |\int_{x_{0}} q (x_{0}, z_{0}) e^{i k ω^{'}} d x| . Ф о р м . 39

Амплитудная функция от всего корпуса:

A (ϑ) = \frac{1}{λ \cos ϑ} |\int \int_{Ω} q (x_{0}, y_{0}) e^{k (- z_{0} + i ω^{'})} d Ω| . Ф о р м . 40

ω^{'} = x_{0} \cos ϑ + y_{0} \sin ϑ;

d Ω = \sqrt{1 + y_{X}^{2} + y_{Z}^{2}} d x d z

Из геометрического построения формулы 40 можно отметить отсутствие корректности при включении в интерференцию волн, излучаемых с участка корпуса от форштевня до точки ② и от точки ② до ахтерштевня (по рис. 11). Получение же аналогичной формулы из волнообразующего потенциала: φ*(ϑ), ввиду формальности преобразований формул: 10 ⇒ 25 ⇒ 33 ⇒ 34, полностью исключает этот вопрос из рассмотрения.

Предлагается к прочтению: Наставление по организации штурманской службы на судах

Для уточнения расчетов волнового сопротивления корабля, которые будут выполняться с использованием уравнений, полученных на основе линейной теории волн, необходимо продолжить геометрическую и физическую интерпретацию формул для волнового сопротивления корабля (формула35) и корабельного волнообразования (формула 40).

Численная реализация расчетов волнового сопротивления

Для более ясного понимания вычислительных алгоритмов и применения эмпирических зависимостей при невозможности прямого численного решения интеграла Мичелла (формулы 40, 41) имеет смысл заменить аргумент в виде фазового угла Кельвина ϑ на длину излучаемой корпусом корабельной волны λ:

d ϑ = \frac{d λ}{2 λ \cdot \sqrt{\land - λ}}

выражение для дифференциала;

λ = \frac{2 π}{k} = 2 π \frac{{V_{0}}^{2} c o s^{2} ϑ}{g}

фазовая длина волны;

\land = 2 {π V_{0}}^{2} / g

критическая/максимальная длина поперечной волны;

M = \frac{V_{0}}{C} = \sqrt{\frac{\land}{λ}} = \frac{1}{c o s ϑ}

аналог волнового число Маха;

C = V_{0} / M

фазовая скорость волны;

H = A \cdot λ \cdot M / 4

функция Кочина.

Тогда основные расчетные формулы примут вид:

ω_{0} = \frac{x_{0}}{M} + \frac{y_{0} \sqrt{M^{2} - 1}}{M};

A (λ) = \frac{M}{λ} \cdot |\int_{Ω} q \cdot e^{k \cdot (- z_{0} + i ω_{0})} d Ω_{0}|;

R_{X} = \frac{ρ \cdot g}{4} \int_{0}^{L} A^{2} (λ) \frac{d λ}{λ \cdot M \sqrt{M^{2} - 1}} .

В общем случае функция A(λ) сильно осциллирует и имеет особенность порядка λ^-3/2 при λ→0. Интеграл (формула 18) для вычисления волнового сопротивления имеет особенности на границах порядка λ^-1/2 при λ→0 и λ→∧.

Указанные особенности могут быть ослаблены при использовании условий, учитывающих особенности волнообразования вблизи поверхности корпуса.

Интеграл по ватерлиниям

A (λ, z) = \int_{- L / 2}^{L / 2} q (x, z) \cdot e x p (\frac{i \cdot k}{M} (x + y \sqrt{M 2 - 1})) d x . Ф о р м . 42

При малых значениях λ интеграл сильно осциллирует, в то же время при λ, имеющей порядок длины корпуса, этот интеграл не представляет никаких особенностей и может быть вычислен по методу Симпсона (“трапеций”). Для оценки степени осцилляции вводится параметр Np, задающий минимальное количество расчетных точек на одну длину волны λ. Критерием допустимости прямого интегрирования может быть поставлено следующее условие:

\frac{L}{N i - 1} \cdot N p \geq \frac{2 π M}{k} = \sqrt{\land \cdot λ},

где:

L – длина между перпендикулярами;
Ni – количество шпангоутов;
Np – допустимое количество точек аппроксимации, приходящихся на один период рассчитываемой корабельной волны.

В случае если условие (формула 21) не выполняется, то можно воспользоваться линейными аппроксимациями подынтегральных функций и аналитическим интегрированием каждой шпации в отдельности.

A (λ, z, ∆ x) = \int_{x_{i}}^{x_{i + 1}} (a + b x) e x p (i (α + β x)) d x,

a = \frac{q (x_{i}) + q (x_{i + 1})}{2}, b = \frac{q (x_{i + 1}) - q (x_{i})}{∆ x},

α = (\frac{x_{i} + x_{i + 1}}{2} + \frac{y_{i} + y_{i + 1}}{2} \cdot \sqrt{M^{2} - 1}) \frac{k}{M},

β = (1 + \frac{y_{i + 1} - y_{i}}{∆ x} \cdot \sqrt{M^{2} - 1}) \cdot \frac{k}{M} .

a (λ, z, ∆ x) = \frac{e x p (i (α + β x))}{β} (i a - i b x + \frac{b}{β}) |_{x_{i}}^{x_{i + 1}} = Ф (x_{i + 1}) - Ф (x_{i}) .

Абсолютное значение интеграла A(λ, z) всегда меньше, чем максимальное значение по абсолютной величине от подынтегральной функции, равное максимуму от

$q (x, z) \sqrt{1 + {y_{x}^{'}}^{2} + {y_{z}^{'}}^{2}},$

достигаемому вблизи штевней. Если заранее рассчитать такие максимумы, то критерием достижения заданной точности при вычислении интеграла по ватерлиниям явится выражение:

e^{- k z} \cdot |m a x (q \cdot Ω)| > e p s .

где:

eps – принятая в расчетах абсолютная точность.

Иначе A(λ, z) = 0, если

e^{- k z} \cdot |m a x (q \cdot Ω)| > e p s .

Интегрирование результатов расчета по ватерлиниям

A (λ) = \int_{0}^{T} A (λ, z) \cdot e^{- k z} d z Ф о р м . 43

имеет экспоненциальную особенность при z→, которая определяет его величину при больших значениях k (то есть малых λ). Знак абсолютной величины ослабит, но не исключит возможность осцилляции функции A(λ, z), поэтому выбран метод вычислений, суть которого можно определить как двойную аналитическую аппроксимацию A(λ, z) в точках вблизи действующей ватерлинии (где: z→0).

Аппроксимируя |A(λ, z )| = f (z) с помощью параболы:

\int_{0}^{z} f (z) e^{- k z} d z = \int_{0}^{z} (a + b x + c x^{2}) \cdot e^{β z} d z = I (z),

β = - k; a = f (0);

b = \frac{- 3 f (0) + 4 f^{'} (z_{1}) - f^{″} (z_{2})}{2 \cdot δ z};

c = \frac{f (0) - 2 f^{'} (z_{1}) + f ″ (z_{2})}{2 \cdot δ z^{2}},

где:

$f^{'} = f e^{- b x};$
$f^{″} = f e^{- b x^{2}} .$

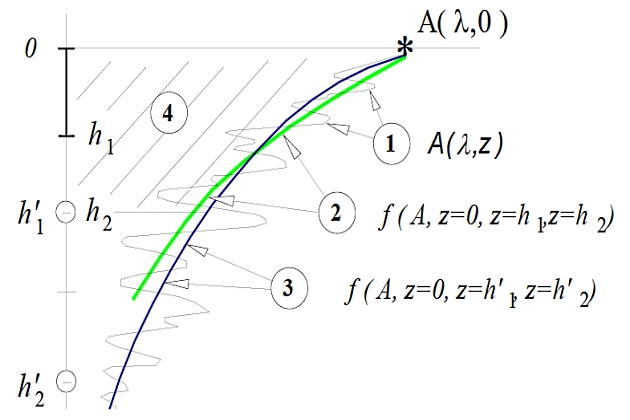
График функции параболы — Рис. 13 Геометрическое представление функции A(λ, z) и ее аналитических аппроксимаций

Ось Z полагается разбитой на равные интервалы:

∆z – расстояние между ватерлиниями;
Z¹ = ∆z;
.Z² = 2²z,

то:

I (z_{2}) = I (z_{1}, z_{2}) = e^{β x} \cdot (\frac{a + b x + c x^{2}}{β} - \frac{b + 2 x}{β^{2}} + 2 \frac{c}{β^{3}}) |_{0}^{z_{2}};

I ({z_{1}}^{'}) = I ({z_{1}}^{'}, {z_{2}}^{'}) = I (2 \cdot z_{1}, 2 \cdot z_{2});

I (2 ∆ z) = \frac{I (z_{2}) + I (z_{1}^{‘})}{2} .

Показанная аналитическая аппроксимация применяется только в том случае, если значения функции |А(λ, z)| в точках z = 0 и z = δz отличаются на порядок. Иначе ведется интегрирование по методу Симпсона.

Если же А(λ, 0)/А(λ¹, z¹) > 12, то используется расчет поправки вида:

δ A (λ, z) = I (2 δ z) - |A (λ, 2 δ z)| δ z / 2

После этого последние две точки в массиве A(λ, zⁱ) обнуляются, и дальнейшее интегрирование ведется по методу трапеций.

Интеграл по волновому спектру, расчет сопротивления

R_{x} = \frac{ρ g}{4} \int_{0}^{\land} \frac{A^{2} (λ) \cdot M}{λ^{2} \sqrt{M^{2} - 1}} d λ = \frac{ρ V_{0}}{4} \sqrt{2 π g} \int_{0}^{\land} \frac{A^{2} (λ)}{λ^{2} \sqrt{\land - λ}} d λ Ф о р м . 44

Здесь A имеет размерность (м²) и обладает экспоненциальным стремлением к нулю при λ→0. Сам же интеграл имеет особенности в точках λ→∧ типа λ^-1/2; λ→0 типа λ^-2, которая гасится экспонентой в выражении:

\frac{A^{2} (λ)}{λ^{2} \sqrt{\land - λ}} = f (λ) .

График подынтегральной функции — Рис. 14 Характер поведения подынтегральной функции

При вычислении интеграла по волновому спектру необходимо постоянно оценивать степень осцилляции функции f(λ). Разбивая этот интеграл на две части:

(λⁱ : ∧) – слабо осциллирующую, но обладающую особенностью типа λ^-1/2 при λ→∧;
(0 : λ_i) – сильно осциллирующая часть интеграла, включающую очень короткие корабельные волны, которые принципиально не могут оторваться от корпуса корабля.

Для поиска критического значения λ_i можно воспользоваться следующей оценкой подынтегральной функции в выражении для интеграла по ватерлиниям:

e x p (\frac{i k}{M} L) = f (λ) = e x p (\frac{i \cdot 2 π \cdot L}{\sqrt{λ \land}}),

где:

L – длина судна.

Если допустить “проход” трех периодов волн в полученной зависимости от аргумента λ, тогда:

λ_{i} = \frac{{(L / \land)}^{2}}{{(L / \land + 3)}^{2}} \cdot \land,

а отношение

\land / L = 2 π \cdot {F_{N}}^{2} .

Для вычисления интеграла

\int_{λ_{i}}^{\land} f (λ) d λ

был использован рекурсивный алгоритм, основанный на использовании полиномов Гаусса 4-й степени, которые удовлетворительно аппроксимируют функции с особенностями на границах интервала интегрирования. Численное решение интеграла Мичелла с использованием полиномов Гаусса позволяет получить точные значения волнового сопротивления даже для сложных форм корпуса. При вычислении интеграла

\int_{0}^{λ_{i}} f (λ) d λ

использовался традиционный «метод трапеций», так как его аппроксимации не приводят к разрывам решений с осциллирующими функциями. Анализ чувствительности волнового сопротивления к изменению параметров корпуса, проводимый с помощью формулы Мичелла, позволяет оптимизировать конструкцию судна.

Автор

Ольга Несветайлова

Фрилансер

Литература

Мичелл, Дж. Х. (1898). Волновое сопротивление судна. Философский журнал, 45(272), 106-123.
Хэвлок, Т. Х. (1908). Распространение групп волн в дисперсионных средах с применением к волнам на воде, вызванным движущимся возмущением. Труды Королевского общества Лондона. Серия А, 81(549), 398-430.
Лэмб, Г. (1932). Гидродинамика. Издательство Кембриджского университета.
Стокер, Дж. Дж. (1957). Водные волны: математическая теория с приложениями. Издательство Interscience.
Веханен, Дж. В., Лайтон, Э. В. (1960). Поверхностные волны. В Справочнике по физике (Том 9, стр. 446-778). Springer, Берлин, Гейдельберг.
Лайтхилл, М. Дж. (1978). Волны в жидкостях. Издательство Кембриджского университета.
Фалтинсен, О. М. (1990). Нагрузки от волн на суда и морские сооружения. Издательство Кембриджского университета.
Тулин, М. П. (1964). Теория судовых волн и волнового сопротивления. В Достижениях гидронауки (Том 1, стр. 307-392). Elsevier.
Эггерс, К. (1981). К теории судовых волн и волнового сопротивления. Schiffstechnik, 28(2), 65-84.
Инуи, Т. (1962). Волновое сопротивление судов. Труды Общества морских архитекторов и инженеров, 70, 283-326.
Маруо, Х. (1963). Избыточное сопротивление судна в штормовом море. Международный прогресс судостроения, 10(105), 326-348.
Сальвесен, Н., Тук, Э. О., Фалтинсен, О. (1970). Движение судна и нагрузки от волн. Труды Общества морских архитекторов и инженеров, 78(1), 250-287.
Огилви, Т. Ф. (1964). Недавний прогресс в понимании и прогнозировании движения судов. В 5-м симпозиуме по морской гидродинамике (стр. 3-79).
Журне, Дж. М. Дж., Массие, В. В. (2001). Морская гидромеханика. Делфтский технический университет.
Ньюман, Дж. Н. (1977). Морская гидродинамика. Издательство MIT.