Использование критерия предельной прочности при проектировании балочных конструкций ледовых усилений предполагает, что переход в предельное состояние не сопровождается изменением конфигурации поперечных сечений балок. Для выполнения данного условия элементы поперечных сечений должны обладать определенным запасом устойчивости. Наряду с этим должна быть исключена реализация наблюдаемых на практике дополнительных механизмов перехода в предельное состояние, связанных с выходом из плоскости (заваливанием) балок основного набора или смятием стенок балок. Ниже обосновывается система дополнительных расчетных требований к элементам поперечных сечений балок, обеспечивающая необходимые запасы прочности при заваливании и смятии.
Основные положения
- Устойчивость элементов поперечных сечений
- Предельная прочность профиля при заваливании
- Предельная прочность стенки при смятии
- Предельная прочность кничных соединений
- Оптимальное проектирование балочных конструкций
- Требования к предельной прочности наружной обшивки
- Существующие требования и усовершенствованная модель локально загруженной пластины
- Требования к толщине наружной обшивки
- Проектирование листовых конструкций по критериям предельной прочности и устойчивости
- Существующие требования к листовым конструкциям
- Расчетные схемы (варианты) листовых конструкций, подлежащих расчетной регламентации
- Нормирование расчетных нагрузок на листовые конструкции
- Расчетные модели и методы, описывающие переход листовых конструкций в предельное состояние
- Требования к размерам листовых конструкций по критерию устойчивости
- Сопоставительный анализ новых и действовавших требований. Выводы
- Выводы по главе 3
При разработке системы считаются заданными:
- расстояния между балами и длины пролетов;
- расстояния между ребрами жесткости, подкрепляющими стенки балок;
- Наружная обшивка, настил палуб и переборкитолщина наружной обшивки.
Задание указанных параметров определяет размеры присоединенного пояска балки.
Поэтому дополнительной регламентации подлежат следующие размеры поперечного сечения:
- h, t – высота и толщина стенки;
- с, δ – ширина и толщина стенки.
Введем индекс типа балки i и присвоим ему следующие значения:
- i = 1 – обыкновенные шпангоуты и продольные балки (основной набор);
- i = 2 – несущие стрингеры;
- i = 3 – рамные шпангоуты.
Примем следующие обозначения:
- ei = (hi, ti, ci, δi)Т – вектор регламентируемых размеров поперечного сечения балки i-го типа;
- ai, li – расстояние между балками и длина пролета балки i-гo типа;
- а = а1 – расстояние между балками основного набора (шпация);
- Sн. о – толщина наружной обшивки;
- σт – предел текучести материала;
- Е – модуль нормальной упругости.
Устойчивость элементов поперечных сечений
Устойчивость плоской формы изгиба
Общее требование к устойчивости плоской формы изгиба согласно решению Г.В. Бойцова
где:
Однако для применения (Формула 1) к конструкциям ледовых усилений требуется выполнение специального анализа.
Условие (Формула 1) получено в рамках следующих допущений.
Свободный поясок рассматривается как бесконечная свободно опертая балка, лежащая на упругом основании, создаваемом стенкой, скрепленной с обшивкой, загруженная постоянными продольными силами Т. При этом коэффициент жесткости упругого основания, эйлерово продольное усилие и длина полуволны потери устойчивости соответственно равняются
где:
- Iп – момент инерции свободного пояска.
Влияние отступления от закона Гука на устойчивость не учитывается, а Напряжения в корпусе судна при его общем продольном изгибеэйлеровы напряжения σэ доводятся до предела текучести, т.е. σэ = σкр = σт (σкр – критические напряжения).
Данные допущения в определенной мере сбалансированы: занижение запаса устойчивости плоской формы изгиба в расчетной модели, введенное первым допущением, компенсируется пренебрежением влияния отступления от закона Гука. Однако, как показывает расчетный анализ, для различных типов балочных связей ледовых усилений мера этой компенсации существенно различна. У рамных шпангоутов длина полуволны потери устойчивости lпi ∼ 5l3, т. е. Конструкция судовых перекрытийрасчетная модель бесконечной балки действительно обеспечивает существенный запас устойчивости и корректировка соотношения (Формула 1) не требуется. У шпангоутов и несущих стрингеров lпi ∼ 1 ÷ 1,5l1 (i = 1,2). Поэтому в рамках принятой расчетной модели не содержится достаточного запаса устойчивости. В связи с этим необходимо в явном виде учесть отступление от закона Гука, приняв
Как показал анализ, а1 = а2 = 2,0.
В выражении для параметра ξ в (Формула 1), входящего в формулу для коэффициента жесткости упругого основания (Формула 2), первое слагаемое определяется изгибом стенки, второе – обшивки (рис. 1).

При потере устойчивости плоской формы изгиба несущих стрингеров изгиб обшивки исключен из-за наличия обыкновенных шпангоутов, поэтому второе слагаемое в ξ2 следует опустить. Кроме того, характер конструктивного оформления узлов пересечения стенки несущего стрингера со шпангоутами позволяет заключить, что и часть стенки стрингера, примыкающая к наружной обшивке, не участвует в изгибе (рис. 2).

Поэтому при рассмотрении потери устойчивости плоской формы изгиба несущего стрингера следует считать, что стенка жестко заделана по линии 0-0′, а эффективная высота стенки, входящая в выражение для параметра ξ2 в (Формула 1),
Дополнительные или усиленные конструкции корпуса суднаСтенка рамного шпангоута, как правило, подкрепляется ребрами жесткости. При наличии подкрепляющих ребер, установленных перпендикулярно наружной обшивке, в соотношении (Формула 1) в коэффициент ξ3 вместо t3 следует вводить приведенную толщину стенки, определяемую из условия
где:
- iр – момент инерции подкрепляющего ребра;
- zр – расстояние между ребрами жесткости.
Для реального диапазона изменения размеров ребер жесткости после несложных преобразований получим
Если ребра жесткости установлены параллельно наружной обшивке, то внесение изменений (Формула 16) не требуется.
Таким образом, итоговое соотношение, определяющее требование к устойчивости плоской формы изгиба, примет вид
где:
- – если стенка рамного шпангоута подкреплена ребрами жесткости, перпендикулярными к наружной обшивке;
- ξ3 = 1 – в противном случае;
- α1 = α2 = 2,0; α3 = 1.
Из соотношения (Формула 7) вытекает следующее нелинейное алгебраическое уравнение для определения требуемой ширины свободного пояска балки
Решение (Формула 18) относительно величины сi, позволяет установить минимальную ширину свободного пояска в зависимости от остальных элементов вектора ei. Для практического определения сi, на основании расчетного анализа получены следующие аппроксимационные соотношения:
где:
- Ai, Bi, Di – численные коэффициенты.
Устойчивость стенки и свободного пояска
Данные требования сформированы на основании общих требований Правил Регистра. После некоторой корректировки, учитывающей специфику конструкций ледовых усилений, они приведены к следующему виду.
Наружная обшивка и подкрепляющий ее наборТребуемая минимальная толщина стенки (мм)
где:
- c11 = h1; c22 = l1; c12 = h2 – 0,8h1; c22 = α3; c13, c23 – меньшая и большая стороны панели, на которые стенка рамного шпангоута разбивается подкрепляющим его набором; σт> (МПа); cji (м).
Требуемая максимальная ширина свободного пояска (мм)
где:
- ci, δi (мм); σт (МПа).
Предельная прочность профиля при заваливании
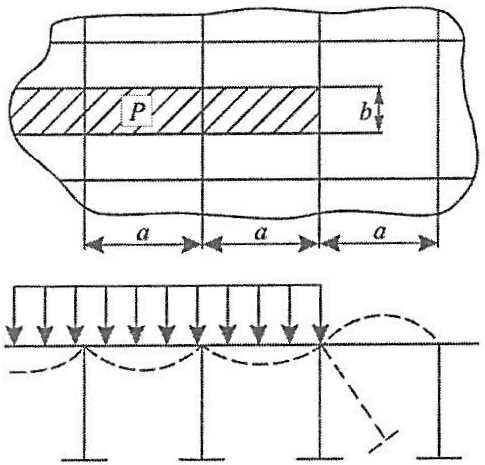
Заваливание (выход из плоскости) обыкновенных шпангоутов на судах ледового плавания согласно анализу разд. “Анализ повреждаемости и обоснование критериев прочности корпусов судов ледового плавания и ледоколовАнализ данных о повреждаемости судов ледового плавания в условиях продленной навигации в Арктике“, “Анализ повреждаемости и обоснование критериев прочности корпусов судов ледового плавания и ледоколовОсобенности и закономерности ледовой повреждаемости. Отдельные (допустимые) и массовые (недопустимые) ледовые повреждения” относится к одному из характерных типов ледовых повреждений. При этом важно отметить, что оно может реализоваться и в конструкциях, обладающих заведомо обеспеченной устойчивостью плоской формы изгиба. Поэтому естественно связать данное повреждение с особенностями воздействия локальных ледовых нагрузок. При действии локальной нагрузки всегда возникает следующая ситуация: шпангоут, расположенный в крайней по длине эпюры нагрузки шпации или продольная балка, расположенная в крайней по высоте распределения нагрузки шпации, поворачиваются вместе с наружной обшивкой согласно схеме рис. 3. При определенных условиях указанный поворот может привести к заваливанию профиля. Пусть расчетная ледовая нагрузка, действующая на бортовое перекрытие, характеризуется величиной
где:
- pR, bR – интенсивность и высота распределения нагрузки.
Величины pR и bR соответствуют некоторым осредненным условиям взаимодействия корпуса со льдом. В действительности на конструкции корпуса может воздействовать нагрузка с параметрами р и b, связанными следующим приближенным соотношением pb ≈ qR. Под действием нагрузки с параметрами pR и bR пластина наружной обшивки переходит в предельное состояние по конвертообразной схеме (см. рис. 4). Длина зоны разрушения (конверта), как показано в п. “Существующие требования и усовершенствованная модель локально загруженной пластины“, при поперечной системе набора определяется следующим приближенным соотношением:
где:
- а – расстояние между шпангоутами.
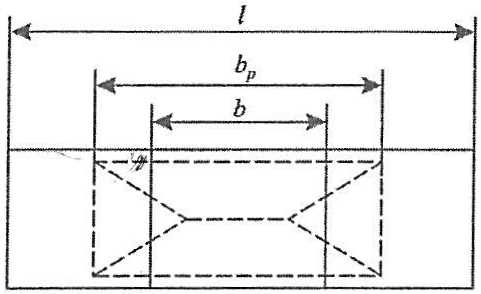
На длине bр в опорном сечении пластины вдоль стенки шпангоута образуется Принципы проектирования элементов днищевых конструкций в носовой оконечностишарнир текучести, в котором действует погонный предельный изгибающий момент
При действии ледовой нагрузки с параметрами bр > bR и p = qR/b пластина может и не достигать предельного состояния, тем не менее вдоль ее кромок успеют образоваться шарниры текучести.
Выполненный с учетом изложенных обстоятельств расчетный анализ показал, что погонный момент mн.о может возникать по всей длине пролета балки 1, на которой возможно заваливание профиля.
Момент mн.о передается на стенку балки и соседнюю незагруженную пластину наружной обшивки. Условия совместности угловых перемещений пластины и стенки (в рамках представлений о цилиндрическом изгибе) определяют следующее соотношение для величины погонного момента, приложенного непосредственно к стенке,
где:
- mc – предельный погонный изгибающий момент стенки.
Зависимость (Формула 14) может быть представлена в следующем виде:
где:
Согласно анализу для рассматриваемых конструкций ϒ ≈ 1 и m = mc.
Рассмотрим изгиб балки. Поскольку она расположена в крайней шпации, то на нее воздействует нагрузка
В соответствии с принятым критерием предельной прочности расчетная нагрузка qR тождественна предельной нагрузке балки. Тогда, пренебрегая влиянием сдвига, получим
где:
- b = 1; М0 – предельный изгибающий момент поперечного сечения;
- l – длина пролета балки при расчете в упругой области, определяемая согласно Правилам Регистра;
- l0 – пролет балки при расчете предельной нагрузки, определяемый согласно п.”Подходы к рациональному проектированию и оценке технического состояния балочных конструкций с кничным и соединениями” по концам книц (рис. 5).
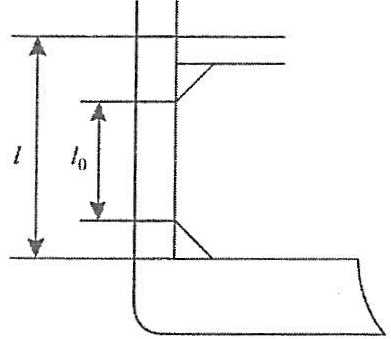
Расчетный анализ показал, что при реальных соотношениях размеров под действием нагрузки q в опорном и среднем сечениях балки на уровне свободного пояска действуют следующие величины относительных (по отношению к пределу текучести) напряжений:
Поскольку нейтральная ось у балок ледовых усилений располагается достаточно близко к присоединенному пояску, эпюра напряжений по высоте сечения может быть принята в виде (рис. 6)
где:
- z – координата, отсчитываемая от присоединенного пояска.
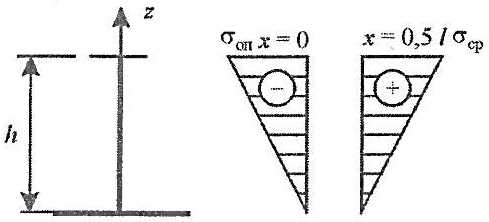
Распределение напряжений в продольных волокнах балки σ (x, z/x = const) между опорным и средним сечениями известно. Таким образом, напряжения σ (x, z) заданы по всей площади пластины стенки.
Определенные усилия m (х) и σ (x, z) Материалы конструкций корпуса, активно используемые в судостроениидействуют на профиль балки, расположенной в крайней относительно пятна приложения нагрузки шпации. Их совместное воздействие может привести к заваливанию ее профиля.
Описание предельного состояния профиля балки под действием усилий m (х) и σ (x, z) осуществим в рамках кинематического метода. Схема образуемого в профиле пластического механизма представлена на рис. 7. Другие схемы пластических механизмов, реализуемые на неполной длине пролета балки, как показал расчетный анализ, не являются истинными.
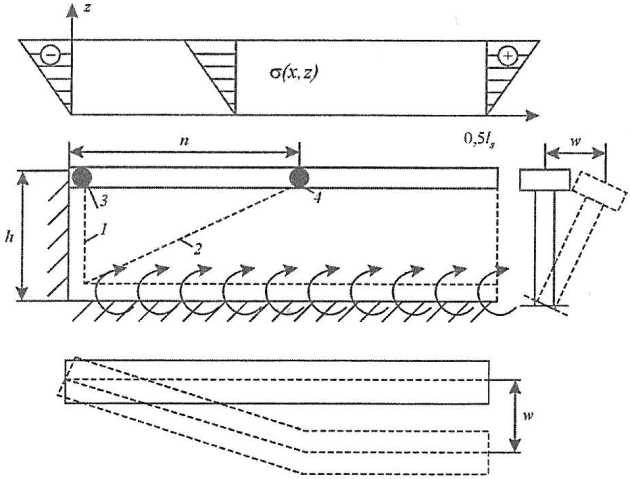
Следуя процедуре кинематического метода, вычислим работу внешних и внутренних сил на перемещении пластического механизма w. У шарниров в стенке (№ 1, 2)
где:
- Tj – работа внутренних сил в шарнире;
- θj – угол слома в шарнире;
- mj (хj) – предельный момент в шарнире;
- lj – длина шарнира текучести;
- xj – координата, направленная вдоль оси шарнира,
(влиянием напряжений σ (x, z) на величину m2 в (Формула 22), как показал анализ, можно пренебречь).
У шарниров в свободном пояске, рассматриваемом как балка прямоугольного сечения,
- — (влияние напряжений σ (n, h) на величину M4, как показал анализ, несущественно);
- – предельный Общий продольный изгиб и общая продольная прочность корпусных конструкций суднаизгибающий момент пояска при чистом изгибе в плоскости его наибольшей жесткости;
- n – параметр пластического механизма (см. рис. 7).
Работа внешних сил на перемещении w
Разрешающая система уравнений имеет вид
Решение системы дает следующие условия предельного равновесия рассмотренного пластического механизма под действием усилий m (х) и σ (x, z):
Соотношение (Формула 26) регламентирует минимальную относительную ширину свободного пояска, обеспечивающую необходимый запас предельной прочности шпангоутов и продольных балок при заваливании профиля. Для несущих стрингеров и рамных шпангоутов данное требование заведомо выполняется.
Предельная прочность стенки при смятии
Стенки балочного набора наряду с участием в изгибе бортовых перекрытий испытывают воздействие ледовых нагрузок, непосредственно прикладываемых к их кромкам и вызывающих их смятие. Исследуем особенности предельного равновесия стенок балок в условиях совместного изгиба и смятия.
Введем, как и ранее, индекс типа балки i и присвоим ему следующие значения:
- i = 1 – шпангоуты и продольные балки (основной набор);
- i = 2 – несущие стрингеры;
- i = 3, 4 – рамные шпангоуты соответственно при поперечной и продольной системах набора.
Рассмотрим первоначально балки типа i = 1 и i = 3, для которых можно полагать, что погонная нагрузка, прикладываемая к кромке стенки, распределена на некоторой длине равномерно и равняется q = ра (р – расчетное давление, а – шпация основного набора).
В этом случае задача предельного равновесия для кромки стенки применительно к условиям чистого смятия (без учета изгиба в составе перекрытия) записывается в виде:
где:
- σ2 – нормальное напряжение на кромке стенки;
- σ1 – нормальное напряжение в площадке, перпендикулярной кромке стенки;
- t1 – толщина стенки.
Решение (Формула 27) дает
Введем гипотезу о линейном распределении напряжений по высоте листового элемента
где:
- z – отстояние от кромки листового элемента;
- h – высота стенки балки.
Гипотеза (Формула 29) позволяет свести задачу о предельном равновесии стенки при совместном действии смятия и изгиба к рассмотрению наиболее нагруженного сечения балки, в котором реализуется максимум изгибающего момента М.
Предлагается к прочтению: Конструкция в районе палубных вырезов
При совместном действии в сечении балки напряжений от смятия (σ1, σ2) И изгиба (σм) условие пластичности для всей совокупности его точек запишется в виде
где:
- z1 – отстояние от нейтральной оси сечения.
Уравнения предельного равновесия будут
где:
- ω – площадь сечения балки.
Соотношения (Формула, а), (Формула 30) позволяют решить задачу об отыскании уравнения предельной кривой:
Результаты численного решения (Формула 31) для типовых сечений балок основного набора (обыкновенных шпангоутов и продольных балок) и рамных шпангоутов при поперечной системе набора представлены на рис. 8. Данные рис. 8 дают представление о сравнительном уровне требований к толщинам стенок балок основного и рамного набора.
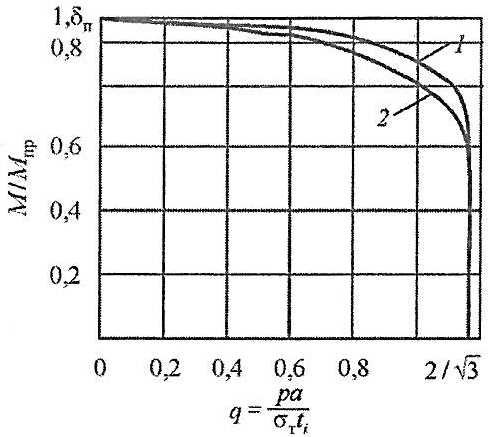
Обозначим:
- – относительное уменьшение изгибающего момента по сравнению с предельным изгибающим моментом при чистом изгибе, обусловленное влиянием смятия.
Будем рассматривать величину δ в качестве независимого параметра и перейдем от (Формула 31) к заданию уравнения предельной кривой в явном виде
Тогда Методы расчета прочности конструкций ледовых усилений при глубоком пластическом деформированиитребование к толщине стенки может быть представлено в виде
где:
- δнi – нормативное значение параметра δ для балки i-го типа.
Применяя сформулированный принцип равнопрочности к рассматриваемой задаче, придем к условию постоянства нормативного значения δ для всех типов балок:
Анализ существующих требований к толщинам стенок позволил установить следующую нормативную величину параметра δ:
Тогда
В рамках изложенной расчетной модели стенки несущих стрингеров и рамных шпангоутов при продольной системе набора находятся в более благоприятных условиях, поскольку приходящаяся на них погонная нагрузка хотя и имеет максимальное значение q = ра, но, в отличие от рассмотренного случая, распределена вдоль кромки не равномерно, а по треугольнику. Однако применительно к указанным балкам, необходимо принимать во внимание следующие обстоятельства. Во-первых, в узлах пересечения с основным набором должна обеспечиваться надежная передача усилий взаимодействия. Во-вторых, стенки ослаблены вырезами для прохода балок основного набора. Учитывая изложенное, принимается:
Таким образом, соотношения (Формула 37), (Формула 38) устанавливают требования к толщинам стенок набора бортовых перекрытий из условий обеспечения предельной прочности при совместном изгибе и смятии.
Предельная прочность кничных соединений
Особенности работы кничных соединений и постановка задачи
В корпусных конструкциях морских судов кницы используются в основном с целью снижения уровня напряженности и повышения усталостной долговечности узлов соединения (пересечения) балок. В конструкциях ледовых усилений согласно представленным в разд. “Анализ повреждаемости и обоснование критериев прочности корпусов судов ледового плавания и ледоколовАнализ данных о повреждаемости судов ледового плавания в условиях продленной навигации в Арктике” данным усталостные повреждения отсутствуют, а типичные для кничных узлов ледовые повреждения связаны с пластическим выпучиванием (выходом из плоскости) книц. Поэтому, положительная с позиций повышения прочности балки роль книц проявляется в основном в уменьшении длины ее свободного пролета. Естественно, что повреждение в виде выпучивания кницы может сопровождаться уменьшением ее способности поддерживать балку и, в связи с этим, снижением предельной прочности балочной конструкции (шпангоутной ветви).
Поскольку проектирование балочных конструкций ледовых усилений осуществляется на основании критерия предельной прочности, то и оценка влияния книц на предельную прочность балочной конструкции, а также определение уровня снижения ее прочности при выпучивании кницы целесообразно выполнить на основании аппарата ТПР. Решение данных задач осуществляется на основании следующей расчетной модели.
Выпучивание кницы происходит под действием погонной нагрузки q, передаваемой на ее катеты соединенными в узле балками. Рассматривая предельное состояние и запредельное деформирование изолированной кницы в рамках обоснованной в разд. “Методы расчета прочности конструкций ледовых усилений при глубоком пластическомМетоды расчета прочности конструкций из жесткопластического материала в геометрически нелинейной постановке” нелинейной постановки, можно получить зависимость указанной нагрузки от максимального прогиба выпучивания кницы w-q (w) (рис. 9, а).
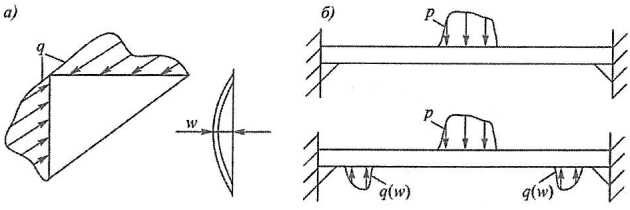
Далее, переходя к балочной конструкции и заменяя кницы реактивными нагрузками (w) (рис. 9, б), можно оценить влияние повреждений в кницах, характеризуемых прогибом w, на уровень предельной прочности балки, а также решить задачу назначения расчетной длины пролета балки с кничными соединениями в опорных сечениях.
Предельное состояние и запредельное деформирование изолированной кницы
Пусть дана прямоугольная симметричная кница со следующими размерами:
- с – длина катета кницы;
- Гк – толщина кницы.
При ее работе в упругой области в составе кничного соединения согласно решению А.З. Локшина на катеты кницы со стороны образующих узел балок (рис. 10, а) действует погонная нагрузка q, которая разлагается на нормальную и касательную составляющие
где:
- х – координата, отсчитываемая от вершины кницы;
- b – длина катета кницы.
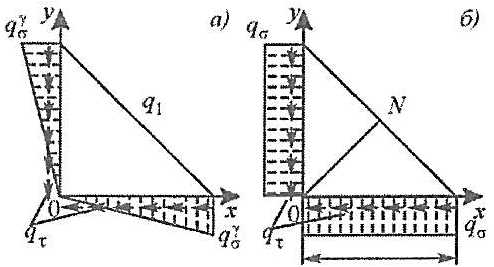
Однако при реализации в книце состояния, близкого к предельному, процесс интенсивного развития пластических деформаций неизбежно должен сопровождаться выравниванием величины усилий, передаваемых со стороны балок, по длине катетов кницы. Поэтому на момент перехода кницы в предельное состояние следует принять
Тогда из условия равновесия кницы, как твердого целого (см. рис. 10, б)
В отношении вертикальных перемещений (перпендикулярных плоскости кницы) будем считать кницу жестко заделанной по катетам.
Рассмотрим первоначально работу кницы без подкрепляющего пояска. Переход кницы в предельное состояние происходит в результате образования пластического механизма, включающего три прямолинейных шарнира текучести: вдоль катетов ОМ и OL и вдоль гипотенузы прямого угла ON (рис. 11). Гипотенуза ON одновременно является осью симметрии пластического механизма. В процессе деформирования пластический Крепление механизмов на фундамент суднамеханизм получает перемещения в двух взаимно перпендикулярных плоскостях: катеты поворачиваются в плоскости кницы вокруг точки О, а гипотенуза в результате слома поверхности кницы в шарнирах текучести поворачивается вокруг точки О в плоскости, перпендикулярной недеформированной поверхности кницы. Имеет место нелинейная связь между указанными перемещениями.
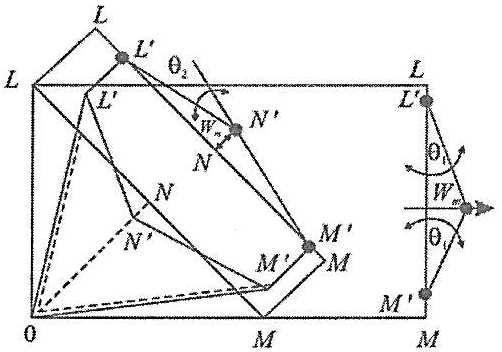
Введем, по аналогии с решениями гл. 2, систему обозначений:
- i – номер шарнира текучести, i = 1 – ОМ (или OL), i = 2 – ON;
- θi – угол в шарнире текучести;
- di – длина шарнира текучести;
- Si – отстояние срединной поверхности от нейтрального слоя в шарнире текучести;
- еi = θi Si – укорочение срединной поверхности в шарнире текучести;
- Gi – сдвиг в шарнире текучести;
- хi – координата, направленная вдоль оси шарнира текучести, отсчитываемая от точки О;
- u (хi), v (xi) – перемещения катета ОМ (OL) в направлении действия нагрузок qi и qσ соответственно;
- w (x2) – перемещение гипотенузы ON в направлении, перпендикулярном недеформированной поверхности кницы.
Поскольку нагрузки qτ и qσ постоянны по длине катета, следует принять
Так как шарнир 2 совпадает с осью симметрии пластического механизма, деформации сдвига в нем отсутствуют и G2 = 0. В виду прямолинейности шарниров текучести
где:
- wmax – максимальный прогиб выпучивания кницы (в точке N).
В рамках введенной в разд. “Методы расчета прочности конструкций ледовых усилений при глубоком пластическомМетоды расчета прочности конструкций из жесткопластического материала в геометрически нелинейной постановке” терминологии пластический механизм характеризуется следующим набором параметров:
- вектор обобщенных перемещений u = {uk} = {wmax, S1, S2, G1} Т, k = 1,…, 4;
- вектор обобщенных деформаций θ = {θ1, θ2, e1, e2, u, v}Т.
Отметим, что в соответствии с положениями разд. “Методы расчета прочности конструкций ледовых усилений при глубоком пластическомМетоды расчета прочности конструкций из жесткопластического материала в геометрически нелинейной постановке” изменение размеров жестких частей механизма за счет обобщенных перемещений S1, S2, G1 должно учитываться при определении работ внешних сил. Обобщенные деформации следующим образом выражаются через элементы вектора обобщенных перемещений {uk} и размеры кницы:
Работа внутренних сил в шарнирах текучести определяется на основании соотношений разд. “Методы расчета прочности конструкций ледовых усилений при глубоком пластическомМетоды расчета прочности конструкций из жесткопластического материала в геометрически нелинейной постановке“.
Шарнир 1 является изгибно-продольно-сдвиговым шарниром с постоянным укорочением срединной поверхности и согласно (Описание работы материала в шарнирах текучестиФормула 78):
где:
Шарнир 2 относится к типу изгибно-продольных шарниров с постоянным укорочением срединной поверхности и для него согласно (Описание работы материала в шарнирах текучестиФормула 77):
Полная работа внутренних сил
Работа внешних сил qт и qσ:
где:
Разрешающая система уравнений кинематического метода (Учет геометрически нелинейных факторов при описании запредельного деформирования конструкцийФормула 50)-(Учет геометрически нелинейных факторов при описании запредельного деформирования конструкцийКФормула 56) в рассматриваемой задаче примет вид
Система (Формула 48), описывающая запредельное деформирование кницы, является системой четырех нелинейных алгебраических уравнений относительно параметров
. После выполнения процедур дифференцирования и алгебраических преобразований система (Формула 48) приведена к следующему виду:
Решение нелинейной системы (Формула 49) осуществляется численно. Без-размерная нагрузка q0 используется в качестве независимого параметра. Из последнего определяется зависимость G (q0), а затем с помощью соотношений остальные обобщенные перемещения: S1 (q0), S2 (q0) и wmax (q0). Результаты определения перечисленных функций, описывающих запредельное деформирование кницы, на основании изложенной процедуры представлены на рис. 12. Анализ численного решения показывает, что при q0 → 0,516, wmax → 0, G → ∞. Значение q0* = 0,516 следует рассматривать в качестве предельной нагрузки кницы.
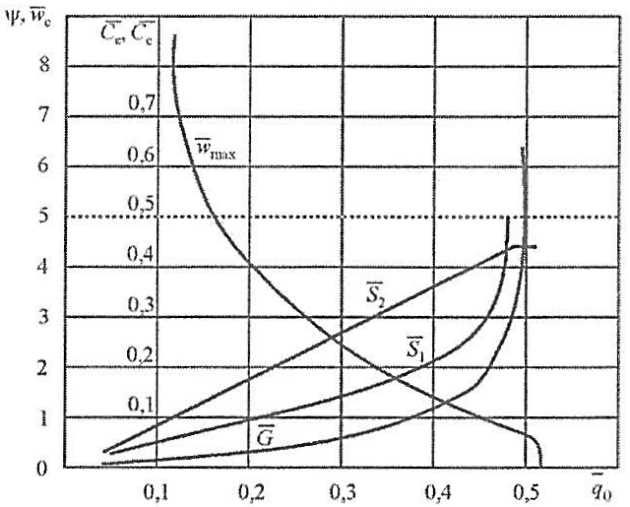
При наличии у кницы подкрепляющего пояска пластический механизм дополняется изгибным пластическим шарниром посередине длины пояска (в точке N). Учет данного обстоятельства приводит к появлению дополнительного члена в выражении для wmax в (Формала 49) и оно приобретает вид
где:
- – высота и толщина подкрепляющего пояска.
Основной практический интерес для дальнейших оценок представляет зависимость нагрузка – Конструкция судовых перекрытийпрогиб кницы (q0 (wmax). Результаты численного определения данной зависимости при вариации размеров подкрепляющего пояска представлены на рис. 13. Они показывают, что поясок не оказывает влияния на предельное состояние кницы (при wmax = 0) однако заметно повышает прочность кницы при запредельном деформировании, значительно замедляя сброс нагрузки в процессе ее выпучивания.
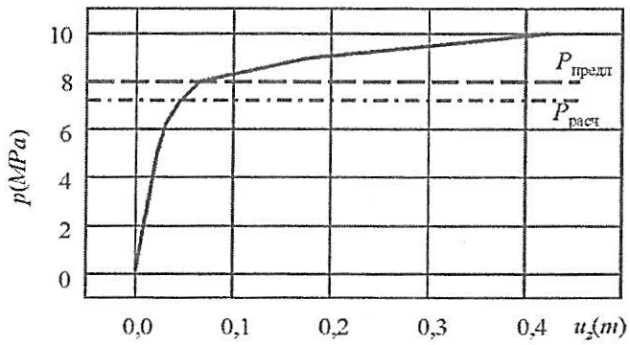
Близкие к описанным результаты получены В.А. Кулешом, рассмотревшим задачу о закритическом поведении книц в несколько иной постановке. Выполненные В.А. Кулешом эксперименты подтвердили достоверность обоих полученных решений.
В заключение дадим физическую трактовку полученных функций q0 (wmax). Если в качестве wmax рассматривать относительный остаточный прогиб, образовавшийся в результате выпучивания кницы, то величина q0 (wmax) соответствует относительной нагрузке, которую поврежденная кница способна воспринять со стороны балочной конструкции.
Предельная прочность балочных конструкций с кничными соединениями
Кничные соединения наиболее часто используются в конструкциях обыкновенных и рамных шпангоутов. Поэтому анализ предельной прочности системы балка – кничное соединение выполняется применительно к шпангоутной ветви.
Пусть шпангоут пересекает две соседние опорные конструкции, расположенные на расстоянии l друг от друга. Ледовая нагрузка в виде сосредоточенной силы P в соответствии с обоснованиями разд. “Методология проектирования конструкций ледовых усилений по критерию предельной прочностиПроектирование балок основного набора и балочных систем (бортовых перекрытий)” приложена симметрично относительно опорных сечений. Согласно решению п. “Обобщённый метод гибкого проектирования сложных бортовых перекрытийОценка предельной прочности и проектирование балок 1-го уровня (обыкновенных шпангоутов)” предельная нагрузка шпангоута составит
где:
- M0, N0 – предельные изгибающий момент и перерезывающая сила поперечного сечения шпангоута.
Если считать, что в опорных сечениях шпангоута установлены кницы с катетом с и переход в предельное состояние происходит на длине пролета между концами книц l = lk – 2с, то предельная нагрузка
Коэффициент
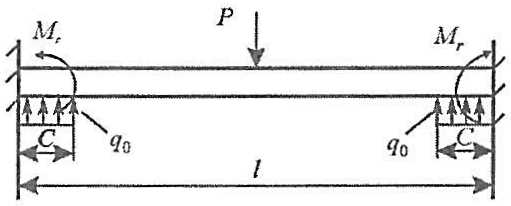
характеризует повышение предельной прочности шпангоута за счет установки книц. График зависимости η (l) (l = l/h) параметр жесткости шпангоута, h – высота поперечного сечения), представленный на рис. 14 (при характерных размерах шпангоутной ветви), демонстрирует, что существенное, до 15-25 %, увеличение предельной прочности наблюдается у шпангоутов с относительно невысокой жесткостью (l = 10 ÷ 15), а с увеличением жесткости (l < 10) этот эффект уменьшается и при l < 5 полностью нивелируется. Данный вывод свидетельствует о необходимости использования дифференцированного подхода к оценке роли кничных соединений.
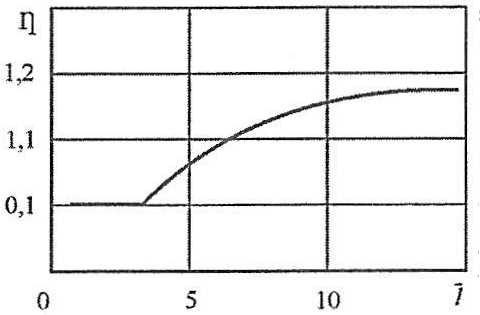
Теперь, в соответствии с изложенным в п. “Особенности работы кничных соединений и постановка задачи” подходом, отбросим кницы и заменим их действием нормальной и касательной нагрузок
равномерно распределенных на длине катетов с. Касательная нагрузка, приложенная к свободному пояску шпангоута, статически эквивалентна продольному усилию
приложенному к центру тяжести сечения, и сосредоточенному изгибающему моменту
где:
- g – отстояние центра тяжести поперечного сечения от свободного пояска.
Оценка показывает, что величина Tт, составляющая около 5 % от предельной продольной силы поперечного сечения, не оказывает заметного влияния на предельное состояние шпангоута и может не учитываться в дальнейшем анализе.
Тогда Справочные показатели для проектирования судового мидель-шпангоута. Приложениерасчетная схема шпангоутной ветви с отброшенными кницами примет вид, представленный на рис. 15. Пусть Pш – предельная нагрузка шпангоутной ветви с отброшенными кницами (см. рис. 15). Очевидно, что Pш ≤ Pк.
Обозначим:
- q0 – уровень нагрузки, передаваемой кницей на шпангоут, при котором его предельная прочность остается на уровне схемы обрушения по концам книц, т. е. Pш = Pк.
Если передаваемая кницей на шпангоут нагрузка
то предельная нагрузка шпангоутной ветви Pш < Pк следовательно, прочность кницы недостаточна. В противном случае, при
, кница имеет избыточную прочность, так как все равно Pш = Pк. Для определения
необходимо составить уравнение предельного равновесия шпангоутной ветви на полной длине пролета 1 и положить в нем
В результате выполнения данной процедуры получим следующее решение
где:
- – толщина и площадь стенки;
- f1 – площадь свободного пояска;
- F – Конструкция поперечных и продольных переборокплощадь поперечного сечения.
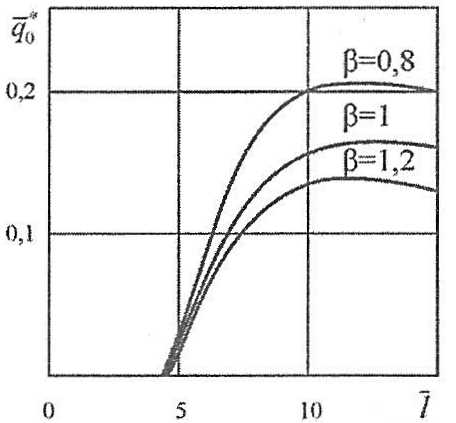
Для практических оценок для нагрузки q0 получено аппроксимационное соотношение (рис. 16)
Учитывая, что, как правило, β ≈ 1, можно заключить, что величина
не превышает значений (см. рис. 16)
Обратимся теперь к полученным в п. “Предельное состояние и запредельное деформирование изолированной кницы” зависимостям q0 (wmax). Из равенства
может быть найдена величина остаточного прогиба
при котором выполняется условие (Формула 52), т. е. предельная прочность шпангоутной ветви с деформированными кницами остается на уровне предельной прочности шпангоута при его обрушении по концам книц
. При
имеет место снижение предельной нагрузки шпангутной ветви с кницами
. Поэтому величина
может рассматриваться как допустимый остаточный прогиб кницы. Согласно данным рис. 13, значениям
(Формула 60) соответствуют величины допустимых прогибов
При увеличении жесткости шпангоутов величина
увеличивается и при
. Это означает, что условие (Формула 57)
выполняется, установка книц не оказывает влияния на запасы предельной прочности шпангоута, а их повреждения не влияют на эксплуатационные качества шпангоутной ветви.
Для практических оценок может использоваться следующая аппроксимационная зависимость для допустимого прогиба (см. рис. 13):
Действующий нормативный документ Регистра по определению технического состояния конструкций не содержит количественных требований для оценки допустимого прогиба деформированных книц и предлагает принимать решение на основании опыта надзора. Соотношение (Формула 63) позволяет заполнить данный методический пробел.
Подходы к рациональному проектированию и оценке технического состояния балочных конструкций с кничным и соединениями
Полученные результаты позволяют сформулировать следующие выводы в отношении подходов к рациональному проектированию и оценке технического состояния балочных конструкций с кничными соединениями в опорных сечениях.
Кницы в опорных сечениях балочных конструкций следует рассматривать как сминающиеся элементы, предохраняющие образующие узел связи от повреждений при воздействии экстремальных нагрузок и способствующие повышению уровня их предельной прочности.
У шпангоутной ветви с неповрежденными кницами даже при наличии технологических погибей
заведомо выполняются условия
Это означает, что при проектировании балочных конструкций с кничными соединениями расчетную длину пролета следует назначать как расстояние между сечениями у концов книц.
У балок с относительно низким уровнем жесткости
в зависимости от наличия у книц подкрепляющего пояска и его размеров уровень допускаемых прогибов составляет
. Если прогибы выпучивания кницы превышают указанный уровень, то существует опасность снижения предельной прочности балки на 15 ÷ 20 %. Поэтому в данном случае целесообразно выполнение конструктивных мероприятий по подкреплению поврежденных книц.
У относительно жестких балок
влияние книц на уровень предельной прочности проявляется относительно слабо, а при l < 5 полностью нивелируется. Поэтому в этом случае подкрепление кничных соединений необходимо только в случае наличия в узле соединения трещин и разрывов. Кницы, имеющие прогибы выпучивания, превышающие допустимые
, подлежат ремонту (подкреплению или замене). При выполнении ремонта следует учитывать, что значительное увеличение прочности подкрепляемой или заменяемой кницы нецелесообразно, поскольку может в будущем привести к повреждению (подмятию) Листовые конструкции корпуса суднастенки балки в районе узла соединения и, как следствие, заметному снижению предельной прочности шпангоутной ветви в целом.
Оптимальное проектирование балочных конструкций
Разработанный в статье “Методология проектирования конструкций ледовых усилений по критерию предельной прочностиПроектирование балок основного набора и балочных систем (бортовых перекрытий)” метод гибкого проектирования балочных систем (перекрытий) включает процедуру варьирования соотношения фактической и требуемой площадей стенок, позволяющую изменять величину требуемого предельного момента сопротивления. Данная процедура обеспечивает потенциальную возможность получения оптимальных проектных решений. Вместе с тем алгоритм определения размеров поперечного сечения балки становится неоднозначным. Представленные в настоящем разделе дополнительные требования к предельной прочности и устойчивости элементов поперечных сечений, часть которых носит нелинейный характер, а также наличие дополнительных конструктивно-технологических ограничений, накладываемых на размеры профиля, способствуют дальнейшему усложнению алгоритма проектирования.
Изложенные соображения определяют целесообразность разработки метода и программы оптимального проектирования балочных конструкций ледовых усилений, развивающих существующие в этой области разработки, ориентированные на анализ деформирования конструкций в упругой области.
Система расчетных требований и конструктивно-технологических ограничений
В соответствии с подходом будем полагать, что геометрия перекрытия, характеристики материала σт, толщина наружной обшивки Sн. о и площадь присоединенного пояска f2 являются общепроектными параметрами, не подлежащими оптимизации по условиям обеспечения предельной прочности перекрытия. Тогда вопрос оптимизации размеров поперечного сечения для каждого из типов входящих в перекрытие балок может рассматриваться изолированно.
Введем, как и ранее (см. п. “Основные положения”**), индекс типа балки i и вектора размеров поперечного сечения
. Элементы векторов e1 являются параметрами оптимизации размеров поперечного усечения (далее индекс i используется только при наличии различий в расчетных требованиях у балок разных типов).
Подстановка элементов вектора е в расчетные требования к геометрическим характеристикам поперечных сечений балок перекрытия (Формула 14), (Формула 20), (Формула 49), полученные в формулах 3-5, приводит к следующим соотношениям:
где:
- – фактические площадь стенки и прельный момент сопротивления;
- ψ – согласно п. “Корректировка и экспериментальная проверка модели деформирования пластины судов ледового плаванияРабота материала в пластических шарнирах“;
- – функции, зависящие от расчетной нагрузки, размеров перекрытия и материала.
Требования к устойчивости стенки (Формула 10) и предельной прочности стенки при изгибе и смятии (Формула 37) приводят к следующему соотношению:
где:
- – функция, определенная в (Формула 10);
- – функция параметров ледовой нагрузки, размеров перекрытия и материала, определенная в (Формула 37).
Требование к устойчивости свободного пояска (Формула 11) дает
Требования к устойчивости плоской формы изгиба (Формула 7) и предельной прочности при заваливании профиля (Формула 26) записываются в виде
где:
- – функция, определенная в (Формула 7);
Дополнительно к расчетным требованиям к ледовой прочности на элементы вектора е налагается система конструктивнотехнологических ограничений, которые в общем виде могут быть представлены следующим образом:
На практике система ограничений (Формула 70) может быть упрощена и, согласно опыту автора, сведена к следующим требованиям:
Таким образом, сформирована система расчетных требований (Формула 65-69) и конструктивно-технологических ограничений (Формула 71), (Формула 72), накладываемых на элементы вектора размеров поперечного сечения балочных конструкций ледовых усилений:
Алгоритм оптимального проектирования
Сформулируем задачу оптимизации размеров поперечного сечения, рассматривая ее как конечномерную экстремальную задачу с ограничениями типа неравенств:
где:
- F0 (е) — функция цели, в качестве которой обычно рассматривается Общие вопросы проектирования судовых конструкцийминимизация веса балочных конструкций, при этом F0 (е) = ht + cδ, хотя в принципе возможны и другие задачи оптимизации, например, минимизация высоты сечения, тогда F0 (е) = h.
Используем принцип Лагранжа для исследования задач с ограничениями. Функция Лагранжа запишется:
где:
- – вектор множителей Лагранжа.
Разрешающая система уравнений, отражающая условия стационарности функции Лагранжа в критической точке и дополняющей нежесткости, примет вид
Анализ показал, что вырожденный случай λ0 = 0 в рассматриваемой задаче не реализуется, т. е. следуя принципу Лагранжа можно положить λ0 = 1.
Тогда разрешающая система (Формула 76) дает 11 уравнений относительно неизвестных множителей Лагранжа (λ0,…, λ7)T и параметров конфигурации профиля e = (h, t, c, δ)T. Учитывая, что часть уравнений (Формула 76) нелинейна, целесообразно исследовать возможности понижения размерности системы. Обратимся к условию
и рассмотрим варианты
При
как показал анализ, решение системы дает
, что противоречит последнему неравенству сформулированной задачи (Формула 74). Это означает отсутствие критических точек функции Лагранжа в области положительных значений параметров с и δ при
или, физически, что требованиям предельной прочности отвечает оптимальный по массе профиль без свободного пояска. Поэтому минимальная величина произведения сδ регламентируется только условиями устойчивости плоской формы и предельной прочности при заваливании (Формула 69), а условие (Формула 77) дает
Последнее равенство в совокупности с условиями дополняющей нежесткости
устанавливают два возможных варианта, однозначно регламентирующих величины с и δ:
Из рассмотрения условий
аналогично предыдущим рассуждениям также выделяются два варианта:
Наконец, из условия
следует, что при
реализуется частный случай
. Поэтому при отыскании решения, соответствующего критической точке, из выражения (Формула 81) получим варианты:
Изложенное позволяет утверждать, что вектор множителей Лагранжа содержит одновременно не менее трех нулевых элементов, причем
а оставшиеся четыре условия дополняющей нежесткости при ненулевых λj образуют систему нелинейных уравнений относительно четырех параметров конфигурации профиля, образующих вектор e.
Читайте также: Малотоннажные стальные суда
Анализ соотношений (Формула 78, 79, 80, 82) позволяет установигь, что поиск критической точки функции Лагранжа, обеспечивающей минимум целевой функции, связан с исследованием восьми вариантов систем разрушающих уравнений. Каждый вариант содержит нелинейное уравнение
Далее, к соотношению (Формула 83) следует добавить одно из уравнений (Формула 82), регламентирующих требования к предельной прочности, т.е.
Последние два уравнения разрешающих систем формируются на основании условий дополняющей нежесткости, накладываемых непосредственно на элементы вектора е. Последовательность рассмотрения вариантов систем, идентичную в рамках каждой группы, целесообразно строить по принципу усиления ограничений, т. е. перехода от ограничений по минимальным размерам к ограничениям максимальных соотношений. В итоге может быть предложен следующий алгоритм:
1)Решается система, образуемая условиями
которая дает абсолютный минимум массы профиля при условии, что выполнены ограничения
2)При нарушении ограничения (Формула 86) формируется разрешающая система
которая приводит к результату
3)При нарушении ограничения (Формула 87) формируется разрешающая система
которая приводит к результату
4)При нарушении ограничений (Формула 86, 87) при решении системы (Формула 85) или одного из них при решении систем (Формула 88, 89) формируется система
дающая
.
Принадлежность каждой из приведенных систем к группе λ1 = 0 или λ2 = 0 определяется на основании выражения (Формула 84).
После определения элементов вектора е необходимо убедиться в существовании решения для оставшихся четырех ненулевых значений λ и выполнении условий их неотрицательности. Эта тривиальная процедура осуществляется на основании рассмотрения системы четырех линейных относительно ненулевых λj уравнений, задаваемых условиями стационарности функции Лагранжа согласно первому соотношению общей системы (Формула 76). Очевидно, что ее выполнение не имеет практического значения, так как элементы е уже вычислены, и носит проверочный характер.
На основании изложенного решения разработано соответствующее Системное программное обеспечение на судахпрограммное обеспечение, позволяющее выполнять оптимизацию размеров поперечных сечении балок бортовых перекрытий судов ледового плавания при альтернативных видах целевой функции. Выполненные при его помощи массовые расчеты, показали, что применение оптимизационных процедур позволяет в среднем на 10 % улучшить описываемые целевой функцией габаритные характеристики или характеристики по массе поперечных сечений по сравнению с подходами к определению размеров сечений, базирующимися на инженерной интуиции проектировщика.
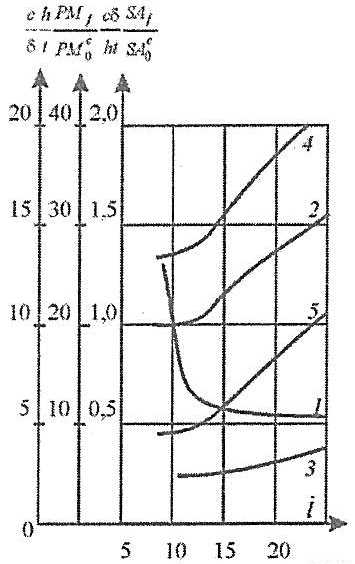
Пример оптимизации размеров поперечного сечения шпангоута по весу при вариации его относительной длины пролета
представлен на рис. 17. Согласно данным рис. 17, для относительно жестких балок
, типичных для конструкций ледовых усилений, оптимальным является профиль, у которого
(отсутствует запас по площади стенки), стенка относительно низкая, а поясок относительной узкий (
минимальны), площадь пояска значительно меньше площади стенки.
Формула
Такая конфигурация профиля, напоминающая приземистый белый гриб, физически полностью оправдана и обеспечивает высокую надежность при восприятии интенсивных локальных ледовых нагрузок. При снижении жесткости балки
, практически наблюдаемом при понижении ледовой категории судна, имеют место следующие тенденции: образуется значительный запас по площади стенки
, у стенки и пояска увеличиваются относительные высоты и ширина (
возрастают), площадь пояска увеличивается по сравнению с площадью стенки (возрастает параметр
). Это означает, что влияниечисто ледовых факторов нивелируется, а главной задачей становится удовлетворение условия по требуемому моменту сопротивления. Конфигурация профиля начинает напоминать гриб на тонкой ножке с широкой шляпкой (мухомор), что, в целом, типично для Конструкция носовой и кормовой оконечностей суднаконструкций морских (не ледовых) судов.
Изложенные соображения подтверждают эффективность и физическую обоснованность разработанной системы расчетных требовании и полученного решения об оптимальном проектировании балочных конструкций ледовых усилений.
Требования к предельной прочности наружной обшивки
Существующие требования и усовершенствованная модель локально загруженной пластины
Существовавшие Правила Регистра базировались на весьма условном подходе к оценке прочности наружной обшивки, основанном на традиционной модели балки-полоски, приводящей к следующему соотношению для требуемой толщины
где:
- а – расстояние между соседними балками основного набора, м;
- pрег – расчетное давление, МПа.
Главным недостатком соотношения (Формула 91) является игнорирование локального характера ледовой нагрузки. В связи с этим требуемая толщина оказывается не зависящей от высоты распределения расчетной нагрузки b. Поскольку в рамках общего подхода величина расчетной ледовой нагрузки характеризуется двумя однозначно связанными парамеграми – интенсивностью р и высотой распределения b, то указанный недостаток расчетной модели весьма неблагоприятно сказывался на всей методологии нормирования ледовой прочности и конкретно проявлялся в необходимости задания в Правилах ледовых нагрузок отдельно на набор бортовых перекрытий (где влияние параметра b учтено) и наружную обшивку.
К сожалению, данный условный подход был сохранен и в упоминавшемся проекте Норм ледовой прочности. В результате при их разработке пришлось использовать дополнительные условные приемы для согласования требований с существующей практикой: в формулу для требуемой толщины искусственно была введена функция, зависящая от водоизмещения судна ледового плавания или мощности ледокола.
Учитывая изложенное, возможности совершенствования требований к наружной обшивке связаны не только с переходом на критерий предельной прочности, но и с использованием уточненной расчетной модели, учитывающей фактор локальности ледовой нагрузки.
Уточненная расчетная модель локально загруженной пластины с конечным соотношением сторон обоснована в разд. “Методы расчета прочности конструкций ледовых усилений при глубоком пластическом деформированииДеформирование локально загруженной пластины наружной обшивки при образовании бухтины” (см. рис. 2.3.1, б). В полученном в разд. “Методы расчета прочности конструкций ледовых усилений при глубоком пластическом деформированииДеформирование локально загруженной пластины наружной обшивки при образовании бухтины” решении об упругопластическом и запредельном деформировании пластины в качестве частного случая представлена система уравнений (Формула 106), описывающая ее предельное состояние.
После выполнения процедур дифференцирования данная система может быть преобразована к следующему виду:
где:
- М, N – параметры пластического механизма, ясные из “Деформирование локально загруженной пластины наружной обшивки при образовании бухтинырис. 6 Обоснование схемы пластического механизма“, г.
Результаты численного решения нелинейной системы (Формула 92) представлены на рис. 18. Данные рис. 18, а наглядно демонстрируют влияние фактора локальности нагрузки на уровень предельной прочности пластины. При высокой степени локализации ледовой нагрузки b, характерной для судов малых водоизмещений, уровень предельной прочности обшивки увеличивается в (2,5 ÷ 1,9) раза по сравнению с моделью балки-полоски. Данный результат хорошо согласуется со сложившейся в отношении малых судов еще в 1960-1970-е годы проектной практикой. Как отмечалось, для учета этого обстоятельства в требованиях Норм к предельной прочности обшивки, основанных на модели балки-полоски, искусственно вводился коэффициент, обеспечивающий увеличение предельной нагрузки пластины наружной обшивки в области малых водоизмещений.
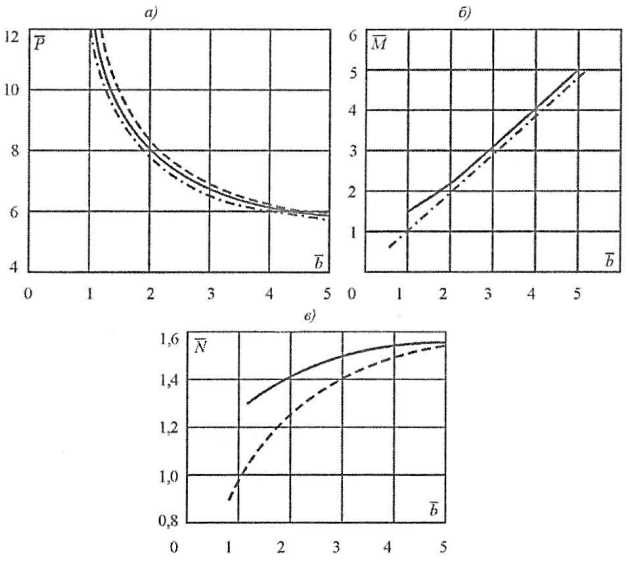
Наряду с этим из данных рис. 18, б следует, что длина зоны разрушения М лишь незначительно превосходит высоту Конструктивные типы транспортных судов и особенности проектирования их конструкцийзоны приложения нагрузки b, а при
. На основании данной тенденции может быть принято допущение М = b, позволяющее получить приближенное решение системы (Формула 92) в виде
Учитывая, что
, можно записать
Формула (Формула 95) дает результаты, с точностью до 1-2 % совпадающие с численным решением системы (Формула 92) (см. рис. 18, а).
Решение (Формула 94), фактически описывающее предельное состояние жестко заделанной пластины с размерами а х b под действием равномерно распределенной нагрузки, хорошо согласуется с получением решением (Формула 92) для локально нагруженной пластины. Данный факт может быть использован для оценки точности результатов.
Как известно, кинематический метод дает для предельной нагрузки оценку сверху. Поэтому решение (Формула 92), основанное на гипотезе о прямолинейных шарнирах текучести, приводит к погрешности, направленной всегда в опасную сторону. В показано, что предельная нагрузка, отвечающая заданию формы разрушенной поверхности квадратной пластины в виде
оказывается на 14 % ниже нагрузки, определенной на основании гипотезы о прямолинейных шарнирах текучести. Для рассматриваемой задачи данное сопоставление соответствует случаю b = 1. Очевидно, что с ростом b погрешность, вносимая допущением о прямолинейных шарнирах, уменьшается, а при b → ∞ реализуется точное решение о предельном состоянии пластины, гнущейся по цилиндрической поверхности. На основании изложенного можно сформулировать следующее условие для корректировки аппроксимации (Формула 95):
где:
- △ = 0,14 – относительная погрешность, вносимая допущением о прямолинейных шарнирах текучести.
Удовлетворение (Формула 96) дает следующее выражение для предельной нагрузки:
Требования к толщине наружной обшивки
На основании полученного соотношения устанавливается требование к толщине наружной обшивки. Переходя в (Формула 97) к размерным параметрам и разрешая его относительно величины Sн.о, входящей в выражение для параметра
~P1, можно получить следующую формулу для толщины наружной обшивки без учета износа:
Соотношение (Формула 98) получено для традиционно используемой в конструкциях ледовых усилений поперечной Конструкция судового наборасистемы набора. Однако на его основании легко перейти к соответствующему соотношению для продольной системы набора.
Для этого следует учесть, что принятая конвертообразная схема пластического механизма распространяется на все поле пластины и размер пластического механизма М заранее известен (М = l, l – расстояние между соседними поперечными связями). Тогда вместо (Формула 98) будем иметь
Соотношения (Формула 98, 99) отражают требования, предъявляемые к уровню предельной прочности наружной обшивки. В соответствии с принятым порядком, требование к строительной толщине наружной обшивки должно включать в явном виде добавку на износ. Величина этой добавки устанавливается следующим выражением:
где:
- Т – срок службы судна;
- u – скорость износа наружной обшивки;
- А – численный коэффициент.
Для конструкций морских транспортных судов в Правилах Регистра принято А = 0.5, что обеспечивает примерное постоянство запасов их прочности в течении всего срока службы. Для обшивки судов ледового плавания арктических категорий, согласно предложениям Г.В. Бойцова, данное условие выполняется при
Наружная обшивка, настил палуб и переборкиСкорости износа наружной обшивки установлены на основании анализа фактических данных о износах существующего ледового флота и согласования требований соотношения (Формула 98) с существующим опытом. Конкретные значения скоростей износа хорошо согласуются с результатами исследований, представленных В.А. Кулешом.
С учетом соотношений (Формула 98-101) итоговое соотношение для строительной толщины наружной обшивки, основанное на критерии предельной прочности и ориентированное на использование в Правилах Регистра, примет вид:
где:
- Sн.с – строительная толщина наружной обшивки, мм;
- р – интенсивность расчетной ледовой нагрузки, кПа;
- σт – предел текучести материала, МПа;
- а – расстояние между балками основного набора, м;
- с = b – при поперечной системе набора, м;
- с = l – при продольной системе набора, м;
- b – высота распределения расчетной ледовой нагрузки, м;
- l – расстояние между соседними поперечными связями, м;
- A = 0,5 – для среднего и кормового районов ледовых усилений судов категорий ЛУ1, ЛУ2, ЛУ3;
- A = 0,75 – в остальных случаях;
- Т – планируемый срок службы судна, годы;
- u – скорость износа наружной обшивки, мм/год.
Проектирование листовых конструкций по критериям предельной прочности и устойчивости
Существующие требования к листовым конструкциям
Этапы разработки требований к листовым конструкциям
Под листовыми конструкциями понимаются прилегающие к наружной обшивке участки настилов палуб, платформ, второго дна, обшивки поперечных переборок, стенок рамных связей (рамных шпангоутов, стрингеров, вертикального киля, сплошных и облегченных флоров, скуловых бракет). Понимание о необходимости четкой регламентации требований к листовым конструкциям сформировалось во второй половине 1980-х годов в связи с их повышенной повреждаемостью в условиях круглогодичной эксплуатации в Арктике (см. разд. “Анализ повреждаемости и обоснование критериев прочности корпусов судов ледового плавания и ледоколовАнализ данных о повреждаемости судов ледового плавания в условиях продленной навигации в Арктике“). До этого в Правилах Регистра существовали отдельные достаточно условные требования к настилам палуб и переборок. В рамках их совершенствования В.А. Курдюмовым были разработаны и включены в Правила Регистра требования к прочности листовых конструкций, основанные, как и остальные разделы Правил, на критерии фибровой текучести.
Данные требования давали практически неприемлемые результаты и при подготовке Правил Регистра 1995 г. подверглись определенному редактированию, которое, однако, объективно не смогло снять всех присущих им недостатков, обусловленных положенными в их основу моделями. Поэтому автором было продолжено совершенствование методов проектирования листовых конструкций по критерию предельной прочности.
Одновременно были систематизированы положения Правил, касавшиеся классификации и конструктивного оформления листовых конструкций.
Анализ существующих расчетных моделей и требований к листовым конструкциям
Положенные в основу требований Правил подходы ориентировались на рассмотрение изолированной листовой конструкции, к кромке которой приложена расчетная погонная нагрузка:
- – для листовых конструкции, ориентированных вдоль корпуса;
- – для листовых конструкций, ориентированных поперек корпуса, где
– интенсивность и высота распределения расчетной ледовой нагрузки согласно;
- а – расстояние между шпангоутами.
Не говоря о том, что по борту может иметь место продольная система набора, для которой способ определения параметра а неясен, обратим внимание на следующее. Задание расчетной погонной нагрузки
соответствует представлению о возможности следующей вариации параметров ледовой нагрузки:
т.е. величина
задается в предположении, что зона приложения ледовой нагрузки может заметно сужаться и при этом значение погонной нагрузки не изменяется. Только при таком подходе величина
может считаться полностью передаваемой на кромку листовой конструкции. Однако возможности аналогичной локализации нагрузки
не учитываются. Требование к приведенной толщине (с размазанными подкрепляющими ребрами жесткости) листовой конструкции задается на основании условной модели, рассматривающей ее изолированную работу, без учета поддерживающего влияния наружной обшивки и/или балок основного набора:
где:
- К – коэффициент запаса;
- К = 3 – для судов ледового плавания и ледоколов ЛЛ4;
- К = 1,5 – для ледоколов ЛЛ3;
- К = 1,2 – для ледоколов ЛЛ2;
- К = 1,15 – для ледоколов ЛЛ1.
При этом имеющийся существенный разброс в величинах коэффициента запаса К = 3,0 ÷ 1,15 можно рассматривать как дополнительное подтверждение условности расчетных подходов.
Количественный анализ требований Правил к листовым конструкциям, приводимый ниже, наряду с условностями расчетных подходов выявил также наличие существенных отклонений в требуемых толщинах палуб от сложившейся практики (см. п. “Сопоставительный анализ новых и действовавших требований. Выводы“, табл. 1-3). Не обсуждая причин указанных отклонений, отметим, что данные требования в предшествующих изданиях Правил, отсутствовали. Поэтому нельзя считать, что они прошли практическую апробацию и устанавливаемый ими уровень толщин листовых конструкций палуб отвечает накопленному опыту эксплуатации судов во льдах.
В связи с изложенным целесообразно рассмотреть также требования к толщинам листовых конструкций (палуб и переборок). Толщины настилов ледовых палуб и платформ вычисляются по формулам:
где:
- а – расстояние между бимсами;
- β – угол наклона шпангоута;
- К1 = 0,86.
Для толщин обшивки переборок устанавливаются следующие соотношения:
- S не менее толщины стенки шпангоута – для УЛА;
S не менее толщины стенки рамного шпангоута – для ледоколов, где aр – расстояние между подкрепляющими листовую конструкцию ребрами жесткости, установленными нормально к борту. Как видно из представленных соотношений, данные требования имеют еще более условный характер. Требования к палубам не зависят от предела текучести материала, требования к переборкам – от параметров ледовой нагрузки. Тем не менее можно говорить о том, что данные требования в определенной мере соответствуют сложившейся практике обеспечения прочности листовых конструкций палуб, платформ и переборок и, в связи с этим, представляют несомненный интерес для сопоставлений.
Изложенные сведения позволяют констатировать, что требования Правил к листовым конструкциям нуждаются в значительном совершенствовании, включающем:
- Дополнительные или усиленные конструкции корпуса суднаклассификацию листовых конструкций;
- обоснование нормативных подходов к назначению расчетных нагрузок на листовые конструкции;
- разработку расчетных моделей, описывающих переход листовых конструкций в предельное состояние с учетом особенностей деформирования совместно с наружной обшивкой, подкрепляющими ребрами жесткости и балками основного набора.
Расчетные схемы (варианты) листовых конструкций, подлежащих расчетной регламентации
В число листовых конструкций, применительно к которым должны устанавливаться расчетные нагрузки и разрабатываться расчетные модели, входят следующие:
- настилы палуб, платформ и второго дна, стенки днищевых стрингеров и вертикального киля;
- обшивка поперечных переборок, стенки флоров, скуловые бракеты.
Из представленного перечня исключены листовые конструкции несущих бортовых стрингеров и рамных шпангоутов, поскольку требования к толщинам стенок рамного набора бортовых перекрытий сформулированы в разд. “Требования к предельной прочности и устойчивости элементов поперечных сечений балочных конструкций судна”**.
Расчетная схема листовой конструкции и величина действующей на нее ледовой нагрузки определяются ориентацией листовой конструкции относительно судового корпуса и балок основного набора.
Для учета этого фактора достаточно ввести набор индексов ориентации, позволяющий в дальнейшем абстрагироваться от конкретного типа корпусной связи:
- i – индекс ориентации листовой конструкции относительно судового корпуса;
- i = 1 – вдоль корпуса;
- i = 2 – поперек корпуса;
- j – индекс ориентации листовой конструкции относительно балок основного набора, идущих по наружной обшивке;
- j = 1 – балки основного набора перпендикулярны листовой конструкции;
- j = 2 — балки основного набора параллельны листовой конструкции.
Тогда могут иметь место следующие четыре варианта ориентации листовой конструкции (номер варианта i, j образуется комбинацией введенных индексов):
- Вариант 1.1 – вдоль корпуса перпендикулярно основному набору.
- Вариант 1.2 – вдоль корпуса параллельно основному набору.
- Вариант 2.1- поперек корпуса параллельно основному набору.
- Вариант 2.2 – поперек корпуса перпендикулярно основному набору.
Вопросы назначения расчетных ледовых нагрузок на листовые конструкции перечисленных вариантов ориентации рассматриваются ниже.
Нормирование расчетных нагрузок на листовые конструкции
В настоящей монографии не рассматривается общая методология регламентации расчетных ледовых нагрузок, положенная в основу требований Правил 1999 г. и последующих изданий. Тем не менее для понимания описываемой ниже специфики назначения расчетных ледовых нагрузок на Наружная обшивка и подкрепляющий ее наборлистовые конструкции необходимо привести некоторые общие положения данной методологии.
В Правилах введена новая ледовая классификация, включающая (в скобках указаны эквивалентные новым категории существовавшей классификации Правил, категории ЛУ6, ЛУ8, ЛУ9 аналогов не имеют):
- девять ледовых категорий судов ЛУ1 (Л4), ЛУ2 (Л3), ЛУ3 (Л2). ЛУ4 (Л 1), ЛУ5 (УЛ), ЛУ6, ЛУ7 (УЛА), ЛУ8, ЛУ9;
- четыре категории ледоколов ЛЛ6 (ЛЛ4), ЛЛ7 (ЛЛ3), ЛЛ8 (ЛЛ2), ЛЛ9 (ЛЛ1).
Из девяти ледовых категории судов первые три (ЛУ1, ЛУ2, ЛУ3) предназначены для плавания в замерзающих (неарктических) морях, остальные шесть (ЛУ4, ЛУ5, ЛУ6, ЛУ7, ЛУ8, ЛУ9) – для арктических морей.
В Правилах РМРС 2010 г. использованы новью названия ледовых категорий:
- Ice1 – ЛУ1, Ice2 – ЛУ2, Ice3 – ЛУ3 – неарктические категории;
- Arc4 – ЛУ4, Arc5 – ЛУ5, Arc6 – ЛУ6, Arc7 – ЛУ7, Arc8 – ЛУ8, Arc9 – ЛУ9 – арктические категории;
- Ibr6 – ЛЛ4, Ibr7 – ЛЛ3, Ibr8 – ЛЛ2, Ibr9 – ЛЛ1 – категории ледоколов.
В Правилах *99 установлены единые для обшивки и набора ледовых усилений расчетные нагрузки, характеризуемые следующими параметрами:
где:
- рр, bр – интенсивность и Руководящие документы для судов, эксплуатирующихся в полярных водах
высота распределения расчетной ледовой нагрузки; - qр – погонная расчетная нагрузка.
При получении (Формула 107) использованы нормативные подходы, учитывающие в основном особенности работы балочных систем и пластин наружной обшивки. Естественно, что нормирование расчетных нагрузок на листовые конструкции имеет свою специфику, которая тесно связана с характером работы листовой конструкции в составе корпуса.
Введем аналогичные (Формула 107) расчетные нагрузки на листовые конструкции
Для перехода от нагрузок (Формула 107) к нагрузкам (Формула 108) требуется принять два нормативных решения:
- определение общего уровня нагрузок на листовые конструкции qk при заданном уровне расчетной нагрузки qр;
- установление соотношения между параметрами рk и bk в рамках заданного уровня нагрузки
В рамках обоснования общего уровня нагрузок необходимо учитывать следующие обстоятельства. Ледовые нагрузки характеризуются существенной изменчивостью. При отклонении реальных характеристик прочности льда и формы ледовой кромки от принятых при получении (Формула 107) осредненных значений возможно превышение расчетного уровня нагрузок, сопровождаемое на практике появлением ледовых повреждений. Однако, как показано в гл. 2, пластины и, в несколько меньшей степени, балочные системы имеют способность воспринимать возрастающие нагрузки, существенно большие, чем предельные нагрузки, соответствующие уровню расчетных (Формула 107).
Данная способность обусловлена поддерживающим влиянием распорных продольных усилий, возникающих на стадии запредельного деформирования в пластинах и балочных системах. Поэтому повреждения, вызванные воздействием нагрузок, превышающих расчетные (Формула 107), проявляются только в появлении в пластинах и балках фиксируемых остаточных прогибов. Листовые конструкции под действием ледовой нагрузки испытывают сжатие.
После перехода в предельное состояние происходит выпучивание листовой конструкции – резкое увеличение прогибов в направлении, перпендикулярном плоскости листовой конструкции, сопровождаемое сбросом нагрузки. Как показано в разд. “Корректировка и экспериментальная проверка модели деформирования пластины судов ледового плаванияДеформирование локально загруженной листовой конструкции совместно с наружной обшивкой при образовании вмятины-выпучины“, процесс сброса нагрузки происходит до тех пор, пока в пластине наружной обшивки не разовьются распорные усилия, достаточные для уравновешивания внешней нагрузки. Такой характер пластического деформирования с позиций негативных последствий повреждений представляет большую опасность, чем наблюдаемое у пластин и балочных систем плавное нарастание прогибов.
Наряду с этим необходимо иметь в виду, что листовые конструкции, создающие опорный контур для бортовых перекрытий и других балочных систем, относятся к корпусным конструкциям повышенной ответственности. Развитие в них повреждений может отрицательно сказаться на уровне ледовой прочности всего корпуса. Изложенные соображения определяют целесообразность повышения общего уровня расчетных нагрузок на листовые конструкции путем введения коэффициента запаса к расчетным нагрузкам (Формула 107):
где:
- – коэффициент запаса;
- – коэффициент, учитывающий влияние изменчивости ледовых нагрузок;
- – коэффициент, учитывающий повышенную ответственность листовых конструкций.
В соответствии с традиционными подходами к нормированию прочности судовых конструкций, в частности, с нормативными решениями Норм прочности морских судов (1992), где коэффициент запаса общей предельной прочности корпуса установлен на уровне 1,15-11,25, может быть принято
В отношении коэффициента изменчивости могут быть сформулированы следующие соображения. В соответствии с принятым порядком нормирования ледовой прочности расчетные параметры ледовых условий увеличиваются с ростом ледовой категории.
При этом в диапазоне категорий ЛУ1-ЛУ5 этот процесс идет параллельно общему ужесточению ледовых условий, в которых эксплуатируется судно. В этом диапазоне коэффициент изменчивости можно считать не зависящим от ледовой категории. Величина
устанавливается следующим физически ясным нормативным условием нагрузка на листовые конструкции i-й ледовой категории равняется среднему арифметическому расчетных нагрузок qp рассматриваемой (i-й) и следующей ((i + 1)-й) ледовых категорий.
Из данного условия с учетом данных гл. 4 следует:
где:
- i — индекс ледовой категории.
У судов и ледоколов высших ледовых категорий (i = 8,9) расчетные Подготовка судна к плаванию во льдахпараметры ледовых условий соответствуют верхнему пределу практически реализуемых, что в значительной мере нивелирует влияние фактора изменчивости. Поэтому может быть принято
Тогда для диапазона i = 5 ÷ 8 логично задать линейное изменение коэффициента изменчивости. В итоге, на основании (Формула 111-113), получим следующее выражение для входящего в (Формула 110) коэффициента запаса:
Таким образом количественно конкретизировано соотношение (Формула 110) между общими уровнями расчетных нагрузок qр и нагрузок на листовые конструкции qk. Перейдем к установлению соотношения между параметрами нагрузки рk и bk в рамках условия (Формула 109). Обратимся к обоснованному в п. “Анализ повреждаемости и обоснование критериев прочности корпусов судов ледового плавания и ледоколовКритерий предельной прочности. Расчётные методы и модели оценки предельной прочности” критерию предельной прочности (Формула 39). Для целей дальнейшего анализа он может быть представлен в следующем виде:
где:
- рр, bр – параметры расчётной ледовой нагрузки, отвечающие критерию предельной прочности;
- р – предельная нагрузка конструкции, определяемая методами ТПР.
Если в (Формула 115) варьировать высоту распределения нагрузки b, то можно получить так называемую кривую предельной прочности р (b) определяющую величину предельного давления, вызывающего переход конструкции в предельное состояние в функции от высоты b. Параметры расчетной нагрузки рр, bр представляют одну из точек на кривой р (b).
Третий параметр, определяющий эпюру ледовой нагрузки, – длина распределения ls при принятом порядке описания формы ледовой кромки в основном зависит от величины b:
В принципе для каждого типа конструкций ледовых усилений на кривой предельной прочности р (b) может быть установлена своя точка, дающая наиболее неблагоприятное сочетание значений р, b, l3. Использованная в процедура выбора точки, устанавливающей значения расчетных параметров рр, bр, ориентирована на оценку прочности бортовых перекрытий при одновременном учете специфики пластин наружной обшивки. Условия выбора параметров рр, bр имеют вид:
Т. е. в качестве расчетных выбираются параметры, дающие максимум погонной нагрузки и большую длину эпюры распределения, при которой в деформирование вовлекается значительная часть бортового перекрытия. Определенная на основании такого подхода расчетная нагрузка, которую в дальнейшем будем называть глобальной, может вполне обоснованно использоваться и для оценки прочности листовых конструкций, ориентированных согласно варианту 1.1, при котором линия действия нагрузки параллельна кромке листовой конструкции, а балки основного набора (шпангоуты) пересекают ее. В этом случае должны быть разработаны модели, описывающие переход в предельное состояние листовой конструкции совместно с балками основного набора и подкрепляющими листовую конструкцию ребрами под действием нагрузки, распределенной на значительной длине и имеющей наибольшее погонное значение. В рамках таких моделей перехода в предельное состояние Методы расчета прочности конструкций ледовых усилений при глубоком пластическом деформированиипроцесс деформирования листовой конструкции в основном определяется значением погонной нагрузки q и слабо зависит от соотношения параметров р и b. Поэтому с учетом (Формула 110) для параметров глобальной нагрузки может быть принято
Однако наряду с глобальными нагрузками (Формула 118) для всех вариантов ориентации необходимо учитывать, что листовая конструкция может разрушаться под действием локализованных нагрузок путем образования локальных механизмов, при которых в предельное состояние переходит участок листовой конструкции на длине, не превосходящей расстояния между балками подкрепляющего листовую конструкцию набора (установленного в направлении к наружной обшивке) или пересекающего ее основного набора. В этом случае в рамках пластического механизма необходимо учитывать взаимодействие листовой конструкции с наружной обшивкой. Расчетная нагрузка вида (Формула 117) для такого типа пластических механизмов, естественно, не является наиболее неблагоприятной. Гораздо опаснее оказывается часть кривой р (b) дающая следующие соотношения параметров:
Параметры (Формула 119) по сравнению с расчетными (Формула 117) дают локализованное пятно высокоинтенсивной ледовой нагрузки. Степень локализации нагрузки может характеризоваться коэффициентом локализации
Как показал анализ, при локализации нагрузки до величин
параметры q и р изменяются в диапазонах
Как показывают соотношения (Формула 122), имеет место определенное снижение погонной нагрузки вследствие локализации. Однако при этом необходимо учитывать, что листовая конструкция обладает существенно большей жесткостью по сравнению с наружной обшивкой. Экспериментально установлено и учтено в Финско-шведских правилах, что в районе конструкций повышенной жесткости имеет место некоторое возрастание интенсивности ледовой нагрузки. Данный фактор не оказывает существенного влияния на оценку прочности бортового набора, а также листовых конструкций с глобальным механизмом перехода в предельное состояние, поскольку речь идет только о перераспределении интенсивностей в рамках общего интеграла ледового усилия. Однако в рассматриваемых локальных механизмах перехода в предельное состояние он должен приниматься во внимание.
Это интересно: Главные и вспомогательные паровые котлы
Тогда можно полагать, что уменьшение погонной нагрузки q за счет локализации количественно компенсируется повышением интенсивности нагрузки в районе жесткой листовой конструкции.
Аналогичное (Формула 122) уменьшение длины распределения ледовой нагрузки ls по сравнению с lsp не принципиально, поскольку при рассматриваемых вариантах ориентации данный параметр не оказывает влияния на характер работы листовой конструкции. Поэтому, с учетом (Формула 110), а также соображений, сформулированных при получении (Формула 118) и остающихся справедливыми и в данном случае, получим следующие соотношения для параметров локализованной расчетной нагрузки (штрих у параметров р и b является признаком локализованной нагрузки):
В качестве расчетного значения Кп, регламентирующего степень локализации расчетной нагрузки, с небольшой ошибкой в безопасную сторону следует принять нижнее значение диапазона (Формула 121):
где:
- β – коэффициент, учитывающий, что для крупнотоннажных судов и ледоколов повышенной мощности локализация нагрузки (ограничение роста b);
- – для судов ледового плавания;
- – для ледоколов;
- △ – водоизмещение судна, тыс. т;
- – коэффициент, зависящий от суммарной мощности ледокола.
Таким образом, согласно выполненному анализу:
- При ориентации листовой конструкции согласно варианту 1.1 в качестве расчетной рассматривается глобальная нагрузка (Формула 110). При этом в соответствующих расчетных моделях должен описываться переход в предельное состояние листовой конструкции совместно с пересекающим ее основным набором и подкрепляющими ребрами жесткости.
- При всех вариантах ориентации должна быть рассмотрена возможность образования локальных механизмов перехода в предельное состояние листовой конструкции совместно с пластиной наружной обшивки под действием локализованной расчетной нагрузки (Формула 121) при коэффициенте локализации (Формула 124).
Расчетные модели и методы, описывающие переход листовых конструкций в предельное состояние
Согласно изложенным требованиям оценка предельной прочности листовых конструкций должна основываться на расчетных моделях, описывающих их переход в предельное состояние совместно с пластинами наружной обшивки, балками основного набора, подкрепляющими ребрами жесткости. При разработке данных моделей следует учитывать результаты полученных в разд. “Корректировка и экспериментальная проверка модели деформирования пластины судов ледового плаванияДеформирование локально загруженной листовой конструкции совместно с наружной обшивкой при образовании вмятины-выпучины” решений об упругопластическом и запредельном деформировании изолированной листовой конструкции и листовой конструкции совместно с наружной обшивкой.
Предельное состояние изолированной листовой конструкции с подкрепляющими ребрами жесткости
Решение п. “Корректировка и экспериментальная проверка модели деформирования пластины судов ледового плаванияПредельное состояние и запредельное деформирование изолированного листа” о предельном состоянии и запредельном деформировании изолированной листовой конструкции в рассматриваемом случае, ограниченном анализом предельного равновесия, может быть упрощено. Вместо пластического механизма с пятью изгибно-продольными шарнирами текучести, описывающими процесс образования выпучины, здесь достаточно ввести один шарнир смятия на кромке листовой конструкции (рис. 19).
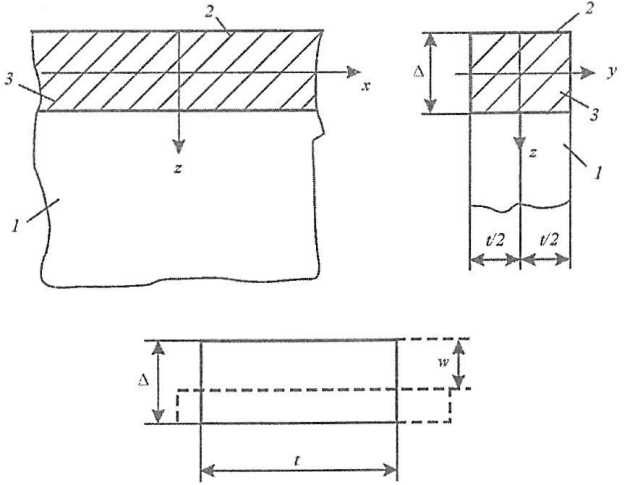
1 – листовая конструкция; 2 – наружная обшивка; 3 – шарнир смятия
Полная работа внутренних сил в шарнире смятия листовой конструкции равняется
где:
- t – толщина листовой конструкции;
- dc – длина шарнира смятия;
- х – координата вдоль оси шарнира смятия;
- z, w(x) – координата, перпендикулярная кромке листовой конструкции и перемещение вдоль нее.
При наличии ребер жесткости, подкрепляющих листовую конструкцию и установленных перпендикулярно наружной обшивке, в (Формула 125) вместо толщины t следует использовать приведенную толщину
где:
- f – площадь ребра жесткости (без присоединенного пояска);
- а1 – расстояние между ребрами жесткости;
- а = 1 – если балки основного набора пересекают листовую конструкцию, а = 1 – в противном случае;
- а – расстояние между балками основного набора;
- а2 – длина неподкрепленной части выреза в листовой конструкции для прохода балок основного набора, измеренная вдоль наружной обшивки.
Предельное состояние и требования к толщинам листовых конструкций, деформирующихся совместно с наружной обшивкой
Согласно классификации п. “Расчетные схемы (варианты) листовых конструкций, подлежащих расчетной регламентации” и соображениям п. “Нормирование расчетных нагрузок на листовые конструкции” локальные пластические механизмы, приводящие к совместному деформированию листовой конструкции и наружной обшивки, могут реализовываться при всех вариантах ориентации. Особенности построения совместных пластических механизмов целесообразно рассмотреть сначала для варианта 2.2, а затем обобщить результаты на остальные варианты.
Рассмотрим момент, предшествующий переходу в предельное состояние листовой конструкции (рис. 20, а).
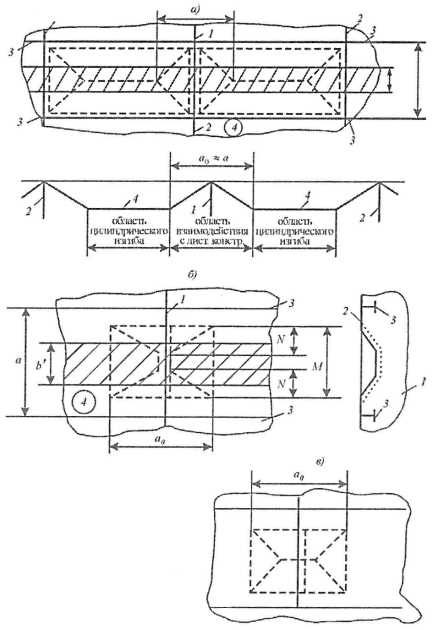
1 – листовая конструкция; 2 – соединение листовых конструкции; 3 – балки основного набора; 4 – наружная обшивка;
– область ледовой нагрузки;
‒ ‒ ‒ ‒ ‒ ‒ шарнир текучести в обшивке;
∙ ∙ ∙ ∙ ∙ шарнир смятия в листовой конструкции
Наружная обшивка, непосредственно воспринимающая нагрузку, на большей части длины находится в состоянии цилиндрического изгиба. Переход листовой конструкции в предельное состояние практически не окажет влияния на состояние обшивки в областях цилиндрического изгиба. Совместное Восстановление размеров и форм деталей деформированиемдеформирование обшивки с листовой конструкцией будет происходить только в узкой области, примыкающей к листовой конструкции. Как следует из геометрических построений рис. 20, а, протяженность этой области
Поэтому можно считать, что после перехода листовой конструкции в предельное состояние совместный пластический механизм локализуется в области а0. При этом в обшивке реализуется конвертообразная форма деформированной поверхности, а в листовой конструкции – шарнир смятия (см. рис. 20, б). Представленная на рис. 20, б форма конверта, аналогичная рассмотренной в разд. “Требования к предельной прочности наружной обшивки“, не является единственной. При высокой степени локализации нагрузки истинной становится другая ориентация конверта (см. рис. 20, в)
В обоих случаях размеры пластического механизма характеризуются неизвестными параметрами М и N (см. рис. 20, б), а также величиной а0 согласно (Формула 126). Как показал анализ, для целей настоящего исследования применительно к реальным соотношениям между высотой локализованной нагрузки b и размером а0 с достаточной степенью точности может быть принята следующая приближенная зависимость между параметрами М и N:
Таким образом, остается неизвестным только параметр М, на величину которого накладывается ограничение, соответствующее условию локализации пластического механизма
где:
- С = а – предельная протяженность деформированной зоны вдоль кромки листовой конструкции;
- а – расстояние между балками основного набора, пересекающими листовую конструкцию.
С учетом решения разд. “Требования к предельной прочности наружной обшивки” и соотношения (Формула 125) получим следующие выражения для перемещения w (x) в (Формула 125), работ внутренних сил в шарнирах текучести пластины Тп.л и в шарнире смятия листовой конструкции Тл.к, а также для работ внешних сил V (в силу симметрии рассматривается четверть системы пластина – листовая конструкция):
где:
- – толщина пластины наружной обшивки;
- – коэффициенты локализации и запаса согласно (Формула 124) и (Формула 114);
- р, b – интенсивность и высота распределения расчетной ледовой нагрузки (введенный в формуле 105 индекс «р» к параметрам расчетной нагрузки ниже опускается);
- φ – поправочная функция, причины введения и структура которой рассматриваются ниже;
- w – максимальное перемещение пластического механизма.
Для определения предельной нагрузки и неизвестного размера пластического механизма m составляется, в соответствии с процедурой кинематического метода, следующая разрешающая система уравнений
где:
Обратим внимание, что в разрешающей системе (Формула 131), как и в полученном ранее решении разд. “Корректировка и экспериментальная проверка модели деформирования пластины судов ледового плаванияДеформирование локально загруженной листовой конструкции совместно с наружной обшивкой при образовании вмятины-выпучины“, учитывается важный эффект разнесения нагрузки вдоль кромки листовой конструкции, создаваемый наружной обшивкой: длина деформированной зоны листовой конструкции М всегда больше высоты распределения ледовой нагрузки b’. Если расширить решение (Формула 131) на весь диапазон возможных соотношений между величинами b’, аb’, q, отказавшись от упрощающего допущения (Формула 127) в отношении величины N, то можно доказать справедливость следующих соотношений:
Это означает, что даже в предельном случае
рассматриваемая модель характеризуется конечной величиной предельной нагрузки q и к толщине листовой конструкции могут быть предъявлены вполне конкретные требования. В модели изолированной листовой конструкции, как отмечалось выше, возможность локализации нагрузки не поддается корректному учету и вносит неопределенность в процедуру регламентации требований к толщине.
Поясним физические причины, обусловившие введение в (Формула 130) поправочной функции φ. Как показано в разд. “Корректировка и экспериментальная проверка модели деформирования пластины судов ледового плаванияДеформирование локально загруженной листовой конструкции совместно с наружной обшивкой при образовании вмятины-выпучины“, из-за существенного различия в жесткостях обшивки и листовой конструкции предельное состояние и начало запредельного деформирования (выпучивания) последней реализуются в момент, когда пластина еще работает в упругой или упругопластической стадиях. При этом определенная на основе жесткопластического подхода работа внутренних сил в шарнирах текучести пластины оказывается завышенной. Для учета данного обстоятельства в структуру выражения для
в (Формула 130) введена поправочная функция φ, играющая роль редукционного коэффициента.
Численный анализ, выполненный с помощью решения разд. “Корректировка и экспериментальная проверка модели деформирования пластины судов ледового плаванияДеформирование локально загруженной листовой конструкции совместно с наружной обшивкой при образовании вмятины-выпучины” об упругопластическом деформировании системы листовая конструкция – наружная обшивка, позволил установить следующее соотношение для поправочной функции φ:
где:
- – параметр жесткости пластины наружной обшивки;
- z – zминимальный размер в плане деформированной зоны пластины, для рассматриваемого пластического механизма
; - D = 22,5, d = 1,5 – численные коэффициенты.
Решение нелинейной системы (Формула 131) относительно параметров q и m может быть получено только численно. Как показал анализ, применительно к практически реализуемому диапазону изменений параметров b и m может быть принято следующее приближенное соотношение
позволяющее получить аналитическое решение системы (Формула 131). С учетом формулы (Формула 133) для поправочной функции φ после перехода от безразмерных к размерным параметрам решение (Формула 131) относительно предельной нагрузки (предельного давления
) примет вид
где:
Приравнивая согласно критерию предельной прочности предельное и расчетное давления
, после подстановки выражений для К3 и Кл, а также численных значений коэффициентов ϒ, δ, d, D, получим следующее итоговое выражение для требуемой толщины листовой конструкции с вариантом ориентации 2.2:
где:
- – согласно (Формула 114) в зависимости от ледовой категории;
- β – согласно (Формула 124).
Требование (Формула 135) распространяется на Конструкция судовых перекрытийлистовые конструкции поперечных переборок, флоров и скуловых бракер при продольной системе набора соответственно по борту и днищу.
Построение аналогичных решений для остальных вариантов ориентации листовой конструкции не представляет затруднений.
В варианте ориентации 2.1 в соответствии с изложенными соображениями также следует полагать (рис. 21, а)
а единственное изменение сводится к использованию в качестве величины С в (Формула 128) параметра Ср:
где:
- Ср – расстояние между подкрепляющими листовую конструкцию ребрами, установленными нормально к наружной обшивке.
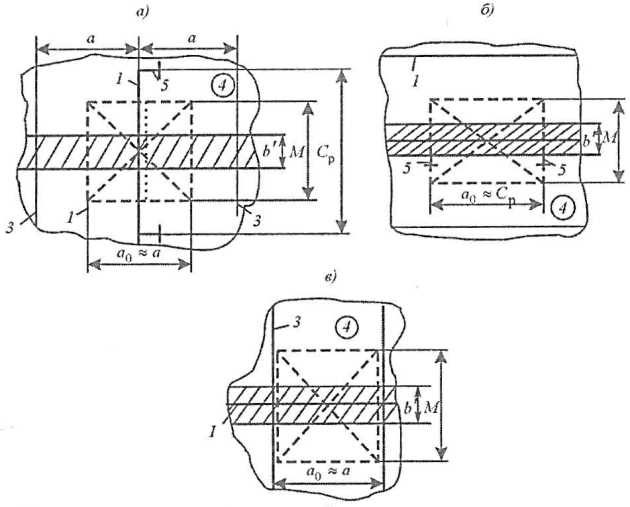
а – вариант 2.1; б – вариант 1.2; в – вариант 1.1:
1 – листовая конструкция; 2 – соединение листовых конструкции; 3 – балки основного набора; 4 – наружная обшивка; 5 – подкрепляющие листовую конструкцию ребра жесткости;
– область ледовой нагрузки;
‒ ‒ ‒ ‒ ‒ шарниры текучести в обшивке;
∙ ∙ ∙ ∙ ∙ шарнир смятия в листовой конструкции
Тогда в итоге для варианта ориентации 2.1 будем иметь
где:
Требование (Формула 138) распространяется на листовые конструкции поперечных переборок, флоров и скуловых бракет при использовании поперечной системы набора соответственно по борту и днищу.
В варианте 1.2 в соответствии со схемой пластического механизма рис. 21, б будем иметь
а аналогичное (Формула 128) ограничение на величину размера пластического механизма М ≤ 2а при принятой степени локализации нагрузки может считаться удовлетворяемым автоматически.
Наряду с этим, вследствие изменения ориентации листовой конструкции, для вычисления работ внутренних сил в шарнире смятия необходимо использовать соотношение
а величину коэффициента ϒ в соотношении (Формула 133), как показал численный анализ, принять равной
С учетом (Формула 139-141) получим следующее соотношение для требуемой толщины листовой конструкции:
Полученные соотношения справедливы в том случае, когда листовая конструкция подкреплена ребрами жесткости, нормальными к наружной обшивке. Если ребра отсутствуют, то шарнир смятия в листовой конструкции может иметь существенную протяженность, и в этих условиях поддерживающее влияние обшивки полностью нивелируется. Следовательно, Гидротехнический расчет плавучей буровой установки и волновая нагрузка ПБУлокализованная нагрузка практически полностью воспринимается листовой конструкцией и к ее толщине должно быть предъявлено следующее очевидное требование:
Требования (Формула 142), (Формула 143) распространяются на листовые конструкции палуб, платформ и второго дна при продольной системе набора по борту, а также днищевых стрингеров и вертикального киля при продольной системе набора по днищу.
В варианте 1.1 снимается ограничение на величину М, а в качестве a0 также используется величина Ср согласно (Формула 139). В частном случае (см. рис. 21, в) она может совпадать со шпацией пересекающего листовую конструкцию набора, т. е.
Соотношения (Формула 140-171) остаются в силе, а требование к толщине полностью совпадает с требованием (Формула 142), откуда
Требование (Формула 145) распространяется на листовые конструкции палуб, платформ, второго дна при поперечной системе набора по борту, а также днищевых стрингеров и вертикального киля при поперечной системе набора по днищу.
Требования к листовым конструкциям палуб и платформ будуг дополнены в результате приводимого ниже рассмотрения глобального механизма перехода в предельное состояние.
Предельное состояние и требования к толщинам листовых конструкций, деформирующихся совместно с бортовым набором
Согласно изложенному этот тип деформирования реализуется только при варианте 1.1 ориентации листовой конструкции.
В данном варианте Корпусные конструкции транспортных судов ледового плаванияледовая нагрузка воспринимается листовой конструкцией, подкрепляющими ее ребрами жесткости и пересекающими ее балками основного набора. В пластический механизм, образуемый при переходе в предельное состояние, включаются все перечисленные связи.
Поскольку нагрузка распределена вдоль кромки листовой конструкции на участке значительной протяженности (порядка 10 и более шпаций основного набора), при рассмотрении работ внутренних сил допустимо использование приема «размазывания» балочных элементов. Поэтому подкрепляющие ребра жесткости могут включаться в пластический механизм в рамках введенного выше представления о приведенной толщине листовой конструкции (Формула 125). На перемещении w работа внутренних сил в элементе единичной длины шарнира смятия листовой конструкции приведенной толщины составит:
Используя прием «размазывания» для балок основного набора, получим следующее выражение для работы внутренних сил в пластических шарнирах:
где:
- l1, l2 – расстояния от рассматриваемой листовой конструкции до опорных сечений балок основного набора на ближайших к ней листовых конструкциях с одной и другой стороны;
- φ (l) поправочная функция, аналогичная функции φ в (Формула 130), определяемая ниже;
- w0 – фактический предельный момент сопротивления поперечного сечения балки основного набора.
Работа внешних сил на элементе единичной длины определяется из очевидного соотношения
Разрешающее уравнение имеет вид
Из (Формула 149) следует выражение для интенсивности предельной нагрузки
Для определения поправочной функции ф (l) используется решение разд. “Корректировка и экспериментальная проверка модели деформирования пластины судов ледового плаванияДеформирование локально загруженной панели при образовании вмятины“, позволяющее учесть упругопластические свойства балок основного набора. На основании выполненного численного анализа получено следующее соотношение для поправочной функции:
где:
Подставляя в (Формула 150) выражения для tпр и φ (l), значения коэффициентов D, d и разрешая его относительно величины t, получим следующее требование к толщине листовой конструкции при ориентации по варианту 1.1:
где:
- а, а1 – согласно (Формула 125).
Требование (Формула 152) распространяется на листовые конструкции палуб и платформ при поперечной системе набора по борту.
Требования к размерам листовых конструкций по критерию устойчивости
Описанный в п. “Расчетные модели и методы, описывающие переход листовых конструкций в предельное состояние” подход к формированию требований к листовым конструкциям на основании критерий предельной прочности предполагает, что вплоть до перехода в предельное состояние листовые конструкции сохраняют свою первоначальную геометрическую форму. Для обеспечения данного допущения к листовым конструкциям, работающим в условиях одностороннего сжатия, должны быть предъявлены соответствующие требования по критерию устойчивости.
Будем исходить из следующей традиционно используемой при оценке устойчивости листовых конструкций расчетной схемы: листовая конструкция находится в условиях одностороннего сжатия, а приложенная к ней погонная нагрузка равномерно распределена вдоль кромки. Тогда условие устойчивости запишется в виде:
где:
- qϒ – равномерно распределенная расчетная погонная нагрузка на кромку листовой конструкции, примыкающей к наружной обшивке;
- σкр – критическое напряжение, определяемое с учетом отступления от закона Гука;
- t – толщина листовой конструкции.
Зависимость критических напряжений от эйлеровых устанавливается согласно Нормам прочности морских судов:
где:
- – эйлеровы напряжения для односторонне сжатой панели листовой конструкции, МПа
– если к наружной обшивке примыкает длинная сторона панели листовой конструкции;
- К1 = 4 – если к наружной обшивке примыкает короткая сторона листовой конструкции;
- t – толщина листовой конструкции, мм;
- c1, c2 – соответственно короткая и длинная стороны панелей, на которые листовая конструкция разбивается подкрепляющим ее набором, м.
Для определения входящей в (Формула 153) величины qϒ необходимо рассмотреть две задачи:
- обоснование нормативных подходов к назначению параметров расчетной нагрузки ру и bу, определяющих требования к устойчивости конструкции;
- построение соотношений для определения величины qϒ в зависимости от параметров ру и bу, а также геометрических размеров конструкции.
Обратимся первоначально к задаче нормирования. В соответствии с изложенными в п. “Нормирование расчетных нагрузок на листовые конструкции” подходами при оценке предельной прочности листовых конструкций используются следующие параметры ледовой нагрузки:
При назначении расчетных нагрузок, определяющих требования к устойчивости, необходимо учитывать физическое различие между опасными состояниями, связанными с исчерпанием предельной прочности и потерей устойчивости конструкции. Расчетные параметры pу и b отвечают принятому в качестве основного критерию предельной прочности. Как указано в разд. “Анализ повреждаемости и обоснование критериев прочности корпусов судов ледового плавания и ледоколовКритерии и методы оценки прочности. Расчётные ледовые нагрузки. Принципы регламентации режимов движения во льдах“, нарушение критерия предельной прочности приводит к появлению в конструкции фиксируемых повреждений. С другой стороны, потерю устойчивости конструкции, рассматриваемую в рамках представлений об упругой работе материала, следует трактовать как некоторое условное опасное состояние, не связанное не только с возможностью непосредственного разрушения конструкции, но даже и с развитием пластических деформаций.
Поэтому критерий устойчивости физически соответствует критерию фибровой текучести (первых пластических деформаций) – именно в такой связке данные критерии традиционно используются в нормативных документах, в частности в Правилах Регистра. Таким образом, расчетная нагрузка, регламентирующая требования к устойчивост и, должна соответствовать уровню нагруженности конструкций, при котором возникает фибровая текучесть.
Согласно выполненному автором представительному расчетному анализу соотношение между расчетными нагрузками, соответствующими критериям предельной прочности и фибровой текучести, устанавливаются следующими
где:
- р, b, q, pф, bф, qф – соответственно параметры предельной нагрузки конструкции и нагрузки фибровой текучести;
- Кпр = 1,8 – нормативная величина коэффициента запаса предельной прочности.
Переходя в (Формула 156) от параметров pф, bф к параметрам нагрузки, определяющей требования к устойчивости, на основании (Формула 155) будем иметь
где:
- ру, bу – интенсивность и высота распределения расчетной ледовой нагрузки при оценке устойчивости.
Поскольку, однако, в соответствии с изложенным подходом величины р’ и b’ соответствуют предельно локализованной нагрузке, дальнейшее уменьшение высоты bу по сравнению с b’ не целесообразно. Поэтому следует принять
Соотношением (Формула 158) определяются расчетные значения параметров ледовой нагрузки, регламентирующие требования к устойчивости листовых конструкций.
Вторая задача, связанная с определением qу,применительно к рассмотренным в п. “Нормирование расчетных нагрузок на листовые конструкции” вариантам ориентации листовых конструкций решается в рамках традиционно используемых при расчетах в упругой области подходов к распределению внешней нагрузки между пересекающимися и параллельными связями.
Для упрощения итоговых зависимостей для вариантов 1.1, 2.2 можно полагать, с некоторой ошибкой в безопасную сторону, что высота распределения локализованной нагрузки сопоставима со шпацией основного набора. Тогда погонная нагрузка имеет распределение вдоль кромки, близкое к треугольному, а ее средняя величина, полагаемая равномерно распределенной в соответствии с принятой расчетной схемой оценки устойчивости, определяется выражением
Для варианта 2.1 можно полагать, что локализованная нагрузка имеет высоты распределения, ориентировочно составляющую половину длины неподкрепленной кромки ср. Тогда при переходе к равномерно распределенной вдоль всей кромки нагрузке получим выражение для qу совпадающее с (Формула 159).
В варианте 1.2 нагрузка на кромку определяется из условия статического распределения реакции между листовой конструкцией и параллельными ей балками основного набора. Из очевидных соображений в этом случае может быть получено:
Решая совместно (Формула 153,154) с учетом соотношений (Формула 159, 160) для qу получим следующее соотношение для требуемой из условия устойчивости толщины листовой конструкции:
где:
- σТ – предел текучести материала, МПа.
Наряду с требованиями к толщине листовых конструкций должны предъявляться требования к устойчивости подкрепляющих их ребер жесткости, установленных в направлении к наружной обшивке. Данные требования достаточно тривиальны и в настоящей монографии не рассматриваются.
Сопоставительный анализ новых и действовавших требований. Выводы
Разработанные в настоящем разделе подходы к назначению расчетных ледовых нагрузок на листовые конструкции и методы расчета их предельной прочности и устойчивости в совокупности определяют новую методику проектирования листовых конструкций, не имеющую аналогов как в отечественных, так и в зарубежных нормативных документах. В связи с этим представляет интерес сопоставление требований данной методики с требованиями Правил, а также, согласно сформулированным в п. “Существующие требования к листовым конструкциям” соображениями, с требованиями предыдущей редакции.
Сопоставительные расчеты выполняются для судов среднего (L = 120 м) И большого (L = 250 м) водоизмещений из сетки судов и ледоколов из ледокольного ряда, разработанного автором совместно с А.Б. Нестеровым в процессе подготовки новых ледовых Правил. Сравнение производится для ледовых категорий действовавших Правил (Л3, Л2, Л1,УЛ, УЛА – суда; ЛЛ4, ЛЛЗ, ЛЛ2, ЛЛ1 – ледоколы) иэквивалентных ледовых категорий новых ледовых Правил (ЛУ2, ЛУ3, ЛУ4, ЛУ5, ЛУ7 – суда; ЛЛ6, ЛЛ7, ЛЛ8, ЛЛ9 – ледоколы).
Поскольку введенные в новой классификации ледовые категории ЛУ6, ЛУ8, ЛУ9 не имели аналогов в действовавшей классификации, при выполнении расчетов полагалось, что их общепроектные параметры (шпация, пролеты балок, форма корпуса и т. п.) соответствуют принятым для ЛУ7 (УЛА), за исключением предела текучести материала у категорий Л8, Л9, для которого были приняты следующие значения:
ЛУ8 –
ЛУ9 – .
Расчеты выполнялись для носового района ледового пояса (район АI). Рассматривались Конструирование и расчет палубных перекрытийлистовые конструкции палуб и поперечных переборок при поперечной системе набора по борту.
Использовались следующие конструктивные схемы листовых конструкций.
Палубы. На судах категорий ЛУ4-е-ЛУ9 и Л1, УЛ, УЛА и ледоколах листовая конструкция считалась подкрепленной Палубные конструкции морских деревянных судовребрами жесткости (бимсами), установленными на каждом шпангоуте нормально к наружной обшивке. На судах категорий ЛУ1 – ЛУЗ и ЛЗ, Л2 листовая конструкций считалась подкрепленной ребрами жесткости (бимсами), установленными на каждом втором (основном) шпангоуте.
Переборки. На судах категорий ЛУ4-нПУ9 и Л1, УЛ, УЛА и ледоколах листовая конструкция считалась подкрепленной ребрами жесткости, установленными через 0,6 м нормально к наружной обшивке. На судах категорий ЛУ1-ЛТУЗ и ЛЗ, Л2 листовая конструкция считалась подкрепленной ребрами жесткости, установленными через 1,0 м нормально к наружной обшивке.
Результаты сопоставительных расчетов представлены в табл. 1, 2 (для судов) и 3 (для ледоколов).
Выполненный сопоставительный анализ позволяет сделать следующие выводы.
В рамках новой системы требований устранено имевшееся в Правилах неоправданное увеличение толщин листовых конструкций палуб (у судов высших ледовых категорий и ледоколов) и переборок (у судов категории УЛА).
Вместе с тем с учетом имеющейся тенденции к ужесточению условий ледовой эксплуатации, уровень требований к листовым конструкциям судов высших ледовых категорий и ледоколов по сравнению с требованиями Правил, несколько повышен.
Результаты сопоставительных расчетов наглядно показывают преимущества разработанной системы требований, обеспечивающей плавное возрастание требуемых толщин листовых конструкций с ростом ледовой категории. Это выгодно отличает разработанные требования от требований действовавших Правил, в которых может иметь место как упомянутый неоправданный poor толщин одних листовых конструкций (см. табл. 1- 3, палубы, УЛ, УЛА, ЛЛ4 – ЛЛ1; см. табл. 2, переборки, УЛА), так и весьма медленное увеличение толщин других листовых конструкций, неадекватное соответствующему увеличению толщин наружной обшивки (см. табл. 1, 2, переборки, ЛЛ1 – УЛА; см. табл. 3, переборки).
Сопоставительные расчеты выполнялись для судов и ледоколов традиционных размерений и апробированных схем листовых конструкций. Однако разработанные требования потенциально позволяют учитывать влияние отклонений от традиционных соотношений. Эго, в частности, проявляется в физически оправданных результатах, полученных для крупнотоннажного судна (L = 250 м) и сверхмощного ледокола
, а также для схем листовых конструкций судов низших ледовых категорий.
Читайте также: Изготовление палубы судна из стеклопластика
Перечисленные преимущества разработанных требований объясняются введенными уточнениями в расчетные модели, позволяющие учитывать поддерживающий эффект, создаваемый окружающими листовые конструкции связями: пластинами наружной обшивки, балками основного набора, подкрепляющими ребрами жесткости. Благодаря учету данных факторов, а также достаточно гибкому подходу к вопросам нормирования расчетных ледовых нагрузок, удалось количественно обосновать наблюдаемый на практике факт, что при наличии мощной наружной обшивки (как у ледоколов высших ледовых категорий) возможна надежная эксплуатация листовых конструкций с весьма умеренными толщинами.
Внедрение разработанных требований в практику проект ирования конструкций ледовых усилений будет способствовать повышению надежности листовых конструкций, а также, в отдельных случаях, исключению избыточных запасов материала.
| Таблица 1. Сопоставление толщин листовых конструкций и наружной обшивки судов среднего водоизмещения (L = 120 м), определенных по новым требования и Правилам 1985 и 1991 гг. | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Документ | Толщины связей, мм | ||||||||
| Вид требования к толщине | ЛУ1 | ЛУ2 Л3 | ЛУ3 Л2 | ЛУ4 Л1 | ЛУ5 УЛ | ЛУ6 | ЛУ7 УЛ А | ЛУ8 | ЛУ9 |
| Листовые конструкции палубы | |||||||||
| Новые требования: | |||||||||
| Предельная прочность | |||||||||
| – по. ф. (Формула 142) | 4,5 | 6,2 | 7,8 | 6,5 | 7,5 | 8,4 | 10,2 | 11,9 | 13,4 |
| – по ф. (Формула 152) | 3,8 | 5,5 | 6,8 | 5,8 | 8,5 | 7,4 | 12,0 | 11,0 | 12,5 |
| Устойчивость | |||||||||
| – по ф. (Формула 161) | 7,9 | 8,5 | 9,0 | 6,5 | 7,5 | 8,4 | 10,2 | 11,9 | 13,4 |
| Принятая толщина | 8 | 9 | 9 | 7 | 9 | 9 | 12 | 12 | 14 |
| Правила 1985 г.: | |||||||||
| Принятая толщина | – | 11 | 12 | 8 | 9 | – | 11 | – | – |
| Правила 1991 г.: | |||||||||
| Принятая толщина | – | 10 | 10 | 13 | 16 | – | 26 | – | – |
| Ледовая конструкция переборки | |||||||||
| Новые требования: | |||||||||
| Предельная прочность | |||||||||
| – по ф. (Формула 135) | 4,6 | 5,8 | 4,9 | 6,9 | 9,0 | 10,0 | 12,6 | 12,7 | 13,4 |
| Устойчивость | |||||||||
| – по ф. (Формула 161) | 8,9 | 9,7 | 10,2 | 8,1 | 8,9 | 10,0 | 11,6 | 13,5 | 15,2 |
| Принятая толщина | 10 | 10 | 11 | 9 | 9 | 10 | 13 | 14 | 16 |
| Правила 1985 г.: | |||||||||
| Принятая толщина | – | 13 | 13 | 8 | 8 | – | 9 | 9 | 9 |
| Правила 1991 г.: | |||||||||
| Принятая толщина | – | 11 | 11 | 9 | 11 | – | 16 | – | – |
| Наружная обшивка | |||||||||
| Новые требования: | |||||||||
| Принятая толщина | 13 | 16 | 18 | 19 | 24 | 26 | 30 | 34 | 36 |
| Правила 1991 г.: | |||||||||
| Принятая толщина | – | 16 | 17 | 22 | 24 | – | 30 | – | – |
| Таблица 2. Сопоставление толщин листовых конструкций и наружной обшивки судов большого водоизмещения (L = 120 м), определенных по новым требования и Правилам 1985 и 1991 гг. | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Документ | Толщины связей, мм | ||||||||
| Вид требования к толщине | ЛУ1 | ЛУ2 Л3 | ЛУ 3 Л2 | ЛУ4 Л1 | ЛУ5 УЛ | ЛУ6 | ЛУ7 УЛ А | ЛУ8 | ЛУ9 |
| Листовые конструкции палубы | |||||||||
| Новые требования: | |||||||||
| Предельная прочность | |||||||||
| – по. ф. (Формула 142) | 6,6 | 9,5 | 11,7 | 9,4 | 15,3 | 18,7 | 23,7 | 26,7 | 29,5 |
| – по ф. (Формула 152) | 6,1 | 7,9 | 8,5 | 7,2 | 9,1 | 13,6 | 17,1 | 15,0 | 22,2 |
| Устойчивость | |||||||||
| – по ф. (Формула 161) | 8,7 | 9,5 | 10,0 | 7,3 | 8,0 | 9,2 | 11,0 | 13,0 | 16,5 |
| Принятая толщина | 9 | 10 | 12 | 10 | 15 | 19 | 24 | 28 | 30 |
| Правила 1985 г.: | |||||||||
| Принятая толщина | – | 14 | 14 | 9 | 9 | – | 10 | – | – |
| Правила 1991 г.: | |||||||||
| Принятая толщина | – | 13 | 13 | 14 | 19 | – | 39 | – | – |
| Листовая конструкция переборки | |||||||||
| Новые требования: | |||||||||
| Предельная прочность | |||||||||
| – по ф. (Формула 135) | 4,8 | 6,0 | 7,0 | 6,2 | 8,0 | 10,7 | 12,8 | 14,3 | 15,3 |
| Устойчивость | |||||||||
| – по ф. (Формула 161) | 9,7 | 10,5 | 11,2 | 8,9 | 9,8 | 10,9 | 12,5 | 14,7 | 18,5 |
| Принятая толщина | 10 | 11 | 12 | 9 | 10 | 11 | 13 | 15 | 19 |
| Правила 1985 г.: | |||||||||
| Принятая толщина | – | 13 | 13 | 8 | 8 | – | 9 | – | – |
| Правила 1991 г.: | |||||||||
| Принятая толщина | – | 13 | 14 | 11 | 14 | – | 28 | – | – |
| Наружная обшивка | |||||||||
| Новые требования: | |||||||||
| Принятая толщина | 16 | 19 | 22 | 22 | 26 | 30 | 36 | 40 | 48 |
| Правила 1991 г.: | |||||||||
| Принятая толщина | – | 20 | 22 | 24 | 28 | – | 39 | – | – |
| Таблица 2. Сопоставление толщин листовых конструкций и наружной обшивки ледоколов, определенных по новым требования и Правилам 1985 и 1991 гг. | ||||||
|---|---|---|---|---|---|---|
| Документ | Толщины связей, мм | |||||
| Вид требования к толщине | ЛЛ6 ЛЛ4 (4 МВт) | ЛЛ6 ЛЛ4 (9,6 МВт) | ЛЛ7 ЛЛ3 (19,1 МВт) | ЛЛ8 ЛЛ2 (30,5 МВт) | ЛЛ9 ЛЛ1 (55 МВт) | ЛУ9 ЛЛ1 (110 МВт) |
| Листовые конструкции палубы | ||||||
| Новые требования: | ||||||
| Предельная прочность | ||||||
| – по. ф. (Формула 142) | 7,2 | 7,4 | 11,6 | 15,4 | 18,7 | 24,8 |
| – по ф. (Формула 152) | 6,9 | 6,4 | 8,1 | 11,9 | 13,1 | 18,3 |
| Устойчивость | ||||||
| – по ф. (Формула 161) | 8,9 | 8,6 | 10,0 | 12,9 | 15,3 | 16,1 |
| Принятая толщина | 9 | 9 | 12 | 16 | 19 | 26 |
| Правила 1985 г.: | ||||||
| Принятая толщина | 7 | 8 | 12 | 14 | 14 | 16 |
| Правила 1991 г.: | ||||||
| Принятая толщина | 15 | 24 | 34 | 38 | 32 | 42 |
| Листовая конструкция переборки | ||||||
| Новые требования: | ||||||
| Предельная прочность | ||||||
| – по ф. (Формула 135) | 10,5 | 9,5 | 11,3 | 14,6 | 17,6 | 16,4 |
| Устойчивость | ||||||
| – по ф. (Формула 161) | 10,1 | 10,0 | 11,5 | 14,2 | 16,8 | 17,7 |
| Принятая толщина | 11 | 10 | 12 | 15 | 18 | 18 |
| Правила 1985 г.: | ||||||
| Принятая толщина | 26 | 26 | 32 | 40 | 44 | 50 |
| Правила 1991 г.: | ||||||
| Принятая толщина | 15 | 16 | 15 | 15 | 16 | 16 |
| Наружная обшивка | ||||||
| Новые требования: | ||||||
| Принятая толщина | 30 | 32 | 40 | 46 | 46 | 46 |
| Правила 1991 г.: | ||||||
| Принятая толщина | – | – | – | – | – | – |
Выводы по главе 3
- Задача проектирования (определения требуемых размеров связей) бортовых перекрытий, испытывающих воздействие ледовых нагрузок, традиционно занимает одно из центральных мест в общей проблеме обеспечения ледовой прочности корпусов судов и ледоколов. Концепция проектирования перекрытия по критерию предельной прочности основывается на иерархическом подходе к идеализации его конструкции: Конструкция и расчеты днищевых перекрытий в корпусе суднасоставляющие перекрытие балки разделяются на несколько иерархических уровней; каждый уровень реагирует на ледовые нагрузки различной степени локализации и вступает в силовое взаимодействие с балками более высокой иерархии; в соответствии с процедурой расчета предельной прочности сложных балочных систем устанавливается иерархическое соответствие между уровнями балок и типами пластических механизмов, описывающих переход в предельное состояние отдельных частей перекрытия; требования к размерам связей перекрытия устанавливаются в рамках принципа равнопрочности балок различных иерархических уровней.
- Перспективы получения рациональных решений при проектировании перекрьггий обеспечиваются в рамках разработанного метода гибкого проектирования бортовых перекрытий, ориентированного на исключение избыточных запасов прочности и представляющего проектанту следующие возможности: учёт различий в величинах расчётных ледовых нагрузок, воздействующих на балки различных иерархических уровней; вариацию соотношения между изгибными и сдвиговыми геометрическими характеристиками при проектировании поперечного сечения балки, позволяющую снижать требуемый момент сопротивления при наличие запаса по площади стенки; учёл’ избыточных запасов материала, образующихся при проектировании поперечных сечений балокболее низких уровней (шпангоутов, стрингеров), позволяющий снижать требуемые размеры балок более высоких уровней (стрингеров, рамных шпангоутов); перераспределение материала межу балками различных иерархических уровней с целью оптимизации размеров перекрытия.
- Разработана система дополнительных требований к предельной прочности и устойчивости элементов поперечных сечений балочных конструкций, обеспечивающая исключение наблюдаемых на практике повреждений, связанных с выходом из плоскости (заваливанием) балок и смятием их стенок. Требования к предельной прочности основаны на оригинальных расчетных моделях, описывающих предельное состояние балочных конструкций при заваливании профиля и совместном смятии и изгибе стенки. Система требований к устойчивости элементов поперечных сечений полноценно учитывает специфику балочных конструкций ледовых усилений.
- Получено оригинальное решение о запредельном деформировании изолированной кницы и предельном состоянии шпангоутной ветви с кницами, позволяющее обосновать следующие положения: при проектировании балочных конструкций с кничными соединениями расчетную длину пролета следует назначать как расстояние между сечениями у концов книц; у балок с относительно низким уровнем жесткости в зависимости от наличия у книц подкрепляющего пояска и его размеров уровень допустимых прогибов составляет 4 + 8 толщин, если прогибы выпучивания кницы превышают указанный уровень, то существует опасность снижения предельной прочности балки на 15 + 20 % и целесообразно выполнение конструктивных мероприятий по подкреплению поврежденных книц; у относительно жестких балок влияние книц на уровень предельной прочности проявляется относительно слабо и подкрепление кничных соединений необходимо только в случае наличия в узле соединения трещин и разрывов.
- Сформирована система расчетных требований к предельной прочности и устойчивости, а также конструктивно-технологических ограничений, накладываемых на размеры поперечного сечения балок и применительно к ней разработаны алгоритм и программа оптимального проектирования балочных конструкций ледовых усилений. Для относительно жестких балок, типичных для судов высоких ледовых категорий, оптимальным является профиль, у которого отсутствует запас по площади стенки, стенка относительно низкая, поясок относительной узкий, площадь пояска значительно меньше площади стенки. Такая конфигурация профиля обеспечивает высокую надежность при восприятии интенсивных локальных ледовых нагрузок. При снижении жесткости балки, практически наблюдаемом при понижении ледовой категории судна, образуется значительный запас по площади стенки, у стенки и пояска увеличиваются относительные высота и ширина, площадь пояска увеличивается по сравнению с площадью стенки и конфигурация профиля приближается к типичной для конструкций морских (не ледовых) судов.
- Построены расчетные требования к толщине наружной обшивки, основанные на уточненной расчетной модели, описывающей предельное состояние локально загруженной пластины и полноценно учитывающей фактор локальности ледовой нагрузки. При высокой степени локализации ледовой нагрузки, характерной для судов малых водоизмещений, уровень предельной прочности обшивки увеличивается в 1,5 ÷ 2 раза по сравнению с использовавшейся ранее моделью балки-полоски. Данный результат хорошо согласуется со сложившейся в отношении малых судов еще в 1960-1970-е годы проектной практикой.
- Требования действующих Правил Регистра к листовым конструкциям нуждаются в значительном совершенствовании, включающем: классификацию листовых конструкций; обоснование нормативных подходов к назначению расчетных нагрузок на листовые конструкции; разработку расчетных моделей, описывающих переход листовых конструкций в предельное состояние с учетом особенностей деформирования совместно с наружной обшивкой, подкрепляющими ребрами жесткости и балками основного набора.
- Назначаемые в качестве расчетных параметры ледовой нагрузки, традиционно учитывающие прежде всего специфику работы балочных конструкций, дают максимум погонной нагрузки и большую длину эпюры распределения и рассматриваются как глобальные. Они применимы для оценки прочности листовых конструкций, переходящих в предельное состояние совместно с пересекающими их балками основного набора, а также подкрепляющими листовую конструкцию ребрами. Для полноценного учета специфики листовых конструкций дополнительно к ним должны вводиться локализованные по высоте распределения высокоинтенсивные расчетные ледовые нагрузки, приводящие к образованию локальных механизмов перехода в предельное состояние листовой конструкции совместно с наружной обшивкой. Максимальная степень локализации соответствует 3-кратному уменьшению высоту распределения ледовой нагрузки. При назначении расчетных нагрузок, определяющих требования к устойчивости листовых конструкций, необходимо учитывать физическое различие между опасными состояниями, связанными с исчерпанием предельной прочности и потерей устойчивости конструкции. Критерий устойчивости физически соответствует критерию фибровой текучести (первых пластических деформаций). Поэтому необходима корректировка расчетных натрузок в соответствии с установленным нормативным соотношением между уровнями предельной прочности и фибровой текучести.
- Воздействие глобальной нагрузки вызывает предельное состояние только в листовых конструкциях, ориентированных вдоль корпуса и перпендикулярно основному набору. Расчетная модель, описывающая предельное состояние листовой конструкции с данной ориентацией, основана на рассмотрении предельного равновесия пластического механизма, включающего наряду с листовой конструкцией балки основного набора и подкрепляющие ребра жесткости. При воздействии локализованных нагрузок во всех вариантах ориентации образуются локальные пластические механизмы, в которых листовая конструкция деформируется совместно с пластиной наружной обшивки. Различие в жесткостях листовой конструкции, балок основного набора и пластин обшивки учитывается введением поправочных функций, установленных с помощью упругопластических решений см. “Ледовые усиления судов Арктического плаванияМетоды расчета прочности конструкций ледовых усилений при глубоком пластическом деформировании” и “Элементы судовых конструкций ледокола, расчет прочностиКорректировка и экспериментальная проверка модели деформирования пластины судов ледового плавания“.
- Разработанная система требований к размерам листовых конструкций позволяет устранить имевшееся в Правилах неоправданное увеличение толщин листовых конструкций палуб (у судов высших ледовых категорий и ледоколов) и переборок (у судов категории УЛА) и количественно обосновать наблюдаемый на практике факт, что при наличии мощной наружной обшивки (как у ледоколов высших ледовых категорий) возможна надежная эксплуатация листовых конструкций с весьма умеренными толщинами. Вместе с тем с учетом имеющейся тенденции к ужесточению условий ледовой эксплуатации уровень требований к листовым конструкциям судов высших ледовых категорий и ледоколов по сравнению с требованиями Правил несколько повышен.
- В совокупности разработанные методы и модели определяют новую методику проектирования конструкций ледовых усилений на основании критериев предельной прочности и устойчивости, не имеющую аналогов как в отечественных, так и в зарубежных нормативных документах. Ее практическое использование в требованиях Правил Регистра к конструкциям ледовых усилений будет способствовать повышению надежности корпусов судов ледового плавания и исключению избыточных запасов материала.
🤝 Поддержите нашу работу
Нашли опечатку? Выделите и нажмите CTRL+Enter
