Разработанная приближенная модель деформирования пластины основана на ряде допущений, справедливость которых требует экспериментального подтверждения. Сформулируем физические принципы экспериментальной проверки модели.
- Деформирование локально загруженной панели при образовании вмятины
- Работа материала в пластических шарнирах
- Запредельное деформирование изолированной балки
- Запредельное деформирование балки со сдвиговым характером перехода в предельное состояние. Учет поддерживающего влияния поясков
- Приближенная модель упругопластического и запредельного деформирования панели
- Определение эмпирических коэффициентов и проверка модели деформирования локально загруженной панели
- Деформирование локально загруженной листовой конструкции совместно с наружной обшивкой при образовании вмятины-выпучины
- Расчетная схема системы «листовая конструкция – наружная обшивка»
- Предельное состояние и запредельное деформирование изолированного листа
- Запредельное деформирование системы листовой элемент – пластина наружной обшивки
- Упругопластическое деформирование системы листовой элемент – пластина наружной обшивки
- Практическое использование решений об упругопластическом и запредельном деформировании конструкций
- Выводы по главе 2
Основным допущением решения является ГМШ. В ее рамках игнорируется процесс постепенного распространения пластических деформаций, что, естественно, приводит к ужесточению модели по сравнению с реальной конструкцией.
Однако, если остальные допущения модели и метод построения теоретического решения в целом достоверно отражают Напряжения в корпусе судна при его общем продольном изгибефизические процессы, происходящие при изгибе пластины за пределом текучести, то вносимая ГМШ погрешность будет достаточно стабильна и может быть устранена путем введения эмпирических поправок, установленных на основе сопоставлений с представительными экспериментальными данными.
Предлагается следующий способ корректировки теоретического решения с целью устранения погрешности, вносимой ГМШ. Пусть имеются данные представительного эксперимента, называемого в дальнейшем базовым, представляющие набор зависимостей
для некоторой вариации геометрических размеров пластины.
Теоретическое решение характеризуется соответствующим набором зависимостей
Согласование с данными базового эксперимента достигается путем введения следующей корректировки в теоретическое решение
где:
- k3 – эмпирический коэффициент;
- F – безразмерная поправочная функция, равная величине абсолютной погрешности в определении f от использования ГМШ.
Относительно структуры функции F могут быть сформулированы следующие физические соображения:
а Как показывает опыт расчетов балок и балок-полосок за пределом упругости, величина погрешности от применения ГМШ в основном зависит от значения параметра гибкости (отношение длины к толщине пластины или высоте сечения) – с увеличением гибкости погрешность уменьшается. Поэтому, если полагать, что полученное теоретическое решение достоверно отражает влияние на процесс пластического деформирования соотношений геометрических размеров пластины и пятна нагрузки, то можно принять
б Погрешность от использования ГМШ в значительной степени определяется ролью изгибных составляющих деформированного состояния в процессе их развития вплоть до образования шарнира текучести. Поэтому на упругопластической стадии погрешность увеличивается с ростом глубины пластического деформирования, характеризуемой величиной пластического прогиба. На запредельной стадии, когда Анализ повреждаемости и обоснование критериев прочности корпусов судов ледового плавания и ледоколовувеличение прогибов происходит за счет деформаций срединной поверхности, рост погрешности прекращается.
С учетом изложенного установлена следующая структура поправочной функции:
где:
- – относительные прогибы пластины в момент появление первых пластических деформаций и при окончании упругопластической стадии.
Для определения величины k3 и оценки достоверности принятой из физических соображений структуры поправочной функции F в качестве базового эксперимента используются испытания пластин, проводившиеся под руководством В. В. Козлякова. В эксперименте исследовалось деформирование пластин со следующими постоянными и варьируемыми параметрами:
Условия нагружения и закрепления пластин – равномерная нагрузка, жесткая заделка и абсолютный распор, соответствующие наиболее простому частному случаю теоретического решения, позволяли исключить влияние других факторов (локальность нагрузки, распора и т. п.) на результаты оценки погрешности ГМШ.
Результаты сопоставления с базовым экспериментом, подробно изложенные в отчетных материалах ЦНИИ им. акад. А. Н. Крылова, выборочно представленные на рис. 1, показали, что введенная поправочная функция (Формула 5) обеспечивает стабильное согласование откорректированного теоретического решения с экспериментальными данными во всем диапазоне варьирования параметров а и l. При этом значение эмпирического коэффициента в (Формула 3)
Проверка откорректированного решения осуществляется путем его сопоставления с результатами испытаний пластин, загруженных локальной нагрузкой и работающих в составе панели (Дополнительные или усиленные конструкции корпуса суднанатурные конструкции) или перекрытий (жестяные модели).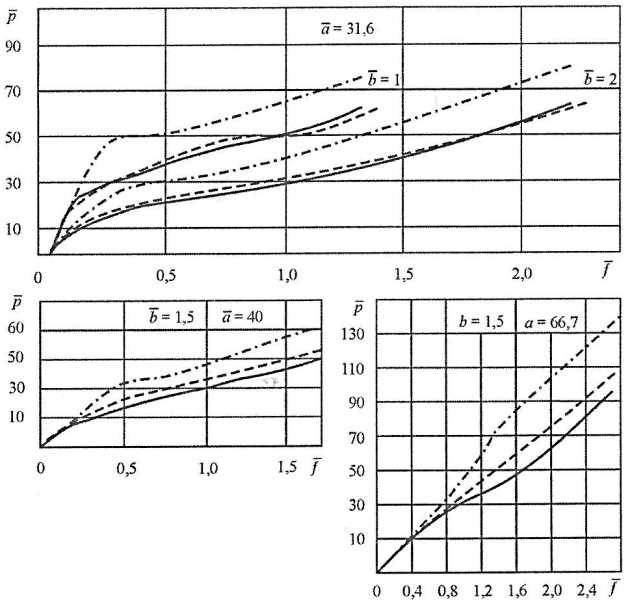
– • – • – • – • – • – – теоретическое решение. См. “Модель запредельного деформирования пластины“, “Модель упругопластического деформирования пластины при активном нагружении и разгрузке“; ———— – откорректированное решение; — — — — – базовый эксперимент
На рис. 2 представлено сопоставление теоретического решения с результатами испытаний 3-пролетной жестяной модели, проводившихся Л. М. Беленьким и В. В. Макаровым в 1992 году в ОНИЛ ПОЛЕКС по заказу автора. Модель имитировала работу локально загруженной пластины наружной обшивки в составе перекрытия (см. рис. 2, а). Как следует из рис. 2, б, имеет место хорошее согласование теоретических и экспериментальных зависимостей «нагрузка – прогиб».
1 – опорный контур; 2 – продольные и поперечные диафрагмы; 3 – обшивка; ———— – теоретические решения;
б – схема модели
На рис. 3 представлены результаты испытаний натурной панели при локальном нагружении, проводившихся под руководством автора в 1992 году в ЦНИИ им. акад. А. Н. Крылова. Сопоставление теоретических и экспериментальных зависимостей «Методы расчета прочности конструкций ледовых усилений при глубоком пластическом деформированиинагрузка – прогиб» (рис. 3, б) также подтверждает достоверность полученного решения.
На рис. 4 представлены результаты сопоставления решения с испытаниями жестяных моделей участков палубных перекрытий, имитирующих работу пластин настила совместно с продольными ребрами жесткости при воздействии локальных нагрузок от колесной техники. На рис. 4, а даны результаты для однопанельной модели (всего испытывалось пять таких моделей) и 3- панельной модели (испытывалось три модели). Хотя соотношения размеров палубных конструкций отличаются от характерных соотношений для конструкций ледовых усилений в сторону большей гибкости, а область работы (начальное упругопластическое деформирование) при полученном теоретическом решении описывается наиболее приближенно, имеет место хорошее согласование результатов как на стадии активного нагружения, так и при определении остаточных прогибов.
а – однопанельная модель; б – трехпанельная модель:
1 – активный прогиб; 2 – остаточный прогиб; ⚫ х экспериментальные точки
Таким образом, представленные результаты сопоставлений позволяют утверждать, что полученное теоретическое решение о деформировании локально загруженной пластины, работающей в составе перекрытия (панели), получило представительное экспериментальное подтверждение в широком диапазоне изменения жесткостных и геометрических параметров, а также при различной глубине развития пластических деформаций.
Деформирование локально загруженной панели при образовании вмятины
Работа материала в пластических шарнирах
Для исследования работы балочных конструкций ледовых усилений в области больших пластических деформаций необходимо конкретизировать условия работы материала в пластических шарнирах. Данный вопрос, несмотря на кажущуюся традиционность задачи, применительно к конструкциям ледовых усилений имеет ряд особенностей и остается в определенной мере дискуссионным.
Дополнительные или усиленные конструкции корпуса суднаПовышенная жесткость балочных конструкций ледовых усилений требует при рассмотрении их напряженного состояния обязательного учета влияния перерезывающих сил. Работа в области больших пластических деформаций связана с появлением растягивающих продольных усилий. Наличие мощного присоединенного пояска, образованного толстой наружной обшивкой, ставит под вопрос используемое в прикладной теории изгиба балок допущение о возможности пренебрежения собственной жесткостью поясков двутавровой балки.
Примем следующую систему обозначений и безразмерных параметров:
- – площади стенки, свободного и присоединенного поясков;
- – площадь поперечного сечения;
- – относительные площади элементов поперечного сечения;
- – толщины свободного и присоединенного поясков;
- h – высота стенки;
- l – длина пролета балки;
- W0 – предельный момент сопротивления поперечного сечения;
- – пределы текучести материала при растяжении и сдвиге;
- M, N, T – изгибающий момент, перерезывающая и продольная сила, действующие в сечении балки,
Рассмотрим первоначально ряд частных случаев.
Для простого изгиба (без продольных сил) в результате исследований Л. М. Беленького, А. М. Бененсона и В. А. Курдюмова, В. В. Козлякова, Б. Е. Топчего и др., а также исследований автора, сформировались следующие представления о работе двутаврового профиля в предельном состоянии:
- Перерезывающая сила воспринимается только стенкой (без участия поясков);
- При достижении перерезывающей силой предельного значения N = N0 сечение неспособно воспринимать изгибающий момент (М = 0), поскольку при этом нарушается взаимосвязь между поясками и они, оставаясь незагруженными, не вовлекаются в изгиб балки.
Изложенным представлениям отвечает условие пластичности (предельная кривая), которое строго может быть представлено только в неявном виде, но, с достаточной точностью аппроксимируется следующим уравнением:
Уравнению (Формула 8) отвечает равномерная по высоте стенки эпюра касательных напряжений, а нормальные напряжения, что важно отметить для дальнейшего изложения, не имеют разрыва в точках соединения поясков со стенкой, т. е.
где:
- zп – координата пояска.
Достоверность уравнения (Формула 8), учитывающего взаимовлияние изгибающего момента и перерезывающей силы (взаимовлияние М – N), подтверждена в проведенном автором экспериментальном исследовании особенностей пластического деформирования конструкций ледовых усилений.
Предлагается к прочтению: Грузовые характеристики морских грузов
Уравнение предельной кривой в этом случае удается представить в явном виде
где:
- ф(Т) – функции.
Для третьего частного случая, при действии в сечении продольной и перерезывающей сил (М = 0), возможны два варианта уравнений предельной кривой, соответствующих двум крайним допущениям о форме эпюры нормальных напряжений.
В первом варианте будем полагать, что выполняются условия неразрывности эпюры (Формула 9). Тогда, сохраняя принятую при получении (Формула 8) равномерную по высоте стенки эпюру касательных напряжений, получим:
Однако, как показывает анализ, использование (Формула 11) при описании запредельного деформирования балки приводит к следующему. Возрастание продольного усилия с ростом перемещений приводит к столь существенному уменьшению перерезывающих сил в опорных сечениях, что сопровождается сбросом нагрузки, продолжающимся до тех пор, пока продольные усилия не достигнут значений, близких к предельному. Поскольку в действительности такой картины деформирования не наблюдается, будем исходить из второго варианта, допускающего возможности разрывов напряжений в точках соединения поясков и стенки. Тогда, согласно условию текучести, получим в пояске
; в стенке
Соотношениям (Формула 12) соответствует следующее уравнение предельной кривой:
При этом, с физических позиций, наличие разрыва (Формула 12) вполне допустимо, поскольку развитие сдвиговых деформаций в стенке не препятствует (в отличие от случая изгиба со сдвигом) подключению поясков к восприятию продольной силы. Отмеченного сброса нагрузки при использовании (Формула 13) не происходит. Поэтому в дальнейшем будем применять уравнение (Формула 13), базирующееся на разрывной эпюре напряжений (Формула 12).
Объединяя уравнения предельных кривых для частных случаев, получим следующее приближенное уравнение предельной поверхности для общего случая действия в сечении всех рассматриваемых компонентов усилий:
где:
Перейдем к рассмотрению перемещений в пластических шарнирах. Поскольку рассматриваемое в дальнейшем запредельное деформирование осуществляется в основном за счет перемещений продольно-изгибного характера, основной интерес представляет величина удлинения Общие вопросы проектирования судовых конструкцийоси балки в пластических шарнирах. Для частного случая чисто сдвигового характера предельного состояния способы определения перемещений, а также уточнения действующих в шарнирах величин силовых параметров, будут изложены в п. см. “Запредельное деформирование балки со сдвиговым характером перехода в предельное состояние. Учет поддерживающего влияния поясков“.
Удлинения оси в пластических шарнирах находятся на основании следующих соотношений:
где:
- – безразмерные функции;
- θk – угол слома в пластическом шарнире;
- Sk – отстояние нейтральной оси от оси центров тяжести балки, положительное при смещении нейтральной оси в сторону присоединенного пояска.
Полученные соотношения описывают работу пластического шарнира в объеме, необходимом для рассмотрения запредельного деформирования балочных конструкций, у которых преобладающим является изгибно-продольный характер деформированного состояния, а влияние перерезывающих сил может рассматриваться в качестве дополнительного фактора. Способы описания перемещений в шарнирах и процесса деформирования балочных конструкций с преимущественно сдвиговым характером перехода в предельное состояние (так называемый механизм чистого сдвига) будут рассмотрены в п. см. “Запредельное деформирование балки со сдвиговым характером перехода в предельное состояние. Учет поддерживающего влияния поясков“.
Запредельное деформирование изолированной балки
Деформирование балки в составе перекрытия под действием локальной нагрузки в рамках балочной идеализации может быть описано с помощью расчетной схемы, представленной на рис. 5.
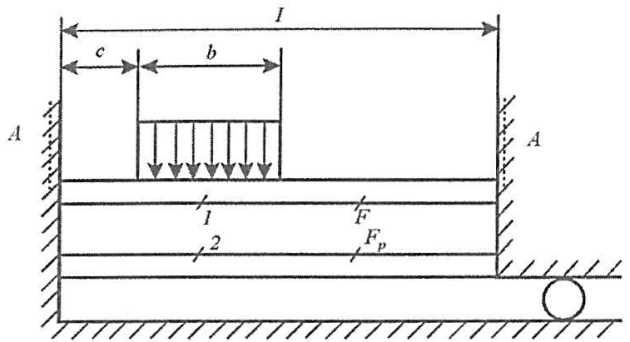
1 – балка; 2 – распорная конструкция
Действующая на балку нагрузка G, произвольно расположенная в пролете балки, характеризуется тремя параметрами – значение погонной нагрузки, g = const; b – высота распределения нагрузки; с — наименьшее расстояние от края нагрузки до ближайшего опорного сечения; G = gb – полная сила. Окружающие балку конструкции накладывают ограничения на угловые и горизонтальные (осевые) перемещения балки. Данные ограничения традиционно характеризуются значениями коэффициента податливости А и площади распорной конструкции
.
Действительные условия работы локально загруженных балок, как правило, характеризуются распором, близким к абсолютному. Однако в отдельных случаях, например, при экспериментальных исследованиях, возможны схемы работы балок с коэффициентом распора kp < 1.
Образуемый при переходе в предельное состояние Технология судоремонта, причины и виды поврежденийпластический механизм в общем случае представляет собой так называемую трехшарнирную схему (рис. 6, а). У опорных сечений возникают пластические шарниры согласно уравнению предельной кривой (Формула 8), в пролете – изгибный шарнир согласно (Формула 10) при Т = 0. В частном случае вместо трехшарнирной возможна реализация схемы чистого сдвига, характерной для высоких тонкостенных балок (см. рис. 6, б). Деформирование балок со сдвиговым характером предельного состояния имеет ряд существенных особенностей,и будет рассмотрено отдельно в п. см. “Запредельное деформирование балки со сдвиговым характером перехода в предельное состояние. Учет поддерживающего влияния поясков“.
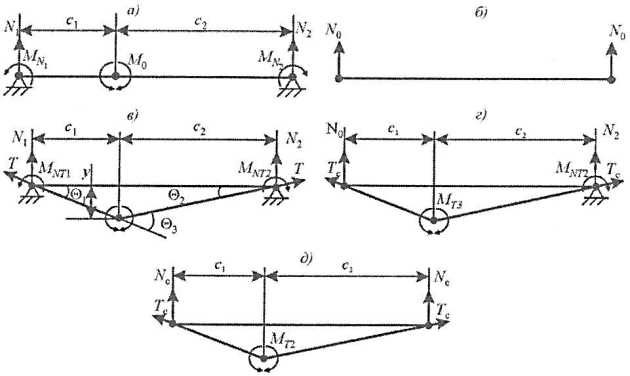
а, б и при последующем запредельном деформировании
После образования трехшарнирной схемы начинается запредельное деформирование, при котором пластический механизм приобретает способность воспринимать возрастающую нагрузку в процессе увеличения прогибов, появления и роста продольных усилий Т распорного характера и перерезывающих сил и соответственно уменьшением изгибающих моментов согласно уравнениям (Формула 10), (Формула 14) (см. рис. 6, в).
При достижении перерезывающей силой предельного значения сначала в опорном шарнире
(рис. 6, г), а затем и шарнире
(рис. 6, д) общее уравнение (Формула 14) переходит в частный случай предельной кривой (Формула 13):
При выполнении условия
перераспределение усилий в шарнирах заканчивается, а дальнейший рост нагрузки уравновешивается возрастанием вертикальных проекций усилий
в процессе интенсивного нарастания прогибов и соответственно углов слома в шарнирах.
Разрешающая система, описывающая запредельное деформирование балки, включает систему уравнений равновесия и условие совместности перемещений, позволяющее раскрыть статическую неопределимость системы пластический механизм – распорная конструкция.
С учетом построений, представленных на рис. 7, а также соотношений (Формула 15) условие совместности примет вид:
где:
- k – номер пластического шарнира;
- еp – сближение опорных сечений в результате Корпусные конструкции транспортных судов ледового плаваниясжатия распорной конструкции;
- еу – сближение опорных сечений вследствие искривления оси балки;
- у – максимальный прогиб балки;
- с1, с2 – расстояния от пролетного шарнира до опор балки.
Уравнение (Формула 16) не может решаться отдельно от уравнений равновесия, поскольку согласно (Формула 15) в него входит ТN, зависящая от N. Система уравнений равновесия в совокупности с уравнениями предельной поверхности в пластических шарнирах применительно к общему случаю трехшарнирной схемы (см. рис. 6, в), включающей частные случаи пластических механизмов (рис. 6, г, д), имеет вид
где:
Разрешающая система (Формула 16), (Формула 17) включает пять нелинейных уравнений относительно неизвестных
и три ограничения в виде неравенств на максимальные значения
Срабатывание ограничений означает, с одной стороны, понижение числа неизвестных, с другой – переход от общего уравнения предельной поверхности к одному из частных случаев предельной кривой. Обеспечение сходимости итерационных алгоритмов решений систем нелинейных уравнений вблизи точек перехода связано с известными математическими трудностями. Для их преодоления дополнительно к стандартным методам решения систем нелинейных уравнений были разработаны специализированные процедуры, управляющие итерационными процессами при прохождении точек перехода и скачкообразном изменении числа неизвестных.
В результате совместного решения уравнений (Формула 16), (Формула 17) определяется следующая система зависимостей:
Распространение полученного решения на упругопластическую стадию осуществляется при помощи подходов, аналогичных использованным в п. см. “Модель упругопластического деформирования пластины при активном нагружении и разгрузке“. Построение упругопластического решения на основании ГМШ применительно к рассматриваемой балке не встречает принципиальных затруднений, хотя и приводит к достаточно громоздкой процедуре в виду наличия несимметрии нагружения и разнообразия кинематических условий в пластических шарнирах.
Процедура корректировки решения, направленная на исключение вносимой ГМШ погрешности, осуществляется аналогично подходу п. см. “Корректировка и экспериментальная проверка модели деформирования пластины судов ледового плавания“. При этом в качестве базового эксперимента используются результаты проведенных автором испытаний натурных балочных конструкций ледовых усилений. Откорректированное решение представляется в виде:
где:
- у(G) – упругопластическое решение на основе ГМШ;
- – эмпирический коэффициент;
- Fδ – поправочная функция, аналогичная по структуре поправочной функции, введенной в решение для пластин.
Как показал анализ, величина эмпирического коэффициента
хорошо согласуется с полученным ранее значением k3 для пластин:
Этот результат показывает, что предложенная процедура корректировки имеет универсальный характер и, следовательно, объективно соответствует протекающим при упругопластическом деформировании физическим процессам.
Вопросы разгрузки для рассматриваемой изолированной балки не имеют принципиального значения, поскольку для балочных конструкций судового корпуса, а тем более жестких конструкций ледовых усилений, при достаточно глубоком пластическом деформировании остаточный прогиб несущественно отличается от активного. Процедура описания разгрузки при работе балок совместно с наружной обшивкой будет рассмотрена в п. см. “Приближенная модель упругопластического и запредельного деформирования панели“.
Запредельное деформирование балки со сдвиговым характером перехода в предельное состояние. Учет поддерживающего влияния поясков
Полученное в п. см. “Запредельное деформирование изолированной балки” решение основывается на традиционном для балочных конструкций представлении о возникновении пластических шарниров в отдельных сечениях балки. Частным случаем такого подхода является переход в предельное состояние по механизму чистого сдвига (см. рис. 6, б), когда в опорных сечениях образуются сдвиговые шарниры, допускающие вертикальные перемещения балки относительно опоры. Данный механизм соответствует чисто линейной постановке задачи и не позволяет описать дальнейшее запредельное деформирование.
С другой стороны, при сдвиговом шарнире пластические деформации сосредоточены только в стенке двутавровой балки, а пояски остаются практически незагруженными.
Естественно предположить, что наличие поясков, а тем более характерного для ледовых усилений мощного присоединенного пояска, должно препятствовать осуществлению вертикальных перемещений в сдвиговом шарнире. Это подтверждается и результатами испытаний балочных конструкций ледовых усилений. Согласно этим испытаниям механизм чистого сдвига позволяет достаточно обоснованно прогнозировать только величину предельной нагрузки балки (рис. 8), а картина деформирования после реализации предельного состояния (рис. 9), связанная с потерей устойчивости стенки (выход из плоскости с образованием диагональных гофров в районе опорных сечений), принципиально отличается от схемы перемещений по механизму чистого сдвига.

Для преодоления отмеченных методологических недостатков необходимо построение более точной модели, позволяющей описать совместные перемещения поясков и стенки при сдвиговом характере 104 предельного состояния.
Однако представление кинематически допустимого поля совместных перемещений поясков и стенки в рамках допущения, что пластические деформации сосредотачиваются только в отдельных сечениях, невозможно. Поэтому введем гипотезу, позволяющую расширить представление о сдвиговом пластическом шарнире: при изгибно-сдвиговом характере предельного состояния пластические деформации в стенке развиваются в некоторой области конечной длины (△).
Предполагая, что по длине пластической области △ деформации постоянны, получим следующие выражения для компонентов деформаций, интенсивности деформаций и работы внутренних сил пластической области стенки △ (рис. 10, а):
где:
- х – координата вдоль нейтральной оси балки;
- z – вертикальная координата, отсчитываемая от нейтральной оси балки;
- △ – длина пластической области;
- θ – угол поворота сечений пластической области за счет изгибных деформаций;
- ψ – угол сдвига пластической области;
- – безразмерная функция;
- tс – Наружная обшивка и подкрепляющий ее набортолщина стенки.
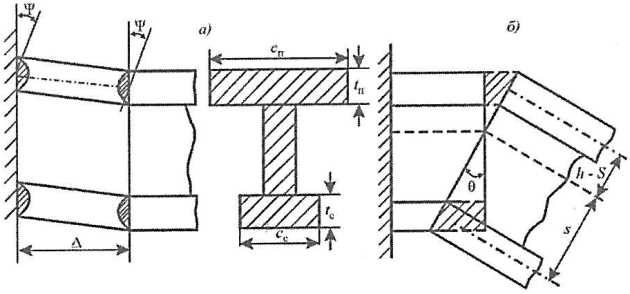
а – сдвиговые деформации; б – изгибные деформации
Перейдем к рассмотрению работы поясков. Введенное допущение о конечности размеров пластической области в стенке и условие совместности поля перемещений стенки и поясков обуславливают следующий кинематический механизм перехода поясков в предельное состояние: в сечениях, ограничивающих область пластических деформаций в стенке (х = 0 и х = △), по ширине поясков вводятся изгибные пластические шарниры, обеспечивающие возможность поворота пояска на угол сдвига ψ (рис. 10, а). При определении работы внутренних сил в поясках будем полагать, что удлинение срединной поверхности поясков в направлении оси х, вызванное поворотом сечений балки на угол θ (см. рис. 10, б), полностью сосредоточено в пластических шарнирах поясков в сечении х = △. Величина указанного удлинения составит:
для свободного пояска (индекс «1»)
для присоединенного пояска (индекс «2»)
Сформулированное предположение позволяет определить работу внутренних сил в поясках как работу в изгибных шарнирах на угле поворота ψ. При этом в шарнирах сечения х = 0 поворот на угол осуществляется вокруг срединной поверхности поясков, а в сечениях х = △ (у заделки) – вокруг оси, отстоящей от срединной поверхности на расстоянии
С учетом изложенного работа внутренних сил в шарнирах поясков
где:
- – толщина свободного (присоединенного) пояска.
Полная работа внутренних сил определится как
Определение работы внешних сил V на обобщенных перемещениях ψ и θ тривиально. Система разрешающих уравнений получается в рамках кинематического метода ТПР путем дифференцирования разности (Т – V) по обобщенным перемещениям. В общем случае указанная система оказывается нелинейной и требует численного решения. Однако применительно к представляющему основной интерес случаю чистого сдвига решение может быть получено в аналитическом виде.
В соответствии со схемой рис. 11 при чистом сдвиге будем иметь:
где:
- – ширина свободного (присоединенного) пояска;
- k – индекс пластической области;
- q – Оценка общей площади судовпогонная нагрузка;
- b – длина зоны действия нагрузки;
- W (х) – уравнение прогибов балки.
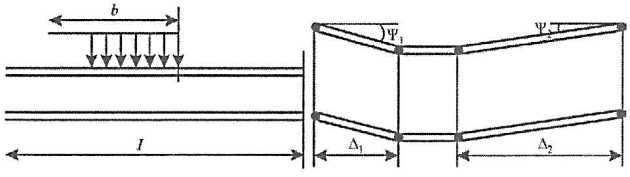
На параметры Ψk и Δk1s накладывается очевидное местности перемещений левой и правой частей балки
Разрешающая система уравнений относительно параметров q, Δ1, Δ2, Ψ1 имеет вид
При симметричном приложении нагрузки данная система имеет следующее аналитическое решение:
где:
- Qc предельная.
Загрузка балки при чистом сдвиге, определяемая на основании традиционного представления о сдвиговых пластических шарнирах.
График зависимости q ( A, b) в реальном диапазоне изменения параметра А, являющегося характеристикой конфигурации поперечного сечения балки, представлен на рис. 12. Он показывает, что учет поддерживающего влияния поясков увеличивает на (15-30) % величину предельной нагрузки чистого сдвига, определенную в рамках традиционной балочной идеализации. Непосредственный учет данного эффекта при оценке предельной прочности балочных конструкций осуществляется путем введения эффективного значения предельной перерезывающей силы:

В случае чистого изгиба эффект поддерживающего влияния поясков полностью исчезает, а пластическая область △ преобразуется в изгибный пластический шарнир. Аналогичный результат имеет место и при наличии продольных усилий: эффект поддерживающего влияния поясков нивелируется с ростом Т. Поэтому для учета рассмотренного эффекта при решении практических задач, касающихся не только чисто сдвиговых, но и изгибно-продольно- сдвиговых механизмов типа описанной в п. см. “Запредельное деформирование изолированной балки” трехшарнирной схемы, необходимо внести изменения в уравнение предельной поверхности (Формула 14):
Представленная модель перехода балки со сдвиговым механизмом в предельное состояние наряду с уточнением предельных характеристик поперечного сечения за счет фактора поддерживающего влияния поясков позволяет описать перемещения на запредельной стадии деформирования.
Отметим, что для случая поперечного изгиба при симметричном приложении нагрузки аналогичное решение независимо было получено В. А. Кулешом. Эффект независимой работы поясков при сдвиговом механизме предельного состояния был экспериментально обнаружен В. В. Макаровым и назван пластическим делением профиля. В дальнейшем Б. Е. Топчим было дано теоретическое описание этого эффекта, базирующееся на несколько иных по сравнению с предложенной моделью подходах.
Тем не менее количественные результаты Б. Е. Топчего в целом согласуются с изложенной моделью, что является лишним доказательством ее достоверности.
После образования пластического механизма в соответствии со схемой рис. 11 и начала перемещений начинается рост распорных продольных усилий, уравновешивающий возрастание нагрузки. Величина внешней нагрузки согласно уравнению равновесия определяется на основании следующего выражения:
Конструкция поперечных и продольных переборокВеличина продольного усилия определяется из аналогичного (Формула 16) уравнения, но при форме перемещений пластического механизма, соответствующей схеме рис. 11, для которой сближение опорных сечений вычисляется по формуле:
Рост продольных усилий продолжается до величины Tс, ив процессе этого роста, как правило, образуется пластический шарнир в пролете. Таким образом, схема деформирования становится полностью идентичной конечной схеме рис. 6, д, к которой в итоге приходит балка с трехшарнирным пластическим механизмом. Полная идентичность процесса деформирования рассматриваемых схем пластических механизмов в том граничном случае, когда оба они образуются при одинаковой предельной нагрузке, естественно, не достигается. Однако это не является недостатком решения, а, напротив, соответствует наблюдаемой реальной картине: потеря устойчивости стенки, сопровождающая переход в предельное состояние по чистому сдвигу, существенным образом изменяет характер дальнейшего деформирования.
Включение уточненного уравнения предельной поверхности (Формула 31), а также схемы запредельного деформирования балки со сдвиговым механизмом в общий алгоритм решения п. см. “Запредельное деформирование изолированной балки” не встречает принципиальных затруднений.
Приближенная модель упругопластического и запредельного деформирования панели
Полученное решение о деформировании изолированной балки может непосредственно использоваться для описания процесса образования длинных вмятин, при котором, в соответствии с изложенными в разд. см. “Анализ повреждаемости и обоснование критериев прочности корпусов судов ледового плавания и ледоколовОсобенности и закономерности ледовой повреждаемости. Отдельные (допустимые) и массовые (недопустимые) ледовые повреждения” соображениями, происходит одновременное деформирование большого числа балок. Однако для представляющего основной практический интерес случая образования отдельных вмятин, когда поврежденный участок конструкции локализован в пределах 2-4 шп. основного набора, процесс деформирования имеет значительно более сложную природу и не может быть сведен к рассмотрению работы изолированной балки. Рассмотрим возможности построения модели, позволяющей описать совместное деформирование балок и наружной обшивки в процессе образования отдельной вмятины.
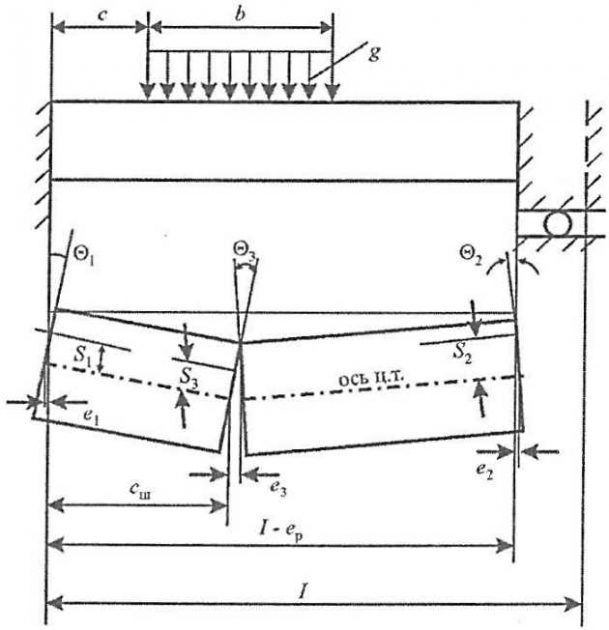
Примем следующую расчетную схему. Панель, образованная балками главного направления, скрепленными с наружной обшивкой и опертыми на недеформируемый опорный контур, загружена локальной нагрузкой, равномерно распределенной в пределах зоны контакта (рис. 13).
Нагрузка и геометрические размеры панели характеризуются следующими параметрами:
- а – расстояние между балками;
- l – длина пролета балки;
- с – отстояние горизонтального края зоны контакта от ближайшего опорного сечения;
- р – давление в зоне контакта;
- b,d – высота и длина зоны контакта, d = anp;
- np – число загруженных шпаций панели.

1 – балки главного направления;
2- опорные конструкции
На начальной стадии деформирования Наружная обшивка, настил палуб и переборкинаружная обшивка изгибается между балками, имеющими относительно небольшие собственные прогибы. Нагрузка воспринимается балками согласно следующим традиционным для балочной идеализации соотношениям:
где:
- gб. = pa – погонная нагрузка на балки, оси которых пересекают зону контакта (загруженные балки);
- gб.к = 0,5 pa – погонная нагрузка на балки, оси которых совпадают с границей зоны контакта (крайние балки).
Рост нагрузки и развитие пластических деформаций сопровождается интенсивным нарастанием прогибов загруженных балок и соответственным изменением формы деформированной поверхности. При этом собственно загруженные балки можно продолжать рассматривать в рамках подходов балочной идеализации. Поэтому на основании решения о деформировании балки (см. рис. 5), полученного в настоящем разделе, можно построить зависимости gб = gб (y). Однако равенство (Формула 34) уже нельзя считать справедливым вследствие кардинального изменения роли наружной обшивки. В результате перераспределения усилий в процессе роста прогибов загруженных балок она начинает работать как единая пластина с размерами в плане l x d, поскольку ее опорный контур образуют крайние балки и недеформированный опорный контур панели (рис. 14).
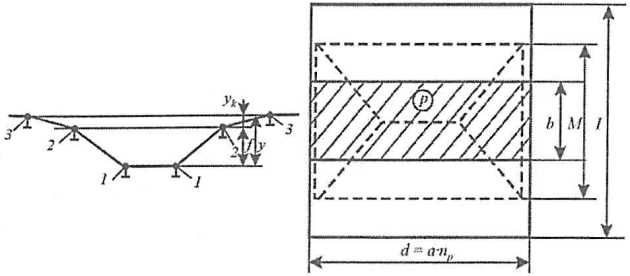
1 – загруженные балки;
2 – полузагруженные балки;
3 – крайние балки;
⚫ – линии шарниров текучести;
▅ – область приложения нагрузки
Деформирование пластины в соответствии со схемой рис. 14 описывается согласно решению разд. см. “Методы расчета прочности конструкций ледовых усилений при глубоком пластическом деформированииДеформирование локально загруженной пластины наружной обшивки при образовании бухтины“, на основании которого, в частности, могут быть определены зависимости pп = pп (f), M = M (f),
где:
- f – максимальный прогиб пластины относительно крайних балок;
- pп – интенсивность нагрузки, вызывающей в пластине прогиб f;
- M – размер образуемого в пластине механизма.
Есть основания предполагать, что при определенной глубине пластического деформирования процессы, протекающие в балках и пластине, становятся практически независимыми. На этом предположении и базируется описываемая ниже модель деформирования локально загруженной панели.
Примем следующую систему допущений, описывающих модель образуемого в процессе деформирования механизма.
1 Механизм состоит из двух частей:
- Пластины наружной обшивки, работающей в соответствии со схемой рис. 14;
- Загруженных балок, работающих в соответствии со схемой рис. 5 в рамках представлений балочной идеализации и концепции присоединенного пояска.
2 На перемещения частей пластического механизма накладывается условие совместности в виде равенства максимальных прогибов:
где:
- у, уk – максимальные прогибы загруженной и крайней балок;
- f – максимальный прогиб пластины.
Располагая результатами расчетов зависимостей нагрузка – прогиб для частей введенного принятыми допущениями механизма, можно, исходя из сформулированных принципов, составить следующее условие:
где:
- – интенсивность нагрузки, вызывающая в загруженной балке прогибу y;
- pф* – интенсивность нагрузки, вызывающая прогиб y в действительной конструкции панели.
Условие (Формула 36) поддается следующей конкретизации. На начальной стадии деформирования, когда, согласно изложенному, характер деформирования наружной обшивки отличается от принятого в модели, (Формула 36) имеет вид строгого неравенства. При глубоком пластическом деформировании картина деформирования модели и конструкции согласуется, и уравнение (Формула 36) может быть заменено приближенным (с практических позиций) равенством.
Читайте также: Подвесные лодочные моторы в малотоннажном судостроении
Следовательно, существует некоторое граничное напряженно-деформированное состояние механизма, начиная с которого его деформирование адекватно действительной конструкции панели. Граничное состояние характеризуется величиной соответствующей ему нагрузки
Поскольку при y < y* (p < p*) различие в поведении конструкции обусловлено способом описания работы наружной обшивки, для его компенсации в (Формула 36) сомножителем к величине pn вводится редукционная поправочная функция, позволяющая во всем диапазоне деформирования записать
где:
- – суммарная редуцированная нагрузка;
- – редуцированная нагрузка, воспринимаемая пластиной;
- – редукционная (поправочная) функция.
Физическая формулировка граничного состояния базируется на следующих представлениях. До наступления граничного состояния в наружной обшивке должно произойти такое развитие пластических деформаций, которое позволяет ей за счет перераспределения внутренних усилий в пластических зонах перейти от схемы деформирования между балками к типичному характеру работы единой пластины во вмятине (см. рис. 14). Сформулированному условию вполне соответствует ситуация, при которой в отдельных пластинах наружной обшивки, деформирующихся между балками, реализуется предельное состояние, обеспечивающее потенциальную возможность для дальнейшего изменения формы деформированной поверхности. Поскольку у конструкций ледовых усилений, как, впрочем, и у большинства судо-корпусных конструкций, имеет место примерное равенство предельных нагрузок пластин наружной обшивки
и балок главного направления
, то при
отмеченная потенциальная возможность реализуется за счет возрастания прогибов балок. Полагая, в соответствии с изложенным,
, примем следующую структуру редукционной функции:
где:
- ϒ3 – эмпирический коэффициент, ϒ3 ≈ 2,0.
Величина ϒ3 определяется на основании специального исследования, описанного в п. см. “Определение эмпирических коэффициентов и проверка модели деформирования локально загруженной панели“.
Для применения формул (Формула 37), (Формула 38) необходимо раскрыть неопределенность этих соотношений относительно входящей в них согласно (Формула 35) величины прогиба крайней балки уk. Не описывая подробно эту процедуру, отметим, что при определении уk учитывается, что пластина, примыкающая к крайней балке со стороны незагруженного участка, создает для нее поддерживающий эффект типа упругого основания (рис. 15). В частном случае, когда нагрузка приложена в пределах одной шпации и действует только на пластину (загруженные балки отсутствуют), оно соответствует рассмотренному в разд. см. “Методы расчета прочности конструкций ледовых усилений при глубоком пластическом деформированииДеформирование локально загруженной пластины наружной обшивки при образовании бухтины” решению для пластины.
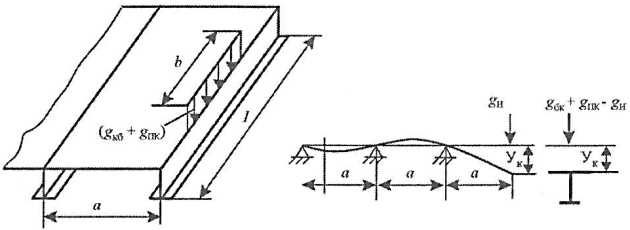
Однако в данном случае оно позволяет учесть деформируемость составляющих две противоположные стороны опорного контура пластины крайних балок. При этом отметим, что влияние деформируемости учитывается и при установлении значений коэффициентов опорной пары æ2 (см. рис. 5 Расчетная схема пластины), которые при этом также оказываются функциями прогиба крайних балок.
Описание процесса разгрузки в рамках уже полученных решений для балки и пластины применительно к рассматриваемой модели осуществляется с учетом силового взаимодействия, возникающего в условиях совместного перемещения балок и пластины, а также особенностей деформирования крайних балок.
Таким образом, получено решение об упругопластическом и запредельном деформировании балок совместно с наружной обшивкой при образовании вмятины, позволяющее учесть ряд новых физических эффектов. Несмотря на приближенный характер, решение адекватно отражает основные физические процессы, происходящие во вмятине. В его рамках дается количественное описание роли наружной обшивки в восприятии локальной нагрузки, позволяющее существенно уточнить представления о несущей способности конструкции панели по сравнению с традиционными подходами, основанными на балочной идеализации. Для иллюстрации данного утверждения на рис. 16 представлены результаты расчета бортовой конструкции, размеры которой приближенно соответствуют требованиям Правил Регистра, предъявляемым к судам высоких ледовых категорий: l = 3 м, а = 0,4 м, t = 25 мм, h = 420 мм, W0 = 1 700 см³, b = 0,8 м.
Согласно данным рис. 16 поддерживающий эффект, обеспечиваемый наружной обшивкой, в значительной степени изменяет представления о запасах прочности локально загруженной панели. При относительно малой длине зоны нагружения (d = 2a) нагрузка, вызывающая остаточный прогиб панели порядка двух толщин наружной обшивки, более чем в 2 раза превышает соответствующую нагрузку при балочной идеализации. При дальнейшем увеличении остаточного прогиба Наружная обшивка и подкрепляющий ее наборроль наружной обшивки в восприятии нагрузки еще более возрастает.
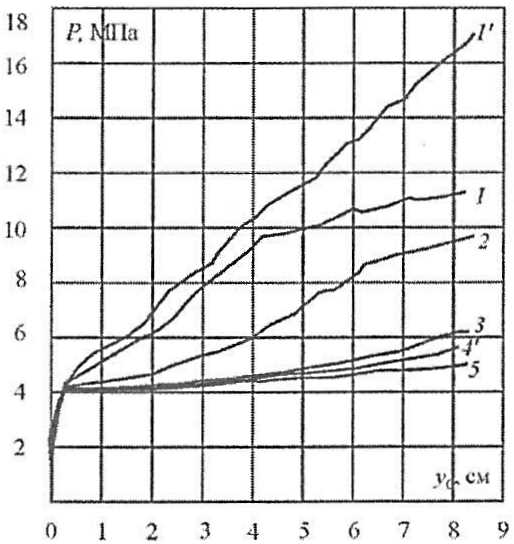
1 – d = 2a;
2 – d = 3a;
3 – d = 6a;
4 – d = 9a;
без учета деформации крайних балок:
1′ – d = 2a;
4′ – d = 9a;
5 – при балочной идеализации;
d – длина эпюры ледовой нагрузки
С увеличением длины зоны нагружения влияние наружной обшивки уменьшается. Одновременно важно подчеркнуть, что роль наружной обшивки и не переоценивается, поскольку учитывается вовлечение в процесс деформирования крайних балок (точки перегиба на кривых 1 2 соответствуют моменту начала интенсивного нарастания пластических прогибов крайних балок). Прогибы крайних балок сближаются с прогибами загруженных балок, увеличивая длину деформированной зоны панели и, тем самым, нивелируя роль обшивки (см. рис. 16, кривые 1 и 1′).
Определение эмпирических коэффициентов и проверка модели деформирования локально загруженной панели
Разработанная приближенная модель деформирования локально загруженной панели основана на ряде допущений, а также включает эмпирический коэффициент ϒ3, входящий в соотношение (Формула 38).
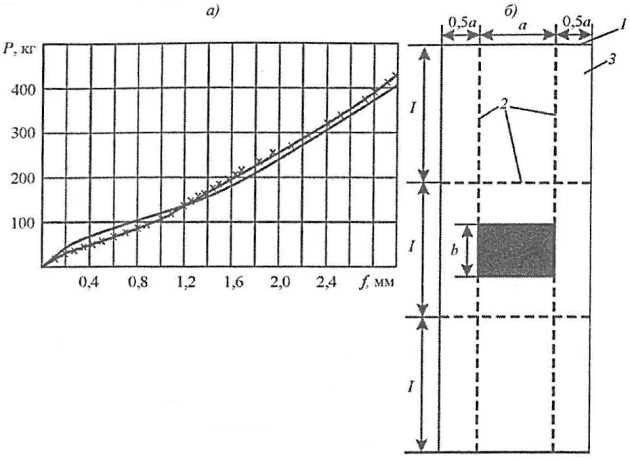
Принятое в решении значение ϒ3 ≈ 2,0 установлено на основании подхода, использованного в п. см. “Корректировка и экспериментальная проверка модели деформирования пластины судов ледового плавания“. В качестве базового эксперимента использованы испытания жестяных моделей (разд. см. “Методы расчета прочности конструкций ледовых усилений при глубоком пластическом деформированииДеформирование локально загруженной пластины наружной обшивки при образовании бухтины“), проводившиеся Л.М. Беленьким и В.В. Макаровым в 1992 году в ОНИЛ ПОЛЕКС по заказу автора. Программа эксперимента, разработанная автором, включала проведение испытаний трехпролетных изолированных двутавровых балок и трехпролетных панелей состоящих из тавровых балок, скрепленных с наружной обшивкой. Конструкция модели с панелью состояла из пластины наружной обшивки и приваренного к ней шпангоута, которые опирались на жесткие продольные диафрагмы и закреплялись на жестком опорном контуре (рис. 17).
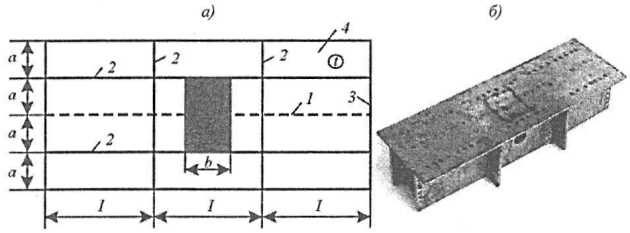
а – схема модели; б – вид моделей после испытаний:
1 – тавровая балка;
2 – продольные и поперечные диафрагмы;
3 – жесткий опорный контур;
4 – пластины наружной обшивки t = 1,07 мм;
a = 15 мм;
b = 22,5 мм;
σT = 285 Мпа;
▄ – область приложения нагрузки
В моделях изолированных балок пластина отсутствовала, а вместо нее к балке приваривался второй поясок. В совокупности модели имитировали работу балок ледовых усилений в составе бортового перекрытия совместно с наружной обшивкой (модель панели) и при балочной идеализации (модель изолированной балки). На основании сопоставления результатов испытаний панелей и изолированных балок установлено значение эмпирического коэффициента в соотношении (Формула 38), ϒ3 ≈ 2,0. Сопоставление результатов испытаний модели панели и расчета на основании полученного теоретического решения представлено на рис. 18. Как следует из рис. 18, теоретическое решение достаточно хорошо описывает зависимость остаточного прогиба от нагрузки.
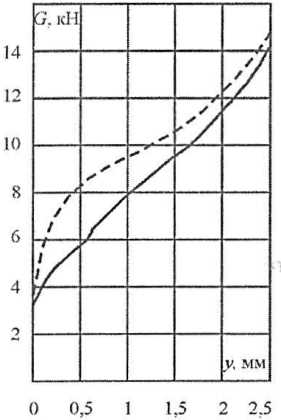
———— – теоретическое решение;
— — — — – эксперимент
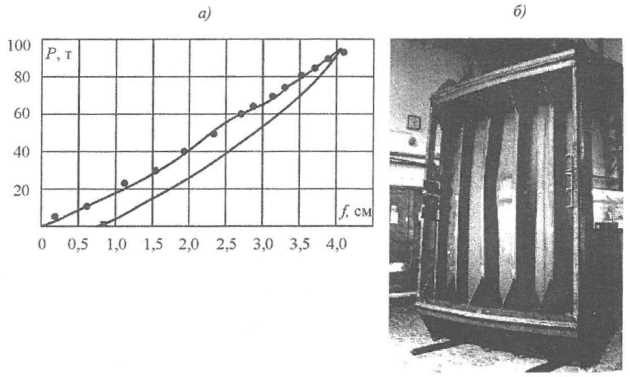
На рис. 19 представлено сопоставление теоретического решения с расчетом по МКЭ натурной конструкции участка бортового Особенности подготовки судна к плаванию во льдахперекрытия судна с высокой ледовой категорией, также демонстрирующее хорошее согласование результатов (конечно-элементный расчет выполнялся Е. А. Маслич). Некоторое расхождение результатов в области начала пластического деформирования имеет следующее физическое объяснение. Рассчитываемая конструкция имела сдвиговой механизм перехода в предельное состояние. Момент перехода в предельное состояние по чистому сдвигу сопровождается образованием диагональных гофров в стенке и последующим интенсивным нарастанием прогибов. Данный физический процесс полноценно учитывается в полученном теоретическом решении, о чем свидетельствует наличие точки перегиба на зависимости нагрузка – прогиб (см. рис. 19, кривая 7). В расчете по МКЭ возможность нелинейной потери устойчивости стенки не учитывается, чем и обусловлено отмеченное различие в результатах на начальной стадии пластического деформирования.

Изложенные сопоставления подтверждают достоверность полученного теоретического решения об упругопластическом и запредельном деформировании локально загруженной панели, описывающего процесс образования вмятин в конструкциях ледовых усилений судов ледового плавания.
Деформирование локально загруженной листовой конструкции совместно с наружной обшивкой при образовании вмятины-выпучины
Расчетная схема системы «листовая конструкция – наружная обшивка»
К листовым конструкциям относятся Палубные покрытиянастилы палуб и платформ, обшивка переборок, стенки рамных связей и другие подобные конструкции, привариваемые к наружной обшивке. Будем в дальнейшем считать, что листовая конструкция состоит из непосредственно листа (листового элемента) и подкрепляющего набора, установленного, в общем случае, в двух направлениях – перпендикулярно и параллельно наружной обшивке (рис. 20). В целом (см. гл. 3**) возможны четыре варианта расчетных схем листовых конструкций в зависимости от взаимной ориентации листа и балок главного направления относительно линии действия нагрузки. Применительно к обычно встречающейся поперечной системе набора по борту расчетные схемы представлены на рис. 21 соответственно для листовых конструкций, ориентированным поперек а и вдоль б судна. Трансформация данных схем к продольной системе набора осуществляется путем перестановки размеров пятна нагрузки b и d.
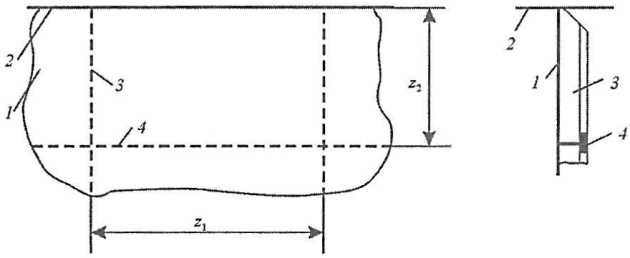
1 – лист (листофой элемент;
2 – наружная обшивка;
3, 4 – подкрепляющий набор
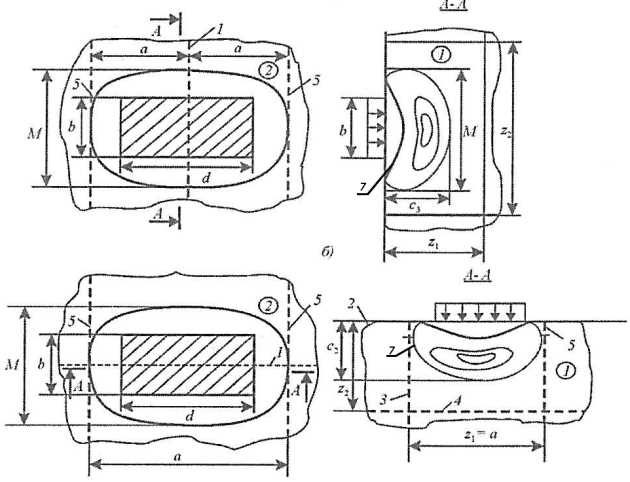
1-4 см. рис. 20;
5 – балка главного направления;
⬭ – контур вмятины в наружной обшивке;
7 – контур выпучины в листовой конструкции
В соответствии с изложенными в разд. см. “Анализ повреждаемости и обоснование критериев прочности корпусов судов ледового плавания и ледоколовОсобенности и закономерности ледовой повреждаемости. Отдельные (допустимые) и массовые (недопустимые) ледовые повреждения” данными о повреждениях воздействие локальных нагрузок на систему наружная обшивка – листовая конструкция приводит к образованию вмятины-выпучины, включающей вмятину в наружной обшивке и выпучину в листе. Поскольку целью исследований настоящей главы является описание деформирования конструкций под действием локализованных нагрузок, приводящих к отдельным повреждениям, следует считать, что выпучина не выходит за пределы ячейки, образованной подкрепляющим лист набором (рис. 21).
Естественно, что при этом особую роль приобретает наружная обшивка, способная в виду своей относительно высокой жесткости (толщина наружной обшивки, как правило, в 2-3 раза и более превышает толщину листа), не только непосредственно воспринимать часть нагрузки, воздействующей на конструкцию, но и разносить локализованную нагрузку по длине кромки листа.
Исследуем возможности построения расчетной модели, позволяющей описать процесс образования вмятины-выпучины с учетом взаимодействия листовой конструкции с наружной обшивкой. Для этого, в соответствии со сложившейся методологией, первоначально рассмотрим предельное состояние изолированного листа и последующий процесс его выпучивания под действием сжимающей нагрузки, а затем совместное деформирование листа и наружной обшивки в процессе образования вмятины-выпучины.
Предельное состояние и запредельное деформирование изолированного листа
В соответствии с изложенными соображениями введем в рассмотрение представленный на рис. 22 пластический механизм, описывающий выпучивание (выход из плоскости) полубесконечного листа после перехода в предельное состояние под действием локальной погонной нагрузки q, равномерно распределенной вдоль кромки на длине 2с. Форма деформированной поверхности листа, образуемая в результате перемещения пластического механизма, соответствует (в рамках представлений о прямолинейных шарнирах текучести) наблюдаемой в действительности типичной складке (выпучине) в листовой конструкции.
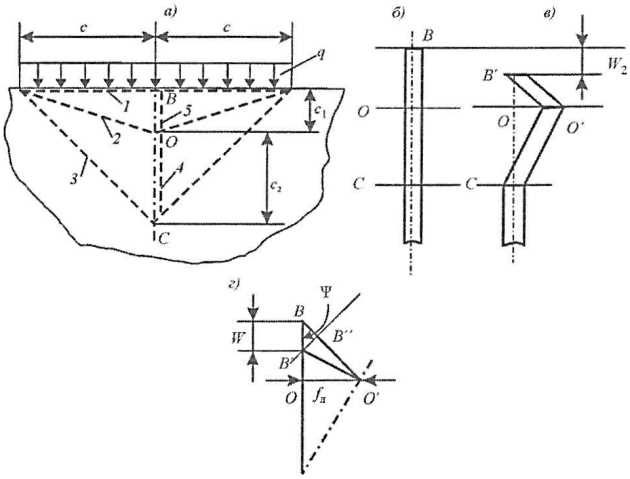
— — — — – линия шарниров текучести
Граничные условия на кромке листа исключают возможность ее углов поворота и Перемещений, перпендикулярных плоскости листа.
В процессе деформирования пластический механизм получает перемещения в двух взаимно перпендикулярных плоскостях (рис. 22): Перемещение перпендикулярно плоскости листа (выход из плоскости), характеризуемое величиной максимального прогиба fл (в точке О); перемещение в плоскости листа (в направлении действия нагрузки), характеризуемое величиной максимального прогиба w2 (в точке В). Как будет показано ниже, связь меду величинами fл и w2 нелинейна.
Введем систему обозначений, аналогичную использованной в разд. см. “Методы расчета прочности конструкций ледовых усилений при глубоком пластическом деформированииДеформирование локально загруженной пластины наружной обшивки при образовании бухтины“:
- i – номер шарнира текучести, i = 1-AB;
- i = 2-AO;
- i = 3-АС;
- i = 4-СО;
- i = 5-OB;
- j – номер конца шарнира текучести, j = 1,2;
- xi – координата, направленная вдоль оси i-го шарнира текучести и отсчитываемая от 1-го (j = l) конца;
- θi – угол слома в i-м шарнире;
- di – длина i-го шарнира;
- ei – удлинение (укорочение) срединной поверхности в i-м шарнире;
- Si – отстояние срединной поверхности от нейтрального слоя в i-м шарнире;
- с1, с2 – размеры пластического механизма, ясные из рис. 22;
- tл – толщина листа.
В рамках представлений о прямолинейных шарнирах текучести величины ei, и Si линейно распределены по длине шарнира текучести или, в частном случае, постоянны. В рассматриваемой задаче для случая действия постоянной нагрузки на изолированную полуплоскость, для шарниров 1, 2, 3 следует положить
Следует обратить внимание, что в шарнирах 1, 2, 3 происходит укорочение срединной поверхности пластины, обусловленное действием сжимающей нагрузки q. В шарнирах 4, 5, напротив, имеет место удлинение срединной поверхности, вызванное геометрически нелинейным фактором искривления ее поверхности в процессе выпучивания.
При этом величины е в шарнирах 4, 5 находятся из условия совместности деформирования элементов пластического механизма.
Пластический механизм характеризуется следующим набором параметров:
вектор обобщенных перемещений
вектор обобщенных деформаций
вектор координат шарниров текучести
В отличие от конвертообразного пластического механизма в пластине, рассмотренного в разд. см. “Методы расчета прочности конструкций ледовых усилений при глубоком пластическом деформированииДеформирование локально загруженной пластины наружной обшивки при образовании бухтины“, пластический механизм, образуемый в листе, имеет четыре обобщенных перемещения.
Причем, в соответствии с замечанием разд. см. “Методы расчета прочности конструкций ледовых усилений при глубоком пластическом деформированииМетоды расчета прочности конструкций из жесткопластического материала в геометрически нелинейной постановке“, изменения размеров жестких частей пластического механизма за счет перемещений е1, е2, е3 должны учитываться при определении работы внешних сил.
После достаточно громоздких преобразований и с учетом построений, представленных на рис. 22 и рис. 23, обобщенные деформации 0, размеры пластического механизма di, и перемещение в плоскости листа w2 удается выразить через элементы векторов u, r:
где:
- w1 – прогиб в точке A;
- w2 – максимальный прогиб кромки листа (в точке В);
– функции векторов u, r;
Работа внутренних сил в шарнирах текучести и внешних сил на перемещениях пластического механизма определяются из соотношений:
где:
Полученные соотношения позволяют сформировать разрешающую систему (Формула 50) – (Формула 56), которая с учетом представленных в п. см. “Модель запредельного деформирования пластины” при формировании системы (Формула 95) соображений в рассматриваемом случае примет вид
Учитывая нелинейный характер полученной системы (Формула 42), целесообразно исследовать возможности снижения ее размерности.
Выполненный анализ показал, что три уравнения системы (Формула 42) для k = 2,3,4 имеют следующее аналитическое решение:
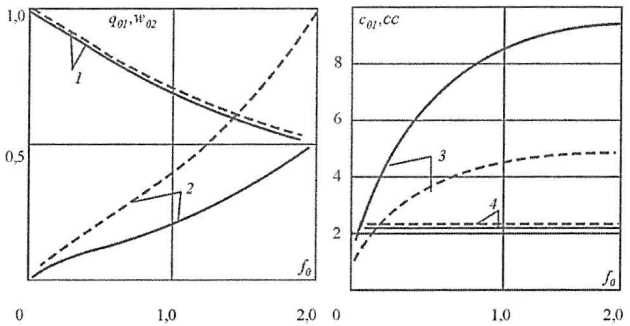
Решение оставшихся уравнений системы (Формула 42) осуществляется численно, с использованием процедур численного дифференцирования и решения систем нелинейных уравнений. Результаты численного решения задачи показаны на рис. 24 графиками следующих безразмерных зависимостей: нагрузка – прогиб выпучивания:
Принципы проектирования конструкций корпуса суднамаксимальный прогиб кромки – прогиб выпучивания
размеры пластического механизма – прогиб выпучивания
Значение
достигаемое в пределе, при
соответствует максимальной погонной нагрузке, которую может воспринять конструкция при плоском напряженном состоянии. С появлением прогиба
происходит интенсивный сброс нагрузки (рис. 24, кривая 1). Форма пластического механизма (
(при развитой пластичности), см. рис. 24) согласуется с наблюдаемым при испытаниях процессом выпучивания сжатых в своей плоскости листовых элементов.
В дальнейшем, при рассмотрении совместной работы листового элемента с пластиной наружной обшивки, представляет интерес описание предельного равновесия пластического механизма, представленного на рис. 25, а.
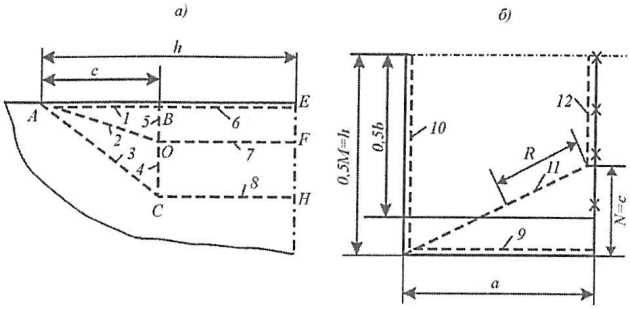
а – наружная обшивка; б — — — — – линия шарниров текучести;
Считается, что нагрузка приложена к кромке пластины на длине 2h, а образующийся в листе пластический механизм по сравнению с описанным (см. рис. 22) включает дополнительный участок призматического изгиба ВСНЕ, содержащий шарниры текучести BE (№ 6), OF (№ 7), CH (№ 8). Наряду с этим, накладывается условие на форму перемещений кромки листа w(x1), сводящееся к требованию отсутствия разрывов в прогибах. Поэтому условие (Формула 39) и вектор обобщенных перемещений запишутся в виде:
Дальнейшая процедура решения не отличается от описанной, а аналитическое решение (Формула 43) имеет вид
Для последующего описания совместной работы листового элемента с пластиной наружной обшивки получены аппроксимационные формулы для определения параметров с1, с2 в зависимости от максимального прогиба f:
где:
– аппроксимационные полиномы.
Полученные аппроксимационные зависимости (Формула 46), а также аналитические решения (Формула 43), (Формула 45) позволяют в существенной степени упростить дальнейшее решение задачи благодаря уменьшению размерности разрешающей системы (Формула 42) с шести до одного уравнения.
Запредельное деформирование системы листовой элемент – пластина наружной обшивки
Решение разд. см. “Методы расчета прочности конструкций ледовых усилений при глубоком пластическом деформированииДеформирование локально загруженной пластины наружной обшивки при образовании бухтины” о конвертообразном механизме перехода в предельное состояние пластины и полученное в п. см. “Предельное состояние и запредельное деформирование изолированного листа” решение о предельном состоянии изолированного листового элемента, допускающее возможность согласования соответствующего ему пластического механизма с конвертообразным механизмом пластины (рис. 25), создают теоретическую основу для решения задачи о предельном состоянии системы листовой элемент – пластина наружной обшивки. В рамках данного решения ограничимся рассмотрением расчетной схемы приложения нагрузки в соответствии с рис. 21, а и случаем реализации в пластине наружной обшивки пластического механизма типа μ = 1 (см. рис. 25, б). Распространение полученного для указанного частного случая решения на другие варианты не представляет принципиальных затруднений.
Введем следующие обозначения:
- p, b, d – как и ранее, параметры ледовой нагрузки;
- а – расстояние между листовым элементом и соседней балкой главного направления;
- t, tл – толщины наружной обшивки и листовой конструкции;
- wн, fл – максимальные прогибы вмятины в наружной обшивке и выпучины в листовом элементе,
Будем полагать, что деформированная зона локализуется в пределах двух шпаций, т.е. балки главного направления (в терминологии разд. см. “Деформирование локально загруженной панели при образовании вмятины” – крайние балки) образуют жесткий опорный контур, а размеры сторон образуемого в пластине конверта и длина зоны нагружения равняются
. Отметим, что учет вовлечения крайних балок в деформационный процесс в рамках разработанного в разд. см. “Деформирование локально загруженной панели при образовании вмятины” подхода не встречает затруднений.
Совместность деформирования пластины и листового элемента обеспечивается условием равенства перемещений пластины и листа по линии их соединения, а также следующим соответствием размеров пластических механизмов (см. рис. 25)
.
Таким образом, введенный пластический механизм имеет 12 шарниров текучести, пронумерованных согласно схеме рис. 25, характеризуется вектором обобщенных перемещений (Формула 44) и расширенным по сравнению с решением п. см. “Предельное состояние и запредельное деформирование изолированного листа” вектором координат шарниров текучести
Построенная по типу (Формула 42) разрешающая система будет включать девять нелинейных уравнений:
где:
- Uл – работа внутренних сил в шарнирах текучести листового элемента, вычисляемая на основании решения п. см. “Предельное состояние и запредельное деформирование изолированного листа“;
- Uп, V – работа внутренних сил в шарнирах текучести пластины и работа внешних сил, определяемые на основании зависимостей (Формула 92–93), при замене параметра f на wн0.
При этом использованный в п. см. “Предельное состояние и запредельное деформирование изолированного листа” прием получения аналитического решения для e1, e2, e3 в рамках системы (Формула 48) не подходит. Эти обобщенные перемещения через параметр w входят в выражения для работ внутренних сил в шарнирах текучести пластины и внешних сил V, что исключает возможность получения замкнутого аналитического решения для общего случая. В связи с этим следует констатировать, что относительно высокая размерность нелинейной разрешающей системы (Формула 48), даже с учетом ее понижения за счет аппроксимационных выражений (Формула 46) для с1, с2 делает проблематичным получение устойчивых и эффективных расчетных алгоритмов.
Это интересно: Методы выявления дефектов силовых установок, устройств, систем и корпуса судна
Исследуем более подробно возможности дальнейшего снижения размерности системы. Наиболее важным фактором, который может быть оценен именно из анализа работы механизма лист – пластина, является влияние размеров листа на величины параметров М и N, количественно характеризующее отмеченное выше явление разнесения нагрузки по кромке листового элемента. Поскольку, в соответствии с данными рис. 24, имеет место следующее соотношение между перемещениями механизма wн << fл, то, очевидно, на стадии развития пластических деформаций и образования пластического механизма в листе влияние геометрически нелинейных факторов на работу пластины проявляется не столь существенно.
Поэтому для анализа зависимости параметров М и N от размеров листа может быть использовано упрощенное геометрически нелинейное решение для пластины, основанное на допущении, что ее кромки не имеют возможности сближаться (абсолютный распор).
При этом можно принять R = 1 и использовать следующие выражения для работ внутренних сил в шарнирах пластины, вытекающие из (Формула 92):
Выражению для работ внутренних сил в шарнирах листового элемента 1-8 применительно к действительному диапазону изменения значений параметров:
может быть придан вид:
где:
Подстановка полученных зависимостей для Uп и Uл, а также выражения (Формула 93) для V в разрешающую систему (Формула 48), позволяет получить после преобразований аналитическое, хотя и достаточно громоздкое, решение для искомых обобщенных перемещений е2, (i = 1,2,3). Полученное решение для е2, в совокупности с аппроксимационными соотношениями (Формула 46) для с1, с2 позволяет понизить число уравнений разрешающей системы до четырех, что является вполне приемлемым для построения устойчивого алгоритма, пригодного для выполнения расчетного анализа. Результаты расчета на основании полученного алгоритма представлены на рис. 26 в виде зависимости

Как видно из рис. 26, величина нагрузки, воспринимаемой конструкцией, зависит не только от толщины листа, как имеет место при рассмотрении изолированного листового элемента, но и от параметров нагрузки и размеров пластины наружной обшивки. Следует обратить внимание на принципиальную особенность запредельного деформирования листового элемента совместно с пластиной наружной обшивки. Она состоит в наличии минимума зависимости
.
Физическое объяснение этого сводится к следующему. При относительно небольших прогибах большую часть нагрузки воспринимает листовой элемент. С ростом прогибов прочность листового элемента уменьшается. Одновременно пластина обшивки за счет наличия распора и фактора самораспора упрочняется.
Сложение этих противоположных процессов и приводит к появлению минимума нагрузки. При больших прогибах Общий продольный изгиб и общая продольная прочность корпусных конструкций суднапрочность конструкции в основном определяется пластиной обшивки.
Для дальнейших исследований, связанных с необходимостью построения упругопластического решения о деформировании конструкции листовой элемент – пластина наружной обшивки, целесообразно получить аппроксимационные соотношения для параметров пластического механизма, образуемого в пластине – M, N и R. В результате расчетного анализа установлено, что для определения М и N могут быть использованы следующие приближенные зависимости.
где:
- – параметры пластического механизма, определенные из решения п. см. “Модель запредельного деформирования пластины” для изолированной пластины.
Для определения параметра R получена следующая расчетная процедура.
Строится решение п. см. “Модель запредельного деформирования пластины” для изолированной пластины (Формула 95), в результате которого находятся значения
Осуществляется корректировка значений данных параметров согласно (Формула 51) и повторно решается задача (Формула 95) при замене 2-го и 3-го уравнений системы зависимостями (Формула 51). В результате определяется третий размер пластического механизма в пластине
.
Следует отметить, что соотношения (Формула 51) позволяют оценить эффект разнесения нагрузки вдоль кромки листового элемента, обеспечиваемый пластиной наружной обшивки. Количественно эффект разнесения характеризуется соотношением высоты распределения нагрузки вдоль кромки листового элемента b и размером пластического механизма М, определяющим длину деформированной зоны вдоль кромки листового элемента (см. рис. 25). При рассмотрении изолированного листа b = M, т.е. длина зоны деформирования совпадает с высотой распределения нагрузки. При учете влияния пластины всегда имеет место соотношение М > b.
Причем при относительно больших b(b > (4 ÷ 6) a) имеет место тенденция b → М, и эффект разнесения нивелируется, а при существенной локализации нагрузки (b → 0) размер М остается конечным и эффект разнесения приобретает существенное значение. Для реального соотношения размеров конструкции и параметров нагрузки, как показывает анализ, имеет место соотношение M = (1,3 ÷ 1,7) b, т.е. за счет эффекта разнесения длина деформированной зоны вдоль кромки листового элемента увеличивается примерно в 1,5 раза. Соответственно возрастает и суммарная сила G = pbd, которую способен воспринять листовой элемент.
Таким образом, получены аппроксимационные соотношения для определения всех элементов вектора r. Их использование позволяет исключить из разрешающей системы (Формула 48) последние пять уравнений и получить приближенное решение, в котором параметры пластических механизмов в листовом элементе и пластине определяются независимо. Данное решение используется ниже при рассмотрении упругопластического деформирования системы листовой элемент – пластина наружной обшивки.
Упругопластическое деформирование системы листовой элемент – пластина наружной обшивки
Полученное решение, основанное на гипотезе об идеальном жесткопластическом материале, имеет следующий принципиальный недостаток.
В решении рассматривается предельное равновесие двух элементов конструкции, обладающих в значительной степени различной жесткостью в направлении действия ледовой нагрузки. Поэтому может реализоваться ситуация, когда в действительности глубокое пластическое деформирование листового элемента происходит одновременно с работой пластины в упругой или начальной упругопластической области.
Для преодоления отмеченного недостатка необходимо отказаться от использования модели жесткопластического материала применительно к пластине наружной обшивки. Элементы конструкции корпуса суднаЛистовой элемент, вследствие его значительной жесткости, можно с достаточным основанием рассматривать в рамках представлений о жесткопластическом материале.
Полученное в предыдущем пункте решение позволяет достаточно легко перейти к рассмотрению работы пластины обшивки в упругопластической области, так как в нем производится разделение общей задачи на две: о предельном состоянии пластины и о предельном состоянии листового элемента. В свою очередь, для пластины наружной обшивки в п. см. “Корректировка и экспериментальная проверка модели деформирования пластины судов ледового плавания” разработана модель упругопластического и запредельного деформирования.
Не останавливаясь подробно на описании процедуры построения упругопластического решения для системы листовой элемент – пластина наружной обшивки, отметим, что она основана на замене выражений для работ внутренних сил в шарнирах текучести пластины на соответствующие выражения для упругих прослоек, полученные в п. см. “Корректировка и экспериментальная проверка модели деформирования пластины судов ледового плавания“.
Характер деформирования системы листовой элемент – пластина наружной обшивки на упругопластической и запредельной стадиях деформирования иллюстрируется на рис. 27. Для сравнения там же дана зависимость нагрузка – прогиб, соответствующая жесткопластическому решению п. см. “Запредельное деформирование системы листовой элемент – пластина наружной обшивки“.
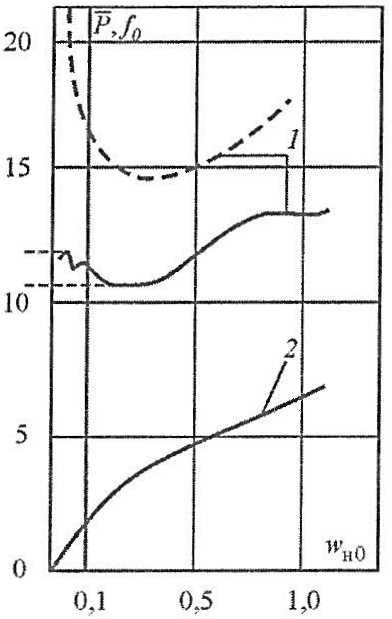
— — — — – жесткопластическое решение п. см. “Упругопластическое деформирование системы листовой элемент – пластина наружной обшивки“;
———— – упругопластическое решение п. см. “Упругопластическое деформирование системы листовой элемент – пластина наружной обшивки“
Согласно представленным данным величины нагрузок, воспринимаемых конструкцией в соответствии с упругопластическим и жесткопластическим подходами, могут существенно различаться (около 1,5 раза). Данное различие обусловлено тем, что при достижении минимума зависимости нагрузка-прогиб пластина находится в условиях начального пластического деформирования, а листовой элемент в стадии глубокого пластического деформирования: минимуму зависимости нагрузка-прогиб (pmin) соответствуют прогибы от выпучивания порядка 4-5 толщин пластинчатого элемента (f0 ≈ 4 ÷ 5) (см. рис. 27, кривая 2).
Теоретически конструкция может воспринимать нагрузку рmax превышающую pmin0, что отражает левая часть кривой p (wн0) (рис. 27, кривая 7), при относительно небольших прогибах f0. Следует, однако, понимать, что данный результат соответствует идеализированной постановке задачи, не учитывающей влияние всегда имеющихся в конструкции начальных несовершенств (начальные погиби листового элемента, неперпендикулярность элемента наружной обшивке и др.). Поэтому значение нагрузки pmin следует рассматривать как границу, после которой в конструкции могут возникнуть ограниченные пластические деформации, сопровождаемые выпучиванием листового элемента до прогибов в несколько толщин.Таким образом, получено решение об упругопластическом и запредельном деформировании Элементы конструкции корпуса суднасистемы листовой элемент-пластина наружной обшивки.
Решение позволяет описать не учитываемые ранее эффекты, связанные с разнесением пластиной локальной нагрузки вдоль кромки листового элемента и участие наружной обшивки в восприятии нагрузки на запредельной стадии деформирования.
Практическое использование решений об упругопластическом и запредельном деформировании конструкций
Полученные в настоящей главе решения и основанные на них расчетные программы обеспечивают возможности регламентации требований к прочности конструкций ледовых усилений по сформулированному в разд. см. “Анализ повреждаемости и обоснование критериев прочности корпусов судов ледового плавания и ледоколовКритерии и методы оценки прочности. Расчётные ледовые нагрузки. Принципы регламентации режимов движения во льдах” критерию ограниченной пластической деформации и соответствующих ему отказах в виде основных типов ледовых повреждений (бухтин, гофрировок, вмятин и вмятин-выпучин), обусловленных воздействием интенсивных локальных ледовых нагрузок.
На стадии проектирования судов ледового плавания и ледоколов применение решений позволяет получить рациональное распределение материала между наружной обшивкой, балками основного набора и листовыми конструкциями, обеспечивающее равнопрочность перечисленных конструктивных элементов в отношении локальных ледовых нагрузок, способных вызвать появление отдельных повреждений Определение и классифицирование нарушения целостности корпуса судов при дефектациив виде бухтин, вмятин и вмятин-выпучин.
При этом необходимо понимать, что вытекающие из критерия ограниченной пластической деформации дополнительные требования могут приводить к некоторому увеличению веса конструкций по отношению к уровню, установленному требованиями Правил Регистра. Поэтому наиболее «безболезненно» данная процедура может применяться при проектировании ледоколов, поскольку увеличение веса корпуса ледокола не оказывает существенного влияния на показатели его эффективности.
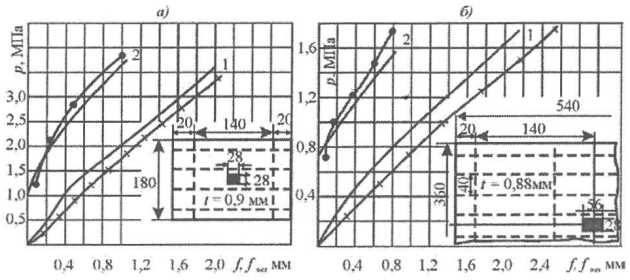
Для эксплуатирующихся судов с помощью полученных решений могут разрабатываться рациональные схемы подкреплений повреждаемых районов, а также оцениваться фактические величины ледовых нагрузок, вызвавших отдельные повреждения конструкций ледовых усилений. Примером такого использования решений может служить выполненное автором по заказу Мурманского морского пароходства комплексное исследование по повышению надежности а/л типа «Арктика». На рис. 28, 29 представлены результаты расчетов величин локальных ледовых нагрузок, вызвавших отдельные повреждения обшивки и набора во время экстремальной навигации 1983 г. в восточном секторе Арктики (а/л «Арктика») и в период высокоширотного рейса к Северному полюсу (а/л «Сибирь», 1987 г.). Данные нагрузки существенно превышали уровень предельной прочности конструкций, установленный без учета резервов запредельного деформирования.
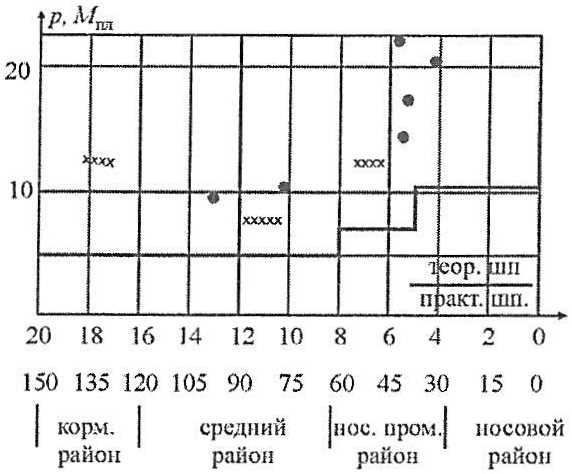
х – отдельные бухтины; ⚫ – гофрировки:
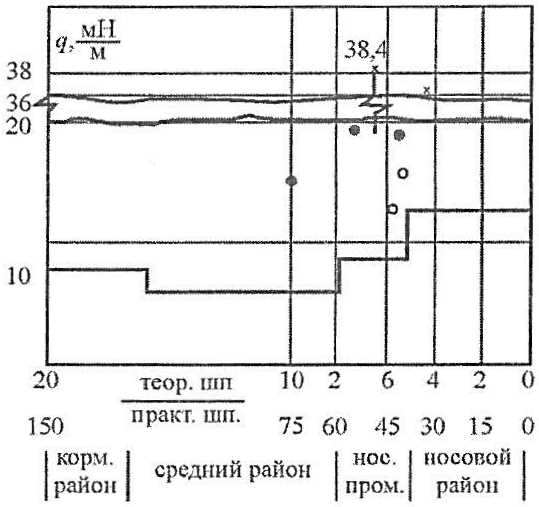
◯ – отдельные вмятины в бортовых конструкциях а/л “Арктика”; ⚫ – отдельные вмятины в бортовых конструкциях а/л “Сибирь”; х – пробоины в бортах а/л “Сибирь” (над вторым дном);
Установленные в результате анализа величины экстремальных нагрузок принимались во внимание при разработке рекомендаций по подкреплению конструкций. Выполненные расчеты прочности конструкций ледовых усилений при образовании отдельных повреждений показали, что наружная обшивка обладает избыточным запасом во всех районах ледовых усилений. Прочность основного набора оказывается лимитирующей в среднем районе, где шпангоуты имеют увеличенный пролет, а толщина наружной обшивки и, следовательно, ее поддерживающее влияние малы. В оконечностях минимальным уровнем прочности обладают листовые конструкции (стенки рамных шпангоутов).
На основании выполненных расчетов построены кривые строительной прочности и определены повреждающие режимы движения ледокола во льдах, приводящие к появлению отказов – недопустимых по нормативам Дефектация судовых технических средствдефектации отдельных повреждений корпусных конструкций.
При решении вопросов нормирование полученные решения позволили установить обоснованные соотношения между уровнями прочности, соответствующими переходу конструкции в предельное состояние (критерий предельной прочности) и возникновению недопустимых отдельных повреждений (критерий ограниченной пластической деформации) (см. разд. “Анализ повреждаемости и обоснование критериев прочности корпусов судов ледового плавания и ледоколовКритерии и методы оценки прочности. Расчётные ледовые нагрузки. Принципы регламентации режимов движения во льдах“).
Полученные решения успешно применялись и при рассмотрении других типов конструкций, подверженных воздействию локальных нагрузок. В частности на их основании были разработаны требований Правил Регистра к конструкциям палуб накатных судов, воспринимающих нагрузки от колесной техники.
Выводы по главе 2
- Расчетные методы, описывающие процесс образования в конструкциях ледовых усилений отдельных повреждений в виде бухтин, вмятин и вмятин-выпучин, должны: обеспечивать получение устойчивых алгоритмов от момента начала упругопластического деформирования до развития глубоких пластических деформаций; учитывать фактор геометрической нелинейности и локальный характер нагружения; описывать взаимодействие деформируемой конструкции с окружающими ее неповрежденными участками перекрытия.
- При разработке расчетных моделей для описания процесса образования отдельных повреждений целесообразно использование следующей общей методологии: построение решения о предельном равновесии жесткопластической конструкции в геометрически линейной постановке; обоснование принципов решения задач о деформировании жесткопластических конструкций в геометрически нелинейной постановке; разработка приближенных расчетных моделей, позволяющих учитывать упругие свойства элементов конструкций в рамках жесткопластического решения; экспериментальная проверка и уточнение основных допущений расчетных моделей.
- Формы деформированной поверхности при образовании в конструкции отдельных повреждений хорошо изучены. Поэтому при рассмотрении предельного состояния в геометрически линейной постановке допустимо использовать упрощенную разрешающую систему кинематического метода ТПР, основанную напредположении, что заранее известен полный Конструкция судового наборанабор пластических механизмов перехода конструкции в предельное состояние.
- В процессе запредельного деформирования пластины конвертообразная форма пластического механизма имеет тенденцию к вырождению в пирамидальную без изменения типа пластического механизма. Для определения типа пластического механизма достаточно решить задачу о предельном состоянии пластины в геометрически линейной постановке.
- Для описания упругопластического изгиба локально загруженной пластины предложена расчетная модель, в рамках которой: деформированная поверхность пластины представляется в виде совокупности жестких частей, соединенных нежесткими прослойками; прослойки могут существовать в состоянии упругого элемента конечной ширины или шарнира текучести; тип состояния определяется в зависимости от величины совершаемой в прослойке работы внутренних сил.
- Влияние степени локализации нагрузки на деформированное состояние пластины проявляется весьма существенно. Использование модели балки-полоски, игнорирующей эффект локального нагружения, приводит к существенному, в 1,5-2,0 раза и более, занижению действительной несущей способности пластины. Влияние на работу пластины условий закрепления опорных кромок (в отношении перемещений в плоскости пластины), существенно проявляющееся в традиционно используемой модели балки-полоски, в модели локально загруженной пластины в значительной степени нивелируется за счет описанного явления самораспора.
- При рассмотрении пластического деформирования балочных конструкций ледовых усилений необходимо учитывать нелинейный эффект взаимовлияния изгибающих моментов и перерезывающих сил в изгибно-сдвиговых пластических шарнирах, а также перераспределение внутренних усилий в изгибно-продольно-сдвиговых пластических шарнирах в процессе увеличения продольных сил, обусловленного распорным эффектом.
- Эффект поддерживающего влияния поясков балки при реализации сдвиговых механизмов перехода в предельное состояние, игнорируемый в рамках балочной идеализации, может быть описан с помощью новой модели, учитывающей пространственное взаимодействие стенки и поясков в пластическом механизме. Учет поддерживающего влияния поясков увеличивает на 15-30 % уровень предельной прочности балочных конструкций со сдвиговым характером предельного состояния.
- Учет эффекта взаимодействия балок основного набора с наружной обшивкой в процессе образования отдельной вмятины позволяет существенно уточнить представления о несущей способности конструкции по сравнению с балочной идеализацией. При относительно малой длине зоны нагружения (около двух шпаций основного набора) нагрузка, вызывающая остаточный прогиб панели порядка двух толщин наружной обшивки, более чем в 2 раза превышает соответствующую нагрузку при балочной идеализации. При увеличении длины зоны нагружения влияние наружной обшивки уменьшается.
- При образовании отдельной вмятины-выпучины существенное влияние на характер деформирования конструкции оказывает пластина наружной обшивки, способная не только непосредственно воспринимать часть нагрузки, но и разносить локализованную нагрузку по длине кромки листовой конструкции. За счет эффекта разнесения суммарная сила, которую она способна воспринять, увеличивается примерно в 1,5 раза. Непосредственный поддерживающий эффект наружной обшивки (восприятие части нагрузки) возрастает по мере увеличения прогибов во вмятине.
- Сложение процессов снижения несущей способности листовой конструкции при развитии в ней выпучины и упрочнения пластины наружной обшивки с ростом прогибов во вмятине приводит к появлению минимума на кривой нагрузка – прогиб. Значение нагрузки – минимума (pmin) следует рассматривать как характеристику несущей способности системы листовая конструкция – пластина наружной обшивки. Игнорирование упругих свойств материала пластины в рамках жесткопластических решений приводит к завышению нагрузки pmin в 1,5 раза и более.
- Полученные в настоящей главе решения и основанные на них расчетные программы обеспечивают возможности регламентации требований к прочности конструкций ледовых усилений по критерию ограниченной пластической деформации, соответствующему отказам в виде основных типов ледовых повреждений (бухтин, вмятин и вмятин-выпучин), обусловленных воздействием интенсивных локальных ледовых нагрузок. На стадии проектирования судов ледового плавания и ледоколов применение решений позволяет получить рациональное распределение материала между наружной обшивкой, балками основного набора и листовыми конструкциями, обеспечивающее равнопрочность перечисленных конструктивных элементов в отношении отказов в виде отдельных повреждений. Для эксплуатирующихся судов с помощью полученных решений могут разрабатываться рациональные схемы подкреплений повреждаемых районов, а также оцениваться фактические величины ледовых нагрузок, вызвавших отдельные повреждения конструкций.
