При перевозке сжиженного газа конструктивные элементы грузовых танков газовозов, их опоры и детали креплений испытывают воздействие различных нагрузок.
Поэтому прочность их должна быть рассчитана на действие любых возможных в эксплуатации нагрузок и их реальных комбинаций, а именно на:
- расчетное Свойства сжиженных газовдавление паров газа (внутренние и внешние давления);
- динамические нагрузки, вызванные перемещениями судна при качке;
- динамические нагрузки от волнообразования жидкости в частично заполненных танках;
- нагрузки, вызванные температурными деформациями;
- нагрузки от силы тяжести (веса) танков и их изоляции, а также силы тяжести (веса) перевозимого газа;
- нагрузки, действующие на выступающие над палубой части танков.
Расчетные нагрузки
Кроме указанного выше, необходимо дополнительно рассчитать конструкции на:
- нагрузки, возникающие в процессе испытаний;
- возможность увеличения расчетного давления паров p0 в танке при стоянке в порту;
- перераспределение нагрузок при статическом крене 30°.
Расчетное давление паров газа. Максимальное манометрическое давление в верхней части грузового танка в соответствии с требованиями Правил Регистра для вкладных грузовых танков типа А и В не должно превышать p0 = 70 кПа, а для танков типа С – величины
где:
- σm – расчетное напряжение в стенке танка, МПа;
- ΔσA – удвоенная амплитуда динамических напряжений (допускаемое цепное напряжение) в стенке танка при уровне вероятности 10-8, ΔσA = 55 МПа – для феррито-мартенситной стали и ΔσA = 25 МПа – для алюминиевых сплавов;
- C – характерный размер танка, определяемый как наибольший из трех величин: h, 0,75b, 0,45l (здесь h, b, l – соответственно высота, ширина и длина танка в вертикальном, поперечном и продольном направлениях, м);
- ρ – относительная плотность перевозимого газа при расчетной температуре (отнесенная к плотности воздуха).
Установка вторичного сжижения газа на судах-газовозах рефрижераторного типаРасчетное давление паров для встроенных грузовых танков не должно превышать p0 = 25 кПа, а при увеличении размеров всех связей корпусных конструкций в районе танков – p0 ≤ 70 кПа:
- для грузовых танков с внутренней изоляцией – p0 = 25 кПа, при условии увеличения прочности конструкций корпуса, поддерживающих грузовой танк p0 ≤ 70 кПа, а если грузовой танк с внутренней изоляцией поддерживается конструкцией вкладного танка, то p0 > 70 кПа;
- для мембранных и Конструкции грузовых танков газовозовполумембранных танков p0 = 25 кПа, а при условии соответствующего увеличения размеров связей корпуса и учета прочности поддерживающей изоляции p0 ≤ 70 кПа.
Внутреннее давление в грузовом танке определяется расчетной максимальной нагрузкой, кПа,
где:
- p0 – расчетное давление паров, кПа;
- hд – давление, создаваемое в результате совместного действия гравитационного и динамического ускорений в ЦТ груза под влиянием качки газовоза при полном заполнении танков – определяется по зависимостям.
Внешнее давление определяется расчетной нагрузкой в виде разности между минимальным внутренним (максимальный вакуум) и максимальным внешним давлением, которым одновременно в процессе эксплуатации может подвергаться танк или любая его часть. Эти нагрузки, характерные в основном для сферических танков, приводящие иногда к потере устойчивости их конструкции, подробно рассмотренные в пункте “Прочность вкладных грузовых танков типа B“.
Расчетные динамические нагрузки, вызванные перемещениями судна-газовоза при качке, должны определяться на основании долговременного распределения его перемещений при продольной, поперечно-горизонтальной, бортовой, вертикальной, килевой качках и рыскании на нерегулярном волнении, которые судно будет испытывать в течение всего срока службы (обычно 108 волновых циклов).
В некоторых случаях, согласованных с Регистром, могут применяться упрощенные спектры динамических нагрузок, а также могут учитываться их снижения в связи с необходимым уменьшением скорости газовоза и изменением курсового угла на волнении.
Для практической оценки скорости распространения трещин можно использовать упрощенное распределение нагрузки в течение 15 сут, рекомендованное Регистром.
Предлагается к прочтению: Грузовые операции на газовозах морского типа
Большие теоретические исследования по определению расчетных динамических нагрузок, вызванных перемещениями газовоза при качке, проведены отделом судовой технологии Норвежского классификационного общества “Дет Норске Веритас” и кафедрой теории корабля Николаевского кораблестроительного института. Отдел судовой технологии разработал методику определения динамических нагрузок при качке с применением ЭВМ, так как считал, что для газовозов, используемые обычно в этих целях различные эмпирические или какие-либо другие формулы, как правило, неприемлемы.
На основе теории плоского течения Салвесен-Так-Фалтинсена отделом судовой технологии общества “Дет Норске Веритас” составлены системы дифференциальных уравнений качки и разработана программа расчета на ЭВМ продольно-горизонтальной, поперечно-горизонтальной, вертикальной, бортовой, килевой качки и рыскания. Таким образом, были учтены шесть степеней свободы газовоза при качке. Расчеты динамических нагрузок с помощью описываемой методики дают хорошие теоретические результаты для качки на нерегулярном волнении с учетом спектров волнения моря в предполагаемых районах эксплуатации газовозов.
По этой методике “Дет Норске Веритас” рассчитывает конструкции танков газовозов.
Регистр РФ, как и “Дет Норске Веритас”, для того чтобы точно определить динамические нагрузки, действующие на грузовые танки при перемещениях газовоза на волнении, находит три вида ускорений в их ЦТ:
- вертикальное ускорение (ускорение при вертикальной, килевой и бортовой качках, направленное нормально к основной плоскости судна);
- поперечное ускорение (ускорение при поперечно-горизонтальной, бортовой качках и рыскании, а также гравитационную составляющую ускорения при бортовой качке);
- продольное ускорение (ускорение при продольной и килевой качках, а также гравитационную составляющую ускорения при килевой качке).
Данные ускорения можно определить с помощью программ, разработанных в НКИ на кафедре теории корабля и одобренных Регистром. Однако, если достоверные данные об инерционных нагрузках, действующих на Конструкции грузовых танков газовозовгрузовые танки при перемещениях судна на волнении, отсутствуют, то Регистр допускает использование величин ускорений, определяемых с помощью формул, приведенных в Правилах Регистра.
Французское Бюро Веритас требует, чтобы расчетная динамическая нагрузка, кПа, была не менее величины
где:
- p0 — расчетное давление паров газа, кПа;
- ρ – истинная плотность перевозимого сжиженного газа, т/м3, равная большому значению из следующих величин:
или
- (здесь ρ0 – плотность перевозимого газа, т/м3, которая принимается за исключением тех случаев, когда представлена точная информация о перевозимом газе, равной 0,5 – для метана, 0,6 – для бутана, 0,58 – для пропана, 0,7 – для аммония (ангидрида);
- at – максимальное ускорение для поперечного сечения танка, вызываемое бортовой качкой газовоза и принимаемое большим из величин, м/с2, at = 60σ2 Aбy или at = 60σ2 Aб (z – 0,8d);
- al – максимальное ускорение, вызываемое продольной качкой судна, м/с3:
- при посадке газовоза на ровный киль,
- при дифференте газовоза на нос;
- частота бортовой качки, c-1;
- d – осадка газовоза, м;
- aM = 384/(L – 7) – ускорение на миделевом сечении газовоза, м/с2 (при этом aAB ≤ 1,2, aAV ≤ 12, aM ≤ 12);
- aAV = 1 450/(L + 60) – ускорение на носовом перпендикуляре газовоза, м/с2;
- aAR = 1 270 /(L + 60) – ускорение на кормовом перпендикуляре газовоза, м/с2;
- h – начальная поперечная Определение поперечной метацентрической высоты судна путем выполнения опыта кренованияметацентрическая высота газовоза, м;
- zg – аппликата ЦТ газовоза, м;
- y – расстояние от расчетной точки до ЦП газовоза, м;
- z – вертикальное расстояние от расчетной точки до палубной линии y борта (если расчетная точка расположена выше палубы, то величина z принимается со знаком минус), м;
- Aб, Aк – максимальные амплитуды соответственно бортовой и килевой качки, рад, Aк = 19/L и Aб = 0,01 (63,0 – 0,9B), при этом Aк ≤ 0,17 и 0,21 ≤ Aб ≤ 0,52;
- L, B – длина и ширина газовоза по КВЛ, м;
- yp, zp – координата точки подволока танка, наиболее удаленной от ДП газовоза, м;
- k – коэффициент, учитывающий направление связей внутри танка, k = 0,6 – для поперечных связей, k = 0,3 – для продольных;
- l – длина грузового танка между поперечными переборками, м.
Расчетные динамические нагрузки от волнообразования жидкости в частично заполненных танках, возникающие из-за наличия свободных поверхностей, необходимо определять при выполнении проверочных расчетов на прочность танков, что позволит определить Архитектурно-конструктивные особенности судов-газовозовопасность нагрузок.
Регистр РФ указывает, что данные нагрузки являются в каждом случае предметом специального рассмотрения. “Дет Норске Веритас” определяет их, как
где:
- hд. д – дополнительная динамическая нагрузка, кПа;
- hx, hy – составляющая нагрузки в продольном и поперечном направлениях, кПа, равные
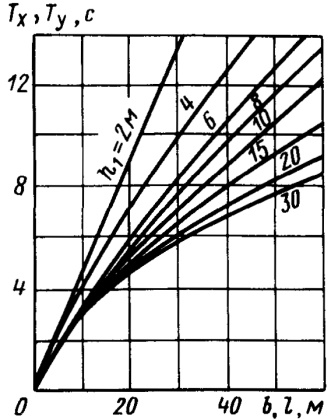
- Tx, Ty – резонансные периоды колебаний жидкости в танках в продольном и поперечном направлениях, c, определяемые с помощью графиков (рис. 1);
- Tк, Tб – периоды килевой и бортовой качек газовоза,
- g – ускорение свободного падения, м/с2;
- l, b – расстояние между поперечными и продольными переборками танка, м;
- x – расстояние от миделя до ЦТ танка, м;
- ускорение ЦТ танка, м/с2;
- ν – скорость судна, уз;
- L, B – длина и ширина судна, м;
- k1, k2 – коэффициенты, значения которых приведены ниже:
| Значение коэффициентов k1, k2 | ||
|---|---|---|
| Для подволока танка | Для днища танка | |
| k1 | 165 | 100 |
| k2 | 45 | 130 |
Формула 4 справедлива при Tx, Ty с Tк/Tх ≥ 1,25 и Tб/Ty ≥ 1,40, что определяет область нерезонансных режимов.
Нагрузки, вызванные температурными деформациями, в каждом случае являются предметом специального рассмотрения Регистром РФ. Кратковременные термические нагрузки, возникающие в период охлаждения, необходимо учитывать в расчетах прочности грузовых танков, если спецификационная температура перевозимого груза ниже -55 °C.
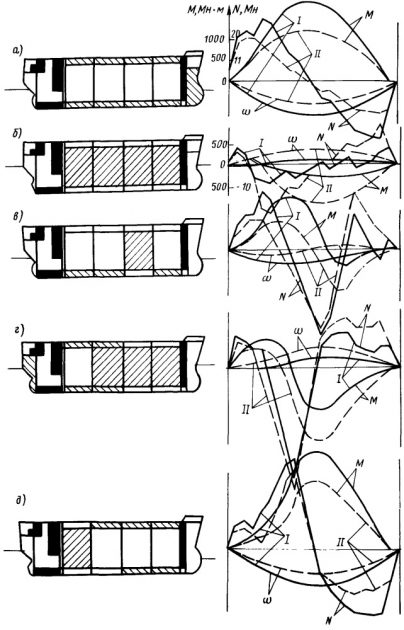
Необходимость учета нагрузок, обусловленных температурными деформациями, вызвана большим перепадом температур, действующих на танки. Связано это с глубоким охлаждением танков в период приемки груза и нагревом их после выгрузки. Для компенсации температурных деформаций на газовозах применяют специальные крепления танков к его корпусу, что позволяет им смещаться при воздействии температурного поля. При этом больших напряжений в конструкциях танков не возникает.
Теплоизоляция танков также снижает влияние перепада температур. Более сложные процессы происходят в конструкциях газовозов в аварийных ситуациях при утечке газов через различного рода неплотности и при возникновении дефектов в изоляции. При этом термическим нагрузкам в случае утечки газов подвергаются конструкции корпуса газовозов, а в случае дефектов теплоизоляции – конструкции танков или корпусные конструкции, если танки выполнены с внутренней изоляцией.
Нагрузки, действующие на выступающие над палубой части танка, создают дополнительное внешнее давление, которое вызывается накатом воды. При отсутствии наката воды на выступающие над палубой части танка нагрузка принимается равной нулю.
Нагрузки, возникающие в процессе испытаний. Гидростатические или гидропневматические испытания, которым должны подвергаться встроенные грузовые танки типов А и В, рассчитывают так, чтобы напряжения в танках этих типов приближались, насколько это практически возможно, к проектным напряжениям, и так, чтобы давление в районе купола танка соответствовало давлению предохранительного клапана. При этом максимальные первичные напряжения в любой точке конструкции танка или максимальные напряжения при изгибе его основных связей не должны превышать 0,9ReH (здесь ReH – предел текучести материала при температуре испытания). Если напряжения, определенные расчетом, превысят 0,75ReH, то следует провести тензометрические испытания прототипа конструкции танка.
Вкладные грузовые танки типа С испытывают под давлением, измеренным в верхней его части, и равным не менее 1,5 p0, а напряжение в них не должно превышать величин, аналогичных величинам при испытаниях вкладных танков типов А и В. На газовозах с мембранными и полумембранными танками все пространства, в которых перевозится жидкий груз и которые являются смежными с конструкциями корпуса, поддерживающими мембрану, должны подвергаться гидростатическому или гидропневматическому испытанию в соответствии с принятыми нормами.
Нагрузки, вызванные возможностью увеличения расчетного давления паров, также специально рассматриваются в соответствии с требованиями Регистра РФ. Допускается увеличение давления паров выше p0 для грузовых танков различных типов, если газовоз находится в порту на стоянке. Существует ряд ограничений (см. выше).
Перераспределение нагрузок при статическом крене 30° учитывается с помощью формул, приведенных в данном параграфе.
Суммирование нагрузок. Грузовые танки газовозов должны рассчитываться в соответствии с требованиями Правил Регистра РФ на раздельное воздействие всех видов нагрузок или одновременное воздействие всех возможных в эксплуатации реальных нагрузок.
Классификационное общество “Дет Норске Веритас” считает, что в один и тот же момент газовоз не испытывает комплекса максимальных нагрузок. Поэтому оно предлагает в качестве расчетной нагрузки использовать значение, вычисляемое как квадратный корень из суммы квадратов составляющих нагрузок. Если предлагается частичное заполнение танков (на 20-90 % их объемов), в качестве расчетной в нерезонансных условиях принимается нагрузка, равная сумме статического давления hc = 7ρ0H и дополнительной динамической нагрузки hд. д, определяемой по формуле 4. Здесь H – высота танка, м.
Французское Бюро Веритас расчетную нагрузку определяет как сумму статического давления hc = 10ρ0H в полностью заполненном грузом танке и динамической нагрузки, определяемой зависимостью (Формула 3). Как видно, при этом не учитываются дополнительные нагрузки, вызываемые частичным заполнением танка.
Таким образом, вопрос о суммировании нагрузок, возникающих в процессе эксплуатации газовозов, окончательно еще не решен из-за его сложности.
Краткий анализ показывает, что для случая полного заполнения танка, нагрузки, определенные по правилам различных классификационных обществ, приблизительно одинаковы. При частичном заполнении танка нагрузки, определенные по Правилам “Дет Норске Веритас”, для его днищевых связей оказываются на 25-40 % меньше, чем при полном заполнении, а для связей подволока или купола – на 10-60 % выше. Таким образом, определяющими могут быть Требования к предельной прочности и устойчивости элементов поперечных сечений балочных конструкций суднарасчетные нагрузки, как при частичном, так и при полном заполнении танка.
Нагрузки, вызванные температурными деформациями, а также возникающие в процессе испытаний или вследствие увеличения расчетного давления паров p0, могут использоваться при проверочных расчетах прочности танков. Перераспределение нагрузок при статическом крене также учитывается при этих расчетах.
Допускаемые напряжения. Для встроенных грузовых танков допускаемые напряжения определяются так же, как для корпусных конструкций традиционных судов, а для мембранных и полумембранных газовозов – особо, в соответствии с требованиями Регистра РФ.
Допускаемые напряжения для конструкций вкладных грузовых танков типа А, образованных плоскими поверхностями, принимаются меньшими из двух величин:
где:
- ReH – спецификационный минимальный предел текучести материала танка при комнатной температуре, МПа (в случае отсутствия на кривой деформации материала танка от напряжений площадки предела его текучести, в качестве ReH принимается напряжение, соответствующее удлинению образца на 0,2 %);
- Rm – спецификационный минимальный предел прочности материала танка при комнатной температуре, МПа.
Допускаемые напряжения, определяемые по формулам 5, могут быть по согласованию с Регистром РФ увеличены на основе уточненных расчетов прочности танков. При этом должны быть учтены изгибные деформации, осевое смещение танка, деформация сдвига и кручения, а также силы взаимодействия между корпусом и танком, обусловленные деформациями двойного дна газовоза и днища танка.
Для вкладных грузовых танков типа В, имеющих форму тел вращения, принимаются следующие виды допускаемых напряжений:
- эквивалентные первичные общие σm ≤ f и местные мембранные σL ≤ 1,5f;
- эквивалентные первичные при изгибе σB ≤ 1,5F;
- суммарные σL + σB ≤ 1,5F;
- σm + σB ≤ 1,5F.
- Здесь f – меньшее значение из Rm/A и ReH/B;
- F – меньшее значение из величин Rm/C и ReH/D;
- А, В, С, D – коэффициенты напряжений (коэффициенты запасов по пределу текучести), которые принимают в соответствии с табл. 1.
| Таблица 1. Значения коэффициентов напряжений в зависимости от материала танка | |||
|---|---|---|---|
| Коэффициенты напряжения | Сталь | Алюминиевые сплавы | |
| Углеродно-марганцовистая и никелевая | Аустенитная | ||
| А | 3,0 | 3,5 | 4,0 |
| В | 2,0 | 1,6 | 1,5 |
| С | 3,0 | 3,0 | 3,0 |
| Д | 1,5 | 1,5 | 1,5 |
Первичные общие Особенности конструкции морских газовозовмембранные напряжения распределены таким образом, что текучесть материала не вызывает перераспределения нагрузок. Первичные местные мембранные напряжения возникают в результате влияния местного давления или другой нагрузки и связаны с первичным эффектом или эффектом нарушения непрерывности. Эти напряжения вызывают чрезмерную деформацию при передаче нагрузки на другие части конструкций танка. Район этих напряжений рассматривается как местный, если выполняются условия
где:
- S1 – расстояние в меридиональном направлении, в пределах которого эквивалентное напряжение превышает 1,1f;
- S2 – расстояние в меридиональном направлении до другого района, в котором пределы первичного общего мембранного напряжения превышены;
- R – средний радиус грузового танка, м;
- t – толщина стенок грузового танка в месте, где предел первичного общего мембранного напряжения превышен, м.
Мембранное напряжение – составляющая нормального напряжения, равномерно распределенная и равная средней величине напряжений по толщине рассматриваемого сечения. Напряжение изгиба – переменное по толщине рассматриваемого сечения напряжение за вычетом мембранного напряжения.
Эквивалентные напряжения:
где:
- σx, σy – суммарные нормальные напряжения в направлениях осей x и y, МПа;
- τxy – суммарные касательные напряжения, МПа.
При определении статических и динамических напряжений суммарные напряжения рассчитываются раздельно:
где:
- σx ст, σy ст, τxy ст, σx д, σy д, τxy д – соответственно статические и динамические компоненты напряжений, МПа.
Величины допускаемых напряжений, выбираемые для конструкций вкладных танков типа В с плоскими поверхностями, должны согласовываться с Регистром РФ.
Допускаемые мембранные напряжения для вкладных грузовых танков типа В должны приниматься меньшими из двух величин, МПа
Прочность вкладных грузовых танков типа А
Общие вопросы проектирования газовозовРассчитаем прочность вкладных грузовых танков типа А, представляющих собой, как уже было сказано, призматические емкости, образованные плоскими поверхностями, устанавливаемые в корпусе газовоза с помощью обычных и клиновых опор. Перекрытия таких танков не являются конструкциями корпуса судна и не участвуют в обеспечении его общей и местной прочности. Расчет прочности таких танков должен выполняться в соответствии с требованиями ч. II “Корпус” Правил Регистра РФ для традиционных судов с учетом внутреннего давления и надбавок на коррозию. Размеры конструкций, расположенных в районе их опор, должны определяться, насколько это возможно, с учетом всех нагрузок, указанных в пункте “Расчетные нагрузки”, и деформаций корпуса судна.
Однако, как показывает анализ формул Правил Регистра РФ и прочностных характеристик конструктивных элементов танков газовозов, эти зависимости, справедливые для традиционных судов, не всегда дают хорошие результаты для танков газовозов. Поэтому предлагаются два варианта определения размеров связей вкладных танков типа А, разработанные авторами данной статьи: основанный на расчетных зависимостях, традиционных для Правил Регистра РФ, и на комбинированном методе проектирования танков.
Вариант 1. Основой полученных расчетных зависимостей явились Правила Французского Бюро Веритас, проекты газовозов с танками типа А, Правила Регистра РФ.
Подволок танков набирается по продольной системе (рис. 2). Основные балки набора – продольные и усиленные продольные; перекрестные – поперечные рамы.
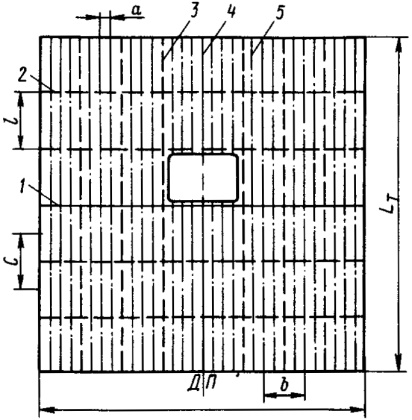
1 — поперечная переборка внутри танка; 2 — поперечная рама подволока; 3 — усиленная продольная балка подволока; 4 — продольная переборка внутри танка; 5 — продольная балка
Расстояние между продольными балками подволока должно быть не более нормальной шпации
где:
- L – длина судна, м.
Для вывода зависимости, определяющей момент сопротивления поперечного сечения продольных балок подволока, использовалась формула Регистра РФ
где:
- a – расстояние между продольными балками, м;
- p – условная нагрузка (напор), МПа;
- l – длина пролета балки, м;
- ReH – спецификационный минимальный предел текучести материала танка, МПа.
При определении условной нагрузки учитывался тот факт, что в танке типа А, рассчитанном на перевозку сжиженных газов при атмосферном давлении, поверхность жидкости при заполнении танка на 98 % находится нескольку выше нижнего среза тройка. Тронк же выполнен так, чтобы над поверхностью жидкости всегда имелся объем газа по всей длине танка, а также, чтобы для обеспечения остойчивости судна поверхность жидкости всегда была минимальной. Учитывая, что Правила Регистра РФ для вкладных танков типа А не требуют расчета дополнительных динамических нагрузок от волнообразования жидкости при их частичном заполнении, можно в качестве условной расчетной нагрузки принимать hэкв = p0. Этот вывод следует из формулы 2, так как для конструктивных связей подволока танка высота жидкого груза над рассматриваемой расчетной точкой равна нулю.
При определении коэффициента k учитывалось, что танки не участвуют в общем продольном изгибе, поэтому их набор необходимо рассчитывать на местные нагрузки. Как показал анализ, значение коэффициента k с учетом условий закрепления балок, запаса прочности, размерности, но без учета надбавок на коррозию следует принимать равным 168.
Таким образом, момент сопротивления, см3, продольных балок подволока должен быть не менее
где:
- p0 – расчетное давление паров газа в верхней части танка, МПа.
Усиленные продольные балки устанавливаются в плоскости стрингеров днища танка. Правила Бюро Веритас не содержат расчетной формулы для этих балок. Для ее вывода была разработана расчетная схема, учитывающая характер закреплений, опор и нагрузок, действующих на балку. Авторами было установлено, что в пролете между поперечными рамами изгибающие моменты меньше, чем в пролете между поперечной рамой и поперечной переборкой танка. Поэтому момент сопротивления усиленных продольных балок, см3,
где:
- k – коэффициент, равный 10(4 + Lт) в пролете между поперечными рамами и 30(4 + Lт) в пролете между поперечной рамой и поперечной переборкой (здесь Lт – длина танка, м);
- b – наибольшая ширина площади подволока, поддерживаемая усиленной продольной балкой, м;
- p0 – расчетное давление паров в верхней части танка, МПа;
- l – длина пролета балки, равная расстоянию между поперечными рамами или между поперечной рамой и поперечной переборкой, м.
Проверочный расчет показал, что величины моментов сопротивлений поперечных сечений усиленных продольных балок реальных газовозов и моментов, определенных по формуле 11, хорошо согласуются.
В грузовых танках между поперечными переборками подволок должен поддерживаться, по крайней мере, двумя поперечными рамами, образующими вместе с рамными стойками по продольным переборкам, бортовыми и днищевыми рамами замкнутые конструкции. Анализ, проведенный для поперечных рам, позволил вывести формулу для момента сопротивления их поперечного сечения, см3:
где:
- c – полусумма длин пролетов продольных балок, примыкающих к рассматриваемой раме, м;
- l – длина пролета рамы, измеренная по настилу горизонтальной части подволока между продольной переборкой и наклонной частью подволока, м.
Толщина настила подволока, мм, должна быть не менее
где:
- a – расстояние между балками продольного набора, м.
Однако в любом случае для любой стали толщина настила подволока, мм, должна быть не менее минимальной толщины Smin = 0,02L + 5, но не более 10,5 мм.
Днищевое перекрытие набирается по продольной системе (рис. 3). Наружная обшивка и подкрепляющий ее наборОсновные балки набора – продольные днищевые, днищевые стрингеры; перекрестные – днищевые рамы (флоры).
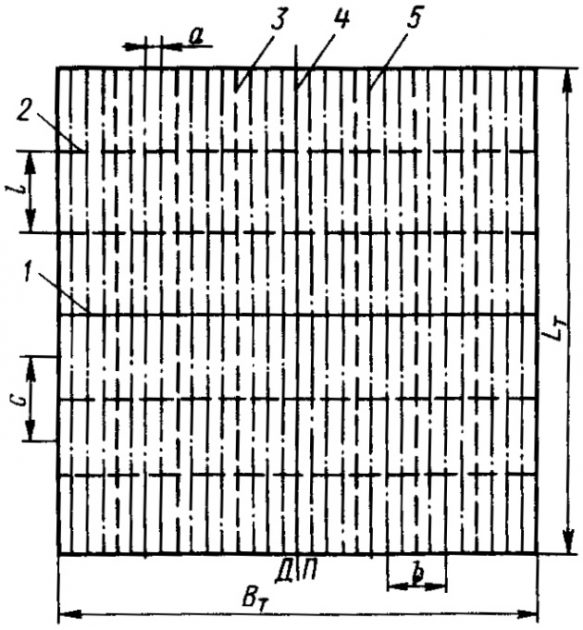
1 – поперечная переборка внутри танка; 2 – днищевая рама; 3 – днищевой стрингер; 4 – продольная переборка внутри танка; 5 – продольная днищевая балка танка
Момент сопротивления поперечного сечения продольных днищевых балок, см3, должен быть не менее
где:
- a – расстояние между продольными днищевыми балками, м;
- hэкв – внутреннее давление в грузовом танке, МПа, определяемое по формуле 2;
- l – длина пролета балки между днищевыми рамами или днищевой рамой и поперечной переборкой, м.
Вывод формулы для днищевых стрингеров основывался на расчетной схеме, которая учитывала характер закреплений балки и опор танка. Анализ реальных конструкций показал, что поперечные сечения стрингеров могут быть переменными по длине. Все это позволило вывести следующие формулы для определения момента сопротивления поперечного сечения, см3, днищевых стрингеров:
где:
- k – коэффициент, равный 231 – для пролетов стрингеров между днищевыми рамами и равный 716 – для пролетов стрингеров между поперечной переборкой и днищевой рамой;
- b – наибольшая ширина площади, поддерживаемой днищевыми стрингером, м;
- hэкв – Контролируемый газоотвод на морских танкерахвнутреннее давление в грузовом танке, МПа, определяемое по формуле 2;
- l – длина пролета стрингера, равная расстоянию между днищевыми рамами или поперечной переборкой и днищевой рамой, м.
Для вывода формулы момента сопротивления днищевой рамы использовались расчеты поперечных рам танков газовозов. Поперечные рамы идеализировались стержневой схемой. Нагрузки на стержни рамы определялись в соответствии с формулой 2. Учитывалось влияние опор и продольных переборок танков. В этом случае момент сопротивления днищевой рамы, см3, должен быть не менее
где:
- k – коэффициент, равный 10(31 – Bт/2);
- Bт – ширина танка, м;
- c – полусумма длин пролетов продольных днищевых балок, примыкающих к рассматриваемой раме, м;
- l – длина пролета днищевой рамы, измеренная по горизонтальной части настила днища, м.
Толщина обшивки танка, мм, должна быть не менее определяемой по формуле 12, в которой напор принимается в соответствии с формулой 2. Однако в любом случае толщина обшивки днища и подволока танка, мм, должна быть не менее s = 9,43α. Здесь a – расстояние между продольными балками набора, м.
Обшивку и набор борта рассмотрим при следующих условиях. Конструкция судовых перекрытийБортовые перекрытия набираются по продольной системе (рис. 4).
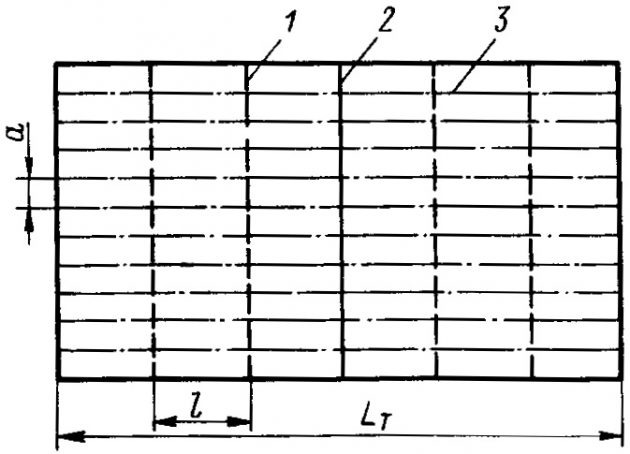
1 — бортовая рама; 2 — поперечная переборка внутри танка; 3 — продольная бортовая балка
Основные балки набора – продольные бортовые, перекрестные – бортовые рамы (рамные шпангоуты). Момент сопротивления поперечного сечения продольных балок борта, см3, должен быть не менее определяемого по формуле 13, момент сопротивления поперечного сечения бортовых рам, см3, – не менее
где:
- b – наибольшая ширина площади бортовой обшивки, поддерживаемой бортовой рамой, м;
- hэкв – внутреннее давление в танке, МПа, определяемое формулой 2;
- l – длина пролета рамы, измеренная по вертикальной части бортовой обшивки, м.
Толщина обшивки бортовой части танка, мм,
где:
- a – расстояние между подкрепляющими обшивку балками набора, м;
- hэкв – Грузовые операции на газовозах морского типавнутреннее давление в танке, МПа, определяемое формулой 2.
Поперечные переборки танка, установленные посредине его длины, должны иметь схему набора (рис. 5), согласованную с системой набора танка.
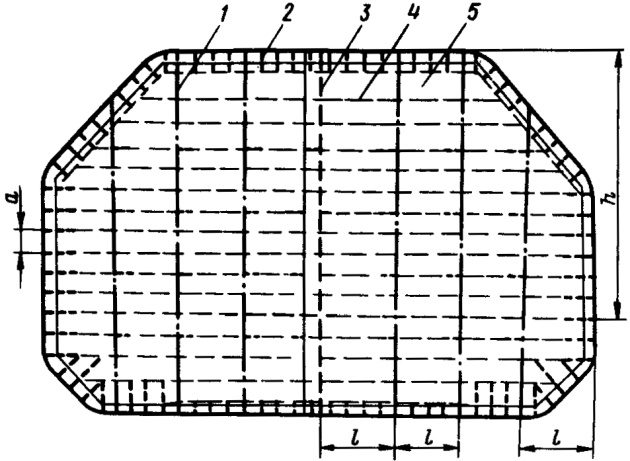
1 – рамная стойка; 2 – продольная балка подволока; 3 – продольная переборка внутри танка; 4 – горизонтальная балка; 5 – обшивка поперечной переборки
При продольной системе набора борта набор переборок состоит из горизонтальных балок и рамных стоек. Толщина стоек поперечных переборок определяется по формуле 14. Зависимость для определения момента сопротивления поперечного сечения горизонтальных балок, см3, получена на основе анализа условий их работы:
где:
- a – расстояние между горизонтальными балками, м;
- hэкв – внутреннее давление в танке на уровне балки, МПа, определяемое формулой 2;
- l – длина пролета балки, измеренная как расстояние между рамными стойками, между рамной стойкой и продольной переборкой или между рамной стойкой и бортом, в зависимости от того, что больше, м.
Аналогично были получены формулы для рамных стоек, установленных в плоскости днищевых стрингеров и усиленных продольных балок подволока. Момент сопротивления поперечного сечения рамных стоек, см3, должен быть не менее
где:
- k – коэффициент, k = 10(55 – Lт);
- Lт – длина танка, м;
- b – наибольшая ширина площади переборки, поддерживаемой рамной стойкой, м;
- hэкв – внутреннее давление в танке, МПа, определяемое по формуле 2 на уровне середины пролета рамной стойки;
- l – длина пролета, равная длине стойки, включая концевые кницы, м.
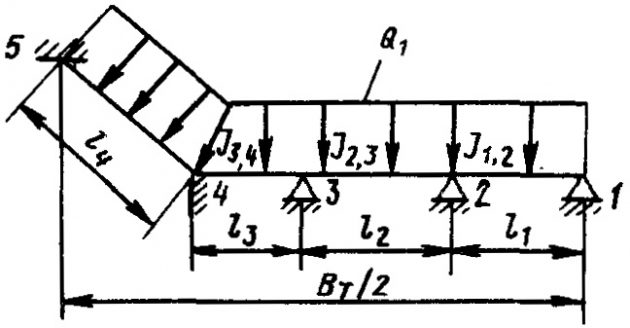
Продольные переборки танка, устанавливаемые в ДП по всей его длине, должны иметь схему набора, согласованную с системой набора танка (рис. 6). При продольной системе набора танка и набора поперечных переборок, состоящего из горизонтальных балок и рамных стоек, основные конструктивные связи продольных переборок должны быть такими же, как и у поперечных переборок.
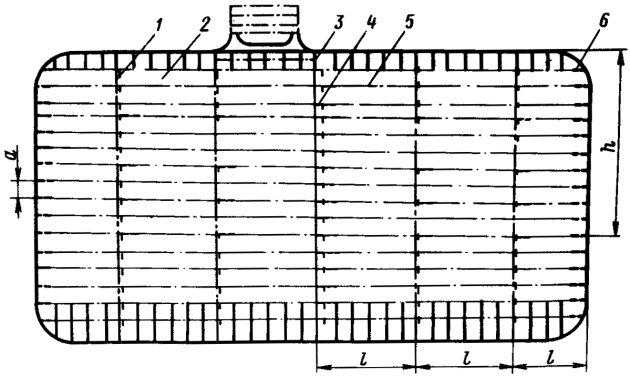
1 – рамная стойка; 2 – обшивка продольной переборки; 3 – поперечная переборка внутри танка; 4 – горизонтальные балки поперечной переборки внутри танка; 5 – горизонтальная балка продольной переборки; 6 – продольные балки борта танка
Листовые конструкции корпуса суднаТолщина листов продольных переборок определяется по формуле 14, а момент сопротивления поперечного сечения их рамных стоек, устанавливаемые в плоскости бортовые рамы-днищевые рамы-поперечные рамы подволока танка – по формуле 19. Момент сопротивления поперечного сечения горизонтальных балок, см3, должен быть не менее
где:
- a – расстояние между горизонтальными балками, м;
- l – длина пролета балки, измеренная как расстояние между рамными стойками или как расстояние между рамной стойкой и поперечной переборкой, в зависимости от того, что больше, м.
Вариант 2. Вследствие сложности напряженно-деформированного состояния перекрытий корпусных конструкций вкладных грузовых танков типа А для более точных расчетов их прочностных размеров необходимо воспользоваться не только эмпирическими зависимостями, предложенными в варианте 1, но и расчетными схемами. В связи с этим целесообразно проектировать корпусные связи танков по заданным нагрузкам, рекомендуемым расчетным схемам, и частично с помощью эмпирических зависимостей, полученных на основе ряда расчетных схем. Такой метод проектирования, названный комбинированным, предлагается ниже.
Комбинированный метод основан на расчете прочностных характеристик в нескольких приближениях в зависимости от степени готовности проекта газовоза. В этом случае Регистр РФ должен потребовать от исполнителя предъявления следующих данных: перечня принятых допущений, программ расчета на ЭВМ, результаты вычислений прочности грузовых танков.
Обшивка танков. Для любой стали или алюминиевых сплавов толщина обшивки, мм, должна быть не менее минимальной толщины smin = 0,02L + 5, но не более 10,5 мм. В первом приближении толщину обшивки следует определять по формуле 14, а во втором – с помощью расчетных схем; при этом обшивка рассматривается как изотропная пластина. В зависимости от того, к какому перекрытию танка относится та или иная пластина, выбирают схему ее нагружения и условия закрепления на кромках. При этом толщина обшивки, мм,
где:
- Mmax – максимальный погонный изгибающий момент, действующий в пластине, H;
- [σ]д – допускаемые напряжения для конструкций вкладных танков типа А, МПа.
В любом случае толщина днища танка и подволока, мм, должна быть не менее s = 9,43a.
Читайте также: Справочные показатели для проектирования судового мидель-шпангоута. Приложение
Продольные балки. В первом приближении моменты сопротивлений продольных балок наборов всех перекрытий рассчитывают по формулам 10 и 13. Во втором приближении размеры балок определяют с учетом перерезывающих сил. Характер распределения их оценивают по следующей схеме: балка считается жестко защемленной на поперечных рамах (рис. 7), испытывающей равномерную нагрузку Q = hэквal, кH (здесь a – расстояние между продольными балками). Эквивалентные напряжения плоского напряженного состояния
не должны превышать допускаемых напряжений [σ]д.
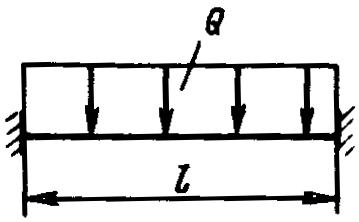
Усиленные продольные подпалубные балки. Моменты сопротивлений поперечных сечений в первом приближении определяют по формуле 13. Во втором приближении размеры балок вычисляют с учетом перерезывающих сил и в соответствии с расчетной схемой (рис. 8).

Усиленная продольная подпалубная балка считается жестко защемленной на поперечных переборках танка, поперечные рамы подволока рассматриваются как ее упругие опоры, поперечное сечение балки принимается переменным по ее длине. Балка нагружена равномерно распределенной нагрузкой, суммарное значение которой, кH, в пролетах
где:
- b – средняя ширина площади палубы, поддерживаемой усиленной продольной балкой, м.
Для усиленных продольных балок, устанавливаемых в районе опор танков, расчетные нагрузки должны быть откорректированы с учетом всех нагрузок, указанных в пункте “Расчетные нагрузки”. Для этого в формуле 19 вместо hэкв необходимо подставлять соответствующие нагрузки. Размеры балок должны быть рассчитаны так, чтобы эквивалентные напряжения, полученные по формуле 18, не превышали [σ]д.
Расчет усиленных продольных балок в третьем приближении ведется по уточненной конструктивной схеме с учетом влияния поперечной переборки и днищевой рамы (рис. 9). Нагрузки определяются в соответствии с требованиями пункта выше, а размеры балок из условия непревышения эквивалентных напряжений по формуле 18 допускаемых напряжений.
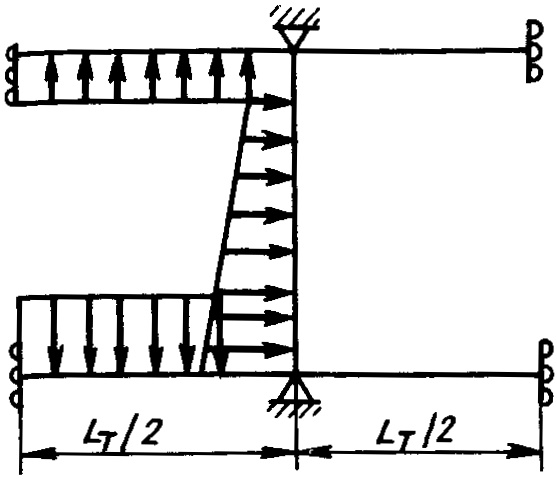
В первом приближении моменты сопротивлений поперечных сечений днищевых стрингеров определяются по варианту 1, во втором по расчетной схеме (рис. 10). Конструкция корпуса газовозовДнищевой стрингер считается балкой, жестко защемленной на поперечных переборках танка, днищевые рамы рассматриваются как его упругие опоры, поперечное сечение балки принимается переменным по ее длине. Стрингер нагружен в соответствии с усилиями, описанными формулой 19, в которых b – средняя ширина площади днища, поддерживаемая стрингером. Дальнейшие расчеты, в том числе и в третьем приближении, необходимо выполнять аналогично расчетам усиленных продольных подпалубных балок.
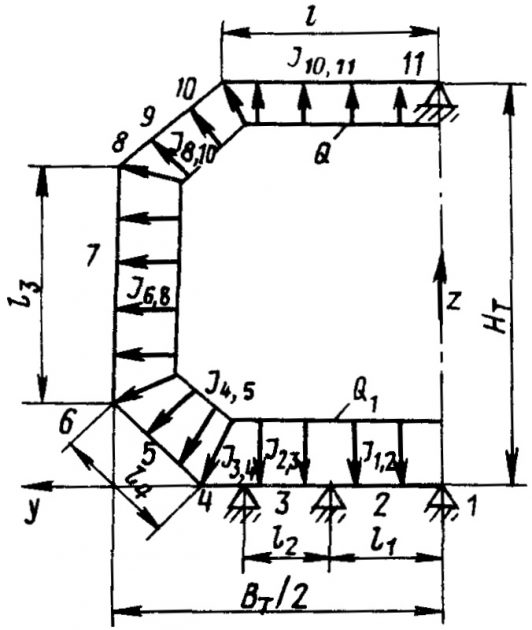
В первом приближении моменты сопротивлений поперечных сечений элементов поперечных рам (подволока, борта, днища) танка определяются с помощью формул варианта 1, во втором – по соответствующим расчетным схемам. При этом рама подволока считается балкой, жестко защемленной на поперечной переборке и на наклонной ветви бортовой рамы (см. рис. 7), нагруженной суммарными усилиями Q = p0lb, кH (здесь l – длина пролета рамы, измеренная между продольной переборкой и наклонной ветвью бортовой рамы, м; b – средняя ширина площади подволока, поддерживаемая рамой, м). В некоторых случаях при соответствующих соотношениях моменты инерций бортовой и подволочной частей рамы расчет во втором приближении необходимо вести по схеме рис. 11. Рама подволока считается балкой, свободно опертой на наклонную ветвь бортовой рамы и жестко заделанной на поперечной переборке танка.
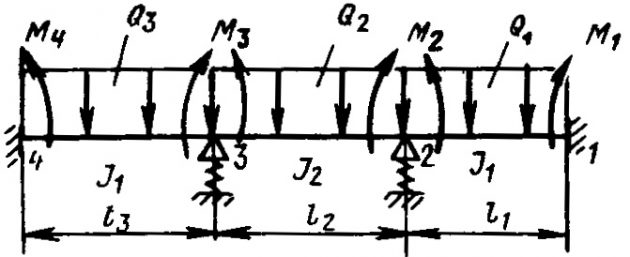
Размеры поперечного сечения рамы подволока в третьем приближении определяют по результатам расчетов максимальных моментов и перерезывающих сил, возникающих в ней и определенных в соответствии с расчетной схемой (рис. 12).
Рама подволока рассматривается как часть общей поперечной рамы танка. В расчетной схеме реальные ветви поперечной рамы танка заменены условными стержнями, нагрузки на которые определяются в соответствии с указаниями пункта “Расчетные нагрузки”. Поперечная рама считается жестко защемленной на продольной переборке, Принципы проектирования элементов днищевых конструкций в носовой оконечностиднищевая часть рамы опирается на жесткие опоры танка, податливость которых не учитывается. В состав площади поперечных сечений стержневой рамы необходимо включать их присоединенные пояски. На рис. 12 обозначено:
- l1, l2 – расстояния, измеренные между жесткими опорами танка, м;
- l3 – пролет бортовой рамы (шпангоута), м;
- l4 – длина пролета наклонной части рамы, м;
- l – длина пролета поперечной рамы подволока, м;
- Bт, Hт – ширина и высота танка, м;
- Q, Q1 – суммарные нагрузки, передаваемые на рамы подволока и днища, кH;
- l1, 2, l2, 3, l3, 4, l4, 5, l6, 8, l8, 10, l10, 11 – моменты инерции поперечных сечений стержней с учетом присоединенных поясков, м4.
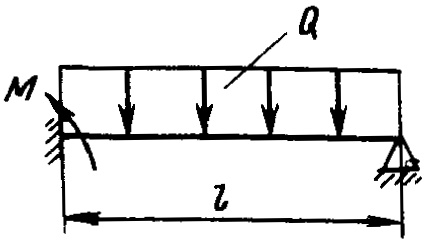
Во втором приближении бортовая рама считается балкой, жестко защемленной по концам, пролет ее рамы принимается равным высоте вертикальной части борта танка. Бортовая рама нагружена давлением в соответствии с расчетной схемой (рис. 13). В третьем приближении размеры рамы определяются по расчетной схеме рис. 12.
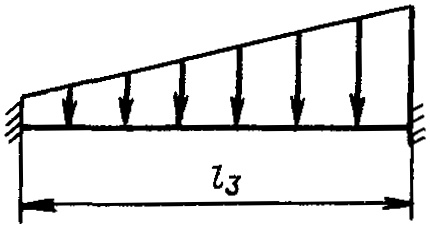
Днищевая рама во втором приближении считается криволинейной балкой, жестко защемленной на продольной переборке и у нижнего конца вертикальной части бортовой рамы. Днищевая часть рамы опирается на жесткие опоры танка. Податливость опор не учитывается (рис. 14). В состав поперечного сечения рамы необходимо включить присоединенный поясок обшивки.
Уточненный расчет в третьем приближении с оценкой влияния бортовой ветви рамы и рамы подволока необходимо вести согласно рис. 12.
Это интересно: Безопасность газовозов и источники воспламенения газов
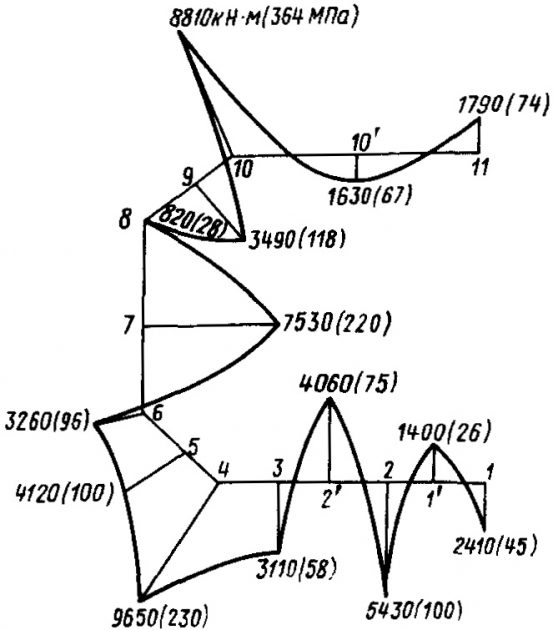
Размеры поперечных рам должны быть рассчитаны так, чтобы эквивалентные напряжения из формулы 18 не превышали [σ]д. Результаты расчетов изгибающих моментов, кH · м, и напряжений, МПа, действующих в поперечной раме танка газовоза типа “Моссовет”, представлены на рис. 15.
Поперечные и продольные рамы переборки танка. Листовые конструкции корпуса суднаТолщина листов обшивки переборок в первом приближении определяется по формуле 14, во втором – из расчета обшивки как изотропной пластины. Моменты сопротивлений поперечных сечений горизонтальных балок по поперечным и продольным переборкам определяются по формулам 15 и 17. Размеры рамных стоек в первом приближении вычисляются в соответствии с моментом сопротивления поперечного сечения, определенным по формуле 16.
Во втором приближении рамные стойки продольных и поперечных переборок считаются балками, жестко защемленными по концам. В случае необходимости учета влияния на размеры поперечных сечений рамных стоек переборок танка днищевой рамы и рамы подволока следует воспользоваться расчетной схемой (см. рис. 9).
Размеры связей переборок танка должны быть такими, чтобы эквивалентные напряжения из формулы 18 не превышали [σ]д.
Моменты сопротивления поперечных сечений, см3, конструктивных связей внутри танков газовозов, определяемые расчетным путем, должны быть не менее
где:
- Mр – максимальный расчетный изгибающий момент, кН · м.
Надбавки на коррозию для толщины обшивок грузовых танков, полученных расчетным путем, вводят, если при эксплуатации газовозов предусматривается Перевозка опасных грузов в таре и наваломперевозка химически активных веществ или не предусмотрен контроль среды, окружающей танк. Надбавки рассчитывают в соответствии с расчетным периодом эксплуатации газовозов и скоростью коррозии конструкций. Если наружная поверхность танков защищена инертным газом или она стойка к воздействию паров груза, то надбавку на коррозию не вводят. Если обшивка танков выполнена из коррозионно-стойких материалов, введение надбавки на коррозию согласуется с Регистром РФ. При этом окраска поверхностей танка или применение специальных тонких покрытий не считается их коррозионной защитой.
Прочность вкладных грузовых танков типа В
Рассчитаем прочность вкладных грузовых танков типа В. Прочностные расчеты таких танков следует вести по уточненным методикам с учетом всех возможных в эксплуатации нагрузок и их комбинаций. Уточненные методики должны включать:
- статистическую оценку волновых нагрузок;
- расчеты прочности методом конечных элементов или эквивалентным методом, одобренным Регистром РФ;
- расчеты усталостной долговечности и скоростей распространения трещин;
- расчет устойчивости конструкций;
- расчеты прочности при воздействии нагрузки, передаваемой на конструкции грузового танка от его опор и деталей крепления с применением трехмерной схемы идеализации.
Статистическая оценка волновых нагрузок, действующих на грузовые танки. Она может быть проведена на основе спектральной теории нерегулярной качки на волнении. Эффективнее всего при статистической оценке волновых нагрузок использовать один из методов статистической динамики – спектральный, устанавливающий статистическую связь между параметрами внешнего возбуждения исследуемой системы и выходного процесса. При этом по известным входным параметрам и свойствам системы определяют характеристики выходного процесса. Спектральный метод может быть применен тогда, когда рассматриваемые процессы имеют достаточную длительность, их корреляционные функции определяются лишь промежутком между рассматриваемыми моментами времени, сама система за время работы не изменяется и подвергается влиянию стационарных случайных воздействий. Таким образом, спектральный метод при статистической оценке волновых нагрузок применим в случаях полностью загруженных и порожних танков.
Читайте также: Применение якорей при маневрировании
Используя данный метод, газовоз будем рассматривать в качестве линейной динамической системы, на вход которой подается стационарный случайный процесс – волнение, частотный спектр которого считается известным. На выходе системы определяются параметры выходного процесса – спектральные плотности различных видов качки Su (ω). Входной и выходной процесс с помощью амплитудно-частотной характеристики (АЧХ) связаны зависимостью Винера-Хинчина
где:
- u – индекс рассматриваемого вида качки;
- Sζ (ω) – спектральная плотность волнения;
- |Φu (iω)| – модуль АЧХ.
Нерегулярное волнение будем считать ветровым, образованным суперпозицией бесконечного множества гармонических волн различной длины с непрерывным частотным спектром ω и случайными бесконечно малыми амплитудами, распределение энергии между которыми характеризуется спектральной плотностью Sζ (ω).
Двухмерное (плоское) нерегулярное волнение – сумма бесконечного числа прогрессивных волн, имеющих свою амплитуду, частоту и фазу. При этом направление волн одинаково, а их гребни – бесконечно длинные. В трехмерном нерегулярном волнении составляющие волны распространяются под различными углами к главному направлению бега волн. Поэтому у такого волнения дополнительным параметром является угол ε между направлением бега простых прогрессивных волн и главным направлением, соответствующим обычно направлению ветра.
При рассмотрении нерегулярного волнения как двухмерного его спектр называют одномерным, так как ордината кривой спектра зависит только от одной переменной – частоты волны ω. Так как спектр трехмерного нерегулярного волнения зависит от двух переменных – частоты волны ω и текущего значения угла ε относительно направления бега волн – его спектр называют двухмерным. Одномерный спектр можно получить интегрированием двухмерного спектра по углу ε в пределах от π/2 до π/2.
Для статистической оценки волновых нагрузок на конструкции танков газовозов при двумерном нерегулярном волнении рекомендуется использовать спектр, который имеет вид
где:
- – дисперсии волновых ординат, частота максимума спектра и средняя частота;
- τm – расчетное значение периода максимума спектра, c-1;
- – частота волны, с-1;
- τв – период волны, с.
Дисперсия волновых ординат, м2,
где:
- h3 % – высота волны 3 %-ной обеспеченности, м.
В зависимости от определяющего вида качки выбирается расчетный спектр волнения. Так, например, для бортовой качки τm = 0,6τθ при движении “резонансным” курсовым углом, τm = τθ – при движении лагом к волне. Для продольной качки средний период волнения должен соответствовать кривой (τm)ср (рис. 16). Кривые (τm)max и (τm)min используются соответственно при оценках наибольших амплитуд продольной качки и затухающего волнения.
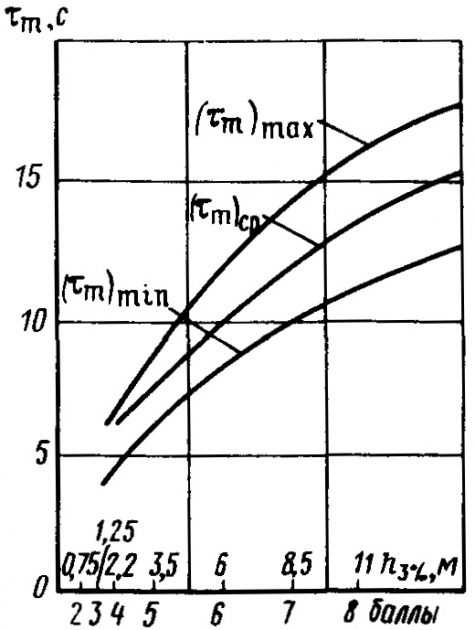
Для трехмерного волнения рекомендуется использовать спектр
где:
- ε – текущее Обозначение судовых технических величинзначение угла относительно направления бега волн;
- m, n – коэффициенты, принимающие значения:
Спектральные плотности углов волнового склона двухмерного и трехмерного волнения
Для определения волновых нагрузок, действующих на грузовые танки газовозов, необходимо знать ускорение в их расчетных точках, дисперсии проекций которых на вертикальную Оζ, поперечную Оη и продольную Оξ оси (Оξ и Оη лежат в плоскости невозмущенной поверхности воды) имеют вид
где:
- ζm, ηm, ξm – проекции перемещений расчетной точки танка, имеющей координаты
z, y, x
в связанной с газовозом подвижной системой координат, начало которой совпадает с его ЦТ,– модули АЧХ преобразования в вертикальное, поперечное и продольное перемещение точки танка газовоза.
Перемещение точки m на оси ζ, η, ξ можно определить с помощью соотношений
где:
- ζg, ηg, ξg – координаты ЦТ судна;
- θ, ψ, φ – График дифферента (Диаграмма осадки носом и кормой)углы крена, дифферента и рыскания.
Квадраты модулей АЧХ преобразований волнения в перемещении точки m танка могут быть определены с помощью модулей АЧХ соответствующих видов качки на основании зависимостей
где:
- u – индекс рассматриваемого вида качки, принимающий последовательно значения ξm, ηm, ζm;
- ν – индекс координат ЦТ газовоза, принимающего последовательно значения ξg, ηg, ζg;
- k, n – индексы сдвигов фаз колебаний газовоза по отношению к волнению, принимающие последовательно значения φ, θ, ψ и ψ, φ, θ;
- α, β – координаты расчетной точки танка газовоза, принимающие последовательно значения y, z, x и z, x, y.
Корреляционные моменты двух видов качки u и ν находят следующим образом:
где:
- – модули АЧХ различных видов качки;
- δu, δν – сдвиги фаз этих колебаний по отношению к волнению.
В случае необходимости дисперсии проекций перемещений, скоростей и ускорений расчетной точки танка с помощью соотношений можно выразить линейной комбинацией соответствующих дисперсий проекций перемещений, скоростей и ускорений ЦТ судна и корреляционных моментов различных видов качки, связанных с коэффициентами корреляции.
Зная дисперсии ускорений точки m, можно определить соответственно средние, с 3 %-ной обеспеченностью и максимальные значения проекций ее амплитуд ускорений, а именно:
где:
- – дисперсия проекции ускорения любого из направлений (
– принимают значения
).
Таким образом, зная выше перечисленные величины проекций ускорений, можно определить динамические нагрузки, действующие на конструкции танков газовозов.
Расчеты прочности вкладных грузовых танков типа В ведут методом конечных элементов (МКЭ) или эквивалентным ему методом. Так, например, можно использовать, разработанный в Николаевском кораблестроительном институте канд. тех., наук доцентом В. Н. Спихтаренко итеративный метод решения пространственных стержневых систем, который намного проще МКЭ при практически одинаковых результатах. Программы для ЭВМ, реализующие итеративный метод, менее громоздки, чем составленные по МКЭ.
В соответствии с итеративным методом танк газовоза можно представить в виде пространственной системы стержневых конструкций – совокупности жестких связей, составляющих каркас определенным образом соединенных перекрытий танка. Поперечные и продольные балки перекрытий жестко соединены между собой в узлах пересечения, а сами перекрытия соединены так, что поперечные рамы танка связаны одна с другой продольными рамами. Такая пространственная конструкция при приложении нагрузки к какому-либо перекрытию или балке вовлекает в работу не только балки данного перекрытия, а и соседнего, несущие нагрузки. При расчете пространственной конструкции танка она расчленяется на отдельные балки или плоские рамы так, чтобы их расчет с учетом взаимного влияния всех ее элементов мог быть выполнен с помощью известных систем уравнений, не требующих составления специальных программ для ЭВМ.
В качестве факторов, определяющих интенсивность взаимного влияния всех связей пространственной конструкции на элементы изгиба каждой из составляющих ее балок при выделении из ее состава любого перекрытия, принимаются условия закреплений балок перекрытия на опорном контуре. Эти условия назначаются с учётом соотношений балок пространственной конструкции танка и действующих на них нагрузок. Принимается, что нагрузка воспринимается поперечными рамами танка, опертыми на жестко смещаемые опоры, а узловые реакции – продольными балками. Величина смещения опор определяется прогибом соответствующих узловых сечений продольных балок. Тогда один из алгоритмов расчета пространственной конструкции танка газовоза, основанный на вышеописанном методе и применении теоремы трех моментов, будет иметь следующий вид.
1 Определение в первом приближении коэффициентов rk(1) узловых реакций Rk = rkQmn (здесь Qmn – расчетная нагрузка на стержень m – n) по формуле
где:
- индекс n – номер приближения;
- αmnk – коэффициент влияния нагрузки Qmn на прогиб стержня m-n в k-м сечении, вычисленный с учетом работы этого стержня в составе поперечной рамы;
- βk, γk – коэффициенты, равные
Здесь:
- βki – коэффициент влияния узловой реакции Ri = riQmn на прогиб стержня m-n в k-м сечении, вычисленный с учетом работы этого стержня в составе поперечной рамы;
- γkj – коэффициент влияния узловой реакции Rj = rjQmn на прогиб перекрестной связи c-d в k-м сечении, вычисленный с учетом работы этой связи в составе продольной рамы;
- Ri(i = 1, 2,…, k,…, s) – реакция в узлах пересечения стержня m-n с перекрестными балками;
- s – число перекрестных балок, с которыми пересекается стержень m-n;
- Ri (i = 1, 2,…, k,…, t) – реакции в узлах пересечения перекрестной связи c-d со стержнями поперечных рам;
- t – число стержней поперечных рам, с которыми пересекается перекрестная (продольная) связь c-d.
Полагая ri(0) = rj(0) = ··· = rk(0), из формул 20 и 21 получаем
где:
2 Определение в первом приближении коэффициентов податливости упругих опор – продольных балок – в k-м узле с помощью выражений (Формула 21) и (Формула 22)
где:
- Lcd – длина перекрестной (продольной) связи пространственной системы, измеренная между поперечными переборками танка c и d;
- Elcd – жесткость перекрестной связи c-d.
3 Определение в первом приближении прогиба балки в k-м узле
4 Расчет поперечных рам танка как рам, опертых в узлах на жесткие смещаемые опоры, величина смещения которых задана прогибом ωk(1) соответствующих сечений продольных рам, загруженных в узлах реакциями Rk(1).
Узловые реакции
где:
5 Определение во втором приближении Ak(2) и ωk(2) в соответствии с формулами пунктов “Прочность вкладных грузовых танков типа А” и “Прочность вкладных грузовых танков типа B“, в которых n = 2.
6 Определение в узловых сечениях поперечных рам Rk(3) = rk(3)Qmn в соответствии с пунктом “Прочность мембранных, полумембранных танков и танков с внутренней изоляцией”.
Процесс последовательных приближений необходимо закончить, когда будет выполнено условие
где:
- lmn – длина стержня поперечной рамы, измеренная между узлами m и n;
- imn – момент инерции поперечного сечения стержня m-n поперечной рамы;
- βkmn(n) = (αmn/rk) – коэффициент;
- (n) = 1, 2, 3 … – номер приближения.
Статическая неопределенность рамы раскрывается методом угловых деформаций. Для этого необходимо определить углы поворотов узлов рамы и вычислить коэффициенты влияний и податливости, используя выражения для прогиба балок от соответствующей нагрузки при заданных углах поворота опорных узлов.
Приведенный алгоритм позволяет рассчитывать пространственные стержневые системы без учета сдвига и с учетом его. Сдвиг в балках перекрытий учитывается с помощью коэффициентов влияния αmnk, βki, γki.
Итеративный метод расчета пространственных конструкций танков позволяет выполнять оптимизацию их по массе в случае работы всех балок в заданном режиме напряжений. Применение итеративного метода требует предварительного одобрения его Регистром РФ.
Расчеты усталостной долговечности и скоростей распространения трещин необходимо проводить для материала танка и его сварки соединений в тех районах, где вероятнее всего могут возникнуть большие динамические напряжения или концентрация напряжений.
Расчет усталостной долговечности танков должен быть выполнен с учетом условно принимаемого 25-летнего срока эксплуатации газовоза и 15-дневного ограниченного времени его пребывания в море. При этом условия пребывания в море газовоза должны быть наиболее неблагоприятными из всех возможных за период его эксплуатации. Рекомендуется проведение обязательного контроля усталостного ресурса конструкций танков газовозов с помощью линейного суммирования усталостных повреждений. При этом долговременный спектр волновых нагрузок и напряжений подчиняется экспоненциальному закону.
Зарубежные фирмы, специализирующиеся на проектировании и постройке газовозов, рекомендуют в расчетах усталостной долговечности учитывать течь перед аварией (Leak befor faibor). В данном случае подразумевается, что появление трещины в какой-либо части конструкции танка не является катастрофическим событием для судна. Газовоз с трещиной в танке может продолжать рейс, даже если эта трещина образовалась в начале рейса. Введя такое понятие, фирмы тем самым несколько ослабили требования, предъявляемые к усталостной долговечности танков, что, по их мнению, не приводит к ухудшению эксплуатационных качеств газовозов.
В первом случае усталостная долговечность определяется в соответствии с наиболее вероятным спектром нагрузок, которым может быть подвержен газовоз в течение 25-летней эксплуатации в Северной Атлантике, или спектром, рекомендованным кодом ИМО (рис. 17).
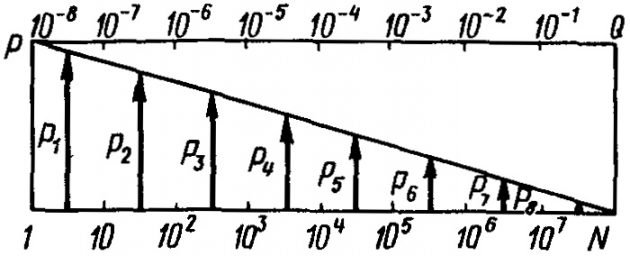
Каждое из восьми значений ординат спектра переменных усталостных нагрузок Pi и число соответствующих циклов их изменений в течение всего срока эксплуатации судна определяются зависимостями
где:
- i – порядковый номер ординат усталостных нагрузок, i = 1, 2, 3, …, 8;
- P0 – наибольшая нагрузка в течение 25-летнего срока эксплуатации при уровне вероятности Q = 10-8.
Влияние нагрузки, вызывающей усталость в соответствии с указанным выше спектром и учетом числа погрузок и разгрузок в портах, должно удовлетворять условию
где:
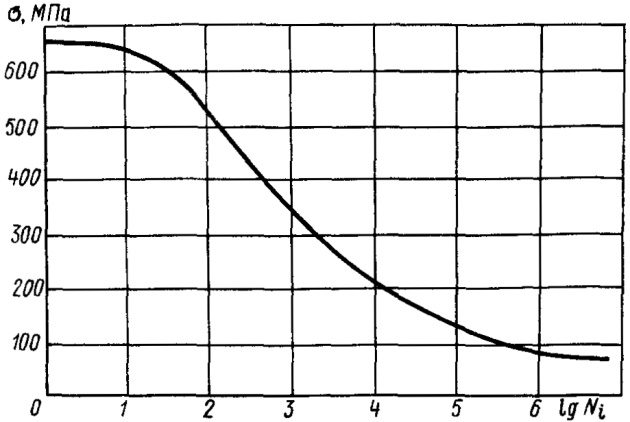
- Ni – число до излома для соответствующего ординате усталостной нагрузки Pi с порядковым номером уровня напряжений, согласно кривой усталости Велера (рис. 18);
- Nj – число циклов до излома для разрушающих усталостных нагрузок, обусловленных погрузочно-разгрузочными операциями и определяемое данными испытаний или на основании обобщения опытов;
- CW = 0,5 – параметр;
- при 0,5 < CW ≤ 1,0 необходимо согласование с Регистром РФ в зависимости от метода модельных испытаний и данных, используемых для построения кривой Велера.
При определении Nj необходимо учитывать Принципы проектирования конструкций корпуса суднастатические нагрузки, описанные в пункте “Расчетные нагрузки”.
Во втором случае усталостная долговечность определяется в течение наихудшего 15-дневного периода нахождения газовоза на волнении в Северной Атлантике, согласно спектру волновых нагрузок (рис. 19).
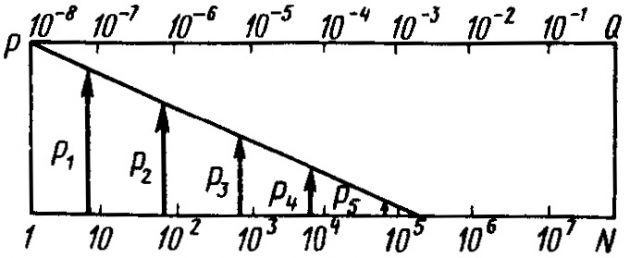
Каждое из пяти значений ординат спектра переменных усталостных нагрузок Pi и число соответствующих циклов их изменений в течение 15-дневного срока пребывания газовоза в море определяются зависимостями
где:
- i – порядковый номер ординат усталостных нагрузок, i = 1, 2, 3, …, 4, 5;
- P0 – наибольшая нагрузка в течение 15-дневного срока пребывания газовоза в море, определенная с учетом динамических нагрузок при качке.
При определении усталостной долговечности узлов конструктивных элементов Регистр РФ может потребовать проведения экспериментальных модельных испытаний. При этом следует особенно обращать внимание на влияние таких факторов, как размеры образца, концентрация напряжений и чувствительность к надрезу, условия и способы сварки, рабочая температура. По результатам испытаний должны быть построены кривые Велера.
Скорость распространения возникшей трещины в конструкции танка газовоза определяется с учетом статических и динамических нагрузок, действующих на танк, на основе усталостной кривой (см. рис. 18) или экспериментальных данных роста трещин.
Предлагается к прочтению: Основы взаимодействия дизеля и устройств автоматического регулирования
При проектировании конструкций танков газовозов с учетом усталостных нагрузок иногда, по согласованию с Регистром РФ, пользуются зависимостями, полученными В. Вит. Козляковым для узлов с напряжениями, распределенными согласно закону Вейбулла и включающими в себя информацию о нагруженности узлов, особенностях их конструктивно-технологического оформления, работоспособности материала и поправок на износ:
где:
- Wy – момент сопротивления поперечного сечения связи;
- fy – площадь поперечного сечения стенки связи;
- M-8, N-8 – изгибающие моменты и перерезывающие силы в рассматриваемом сечении с обеспеченностью 10-8;
- Mт.в. ср, Nт.в. ср – средние за срок эксплуатации значения усилий в узле, принимающие положительные значения при растяжении узла и отрицательных при его сжатии;
- σ 0-1, τ0-1 – пределы усталости базового сварного образца при симметричном цикле нагружения;
- α, α′ – коэффициенты концентрации напряжений.
Расчет устойчивости концентраций грузовых танков типа В выполняется для тех элементов, которые подвержены воздействию сжимающих усилий или больших поперечных усилий, а также при их совместном воздействии. Проверка устойчивости связей танков должна быть проведена для следующих типов деформаций:
- местного изгиба стенок и поясков продольных балок и их опор (поперечных балок);
- кручения продольных балок и их опор;
- общей потери устойчивости подкрепленных пластин.
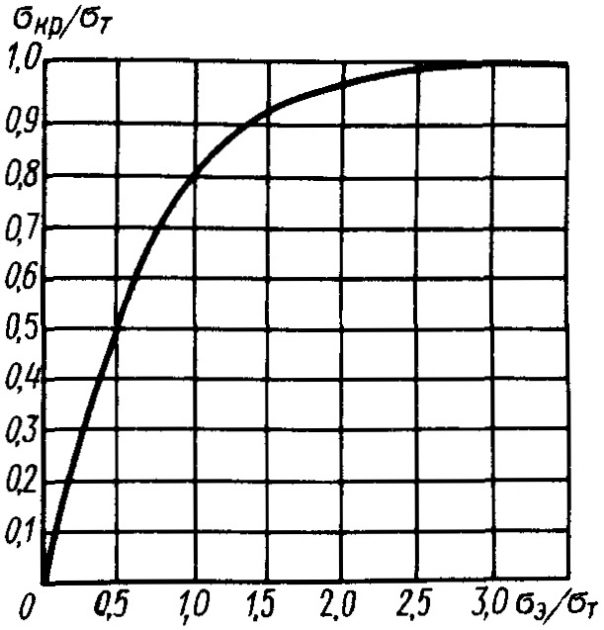
Устойчивость конструктивных элементов можно оценить с помощью расчетного коэффициента устойчивости, сравнив его с допускаемым значением [η]д, при этом η ≤ [η]д. Коэффициент устойчивости, учитывающий одновременное действие нормальных напряжений в направлениях осей х и у и касательных напряжений в плоскости ху, определяется по формуле:
где:
- σx, σy – расчетные (действующие) нормальные напряжения в направлении осей x и y, МПа;
- τxy – расчетные (действующие) касательные напряжения в плоскости xy, МПа;
- σx кр, σy кр, τxy кр – соответствующие значения критических напряжений (исправленные Напряжения в корпусе судна при его общем продольном изгибеЭйлеровы напряжения) в направлении осей x, y и в плоскости xy, МПа, определяемые зависимостями
здесь:
- σx э, σy э, τ э – теоретические Эйлеровы напряжения, определяемые классической теорией устойчивости, МПа;
- ReH – спецификационный минимальный предел текучести материала связей танка при комнатной температуре, МПа.
Допускаемые значения коэффициента устойчивости принимаются в соответствии с табл. 2.
| Таблица 2. Значения допускаемых коэффициентов устойчивости | ||
|---|---|---|
| Вид потери устойчивости | Нагрузка | |
| статическая | суммарная статическая и динамическая | |
| Местная | 0,6 | 1,0 |
| Общая или при кручении | 0,4 | 0,7 |
Расчеты прочности при воздействии нагрузок, передаваемых на конструкции грузового танка от его опор и деталей крепления, возникающих в результате деформаций корпуса газовоза при его общем изгибе и кручении, с помощью трехмерной схемы идеализации можно выполнять итеративным методом, описанным выше.
Прочность вкладных танков типа С
Расчетное внешнее давление pe, кПа, для танков типа С в соответствии с требованиями Правил Регистра РФ
где:
- p1 – установочное давление предохранительных клапанов, кПа, p1 > 25 кПа – для танков без предохранительных клапанов и в каждом случае является предметом специального рассмотрения Регистра;
- p2 – установочное давление предохранительных клапанов для полностью закрытых отсеков корпуса газовоза, в которых расположены грузовые танки или их части, кПа;
- p2 = 0 – для всех других случаев;
- p3 – любые сжимающие усилия от воздействия сил тяжести (веса) обшивки и изоляции и другие сжимающие нагрузки, которым может быть подвержен танк в процессе эксплуатации (в величину p3 должны быть также включены различные местные, распределенные и сосредоточенные нагрузки от сил тяжести куполов, возвышающихся над палубой конструкций и трубопроводов, влияния груза при частичном заполнении танка, деформаций корпуса, сил инерции, местного воздействия внешнего или внутреннего давлений);
- p4 – внешнее давление на танки или их части, расположенные выше палубы, вследствие наката забортной воды, МПа, p4 = 0 – для других случаев.
Формула 23 может быть использована для проверки продольного изгиба под давлением.
При проектировании конструкций танков типа С должны учитываться общие требования, предъявляемые к вкладным танкам, а также все типы нагрузок, описанные в пункте “Расчетные нагрузки”. Прочностные исследования таких танков включают расчеты прочности танков в районе их опор (в стенке танка и в корпусных конструкциях), расчеты устойчивости, если в процессе эксплуатации танки подвергаются воздействию нагрузок, вызывающих напряжения сжатия в их стенках; расчеты усталостной прочности; расчеты с учетом вторичных и термических напряжений.
Это интересно: Малотоннажные стальные суда
При воздействии на сферическую оболочку танка только нормального давления меридианальные σθ и кольцевые σφ напряжения, кПа, могут быть определены по формуле:
где:
- p0 – расчетное давление паров газа в танке, кПа;
- R – радиус срединной поверхности сферы, м;
- t – толщина оболочки сферы, м;
- k – коэффициенты эффективности сварных соединений, k = 1,0 – 0,95 – для сталей, k = 1,0 – 0,8 – для алюминиевых сплавов.
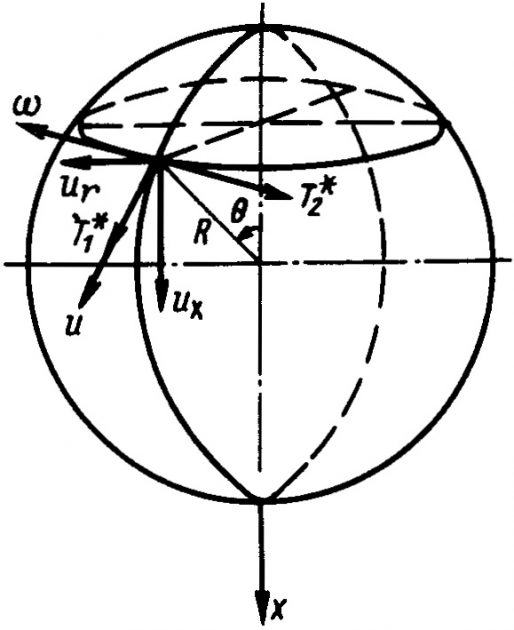
Собственную силу тяжести танка и груза, находящегося в нем, можно учесть на основании безмоментной теории по зависимостям, преобразованных для замкнутой сферической оболочки (рис. 20).
где:
- T*1, T*2 – меридианальные и кольцевые усилия в оболочке, кН/м;
- ϑ* – угол поворота касательной к меридиану, рад;
- θ – угол между осью вращения сферы и радиусом, проведенным в расчетную точку сферы, рад;
- q – распределенная сила тяжести оболочки с грузом, приходящаяся на единицу ее площади серединной поверхности, кПа;
- E – модуль упругости материала оболочки танка, кПа;
- u*x, u*r – осевое и радиальное перемещение расчетной точки сферы, м;
- ν – коэффициент Пуассона;
- ax – перемещение оболочки как жесткого целого в направлении оси x, м.
Выгрузка груза с судна-газовоза рефрижераторного типаГидростатическое давление жидкого груза, действующего на замкнутую оболочку сферы, может быть учтено после преобразований формул из:
где:
- ρmax – максимальная плотность перевозимого груза при расчетной температуре, т/м3.
Входящие в формулы 25-26 осевое
и радиальное
перемещения расчетной точки связаны с меридианальным и нормальным к поверхности оболочки ω перемещениями следующими зависимостями (рис. 20):
или
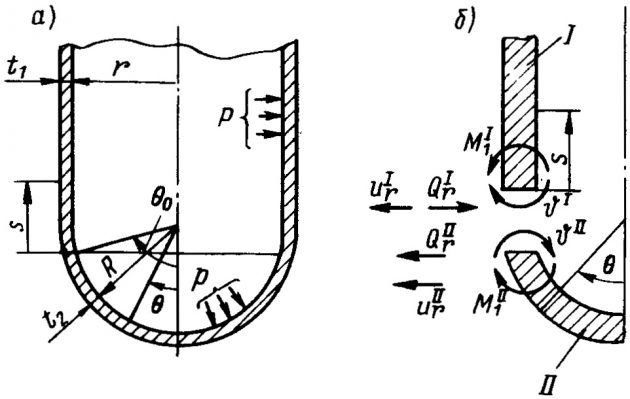
Расчеты прочности сферических танков в районе их опор (в стенке танка и корпусных конструкциях). Зависимости (Формулы 24-26) позволяют рассчитывать прочность сферических танков без учета конструктивных особенностей их соединений с опорами. Однако это может привести к ошибкам в опасную сторону. Так, танк норвежской фирмы “Кварнер-Мосс Розенберг” (Kvaerner – Moss Rozenberg) (рис. 21) представляет собой сферу, опирающуюся на цилиндрическую юбку (седло), приваренную к экваториальной зоне танка, которая выполнена в виде специального профиля с особым усилением, образующим переход от сферы к юбке (рис. 22).
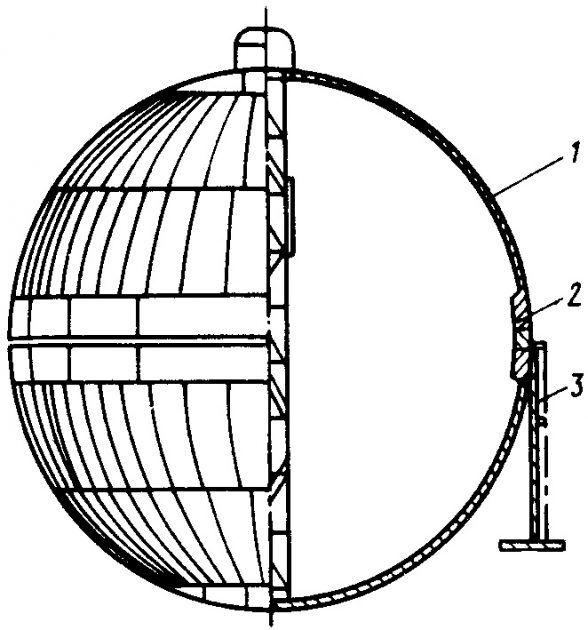
1 — сферическая оболочка танка; 2 — экваториальная зона танка; 3 — цилиндрическая юбка
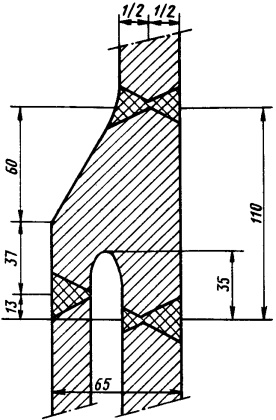
Часть цилиндрической юбки, непосредственно примыкающей к экваториальной зоне, изготавливается из того же материала, что и оболочка сферы, остальная часть – из того же материала, что и корпус газовоза. В этом случае в конструкции юбки предусматриваются специальные переходные детали. Нижняя часть цилиндрической юбки неподвижно соединяется с двойным дном судна.
Предлагается к прочтению: Ремонт коленвала и других основных подвижных деталей дизелей
Танк французской фирмы “Технигаз” (Technigaz), разработанный совместно с фирмой “Кварнер – Мосс Розенберг” представляет собой сферу, отличающуюся от конструкции, описанной выше. Сферический танк крепится к шарнирной конструкции (рис. 23), являющейся его основной опорой и служащей для восприятия вертикальных составляющих инерционных усилий, которые возникают при качке судна на волнении.
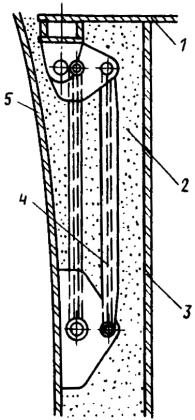
1 — палуба газовоза; 2 — изоляция танка; 3 — обшивка двойного борта газовоза (внутренний борт); 4 — опорные штанги; 5 — сферическая оболочка танка
Как видим, в обеих конструктивных схемах крепления сферических танков к корпусу судна реакции от сил тяжести из оболочки и перевозимого груза воспринимаются экваториальной зоной сферы.
Расчетная схема для определения напряжений и перемещений в оболочке сферы фирмы “Технигаз” изображена на рис. 24, где реакции Qx = 9,8(Pт. и + Pгр)/2πR, кН/м (здесь Pт. и – масса одного грузового танка и его изоляции, т; Pгр – Грузовые операции на газовозахмасса перевозимого газа, т).
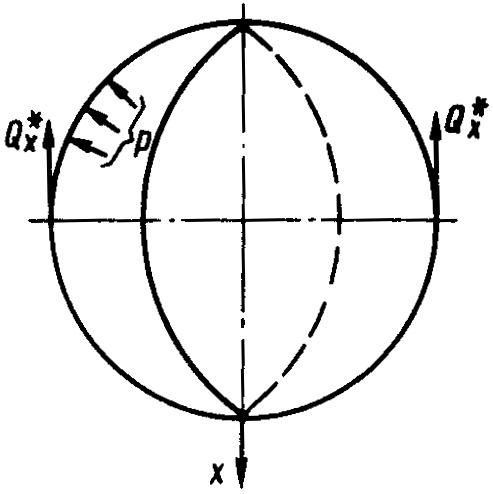
Характер нагружения сферы со стороны ее подвески безмоментный, поэтому можно воспользоваться системой зависимостей для оболочек вращения, предложенной Л. Я. Григорьевым, которая для сферы преобразуется к виду
где:
- – радиальное и осевое усилия в оболочке сферы, кН/м;
- – меридианальный и кольцевой моменты, кН;
- – постоянные интегрирования;
- p – давление, учитывающее избыточное давление перевозимого в танке газа, а также распределенную силу тяжести его оболочки и груза, приходящиеся на единицу площади серединной поверхности сферы, кПа.
Постоянную интегрирования
можно определить из формулы 31, в которой
, т. е. если в качестве точки отсчета осевого перемещения оболочки принять верхний полюс сферы. Тогда
где:
- – меридианальное и осевое усилия в точке верхнего полюса сферы, кН/м.
Размерность
в формуле 32 – метры [м]. Это значит – постоянная интегрирования
характеризует осевое смещение оболочки как твердого целого.
Для определения постоянной интегрирования граничное условие на экваторе сферы (θ = π/2) записывают в виде:
Знак минус в граничном условии формулы 33 появился потому, что действующие на экваториальный пояс сферы осевое усилие противоположно положительному направлению теоретического осевого усилия
для кольцевого сечения.
Из формулы 29 находим значение постоянной интегрирования
Размерность C1 в формуле 34 – килоньютоны [кН], что указывает на учет в зависимостях для усилий в оболочке сферы реакций, передаваемых со стороны подвески танка.
Таким образом, для конструкций танков, аналогичных конструкциям фирмы “Технигаз”, расчетные зависимости (Формулы 27-31 с учетом формул 32 и 34) будут иметь следующий вид:
Напряжения в оболочке сферы определяются делением соответствующих усилий на ее толщину и Сварка корпуса судна на построечном местекоэффициент эффективности сварных соединений k; k = 1,0 ÷ 0,95 – для сталей, k = 1,0 ÷ 0,8 – для алюминиевых сплавов.
При построении расчетной схемы для определения напряжений и перемещений в сферическом танке фирмы “Кварнер – Мосс Розенберг”, изображенной на рис. 25, было положено, что суммарные напряжения и перемещения складываются из основных или безмоментных компонентов и напряжений и перемещений типа краевого эффекта, создаваемых моментами и перерезывающими усилиями, которые распределены в местах стыковки оболочек и возникают в результате действия сил тяжести.
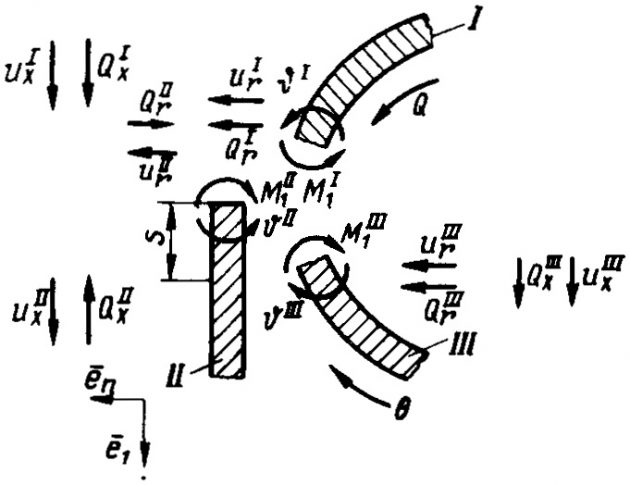
Будем полагать, что в районе экваториального пояса сопрягаются три оболочки: цилиндрическая и две сферические. Цилиндрическая оболочка нагружена равномерно силами тяжести, передаваемыми вдоль ее оси по верхнему кольцевому сечению в районе стыковки со стороны (нормальное давление отсутствует), сферические оболочки – воспринимают нормальное давление p и реакции, возникающие в стыковочном узле. В расчетной схеме различия в свойствах материалов сферы и цилиндрической юбки учитываются различными модулями упругости:
- Eт – модуль нормальной упругости материала сферического танка, кПа;
- Eц – модуль нормальной упругости материалу цилиндрической юбки, кПа.
Усилия, перемещения и моменты определяются для оболочек, сопряженных в узле I (см. рис. 25), зависимостями:
Здесь “звездочка” и “нуль” обозначают соответственно безмоментные и моментные компоненты; M1, M2 – меридианальный и кольцевой моменты.
Читайте также: Особенности перевозки сжиженных газов и жидких химических грузов
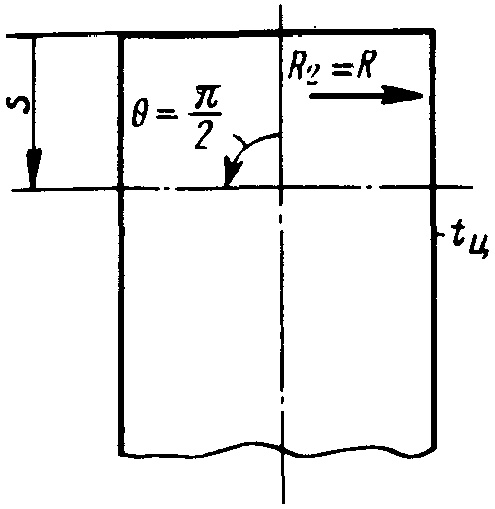
Запишем слагаемые формул 35. Для цилиндрической юбки Радиус цилиндрической юбки принят равным радиусу сферы.x безмоментные компоненты будут выглядеть следующим образом (p = 0, R1 = ∞, R2 = R*; θ = π/2 = const):
где:
- νц – коэффициент Пуассона материала оболочки юбки;
- tц – толщина оболочки цилиндрической юбки, м;
- ds = R1dθ – отрезок образующей цилиндра, отсчитываемый от его верхнего края (рис. 26).
Моментные компоненты цилиндрической юбки запишутся в виде
В формулах 37 обозначено
- cц, βц – переменный параметр, зависящий от длины образующей цилиндра s.
Для сферических оболочек безмоментные компоненты запишутся аналогично (Формулы 27-31), в которых для удобства вычислений постоянные интегрирования C1 и
следует заменить на A1 и
, а вместо E, t, ν поставить значения Eт, tт, νт. Моментные компоненты могут быть представлены как
где:
- – переменный параметр, зависящий от длины дуги меридиана сферы.
Преобразуем (Формулы 36-38) для деформационных и силовых компонент на кромках сопрягаемых элементов.
На кромке цилиндрической юбки (s = 0, βц = 0)
где:
На кромке сферы в узле стыковки танка с цилиндрической юбкой
Так как в данной задаче стыковки сферы с цилиндром сфера замкнута в вершине при θ = 0, то принимаем A′1 = A″1 = 0. Тогда зависимости (Формула 40) преобразуются к виду
где:
- – постоянная интегрирования.
Уравнения 41 справедливы для обеих частей сферического танка (оболочки I и III на рис. 25) в том случае, если отсчет текущих углов θ ведется соответственно от верхнего и нижнего его полюсов, как показано на рис. 25. Для удобства дальнейших расчетов постоянные интегрирования, относящиеся к оболочке I, обозначим буквой А с использованием соответствующих индексов, а относящиеся к оболочке III – буквой B.
Это интересно: Малотоннажные суда из армо- и стеклоцемента
Все силовые и деформационные компоненты, действующие на кромках каждой оболочки в стыковочном узле, обозначим в соответствии с номером оболочки так, как показано на рис. 25.
Для определения значений постоянных интегрирования, входящих в формулы 39 и 41, необходимо записать граничные условия для узла стыковки трех оболочек. При этом необходимо учитывать, что положительные направления деформационных и силовых компонентов определяются положительными направлениями орт
.
Кроме того, если деформационные компоненты на кромках оболочки имеют одинаковые направления, то они приравниваются в граничных условиях с одинаковыми знаками, если противоположные – то с различными знаками. Сумма силовых компонентов в узле стыковки должна быть равна нулю. При этом одинаково направленные компоненты должны иметь одинаковые знаки.
Запишем граничные условия:
где:
- p1 – внешнее усилие, передаваемое на единицу длины меридиана сферы, учитывающее избыточное давление перевозимого в танке газа, а также распределенную силу тяжести его оболочки и груза, кН/м.
Итак, имеем 11 уравнений 42 и 14 неизвестных постоянных интегрирования:
Постоянные интегрирования
, входящие в зависимости (Формула 37), определяют условия закрепления цилиндрической юбки ко второму дну газовоза (для бесконечно длинного цилиндра, закрепленного только в узле стыковки,
). Поэтому три дополнительных граничных условия можно записать для нижнего края цилиндрической юбки, учитывая, что она Конструкция и расчеты днищевых перекрытий в корпусе суднажестко приварена ко второму дну (цилиндр жестко заделан в опоре) в виде:
где
- – радиальное и осевое перемещения нижнего края цилиндрической юбки, м;
- ϑн – угол поворота касательной к меридиану нижнего края цилиндрической юбки.
Таким образом, имеем 14 уравнений (Формулы 42-43) и 14 неизвестных постоянных интегрирования.
Записав выражения для радиального перемещения и угла поворота нижнего края юбки, а затем, подставив соотношения (Формула 39), (Формула 41) в граничные условия (Формула 42), (Формула 43), получим следующую систему расчетных уравнений:
Решив систему уравнений (Формула 44), находим численные значения постоянных интегрирования. Затем с помощью формул 55-58, а также зависимостей (Формулы 27-31), в которые вместо постоянных интегрирования, обозначенных буквой С, подставляем постоянные интегрирования, обозначенные для соответствующих частей сферической оболочки буквами А и В. Определяем внутренние усилия, моменты и перемещения в любом сечении конструкции, т. е. для различных s и θ. С целью получения общей картины напряженного состояния конструкции сферического танка, опирающегося на цилиндрическую юбку, необходимо построить эпюры напряжения по её меридианальному сёчению.
При проведении исследований взаимодействия сферических грузовых танков с корпусом газовоза могут быть полезны формулы для перемещений кромки углубления во втором дне газовоза в районе крепления к нему цилиндрической юбки (рис. 27). Возникающие в корпусе газовоза при его общем изгибе деформации вызывают появление реакций взаимодействия корпуса с танками. Знать эти усилия необходимо для уточнения расчетов прочности экваториального стыковочного узла сферы с цилиндрической юбкой на основе вышеописанных зависимостей, в которые вводят поправку в граничные условия (Формула 42). Возрастает влияние реакций взаимодействия между корпусом и танками во Планирование рейса суднавремя балластного перехода газовоза, когда они могут вызвать потерю устойчивости сферической оболочки.

Рис. 27 К расчету взаимодействия вкладного сферического танка с корпусом газовоза Вертикальное ν, м, и тангенциальное (горизонтальное) u, м, перемещения кромок углублений определяют по универсальным зависимостям:
где:
здесь:
- d – осадка газовоза, м;
- Pгр – масса перевозимого газа в танке, т;
- Pт. и – масса танка и изоляции, т;
- M – изгибающий момент, действующий в расчетном сечении корпуса судна и принимаемый положительным при прогибе, кН · м.
Формулы 45 получены по результатам обработки восстановлением зависимостей расчетов МКЭ части корпуса газовоза вместе со сферическим танком. В расчетную схему входили бортовые, палубные и днищевые перекрытия корпуса газовоза, скуловой пояс, поперечные переборки, опорные конструкции цилиндрических юбок. В качестве внешних нагрузок были приняты гидростатическое давление воды, силы тяжести грузовых сферических танков вместе с изоляцией и грузом, корпуса с запасами топлива, перерезывающие силы и изгибающие моменты, действующие в районе выделенного отсека, вертикальные и горизонтальные (тангенциальные) силы, приложенные к опорным конструкциям цилиндрической юбки.
С помощью зависимостей (Формула 45), учитывая связь между перемещениями и реакциями взаимодействия корпуса с танками и имея данные о жесткостных параметрах системы юбка-танк, можно определить реакции, а затем – суммарные деформации от действия внешних сил и реакций.
Расчеты устойчивости. Вкладные грузовые танки типа С, которые в процессе эксплуатации могут подвергаться воздействию нагрузки, вызывающей напряжение сжатия в стенках танка, должны быть проверены на устойчивость.
Для цилиндрических танков расчетное внешнее давление pe, кПа, определенное по формуле 23, как требуют для обеспечения их устойчивости правила Норвежского Бюро Веритас, не должно превышать 0,25pкр и 0,333pу. Здесь критическая нагрузка, кПа,
где:
- E – модуль нормальной упругости материала оболочки танка при комнатной температуре, кПа;
- D – наружный диаметр оболочки танка, м;
- t – толщина стенки оболочки без учета надбавки на коррозию, м;
- n – число волн при потере устойчивости, n ≥ 2;
- z – коэффициент, принимаемый равным 0,5πD/L;
- L – расстояние между ребрами жесткости оболочки танка, м;
- ν – коэффициент Пуассона.
Мембранные напряжения
где:
- ReH – спецификационный минимальный предел текучести материала танка при комнатной температуре, кПа.
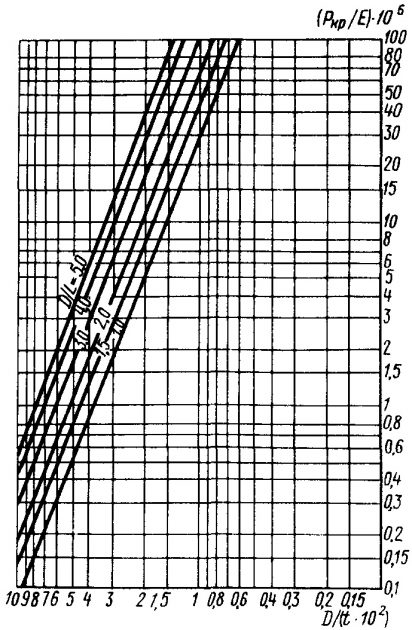
Величины критических напряжений, обычно вычисляемые по формуле 46, могут быть определены и с помощью графических зависимостей (рис. 28).

Рис. 28 График для определения критических нагрузок в расчетах устойчивости вкладных танков типа C Для сферических танков расчетное внешнее давление pe, кПа, не должно превышать
и 0,333pу. Критическая нагрузка, кПа, в этом случае
, где R – радиус оболочки, м.
Читайте также: Крепление механизмов на фундамент суднаКроме формулы 46, для расчета критических нагрузок в цилиндрических оболочках танков, нагруженных всесторонним давлением, можно воспользоваться полуэмпирической зависимостью, принятой в практике судостроительных расчетов:
где:
- pэ – Эйлерово давление оболочки, вычисленное по теоретическим формулам устойчивости для идеальной круговой оболочки без учета начальных погибов и отступлений от закона Гука, кПа;
- η1 – поправочный коэффициент, определенный по результатам испытаний оболочки на устойчивость и учитывающий отступления от идеальной круговой формы цилиндрической оболочки, 0,6 < η1 < 0,8;
- η2 – коэффициент, определяемый по графикам рис. 29 в зависимости от отношений σэ/ReH, η2 = σкр/σэ;
- σэ – Эйлерово напряжение, соответствующее верхнему Эйлерову давлению, σэ = 0,95η1pэRt, кПа, коэффициент 0,95 учитывает технологические различия в толщине оболочки;
- σкр – критические напряжения, кПа.
Эйлерово давление, кПа, может быть определено либо по второй формуле Мизеса в обработке П. Ф. Папковича либо по формуле Американского опытового бассейна;
где:
- l – длина цилиндрического танка, м.
Для цилиндрических оболочек грузовых танков, подкрепленных круговыми ребрами жесткости, с помощью соотношений (Формулы 47 и 48) необходимо проверить местную устойчивость между ребрами жесткости и общую устойчивость между донышками оболочек.

Рис. 29 Обобщенные графики для определения критических напряжений в функции от эйлеровых напряжений для судостроительных сталей и алюминиево-магниевых сплавов Напряжения, кПа, от продольного сжатия оболочек не должны превышать
Расчет прочности цилиндрических танков. Танки данного типа представляют собой находящиеся под давлением цилиндрические емкости, вертикально или горизонтально расположенные в корпусе газовоза, со сферическими оконечностями, что позволяет наиболее рационально использовать материал конструкции. Самая простая формула, позволяющая определить минимальную толщину оболочки танка, м, имеет вид
где:
- p1 – установочное давление предохранительных клапанов, кПа;
- R – радиус цилиндрической оболочки, м;
- [σ]д – допускаемые напряжения для вкладных грузовых танков типа С, определяемые в соответствии с требованиями пункта “Расчетные нагрузки”, кПа;
- k – коэффициент эффективности сварных соединений, k = 1,0-0,95 для ферритно-мартенситных и аустенитных сталей, k = 1,0-0,8 для алюминиевых сплавов.
Если предусматривается визуальный и неразрушающий контроль сварных соединений, то коэффициент их эффективности (коэффициент прочности сварных соединений) в соответствующих с требованиями Правил Регистра РФ следует (можно) принимать равным 0,95. По согласованию с Регистром РФ он может быть увеличен до 1,0 в зависимости от свойств материала, типа соединения, способа сварки и вида нагрузки. Если по специальному согласованию с Регистром РФ предусматривается неразрушающий контроль технологических сосудов под давлением сокращенного, то коэффициент эффективности сварных соединений можно принимать равным не более 0,85.
Толщина обшивки оконечностей, м, цилиндрических танков может быть определена с помощью зависимости
где:
- D0 – наружный диаметр донышка, м;
- k1 – коэффициент, учитывающий технологию изготовления донышка k1 = 1,0 – для донышка, изготовленного из одного листа, k1 = 0,95 – для донышек, изготовленных из двух листов или более;
- – высота донышка, м;
- r, r0 – соответственно внутренний и наружный радиусы переходного участка между донышком и цилиндрической частью танка, м;
- R, R0 – соответственно внутренний и наружный радиусы кривизны донышка, м.
При определении толщин Концепция конструкции грузовой системы морских газовозовоболочки цилиндрического танка расчетным методом целесообразно воспользоваться соотношениями из работы. Геометрические и силовые параметры, а также расчетная схема стыков цилиндрической и сферической частей танка представлены на рис. 30.

Рис. 30 К расчету цилиндрического танка:
а – геометрические параметры и внешние нагрузки, действующие на танк; б – схема стыковки цилиндрической и сферической частей танкаПусть оболочки нагружены нормальным расчетным давлением p, кПа, толщина сферической оболочки – t2, м, цилиндрической – t1, м. Оболочки изготовлены из одинакового материала, поэтому модули нормальных упругостей обеих частей танка обозначим E, кПа, а коэффициент Пуассона ν. Тогда для цилиндрической части оболочки танка
где:
- – коэффициент;
- A1, B1, C2ц – постоянные интегрирования;
- s – длина образующей цилиндра, м;
- r – радиус внутренней поверхности цилиндрической оболочки, м.
Для сферической части оболочки танка, замкнутой в вершине
и нагруженной нормальным давлением, расчетные зависимости имеют вид
где:
- – постоянные интегрирования;
- R – радиус внутренней поверхности сферы, м;
- βc – переменный параметр, определяемый как
- θ – текущее значение угла между вертикальной осью симметрии оболочки танка и радиусом, проведенным в точку стыковки сферы с цилиндром, рад.;
- cc – коэффициент, равный
На основании расчетной схемы (рис. 30, б) и данных запишем граничные условия для узла стыковки сферы с цилиндром. Обозначим при этом все силовые и деформационные компоненты, относящиеся к цилиндрической оболочке, индексом I, а относящиеся к сферической оболочке – индексом II:
*Осевые усилия QxI и QxII — статически определимы, и поэтому нет необходимости использовать их в граничных условиях; по осевым перемещениям uxI и uxII также нет необходимости определять граничные условия.
Предлагается к прочтению: Основные материалы применяемые в морском деревянном судостроении
Определим значения деформационных и силовых компонентов на кромке цилиндра (s = 0; βц = 0):
Деформационные и силовые компоненты на кромке сферы имеют вид (θ = θ0; βс = 0):
Подстановка соотношений формул 52, 53 в граничные условия формулы 51 дает систему четырех уравнений, необходимых для отыскания четырех неизвестных постоянных интегрирования
:
Решение системы уравнений (Формула 54) дает зависимости для определения постоянных интегрирования:
где введены обозначения:
Постоянные интегрирования C2ц и C2ц, входящие в формулы 49 и 50, можно найти, если отсчет осевого перемещения ux сферы и цилиндра вести от точки их стыковки. Тогда для цилиндрической оболочки при s = s1 и ux и 0 получим C2ц = 0, а для сферической оболочки при θ = θ0 и ux = 0, βc = 0, а
где:
T2θ0 – кольцевое усилие в сферической оболочке в узле стыковки ее с цилиндрической оболочкой, равное
Определив с помощью соотношений формул 55 и 56 постоянные интегрирования, по формулам 49 и 50 найдем усилия и моменты в различных точках меридианального сечения конструкции цилиндрического вкладного танка, т. е. для различных s и θ. Затем построим графики распределения в ней напряжений.
Расчеты танков с учетом термических напряжений. Существующие конструкции танков их опор и изоляции позволяют в значительной степени уберечь обшивки корпуса газовоза и танков от влияния значительных температурных напряжений. Однако в аварийных ситуациях, когда происходит утечка сжиженного газа через какие-либо неплотности или при возникновении дефектов в изоляции, газ испаряется, а конструкции, соприкасающиеся с ним, охлаждаются. Оценка величины температурных напряжений в таких случаях представляет определенный интерес. Поэтому Регистр РФ может дополнительно к расчетам прочности вкладных танков типа С потребовать проведения расчетов с учетом термических напряжений.
В случае продолжительного воздействия источника холода на конструкцию в ней возникает небольшая охлажденная зона – пятно охлаждения. Размеры пятна обусловлены малостью зон нарушения изоляции по сравнению с размерами конструкции танка. Внутри этого пятна металл может быть охлажден до температуры вытекающего сжиженного газа. С увеличением расстояния от пятна охлаждения температура обшивки танка будет повышаться до температуры окружающей среды.
Температурные напряжения в обшивке вкладных танков можно определить с помощью методов термоупругости для оболочки при неоднородном температурном поле, закон распределения температуры внутри которого при круглом пятне охлаждения может быть представлен в виде:
где:
- R0 – радиус пятна охлаждения;
- r – расстояние от центра пятна охлаждения;
- t – Дополнительные или усиленные конструкции корпуса суднатолщина обшивки;
- Тo – температура обшивки танка в районе качественной изоляции;
- Tн – температура на наружной поверхности z = 0,5t обшивки танка в районе дефекта изоляции;
- Tвн – температура на внутренней поверхности z = – 0,5t обшивки танка, контактирующей со сжиженным газом, в зоне дефекта изоляции;
- θн, θв – относительные температуры наружной и внутренней поверхностей обшивки танка в зоне дефекта;
- θc, θa – соответственно амплитудные значения симметричной и антисимметричной по толщине составляющей температурного поля в зоне дефекта.
Таким образом, при расчете вкладных танков с учетом термических напряжений, возникающих под воздействием линейного закона (Формула 57) изменения температуры по толщине обшивки, помимо плоского напряженного состояния появляются деформации изгиба. При этом учитывается, что температурные деформации вызываются только симметричной по толщине оболочки составляющей температурного поля, а температурные деформации изгиба – только антисимметричной его частью.
При решении указанной задачи для сферического грузового танка Ю. П. Кочанов условно отделяет сферический сегмент, подверженный охлаждению, от остальной части оболочки и прикладывает к границам участков неизвестные внутренние усилия и моменты, которые находят из условий сопряжения частей оболочки с учетом температурных деформаций охлажденной зоны. При этом он рассматривает две задачи: первая соответствует симметричному распределению температуры по толщине, вторая – антисимметричному распределению. На основании результатов работ Г. Б. Талыпова и В. В. Новожилова Ю. П. Кочанов получил зависимости для суммарных усилий, вызванных симметричной и антисимметричной составляющими температурного поля
где:
- T1, T2 – нормальные усилия в сечениях оболочки, действующие соответственно в направлении меридианов и параллелей;
- M1, M2 – изгибающие моменты;
- E – модуль упругости материала оболочки;
- ν – коэффициент Пуассона;
- R – радиус внутренней поверхности оболочки сферы;
- φ0 – угол между осью вращения сферы и радиусом, проведенным к границе охлажденного сферического сегмента;
- αт – среднее значение коэффициента линейного температурного расширения материала оболочки сферы в интервале температур 0 – θ , равное
- α(θ) – зависимость коэффициента линейного температурного расширения от температуры.
Усилия по границам охлажденного сегмента и нижней части сферы на основании формулы 58 запишутся в виде:
Мембранные температурные напряжения в охлажденном сегменте и нижней части сферы вдоль-границы составляют
Абсолютные значения наибольших изгибных напряжений
Приведенные напряжения могут быть представлены как:
где:
- σi – суммарные напряжения.
Указанные зависимости позволили сделать вывод о том, что при полном нарушении изоляции или утечке сжиженного газа в небольшой зоне обшивки танка могут возникнуть большие температурные напряжения. Кроме того, в обшивке сферического танка эти напряжения при прочих равных условиях примерно в 1,5 раза меньше, чем в плоской обшивке. Для устранения температурных напряжений необходимо качественное нанесение теплоизоляции на поверхность обшивки и осторожное обращение с изоляцией в процессе ее эксплуатации. Ю. П. Кочанов предлагает не нормировать Охлаждение груза перед погрузкой в грузовые танкиместные температурные напряжения, так как появление значительных дефектов в изоляции случайно и мало вероятно, при суммировании температурных напряжений с напряжениями от внешних нагрузок суммарные напряжения не превосходят предела прочности материала танков. Однако Правила Регистра РФ требуют проведения дополнительных расчетов термических напряжений, поэтому вышеописанные зависимости могут быть использованы при их проведении.
Прочность мембранных, полумембранных танков и танков с внутренней изоляцией
В соответствии с требованиями Правил Регистра РФ в расчете прочности конструкции мембранных танков должно учитываться влияние всех возможных в эксплуатации статических и динамических нагрузок. Одновременно с расчетом прочности Регистру РФ должны быть представлены для сведения результаты модельных испытаний конструкции, подтверждающие целесообразность принятых в расчетах допущений и достаточную точность, а также достоверность их результатов. Условия проведения испытаний должны соответствовать наиболее неблагоприятным условиям эксплуатации танка. В ходе испытаний материалов мембранных танков следует убедиться, что их старение не ведет к потере эксплуатационных функций.
В расчетах прочности мембранных танков необходимо учитывать, что температурные деформации в оболочках гофрированных мембран компенсируются деформацией их гофров, а в обшивке плоских мембран — за счет малого коэффициента линейного расширения их материала, например инвара.
В тех случаях, когда отсутствуют достоверные данные о внешних нагрузках на судах, однотипных проектируемым, диапазон и виды испытательных нагрузок должны соответствовать всем возможным в эксплуатации комбинациям реальных нагрузок. Испытания должны подтвердить, что при воздействии избыточного давления на конструкции в межбарьерном пространстве газовоза, вакуума в грузовом танке, динамических нагрузок в случае наличия свободных поверхностей внутри танка, а также вибрации целостность мембраны не будет нарушена.
Допускаемые напряжения для расчета мембраны, ее опор и изоляции, а также методика расчета прочности полумембранных танков являются в каждом случае предметом специального рассмотрения Регистром РФ.
При проведении расчетов прочности грузовых танков с внутренней изоляцией должны быть учтены все возможные в эксплуатации случаи статических и динамических нагрузок, действующих на конструкции танков, а также их реальные комбинации. В соответствии с требованиями Правил Регистра РФ Элементы конструкции корпуса суднаэлементы конструкции, образующие стенки грузовых емкостей, должны быть оценены с точки зрения усталостной прочности, склонности к распространению трещин, адгезионной способности изоляции танков, обеспечения прочности при сжатии, растяжении и сдвиге. На одобрение Регистра должны быть представлены статистический анализ волновых нагрузок, расчеты конструкций по МКЭ или какому-либо другому эквивалентному методу, анализ механизма разрешения конструкции грузовых танков.
Кроме того, должны быть выполнены расчеты (с применением трехмерной схемы идеализации) прочности внутреннего корпуса газовоза и определены уровень напряжений и соответствующих им деформаций с целью выявления возможности отслоения и разрушения материала изоляции танков под воздействием указанных деформаций. В данных расчетах необходимо учитывать избыточное давление внутри грузовых танков и динамические нагрузки, вызываемые волнообразованием в балластных отсеках, прилегающих к стенкам грузовых танков.
Допускаемые напряжения для стенок грузовых танков и допускаемые их совместные деформации с материалом изоляции являются в каждом случае предметом специального рассмотрения Регистром РФ.
Расчеты прочности танков с внутренней изоляцией должны быть сравнены с результатами испытаний моделей конструкций танков и их отдельных конструктивных элементов с учетом совместного воздействия на них статистических, динамических и термических нагрузок. Условия испытаний моделей танков и их узлов должны соответствовать экстремальным условиям эксплуатации грузосодержащей системы газовоза, т. е. испытаны (в том числе) в условиях 400 тепловых циклов при 19 рейсах газовоза в год. Если судно совершает более 19 рейсов в год, то испытания моделей танков должны быть проведены при большем числе тепловых циклов. В процессе испытаний 400 тепловых циклов могут быть разделены на 20 полных циклов (температура груза до 45 °C) и 380 частичных циклов (температура достигает предполагаемой величины во время рейса газовоза в балласте).
Испытываемые модели должны реально отображать моделируемые конструкции, включая углы, соединения, крепления насосов, места проходов трубопроводов и другие концентраторы напряжений. Кроме того, они должны учитывать различие свойств материалов грузовой емкости, технологии изготовления и контроль качества. С целью выявления поведения материала изоляции при развитии сквозной трещины в конструкции внутреннего корпуса должны быть проведены испытания моделей конструктивных элементов танков на растяжение и усталостную прочность. При этом конструкция в районе трещины по возможности должна быть подвергнута максимальному гидростатическому давлению балластной воды.
Прочность корпусных конструкций газовозов
Анализ корпусных конструкций газовозов, выполненный в статье Конструкция газовоза, корпусные перекрытия и переборки“Конструкция корпуса газовозов”, позволяет сделать вывод о том, что отличительными особенностями судов-газовозов являются их большая длина и относительно малая осадка. Это приводит к необходимости размещения больших балластных объемов для достаточного погружения гребного винта и во избежание возникновения слеминга. В частности, грузовые танки газовозов приходится устанавливать на специальные опоры, что вносит изменения в их конструкцию. На газовозах с призматическими мембранными и полумембранными танками отсутствуют большие вырезы в палубе, а на газовозах со сферическими танками они имеются.
Предлагается к прочтению: Элементы автоматических систем судна
Еще одна характерная особенность конструкции газовозов – большое расстояние между поперечными переборками. Однако в целом корпуса судов-газовозов с вкладными призматическими и сферическими танками напоминают корпуса судов для перевозки навалочных грузов и нефтерудовозов, а газовозов с мембранными танками – корпуса танкеров и нефтерудовозов.
Таким образом, несмотря на то, что конструкция корпуса газовоза значительно усложнена по сравнению с конструкцией корпусов традиционных грузовых судов, при расчетах их прочности не имеет смысла выделять их в особый класс по условиям обеспечения прочности. Поэтому в соответствии с требованиями Регистра РФ размеры элементов конструкции корпуса газовозов можно определять так же, как при определении размеров наливных или сухогрузных судов, в зависимости от его типа, типа грузовых емкостей и высоты надводного борта. Однако такое утверждение не всегда закономерно. Исследования показали, что в ряде случаев формулы Правил Регистра РФ применительно к судам-газовозам требуют определенной коррекции. Поэтому ниже приводятся формулы для определения размеров элементов корпусных конструкций газовозов с учетом их особенностей (применительно к газовозам с вкладными призматическими танками).
Продольная прочность. Существуют различные мнения о величине расчетного изгибающего момента MSW на тихой воде для газовоза. Так, например, правила Французского Бюро Веритас допускают, что максимальная его величина MSW, кН · м, на тихой воде должна быть не менее 0,55MH, где MH – максимальное значение волнового изгибающего момента, вычисляемое по формуле:
Здесь:
Таким образом, данные формулы получены при условии малой загрузки корпуса газовозов при плавании на тихой воде. Однако, как показывают исследования, проведенные для различных вариантов газовозов на тихой воде (рис. 31), при частичной загрузке газовозов возможны превышения граничного значения изгибающего момента.

Рис. 31 Эпюры изгибающих моментов М, прорезывающих сил N и стрелки прогиба ω для различных типовых и экспериментальных вариантов загрузки газовоза „Моссовет” на тихой воде:
а — в балласте; б — с грузом; в, г, д — при частичной загрузке.
I — в начале рейса; II — в конце рейсаСледовательно, результаты исследований в какой-то мере дают основание считать расчетным максимальный Общий продольный изгиб и общая продольная прочность корпусных конструкций суднаизгибающий момент на тихой воде при частичной загрузке газовоза. И первое и второе мнение о величине расчетных изгибающих моментов на тихой воде являются крайними. Требования правил Французского Бюро Веритас явно занижены, а варианты загрузки газовозов, приводящие к завышенным изгибающим моментам, с эксплуатационной и расчетной точек зрения являются предельными, так как океанские газовозы совершают переходы между портами в одном направлении с полным грузом (все танки заполнены газом), а в другом – в балласте.
Частичное же заполнение танков бывает только на коротких переходах при разгрузке газа в близко расположенных портах. Однако и в этих случаях можно проводить грузовые операции так, чтобы газовоз не был загружен только в концевых танках. Иными словами, при проектировании и эксплуатации газовозов, несмотря на требование Регистра РФ рассматривать все возможные в эксплуатации случаи нагрузки судна на тихой воде для любого его поперечного сечения по длине и определять (например, путем наложения эпюр и построения огибающей) наибольшие по абсолютному значению изгибающий момент и перерезывающую силу, которые должны приниматься в качестве расчетных, общую продольную прочность газовоза всегда можно обеспечить при
когда загрузка оптимальная. Здесь
– максимальные и граничные значения изгибающих моментов и перерезывающих сил на тихой воде.
Таким образом, изгибающие моменты и перерезывающие силы для газовозов на тихой воде должны, как правило, определяться методом интегрирования кривой нагрузки судна с построением соответствующих эпюр для следующих расчетных положений:- газовоз в полном грузу и в балласте в начале и в конце рейса;
- газовоз при оптимальной с точки зрения прочности частичной загрузки танков (в этом случае для эксплуатационников составляется инструкция по оптимальной загрузке-разгрузке газовоза).
В качестве расчетного изгибающего момента на тихой воде в любом поперечном сечении корпуса по длине газовоза должно приниматься его наибольшее абсолютное значение для расчетных положений загрузки судна. Аналогично необходимо поступать и с перерезывающими силами. Если продольная прочность газовоза на тихой воде проверяется для расчетных положений в любом поперечном сечении корпуса в корму от носового перпендикуляра до 0,6L (здесь L – длина газовоза на уровне летней грузовой ватерлинии), то в качестве расчетного изгибающего момента на тихой воде принимается наибольший прогибающий момент либо наименьший перегибающий момент, если в данном поперечном сечении корпуса действуют только перегибающие изгибающие моменты.
Внешние волновые изгибающие моменты и перерезывающие силы в корпусах газовозов как и в Правилах Регистра РФ, так и в правилах других классификационных обществ, определяются долговременными распределениями с помощью экспоненциального закона с обеспеченностью 10-4-10-8. При этом волновые нагрузки учитывают в неявном виде.
Как показывает проведенный анализ эпюр изгибающих элементов (см. рис. 31), наибольшие расчетные изгибающие моменты на тихой воде для газовозов всегда соответствуют состоянию перегиба. Поэтому, относя проектируемый газовоз в зависимости от его конструктивного типа и типа грузовых танков к соответствующей (см. разд. “Продольная прочность”. Правил Регистра РФ; группа 1 – сухогрузные суда; группа 3 – наливные суда) группе судов, можно с помощью формул, приведенных в Правила Регистра РФ, определить моменты сопротивлений поперечных сечений корпуса в средней части газовоза, в любом сечении по его длине, а также в корму от носового перпендикуляра до 0,06L, моменты сопротивлений палубы и днища.
Таким образом, стандарт общей прочности газовозов будет иметь следующий вид.
Момент сопротивления поперечного сечения палубы, см3 в средней части судна должен быть не менее
Момент сопротивления поперечного сечения днища, см3, в средней части судна должен быть не менее
Здесь
- W0 – базисный минимальный момент сопротивления, см3, поперечного сечения корпуса, равный CWBL2(cb + 0,7)Φ;
- η – коэффициент, значения которого приведены ниже в зависимости от предела текучести стали ReH:
Предел текучести стали ReH 235 315 355 390 η, МПа 1,00 0,78 0,72 0,68 - ReH п, ReH дн – пределы текучести стали соответственно для палубы и днища газовоза, МПа;
- MSW – расчетный изгибающий момент на тихой воде, действующий в средней части судна, кН · м;
M S W 0 = W 0 σ S W · 10 – 3 – граничное значение изгибающего момента, кН · м;
- σSW – нормальное напряжение, равное 73,6 МПа для палубы судов группы 1;
- 78,5 МПа для днища судов группы 1;
- 66,7 МПа для палубы судов группы 3;
- 71,6 МПа для днища судов группы 3;
- B, L – ширина и длина, м;
- cb – коэффициент общей полноты газовоза (cb ≥ 0,6);
- Cn – коэффициент, определяемый формулами Cn = 10,75 – (300 – L/100)3/2 при L ≤ 300 м;
- Cn = 10,75 при L > 300 м;
- Φ – коэффициент, определяемый в виде
Здесь:
C ω - ρп – коэффициент, определяемый по следующим формулам:
- при обычных обводах носовой оконечности (без бульба),
ρ п = 0 , 5 + 2 sin β ≤ 1 ;
при бульбовой форме носовой оконечностиρ п = 1 + C ω 2 ; - β – угол между касательной к шпангоуту и вертикалью на уровне ЛГВЛ в сечении, расположенном на 0,1L от носового перпендикуляра, град.;
ν – спецификационная скорость газовоза, уз, которая, не должна превышать скорость, определенную по формуле
ν = 2 , 2 L 1 + 0 , 35 L 1 / 100 – 1 2 / 3 ; L 1 = 100 м при L ≤ 100 м ; L 1 = L при L > 100 м . Значение Φ должно приниматься не менее 1.
Площадь стенки эквивалентного бруса должна быть не менее:
где:
ω 0 = 5 , 74 C n B L ( c b + 0 , 7 ) α x · 10 – 6 – базисная минимальная площадь стенки эквивалентного бруса, см2;- ReH б – предел текучести стали борта судна, МПа;
- NSW – расчетное значение перерезывающей силы на тихой воде в средней части судна, кН;
N S W 0 – граничное значение перерезывающей силы, кН, определяемой формулой NSW = ω0 τSW;- τSW – базовое значение касательных напряжений, МПа;
α x α x = 0 , 6 ÷ 1 , 1 .
Требования стандарта общей прочности, описанные выше, учитывают проектное состояние корпуса газовоза со стандартными добавками на износ.
Местная прочность. Перекрытия корпусов газовозов должны быть рассчитаны на местную прочность. При этом следует учитывать внешние гидростатические, гидродинамические и инерционные нагрузки, а также нагрузки, действующие со стороны грузосодержащей системы, для случаев положения газовоза на тихой воде, волнении, при испытаниях танков. Внешние гидростатические нагрузки на тихой воде определяют следующим образом: днищевые перекрытия воспринимают равномерно распределенное давление, бортовые – по закону треугольника с максимальным гидростатическим напором на уровне днища и с нулевым – на уровне ЛГВЛ. Внешние гидродинамические нагрузки в различных правилах и нормах определяются по-разному. Чаще всего в правилах и нормах гидродинамические нагрузки задают с обеспеченностью 10-8. Целесообразно определять внешние гидродинамические нагрузки с помощью зависимостей, рекомендуемых правилами Французского Бюро Веритас.
Для средней части длины судна дополнительное волновое гидродинамическое давление на уровне ватерлинии, МПа,
на уровне днищевой обшивки и палубы, МПа,
где:
- L, d – длина и осадка газовоза, м.
Инерционные нагрузки оценивают величиной относительного вертикального ускорения (в долях от ускорения свободного падения), которое можно определить в соответствии с откорректированной формулой кодекса ИМО:
где:
ν в = ν 0 [ 0 , 25 + 0 , 12 ( L / 100 – 1 ) 2 / 3 ] ; - ν0 – Обеспечение безопасности экипажа на танкере-газовозескорость газовоза на тихой воде, уз.
Анализ инерционных нагрузок показывает, что в положении на вершине волны силы инерции как бы уменьшают массу грузов, а на подошве волны – увеличивают, совпадая по знаку с соответствующим изменением гидродинамических давлений. В качестве верхней оценки суммарных волновых нагрузок на днищевые перекрытия на вершине и подошве волны можно использовать суммы соответствующих абсолютных значений гидродинамических и инерционных нагрузок.
Нагрузки при испытаниях танков, МПа, определяются в соответствии с требованиями Французского Бюро Веритас для грузового напора, полученного в результате налива водой, pисп = (Hт + 2,4) · 10-2, где Hт – высота танка, м.
При испытательной нагрузке танков газовоз должен быть поставлен на волну при осадке, м, dисп = 0,4d.
При расчетах наклонных стенок подпалубных и скуловых балластных цистерн газовозов с вкладными грузовыми танками расчетными местными нагрузками является одностороннее гидростатическое давление балласта изнутри цистерн. При этом контактные взаимодействия грузовых танков через жесткие опоры с палубными и скуловыми цистернами не имеет смысла учитывать.
Расчетные комбинации общих и местных нагрузок. Можно предположить, что наиболее опасная комбинация общих и местных нагрузок возникает при чередующейся загрузке трюмов на вершине волны и равномерной их загрузке на подошве волны. Так, например, правила Французского Бюро Веритас рекомендуют суммировать общие и местные нагрузки при чередующейся загрузке танков в случае постановки на вершине газовоза с осадкой
d = 1 , 1 ( d + 0 , 75 p в 0 ) , где:
pв 0 – дополнительное волновое гидродинамическое давление на уровне волновой ватерлинии, м, определяемое формулой
p в 0 = 60 + L 100 L 1 , 15 – c b d , и при равномерной загрузке танков в случае постановки на подошву волны газовоза с осадкой
d 2 = 0 , 9 ( d – 0 , 75 p в 0 ) .
Минимальные толщины определяются в соответствии с требованиями Правил Регистра РФ, так как толщины связей корпусов газовозов, определенные из условий прочности, могут оказаться недостаточными по условиям износа и величинам деформаций при сварке.
Определение размеров элементов корпуса. Классификация морских газовозовПравила классификации и постройки газовозов Регистра РФ требуют определять размеры элементов конструкций корпуса газовозов по формулам, справедливым для наливных или сухогрузных судов. Однако анализ размеров элементов конструкций реальных газовозов, проведенный В. В. Зайцевым, показывает, что эти формулы не всегда справедливы. Ниже приводятся расчетные зависимости для основных элементов корпусов газовозов с вкладными призматическими танками, полученные авторами на основе правил иностранных классификационных обществ, Правил Регистра РФ, анализа конструкций эксплуатируемых газовозов и расчетов перекрытий методами строительной механики корабля.
Полученные зависимости отвечают структуре формул Правил Регистра РФ, удобны на практике. Результаты определения размеров элементов корпусов газовозов по предложенным формулам хорошо совпадают с размерами реальных газовозов и поэтому могут послужить основой при разработке новой редакции правил классификации и постройки газовозов.
Нормальная шпация. В средней части газовозов размер нормальной шпации, м,
Принятый размер шпации может отклоняться от нормальной шпации в пределах ± 25 % и должен согласовываться со стандартным размером, устанавливаемым отраслевой нормалью. Шпация продольного набора (расстояние между балками днища, второго дна, верхней палубы) должна быть принята с учетом рекомендаций, изложенных ниже.
Двойное дно. Днищевое перекрытие газовозов с вкладными призматическими танками обычно набирают по продольной системе набора. По конструкции оно похоже на днищевые перекрытия сухогрузов и рудовозов. Однако условия его работы несколько иные. Передача нагрузки от прочного призматического вкладного танка на второе дно и днище осуществляется через специальные опоры, установленные между вторым дном судна и днищем танка в районах стрингеров, киля и сплошных флоров. Большое значение в этом случае приобретает работа связей на срез. Учет этого позволил вывести формулы для расчетов элементов второго дна, в частности, формул для определения площади поперечного сечения сплошных флоров газовозов.
Конструкция носовой и кормовой оконечностей суднаКоличество днищевых стрингеров с каждого борта газовозов в средней части его корпуса определяют по Правилам Регистра РФ в зависимости от ширины судна в метрах:
- если 10 < B ≤ 18, то следует устанавливать один стрингер;
- если 18 < B ≤ 28, то – два;
- если B > 28, то – три стрингера.
Расстановку их по ширине согласуют с палубным набором и системой опор вкладного призматического танка. Расстояние между сплошными флорами не должно превышать 3,2 м и должно быть кратно трем шпациям.
Высота двойного дна, мм, у вертикального киля должна быть не менее наибольшей из величин
где:
- H – отстояние верхней кромки настила грузового танка от нижней кромки горизонтального киля, м.
Толщина настила второго дна, мм, должна быть не менее определяемой по формуле:
где:
- a – расстояние между подкрепляющими балками, м;
- ρ – Грузовые операции на газовозах морского типарасчетная плотность перевозимого газа, кг/м3;
- Hт – высота грузового танка, м;
- p1 – давление силы тяжести изоляции, оболочки и набора грузового танка, вторичного барьера, МПа;
- k – коэффициент, учитывающий распределение динамических нагрузок, вызванных качкой газовоза.
Момент сопротивления поперечного сечения балок, см3, подкрепляющий настил второго дна (в том числе поперечных балок туннельного киля), должен быть не меньше
где:
- l – пролет, измеренный как расстояние между флорами для продольных балок второго дна или как расстояние между стенками, туннельного киля для поперечных балок, его подкрепляющих, м.
Вертикальный киль должен быть продлен как можно дальше в нос и в корму к штевням и по возможности крепиться к ним. Высота его, мм, в средней части длины судна должна быть не менее высоты, определяемой в соответствии с формулой 60, а толщина, мм, – не менее толщины сплошных флоров.
Вместо вертикального киля может устанавливаться туннельный киль, состоящий из двух стенок, расположенных по обе стороны от ДП. Расстояние между стенками туннельного киля, м.
Высота стенок должна удовлетворять требованию формулы 60. По днищу и настилу второго дна между стенками туннельного киля в плоскости каждого шпангоута следует устанавливать бракеты или поперечные балки с кницами. Восприятие корпусными конструкциями внешних нагрузок, действующих на судноПоперечные балки должны удовлетворять требованиям формулам 62, кницы – требованиям Правил Регистра РФ.
Ребра жесткости вертикального и туннельного килей должны удовлетворять требованиям Правил Регистра РФ.
Площадь поперечного сечения стенки сплошного флора (исключая вырезы), см3, должна быть не менее
где:
- B1 – ширина двойного дна между внутренними кромками скуловых бортовых цистерн, м;
- l – расстояние между сплошными флорами, м;
- p = 0,01d – ρHg – p1 – условная нагрузка, МПа, на днищевое перекрытие;
- n1, n2, n3 – коэффициенты, равные
Толщина флора должна быть не менее минимальной толщины. На всех сплошных флорах в плоскости каждой продольной днищевой балки и продольной балки второго дна следует ставить ребра жесткости. Водонепроницаемые флоры должны иметь толщину, мм, не менее требуемой Правилами Регистра РФ.
Площадь поперечного сечения, см2, днищевых стрингеров должна быть не менее площади поперечного сечения сплошных флоров, определенной по формуле 64. Стрингеры нужно размещать под опорами вкладных призматических танков.
Продольные балки днища. Момент сопротивления поперечного сечения, см3, продольных балок днища должен быть не менее
где:
- a – расстояние между балками, м;
- l – расстояние между сплошными флорами, м.
Конструкция судового набораБортовой набор. Бортовые перекрытия большинства газовозов с вкладными призматическими танками набираются по поперечной системе. Основными связями являются шпангоуты. Нормальные расстояния между шпангоутами определяются по формуле 59 для средней части судна.
Шпация в оконечностях должна быть не более шпации в средней части судна и не должна превышать нормального расстояния между шпангоутами.
Шпангоуты. Момент сопротивления поперечного сечения шпангоута, см3, должен быть не менее определенного по приведенным ниже формулам (в зависимости от того, что больше):
где:
- a – расстояние между шпангоутами, м;
- k – коэффициент, k = 198(1,425 – d/D);
- l – длина пролета шпангоута, измеренная по бортовой обшивке между верхней точкой скуловой и нижней точкой бортовой подпалубных цистерн, м;
- p – напор, МПа, измеряемый между срединой фактического пролета и летней грузовой ватерлинией или ватерлинией, соответствующей осадке d = 0,65D, в зависимости от того, что больше, но не менее 0,015 МПа;
где:
- k – коэффициент, k = 321(1,425 – d/D);
- p – напор, МПа, измеряемый между срединой фактического пролета и летней грузовой ватерлинией, соответствующей осадке d = 0,65D, в зависимости от того, что больше.
Расчетное значение l следует принимать средним для рассматриваемого района по длине судна. Размеры книц, при помощи которых шпангоуты крепятся к подпалубным и скуловым цистернам, определяются в соответствии с требованиями Правил Регистра РФ.
Палубный набор. Верхняя палуба газовозов с вкладными призматическими танками набирается по продольной системе. Основными связями являются продольные подпалубные балки, расстояние между которыми определяется продольной шпацией. Тронковая палуба, если она предусматривается, должна конструироваться по этой же системе. Для получения зависимости, определяющей условную расчетную нагрузку на верхнюю палубу, воспользуемся формулой, применяемой для определения напора на верхнюю открытую палубу надводных кораблей в функции от их длины и высоты надводного борта, так как у газовоза, подобно этим судам, высокий надводный борт. Применительно к газовозам условная расчетная нагрузка на верхнюю палубу (напор), МПа,
Момент сопротивления поперечного сечения продольных подпалубных балок
где:
- a – расстояние между балками продольного набора, м;
- l – длина пролета балки, измеренная между рамными бимсами, м.
Определенные в соответствии с формулой 69 прочные размеры продольных подпалубных балок в районе 0,5L средней части судна между бортом и линией вырезов, если такие имеются, должны быть проверены по моменту инерции их поперечного сечения с присоединенным пояском в соответствии с требованиями Правил Регистра РФ.
Рамные бимсы. Эти бимсы устанавливают по верхней палубе на расстоянии не менее шести нормальных шпаций друг от друга в плоскости каждого второго сплошного флора. Момент сопротивления поперечного сечения Палубные конструкции морских деревянных судоврамного бимса, см3, должен быть не менее
где:
- a – расстояние между рамными бимсами, м;
- p – условная расчетная нагрузка, определяемая по формуле 68, МПа;
- l – пролет рамного бимса, измеренный по настилу верхней палубы между бортовыми подпалубными цистернами, м.
Момент инерции поперечного сечения рамных бимсов, см4, в средней части судна расчетной палубы не может быть менее требуемого Правилами Регистра РФ.
Продольные связи тронковой палубы, если такая предусматривается, должны отвечать требованиями формулы 69, а рамные бимсы тронковой палубы – требованиям формулы 70.
Наружная обшивка, настил палуб и переборкиНастил палубы. Площадь поперечного сечения палубы должна быть не менее величины, требуемой Регистром РФ. Ширина палубного стрингера или стрингера тронковой палубы, м, в средней части судна должна быть не менее
Ширина палубного стрингера в оконечностях должна быть не менее 0,65 его ширины в средней части.
Толщины палубного стрингера и стрингера тронковой палубы, мм, должны быть не менее толщины настила палубы и не менее величины s = 0,05L + 5,5. Кроме того, толщина стрингера должна быть не менее толщины бортовой обшивки.
Сплошной стальной настил должен быть поставлен по всей длине палубы. Принятая толщина листов расчетной палубы, мм, или палубы тронка в пределах 0,6L, в средней части должна быть не менее s = 4,0 + 0,05L + 5 (a – a0), где a – нормальная шпация, определенная по формуле, м; a0 – расстояние между продольными подпалубными балками, м.
Толщина палубных настилов в оконечностях, мм, должна быть не менее s = 0,02L + 5,5. В любом случае толщина настила верхней палубы или палубы тронка, мм, в средней части судна должна быть не менее s = 9,43a.
Наружная обшивка. Толщина наружной обшивки газовозов должна быть определена в соответствии с п. 2.10 Правил Регистра РФ.
Толщину скулового пояса (до верхнего поворота скулы) при подкреплении скулы продольным или поперечным набором следует принимать равной толщине обшивки днища или борта, в зависимости от того, что больше. Толщина пояска бортовой обшивки, расположенного над скуловым пояском, должна быть не менее требуемой Правилами Регистра РФ. Толщины расположенных выше поясов могут постепенно уменьшаться. Площадь поперечного сечения обшивки борта определяется в соответствии с указаниями требований, предъявляемых к общей продольной прочности.
Это интересно: Изменение технологии грузовых работ и перевозки грузов — определяющий фактор в развитии конструктивных типов судов
Ширина горизонтального киля принимается равной ширине палубного стрингера. В том случае, если устанавливается туннельный вертикальный киль, ширина горизонтального киля должна быть не менее расстояния между стенками киля. Толщина горизонтального киля в районе грузовых танков должна быть на 4 мм больше толщины днищевой оболочки. При значительной толщине горизонтального киля (более 35 мм) допускается принимать толщину горизонтального киля на 2 мм больше толщины наружной обшивки. Ширина ширстрека, м, принимается равной ширине палубного стрингера, но не менее b = 0,1D (при этом 3,0 ≤ b ≤ 2,0).
Толщина ширстрека должна быть равна толщине палубного стрингера или бортовой обшивки, смотря по тому, что больше.
Бортовые подпалубные цистерны. Газовозы с вкладными призматическими грузовыми танками оборудуют бортовыми цистернами, размещенными под палубой. В подпалубных цистернах применяется продольная Конструкция судового наборасистема набора.
Момент сопротивления продольных балок по продольным переборкам внутри цистерны, по борту и ограничивающим цистерну переборкам должен быть не меньше
где:
- a – расстояние между балками, м;
- p – напор, МПа, эквивалентный расстоянию от горизонтального ребра до точки, расположенной на 0,65 расстояния от верха цистерны до уровня воздушной трубы, но не менее 0,02 МПа;
- l – полная длина балки, м.
Момент инерции указанных балок должен быть проверен по соответствующим формулам.
Момент сопротивления любой части поперечной рамы, см3, кроме рамы по наклонной стенке цистерны, должен быть не менее величины
предложенной Регистром,
где:
- a – расстояние между поперечными рамами, м;
- l – длина пролета соответствующей части рамы, измеренная по настилу, к которому он присоединен, м;
- p – напор, МПа, эквивалентный расстоянию от середины пролета соответствующей части поперечной рамы до точки, находящейся на 0,65 возвышения воздушной трубы над палубой.
Момент сопротивления рамы по наклонной стенке цистерны должен быть не менее определяемого по формуле 72; при этом пролет рамы измеряется по настилу наклонной стенки цистерны от вертикальной стенки до середины опоры призматического танка, установленной под наклонной стенкой.
Размеры и конструкция поперечных рамных связей и ребер жесткости на поперечных рамах должны удовлетворять требованиям. Размеры элементов бортовых скуловых цистерн определяются по Правилам Регистра РФ.
Поперечные переборки. На газовозах с вкладными призматическими танками обычно устанавливают плоские водонепроницаемые переборки. Их доводят до верхней палубы, делают либо с вертикальными стойками, либо с горизонтальными балками. Каждый грузовой отсек должен быть отделен балластными коффердамами, которые, в свою очередь, ограничиваются поперечными водонепроницаемыми переборками. Вертикальные стойки поперечных водонепроницаемых переборок устанавливают в плоскости продольных балок днища и верхней палубы.
Обшивка переборок. Толщина листов переборок, мм, должна быть не менее большей из величин
где:
- a – расстояние между балками набора, м;
- p – напор, эквивалентный расстоянию от каждой кромки листа до точки, расположенной на 0,65 расстояния от верха цистерны до уровня воздушной трубы, МПа.
Толщина обшивки переборок, мм, балластных коффердамов должна быть не менее большей из величин
где:
- p – напор, эквивалентный расстоянию от нижней кромки листа до точки, расположенной на 2,4 м выше верхней палубы, МПа.
Расстояние между переборками коффердама, м;
где:
- Lт – длина грузового танка между переборками коффердама, м;
- Bт – ширина танка, м;
- H – отстояние верхней кромки настила грузового танка от нижней кромки горизонтального киля.
Стойки переборок. Плоские переборки подкрепляются вертикальными стойками. Расстояние между ними не должно превышать 0,9 м. При применении сварных симметричных тавровых профилей толщина стенки профиля должна составлять не менее 0,9 толщины обшивки переборки посредине высоты стойки. Момент сопротивления поперечного сечения вертикальных стоек переборки должен быть не менее
где:
- a – расстояние между стойками, м;
- p – напор МПа, эквивалентный расстоянию в ДП судна от средины длины стойки до палубы переборок, однако не менее 0,016 МПа;
- l – полная длина стойки, включая кницы, м.
Момент сопротивления поперечного сечения горизонтальных балок поперечных переборок может быть определен по установленным формулам.
Крепление концов стоек водонепроницаемых переборок выполняется при помощи книц.
Прежде чем приступить к проектированию поперечной переборки, необходимо вычертить ее обводы, нанести пазы и стыки поясов, руководствуясь габаритными размерами листов, рекомендуемых для применения в судостроении, а также нанести линии примыкании набора (вертикальных стоек). Далее с учетом данных эскиза замеряются расчетные величины напора для определения толщин листов.
Листы переборок обычно располагаются горизонтальными поясьями. Разбивка обшивки переборок начинается с нанесения нижнего пояса, ширина которого, измеренная от уровня второго дна, должна быть не менее 0,9 м. Очевидно, принимать его шире также нерационально, так как это утяжелит конструкцию. Оставшуюся часть трюмной переборки и высоту переборок в межпалубных помещениях разбивают на поясья в соответствии с ГОСТ на листовую сталь; в случае необходимости предусматривают забойный пояс. После этого можно приступать к определению толщины листов обшивки переборки в соответствии с формулами 73-74.
Читайте также: Методы расчета прочности конструкций ледовых усилений при глубоком пластическом деформировании
Поперечные переборки подпалубных цистерн. Поперечные переборки, ограничивающие бортовые подпалубные цистерны, обычно плоские. Переборки доводятся до верхней палубы, борта и наклонной стенки цистерны. Обшивку переборки подкрепляют ребрами жесткости.
Толщина листов, мм, поперечных переборок должна быть не менее
где:
- a – расстояние между ребрами жесткости, м;
- p – напор, МПа, эквивалентный расстоянию от нижней кромки листа до точки, расположенной на 0,65 расстояния от верха цистерны до уровня воздушной трубы.
Уровень воздушной трубы над верхней палубой принимается равным 2,4 м.
Надбавку на коррозию принимают для всех листов равной 1,25 мм, так как переборка имеет малую высоту. Толщина листов переборки должна быть не менее минимальной толщины smin = 0,03L + 4,5, однако ее значение должно находиться в пределах 6,0 мм ≤ s ≤ 7,5 мм. Листы обшивки переборок могут иметь толщину, не превышающую толщину соответствующих поясьев наружной обшивки при одинаковых пролетах пластин и пределах текучести стали.
Момент сопротивления поперечного сечения ребер жесткости, см3, должен быть не менее
где:
- l – полная длина ребер жесткости, м.
Сноски🤝 Поддержите нашу работу
Чтобы продолжить проекту существовать нам нужна ваша помощь!👥 Нас поддерживают:Геннадий, safebridge, Capt Mohee, Dim, Tika, Anto Serviceи ещё 26 человекТакже есть переводы на карту • Спасибо каждому!Нашли опечатку? Выделите и нажмите CTRL+Enter
Апрель, 15, 2022 3167 0Пометки